Abstract
In this work, we test the idea that most, if not all, cellular Cl- of Amphiuma red blood cells is contained in the cytoplasm. If true, this could resolve the difference between the measured plasma membrane potential (Em) and that expected from the Donnan equilibrium distribution of Cl-. We studied the changes in the fluorescence intensity of the Cl--sensitive dye, MQAE, entrapped in red cells that occurred when intracellular Cl- was exchanged with 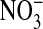 . We could thus monitor the distribution of Cl- between the nuclear and cytoplasmic compartments. We found that essentially all of the cell's Cl- resides in the cytoplasm. Knowing the volume of the cell occupied by the nucleus, we could accordingly correct the measured values of cell Cl-. This resulted in establishing a concordance between the measured values of Em and those calculated from the corrected values of the Cl- ratio, thus explaining the discrepancy. The exclusion of Cl- from the nucleus may result from its unusually high content of “excess” DNA that imposes an imbalance of net negative charge.
. We could thus monitor the distribution of Cl- between the nuclear and cytoplasmic compartments. We found that essentially all of the cell's Cl- resides in the cytoplasm. Knowing the volume of the cell occupied by the nucleus, we could accordingly correct the measured values of cell Cl-. This resulted in establishing a concordance between the measured values of Em and those calculated from the corrected values of the Cl- ratio, thus explaining the discrepancy. The exclusion of Cl- from the nucleus may result from its unusually high content of “excess” DNA that imposes an imbalance of net negative charge.
Keywords: MQAE, nuclear/cytoplasmic ratios
The equilibrium distribution of permeable ions such as Cl- across the plasma membrane of red blood cells should be determined by the membrane potential (Em) that is set by the relative permeability to Na+ and K+ and their concentration gradients. This paper addresses the Em of Amphiuma red blood cells and the reason why the measured Em appears to differ significantly from that expected from the equilibrium distribution of Cl-. The idea that the Em of red blood cells in general and of human red cells in particular could be described by a Donnan potential is based on analyses (1-4) of the passive equilibrium distribution of permeable ions between the cytoplasm (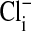 ) and the external medium (Clo). The Em of human red cells, measured indirectly with the use of fluorescent dyes (5), was found to vary quantitatively with the Donnan ratio of Cli/Clo (rCl). This was so when rCl was varied either by changes in external pH (pHo) (5-7) or by altering the concentration of Clo by substitution with an impermeable anion (5). Validation that the fluorescence technique provided an accurate assessment of Em in human red cells stemmed from the concordance of Em determined directly in Amphiuma red blood cells by impalement with microelectrodes (8, 9, †) with those determined by the use of fluorescent dyes (5). These results established the basis for expecting measurements of Em in Amphiuma red blood cells to conform to a Donnan potential. However, analyses showed that, although the Em of Amphiuma responded to changes in Cli produced by changes in pHo, the calculated values of Em based on measured values of Cli and Clo were significantly higher than the observed Em values. Em was calculated by use of the Nernst equation, Em = 58 log Cli/Clo, where 58 is the value of RT/F at 20°C., with R being the gas constant, T the temperature, and F, the Faraday constant. It turns out that the problem lies with the interpretation of the measured values of Cli. These values of whole-cell Cl- were based on units of mmol Cli per liter of cell water. With the assumption that Cl- is excluded from the nucleus of the Amphiuma red blood cell, the cytoplasmic concentration of Cl- is thereby increased, resulting in agreement between the measured values of Em and those calculated from rCl. Evidence is presented below that Cl- is excluded from the cell's nucleus.
) and the external medium (Clo). The Em of human red cells, measured indirectly with the use of fluorescent dyes (5), was found to vary quantitatively with the Donnan ratio of Cli/Clo (rCl). This was so when rCl was varied either by changes in external pH (pHo) (5-7) or by altering the concentration of Clo by substitution with an impermeable anion (5). Validation that the fluorescence technique provided an accurate assessment of Em in human red cells stemmed from the concordance of Em determined directly in Amphiuma red blood cells by impalement with microelectrodes (8, 9, †) with those determined by the use of fluorescent dyes (5). These results established the basis for expecting measurements of Em in Amphiuma red blood cells to conform to a Donnan potential. However, analyses showed that, although the Em of Amphiuma responded to changes in Cli produced by changes in pHo, the calculated values of Em based on measured values of Cli and Clo were significantly higher than the observed Em values. Em was calculated by use of the Nernst equation, Em = 58 log Cli/Clo, where 58 is the value of RT/F at 20°C., with R being the gas constant, T the temperature, and F, the Faraday constant. It turns out that the problem lies with the interpretation of the measured values of Cli. These values of whole-cell Cl- were based on units of mmol Cli per liter of cell water. With the assumption that Cl- is excluded from the nucleus of the Amphiuma red blood cell, the cytoplasmic concentration of Cl- is thereby increased, resulting in agreement between the measured values of Em and those calculated from rCl. Evidence is presented below that Cl- is excluded from the cell's nucleus.
Amphiuma red blood cells, first described in 1875 (10), are one of the largest known red cells (10-14). They are nucleated and elliptical in shape, with average dimensions of 62 μm (range, 48-78 μm) in length and 36 μm (range, 27-46 μm) in width (10-13). The average size of the elliptical nucleus is estimated to be 24 μm long and 14 μm wide (10, 15). We estimate the average thickness of the cell in the region of the bulging nucleus to be ≈14-16 μm and that of the nuclear-free cytoplasm to be 6-9 μm. The cells' surface area and volume are ≈3,700 μm2 and 14,000 femtoliters, respectively.
Materials and Methods
Amphiuma tridactylum, three-toed salamanders (“congo eels”), were obtained from either Carolina Biological Supply or Mogul-Ed Company (Oshkosh, WI). They were kept singly at room temperature (≈20-22°C) in buckets of moss and fresh water that was changed frequently, with occasional feeding of either frozen shrimp or beef heart. Animals anesthetized by exposure to dissolved urethane were bled by shallow puncture of the ventral skin (18-gauge needle) aimed posterially in the region of the heart located between the two anterior legs. Blood was drawn into heparin and, upon dilution with ≈10 volumes of modified amphibian Ringer, was immediately centrifuged for 2-3 min at 800-1,000 rpm in a swinging bucket rotor (Sorvall, HB-4). After removal of the buffy coat, the cells were washed (equilibrated) twice with media as specified below.
Analytical Techniques. For determination of the concentrations of 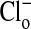 ,
, 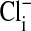 ,
, 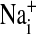 ,
, 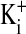 , and cell water, the freshly drawn Amphiuma red blood cells were centrifuged and, after removal of the buffy coat, first were pH-equilibrated with each of one to three washes at 20°C with ≈10-15 volumes of amphibian Ringer's solution that consisted of 110 mM NaCl, 2.5 mM KCl, 1.8 mM CaCl2, and 10 mM Tris·Cl, with the pH adjusted to pH 6.80, 7.20, or 7.60 at 20°C (≈220 milliosmolar per liter). The cells were then packed by using an HB-4 rotor as above at 25,000 × g for 10 min in the bottom of a Lucite tube whose inside, holding ≈20 ml, was shaped wide at the top tapering to a small-diameter column (≈1.5 ml) at the bottom. The fraction of medium that was trapped in the packed column of cells was found to average 7.1%, as determined by the use of 14C-inulin and 14C-para-aminohypurate. Na+ and K+ were determined by flame analysis. Cli and Clo were determined analytically with the use of a Cotlove chloridometer (Buchler). The ratio, rCl, was also determined with 36Cl, as described (5), and was found to be the same as that found analytically. Cell water (wt/wt) was determined by weighing aliquots before and after drying at 90°C for >12 h. The density of Amphiuma cells was found to average 1.0864 and used to convert the fraction of cell water from wt/wt to vol/vol. Cli in mmol Cl per liter cells was converted to mmol per liter cell H2O by division with the fraction cell water (vol/vol); this value was then corrected for trapped Clo with readjustment for the trapped medium volume. Amphiuma red cells, washed with Ringer's solution at pH 7.2, were typically found to contain 10.0 ± 0.5 mmol Na+, 117 ± 4 mmol K+, ≈50 mmol Cl cell per liter cell water (vol/vol) and 76.2 ± 0.6% water (vol/vol), ± SEM. (n = 4). All chemicals used were, wherever possible, reagent grade.
, and cell water, the freshly drawn Amphiuma red blood cells were centrifuged and, after removal of the buffy coat, first were pH-equilibrated with each of one to three washes at 20°C with ≈10-15 volumes of amphibian Ringer's solution that consisted of 110 mM NaCl, 2.5 mM KCl, 1.8 mM CaCl2, and 10 mM Tris·Cl, with the pH adjusted to pH 6.80, 7.20, or 7.60 at 20°C (≈220 milliosmolar per liter). The cells were then packed by using an HB-4 rotor as above at 25,000 × g for 10 min in the bottom of a Lucite tube whose inside, holding ≈20 ml, was shaped wide at the top tapering to a small-diameter column (≈1.5 ml) at the bottom. The fraction of medium that was trapped in the packed column of cells was found to average 7.1%, as determined by the use of 14C-inulin and 14C-para-aminohypurate. Na+ and K+ were determined by flame analysis. Cli and Clo were determined analytically with the use of a Cotlove chloridometer (Buchler). The ratio, rCl, was also determined with 36Cl, as described (5), and was found to be the same as that found analytically. Cell water (wt/wt) was determined by weighing aliquots before and after drying at 90°C for >12 h. The density of Amphiuma cells was found to average 1.0864 and used to convert the fraction of cell water from wt/wt to vol/vol. Cli in mmol Cl per liter cells was converted to mmol per liter cell H2O by division with the fraction cell water (vol/vol); this value was then corrected for trapped Clo with readjustment for the trapped medium volume. Amphiuma red cells, washed with Ringer's solution at pH 7.2, were typically found to contain 10.0 ± 0.5 mmol Na+, 117 ± 4 mmol K+, ≈50 mmol Cl cell per liter cell water (vol/vol) and 76.2 ± 0.6% water (vol/vol), ± SEM. (n = 4). All chemicals used were, wherever possible, reagent grade.
Centrifugation in Dense Solutions. With the object being to chemically measure the Cl-, Na+, and K+ content of the Amphiuma red cell nucleus compared with the cytoplasm, we used several methods for isolating nuclei (e.g., refs. 16 and 17). When we found that the ionic composition of the nucleus changed with the isolation procedure, we, together with Victor Nadler, attempted to separate the cells, in their natural intracellular environment, into nuclear- and cytoplasmic-rich fractions by centrifugation at 250,000 × g for 2-4 h at 4°C in high concentrations (40-79 g/dl) of BSA (18) dissolved in modified amphibian Ringer's solution (pH 7.2-7.4, 220-240 milliosmolar per liter). We were often able to split the cells, without hemolysis, into two not-pure fractions of nucleus-containing vesicles (on the bottom) and clear vesicles (on the top), both containing hemoglobin, but in insufficient quantities for quantitative analysis. However, qualitatively, in two preliminary studies, the relative Cl- concentration was >6× lower in the bottom compared with the top fraction and served as the basis for our assumption that the nucleus was Cl- poor relative to the cytoplasm (see refs. 8 and 9 and †). Because of the intractable nature of this approach, we pursued further analyses with a Cl-- sensitive fluorescence dye described below.
Membrane Potentials. The Em values of Amphiuma red blood cells at pH 6.5, 7.2, and 7.9 were taken from previously published work carried out in collaboration with U. V. Lassen (8, 9, †) in which the procedures and solutions used were similar to those described above but with either 4-morpholinepropanesulfonic acid (Mops) or Hepes substituted for Tris for pH stabilization. The convention for the sign of the Em is inside negative.
Fluorescence Measurements. Fluorescence imaging of Amphiuma red blood cells was carried out on cells labeled with the Cl-- sensitive dye, MQAE, or with the pH-sensitive dye, LysoSensor Green DND-153 (19), both obtained from Molecular Probes. Fluorescence imaging with either of these dyes appears to be independent of cellular hemoglobin. With regard to MQAE, the cells were first washed two times with ≈30 volumes of a Cl--free medium containing 95 mM NaNO3, 2.5 mM KNO3, 1.8 mM Ca(NO3)2, and 10 mM Mops, pH 7.2, at 23°C (≈220 milliosmolar per liter). The cells were pipetted into a coverslip chamber coated with Cell-Tak (BD Biosciences, San Jose, CA) to which they adhered. After 5 min, the cells were incubated in the dark for 20 min in the presence of 10 mM MQAE in the 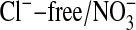 solution. The excess dye was then flushed off and the coverslip transferred to the stage of an inverted microscope to be examined at ×60 (IX70, Olympus, Melville, NY). The solution bathing the attached cells could be exchanged in <5 sec (≈4 ml/min) by gravity flow of new solution coupled to aspiration of the excess. Thus, the bathing medium was alternately changed with a Cl-containing medium (101 mM Cl-), where Cl- substituted for
solution. The excess dye was then flushed off and the coverslip transferred to the stage of an inverted microscope to be examined at ×60 (IX70, Olympus, Melville, NY). The solution bathing the attached cells could be exchanged in <5 sec (≈4 ml/min) by gravity flow of new solution coupled to aspiration of the excess. Thus, the bathing medium was alternately changed with a Cl-containing medium (101 mM Cl-), where Cl- substituted for 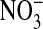 in the previous solution. Importantly, the fluorescence of MQAE is insensitive to
in the previous solution. Importantly, the fluorescence of MQAE is insensitive to 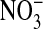 (20). Because the fluorescence intensity of MQAE is quenched by Cl-, we used a Flurmax-3 fluorimeter (Edison, NJ) and found, with Gordon MacGregor, that with excitation at 363 nm, the fluorescence intensity that peaked at 451 nm, for the same MQAE concentration, was 11.9 times higher in the
(20). Because the fluorescence intensity of MQAE is quenched by Cl-, we used a Flurmax-3 fluorimeter (Edison, NJ) and found, with Gordon MacGregor, that with excitation at 363 nm, the fluorescence intensity that peaked at 451 nm, for the same MQAE concentration, was 11.9 times higher in the 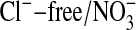 solution than in the 101 mM Cl- medium (6,465 vs. 544, respectively, in arbitrary units). The results presented are typical of several experiments of the same type.
solution than in the 101 mM Cl- medium (6,465 vs. 544, respectively, in arbitrary units). The results presented are typical of several experiments of the same type.
With regard to the LysoSensor dye, the cells were first washed with a medium containing 90 mM NaCl and 20 mM Mops at pHo 7.2 at 23°C (≈210 milliosmolar per liter). The cells were then added to the coverslip chamber, as before, and after 5 min were incubated in the dark for 20 min in the presence of 1 μm LysoSensor Green DND-153 in the NaCl-Mops medium. The excess dye was then flushed off before viewing the fluorescence of the cells in the microscope (excitation at 442 nm, emission at 505 nm). The solution bathing the attached cells was then alternately changed with NaCl-Mops media whose pHo was 6.2, 7.2, or 8.0. Importantly, this dye increases its fluorescence in acid compartments and is quenched in alkaline environments.
The Amphiuma red cells were imaged and the intracellular fluorescence intensity recorded by use of a commercial imaging program (metaf luor, Universal Imaging, Downington, PA). We could thus examine multiple cells in real time and record the relative intracellular fluorescence intensity while simultaneously recording the images from the system. The data were acquired by use of a DGB5 excitation light source (Sutter Instruments, Novato, CA) and a photometrics cooled charge-coupled device camera (Roper Scientific, Trenton, NJ). Because any autofluorescence of cells without dye was minimal, there was no need to correct the final images. All imaging observations were made at 23°C and expressed in arbitrary units.
Results
The prime concern of this paper is to assess the cellular distribution of Cl- in Amphiuma red blood cells. This was studied by preloading the cells with the fluorescence-sensitive Cl- dye, MQAE, with subsequent analysis of the changes in fluorescence that occurred when the intracellular Cl- was exchanged with 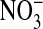 . MQAE fluorescence is quenched by Cl- but is not affected by
. MQAE fluorescence is quenched by Cl- but is not affected by 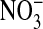 or by changes in pH (20). Fig. 1 shows the changes in two separate fields of the fluorescence intensity that occur when the
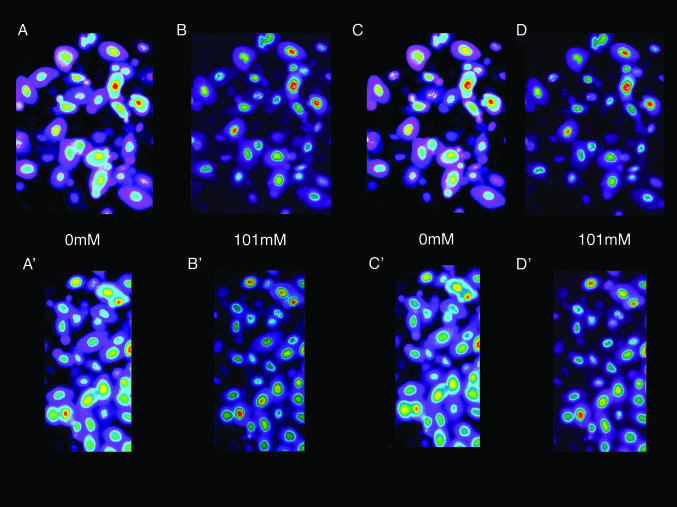
or by changes in pH (20). Fig. 1 shows the changes in two separate fields of the fluorescence intensity that occur when the 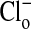 concentration is alternately changed from zero (Fig. 1 A and A′) to 101 mM Clo (Fig. 1 B and B′), and Fig. 1 C (and C′) and D (and D′) show that these changes are readily reversible. These changes in fluorescence intensity take place faster than the time involved in the switch of bath solutions (seconds) and reflect the fact that Cl/NO3 exchange via band 3 is a rapid process. Our measurements with a filter-based technique (21), carried out with Philip Knauf, showed that the half-time, measured in four experiments, of 36Cl efflux at 0°C from preloaded Amphiuma red cells was 5.9 ± 0.35 sec (where n = 8, ±SEM). Once the changes in fluorescence have occurred, the images remain stable for at least several minutes. The important result, seen in both sequences, is that even though the fluorescence intensity of the cytoplasmic compartment is high (bright) when
concentration is alternately changed from zero (Fig. 1 A and A′) to 101 mM Clo (Fig. 1 B and B′), and Fig. 1 C (and C′) and D (and D′) show that these changes are readily reversible. These changes in fluorescence intensity take place faster than the time involved in the switch of bath solutions (seconds) and reflect the fact that Cl/NO3 exchange via band 3 is a rapid process. Our measurements with a filter-based technique (21), carried out with Philip Knauf, showed that the half-time, measured in four experiments, of 36Cl efflux at 0°C from preloaded Amphiuma red cells was 5.9 ± 0.35 sec (where n = 8, ±SEM). Once the changes in fluorescence have occurred, the images remain stable for at least several minutes. The important result, seen in both sequences, is that even though the fluorescence intensity of the cytoplasmic compartment is high (bright) when 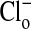 is zero and lower (dim) in high
is zero and lower (dim) in high 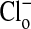 , the fluorescence intensity of the nucleus is not only high but changes only slightly (see Fig. 2) with changes in cytoplasmic Cl-. That the fluorescence intensity of the nucleus remains high indicates that its Cl- concentration is low if not zero. The conclusion to be drawn is that the nucleus excludes Cl-, and that this exclusion is essentially independent of the cytoplasmic concentration of Cl-.
, the fluorescence intensity of the nucleus is not only high but changes only slightly (see Fig. 2) with changes in cytoplasmic Cl-. That the fluorescence intensity of the nucleus remains high indicates that its Cl- concentration is low if not zero. The conclusion to be drawn is that the nucleus excludes Cl-, and that this exclusion is essentially independent of the cytoplasmic concentration of Cl-.
Fig. 1.
Fluorescence imaging with the dye, MQAE, of 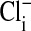 in Amphiuma red blood cells. The changes in the distribution of intracellular Cl- between the nucleus and cytoplasm are quickly evident (<5 sec) upon the sequential changes in Clo. Because the fluorescence of the dye is not affected by
in Amphiuma red blood cells. The changes in the distribution of intracellular Cl- between the nucleus and cytoplasm are quickly evident (<5 sec) upon the sequential changes in Clo. Because the fluorescence of the dye is not affected by 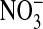 , we could rapidly and reversibly monitor fluorescence changes in
, we could rapidly and reversibly monitor fluorescence changes in 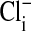 mediated by the exchange, via Band 3, of intracellular
mediated by the exchange, via Band 3, of intracellular 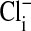 with
with  by exchanging the 101 mM
by exchanging the 101 mM 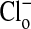 solution with a solution containing 101 mM
solution with a solution containing 101 mM 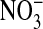 . Here the compositions of the two solutions were the same, with equal osmolalities, except for the change of anions. All changes in fluorescence (images are comprised of pseudocolors) were stable for at least 5 min. It should be emphasized that the fluorescence of the dye is decreased (quenched) by Cl-). In A, with the cells suspended in a
. Here the compositions of the two solutions were the same, with equal osmolalities, except for the change of anions. All changes in fluorescence (images are comprised of pseudocolors) were stable for at least 5 min. It should be emphasized that the fluorescence of the dye is decreased (quenched) by Cl-). In A, with the cells suspended in a 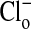 -free
-free 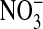 solution, the fluorescence intensity of the cytoplasm is high. In B, upon exchange of the medium with 101 mM
solution, the fluorescence intensity of the cytoplasm is high. In B, upon exchange of the medium with 101 mM 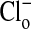 , the relative fluorescence of the cytoplasm is markedly decreased due to Cl- entry into the cell. As shown in C and D, these changes are readily reversible. A′-D′ present another separate (representative) sequence of changes in the fluorescence intensity of MQAE in Amphiuma red blood cells treated the same as those cells in A-D. Of special note is that the relative fluorescence of the nucleus is only slightly affected by the changes in
, the relative fluorescence of the cytoplasm is markedly decreased due to Cl- entry into the cell. As shown in C and D, these changes are readily reversible. A′-D′ present another separate (representative) sequence of changes in the fluorescence intensity of MQAE in Amphiuma red blood cells treated the same as those cells in A-D. Of special note is that the relative fluorescence of the nucleus is only slightly affected by the changes in 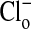 , that is, by changes in
, that is, by changes in 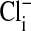 . Because the fluorescence intensity is high, even in the presence of cytoplasmic Cl-, the nucleus appears to contain little or no Cl-.
. Because the fluorescence intensity is high, even in the presence of cytoplasmic Cl-, the nucleus appears to contain little or no Cl-.
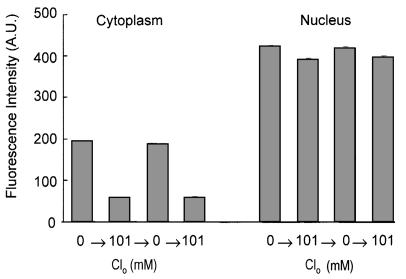
Fig. 2.
Depiction of the quantitative changes in the fluorescence intensity of nucleus and cytoplasm (in arbitrary units) for the results presented in Fig. 1. The analysis was made on the summed intensity of pixels in equal areas of nucleus and cytoplasm in 44 different cells taken from the upper and lower sequences of the cells in the focal plane depicted in Fig. 1. The size of the area chosen for analysis was somewhat smaller than the size of any nucleus to avoid any ambiguity of the latter's boundary. Several repetitions gave comparable results. The mean ± SEM values of fluorescence intensity of the cytoplasm in zero 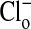 media, A, A′ and C, C′ were 193 ± 3 (range, 169-268) and 187 ± 3 (range, 140-268), respectively; for B, B′ and D, D′, where
media, A, A′ and C, C′ were 193 ± 3 (range, 169-268) and 187 ± 3 (range, 140-268), respectively; for B, B′ and D, D′, where  mM were 57 ± 3 (range, 29-101) and 59 ± 3 (range, 30-100), respectively. Comparable values for the mean ± SEM of the fluorescence intensity of the nucleus in zero
mM were 57 ± 3 (range, 29-101) and 59 ± 3 (range, 30-100), respectively. Comparable values for the mean ± SEM of the fluorescence intensity of the nucleus in zero 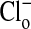 media, for A, A′ and C, C′ were 423 ± 6 (range, 369-498) and 419 ± 6 (range, 363-490), respectively; for B, B′ and D, D′ where
media, for A, A′ and C, C′ were 423 ± 6 (range, 369-498) and 419 ± 6 (range, 363-490), respectively; for B, B′ and D, D′ where  mM, the values were 391 ± 6 (range, 300-467) and 397 ± 5 (range, 321-468), respectively. It is clear that the nuclear content of Cl- is low and responds only modestly to changes in cytoplasmic Cl-.
mM, the values were 391 ± 6 (range, 300-467) and 397 ± 5 (range, 321-468), respectively. It is clear that the nuclear content of Cl- is low and responds only modestly to changes in cytoplasmic Cl-.
Relevant to the distribution of MQAE between the nuclear and cytoplasmic compartments are as-yet-unpublished results of studies we have made on colon, stomach, and kidney tissues from mice, rats, and humans (J.P.G., unpublished results). In all cases, the fluorescence intensity of the cytoplasm was matched by that of the nucleus, and both changed proportionally with changes in Cli (data not shown).
As explained in the legend, the results depicted in Fig. 2 quantitate the changes in fluorescence intensity presented in Fig. 1 that occurred in the cytoplasmic and nuclear compartments with alterations of the concentration of 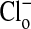 . (An analysis of other similar experiments of the type shown gave comparable results.) We assume that the relative fluorescence intensities so obtained reflect equilibrium concentrations of cellular Cl-. Remembering that the fluorescence intensity is inversely proportional to the Cl- concentration, it is clear that the cytoplasm still retains some Cl- (or at least fluorescence) relative to the nucleus, when
. (An analysis of other similar experiments of the type shown gave comparable results.) We assume that the relative fluorescence intensities so obtained reflect equilibrium concentrations of cellular Cl-. Remembering that the fluorescence intensity is inversely proportional to the Cl- concentration, it is clear that the cytoplasm still retains some Cl- (or at least fluorescence) relative to the nucleus, when 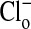 is zero. We do not know the significance or the locale of this retained
is zero. We do not know the significance or the locale of this retained 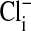 . Curiously, this residual
. Curiously, this residual 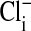 persists even though, as pointed out before, all of the cellular Cl is exchangeable, as shown by equivalent Donnan ratios of 36Cl and chemical Cl. We found, with Gordon MacGregor, that Amphiuma red cells equilibrated 3 times for 10 min each with 30 volumes of an all
persists even though, as pointed out before, all of the cellular Cl is exchangeable, as shown by equivalent Donnan ratios of 36Cl and chemical Cl. We found, with Gordon MacGregor, that Amphiuma red cells equilibrated 3 times for 10 min each with 30 volumes of an all 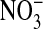 (Cl--free) medium retained ≈12.5% of the Cl- they contained in 110 mM Cl- media. Evidently this Cl- is associated with sites that are not exchangeable with
(Cl--free) medium retained ≈12.5% of the Cl- they contained in 110 mM Cl- media. Evidently this Cl- is associated with sites that are not exchangeable with 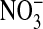 .
.
We also attempted to measure by fluorescence the changes in cytoplasmic Cl- that are known to occur with changes in pHo. We were unable to discern any differences in the fluorescence intensity of Amphiuma red cells equilibrated in 101 mM Clo at pH 6.7, 7.2, and 7.7 (data not shown). This was presumably due to the quenching of entrapped MQAE at high cytoplasmic Cl- concentrations.
It should be emphasized that we have no measure of the distribution of the concentrations of MQAE in the cellular population, its distribution between the nucleus and cytoplasm, nor its possible exclusion/unequal distribution among various cytoplasmic structures such as marginal bands (22) or other types of organelles. We also have no information on the relative path lengths of the emission intensity through either the cytoplasm or nucleus of the cell. On the other hand, that the thickness (path length) of the nucleus is about twice that of the cytoplasm may be a factor underlying the observed differences, depicted in Figs. 1 and 2, in the fluorescence intensity between the nuclear and cytoplasmic compartments in zero Clo, assuming that the relative dye concentrations are likewise proportional. The level of fluorescence intensity of the cytoplasm may also reflect the fact that the cells still retain some Cl- after exposure to the Cl-free 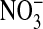 medium, as mentioned before.
medium, as mentioned before.
It is important to understand that we assume MQAE in the nucleus is in a physical state, such that it could respond to Cl- if the latter were present. If this were not so, then interpretation of the Cl- content of the nucleus becomes uncertain. Therefore, in collaboration with Ann Cowan and Dennis Koppel at the University of Connecticut Health Center, we carried out fluorescence bleaching studies of MQAE dye-filled red cells suspended as before in Cl- and 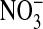 media. We found that photobleaching half the nucleus results in depletion of the dye from the unbleached half, indicating that the probe is free to diffuse in the nucleus (data not shown). These results suggest that the high fluorescence observed in the nucleus, as in Figs. 1 and 2, is not due to stable binding of the dye but reflects that the dye is accurately sensing and reporting the low Cl- content of the nucleus.
media. We found that photobleaching half the nucleus results in depletion of the dye from the unbleached half, indicating that the probe is free to diffuse in the nucleus (data not shown). These results suggest that the high fluorescence observed in the nucleus, as in Figs. 1 and 2, is not due to stable binding of the dye but reflects that the dye is accurately sensing and reporting the low Cl- content of the nucleus.
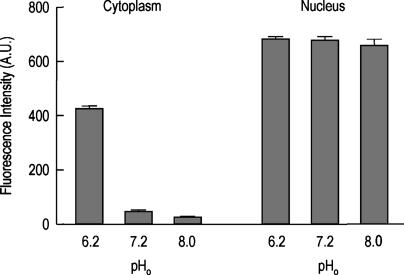
Fig. 3 shows the results of the changes in the relative fluorescence of Amphiuma red blood cells that have been loaded with the pH-sensitive dye, LysoSensor Green DND-153. Depicted here are the averaged values in the relative fluorescence intensities of the dye that occur in the cytoplasm and the nucleus of these cells when the pHo is 6.2, 7.2, or 8.0. It is evident that the nucleus is acidic at all of these values of pHo, whereas the relative fluorescence of the cytoplasm changes in concert with changes in pHo.
Fig. 3.
Depiction of the quantitative changes in the fluorescence intensities of nucleus and cytoplasm (in arbitrary units) that occurred in Amphiuma red cells with changes in pHo as monitored by the pH-sensitive dye, LysoSensor Green DND-153. The analyses were carried out in a completely analogous manner as described in the legend to Fig. 2. Here the relative fluorescence of the dye increases in acidic environments and is quenched in more basic situations. Mean ± SEM value (n = 13) of the fluorescence intensity (in arbitrary units) of the cytoplasm was, at pHo 6.2, 924 ± 12 (range, 352-486); at pHo 7.2, 45 ± 6 (range, 12-88); and at pHo 8.0, 27 ± 4 (range, 7-50). Comparable values for the nucleus were at pHo 6.2, 681 ± 12 (range, 586-788); at pHo 7.2, 678 ± 12 (range, 577-780); and at pHo 8.0, 658 ± 24 (range, 410-777). It is clear that the pH of the cytoplasm changes in concert with changes in pHo. In contrast, the nuclear compartment remains acidic independent of these changes in pHo.
Important for the work that follows is the fraction of the cell's volume occupied by the nucleus. Two ways to estimate this fraction are by (i) the cell's mean corpuscular hemoglobin concentration (MCHC) and (ii) morphometric analysis. Two estimates of MCHC Amphiuma red cells are 24 (14) and 24.8 (23) g/dl of cells. Assuming that all of the hemoglobin is in the cytoplasm, where MCHC approximates 34 g/dl cells, then the fractional nuclear volume of the cell is 0.282% or 28.2%, respectively. The value of 34 g/dl represents an estimated average value of the MCHC of various vertebrate red blood cells, regardless of phyla, upon correction for the volume of the cell occupied by the nucleus (14). The morphometric analysis (kindly performed for us by David Danon) used a procedure (24, 25) that involved taking electron microscopic pictures of random sections of whole Amphiuma red blood cells. From 100 such prints, each cell was cut out and weighed. Then the nucleus (if any) was cut out and weighed. The ratio of the nuclear weights to the total weights gives an estimate of the volume fraction of the cell occupied by the nucleus. This value was 0.287 ± 0.009% (SEM, n = 100) or 28.7%.
Having established by fluorescent imaging that most if not all of the intracellular Cl- in Amphiuma red cells is in the cytoplasm, it is of interest to evaluate the electrical consequences of this distribution of 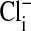 on the cell's plasma membrane potential. This is considered in Fig. 4 and Table 1 where a comparison is made between the values of
on the cell's plasma membrane potential. This is considered in Fig. 4 and Table 1 where a comparison is made between the values of 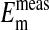 with values of
with values of 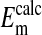 .
. 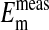 represent averaged values of plasma membrane potentials the we measured electrically as previously published (8, 9, †), and
represent averaged values of plasma membrane potentials the we measured electrically as previously published (8, 9, †), and 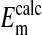 represent values of Em calculated from our measured values of rCl (see Materials and Methods). The comparison is made at three different pH values (Fig. 4) where the values at each pH were calculated on the basis that the Cl- concentration in the cytoplasm depends on the relative size of the nucleus where the nucleus is assumed to be Cl--free. It is evident that the best fit of
represent values of Em calculated from our measured values of rCl (see Materials and Methods). The comparison is made at three different pH values (Fig. 4) where the values at each pH were calculated on the basis that the Cl- concentration in the cytoplasm depends on the relative size of the nucleus where the nucleus is assumed to be Cl--free. It is evident that the best fit of 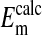 to
to 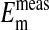 values as seen in Fig. 4 is where the percent volume of the cells occupied by the nucleus is 28.7% (open circles). The quantitative values at pH 7.2 as seen in Fig. 4 are presented in Table 1. Here it is evident that the value of
values as seen in Fig. 4 is where the percent volume of the cells occupied by the nucleus is 28.7% (open circles). The quantitative values at pH 7.2 as seen in Fig. 4 are presented in Table 1. Here it is evident that the value of 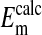 (-16.1 ± 0.3 mV) is equivalent to
(-16.1 ± 0.3 mV) is equivalent to 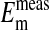 (-14.9 ± 0.16 mV). In addition, it is also evident in Fig. 4 that the slopes of the curves based on
(-14.9 ± 0.16 mV). In addition, it is also evident in Fig. 4 that the slopes of the curves based on 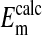 are the same as that for
are the same as that for 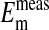 and conform to the theoretical expectation of 58 mV.
and conform to the theoretical expectation of 58 mV.
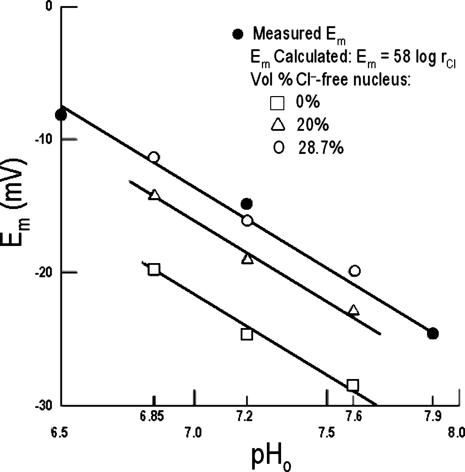
Fig. 4.
The effect of changes in pH on the Em of Amphiuma red blood cells: comparison of measured (solid symbols) and calculated (open symbols) values of Em. The measured value (taken from refs. 8 and 9 and †) of Em± SEM at pH 6.5 was -8.15 ± 0.23 (n = 208), at pH 7.2-14.9 ± 0.16 (n = 184), and at pH 7.9-24.6 ± 0.34 (n = 224). 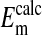 was calculated from the Nernst equation, Em = 58 log rCl, where rCl represents measured values of
was calculated from the Nernst equation, Em = 58 log rCl, where rCl represents measured values of 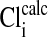 and
and 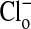 (see Materials and Methods and Table 1). The lines were drawn by eye. The open symbols represent values of
(see Materials and Methods and Table 1). The lines were drawn by eye. The open symbols represent values of 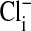 that first assumed that the cell nucleus was free of Cl- and then correcting the measured values of
that first assumed that the cell nucleus was free of Cl- and then correcting the measured values of 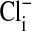 by assuming that the percent of the cell volume occupied by the nucleus was zero (□), 20% (▵), or 28.7% (○).
by assuming that the percent of the cell volume occupied by the nucleus was zero (□), 20% (▵), or 28.7% (○).
Table 1. Comparison of the measured value of 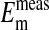 of Amphiuma red blood cells with those calculated from the measured value of rCl, at pH 7.2.
of Amphiuma red blood cells with those calculated from the measured value of rCl, at pH 7.2.
| Percent cell volume of Cl−-free nucleus
|
|||
|---|---|---|---|
| 0 | 20 | 28.7 | |
| rcl, n = 4 | 0.371 ± 0.005 | 0.470 ± 0.006 | 0.527 ± 0.007 |
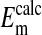 , mV , mV |
−24.9 ± 0.2 | −19.0 ± 0.3 | −16.1 ± 0.3 |
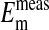 , mV , mV |
−14.9 ± 0.16 | ||
All values are mean ± SEM, where n = 4 for rcl and 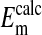 n = 284 for
n = 284 for 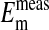 . rcl was measured as described in Materials and Methods.
. rcl was measured as described in Materials and Methods. 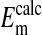 was calculated from rcl by the Nernst equation, in which values of
was calculated from rcl by the Nernst equation, in which values of 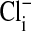 were modified by first assuming that the cell nucleus was free of Cl−, and then correcting the measured values of
were modified by first assuming that the cell nucleus was free of Cl−, and then correcting the measured values of 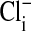 by assuming that the percent volume occupied by the nucleus was either 0%, 20%, or 28.7%. As noted before, 28.7% was the experimentally determined value of the cell volume occupied by the nucleus. The value of
by assuming that the percent volume occupied by the nucleus was either 0%, 20%, or 28.7%. As noted before, 28.7% was the experimentally determined value of the cell volume occupied by the nucleus. The value of 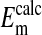 is not significantly different from
is not significantly different from 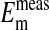 (P=0.375, two-tailed t test) when it is assumed for
(P=0.375, two-tailed t test) when it is assumed for 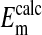 that the percent volume occupied by a Cl−-free nucleus is 28.7%. There was however, a significant difference between
that the percent volume occupied by a Cl−-free nucleus is 28.7%. There was however, a significant difference between 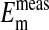 and
and 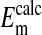 when the percent volume occupied by a Cl−-free nucleus was either zero (P < 0.0001) or 20% (P = 0.0026). See text for discussion.
when the percent volume occupied by a Cl−-free nucleus was either zero (P < 0.0001) or 20% (P = 0.0026). See text for discussion.
Discussion
The main finding presented in this paper is that most, if not all, of the Cl- in an Amphiuma red cell is contained in its cytoplasmic compartment, as documented in Figs. 1 and 2. A major consequence of this result is that, by restricting the cellular concentration of Cl- to the cytoplasm, there is concordance between the measured plasma membrane potentials (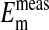 ) and those calculated from the measured values of rCl, as shown in Fig. 4 (comparison of filled and empty circles) and Table 1. It should be noted that the Em measured by others (26, 27) at different values of pHo are in essential agreement with those depicted in Fig. 3. However, there is a difference between our value of 58 mV for the slope of this relationship (from the Nernst equation, Em = 58 log rCl) and that of 33 mV claimed by others (26). We have no explanation for this difference, but it should be recognized that the analytical and electrical methodologies used were not the same.
) and those calculated from the measured values of rCl, as shown in Fig. 4 (comparison of filled and empty circles) and Table 1. It should be noted that the Em measured by others (26, 27) at different values of pHo are in essential agreement with those depicted in Fig. 3. However, there is a difference between our value of 58 mV for the slope of this relationship (from the Nernst equation, Em = 58 log rCl) and that of 33 mV claimed by others (26). We have no explanation for this difference, but it should be recognized that the analytical and electrical methodologies used were not the same.
It has been suggested (28) that Cl- may be excluded from the nuclei of red cells of the dogfish, Musteleis canis. This conclusion was based on the unresolved discrepancy between rCl (≈0.59) and rCO2, i.e., 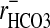 (≈1.32) by assuming that the nucleus was alkaline relative to the cytoplasm. It was suggested that the exclusion of Cl- was compensated for by
(≈1.32) by assuming that the nucleus was alkaline relative to the cytoplasm. It was suggested that the exclusion of Cl- was compensated for by 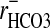 . The cells are said to contain 9.2 pg of DNA per cell (29), but the nuclear volume fraction of the cell is unknown as is its excess DNA content. Given the results reported here, we anticipated the nucleus of the Amphiuma red cell to be acidic relative to the cytoplasm. This proved to be the case, as described in Results (Fig. 3).
. The cells are said to contain 9.2 pg of DNA per cell (29), but the nuclear volume fraction of the cell is unknown as is its excess DNA content. Given the results reported here, we anticipated the nucleus of the Amphiuma red cell to be acidic relative to the cytoplasm. This proved to be the case, as described in Results (Fig. 3).
It is known that the DNA content of a red blood cell is correlated with its size: the more DNA, the larger the cell volume (30-32). The Amphiuma red blood cell, thought to be diploid, has 168 pg of DNA per cell, ≈26 times the amount found in mammalian cells (30). The nature of this excess or extra DNA (whether noncoding, junk, selfish, etc.) is unknown (see ref. 32). Nevertheless, the excess DNA is evidently not balanced by increased histone content, resulting in an imbalance of net negative charge in the nucleus. This imbalance could be further amplified if mucopolysaccharides were also present in the nucleus (33).
What is the basis in Amphiuma red cells for the nuclear exclusion of Cl-? As stated above, because the cell's DNA content is extremely high (see Materials and Methods), it may be there is an uncompensated net negative charge within the nucleus due to histone imbalance in the chromatin. If so, it would provide a rational basis for the exclusion of Cl- from the nucleus. We assume that the distribution of Cl- between nucleus and cytoplasm is passive given the high ionic conductance of the nuclear membrane (34, 35). We measured, with U. V. Lassen, (8, 9, †) the potential difference at pH 7.2 across the nuclear to cytoplasmic (N/C) membrane (inside negative) and found in two experiments (n = 30) the 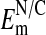 to range from -8 to -54 mV, with the mean = -23 ± 2.0 mV (±SEM). This value is too low to account for the extent of Cl- exclusion seen in Fig. 2. On the other hand, our measured values of
to range from -8 to -54 mV, with the mean = -23 ± 2.0 mV (±SEM). This value is too low to account for the extent of Cl- exclusion seen in Fig. 2. On the other hand, our measured values of 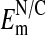 may be low due presumably to nuclear membrane damage caused by electrode impalement. If so, then the highest values of the
may be low due presumably to nuclear membrane damage caused by electrode impalement. If so, then the highest values of the 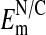 should be taken to reflect the more accurate values of
should be taken to reflect the more accurate values of 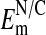 . Values of -54 mV (or higher) would be in the expected range for an
. Values of -54 mV (or higher) would be in the expected range for an 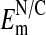 where the nucleus has little or no Cl- relative to the cytoplasm.
where the nucleus has little or no Cl- relative to the cytoplasm. 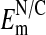 measured in the salivary gland cells of Drosophila was found to be approximately -13 mV (36), and in a variety of other cell types ranged from 0 to -33 mV (34, 36, 37) where the N/C ratio of Cl- was either close to one or unknown. Note that we have assumed throughout that the activities of Cl- are the same as their concentrations in both the nucleus and cytoplasm of Amphiuma red cells.
measured in the salivary gland cells of Drosophila was found to be approximately -13 mV (36), and in a variety of other cell types ranged from 0 to -33 mV (34, 36, 37) where the N/C ratio of Cl- was either close to one or unknown. Note that we have assumed throughout that the activities of Cl- are the same as their concentrations in both the nucleus and cytoplasm of Amphiuma red cells.
The nuclear exclusion of Cl- that occurs in Amphiuma red blood cells is unusual if not unique among various cell types so far examined, whereas the N/C ratio for Na+ hovers around 1. For instance, by use of ion-specific microelectrodes, the N/C ratio in Chironomus salivary gland was found to be ≈1 for both Cl- and Na+ (38, 39). With electron microprobe analysis, maturating chick red blood cells (18 day, near hatching) had N/C ratios = 0.48 for Cl- and 0.63 for Na+ (40); toad oocytes had N/C ratios = 0.84 for Cl- and 0.93 for Na+ (41); in mouse enterocytes, N/C = 0.75-0.85 for Cl- (42); in rabbit ileum, N/C = 0.68 for Cl- and 0.56 for Na+ (43); in rabbit smooth muscle, N/C = 1.0 for Cl- and 0.56 for Na+ (44); for rat renal tubular cells, the N/C ratios for Cl- and Na+ varied somewhat depending on the cytoplasmic region analyzed (45, 46); and in rat hepatocytes, where N/C = 0.9 for Cl- and 1.1 for Na+ (47). It is evident that in all of these studies, there are only small variations in N/C values for Cl- and Na+. Exceptions to these types of results, where N/C ratios were assessed by analyzing nuclei in nonaqueous media, were seen in rat liver, where N/C = 7.9 for Cl- and 11.0 for Na+ (48) and in Ehrlich acites cells, where N/C ≫ 1 for both Cl- and Na+ (49). These studies may be flawed due to redistribution of cellular ions during the preparative procedure. The cellular content of DNA in rat liver nuclei and Ehrlich cells has presumably <6 pg per cell, indicating that excess DNA is unlikely to be present. It would be of interest to know to what extent other cells with high DNA content, e.g., lungfish red blood cells with >160 pg DNA/cell (50, 51), would, like Amphiuma red blood cells, show nuclear exclusion of Cl-.
The red blood cells of fish and amphibians, in contrast to those of reptiles, birds, and mammals, are known to vary greatly in size as well as DNA content. However, the physiological consequences of possible differences in the distribution of intracellular ions in these and perhaps other cell types have yet to be determined. It should also be kept in mind that estimates of concentration gradients between cells and their environment could be influenced by unequal distributions of substances/ions within the cell because of compartmentation.
Acknowledgments
We thank Drs. Knox Chandler, William D. Cohen, David Danon, Philip A. Knauf, Gordon MacGregor, Reiko Maki-Fitzsimonds, Victor Nadler, Achim Seeger, Ewald R. Weibel, Duncan Wong, and David Zenisek for help and advice during the course of this work. We also thank Ann Cowan and Kennis Koppel of the Center for Cell Analysis and Modeling at the University of Connecticut Health Center for carrying out the fluorescence photobleaching studies. This work was supported in part by National Institutes of Health Grants HL 09906 (to J.F.H.); DK 50230, 60069, and 17433 (to J.P.G.); and RR13186 (to the Center for Cell Analysis and Modeling, University of Connecticut Health Center).
Abbreviations: Em, membrane potential; rCl, Donnan ratio of Cli/Clo; Mops, 4-morpholinepropanesulfonic acid; N/C, nuclear to cytoplasmic; pHo, external pH.
Footnotes
Hoffman, J. F. & Lassen, U. V. (1971) XXVth Congress of the International Union of Physiological Sciences, Jul. 25-31, Munich (IUPS), p. 253, abstr.
References
- 1.Warburg, E. J. (1922) Biochem. J. 16, 154-340. [Google Scholar]
- 2.Barcroft, J., Bock, A. V., Hill, A. V., Parsons, T. R., Parsons, W. & Shoji, R. (1922) J. Physiol. 56, 157-178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Van Slyke, D. D., Wu, H. & McLean, F. C. (1923) J. Biol. Chem. 56, 765-849. [Google Scholar]
- 4.Fitzsimons, E. J. & Sendroy, J. (1961) J. Biol. Chem. 236, 1595-1601. [Google Scholar]
- 5.Hoffman, J. F. & Laris, P. C. (1974) J. Physiol. 239, 519-552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Harris, E. J. & Maizels, M. (1952) J. Physiol. 118, 40-53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Funder, J. & Wieth, J. O. (1966) Acta Physiol. Scand. 68, 234-245. [Google Scholar]
- 8.Lassen, U. V. (1972) in Oxygen Affinity of Hemoglobin and Red Cell Acid Base Status, eds. Rørth, M. & Astrup, P. (Munksgaard, Copenhagen), pp. 291-304.
- 9.Lassen, U. V. (1977) in Membrane Transport in Red Cells, eds. Ellory, J. C. & Lew, V. L. (Academic, New York), pp. 137-172.
- 10.Gulliver, G. (1875) Proc. Zool. Soc. London, Plate LV, 473-495.
- 11.Cupp, C. D. (1914) Anat. Record 9, 259-280. [Google Scholar]
- 12.Smith, H. M. (1925) Biol. Bull. 48, 347-378. [Google Scholar]
- 13.Seifriz, W. (1926) Protoplasma 1, 345-363. [Google Scholar]
- 14.Wintrobe, M. M. (1933) Folia Haematol. 51, 32-49. [Google Scholar]
- 15.Hartman, F. A. & Lessler, M. A. (1964) Biol. Bull. 126, 83-88. [Google Scholar]
- 16.Gilbert, I. G. F. & Radley, J. B. (1964) Biochim. Biophys. Acta 82, 618-621. [DOI] [PubMed] [Google Scholar]
- 17.Philpot, J. S. & Stanier, J. E. (1956) Biochem. J. 63, 214-223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Leif, R. C. & Vinograd, J. (1964) Proc. Natl. Acad. Sci. USA 51, 520-528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Millard, E. E., Srivastava, K., Traub, L. M., Schaffer, J. E. & Ory, D. S. (2000) J. Biol. Chem. 275, 38445-38451. [DOI] [PubMed] [Google Scholar]
- 20.Verkman, A. S., Sellers, M. C., Chao, A. C., Leung, T. & Ketcham, R. (1989) Anal. Biochem. 178, 355-361. [DOI] [PubMed] [Google Scholar]
- 21.Dalmark, M. & Wieth, J. O. (1972) J. Physiol. (London) 224, 583-610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cohen, W. D. (1978) J. Cell Biol. 78, 260-273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lenfant, C. & Johansen, K. (1967) Respir. Physiol. 2, 247-260. [DOI] [PubMed] [Google Scholar]
- 24.Delesse, M. A. (1847) C. R. Acad. Sci. 25, 544-545. [Google Scholar]
- 25.Weibel, E. R. (1979) in Stereological Methods (Academic, San Francisco), Vol. 1, pp. 1-415. [Google Scholar]
- 26.Stoner, L. C. & Kregenow, F. M. (1980) J. Gen. Physiol. 76, 455-478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cala, P. M. (1980) J. Gen. Physiol. 76, 683-708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ferguson, J. K. W., Horvath, S. M. & Pappenheimer, J. R. (1938) Biol. Bull. 75, 381-388. [Google Scholar]
- 29.Hinegardner, R. (1976) Comp. Biochem. Physiol. 55B, 367-370. [DOI] [PubMed] [Google Scholar]
- 30.Mirsky, A. E. & Ris, H. (1951) J. Gen. Physiol. 34, 451-462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kregenow, F. M. (1977) in Water Relations in Membrane Transport in Plants and Animals, ed. Jungreis, A. M. (Academic, San Diego), pp. 291-302.
- 32.Gregory, T. R. (2001) Biol. Rev. 76, 64-101. [Google Scholar]
- 33.Bhavanandan, V. P. & Davidson, E. A. (1975) Proc. Natl. Acad. Sci. USA 72, 2032-2036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mazzanti, M., Bustamante, J. O. & Oberleithner, H. (2001) Physiol. Rev. 81, 1-19. [DOI] [PubMed] [Google Scholar]
- 35.Wente, S. R. (2000) Science, 288, 1374-1377. [DOI] [PubMed] [Google Scholar]
- 36.Loewenstein, W. R. & Kanno, Y. (1962) Nature 195, 462-464. [DOI] [PubMed] [Google Scholar]
- 37.Kanno, Y., Ashman, R. F. & Loewenstein, W. R. (1965) Exp. Cell Res. 39, 184-189. [DOI] [PubMed] [Google Scholar]
- 38.Palmer, L. G. & Civan, M. M. (1977) J. Membr. Biol. 33, 41-61. [DOI] [PubMed] [Google Scholar]
- 39.Civan, M. M. (1978) Am. J. Physiol. 234, F261-F269. [DOI] [PubMed] [Google Scholar]
- 40.Jones, R. T., Johnson, R. T., Gupta, B. L. & Hall, T. A. (1979) J. Cell Sci. 35, 67-85. [DOI] [PubMed] [Google Scholar]
- 41.Dick, D. A. T. (1976) J. Physiol. (London) 258, 102P-103P. [PubMed] [Google Scholar]
- 42.Cameron, I. L., Sparks, R. L., Horn, K. L. & Smith, N. R. (1977) J. Cell Biol. 73, 193-199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gupta, B. L., Hall, T. A. & Naftalin, R. J. (1978) Nature 272, 70-73. [DOI] [PubMed] [Google Scholar]
- 44.Somlyo, A. P., Somlyo, A. V. & Shuman, H. (1979) J. Cell Biol. 81, 316-335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Thurau, K., Dorge, A., Mason, J., Beck, F. & Rick, R. (1979) Klin. Wochenschr. 57, 993-999. [DOI] [PubMed] [Google Scholar]
- 46.Beck, F., Bauer, R., Bauer, U., Mason, J., Dorge, A., Rick, R. & Thurau, K. (1980) Kidney Int. 17, 756-763. [DOI] [PubMed] [Google Scholar]
- 47.Horvath, I., Zs-Nagy, I., Lustyik, G. Y. & Varadi, G. Y. (1983) Tissue Cell 15, 515-521. [DOI] [PubMed] [Google Scholar]
- 48.Siebert, G., Langendorf, H., Hannover, R., Nitz-Litzow, D., Pressman, B. C. & Moore, C. (1965) Hoppe-Seyler's Z. Physiol. Chem. 343, 101-115. [PubMed] [Google Scholar]
- 49.Pietrzyk, C. & Heinz, E. (1974) Biochim. Biophys. Acta 352, 397-411. [DOI] [PubMed] [Google Scholar]
- 50.Pedersen, R. A. (1971) J. Exp. Zool. 177, 65-78. [DOI] [PubMed] [Google Scholar]
- 51.Gregory, T. R. (2001) Blood Cells Mol. Dis. 27, 830-843. [DOI] [PubMed] [Google Scholar]