Constructing Abstraction Hierarchies Using a Skill-Symbol Loop

Abstract

We describe a framework for building abstraction hierarchies whereby an agent alternates skill- and representation-construction phases to construct a sequence of increasingly abstract Markov decision processes. Our formulation builds on recent results showing that the appropriate abstract representation of a problem is specified by the agent’s skills. We describe how such a hierarchy can be used for fast planning, and illustrate the construction of an appropriate hierarchy for the Taxi domain.

1 Introduction

One of the core challenges of artificial intelligence is that of linking abstract decision-making to low-level, real-world action and perception. Hierarchical reinforcement learning methods [Barto and Mahadevan, 2003] approach this problem through the use of high-level temporally extended macroactions, or skills, which can significantly decrease planning times [Sutton et al., 1999]. Skill acquisition (or skill discovery) algorithms (recently surveyed by Hengst [2012]) aim to discover appropriate high-level skills autonomously. However, in most hierarchical reinforcement learning research the state space does not change once skills have been acquired. An agent that has acquired high-level skills must still plan in its original low-level state space—a potentially very difficult task when that space is high-dimensional and continuous. Although some of the earliest formalizations of hierarchical reinforcement learning [Parr and Russell, 1997; Dietterich, 2000] featured hierarchies where both the set of available actions and the state space changed with the level of the hierarchy, there has been almost no work on automating the representational aspects of such hierarchies.

Recently, Konidaris et al. [2014] considered the question of how to construct a symbolic representation suitable for planning in high-dimensional continuous domains, given a set of high-level skills. The key result of that work was that the appropriate abstract representation of the problem was directly determined by characteristics of the skills available to the agent—the skills determine the representation, and adding new high-level skills must result in a new representation.

We show that these two processes can be combined into a skill-symbol loop: the agent acquires a set of high-level skills, then constructs the appropriate representation for planning using them, resulting in a new problem in which the agent can again perform skill acquisition. Repeating this process leads to an abstraction hierarchy where both the available skills and the state space become more abstract at each level of the hierarchy. We describe the properties of the resulting abstraction hierarchies and demonstrate the construction and use of one such hierarchy in the Taxi domain.

2 Background

Reinforcement learning problems are typically formalized as Markov decision processes or MDPs, represented by a tuple M = (S, A, R, P, γ), where S is a set of states, A is a set of actions, R(s, a, s′) is the reward the agent receives when executing action a in state s and transitioning to state s′, P(s′|s, a) is the probability of the agent finding itself in state s′ having executed action a in state s, and γ ∈ (0, 1] is a discount factor [Sutton and Barto, 1998].

We are interested in the multi-task reinforcement learning setting where, rather than solving a single MDP, the agent is tasked with solving several problems drawn from some task distribution. Each individual problem is obtained by adding a set of start and goal states to a base MDP that specifies the state and action spaces and background reward function. The agent’s task is to minimize the average time required to solve new problems drawn from this distribution.

2.1 Hierarchical Reinforcement Learning

Hierarchical reinforcement learning [Barto and Mahadevan, 2003] is a framework for learning and planning using higher-level actions built out of the primitive actions available to the agent. Although other formalizations exist—mostly notably the MAX-Q [Dietterich, 2000] and Hierarchy of Abstract Machines [Parr and Russell, 1997] approaches—we adopt the options framework [Sutton et al., 1999], which models temporally abstract macro-actions as options.

An option o consists of three components: an option policy, π_o, which is executed when the option is invoked; an initiation set, which describes the states in which the option may be executed; and a termination condition, β_o(s) → [0, 1], which describes the probability that an option will terminate upon reaching state s.

An MDP where primitive actions are replaced by a set of possibly temporally-extended options (some of which could simply execute a single primitive action) is known as a semi Markov decision process (or SMDP), which generalizes MDPs to handle action executions that may take more than one time step. An SMDP is described by a tuple M = (S, O, R, P, γ), where S is a set of states; O is a set of options; R(s′, τ|s, o) is the reward received when executing option o ∈ O(s) at state s ∈ S, and arriving in state s′ ∈ S after τ time steps; P(s′, τ|s, o) is a PDF describing the probability of arriving in state s′ ∈ S, τ time steps after executing option o ∈ O(s) in state s ∈ S; and γ ∈ (0, 1] is a discount factor, as before.

The problem of deciding which options an agent should acquire is known as the skill discovery problem. A skill discovery algorithm must, through experience (and perhaps additional advice or domain knowledge), acquire new options by specifying their initiation set, I_o, and termination condition, β_o. The option policy is usually specified indirectly via an option reward function, R_o, which is used to learn π_o. Each new skill is added to the set of options available to the agent with the aim of either solving the original or subsequent tasks more efficiently. Our framework is agnostic to the specific skill discovery method used (many exist).

Very few approaches combine temporal abstraction with state abstraction to construct a hierarchy. For example, Mehta et al. [2008] is able to recover a MaxQ hierarchy from demonstration trajectories, but assumes a factored, discrete state space. The most common approach [Hengst, 2002; Jonsson and Barto, 2005; Vigorito and Barto, 2010; Mugan and Kuipers, 2012] assumes a factored (but possibly continuous) state MDP, finds a ranking of state factors from “lowest-level” to “highest-level”, and successively constructs options to change each state factor; these algorithms differ primarily in the method used to order the state factors. The resulting options are hierarchical in the sense that the options for modifying higher-level state variables can execute those for modifying lower-level state variables. However, the agent has access to all options at the same time, and at the same level, when learning to solve the task. Similarly, state abstraction is generally limited to finding option-specific state abstractions for learning each option policy (typically using only state factors at a lower-level than the factor the option is constructed to modify).

2.2 Representation Acquisition

While skill acquisition allows an agent to construct higher-level actions, it alone is insufficient for constructing truly useful abstraction hierarchies because the agent must still plan in the original state space, no matter how abstract its actions become. A complementary approach is taken by recent work on representation acquisition [Konidaris et al., 2014], which considers the question of constructing a symbolic description of an SMDP suitable for high-level planning. Key to this is the definition of a symbol as a name referring to a set of states:

Definition 1

A propositional symbol σ_Z is the name of a test τ_Z, and corresponding set of states Z = {s ∈ S|τ_Z(s) = 1}.

The test, or grounding classifier, is a compact representation of a (potentially uncountably infinite) set of states in which the classifier returns true (the grounding set). Logical operations (e.g., and) using the resulting symbolic names have the semantic meaning of set operations (e.g., ∩) over the grounding sets, which allows us to reason about which symbols (and corresponding grounding classifiers) an agent should construct in order to be able to determine the feasibility of high-level plans composed of sequences of options. We use the grounding operator 𝒢 to obtain the grounding set of a symbol or symbolic expression; for example, 𝒢(σ_Z) = Z, 𝒢(σ_A and σ_B) = A ∩ B. For convenience we also define 𝒢 over collections of symbols; for a set of symbols A, we define 𝒢(A) = ∪_i𝒢(a_i), ∀a_i ∈ A.

Konidaris et al. [2014] showed that defining a symbol for each option’s initiation set and the symbols necessary to compute its image (the set of states the agent might be in after executing the option from some set of starting states) are necessary and sufficient for planning using that set of options. The feasibility of a plan is evaluated by computing each successive option’s image, and then testing whether it is a subset of the next option’s initiation set. Unfortunately, computing the image of an option is intractable in the general case. However, the definition of the image for at least two common classes of options is both natural and computationally very simple.

The first is the subgoal option: the option reaches some set of states and terminates, and the state it terminates in can be considered independent of the state execution began in. In this case we can create a symbol for that set (called the effect set—the set of all possible states the option may terminate in), and use it directly as the option’s image. We thus obtain a symbolic vocabulary that contains 2n symbols for n options (a symbol for each option’s initiation and effect sets) and is provably sufficient for planning. Building a forward model using this vocabulary leads to a plan graph representation: a graph with n nodes, and an edge from node i to node j if option j’s initiation set is a superset of option i’s effect set. Planning amounts to finding a path in the plan graph; once this graph has been computed, the grounding classifiers can be discarded.

The second class of options are abstract subgoal options: the low-level state is factored into a vector of state variables, and executing each option sets some variables to a subgoal (again, independently of the starting state) while leaving others unchanged. In this case the image operator can be computed using the intersection of the effect set (as in the subgoal option case) and a modified starting state classifier (where the variables that are changed by the option are projected out). The resulting symbols are again necessary and sufficient for planning, and constructing a forward model using them results in a STRIPS-like factored representation which can be automatically converted to PDDL [McDermott et al., 1998]. After conversion the grounding classifiers can be discarded, and the PDDL model used as input to an off-the-shelf task planner.

Representation acquisition as described above constructs an MDP from a low-level SMDP. The low-level SMDP may be stochastic and have continuous states and continuous primitive actions (though the set of options must be discrete), but the constructed abstract MDP is discrete and deterministic. This occurs because the abstract MDP is constructed for the purposes of finding plans that are guaranteed to succeed. This approach has recently been generalized to enable the agent to instead compute the probability that a plan succeeds [Konidaris et al., 2015], which results in a stochastic (but still discrete) abstract MDP; we leave the construction of probabilistic hierarchies to future work.

3 Constructing Abstraction Hierarchies

The results outlined above show that the two fundamental aspects of hierarchy—skills and representations—can be tightly coupled: skill acquisition drives representational abstraction. An agent that has performed skill acquisition in an MDP to obtain higher-level skills can automatically determine a new abstract state representation suitable for planning in the resulting SMDP. We now show that these two processes can be alternated to construct an abstraction hierarchy.

We assume the following setting: an agent is faced with some base MDP M₀, and aims to construct an abstraction hierarchy that enables efficient planning for new problems posed in M₀, each of which is specified by a start and goal state set. M₀ may be continuous-state and even continuous-action, and the options defined in it may be stochastic, but all subsequent levels of the hierarchy will be constructed to be discrete-state, discrete-action, and deterministic. We adopt the following definition of an abstraction hierarchy:

Definition 2

An n-level hierarchy on base MDP M₀ = (S₀, A₀, R₀, P₀, γ₀) is a collection of MDPs M_i = (S_i, A_i, R_i, P_i, γ_i), i ∈ {1, …, n}, such that each action set A_j, 0 < j ≤ n, is a set of options defined over M_j−1 (i.e., M_j−1⁺ = (S_j−1, A_j, R_j−1, P_j−1) is an SMDP).

Here, M_j−1⁺ is the SMDP created by adding options to M_j−1 but leaving the state space unchanged.

This captures the core assumption behind hierarchical reinforcement learning: hierarchies are built through macroactions. Note that this formulation retains the downward refinement property from classical hierarchical planning [Bacchus and Yang, 1991]—meaning that a plan at level j can be refined to a plan at level j − 1 without backtracking to level j or higher—because a policy at any level is also a (not necessarily Markovian [Sutton et al., 1999]) policy at any level lower, including M₀. However, while Definition 2 links the action set of each MDP to the action set of its predecessor in the hierarchy, it says nothing about how to link their state spaces. To do so, we must in addition determine how to construct a new state space S_j, transition probability function P_j, and reward function R_j.¹

Fortunately, this is exactly what representation acquisition provides: a method for constructing a new symbolic representation suitable for planning inM_j−1⁺ using the options in A_j. This provides a new state space S_j, which, combined with A_j, specifies P_j. The only remaining component is the reward function. A representation construction algorithm based on sets [Konidaris et al., 2014]—such as we adopt here—is insufficient for reasoning about expected rewards, which requires a formulation based on distributions [Konidaris et al., 2015]. For simplicity, we can remain consistent and simply set the reward to a uniform transition penalty of −1; alternatively, we can adopt just one aspect of the distribution-based representation and set R_j to the empirical mean of the rewards obtained when executing each option.

Thus, we have all the components required to build level j of the hierarchy from level j − 1. This procedure can be repeated in a skill-symbol loop—alternating skill acquisition and representation acquisition phases—to construct an abstraction hierarchy. It is important to note that there are no degrees of freedom or design choices in the representation acquisition phase of the skill-symbol loop; the algorithmic questions reside solely in determining which skills to acquire at each level.

This construction results in a specific relationship between MDPs in a hierarchy: every state at level j refers to a set of states at level j − 1.² A grounding in M₀ can therefore be computed for any state at level j in the hierarchy by applying the grounding operator j times. If we denote this “final grounding” operator as 𝒢₀, then ∀j, s_j ∈ S_j, ∃Z₀ ⊆ S₀ such that 𝒢₀(s_j) = Z₀.

We now illustrate the construction of an abstraction hierarchy via an example—a very simple task that must be solved by a complex agent. Consider a robot in a room with two boxes, one containing an apple (Figure 1a). The robot must occasionally move the apple from one box to the other. Directly accomplishing this involves solving a high-dimensional motion planning problem, so instead the robot is given five motor skills: move-gripper-above1 and move-gripper-above2 use motion planning to move the robot’s gripper above each box; pregrasp controls the gripper so that it cages the apple, and is only executable from above it; grasp can be executed following pregrasp, and runs a gradient-descent based controller to achieve wrench-closure on the apple; and release drops the apple. These form A₁, the actions in the first level of the hierarchy, and since they are abstract subgoal options (though release must be split into two cases, one for each box) the robot automatically constructs a factored state space (see Figure 1b) that specifies M₁.³ This enables abstract planning—the state space is independent of the complexity of the robot, although S₁ contains some low-level details (e.g., pregrasped).

Figure 1.

A robot must move an apple between two boxes (a). Given a set of motor primitives it can form a discrete, factored state space (b). Subsequent applications of skill acquisition result in successively more abstract state spaces (c and d).

Next, the robot detects (perhaps by applying a skill discovery algorithm in M₁) that pregrasp is always followed by grasp, and therefore replaces these actions with grab-apple, which together with the remaining skills in A₁ forms A₂. This results in a smaller MDP, M₂ (Figure 1c), which is a good abstract model of the task. The robot then creates a skill that picks up the apple in whichever box it is in, and moves it over the other box (perhaps by applying a skill discovery algorithm toM₂). A₃ now consists of just a single action, swap-apple, requiring just two propositions to define S₃: apple-in-box-1, and apple-in-box-2 (Figure 1d). The abstraction hierarchy has abstracted away the details of the robot (in all its complexity) and exposed the (almost trivial) underlying task structure.

4 Planning Using an Abstraction Hierarchy

Once an agent has constructed an abstraction hierarchy, it must be able to use it to rapidly find plans for new problems. We formalize this process as the agent posing a plan query to the hierarchy, which should then be used to generate a plan for solving the problem described by the query. We adopt the following definition of a plan query:

Definition 3

A plan query is a tuple (B, G), where B ⊆ S₀ is the set of base MDP states from which execution may begin, and G ⊆ S₀ (the goal) is the set of base MDP states in which the agent wishes to find itself following execution.

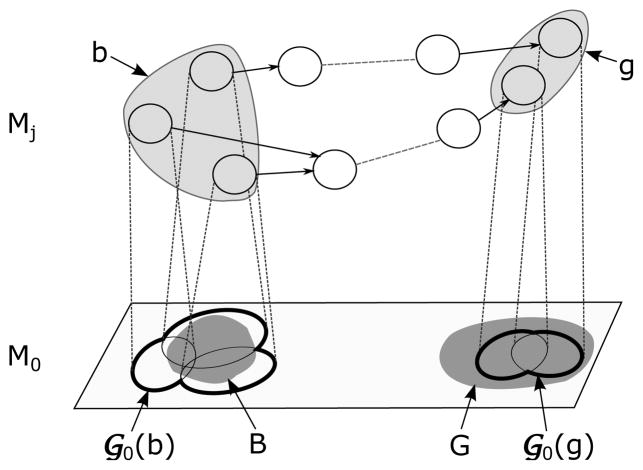
The critical question is at which level of the hierarchy planning should take place. We first define a useful predicate, planmatch, which determines whether an agent should attempt to plan at level j (see Figure 2):

Figure 2.

The conditions under which a plan at MDP M_j answers a plan query with start state set B and goal state set G in the base MDP M₀. A pair of state sets b, g ⊆ S_j are required such that B ⊆ 𝒢₀(b), 𝒢₀(g) ⊆ G, and a plan exists in M_j from every state in b to some state in g.

Definition 4

A pair of abstract state sets b and g match a plan query (B, G) (denoted planmatch(b, g, B, G)) when B ⊆ 𝒢₀(b) and 𝒢₀(g) ⊆ G.

Theorem 1

A plan can be found to solve plan query (B, G) at level j iff ∃b, g ⊆ S_j such that planmatch(b, g, B, G), and there is a feasible plan in M_i from every state in b to some state in g.

Proof

The MDP at level j is constructed such that a plan p starting from any state in 𝒢(b) (and hence also 𝒢₀(b)) is guaranteed to leave the agent in a state in 𝒢(g) (and hence also 𝒢₀(g)) iff p is a plan in MDP M_j from b to g [Konidaris et al., 2014].

Plan p is additionally valid from B to G iff B ⊆ 𝒢₀(b) (the start state at level j refers to a set that includes all query start states) and 𝒢₀(g) ⊆ G (the query goal includes all states referred to by the goal at level j).

Note that b and g may not be unique, even within a single level: because S_j is not necessarily a partition of S_j−1, there may be multiple states, or sets of states, at each level whose final groundings are included by G or include B; a solution from any such b to any such g is sufficient. For efficient planning it is better for b to be a small set to reduce the number of start states while remaining large enough to subsume B; if b = S_j then answering the plan query requires a complete policy for M_j, rather than a plan. However, finding a minimal subset is computationally difficult. One approach is to build the maximal candidate set b = {s|𝒢₀(s) ∩ B ≠ ∅, s ∈ S_j}. This is a superset of any start match, and a suitable one exists at this level if and only if B ⊆ ∪_s∈b𝒢₀(s). Similarly, g should be maximally large (and so easy to reach) while remaining small enough so that its grounding set lies within G. At each level j, we can therefore collect all states that ground out to subsets of G: g = {s|𝒢₀(s) ⊆ G, s ∈ S_j}. These approximations result in a unique pair of sets of states at each level—at the cost of potentially including unnecessary states in each set— and can be computed in time linear in |S_j|.

It follows from the state abstraction properties of the hierarchy that a planmatch at level j implies the existence of a planmatch at all levels below j.

Theorem 2

Given a hierarchy of state spaces {S₀, …, S_n} constructed as above and plan query (B, G), if ∃b, g ⊆ S_j such that planmatch(b, g, B, G), for some j, n ≥ j > 0, then ∃b′, g′ ⊆ S_k such that planmatch(b′, g′, B, G), ∀k ∈ {0, …, j − 1}.

Proof

We first consider k = j − 1. Let b′ = 𝒢(b), and g′ = 𝒢(g). Both are, by definition, sets of states in S_j−1. By definition of the final grounding operator, 𝒢₀(b) = 𝒢₀(b′) and 𝒢₀(g) = 𝒢₀(g′), and hence B ⊆ 𝒢₀(b′) and 𝒢₀(g′) ⊆ G. This process can be repeated to reach any k < j.

Any plan query therefore has a unique highest level j containing a planmatch. This leads directly to Algorithm 1, which starts looking for a planmatch at the highest level of the hierarchy and proceeds downwards; it is sound and complete by Theorem 1.

Algorithm 1.

A simple hierarchical planning algorithm.

The complexity of Algorithm 1 depends on its two component algorithms: one used to find a planmatch, and another to attempt to find a plan (possibly with multiple start states and goals). We denote the complexity of these algorithms as matching cost m(|S|) (linear using the approach described above) and planning cost p(|S|), for a problem with |S| states, respectively. The complexity of finding a plan at level l, where the first match is found at level k ≥ l, is given by $h(k,l,M)={\sum }_{a=k+1}^{n}m(\mid S_a\mid )+{\sum }_{b=l}^k[m(\mid S_b\mid )+p(\mid S_b\mid )]$, for a hierarchy M with n levels. The first term corresponds to the search for the level with the first planmatch; the second term for the repeated planning at levels that contain a match but not a plan (a planmatch does not necessarily mean a plan exists at that level—merely that one could).

5 Discussion

The formula for h highlights the fact that hierarchies make some problems easier to solve and others harder: in the worst case, a problem that should take p(|S₀|) time—one only solvable via the base MDP—could instead take ${\sum }_{a=0}^n[m(\mid S_a\mid )+p(\mid S_b\mid )]$ time. A key question is therefore how to balance the depth of the hierarchy, the rate at which the state space size diminishes as the level increases, which specific skills to discover at each level, and how to control false positive plan matches, to reduce planning time.

Recent work has highlighted the idea that skill discovery algorithms should aim to reduce average planning or learning time across a target distribution of tasks [Şimşek and Barto, 2008; Solway et al., 2014]. Following this logic, a hierarchy M for some distribution over task set T should be constructed so as to minimize ∫_T h(k(t), l(t), M)P(t)dt, where k and l now both depend on each task t. Minimizing this quantity over the entire distribution seems infeasible; an acceptable substitute may be to assume that the tasks the agent has already experienced are drawn from the same distribution as those it will experience in the future, and to construct the hierarchy that minimizes h averaged over past tasks.

The form of h suggests two important principles which may aid the more direct design of skill acquisition algorithms. One is that deeper hierarchies are not necessarily better; each level adds potential planning and matching costs, and must be justified by a rapidly diminishing state space size and a high likelihood of solving tasks at that level. Second, false positive plan matches—when a pair of states that match the query is found at some level at which a plan cannot be found—incur a significant time penalty. The hierarchy should therefore ideally be constructed so that every likely goal state at each level is reachable from every likely start state at that level.

An agent that generates its own goals—as a completely autonomous agent would—could do so by selecting an existing state from an MDP at some level (say j) in the hierarchy. In that case it need not search for a matching level, and could instead immediately plan at level j, though it may still need to drop to lower levels if no plan is found in M_j.

6 An Example Domain: Taxi

We now explain the construction and use of an abstraction hierarchy for a common hierarchical reinforcement learning benchmark: the Taxi domain [Dietterich, 2000], depicted in Figure 3a. A taxi must navigate a 5×5 grid, which contains a few walls, four depots (labeled red, green, blue, and yellow), and a passenger. The taxi may move one square in each direction (unless impeded by a wall), pick up a passenger (when occupying the same square), or drop off a passenger (when it has previously picked the passenger up). A state at base MDP M₀ is described by 5 state variables: the x and y location of the taxi and the passenger, and whether or not the passenger is in the taxi. This results in a total of 650 states (25 × 25 = 625 states for when the passenger is not in the taxi, plus another 25 for when the passenger is in the taxi and they are constrained to have the same location).

Figure 3.

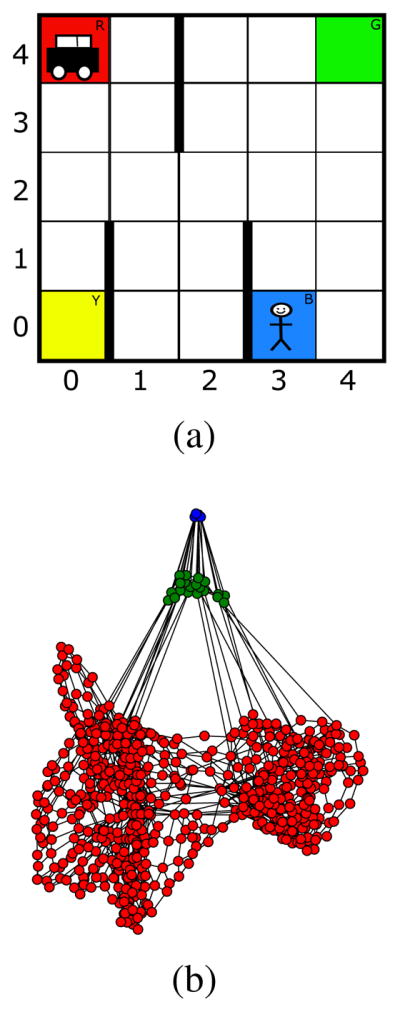
The Taxi Domain (a), and its induced 3-level hierarchy. The base MDP contains 650 states (shown in red), which is abstracted to an MDP with 20 states (green) after the first level of options, and one with 4 states (blue) after the second. At the base level, the agent makes decisions about moving the taxi one step at a time; at the second level, about moving the taxi between depots; at the third, about moving the passenger between depots.

We now describe the construction of a hierarchy for the taxi domain using hand-designed options at each level, and present some results for planning using Algorithm 1 for three example plan queries.

Constructing M₁

In this version of taxi, the agent is able to move the taxi to, and drop the passenger at, any square, but it expects to face a distribution of problems generated by placing the taxi and the passenger at a depot at random, and selecting a random target depot at which the passenger must be deposited. Consequently, we create navigation options for driving the taxi to each depot, and retain the existing put-down and pick-up options.⁴ These options over M₀ form the action set for level 1 of the hierarchy: A₁ = {drive-to-red, drive-to-green, drive-to-blue, drive-to-yellow, pick-up, put-down}.

Consider the drive-to-blue-depot option. It is executable in all states (i.e., its initiation set is S₀), and terminates with the taxi’s x and y position set to the position of the blue depot; if the passenger is in the taxi, their location is also set to that of the blue depot; otherwise, their location (and the fact that they are not in the taxi) remains unchanged. It can therefore be partitioned into two abstract subgoal options: one, when the passenger is in the taxi, sets the x and y positions of the taxi and passenger to those of the blue depot; another, when the passenger is not in the taxi, sets the taxi x and y coordinates and leaves those of the passenger unchanged. Both leave the in-taxi state variable unmodified. Similarly, the put-down and pick-up options are executable everywhere and when the taxi and passenger are in the same square, respectively, and modify the in-taxi variable while leaving the remaining variables the same. Partitioning all options in A₁ into abstract subgoal options results in a factored state space consisting of 20 reachable states where the taxi or passenger are at the depot locations (4 × 4 states for when the passenger is not in the taxi, plus 4 for when they are).

Constructing M₂

Given M₁, we now build the second level of the hierarchy by constructing options that pick up the passenger (wherever they are), move them to each of the four depots, and drop them off. These options become A₂ = {passenger-to-blue, passenger-to-red, passenger-to-green, passenger-to-yellow}. Each option is executable whenever the passenger is not already at the relevant depot, and it leaves the passenger and taxi at the depot, with the passenger outside the taxi. Since these are subgoal (as opposed to abstract subgoal) options, the resulting MDP, M₁, consists of only 4 states (one for each location of the passenger) and is a simple (and coincidentally fully connected) graph. The resulting hierarchy is depicted in Figure 3b.

We used the above hierarchy to compute plans for three example queries, using dynamic programming and decision trees for planning and grounding classifiers, respectively. The results are given in Table 1; we next present each query, and step through the matching process in detail.

Table 1.

Timing results for three example queries in the Taxi domain. The final three columns compare the total time for planning using the hierarchy, by planning in the SMDP obtained by adding all options into the base MDP (i.e., using options but not changing the representation), and by flat planning in the base MDP. All times are in milliseconds and are averaged over 100 samples, obtained using a Java implementation run on a Macbook Air with a 1.4 GHz Intel Core i5 and 8GB of RAM.

Query	Level	Hierarchical Planning			Base + Options	Base MDP
		Matching	Planning	Total
1	2	<1	<1	<1	770.42	1423.36
2	1	<1	10.55	11.1	1010.85	1767.45
3	0	12.36	1330.38	1342.74	1174.35	1314.94

Example Query 1

Query Q₁ has the passenger start at the blue depot (with the taxi at an unknown depot) and request to be moved to the red depot. In this case B₁ refers to all states where the passenger is at the blue depot and the taxi is located at one of four depots, and G₁ similarly refers to the red depot. The agent must first determine the appropriate level to plan at, starting from M₂, the highest level of the hierarchy. It finds state s_b where 𝒢₀(s_b) = B₁ (and therefore B₁ ⊆ 𝒢₀(s_b) holds), and s_r where 𝒢₀(s_r) = G₁ (and therefore 𝒢₀(s_r) ⊆ G₁), where s_b and s_r are the states in M₂ referring to the passenger being located at the blue and red depots, respectively. Planning therefore consists of finding a plan from s_b to s_r at level M₂; this is virtually trivial (there are only four states in M₂ and the state space is fully connected).

Example Query 2

Query Q₂ has the start state set as before, but now specifies a goal depot (the yellow depot) for the taxi. B₂ refers to all states where the passenger is at the blue depot and the taxi is at an unknown depot, but G₂ refers to a single state. M₂ contains a state that has the same grounding set as B₂, but no state inM₂ is a subset of G₂ because no state in M₂ specifies the location of the taxi. The agent therefore cannot find a planmatch for Q₂ at level M₂.

At M₁ no single state is a superset of B₂, but the agent finds a collection of states s_j, such that 𝒢₀(∪_js_j) = B₂. It also finds a single state with the same grounding as G₂. Therefore, it builds a plan at level M₁ for each state in s_j.

Example Query 3

In query Q₃, the taxi begins at the red depot and the passenger at the blue depot, and its goal is to leave the passenger at grid location (1, 4), with the taxi goal location left unspecified. The start set, B₃, refers to a single state, and the goal set, G₃, refers to the set of states where the passenger is located at (1, 4).

Again the agent starts at M₂. B₃ is a subset of the grounding of the single state in M₂ where the passenger is at the blue depot but the taxi is at an unknown depot. However, G₃ is not a superset of any of the states in M₂, since none contain any state where the passenger is not at a depot. Therefore the agent cannot plan for Q₃ at level M₂.

At level M₁, it again find a state that is a superset of B₃, but no state that is a subset of G₃—all states in M₁ now additionally specify the position of the taxi and passenger, but like the states in M₂ they all fix the location of the passenger at a depot. All state groundings are in fact disjoint from the grounding of G₃. The agent must therefore resort to planning in M₀, and the hierarchy does not help (indeed, it results in a performance penalty due to the compute time required to rule out M₁ and M₂).

7 Summary

We have introduced a framework for building abstraction hierarchies by alternating skill- and representation-acquisition phases. The framework is completely automatic except for the choice of skill acquisition algorithm, to which our formulation is agnostic but upon which the usefulness of the hierarchy entirely depends. The resulting hierarchies combine temporal and state abstraction to realize efficient planning and learning in the multi-task setting.