Weighted Genome Trees: Refinements and Applications

Abstract

There are many ways to group completed genome sequences in hierarchical patterns (trees) reflecting relationships between their genes. Such groupings help us organize biological information and bear crucially on underlying processes of genome and organismal evolution. Genome trees make use of all comparable genes but can variously weight the contributions of these genes according to similarity, congruent patterns of similarity, or prevalence among genomes. Here we explore such possible weighting strategies, in an analysis of 142 prokaryotic and 5 eukaryotic genomes. We demonstrate that alternate weighting strategies have different advantages, and we propose that each may have its specific uses in systematic or evolutionary biology. Comparisons of results obtained with different methods can provide further clues to major events and processes in genome evolution.

Although the number of sequenced microbial genomes has increased tremendously in recent years, inferring the phylogeny of microorganisms from the sequences of their genes remains an elusive goal. No single phylogenetic model can perfectly accommodate variations in rates of evolution across genes, between genes, or among lineages or can make up for the lack of phylogenetic signal at depth (15, 33). Even with perfect models and strong signals, we can be misled by mistaking paralogs for orthologs. Most seriously, different genes in the same genome can have different true phylogenies, because of lateral (horizontal) gene transfer (LGT); indeed, most genomes show many genes that have been introduced by LGT. Thus, strictly speaking, the relationships between genomes cannot truthfully be represented by a unique tree (10). A web-like pattern would be a more accurate representation.

Nevertheless, there are good reasons to want to represent the relationships between the organisms harboring those genomes as if they comprise a single bifurcating branching pattern (tree), and thus there is good justification for exploring and comparing methods which reduce the web-like pattern of genomic relationships to single trees. Some such reductions will be less arbitrary than others, and different methods may find different uses.

Concerns about LGT and the weakness of phylogenetic signal in individual genes have increasingly led to the combined use of many, or as many as possible, of a genome's genes for tree construction (multigene or genome trees). Several distinct methods have been described. These include (i) phylogenetic reconstructions using concatenated gene sets, comprising all genes shared by the genomes to be related, or the subsets of those genes involved in transcription and/or translation (3, 17, 24); (ii) supertree methods, which assemble subtrees that may themselves be based on different genes (9); and (iii) distance-based methods using the number of apparently orthologous genes shared by pairs of genomes or some collective measure of the similarity between such genes (6, 8, 32, 37). Although often these methods are introduced with the aim of minimizing or canceling out the effect of LGT, which is regarded as “noise,” gene content methods can actually maximize its influence, while robust supertrees can be expected even if all genes providing strong signals have experienced recent transfer. Analyses which focus only on a core of shared genes (see, e.g., reference 21) probably do target genes least likely to have been recently transferred, but even here, orthologous replacement may have occurred, and phylogenetic signals are often too weak to rule this out.

These concerns aside, trees prepared by these different multigene and whole-genome methods often do agree with each other and with trees based on popular single-gene data sets, such as that for small-subunit rRNA (SSU rRNA). (Agreement in this context usually means recreation of the Bacteria-Archaea divide and support for many of the bacterial phyla first defined by SSU rRNA, but not necessarily consistency in the branching order of phyla or the placement of all individual species within them.) Some argue that the observed agreement means that there indeed is a core of nontransferred or rarely transferred shared genes which, collectively, have adequate phylogenetic signal (9, 21). Others, who believe transfer to be pervasive and ubiquitous, point out that consistency between various sorts of trees might be expected, even if no genes have escaped transfer in the long term (14, 26). Furthermore, they note that plausible constraints on transfer, making it more frequent between organisms with more similar biology, genome content, and gene sequences, could reinforce and even create the patterns of consistency observed among trees (14). Whatever the mapping of multigene and whole-genome trees to any underlying organismal “tree of life,” they usefully distill much information about the sum of genes and the influences which define organisms and their relationships today.

A range of methods for reconstructing whole-genome trees, in particular methods which can reduce or enhance the contribution to the trees' topologies of genes that have been more or less frequently transferred and are more or less commonly found in genomes, would be valuable. We could then start to evaluate the relative roles of transfer and vertical descent in the making up of individual genomes and the degree to which genes in a genome can be seen as comprising classes or compartments (such as “variable shell” [22] and “soft core” and “hard core” [27]) of different intrinsic transferabilities. In the long run, it is likely that no single method will be best for untangling all the complexities of genomic history but that different methods will have different strengths.

One of us (R.L.C.) has developed methods for constructing distance trees from comparisons of average BLAST scores of genes shared between genome pairs (8). Acknowledging that some genes will show conflicting patterns of relationship, Charlebois et al. (7) identified “phylogenetically discordant sequences” (PDS) and eliminated them from these analyses. In general, such trees agree with other genome trees and with common versions of the SSU rRNA tree and show good stability; we see little change in overall topology as new genomes are added (R. L. Charlebois, unpublished data). Because individual BLAST scores are poor measures of evolutionary distance, these methods must owe this agreement and stability to the very large amount of sequence information they bring to bear. Nevertheless, BLAST scores are nonlinear measures of evolutionary distance, and simple averaging of such scores is unlikely to be the best way to extract the information they do contain; some further correction through differential weighting seems appropriate. We must also be aware of, and if possible correct for, artifacts introduced by nonorthologous matches (where orthologs were reciprocally lost, leaving paralogs to become reciprocal best matches [RBMs]) and by matches between single- and multidomain proteins. In our averaging scheme, such uncommon artifacts contribute only a small error to an intergenomic evolutionary distance, but where phylogenetic resolution is already poor, they may suggest erroneous relationships.

Here we report several additional refinements of these methods, which should enhance the utility of whole-genome trees. Each may have specific uses in systematic or evolutionary biology, while comparisons of results obtained with different methods can provide clues to major events and processes in genome evolution, pointing to further hypotheses that can be tested by new bioinformatic analyses and genetic experimentation.

MATERIALS AND METHODS

Measuring the phylogenetic concordance of an ORF.

In a previous publication, one of us (R.L.C.) described a statistic for computing phylogenetic discordance (8). In brief, each open reading frame (ORF) has a distribution of reciprocally best-matching scores with a subset of the available genomes. Each genome, similarly, has a distribution of median scores for all of its genes compared with their counterparts in each other's genomes. We perform ranked correlations of randomizations of these two distributions in order to compute a statistic that estimates the discordance (correlations with P values near zero) or concordance (correlations with P values near 1) of each gene in the context of its bulk genomic phylogenetic signal.

Measuring the prevalence of an ORF by using the consensus gene name. (i) Establishing orthology.

Ideally, one wishes to measure a gene's prevalence by counting the proportion of genomes in which an ortholog of that gene is present. Orthology is difficult to determine in bulk, and we use the RBM as a surrogate. Here, any ORF's best match must have the same ORF as its own best match, using a comparison tool such as BLASTP (1). BLASTP scores are only approximations to evolutionary distances, so we extend the definition of RBM to allow for near ties in BLASTP scores, such that an ORF's best match or anything 95% as good, which has the former ORF as its best match or 95% as good, is still considered a reciprocal best match. (If several satisfy the criteria, the best of these is the RBM.) Distantly related orthologs may perhaps not be recognized by such methods, owing to a BLASTP similarity score falling below any arbitrary threshold. Such disconnected sets might be united by bridging with homologs that match, as the RBM, members of both parts.

(ii) Consensus gene name.

We implemented an extra layer of orthology detection by considering the information found in genomic annotations. Although there is variation in the names assigned to genes by annotators, many of the genes in most genomes are annotated consistently. Annotated names alone cannot be trusted in computing an ORF's prevalence, given the variable conventions used, but a consensus gene name (the most common annotated name from among an ORF's set of reciprocal best matches) should add some reliability to assessments of orthology. In a sense, we are computing something analogous to the “clusters of orthologous groups” (35), perhaps more crudely but with greater facility. We calculated that on average, in RBM sets where a gene is shared by 90% of the genomes, over 95% of the ORFs have the same consensus gene name; in sets where a gene is shared by 50% of genomes, this number drops to 81%, and in sets of relatively rarely occurring genes, present in 10% of the genomes, the value drops to 43%.

An ORF's prevalence, therefore, is the proportion of genomes that possess an ORF with that same consensus gene name. Prevalence affects the contribution of each individual gene to the overall phylogeny but does not interfere with the BLASTP scores themselves (Hypothetical proteins annotated with unique or anonymous gene names, and thus displaying uncertain functional orthology, will necessarily have a reduced impact on a prevalence-weighted phylogeny.)

Weighting matrices based on prevalence and concordance.

A genomic distance can be computed from the mean normalized BLASTP score of all genes shared (by reciprocal best match) between two genomes. Matrices of such distances have been used in constructing genomic phylogenies, based on an equal weighting of each contributing gene, or by first excluding phylogenetically discordant sequences (6, 8) at some alpha threshold. Bootstrapping is accomplished by resampling, with replacement, from the set of genes shared by a pair of genomes. This is not directly comparable to the more usual bootstrapping in which positions within aligned sequences are resampled, but it is the only method applicable to our analysis.

Here, we took measures to construct genomic phylogenies both correctly and altogether wrongly in order to see how the trees' topology might change. We constructed the following six trees with the 147 genomes currently available to us within our genomic analysis system, NGIBWS (7).

(i) Unweighted tree.

The reference tree is based on a distance matrix with equal weighting of all genes. All reciprocally best-matching sequences are used.

(ii) Filtered tree.

Sequences exhibiting phylogenetic discordance above a threshold value are excluded. All included genes are weighted equally. Specifically, the filtered tree used excludes from consideration genes which are phylogenetically discordant, at alpha threshold of <0.05 (8).

(iii) Concordance-weighted tree.

Each gene is weighted in relation to its degree of concordance with other genes in its genome. This tree is weighted in favor of phylogenetically concordant genes by using mean normalized BLASTP scores that are computed from the sum of the product of (1) each gene pair's normalized BLASTP score and (ii) the mean phylogenetic concordance of the pair of genes. (For normalization purposes, the mean's denominator is the sum of the mean phylogenetic concordance of the pair of genes; the same applies for the next three trees described below.)

(iv) Discordance-weighted tree.

Each gene is weighted in relation to its discordance with other genes in its genome (discordance + concordance = 1.0). This tree is weighted in favor of phylogenetically discordant genes by using mean normalized BLASTP scores that are computed from the sum of the product of (i) each gene pair's normalized BLASTP score and (ii) the mean phylogenetic discordance of the pair of genes.

(v) Prevalence-weighted tree.

Each gene is weighted in relation to its representation among genomes. This tree is weighted in favor of prevalent genes by using mean normalized BLASTP scores that are computed from the sum of the product of (i) each gene pair's normalized BLASTP score and (ii) the proportion of genomes that possess a gene with that consensus gene name.

(vi) Rarity-weighted tree.

Each gene is weighted in relation to its rarity among genomes (prevalence + rarity = 1.0). This tree is weighted in favor of rare genes, using mean normalized BLASTP scores that are computed from the sum of the product of (i) each gene pair's normalized BLASTP score and (ii) the proportion of genomes that do not possess a gene with that consensus gene name.

Tree reconstruction.

Trees were generated from all of the distance matrices obtained by using the Fitch-Margoliash (least-squares) method (12) as modified and implemented in the PHYLIP package as FITCH (11). This method has been shown in simulation studies to be more accurate than neighbor joining, the alternative distance-based method (20), and less sensitive to long-branch artifacts (4).

Competitive matching.

In order to examine the possibility of a major gene flux between genomes through LGT, we used the competitive matching analysis available in NGIBWS (7), a method which returns a genome's ORFs that match an ORF from a member of one group of genomes better than they match any ORF from any member of a second group of genomes. In this study we used an inclusion cutoff e value of 10⁻⁵ and a minimum difference in normalized BLASTP scores of 0.05.

RESULTS AND DISCUSSION

We constructed Fitch-Margoliash (least-squares) trees (Fig. 1 to 6) based on ORFs with reciprocally best-matching BLAST scores (6) from a database containing 147 genomes (126 Bacteria, 16 Archaea, and 5 Eukarya). The trees, the construction of which is described in detail in Materials and Methods, were of six types: unweighted, filtered, concordance weighted, discordance weighted, prevalence weighted, and rarity weighted.

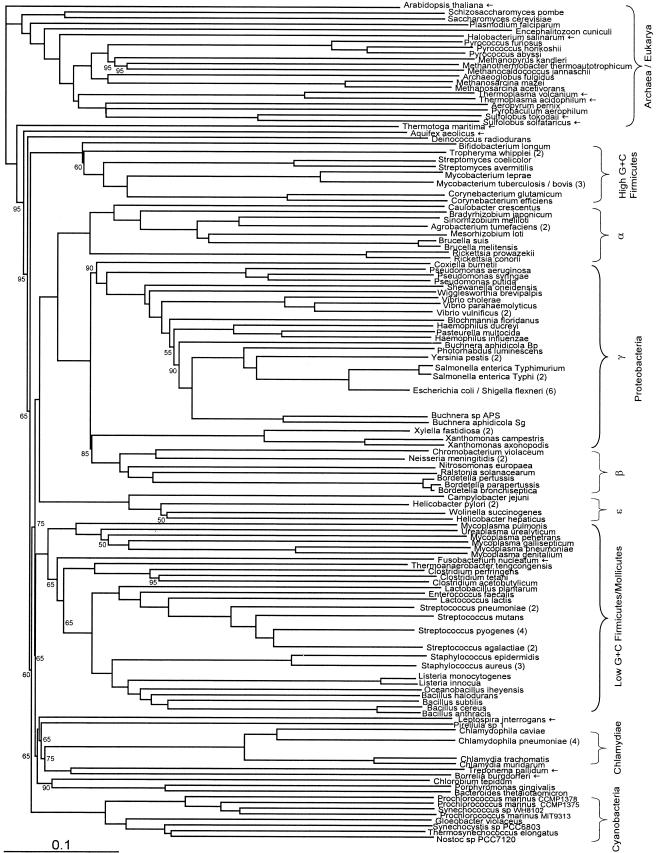
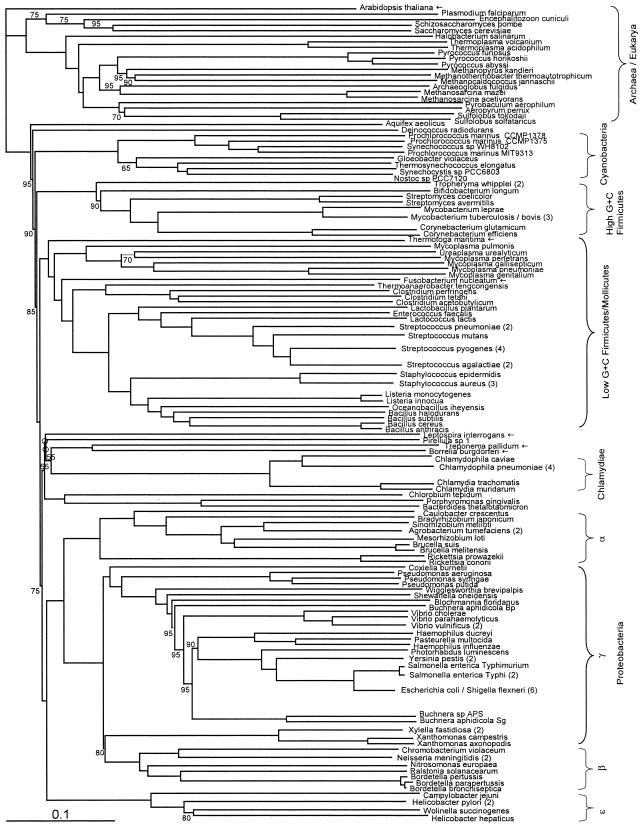
FIG.1.

Fitch-Margoliash tree based on conceptually translated complete genomic ORF sets, with equal weighting of all genes shared between a pair of genomes (see text for details). Bootstrap support (percentage of 20 replicates) was determined in a separate analysis by strict consensus. Where support is not shown, it is 100%. Where a node is marked with an empty circle, support is less than 50%. Taxa of particular interest are marked with an arrow. Whenever different strains of a single species form a single clade, they have been united to a single branch and the number of strains is given in parentheses as follows: Tropheryma whipplei includes T. whipplei Twist and TW0827; Mycobacterium tuberculosis/bovis includes M. bovis, M. tuberculosis H37Rv, and M. tuberculosis CDC1551; Agrobacterium tumefaciens includes A. tumefaciens C58 from both the Cereon and Dupont genomes; Vibrio vulnificus includes V. vulnificus strains CMCP6 and YJ016; Salmonella enterica Typhi includes S. enterica serovar Typhi strains CT18 and Ty2; Escherichia coli/Shigella flexneri includes E. coli strains O157:H7 EDL933, O157:H7, CFT073, and K-12 and S. flexneri strains 2a 2457T and 2a 301; Xylella fastidiosa includes X. fastidiosa strains 9a5c and Temecula1; Neisseria meningitidis includes strains MC58 and Z2491; Helicobacter pylori includes strains 26695 and J99; Streptococcus pneumoniae includes strains R6 and TIGR4; Streptococcus pyogenes includes strains MGAS315, SSI1, SF370, and MGAS8232; Streptococcus agalactiae includes strains 2603VR and NEM316; Staphylococcus aureus includes strains N315, Mu50, and MW2; and Chlamydophila pneumoniae includes strains AR39, TW183, J138, and CWL029. Branch end points for these species correspond to the former root of the clade of strains. For the full trees, which include all strains, see the supplemental material.

FIG. 6.

Fitch-Margoliash tree, as in Fig. 1, but with preferential weighting of genes in the distance matrix according to their rarity within the set of 147 genomes.

The default or unweighted tree (Fig. 1) is broadly similar to other proposed organismal trees, such as bacterial trees based on SSU rRNA or concatenated sequences of proteins involved in translation (3) and archaeal phylogenies based on concatenated sequences of ribosomal proteins or large- and small-subunit rRNA (24). Most nodes in this tree (and in the other trees presented here) are supported by bootstrap values of 100%; lower values are explicitly indicated. These bootstrap values are based on resampling of the genes used in pairwise comparisons (see Materials and Methods). Many familiar taxonomic groups appear as strongly supported monophyletic clades, such as cyanobacteria, high-G+C firmicutes, low-G+C firmicutes, chlamydiae, and alpha, beta, and epsilon proteobacteria (beta being embedded within the gamma subdivision of proteobacteria). However, some major differences can be observed between our analysis and those based on concatenated translational proteins or rRNA. (i) In the Archaea, Halobacterium does not cluster with Methanosarcina among the Euryarchaeota but branches outside Archaea. (ii) Both Thermoplasma species cluster with Crenarchaeota instead of Euryarchaeota. (iii) Clustering of Methanothermobacter and Methanocaldococcus as sister groups is now well supported (24). (iv) In the Bacteria, Spirochaetes (Borrelia, Treponema, and Leptospira) are not monophyletic (Fig. 1). Unlike the monophyletic prokaryotic domains, eukaryotes do not form a single clade in this tree. In the distance matrix Arabidopsis is closer to cyanobacteria than to the other eukaryotes, reflecting numerous chloroplast genes which have had less time to diverge than those sequences shared by all eukaryotes. In fact, on average Arabidopsis is slightly closer to prokaryotes than to eukaryotes (0.730 versus 0.732, respectively). However, removal of Arabidopsis does not restore the other eukaryotes to monophyly, even though they are each others' closest relatives in the distance matrix. This may be because eukaryotes are not equally distant from all prokaryotic phyla, perhaps due to the relative abundance of eukaryotic fusion proteins, whose multiple domains may have best matches in different prokaryotic phyla, leading to a score which artificially averages two conflicting phylogenetic signals into a false distance.

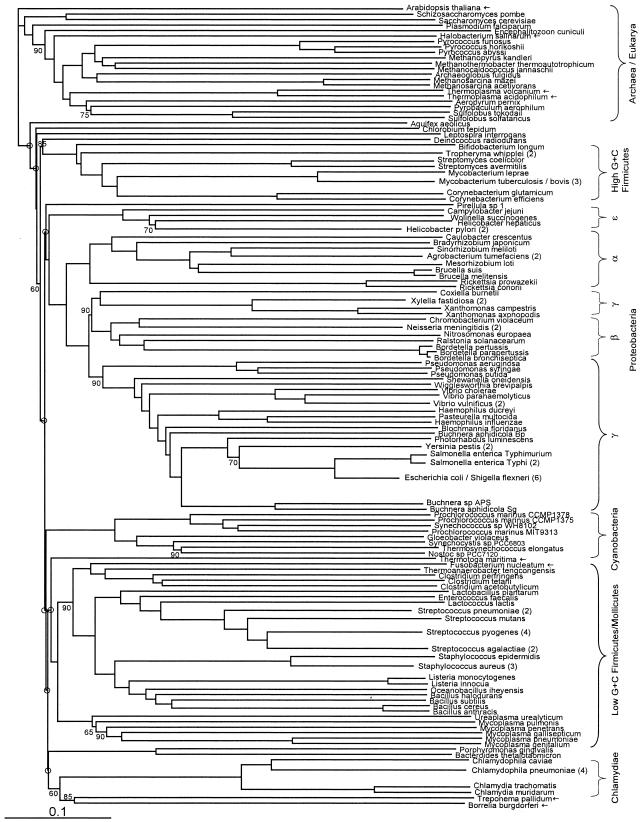
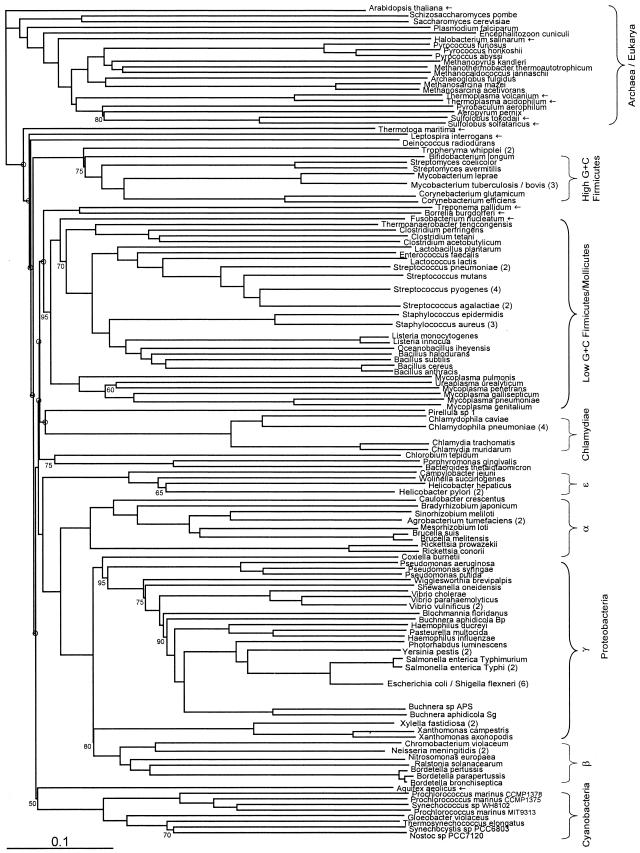
We reasoned that filtered, concordance-weighted, and prevalence-weighted trees, by minimizing effects of noise and conflicting signal and focusing on more widely shared genes, might produce trees that are in general more stable (to added taxa) and more congruent with traditional classification schemes than unweighted trees. These modified trees (Fig. 2, 3, and 5) are broadly similar to the default tree, and some of the ways in which they are different from the unweighted tree (Fig. 1) are indeed more in line with traditional classifications. In the concordance-weighted tree (Fig. 3), but not the filtered tree (Fig. 2), Spirochaetes do form one clade, although with weak (50%) statistical support. In the epsilon proteobacteria, there is better support for the clade of Helicobacter species in the filtered tree (65%) and the concordance-weighted tree (90%) than in the unweighted tree (50%). In the prevalence-weighted tree, however, Helicobacter hepaticus clusters with Wolinella and not with Helicobacter pylori. Furthermore, in the concordance-weighted tree there is some support (70%) for a higher-order grouping including Spirochaetes and Chlamydiales that was observed previously in at least two independent concatenated-protein studies (3, 37). From our analysis, this clade would also include the more recently sequenced planctomycete Pirellula.

FIG. 2.

Fitch-Margoliash tree, as in Fig. 1, but excluding genes deemed phylogenetically discordant (8), at an alpha threshold of 5%.

FIG. 3.

Fitch-Margoliash tree, as in Fig. 1, but with preferential weighting of genes in the distance matrix according to their phylogenetic concordance (8) relative to the bulk of genes in the genome.

FIG. 5.

Fitch-Margoliash tree, as in Fig. 1, but with preferential weighting of genes in the distance matrix according to their prevalence within the set of 147 genomes.

For Archaea, an interesting difference between unweighted, filtered, concordance-weighted, and prevalence-weighted trees is the location of Thermoplasma species. These are found within the Crenarchaeota clade with 100% support in both the unweighted and filtered trees, but the support drops to 65% in the concordance-weighted tree. In the prevalence-weighted tree they branch more basally, after Halobacterium. This difference probably reflects the fact that over 16% of Thermoplasma acidophilum ORFs are closely related to ORFs in the crenarchaeote Sulfolobus (29), especially those encoding proteins involved in metabolism. We surveyed both Thermoplasma species for ORFs suspected to have been acquired by LGT, using the competitive matching analysis available from NGIBWS (7). This analysis provides a list of all ORFs that have a better match (normalized BLASTP score, given a user-defined threshold) in one or more genomes than they do in another set of genomes (see Materials and Methods). In T. acidophilum, 213 ORFs had a better match in Sulfolobus species than in any non-Thermoplasma euryarchaeote, and 87 ORFs had no significant match in Euryarchaeota but had matches in Sulfolobus. (In Thermoplasma volcanium the corresponding ORF counts were 201 and 84, respectively.) Since (as we observe) many metabolic proteins are restricted to only a few Archaea, the prevalence-weighted tree rejects the association of Thermoplasma with Crenarchaeota, and since metabolic proteins may be more susceptible to LGT (28), the concordance-weighted tree only weakly supports it.

Halobacterium occupies an unexpected position in all trees. Although there are unquestionably bacterial genes introduced into this genome by LGT (19), it has also been demonstrated that haloarchaeal protein sequences are highly divergent from sequences of nonhalophiles, as a result of amino acid composition biases (13). Since haloarchaea branch deeply even in our prevalence-weighted tree, we believe the latter to be the dominant effect. Unfortunately, there is as yet no effective approach for correcting for amino acid bias in sequence alignment or comparison (30, 31), and this problem is restricted neither only to Halobacterium nor only to our type of phylogenetic analysis.

Generally speaking, filtering or concordance weighting appears to be more productive than restricting the analysis to prevalent genes, in terms of improving bootstrap values or consistency with other classifications. This, in our opinion, is further evidence that gene content may be misleading in inferring phylogenies and that by no means do genes that are taxonomically abundant show a lesser degree of lateral gene transfer or gene loss. Although the concordance-weighted tree does not differ significantly from the PDS-filtered tree in terms of increased bootstrap values, it does reunite a few groups for which there is good corroborative support. Furthermore, a concordance-weighted tree has the inherent advantage of not relying on an arbitrary threshold, which may turn out to be either too high or too low. Future analyses could create even more refined (though perhaps more computationally intensive) weighting algorithms.

The lack of eukaryotic monophyly noted in the unweighted tree was also observed in the concordance-weighted and prevalence-weighted trees, despite the fact that Arabidopsis moved closer to eukaryotes in the distance matrix. The average distances between Arabidopsis and either eukaryotes or prokaryotes were 0.695 versus 0.718 in the concordance-weighted matrix and 0.683 versus 0.706 in the prevalence-weighted matrix, respectively. Removal of Arabidopsis restored the other eukaryotes to monophyly in the prevalence-weighted tree but not in the concordance-weighted tree. The relative success of the prevalence-weighted tree in this instance may be attributed to the fact that by weighting in favor of highly prevalent genes with assigned function in a predominantly prokaryotic data set, the impact of misleading BLAST scores with eukaryotic multidomain proteins is reduced (see above). We expect that explicitly omitting such multidomain proteins from the computation of genomic distances would be effective in further correcting the placement of eukaryotic taxa in our trees. This can be accomplished by identifying ORFs where different parts of the protein have different best matches.

A few of the differences between unweighted, filtered, and concordance- or prevalence-weighted trees were surprising and may point to important biological patterns. In the prevalence-weighted (Fig. 5) and concordance-weighted (Fig. 3) trees, Thermotoga clusters significantly with low-G+C firmicutes, an unexpected observation since Thermotoga is usually found on a basal branch of the bacterial tree (Fig. 1) or branches with Aquifex as a sole sister group (3, 37). The location of Thermotoga within or at the base of low-G+C firmicutes has, however, been suggested several times before, on a variety of grounds (5, 16), and it is well established that the Thermotoga maritima genome is heavily influenced by gene acquisition through LGT from Archaea (25). The topology depicted by the filtered and concordance-weighted trees may be more accurate, in terms of the history of the bulk of Thermotoga's genome, than that of the unweighted tree.

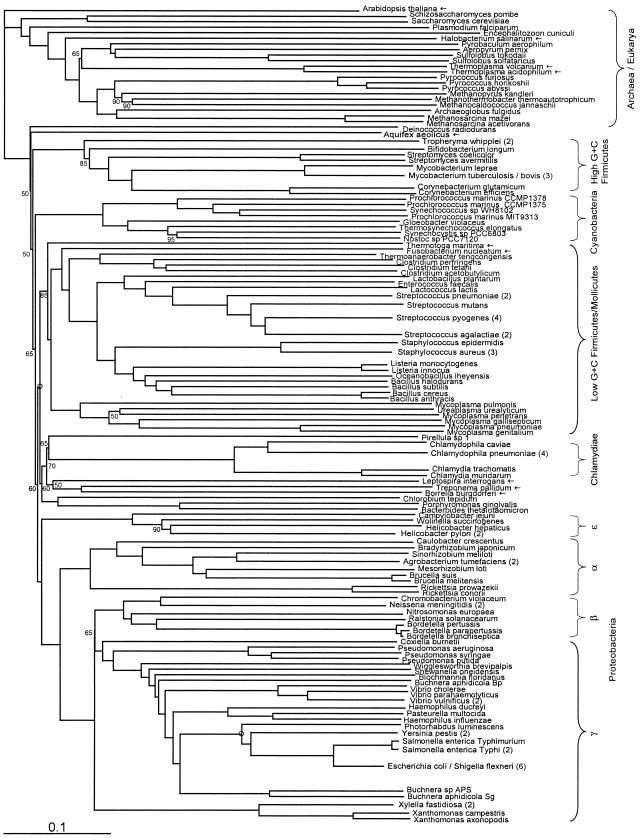
We also constructed two “counterintuitive,” or reverse-weighted, trees, one weighted in favor of phylogenetically discordant sequences (discordance weighted) (Fig. 4) and one favoring rare genes (rarity weighted) (Fig. 6). We see that in the discordance-weighted tree Arabidopsis branches with cyanobacteria, while Thermotoga branches with Pyrococcales, Aquifex is basal within the Archaea, and Chlamydiales, Treponema, and Borrelia cluster with nonphotosynthetic eukaryotes. These unusual clusterings no doubt hint at major evolutionary processes: the endosymbiotic incorporation of cyanobacteria by organisms which evolved to land plants, the high fraction of Thermotoga genes acquired from thermophilic Archaea (25), and quite possibly a similar effect in Aquifex (23). The robustness of the weighted trees, as reflected by bootstrap values and sister group relationships, is dependent on a balance between concordance and discordance, determined by the weighting parameter assigned to different genes (which equals 1 for the unweighted tree). The topology of several tree nodes is therefore determined by the weighting regimen, as can be observed by comparing unweighted, concordance-weighted, and discordance-weighted trees. Ideally one can strive to establish a weighting-correction function, which will come closest to the optimum in this concordance-discordance axis and thus generate the best trees.

FIG. 4.

Fitch-Margoliash tree, as in Fig. 1, but with preferential weighting of genes in the distance matrix according to their phylogenetic discordance (8) relative to the bulk of genes in the genome.

Another interesting case in which trees show conflicting topologies is that of Fusobacterium, a genus of phenotypically and morphologically gram-negative bacteria which more resemble low-G+C firmicutes in both SSU rRNA and protein sequences (6, 18). The discordance-weighted and rarity-weighted trees place Fusobacterium as the deepest branching member of the Clostridium-Thermoanaerobacter group, whereas the filtered, concordance-weighted, and prevalence-weighted trees place it as deep branching between mollicutes and other low-G+C firmicutes. However, in general, the rarity-weighted tree has few significant differences from the unweighted tree, indicating that the phylogenetic signal displayed by genes shared among few organisms is not necessarily weaker or more discordant than genes from the bulk of the genome.

We have as yet no explanation for the clustering of Chlamydiales and Treponema-Borrelia with nonphotosynthetic eukaryotes, which has moderate support (60%) in the discordance-weighted tree (Fig. 4). Some transfers from eukaryotic hosts to the genomes of these parasitic bacteria have been claimed (34, 36), but we think that such genes are too few to so disrupt overall relationships, and we expect that the fact that these bacterial groups have reduced genomes may be relevant in some way. The failure of nonphotosynthetic eukaryotes to group with alpha proteobacteria, even in discordance-weighted trees, is consistent with other reports that nuclear genes for mitochondrial function do not as a rule show alpha-proteobacterial affinities, the alpha-proteobacterial origins of the organelles notwithstanding (2). The unexpected clustering of mollicutes with high-G+C firmicutes and Deinococcus (Fig. 4) cannot be explained directly by LGT, since we could detect fewer than five suspected LGT events between mollicutes and either Deinococcus or high-G+C firmicutes by competitive matching. The branching of high-G+C firmicutes with Deinococcus is not surprising, as it has been observed before for the subset of proteins involved in translation (3) and explained by the compositional bias in amino acids which results from the high G+C content of those organisms.

Discordance- and rarity-weighted trees are both potentially valuable tools for indicating cases in which genes acquired by LGT originate primarily from one source, as expected for endosymbiosis or other relationships involving close and prolonged interaction between recipient and donor. The extent to which discordance- and rarity-weighted trees show topologies similar to each other and to unweighted or concordance-weighted trees will be a measure of the extent to which constraints on LGT, by favoring within-group transfer, serve to maintain or even create apparent phylogenetic patterns. We find it remarkable, in this connection, that the discordance- and rarity-weighted trees, which should dramatically exaggerate the effects of LGT, nevertheless show as many similarities to filtered, concordance-weighted, or prevalence-weighted trees as they do. Preferential within-group LGT indeed seems the best explanation (14).

None of the trees presented here can be a complete or completely accurate representation of the histories of genomes, because any such representation must be reticulated, not exclusively a pattern of successive bifurcations. However, some must be less inaccurate than others in this regard, and some will be more useful for one or another purpose. As a basis for classification, stability to the addition of new genomes will be an important feature. The unweighted trees produced over the last few years by Charlebois and collaborators have changed relatively little with the growth of the genomic database (7, 8). We suspect, and will systematically confirm as more genome sequences appear, that concordance-weighted trees will be the most stable in this regard.

The concordance- and prevalence-weighted trees, and particularly the similarities between them, speak to the coherence and size of any LGT-resistant (or restricted) “core” of genes (27), while discordance- and rarity-weighted trees focus on more unstable genomic components. Differences between trees will generate hypotheses about the histories of individual genomes. Tests and interpretations will be complex, but genome history is itself complex, and the central but most difficult task of comparative genomics is to unravel it. Multiple methods for analyzing data will be required, and it is through the comparison of results obtained by different methods that fruitful insights will most frequently emerge. Stable trees are also needed as the basis of stable taxonomies. We suggest that the methods presented here will more reliably play that role than any other single- or multigene methods currently in use. Whole-genome methods seem in general to be preferred for establishing relationships between existing organisms, because they embrace as much as possible of the underlying genotypes. Weighted methods, such as those we describe here, offer further refinement and stability.