Parallel Transmission RF Pulse Design with Strict Temperature Constraints

Abstract

RF safety in parallel transmission (pTx) is generally ensured by imposing specific absorption rate (SAR) limits during pTx radiofrequency (RF) pulse design. There is increasing interest in using temperature to ensure safety in MRI. In this work, we present local temperature correlation matrix formalism and apply it to impose strict constraints on maximum absolute temperature in pTx RF pulse design for head and hip region. Electromagnetic field simulations were performed on head and hip of the virtual body models. Temperature correlation matrices were calculated for four different exposure durations ranging between 6 and 24 minutes using simulated fields and body-specific constants. Parallel transmission RF pulses were designed using either SAR or temperature constraints and compared to each other and unconstrained RF pulse design in terms of excitation fidelity and safety. The use of temperature correlation matrices resulted in better excitation fidelity compared to the use of SAR in parallel transmission RF pulse design (for the 6-minute exposure period, 8.8% vs 21.0% for the head and 28.0% vs 32.2% for the hip region). As RF exposure duration increases (from 6 mins to 24 mins), the benefit of using temperature correlation matrices on RF pulse design diminishes. However, safety of the subject is always guaranteed (the maximum temperature was equal to 39°C). This trend was observed in both head and hip regions, where the perfusion rates are very different.

Introduction

Radiofrequency (RF) fields are used in MRI to excite nuclei to a state where they can produce a detectable signal. The interaction between RF electromagnetic fields and conducting body tissues generates electrical currents which cause tissue heating. Heat absorbed by biological tissues can lead to significant changes in the underlying temperature distribution^1-8. For this reason, in applications involving RF exposure, it becomes crucial to predict temperature change in order to avoid unsafe temperatures that may cause tissue damage. The International Electrotechnical Commission (IEC) has provided guidelines to guarantee the safety of the patient during MRI ⁹. Limits are imposed primarily on the maximum temperature reached in the human body. Due to the complexity of measuring temperature in-situ, the maximum RF power absorbed per unit mass (Specific energy Absorption Rate; SAR) is used as a secondary surrogate metric for safety. Equivalent SAR is computed to comply with temperature recommendations of IEC using simple models. Typically, SAR, either averaged over a 10-gram tissue volume (10g SAR) or averaged over a whole exposure volume (global SAR), is the quantity most used to monitor safety, even though temperature has a more direct relationship to tissue damage and accepted as a safety metric internationally ⁹.

Several RF pulse design strategies ^10-14 have been proposed for incorporating 10g and/or global SAR into pulse design aiming to achieve safe operation of parallel transmit systems by controlling SAR while achieving design goals, such as inhomogeneity mitigation and SAR minimization. SAR-based safety control of multichannel transmit systems during RF pulse design has been made tractable by using Virtual Observation Points (VOPs) ¹⁵ in electromagnetic (EM) field simulations for reducing the number of monitored locations with predefined SAR overestimation. For transmit arrays, where the field distribution can change through time, utilizing VOPs dramatically speeds up optimization and design processes of RF pulses with SAR constraints ^12,14. In addition to the methods using VOP compression, another fast RF pulse design method ¹⁶ has become available to eliminate the need for SAR overestimation by using SAR at all voxels without compression aiming better SAR control during pulse design.

Temperature has attracted interest as a safety metric for parallel transmit pulse design instead of SAR. For example, one group suggested that it would be possible to find worst-case local temperature increase ¹⁷ with use of temperature matrices as developed for use in hyperthermia ^18-20 but did not implement their use for that purpose. Moreover, a parallel transmission RF pulse design approach has been proposed for a 3D time-of-flight sequence imposing strict temperature constraints by updating strict SAR constraints based on temperature simulations at each iteration ²¹. It was shown that the use of strict temperature constraints enabled the use of high-SAR RF pulses while keeping the local temperature within defined IEC safety limits via relaxing SAR limits. Recently, RF pulse design approaches aiming to overcome B₁⁺ inhomogeneity while explicitly constraining the temperature rise have been demonstrated using EM field simulations involving a head coil loaded with a human subject ^22-24 and local temperature correlation matrices ^18,20.

In this work, we present local temperature correlation matrix formalism for parallel transmission that is applied to identify the maximum temperature inside the subject due to RF exposure for a specific heating time. Local temperature correlation matrices are incorporated into RF pulse design aiming to satisfy limits on local maximum absolute temperature during pulse design. In previous work ^22-24, local temperature matrices were used to constrain only temperature increase. Our aim in this study is to use the maximum absolute temperature as a strict safety constraint in RF pulse design using local temperature correlation matrices. Fast parallel transmit RF pulse design is achieved by using the VOP approach to reduce the number of calculated local temperature correlation matrices from EM field simulations. In order to investigate the effect of perfusion characteristics of the region of interest on RF pulse design with strict maximum temperature constraints, simulations were performed on the head (with brain having relatively high perfusion rates) and the hip (containing only tissues with relatively low perfusion rates) using two different local multichannel transmit arrays. RF pulse designs for multiple RF exposure durations (ranges from 6 minutes to 24 minutes with 6 minute intervals) were performed in order to investigate the characteristics of using maximum temperature constraints rather than SAR constraints in different parts of the body. A preliminary description of this work was presented previously ^22,25.

Theory

Let us suppose we have a series of M RF pulses in one interval TR (Fig. 1), and for each of these pulses there is a combination of amplitudes and phases of the N channels of a transmit array. These M RF pulses can hypothetically have different durations and amplitudes within the same sequence with short TR. This combination associated with the m^th pulse is stored in the complex vector v_m = [v_1,m … v_N,m]^T. For each RF pulse and for each voxel of the inspected subject, r, it is possible to associate a local electric field correlation matrix Λ

Figure 1.

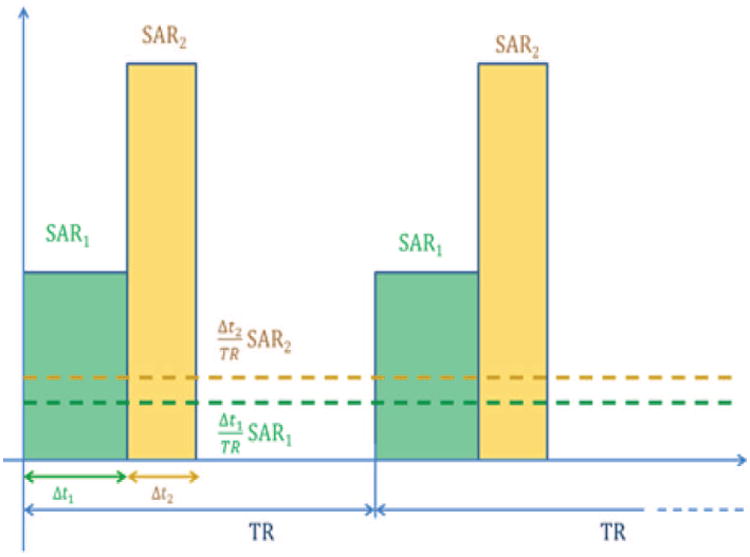
Schematic of two different hard RF pulses in the time interval TR (solid bars), and the relative levels associated with them averaged over each TR (dashed lines).

$$\mathbf{\Lambda }(\mathbf{r})=[\begin{array}{ccc}\frac{\sigma (\mathbf{r})}{\rho (\mathbf{r})}{\mathbf{E}}_1^{\ast }(\mathbf{r}){\mathbf{E}}_1(\mathbf{r})& \cdots & \frac{\sigma (\mathbf{r})}{\rho (\mathbf{r})}{\mathbf{E}}_N^{\ast }(\mathbf{r}){\mathbf{E}}_1(\mathbf{r})\\ ⋮& \ddots & ⋮\\ \frac{\sigma (\mathbf{r})}{\rho (\mathbf{r})}{\mathbf{E}}_1^{\ast }(\mathbf{r}){\mathbf{E}}_N(\mathbf{r})& \cdots & \frac{\sigma (\mathbf{r})}{\rho (\mathbf{r})}{\mathbf{E}}_N^{\ast }(\mathbf{r}){\mathbf{E}}_N(\mathbf{r})\end{array}$$ [1]

where σ is the electrical conductivity, ρ is the material density, and E_n is the electric field generated by the n^th channel when driven with unit voltage and * denotes complex conjugate transpose.

The definition of the matrix Λ allows the computation of the SAR as a result of m^th pulse in each location r by multiplying

$${\mathit{\text{SAR}}}_m(\mathbf{r})={\mathit{v}}_{\mathit{m}}^{\ast }\mathbf{\Lambda }(\mathbf{r}){\mathit{v}}_{\mathit{m}}=v_{1,m}^{\ast }{\mathrm{\Lambda }}_{11}(\mathbf{r})v_{1,m}+v_{1,m}^{\ast }{\mathrm{\Lambda }}_{12}(\mathbf{r})v_{2,m}+\cdots +v_{N,m}^{\ast }{\mathrm{\Lambda }}_{NN}(\mathbf{r})v_{N,m}$$ [2]

SAR absorption induces temperature increase inside the sample that can be computed with a well-known bioheat equation ²⁶

$$\rho (\mathbf{r})c(\mathbf{r})\frac{\partial T(\mathbf{r})}{\partial t}=\nabla \cdot (k\nabla T(\mathbf{r}))-W(\mathbf{r}){\rho }_{bl}{c}_{bl}(T(\mathbf{r})-T_{bl})+Q(\mathbf{r})+\rho (\mathbf{r})\mathit{\text{SAR}}(\mathbf{r})$$ [3]

where ρ is the material density, c is the heat capacity, k is the heat conductivity, W is a blood perfusion related parameter^27,28, Q is the heat generated by metabolism, the subscript bl indicates blood and T_bl is the blood temperature.

For short TR, the temperature increase depends mainly on the average value of SAR over the time interval TR ²⁹. Incorporating SAR associated with all M pulses using Eq. [2] in Eq. [3] yields:

$$\rho (\mathbf{r})c(\mathbf{r})\frac{\partial T(\mathbf{r})}{\partial t}=\nabla \cdot (k\nabla T(\mathbf{r}))-W(\mathbf{r}){\rho }_{bl}{c}_{bl}(T(\mathbf{r})-T_{bl})+Q(\mathbf{r})+\rho (\mathbf{r})(\frac{\mathrm{\Delta }{t}_1}{TR}{\mathit{\text{SAR}}}_1(\mathbf{r})+\frac{\mathrm{\Delta }{t}_2}{TR}{\mathit{\text{SAR}}}_2(\mathbf{r})+\dots +\frac{\mathrm{\Delta }{t}_M}{TR}{\mathit{\text{SAR}}}_M(\mathbf{r}))$$ [4]

where Δt_m is the pulse length defined on m^th hard RF subpulse. Since Eq. [4] is linear assuming (most importantly) that perfusion does not change with temperature, it is possible to focus on the contribution from each single generic pulse separately within short TR. Defining T₀ as the equilibrium temperature or the temperature distribution prior to RF excitation, and T_SARm as the temperature increase due to RF power absorption of the m^th pulse, the total temperature can be expressed as a linear combination of individual temperature increase contributions $T=T_0+{\sum }_{m=1}^M{T}_{\mathit{\text{SARm}}}$. Using the linearity of Eq. [4], it is possible to find independent relationships to determine T₀ and each T_SARm.

$$\rho (r)c(r)\frac{\partial T_0(r)}{\partial t}=\nabla \cdot (k\nabla T_0(r))-W(r){\rho }_{bl}{c}_{bl}(T_0(r)-T_{bl})+Q(r)$$ [5]

$$\rho (r)c(r)\frac{\partial T_{\mathit{\text{SARm}}}(r)}{\partial t}=\nabla \cdot (k\nabla T_{\mathit{\text{SARm}}}(r))-W(r){\rho }_{bl}{c}_{bl}{T}_{\mathit{\text{SARm}}}+\rho (r)\frac{\mathrm{\Delta }{t}_m}{TR}{\mathit{\text{SAR}}}_m(r)$$ [6]

Substituting Eq. [2] into Eq. [6] we find

$$\rho (r)c(r)\frac{\partial T_{\mathit{\text{SARm}}}(r)}{\partial t}=\nabla \cdot (k\nabla T_{\mathit{\text{SARm}}}(r))-W(r){\rho }_{bl}{c}_{bl}{T}_{\mathit{\text{SARm}}}+\rho (r)\frac{\mathrm{\Delta }{t}_m}{TR}{v}_{1,m}^{\ast }{\mathrm{\Lambda }}_{11}(r)v_{1,m}+\rho (r)\frac{\mathrm{\Delta }{t}_m}{TR}{v}_{1,m}^{\ast }{\mathrm{\Lambda }}_{12}(r)v_{2,m}+\cdots +\rho (r)\frac{\mathrm{\Delta }{t}_m}{TR}{v}_{N,m}^{\ast }{\mathrm{\Lambda }}_{NN}(r)v_{N,m}$$ [7]

For a given heating time t_end, and for the superposition of the effects in Eq. [3], it is possible to write

$$T_{\mathit{\text{SARm}}}(r)=\frac{\mathrm{\Delta }{t}_m}{TR}{v}_{1,m}^{\ast }{T}_{11}(r)v_{1,m}+\frac{\mathrm{\Delta }{t}_m}{TR}{v}_{1,m}^{\ast }{T}_{12}(r)v_{2,m}+\cdots +\frac{\mathrm{\Delta }{t}_m}{TR}{v}_{N,m}^{\ast }{T}_{NN}(r)v_{N,m}=\frac{\mathrm{\Delta }{t}_m}{TR}{\mathit{v}}_{\mathit{m}}^{\ast }{\mathbf{T}}_{\mathit{\text{increase}}}(r){\mathit{v}}_{\mathit{m}}$$ [8]

where each value T_ij(r) of the temperature correlation matrix, T_increase, is a solution of the equation

$$\rho (r)c(r)\frac{\partial T_{ij}(r)}{\partial t}=\nabla \cdot (k\nabla T_{ij}(r))-W(r){\rho }_{bl}{c}_{bl}{T}_{ij}+\rho (r){\mathrm{\Lambda }}_{ij}(r)$$ [9]

calculated numerically from t = 0 to t = t_end. Once all the values T_ij are computed with Eq. [9], the number of locations where the matrix T_increase is evaluated can be reduced with the use of the VOP compression used for the SAR ¹⁵. In fact, Eq. [2] and Eq. [8] reveal that T_increase has the same structure of the Λ matrix, in that they are both positive definite and Hermitian. The temperature increase T_inc from an applied RF pulse can be finally computed with the sum

$$T_{\mathit{\text{inc}}}(\mathbf{r})=\sum _{m=1}^M\frac{\mathrm{\Delta }{t}_m}{TR}{\mathit{v}}_{\mathit{m}}^{\ast }{\mathbf{T}}_{\mathit{\text{increase}}}(\mathbf{r}){\mathit{v}}_{\mathit{m}}$$ [10]

such that the absolute temperature becomes

$$T(\mathbf{r})=T_0(\mathbf{r})\sum _{m=1}^M\frac{\mathrm{\Delta }{t}_m}{TR}{\mathit{v}}_{\mathit{m}}^{\ast }{\mathbf{T}}_{\mathit{\text{increase}}}(\mathbf{r}){\mathit{v}}_m$$ [11]

This matrix formalism allows very fast computation of the temperature during RF pulse design or other purposes, such as RF safety monitoring using T_increase matrices for temperature prediction.

Methods

Electromagnetic Field Simulations for Head and Hip Transmit Array

Electromagnetic (EM) field simulations were performed to obtain electric and magnetic field distributions induced by a head-sized 8 element 7T transmit array containing the numerical head model including shoulders with 5mm isometric resolution ³⁰ (Figure 2). A commercial finite difference time domain solver (xFDTD 6.6, Remcom Inc., PA, USA) was used for simulations. Individual coils were designed as copper stripline transmitters with dimensions of 30 × 2 cm on a 36 cm diameter shield. Individual coil electric and magnetic field distributions within the HUGO head model were exported from a number of voxels R = 48566.

Figure 2.

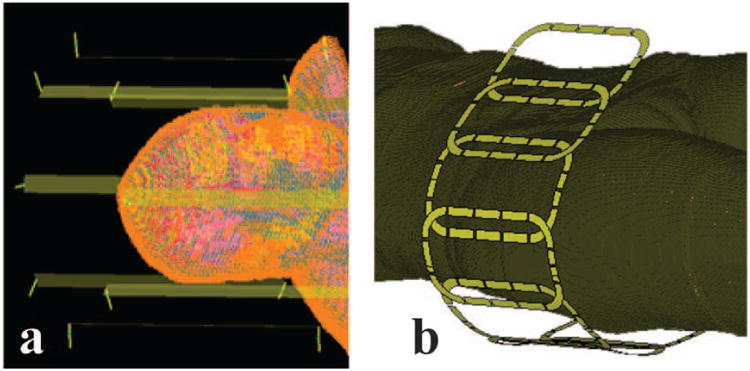
Simulation geometries. a) 8 channel head transmit array with the head model (shield not shown). b) 8 channel hip transmit array with Ella virtual body model.

In addition to the simulations performed on the head array, we used experimentally-validated EM field simulations of a hip transmit array ^31,32 in order to investigate the effect of RF pulse design with temperature-based safety metrics in regions with no tissues as highly perfused as brain. EM field simulation of an 8-channel hip array and torso phantom setup was performed with CST Microwave Studio (CST 2014, Darmstadt, Germany). Each simulated coil was tuned to 297.2 MHz and matched using co-simulation ^33,34 based S-parameter analysis by aligning with the bench measurements of S-parameters in the actual coil. 125 million mesh cells with edge lengths ranging from 0.05 mm to 28 mm were used in the EM field calculations. The loss and phase delay between the RF coil plug and individual coils (including T/R switches, coaxial cables, and cable traps) were measured and applied to the EM field simulations. The simulated electric and magnetic fields of each coil were compared to the measured MR field ³⁵ and temperature measurements ^32,36. Using the validated hip transmit array, EM field simulations of the Ella body model ³⁷ (1mm isometric resolution) was performed. Individual coil electric and magnetic field distributions within the model were exported from a number of voxels R = 10958786.

At each spatial location r, temperature correlation matrices, T_increase, of a multi-channel RF transmit system were calculated from EM field simulations. The elements of local electric field correlation matrices, Λ, were used as source terms in Eq. [9] for a specific imaging sequence length, t_end = 6 minutes (recommended SAR averaging duration by IEC⁹), of gradient-echo based sequence with TR = 9 ms. Simulations performed for analyzing the effect of scan durations on SAR and temperature constraints have the same duty cycle. Voxel specific constants in Eq. [9], such as metabolic rate, density, heat capacity, and electrical properties at 297.2 MHz, were obtained from the literature ³⁸. Initial temperature distributions, T₀(r), were obtained by calculating the steady state temperature distribution of the body using ambient air temperature of 23 °C. Temperature simulations were performed using a finite-difference approximation based temperature simulator ³⁹. The equilibrium temperature computed with no SAR applied until the average temperature distribution of two consecutive time steps was less than 10⁻²¹°C.

The concept of virtual observation points (VOPs) ¹⁵ was incorporated to replace complete T_increase matrices with a smaller number of constructed matrices with VOPs, Z^j j=1, …, N (N, the number of temperature VOPs ≪ R, the number of voxels in the EM field simulation), designed to provide an acceptable maximum 5% overestimation of the worst-case temperature increase per unit RF excitation. The overestimation percentage is chosen such that the number of VOPs is small enough to accelerate the RF pulse design without causing too much overestimation of the SAR and temperature which will reduce performance. When calculating the VOPs for 10s average SAR, for every voxel r, Λ(r) matrices were averaged over a spherically defined 10 g mass, thus yielded Λ^10g matrices. Λ^10g matrices were used to calculate SAR VOPs, ${\mathbf{Z}}_k^{10g}$ k=1, …, K (K: the number of 10g SAR VOPs≪R), with maximum 5% overestimation of the worst-case 10g SAR and were used to guarantee 10g SAR limits during constrained RF pulse design. This smaller number of VOPs enable fast calculation of parallel transmits RF pulses. A spherical volume, rather than cubic, was chosen because thermal conduction from one location in an unconfined homogeneous region occurs equally in all directions making a spherical volume naturally more relevant for safety assurance.

RF Pulse Design

The temperature contribution summation of each hard pulse v_m of length Δt in Eq. [10] can be written as a quadratic function of input RF pulse ${\mathit{v}}_{\text{full}}={[\begin{array}{ccc}{\mathit{v}}_1^{\mathrm{T}}& \cdots & {\mathit{v}}_M^{\mathrm{T}}\end{array}]}^{\mathrm{T}}$, where M is the number of hard RF subpulses, which is the concatenation of coil RF pulse waveforms, v_m:

$$T_{\mathit{\text{inc}}}(\mathbf{r})={\mathit{v}}_{\text{full}}^{\ast }{\mathbf{T}}_{\text{full}}(\mathbf{r}){\mathit{v}}_{\text{full}},\mathit{\text{where}}{\mathbf{T}}_{\text{full}}=\frac{\mathrm{\Delta }t}{TR}\left[\begin{array}{ccc}{\mathbf{T}}_{\mathit{\text{increase}}}& & 0\\ & \ddots & \\ 0& & {\mathbf{T}}_{\mathit{\text{increase}}}\end{array}\right]$$ [12]

Using Eq. [12], temperature increase resulting from any RF pulse excitation can be calculated easily for each location inside the sample and TR. One way of integrating temperature increase prediction capability into RF pulse design is to use the following quadratic inequalities for a given temperature increase limit T_lim:

$${\mathit{v}}_{\text{full}}^{\ast }{\mathbf{T}}_{\text{full}}(\mathbf{r}){\mathit{v}}_{\text{full}}\le T_{\mathit{\text{lim}}}\forall \mathbf{r}$$ [13]

Similarly, maximum tissue temperature limits as specified by the standards ⁹ can be incorporated into the RF pulse design by closely tracking the tissue temperature before RF exposure, T₀(r):

$$T_0(\mathbf{r})+{\mathit{v}}_{\text{full}}^{\ast }{\mathbf{T}}_{\text{full}}(\mathbf{r}){\mathit{v}}_{\text{full}}\le \mathbf{39}°\mathrm{C}\forall \mathbf{r}$$ [14]

Using the small-tip-angle approximation ⁴⁰ and discretizing in N_m time and N_s spatial positions similar to Ref. ⁴¹, transverse magnetization after RF excitation can be written in a matrix form by defining a full system matrix A_full = [A₁ ⋯ A_N] in which A_l's are N_s × N_m system matrices with elements a_ij = iγΔtM₀(r_i)S^(l)(r_i)e^{iγΔB₀(r_i)(t_j − T)}e^ir_i·k(t_j) where γ is the gyromagnetic ratio, M₀(r) is the equilibrium magnetization, S^(l)(r) is the B₁⁺ sensitivity patterns of transmit coils, ΔB₀(r) is the local off-resonance field map, k(t) is the excitation k-space trajectory, N is the number of transmit coils and m is the hard RF subpulse index. Using the matrix form of the system matrix and temperature increase limits, the parallel excitation RF pulse design problem with strict temperature increase constraints can be written as:

$${\widehat{\mathit{v}}}_{\text{full}}=\begin{array}{c}arg\; min\\ {\mathit{v}}_{\text{full}}\end{array}{\Vert {\mathbf{A}}_{\text{full}}{\mathit{v}}_{\text{full}}-{\mathbf{m}}_{\text{des}}\Vert }_2^2\text{subject to}{\mathit{v}}_{\text{full}}^{\ast }{\mathbf{Z}}_{\text{full}}^j{\mathit{v}}_{\text{full}}\le T_{\mathit{\text{lim}}}\mathit{\text{OR}}{T}_{0,j}+{\mathit{v}}_{\text{full}}^{\ast }{\mathbf{Z}}_{\text{full}}^j{\mathit{v}}_{\text{full}}\le \mathbf{39}°\mathrm{C}\forall j$$ [15]

where m_des is the desired magnetization profile from RF excitation, and ${\mathbf{Z}}_{\text{full}}^j$ are the block diagonal matrices that contain temperature increase information, temperature VOPs, to be used in conjunction with v_full. T_0,j is the maximum initial temperature located within the cluster of jth VOP. RF pulses designed with temperature constraints (“temperature constrained”) were compared to RF pulses designed with 10g averaged SAR constraints (“10g SAR constrained”) as well as RF pulses designed without any constraints (“unconstrained”). All RF pulses were designed with maximum absolute temperature constraints by solving Eq. [15]. In order to study the effect of scan durations on SAR and temperature constraints, all three types of RF pulses were designed for multiple RF exposure durations (varying between 6 minutes and 24 minutes) by using the corresponding temperature correlation matrices that are calculated based on the RF exposure duration. In Eq. [15], error minimization term with respect to the desired target profile is defined as a quadratic cost functional of the desired RF pulse and system matrix. Temperature constraints in the optimization problem are defined as quadratic functions of the desired RF pulse. Since local temperature correlation, T_increase, matrices are positive definite and defined constraints are quadratic functions; the optimization problem can be solved inside the convex search space defined by quadratic constraints. The optimization problem in Eq. [15] can be solved by using a range of efficient strategies for convex optimization. Similar to previous RF pulse design approaches ^11,14, a least-squares projection strategy was employed for solving the optimization problem, using, specifically, a Lanczos algorithm with Gram-Schmidt re-orthogonalization steps ⁴². Using Lancsoz algorithm, the number of basis vectors were reduced into 50 with exact temperature constraints enabling fast and memory efficient calculation of the solution to the optimization problem. This reduced basis convex optimization problem was solved efficiently using the SeDuMi ⁴³ v1.2.1 solver interfaced with YALMIP ⁴⁴.

Head Transmit Array

In the present study, a constant rate spiral-in excitation k-space trajectory was used in a gradient-echo based sequence with TR = 9 ms with the following parameters: duration=3.1ms, excitation resolution=2.5mm, sampling interval=10μs, maximum gradient slew rate=150mT/m/s and gradient amplitude=40mT/m. Parallel excitation RF pulses for uniform 30° excitation in a 2D rectangular region on the center axial slice were designed by solving Eq. [15] with maximum temperature constraints. T_increase matrices were replaced by 252 temperature VOPs, Z, in RF pulse design enabling a predefined maximum 5% overestimation of the worst-case temperature increase per unit RF excitation at each subvolume. The local temperature limit on the constraint was defined as 39° C. Similarly, VOP compression on Λ^10g matrices resulted in 364 10g SAR VOPs, Z^10g. The local 10g SAR limit was defined as 10 W/kg.

Hip Transmit Array

For the hip transmit array, a constant rate spiral-in excitation k-space trajectory was used in a gradient-echo based sequence with TR = 9 ms with the following parameters: duration=2.2ms, sampling interval=10μs, maximum gradient slew rate=150mT/m/s and gradient amplitude=40mT/m. Parallel excitation RF pulses for uniform 25° excitation in a 2D disk on the hip region were designed by solving Eq. [15] with maximum temperature constraints. T_increase matrices were replaced by 932 temperature VOPs, Z, (maximum 5% overestimation of the worst-case). The local temperature limit on the constraint was defined as 39° C. Similarly, VOP compression on Λ^10g matrices resulted in 1010 10g SAR VOPs, Z^10g. The local 10g SAR limit was defined as 10 W/kg.

Results

Head Transmit Array

Desired 2D excitation profile and simulated axial flip angle maps resulting from RF pulses designed with different constraints are shown in Figure 3. Defined constraints were always satisfied by the convex optimization and remaining degrees of freedom were used to minimize the excitation error. Temperature constrained design result in lower excitation errors compared to 10g SAR constrained design, while satisfying current MR safety standards ⁹. The maximum local spatial average 10g SAR was 18.0 W/kg for the temperature constrained design, 10 W/kg for 10g SAR constrained design and 20.9 W/kg for the unconstrained design (Table 1).

Figure 3.

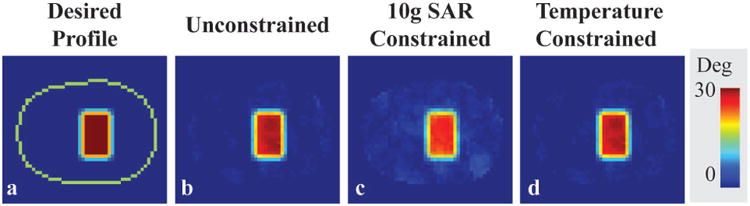
Desired profile on an axial slice of the head model (a) and flip angle distributions of RF pulses designed without constraints (b), with 10g SAR constraints (c), and with temperature constraints (d) for 6 minutes of RF exposure. The periphery of the head is indicated with a green line.

Table 1.

Maximum temperature, maximum 1g SAR, maximum 10g SAR, and NRMSE resulting from RF pulses designed with various strict constraints for the head model in head transmit array for 6 minutes of RF exposure. (NRMSE is defined as the flip angle root mean square error between the achieved and the targeted profile divided by the root mean square of the target excitation flip angle profile)

Pulse Design Type	Unconstrained	10g SAR Constrained	Temperature Constrained
Maximum local temperature (°C)	39.3	38.4	39.0
Maximum 1g SAR (W/kg)	35.1	17.6	30.5
Maximum 10g SAR (W/kg)	20.9	10.0	18.0
NRMSE (%)	7.8	21.0	8.8

Figure 4 shows temperature and 10g SAR resulting from RF pulses designed with temperature constraints on one slice of the head. As depicted by the black squares, the maximum temperature and 10g SAR are located in different regions within the slice.

Figure 4.

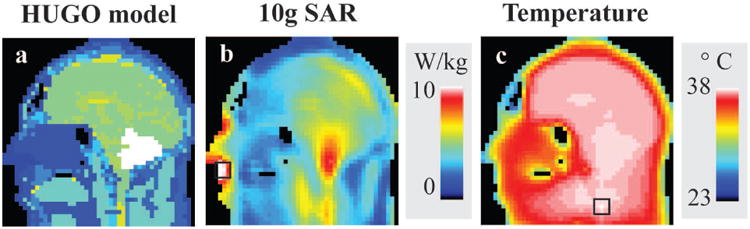
Material distribution of the head model is shown in a. 10g SAR (b) and temperature (c) resulting from temperature-constrained RF pulse designs. Maximum 10g SAR and temperature in the slice are indicated by the black squares located in different regions of the head.

Hip Transmit Array

Figure 5 shows desired 2D excitation profile and simulated axial flip angle maps resulting from RF pulses designed with different constraints. Similar to the head transmit array simulation results, defined constraints were always satisfied by the convex optimization and remaining degrees of freedom were used to minimize the excitation error. The maximum local spatial average 10g SAR was 20.7 W/kg for the temperature constrained design, 10 W/kg for 10g SAR constrained design and 30.1 W/kg for the unconstrained design (Table 2). Maximum local temperature limit of 39 °C was exceeded around 1°C with the RF pulse design having no constraints. The temperature constrained design result in around 15% lower error in excitation profile compared to the SAR constrained design, while satisfying current MR safety standard ⁹.

Figure 5.

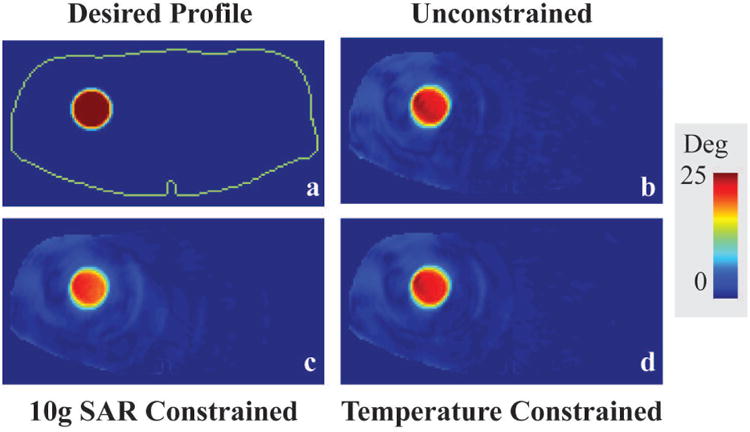
Desired profile (in red) on an axial slice through the Ella virtual model (a) and Bloch simulation resulting from RF pulses designed without safety constraints (b), with 10g SAR constraints (c), and with temperature constraints (d) for 6 minutes of RF exposure. The periphery of the body is indicated with a green line (a).

Table 2.

Maximum temperature, maximum 1g SAR, maximum 10g SAR, and NRMSE resulting from RF pulses designed with various strict constraints for Ella virtual body model in hip transmit array for 6 minutes of RF exposure.

Pulse Design Type	Unconstrained	10g SAR Constrained	Temperature Constrained
Maximum local temperature (°C)	39.9	38.1	39.0
Maximum 1g SAR (W/kg)	75.9	19.9	46.9
Maximum 10g SAR (W/kg)	30.1	10.0	20.7
NRMSE (%)	27.0	32.2	27.5

Figure 6 shows temperature and 10g SAR resulting from RF pulses designed with temperature constraints in the hip region. Similar to head simulations, as depicted by the black squares, the maximum temperature and 10g SAR are located in different regions for hip simulations within the slice.

Figure 6.

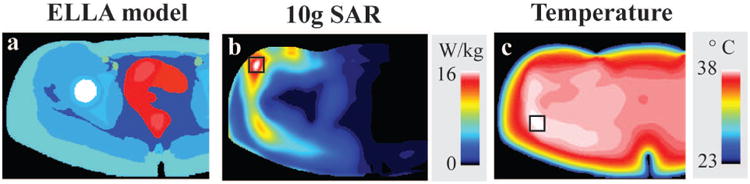
Material distribution of the Ella virtual body model is shown in a. Multiple intensity projections of 10g SAR (b) and temperature (c) results from temperature constrained RF pulse designs. Maximum temperature and 10g SAR are indicated by the black squares which are located in different regions of the head. The right side of the simulations, which was not covered by the hip array, was cropped for visualization.

RF exposure duration

Figure 7 shows the maximum temperature, maximum SAR, and flip angle normalized root mean square error (NRMSE) resulting from RF pulses designed for different RF exposure durations in both head and hip regions. In both regions, designed unconstrained RF pulses, as expected, resulted in constant NRMSE and the maximum SAR for all exposure durations. On the other hand, the maximum temperature increased with exposure duration reaching 40.4 °C and 43.7 °C at the end of 24 minutes of imaging for head and hip regions, respectively. In 10g SAR constrained design, the maximum temperature increased from 38.4°C to 38.9°C and 38.2°C to 39.3°C for head and hip regions, respectively, while NRMSE and the maximum SAR were constant as the exposure duration is increased. Contrary to the trends observed for unconstrained and 10g SAR constrained RF pulse designs, in temperature constrained design for the hip region, the NRMSE increased (from 28.0 % to 33.6 %) and the maximum SAR decreased (from 18.2 W/kg to 8.9 W/kg) as RF exposure duration is increased (from 6 mins to 24 mins). In the head, the NRMSE increased (from 8.8% to 19.7%) and the maximum SAR decreased (from 18.0 W/kg to 10.6 W/kg) as the RF exposure duration is increased (from 6 mins to 24 mins). In both head and hip regions, the maximum temperature remained constant at 39°C as RF exposure duration changed. In order to meet strict temperature safety requirements, some compromise in NRMSE was required during temperature constrained RF pulse design. For sequence durations up to 18 mins and above 24 mins, lower NRMSE was obtained using strict temperature constraints compared to SAR constraints in the hip region and head region, respectively. For both head and hip regions, higher benefits of using temperature constraints are obtained for shorter sequence durations.

Figure 7.

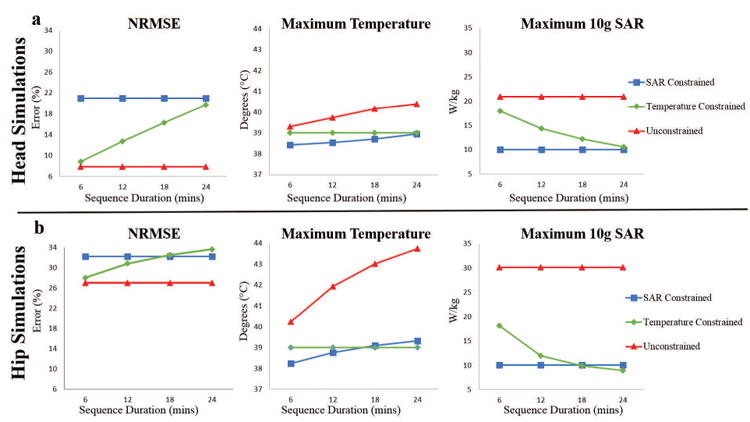
The effect of RF exposure duration in RF pulse design using temperature correlation matrices. NRMSE, maximum temperature, and maximum 10g SAR resulting from RF pulses designed with various strict constraints for head and hip regions are given in a and b respectively.

Discussion

In this work, we demonstrated the concept of using a local temperature correlation matrix, T_increase, calculated from local electric field correlation matrices using EM field and temperature simulations of human models, for safety assurance in pulse design. Calculated T_increase matrices are compressed using VOPs and used in design of parallel RF transmission pulses with strict maximum temperature constraints. The use of temperature correlation matrices in RF pulse design resulted in increased excitation fidelity and provided a more relevant safety metric compared to SAR.

Calculation of T_increase matrices needs to be performed prior to RF pulse calculations with predefined t_end and TR. To the extent that the T_increase matrices match the true tissue characteristics in vivo, using predefined temperature limits in parallel transmission RF pulse design will ensure a safe MR scan. The proposed RF design process with T_increase matrices is fully capable of enforcing different temperature increase limits for different parts of the body, e.g. in the eyes, by predefining VOP clusters in those regions. In addition to the constraints involving temperature predictions for a specific t_end, system related constraints such as individual channel forward and reflected peak and average power can be incorporated into RF pulse optimization problem in Eq. [15] using calibrated power correlation matrices ¹⁴.

In this study, we incorporated limits on the absolute temperature into the RF pulse design by adding the maximum pre-determined temperature before RF excitation to each VOP cluster in the constraints as defined in Eq. [11]. Similarly, local temperature increase limits ^22,24 can easily be incorporated into the RF pulse design. Methods for fast tracking body temperature during an MR exam for safety purposes have also been proposed ²⁹. In the future, further development of those approaches will enable the integration of temperature correlation matrices into MR scanners for closely monitoring safe operation and proactively managing RF pulse design.

We demonstrate that using temperature correlation matrices for parallel transmission RF pulses constraining maximum absolute temperature is beneficial in both head and hip regions. Our results are in agreement with previous investigations obtained in the head using constraints on temperature increase ^22-24, indicating that better excitation profiles can be achieved with temperature constraints than with SAR constraints. We also investigated the hip region, which has lower perfusion rates than those present in the brain. Regardless of the perfusion characteristics differences, our results indicate using temperature correlation matrices enable lower excitation errors especially for shorter RF exposure durations and still ensure patient safety, remaining below the maximum temperature limits. Only for the hip at the longest exposure duration studied does the SAR-constrained pulse provide a slightly better NRMSE than the temperature-constrained one, but it does so at a cost of temperatures slightly exceeding 39 °C. As the RF exposure duration is increased, the benefit of using temperature correlation matrices diminishes for both head and hip regions. However, safe operation (the maximum temperature always below 39 °C) is always guaranteed by using temperature correlation matrices with the expense of increased excitation error, while using strict SAR constraints may result in exposure conditions where the maximum local temperature exceeds 39 °C. It is also important to note that continuous exposures to a single SAR distribution and level (single sequence) lasting up to 24 minutes is increasingly rare in practice. Rather, shorter sequences with different SAR levels are applied in series, often with breaks in between them during which temperature will progress towards baseline. Thus, we believe that the results for exposure periods shorter than 24 minutes are more relevant in practice. Related to this, the methods discussed here are intended for pulse design more than for safety assurance of an actual patient exam, which can be accomplished very rapidly even with consideration of multiple thermo-regulatory effects and the increase of whole-body temperature²⁹.

The comparison with different parts of the body reveals the benefit of using temperature correlation matrices up to a specific exposure duration to be region independent. Also, while it has been shown that the perfusion can be a function of local tissue temperature, here the perfusion of tissues was kept constant with respect to temperature. This may result in reduced RF pulse design performance; however, it provides an additional safety factor. Computational demands for performing high resolution simulations and actual resolutions of the virtual body models limit the use of very fine resolutions. In this study, EM field simulations were performed using two different virtual body models with resolutions 1mm isometric for the hip region and 5mm isometric for the head. While 5mm may seem coarse, in a study of the effects of model resolution on whole-head and 1g averaged SAR, no notable difference was seen between resolutions of 5mm isometric and 2×2×2.5 mm^{3 45}.

In simulations, we incorporated the proposed local temperature correlation matrices and RF pulse design approach to short-TR SAR-limited 3D GRE-based hip microarchitecture scans at high field strengths ⁴⁶. This type of sequence is expected to benefit from the proposed RF pulse design with temperature constraints as opposed to the existing SAR constraints ²¹. In the future, we plan to use this approach for in vivo studies targeting safe operation and minimal excitation error. Current practice for ensuring subject safety of parallel RF excitations using SAR as a metric relies on estimating field distributions from simulations of the RF array with multiple virtual subjects covering the population of interest and their positions with respect to the array ^47-50 and making sure that the worst-case 10g SAR distributions are below what has been traditionally obtained from quadrature excitations ⁹. Similar approaches for estimating field distributions and validated thermal properties of the virtual subjects could enable calculation of the temperature correlation matrices for specific RF exposure duration. Thus, temperature correlation matrices for multiple exposure durations could be calculated once prior to RF pulse design and used later for RF pulse design as long as temperature prior to RF exposure is tracked accurately ²⁹.

Although computation of SAR-induced temperature rather than SAR alone can be seen to add a layer of complexity and uncertainty to assurance of safety, the result is more relevant to the actual risk to the subject and it is always possible to ensure safety with conservative methods designed to ensure an overestimate of temperatures compared to what is expected in vivo. The method implemented here, for example, does not allow for a thermoregulatory increase in perfusion rates at locations of high temperature, as occurs in vivo. This approach has been seen to overestimate temperature increases observed in vivo, even while giving very good estimated of temperature in a phantom ⁸. Another related study showed that very dramatic increases in perfusion with temperature were required to avoid overestimation of temperatures observed in vivo ⁵¹. Thus, in this work use of temperature rather than SAR to maximize safety in pulse design allows for lower constraints in many cases despite the temperature predictions being conservative, which is a clear advantage to use of temperature. The existing limits on SAR are designed to be conservative, and our results indicate that in many cases they are conservative to the point of being more restrictive than use of the temperature limits. Although the method used here for pulse design does not allow for increase in the whole-body core temperature and thus the temperature of incoming blood at each location, after the pulse design is completed fast methods of temperature prediction allowing for core body temperature to increase with consideration of whole-body SAR and many other heat transfer mechanisms such as respiration, perspiration, and convection ^29,52 can be used to ensure safety while also allowing for conservative increases in local perfusion to avoid overly restrictive safety assurance measures. Other methods for computing temperature increase considering additional factors have also been proposed to consider additional factors ²⁸, including discrete vasculature to a fairly high resolution ⁵³. In general, however, they are nonlinear and are not suitable for fast pulse design.

Conclusions

We have demonstrated that temperature correlation matrices can facilitate integration of limits on maximum absolute temperature into parallel transmission RF pulse design. Because temperature is ultimately more relevant to subject safety than SAR, we hope this will inspire further advances in making temperature a routine consideration for ensuring RF safety in MRI.

List of Abbreviations

EM

Electromagnetic

NRMSE

Normalized root mean square error

pTx

Parallel transmission

RF

Radiofrequency

S-parameters

Scattering parameters

SAR

Specific absorption rate

B₁⁺

Transmit radiofrequency magnetic field

VOPs

Virtual observation points