Surface transport and quantum Hall effect in ambipolar black phosphorus double quantum wells

Few-layer black phosphorus acts as tunable ambipolar wide quantum wells.

Abstract

Quantum wells (QWs) constitute one of the most important classes of devices in the study of two-dimensional (2D) systems. In a double-layer QW, the additional “which-layer” degree of freedom gives rise to celebrated phenomena, such as Coulomb drag, Hall drag, and exciton condensation. We demonstrate facile formation of wide QWs in few-layer black phosphorus devices that host double layers of charge carriers. In contrast to traditional QWs, each 2D layer is ambipolar and can be tuned into n-doped, p-doped, or intrinsic regimes. Fully spin-polarized quantum Hall states are observed on each layer, with an enhanced Landé g factor that is attributed to exchange interactions. Our work opens the door for using 2D semiconductors as ambipolar single, double, or wide QWs with unusual properties, such as high anisotropy.

INTRODUCTION

Quantum confinement of atoms and electrons to two dimensions (2D) profoundly alters their electronic properties, giving rise to celebrated phenomena, such as the integer and fractional quantum Hall (QH) effect (1), quantum spin Hall effects (2–4), and interfacial superconductivity and magnetism (5), as well as technological development, such as quantum well (QW) lasers and photovoltaic solar cells. In double QWs, electrons can reside on either one or both potential wells; this “which-layer” degree of freedom is analogous to spin and often referred to as the pseudospin, thus providing a fascinating platform for the investigation of multicomponent physics and competing symmetries (6–16).

Traditional QWs are fabricated on the basis of GaAs/AlGaAs heterostructures, and double QWs are fabricated by inserting a very thin layer of large-bandgap material between two adjacent single QWs. More recently, the advent of 2D materials (17) has opened the door for manipulating low-dimensional material systems with an unprecedented level of control. For instance, single QWs based on single- and few-layer graphene (18, 19) led to the observation of tunable integer and fractional QH effect (20–24), magnetic focusing (25, 26), Veselago lensing (27–31), and specular Andreev reflection (32, 33).

An alternative route to realizing double QWs is to use a wide QW structure (34–38), in which, instead of physically inserting a high barrier separating two layers of charges, the Coulomb repulsion among electrons spontaneously causes electrons to reside on the opposite walls, thus forming a double-layer system with a “soft” potential barrier. Compared with double QWs, wide QWs afford similar physics, except that the soft barrier leads to enhanced interlayer coupling that hybridizes the two layers, giving rise to the formation of symmetric and antisymmetric states that are separated by an energy gap Δ_SAS. By modulating width of the well d, charge density n, Δ_SAS, and magnetic length l_B, inter- and intralayer Coulomb interactions can be tuned, hence yielding insight into the competing interactions in low-dimensional systems. Despite the recent progress, these wide QW structures have not been demonstrated in 2D materials to date because of the lack of high-mobility 2D semiconductors with sizable bandgaps.

Black phosphorus (BP), consisting of layered phosphorus atoms in orthorhombic structure (39, 40), is such a candidate. A plethora of fascinating properties have been predicted or observed in few-layer BP (41–45), such as a layer-, strain-, and electric field–dependent bandgap (46–48); highly anisotropic electrical, thermal, and optical properties (44, 49–52); and very high mobility (40, 53–55) that rival that of first generation graphene devices. Here, we show a simple realization of wide QWs with a double layer of charge carriers in few-layer BP devices, with a mobility up to 6500 cm²/Vs. Two independent sets of Shubnikov–de Haas oscillations are observed, indicating the presence of two parallel conducting surface states that are well separated by an intrinsically insulating bulk. Integer QH plateaus are observed on both surface states. In contrast to traditional GaAs/AlGaAs QWs, BP-based wide QW devices are ambipolar and highly tunable—by independently adjusting top and back gate voltages, we can tune the system into the single or double QW regime with unipolar or bipolar charge distributions, which host QH states at high magnetic fields. From temperature- and density-dependent measurements, an enhanced Landé g factor of 2.7 is observed. Our work paves the way for using 2D materials as wide QWs for investigating phenomena, such as Landau level hybridization, interwell Coulomb interactions, or multicomponent QH ferromagnetism (34, 56, 57) in this highly anisotropic system.

RESULTS

Here, we focus on a device with BP that is ~20 nm thick with Si/SiO₂ back gate and hBN/Al₂O₃/Au top gate at T = 0.3 K. The schematic of the device is shown in Fig. 1A, and an optical image is shown in Fig. 1B. The devices are measured in a pumped He⁴ or He³ cryostat. Similar data are observed in multiple devices. Figure 2A presents the four-terminal resistance R of the device (color) as a function of top gate V_tg (horizontal axis) and back gate V_bg voltages (vertical axis), where green and brown colors indicate conductive (R ~ 10³ to 10⁴ Ω) and highly resistive (R ~ 10⁷ to 10⁸ Ω) states, respectively. Because of the thinner dielectric layers and higher dielectric constant of Al₂O₃, the coupling efficiency of the top gate is approximately four times that of the back gate. The white area in the center of the plot corresponds to an insulating regime (R > 10⁸ Ω) where the high resistance saturates the amplifier, indicating that the Fermi level is within the bandgap. Ambipolar transport can be attained by modulating either V_bg or V_tg: The device is very conductive when highly hole-doped, with a high field effect mobility ~6000 cm²/Vs; because either gate is tuned close to 0, its resistance increases precipitously; when the gate voltages are highly positive, electron conduction is turned on, with a field effect mobility ~1000 cm²/Vs. This electron-hole asymmetry in mobility has been observed previously (53, 55, 59) and attributed to the Cr/Au electrodes that favor contacts to p-doped semiconductors. Another notable feature is the triangular shape of the insulating region: Its lower boundary at negative gate voltages (−6.5 < V_tg < 3 and −40 < V_bg < −5) moves with a negative slope, indicating that the “on”-state threshold voltage in the hole-doped regime is dependent on the total charge density induced by both gates; in contrast, the boundaries at positive gate voltages (V_bg ~ 14 V and V_tg ~ 6 V, respectively) remain constant, signifying that the on-state threshold voltage in the electron-doped regime is controlled by a single gate. We attribute the flat upper and right boundaries to bulk impurities that give rise to unoccupied localized states within the bandgap; because the Fermi level is located very close to the valence band, these states have minimal effect on the transport of BP in the hole-doped regime. Because an increasing gate voltage raises the Fermi level toward the conduction band, these unoccupied mid-gap states must first be filled. Thus, the back (top) gate cannot effectively switch on the top (bottom) surface state because of the large number of localized states within the bulk of the BP device. This effect, in combination with the Fermi level pinning that reduces the effect of gating, results in the flat boundaries of the insulating region.

Fig. 1. Device schematics and image.

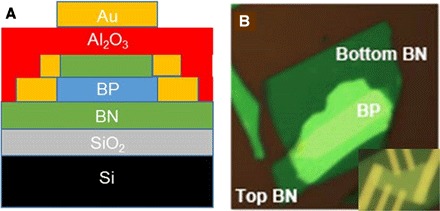
(A) Side view of device schematics. (B) Optical microscope image of an hBN/BP/hBN stack and a finished device without top gate (inset).

Fig. 2. Transport data.

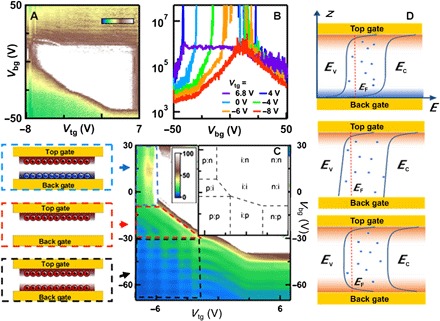
(A and B) R(V_bg, V_tg) and line traces R(V_bg) at different V_tg at T = 1.7 K and B = 0. Note the logarithmic color scale (in Ω). (C) Right: R(V_bg, V_tg) at T = 0.5 K and B = 18 T, featuring a complicated quantum oscillations pattern. The color scale is in kΩ. Left: Schematics of the charge distributions that correspond to bipolar double-layer, single-layer, and unipolar double-layer regimes, respectively. Inset: Charge types for top and bottom surfaces at different combinations of gate voltages. p, hole-doped; n, electron-doped; i, intrinsic insulating state. (D) Band diagrams that correspond to the three regimes in (C), with dots illustrating mid-gap impurity states.

Strikingly, at very large positive or negative V_tg values, the insulating region almost completely disappears. For instance, at V_tg = −8 V, the resistance maximum near the charge neutrality point is ~600 kΩ, which is reduced from the global resistance maximum by more than two orders of magnitude. Such a disappearance of the insulating region may arise from the nontrivial closure of the bandgap by a large out-of-plane electric field (47); alternatively, it could also be a consequence of a nonuniform charge distribution, in which spatially separated surface states contribute to the transport even though the overall net charge is zero.

To determine the origin of the disappearing insulating region, we perform magnetotransport measurements. Figure 2C plots R(V_bg, V_tg) at a magnetic field B = 18 T, where quantum oscillations are visible. Several different patterns are observed, indicating distinct transport regimes. We first focus on the lower left quadrant: For negative V_bg and V_tg, a checkerboard pattern is observed. The presence of horizontal and vertical sets of oscillations indicates the coexistence of two separate high-mobility 2D hole systems (2DHS), each independently tuned by the adjacent gate. The absence of diagonal features in this quadrant indicates that the effect of the farther gate on each layer is fully screened. From a simple Schrödinger-Poisson calculation, the gate-induced 2D hole wave function is expected to tightly confine to the outermost five or six atomic layers at the surface (60), thus limiting the screening length to <4 nm. Thus, the device forms a “naked” wide QW, with two distinct 2DHS residing at the top and bottom surfaces, separated by an intrinsic or insulating region. Similarly, the upper right quadrant of the figure corresponds to the formation of two distinct 2D electron systems (2DES) that, in principle, will display similar checkerboard patterns of oscillations at sufficiently high fields. However, because of the relatively low electron mobility, quantum oscillations are not observed at B = 18 T.

In the upper left (lower right) quadrants, that is, when both V_tg and V_bg have large magnitudes but different signs, only vertical (horizontal) oscillations are observed. Here, similar to the unipolar case, the device hosts top and bottom surface states; however, what distinguishes this case is that the states carry charges of opposite signs. Because the electron-doped regime has lower mobility, quantum oscillations are not observed; thus, a single set of oscillations emerges parallel to (that is, independent of) the axis that corresponds to the farther gate. Hence, these quadrants correspond to a wide QW with 2DHS and 2DES on opposite surfaces, which has not been realized in GaAs-based devices.

Last, when either V_bg or V_tg are tuned close to 0, we observe only a single set of diagonal oscillations, that is, the charge density is controlled by both V_tg and V_bg. In this regime, one of the surfaces is tuned into the intrinsic regime and no longer screens the nearby gate; thus, the remaining surface state in this QW is subjected to field lines from both the back and top gates. The configurations of the top and bottom surface states that correspond to various regions of the R(V_bg, V_tg) map are summarized in the inset and left of Fig. 2C and the band diagrams in Fig. 2D, where the hole (h)–doped, electron (e)–doped, and intrinsic (i) states are represented by red, blue, and white regions, respectively. These configurations also establish that the disappearance of the insulating region arises from the formation of 2DHS or 2DES on either surface at large doping.

DISCUSSION

To summarize our experimental observations thus far, we demonstrate that a thin BP device acts as a wide QW, which can host surface states on the top and bottom surfaces, whereas the interior is a gapped intrinsic semiconductor that acts as a soft tunnel barrier. Unlike conventional GaAs-based counterparts, these BP-based QWs support both single- and double-layer states that are exceedingly tunable, as each of the top and bottom surfaces may be independently tuned to intrinsic, 2D electron gas or 2D hole gas states. These novel wide QWs may be further optimized by improving mobility or reducing the BP flake thickness and, hence, the center barrier width so as to enhance Coulomb interactions between the surface states and tuning parameters, such as the symmetric-antisymmetric gap, thus allowing investigation of 2D correlated physics, such as two-component solid, Wigner crystals, interlayer coherence, and reentrant integer and fractional QH states (61–63) with charges of either or both polarities.

Furthermore, we can extract information about the 2D surface states by analyzing the temperature and density dependence of the quantum oscillations. Here, we focus on the (p:p) region. Figure 3 (A and B) plots the background-subtracted resistance ΔR(V_bg) at different temperatures and at constant V_tg = −6 and −4.4 V, respectively. The oscillation amplitudes decrease with temperature and can be fitted within the Lifshitz-Kosevich approach for 2D systems, yielding an effective mass m* ~0.43 ± 0.1 m_e, where m_e is the electron rest mass. This value is in good agreement with that obtained from density functional theory calculations (53). Notably, we find no clear density dependence of m* within error bars.

Fig. 3. Quantum oscillations at B = 18 T.

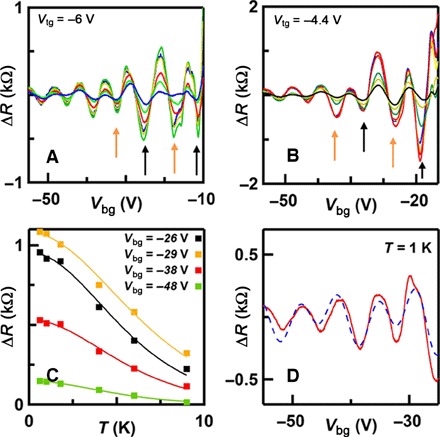
(A) Background-subtracted resistance ΔR at V_tg = −6 V and T = 0.6, 1, 1.8, 4, 6, and 9 K, respectively. Arrows indicate nonmonotonic amplitude dependence on density. (B) Similar data set at V_tg = −4.4 V. (C) Oscillation amplitude as a function of temperature at V_tg = −3 V and different V_bg values (squares), fitted to Lifshitz-Kosevich formula (solid lines). The fits yield an effective mass m* ~ 0.43 ± 0.1 m_e. (D) ΔR(V_bg) at V_tg = 0 V and T = 1 K (solid lines) and fitted curve using Eq. 1 (dashed line), T_D = 2 K and gm* = 1.15.

A close examination of Fig. 3 (A and B) reveals a salient feature: The oscillation amplitude is not monotonic in density; at some gate voltages, the peak height alternates between adjacent oscillations, as indicated by arrows. These nonmonotonic and/or alternating peak heights are not expected in conventional quantum oscillations, where the equally spaced Landau levels at constant B yield oscillation amplitudes that scale as n^−1/2. They have been observed in a number of systems, such as ZnO heterostructures (64), Si inversion layers (65, 66), SrTiO₃ (67), and, more recently, thin BP sheets (53, 55), and are commonly attributed to the appearance of the Zeeman gap that is smaller than the single particle cyclotron gaps, where the oscillation amplitude is given by (67)

$$\frac{\mathrm{\Delta }\mathit{R}}{{\mathit{R}}_0}=\frac{5}{2}{\displaystyle {\sum }_{\mathit{s}=1}^{\infty }}{\mathit{b}}_{\mathit{s}}\text{cos}(\frac{2\mathrm{\pi }\mathit{n}\mathit{h}}{2\mathit{e}\mathit{B}}\mathit{s}-\frac{\mathrm{\pi }}{4})$$ (1)

$${\mathit{b}}_{\mathit{s}}=\frac{{(-1)}^{\mathit{s}}}{\sqrt{\mathit{s}}}{\left(\frac{\mathit{e}\mathit{B}}{\mathit{n}\mathit{h}}\right)}^{1/2}\frac{2{\mathrm{\pi }}^2\mathit{s}{\mathit{k}}_{\mathrm{B}}\mathit{T}/\hslash {\mathrm{\omega }}_{\mathrm{c}}}{\text{sinh}(2{\mathrm{\pi }}^2\mathit{s}{\mathit{k}}_{\mathrm{B}}\mathit{T}/\hslash {\mathrm{\omega }}_{\mathrm{c}})} \text{exp}\left(\frac{-2{\mathrm{\pi }}^2\mathit{s}{\mathit{k}}_{\mathrm{B}}{\mathit{T}}_{\mathrm{D}}}{\hslash {\mathrm{\omega }}_{\mathrm{c}}}\right)\text{cos}\left(\frac{\mathrm{\pi }\mathit{s}\mathit{g}{\mathit{m}}^{*}}{2{\mathit{m}}_{\mathrm{e}}}\right)$$

where ℏ is the reduced Planck constant, g is the Lande g factor, n is the carrier density, ω_c = eB/m* is the cyclotron frequency, m* is the effective mass, k_B is the Boltzmann constant, T_D is the Dingle temperature, and s = 1, 2. In these equations, the periodicity of the oscillations is controlled by n, and our data yield a capacitive coupling ~6.5 × 10¹⁰ cm⁻² V⁻¹ between the back gate and the bottom surface state. The ratio between the alternative peak heights is controlled by the combined product gm*. By fitting ΔR(V_bg) curves to Eq. 1, we obtain a good agreement using T_D = 2 K and gm* = 1.15 ± 0.05 (Fig. 3D). As we have determined m* ~ 0.43 from the temperature dependence of the oscillations, the fitting results indicate that the Landé g factor is ~2.7, which represents a ~33% enhancement over the free hole value of 2.0. This enhancement likely originates from the exchange interaction among electrons in spin-polarized Landau levels (68–70).

Finally, at sufficiently high magnetic field, the QH effect, which is a prototypical 2D phenomenon, can be observed on both 2DHS. Figure 4A exhibits the Landau fan R(V_bg, B) at V_tg = 0 V for 18 < B < 31 T, and several line traces are shown in Fig. 4B. At V_tg = 0 V, the top layer is turned off, and only the bottom layer participates in electrical transport. Quantized plateaus at filling factor ν = 1, 2, 3, 4, 5, and 6 are observed, indicating full lifting of the spin degeneracy. On the other hand, at V_tg = −8 V, the R(V_bg, B) data exhibit additional vertical strips superimposed on top of the Landau fan, signifying the presence of QH states on the highly hole-doped top layer (Fig. 4C), with an estimated hole density of 2.4 × 10¹² cm⁻². No quantized plateau is observed in the raw data (Fig. 4D, dashed lines) because of the coexistence of QH states on both the top and bottom surfaces. Because B sweeps from 18 to 31 T, the filling factor of the top surface state is estimated to decrease from ν = −4.5 to −2; thus, we model its conductance as stepwise quantized plateaus at appropriate filling factors (Fig. 4C, inset). By subtracting this calculated parallel conductance from the raw data, plateaus are recovered in R(V_bg) data, similar to those in Fig. 4 (A and B). Together, these results indicate that both the top and bottom 2DHS host QH states, with spin degeneracy fully lifted.

Fig. 4. QH states at high magnetic field.

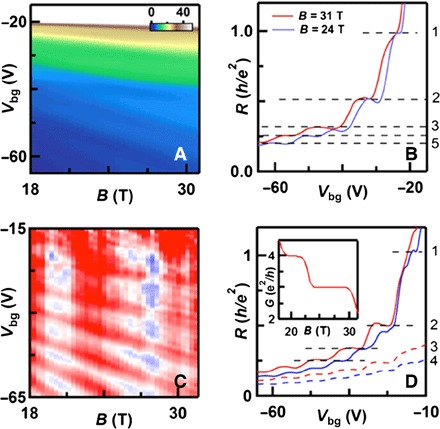
(A) R(V_bg, B) with the top gate disconnected for 18 < B < 31 T. Quantized plateaus at filling factors ν = 1, 2, 3, 4, 5, and 6 are observed. (B) Line traces of (A) at B = 24 T (blue) and B = 31 T (red), respectively. The dashed lines mark expected values of resistance plateaus. (C) Differentiated dR/dB(V_bg, B) at V_tg = −8 V. (D) Line traces of (D) at B = 20.3 T (blue) and B = 27.7 T (red). The dashed lines correspond to raw data, and solid lines are obtained by subtracting parallel conductance contributed by top surface states. Inset: Calculated conductance of the top surface states at V_tg as a function of B.

In conclusion, we have demonstrated the formation of ambipolar highly tunable wide QWs in hBN-encapsulated dual-gated BP devices, in which either or both surfaces may be tuned into intrinsic insulator or hole- or electron-doped surface states. At high magnetic fields, fully spin-resolved integer QH states are observed in both the top and bottom surface states. By further optimization, such as mobility improvement and thickness reduction, these BP-based wide QW devices may open the door to a wide range of novel physics in this highly anisotropic 2D system, ranging from Wigner crystallization and interlayer coherence to integer and fractional QH states with possible reentrant behavior.

MATERIALS AND METHODS

Bulk hBN and BP crystals were grown via high-temperature and high-pressure techniques (39) and were exfoliated into thin sheets onto Si/SiO₂ substrates. A dry transfer technique was used to assemble hBN/BP/hBN stacks (58) inside a Vacuum Technology Inc. glove box with moisture and oxygen concentration <0.1 parts per million. The top hBN layer was etched in SF₆ plasma to expose the BP layer, and Cr/Au electrodes were deposited thereafter by electron beam evaporation. To fabricate the top gate, a dielectric layer of 50- to 70-nm Al₂O₃ was deposited onto the entire stack. The devices were measured in an He³ cryostat using standard direct current or lock-in techniques at the National High Magnetic Field Laboratory at magnetic fields ranging from 0 to 30 T.