Communication: Direct evidence for sequential dissociation of gas-phase Fe(CO)₅ via a singlet pathway upon excitation at 266 nm

Abstract

We prove the hitherto hypothesized sequential dissociation of Fe(CO)₅ in the gas phase upon photoexcitation at 266 nm via a singlet pathway with time-resolved valence and core-level photoelectron spectroscopy with an x-ray free-electron laser. Valence photoelectron spectra are used to identify free CO molecules and to determine the time constants of stepwise dissociation to Fe(CO)₄ within the temporal resolution of the experiment and further to Fe(CO)₃ within 3 ps. Fe 3p core-level photoelectron spectra directly reflect the singlet spin state of the Fe center in Fe(CO)₅, Fe(CO)₄, and Fe(CO)₃ showing that the dissociation exclusively occurs along a singlet pathway without triplet-state contribution. Our results are important for assessing intra- and intermolecular relaxation processes in the photodissociation dynamics of the prototypical Fe(CO)₅ complex in the gas phase and in solution, and they establish time-resolved core-level photoelectron spectroscopy as a powerful tool for determining the multiplicity of transition metals in photochemical reactions of coordination complexes.

The photochemistry of metal carbonyls has been the subject of numerous investigations,^1,2 and Fe(CO)₅ has always occupied a prominent role as a prototypical benchmark case for organometallic photoreactions.³ To date, the photo-induced dissociation of metal carbonyls,^4,5 specifically Fe(CO)₅,^6–10 has attracted great interest. In the quest for understanding what determines reactivity in organometallic photoreactions, it is essential to understand how intra- and intermolecular relaxation processes interplay as both determine the photochemical reactivity.^1–3,11 Contrasting the photodissociation of Fe(CO)₅ in the gas phase and in solution thus helps understanding how fundamental processes of bond dissociation and formation, intersystem crossing, and vibrational relaxation in solution influence the excited-state dynamics of the reactive intermediates on fs to ps time scales.^12,13 Owing to its reduced complexity and the missing solute-solvent interactions, gas-phase Fe(CO)₅ can be regarded as a reference case and the question occurs about how well we actually know this reference.

As summarized by Poliakoff and Turner in 2001,¹⁴ the loss of multiple CO molecules upon UV photolysis of gas-phase Fe(CO)₅ (a singlet ground state) has been established early in Refs. 6, 15, and 16 while the time scale of photodissociation remained unknown as well as whether dissociation proceeded sequentially or synchronously. Similarly, the multiplicity of the transient intermediates Fe(CO)₄ and Fe(CO)₃ remained elusive. The ground states of Fe(CO)₄ and Fe(CO)₃ in rare-gas matrices were found to be triplets.^16,17 The triplet ground state of gas-phase Fe(CO)₄ was confirmed theoretically^18–20 hence suggesting a triplet pathway from excited singlet-state Fe(CO)₅ to triplet-state Fe(CO)₄ via intersystem crossing.¹⁹ In a seminal investigation of the gas-phase photodissociation of Fe(CO)₅ upon excitation at 266 nm with femtosecond-resolution optical ionization experiments, Fuss and co-workers²¹ accurately measured time constants ranging from tens of fs to few ps albeit without the ability to uniquely assign species. They further assumed that intersystem crossing could not occur on such short time scales and thus proposed a sequential singlet pathway. Dissociation was proposed to proceed from excited singlet-state Fe(CO)₅ to excited singlet-state Fe(CO)₄ (¹A₁) within less than 100 fs with a subsequent dissociation of a second CO to Fe(CO)₃ with a time constant of 3.3 ps.²¹ Singlet-state Fe(CO)₄ in the gas phase was indeed detected with time-resolved electron diffraction by Ihee, Cao, and Zewail,²² but their temporal resolution was limited to 10–20 ps and excitation was indirect with two-photon absorption at 620 nm.

An experimental proof for sequential Fe(CO)₅ photodissociation in the gas phase is still missing. This is essential as successive dissociation motivates designing strategies to stabilize the reactive intermediate Fe(CO)₄ for subsequent reactions. Furthermore, the experimental verification of singlet-state Fe(CO)₄ at short time scales of 1 ps or less and thus the validation or disproval of the proposed singlet²¹ or triplet pathway¹⁹ are still missing. This is important because the triplet ground state of Fe(CO)₄ was detected in solution^7,8 thus indicating a corresponding reaction barrier.²⁰ The incomplete knowledge of gas-phase Fe(CO)₅ photodissociation is largely due to limitations of currently established experimental techniques. These limitations are overcome in the present study with optical pump and x-ray probe spectroscopy at the x-ray free-electron laser FLASH,²³ and the open questions are answered. The new insight is based on probing the reaction intermediates with time-resolved valence and core-level photoelectron spectroscopy.^24–31

Fe(CO)₅ was pumped at 266 nm and probed with soft x-ray pulses from the x-ray free-electron laser FLASH in Hamburg (Germany)²³ with time-resolved x-ray photoelectron spectroscopy (repetition rate, 10 Hz; x-ray photon energy, 123 eV; photon-energy bandwidth, 0.1 eV; x-ray pulse energies of 20–40 μJ/pulse before the monochromator; spot size, 280 μm horizontal and 400 μm vertical, Gaussian FWHM; x-ray pulse duration, 100 fs). A comparison of rare-gas photoelectron spectra measured at these conditions with previously published and with previously measured rare-gas spectra with the same setup at FLASH showed no indication for an influence of the comparably low probe-pulse energy on our measurements. Fe(CO)₅ and CO were prepared as effusive jets in an ultrahigh-vacuum chamber where the photodecomposition of Fe(CO)₅ prior to measurements was prevented by keeping it in the dark and using a fresh sample for each measurement shift. Photoelectron kinetic energies were analyzed with a magnetic-bottle-type time-of-flight electron spectrometer (electron-energy bandwidth: 0.4–1.2 eV, for valence photoelectron kinetic energies of 118–103 eV, and 1.5 eV, for Fe 3p core-level photoelectron kinetic energies around 60 eV). Pump and probe pulses propagated nearly collinearly through the interaction region. Pump pulses at 266 nm were obtained by the third-harmonic generation of a Ti:Sa laser (pulse duration, 150 fs; pulse energy, 25 μJ/pulse; pump fluence, 7 mJ/cm²; pump peak intensity, 1.2 × 10¹¹ W/cm²; spot size, 500 μm horizontal and 700 μm vertical, Gaussian FWHM). The pump-probe signals were found to saturate at higher pump fluences, and no indication of multiphoton or other non-linear effects by the pump laser were detected. Our pump intensity is higher than the intensity of 10⁹ W/cm² used in Ref. 21 but much lower than the intensity of 10¹⁴ W/cm² used in Ref. 6 or the intensity of 10¹³ W/cm² for the 2-photon excitation with 620 nm in Ref. 22. In a post processing analysis, data were sorted to correct for unintentional changes of pump-probe delay times (detected with a streak camera correlating the radiation of the optical laser and dipole radiation from FLASH). This average (in contrast to shot-to-shot) correction ensured the correction of long-term drifts (minutes/hours) of the pump-probe delay. A shot-to-shot correction, as required for a better temporal resolution, could unfortunately not be realized at the time of data acquisition at FLASH for the present study. More details of the experimental design and realization will be presented in a forthcoming publication.

The kinetic rate-model fit was performed with the following set of equations:

$$\begin{array}{cc}\hfill \text{Fe}{\left(\text{CO}\right)}_5{N}_5\left(t\right)& =1-f_s\left(\mathit{w},t\right),\hfill \\ \hfill \text{Fe}{\left(\text{CO}\right)}_4{N}_4\left(t\right)& =f_d\left({\tau }_4,\mathit{w},t\right),\hfill \\ \hfill \text{Fe}{\left(\text{CO}\right)}_3{N}_3\left(t\right)& =1-N_5\left(t\right)-N_4\left(t\right)=f_s\left(\mathit{w},t\right)-f_d\left({\tau }_4,\mathit{w},t\right),\hfill \\ \hfill \text{C}\text{O}1N_{\text{C}\text{O}1}\left(t\right)& =1-N_5\left(t\right)=f_s\left(\mathit{w},t\right),\hfill \\ \hfill \text{C}\text{O}2N_{\text{C}\text{O}2}\left(t\right)& =N_3\left(t\right)=f_s\left(\mathit{w},t\right)-f_d\left({\tau }_4,\mathit{w},t\right)\hfill \end{array}$$

with

$$f_s\left(\mathit{w},t\right)=\frac{1}{2}\left[1+\text{erf}\left(\frac{2\sqrt{ln2}}{\mathit{w}}t\right)\right]$$

and

$$f_d\left({\tau }_4,\mathit{w},t\right)=e^{-\left(t-\beta \right)∕{\tau }_4}{f}_s\left(\mathit{w},t-2\beta \right)$$

with

$$\beta =\frac{{\mathit{w}}^2}{{\tau }_4\left(16ln2\right)}.$$

$N_{\text{i}}\left(t\right)$ are the fitted populations of the respective species, $f_s\left(\mathit{w},t\right)$ is the convolved step function for a temporal resolution w (Gaussian FWHM), $f_d\left({\tau }_4,\mathit{w},t\right)$ is the convolved exponential decay for a temporal resolution w and the lifetime (time constant) ${\tau }_4$ for the decay, and $N_5\left(t\right)$ encodes the depletion of Fe(CO)₅. The parameter w (temporal resolution) was fitted to 1 ± 0.3 ps (Gaussian FWHM). The time constant ${\tau }_4$ for the exponential decay of Fe(CO)₄ and rise of CO2 was fitted to 2.8 ± 1.9 ps.

Valence-electron binding energies were computed in multiconfigurational self-consistent-field (MCSCF) calculations similar to the approach of Grell et al.³² as energy differences between the CASPT2(10,10) initial ground and final ionic states with one electron less, and they included scalar relativistic effects and spin-orbit coupling.³³ The geometries of the complexes were optimized at the CASPT2(12,12) level. Within the crystal-field multiplet (CFM) model,^34,35 Fe 3p photoelectron spectra of the singlet ground-state (¹A₁) and the excited triplet-state (³B₂) of Fe 3d⁸ 4s⁰ were calculated. Minimal assumptions were introduced to robustly extract the spectral contrast between low-spin (singlet) and high-spin (triplet) states by matching the valence energy-level structure of Fe(CO)₅, Fe(CO)₄, and Fe(CO)₃ from the CFM calculation with that of the MCSCF calculations by using parameters 10Dq = 1 eV and Ds = −5 eV in the CFM calculations. For each final ionic state, a Lorentzian profile with a FWHM of 1.2 eV was calculated reflecting the lifetime broadening of the core-hole states,³⁶ and all Lorentzians were summed and convoluted with the experimental bandwidth of 1.5 eV (Gaussian FWHM reflecting combined photon-energy and electron-kinetic-energy bandwidths).

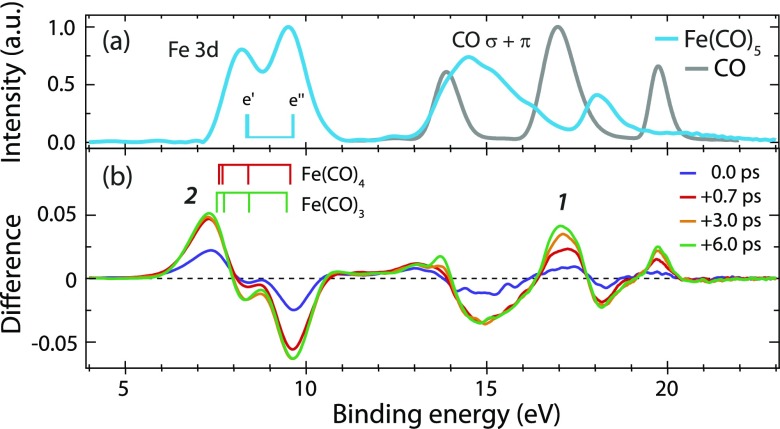
Our time-resolved valence photoelectron spectra are shown in Fig. 1. The spectrum of Fe(CO)₅ [Fig. 1(a)] was studied earlier and shows peaks assigned to Fe 3d and CO σ and π orbitals.^37,38 The difference spectra extracted for the indicated time delays [Fig. 1(b)] exhibit the rise of new species (peaks 1 and 2) and depletion of Fe(CO)₅ (mainly at 9.5 and 15 eV). We concentrate here on peaks 1 and 2 and note that all other changes in the spectrum can be consistently interpreted.

FIG. 1.

(a) Valence photoelectron spectra of Fe(CO)₅ and CO (photon energy 123 eV, intensities normalized to one at maximum). (b) Difference spectra at indicated delay times after the excitation of Fe(CO)₅ at 266 nm (positive delays correspond to the pump before probe pulses; the spectrum of unpumped molecules at −3 ps was subtracted from the measured intensities at the given delays). Calculated final ionic-state energies are indicated by vertical bars for Fe(CO)₅ in (a) and for Fe(CO)₄ and Fe(CO)₃ in (b) with ionization from, with increasing binding energy, (e′, e″) orbitals in Fe(CO)₅, (a₁, b₂, b₁, a₂) in Fe(CO)₄, and (a′, a″, a′, and a″) in Fe(CO)₃.

Since our temporal resolution is 1 ps, we do not expect to probe the initial dynamics of excited-state Fe(CO)₅ on the 100 fs time scale and rather focus on the dissociation dynamics with the formation of Fe(CO)₄ and Fe(CO)₃. With the CO valence photoelectron spectrum [Fig. 1(a)] measured under identical conditions shortly after the pump-probe measurements of Fe(CO)₅, peak 1 in the transient spectra in Fig. 1(b) can be unambiguously assigned to free CO molecules arising from dissociation. Its intensity continues rising up to the maximum measured delay of 6 ps while Fe(CO)₅ depletion saturates with a delay of 0.7 ps. This already indicates a successive dissociation where Fe(CO)₅ depletes during the first dissociation step only and CO continues rising as it is formed in one or more consecutive dissociation steps.

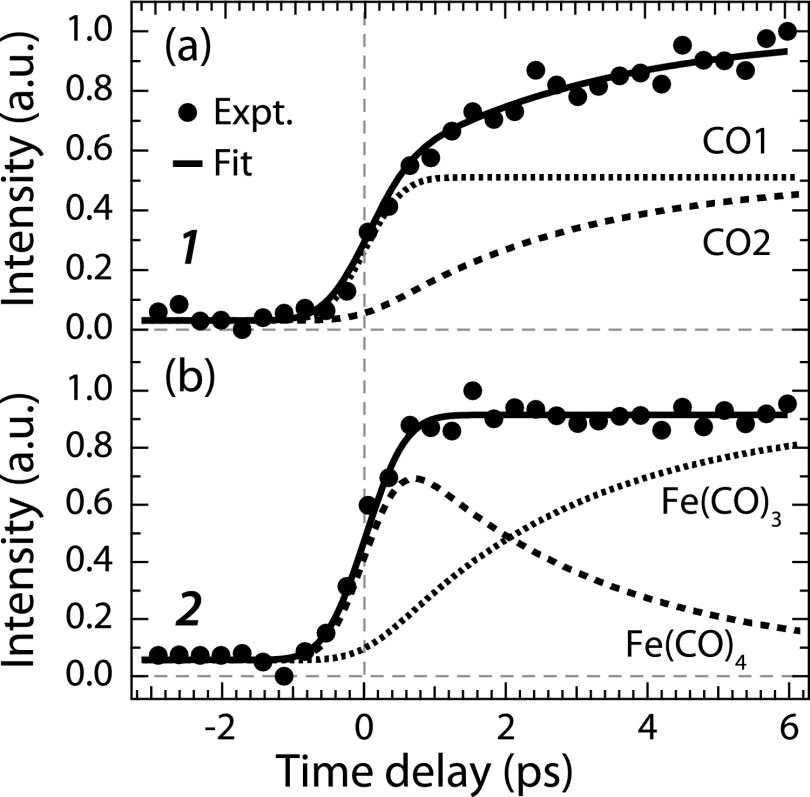
The temporal evolution of intensities of peaks 1 and 2 is plotted in Fig. 2 and compared to a kinetic rate-model fit employing the minimum necessary number of parameters to fit the experimental data.

FIG. 2.

Integrated intensities of CO, Fe(CO)₄, and Fe(CO)₃ valence photoelectron peaks (1 and 2 in Fig. 1) versus pump-probe delay time (closed circles, integration intervals 16.6–17.3 eV for 1 and 6.6–8 eV for 2, intensities normalized to one at maximum). The best fit of a kinetic model is shown as solid lines with the respective components.

The steadily increasing intensity of peak 1 is found to result from two components. First, it increases within temporal resolution due to the appearance of the first free CO from Fe(CO)₅ to Fe(CO)₄ dissociation [CO1 in Fig. 2(a)]. Second, it rises due to the second free CO from successive Fe(CO)₄ to Fe(CO)₃ dissociation [CO2 in Fig. 2(a), exponential rise with a time constant of 2.8 ± 1.9 ps]. Our data thus directly validate successive Fe(CO)₅ photodissociation at 266 nm as proposed by Fuss and co-workers²¹ in two consecutive steps. Extending their work, our valence photoelectron spectroscopy results allow for unambiguously assigning species to the measured time constants.

With our multiconfigurational self-consistent-field (MCSCF) calculations using a basis set of triple-zeta valence with polarization quality (ANO-RCC-VTZP) shown as bar diagrams in Fig. 1(b), peak 2 in particular can be assigned to Fe(CO)₄ and Fe(CO)₃. Consistent with our findings on CO evolution in Fig. 2(a), peak 2 is found to rise within the temporal resolution and to stay constant thereafter [Fig. 2(b)]. Its intensity evolution apparently results from the mutually varying populations of Fe(CO)₄ and Fe(CO)₃. The intensity component of Fe(CO)₄ rises within 1 ps due to Fe(CO)₅ to Fe(CO)₄ dissociation paralleling CO1 evolution, and it decays exponentially with a fitted time constant of 2.8 ± 1.9 ps concomitant with the rise of CO2 due to the successive dissociation of Fe(CO)₄ to Fe(CO)₃ [the Fe(CO)₃ signal rises concomitantly].

Having established the kinetics, we now turn to exploiting the element- and site-specificity of core-level photoelectron spectroscopy. The measured time-resolved Fe 3p photoelectron spectra, their differences for selected delays, and the temporal evolution of selected spectral regions with the kinetic rate-model fit are shown in Fig. 3.

FIG. 3.

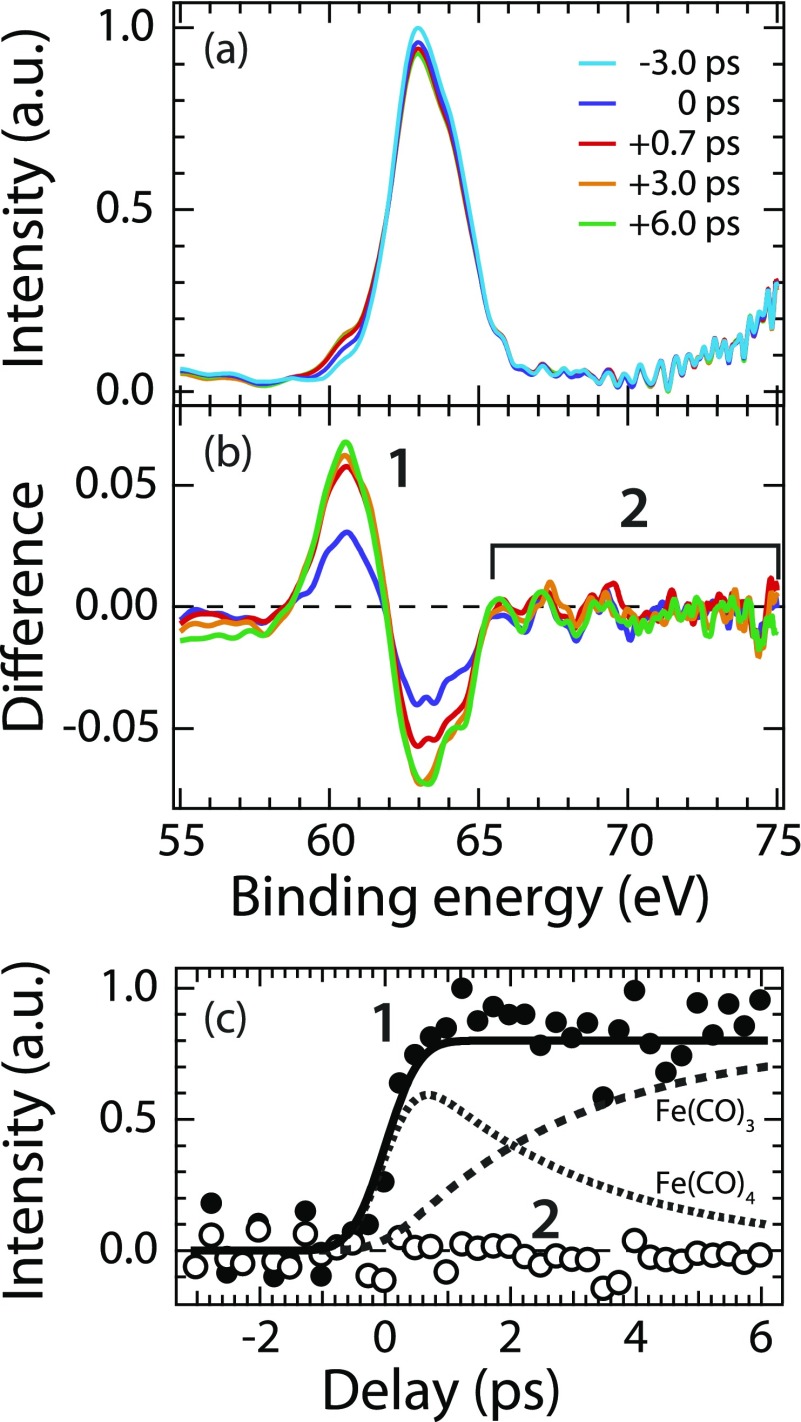
(a) Fe 3p core-level photoelectron spectra of Fe(CO)₅ at indicated delay times after excitation at 266 nm (photon energy 123 eV, intensity of the −3.0 ps spectrum normalized to one at maximum). (b) Difference spectra (the spectrum corresponding to unpumped molecules at −3 ps was subtracted from the intensities at the given delays). (c) Integrated intensities versus pump-probe delay time of the Fe(CO)₄ and Fe(CO)₃ peak (1, closed circles, integration interval 58.5–62 eV, intensities normalized to one at maximum) and of the high-energy side of the Fe 3p peak (2, open circles, integration interval 65.5–75 eV) with the kinetic model (solid lines) taken from Fig. 2 without changes.

The peak at 63 eV in Fig. 3(a) is due to emission from the Fe 3p core level in Fe(CO)₅,³⁸ thereby establishing elemental specificity of our probe. It depletes with the increasing time delay due to Fe(CO)₅ dissociation at the expense of the increasing peak 1 at 60–61 eV assigned to the photofragments [Fig. 3(b)]. The temporal evolution of peak 1 is well explained with our kinetic model [Fig. 3(c)] with the mutually varying contributions of Fe(CO)₄ and Fe(CO)₃. This is consistent with a chemical shift of the Fe 3p photoelectron peak by −2 to −3 eV when going from Fe(CO)₅ to Fe(CO)₄ or Fe(CO)₃. The details of this chemical shift and a closer inspection of the time-dependent changes in the valence photoelectron spectra will be analyzed in a forthcoming publication together with a discussion about how to, potentially, further distinguish spectroscopically between Fe(CO)₄ and Fe(CO)₃.

More interestingly, we find no intensity arising on the high-binding energy side of the Fe 3p line at 65–75 eV [see region 2 in Fig. 3(b)]. Intensity of region 2 is constant at zero within the delay range of 6 ps as measured here and within the statistical uncertainty of our experiment [Fig. 3(c)]. This absence of intensity proves that Fe(CO)₄ and Fe(CO)₃ occur in a singlet state as is explained with the help of Fig. 4.

FIG. 4.

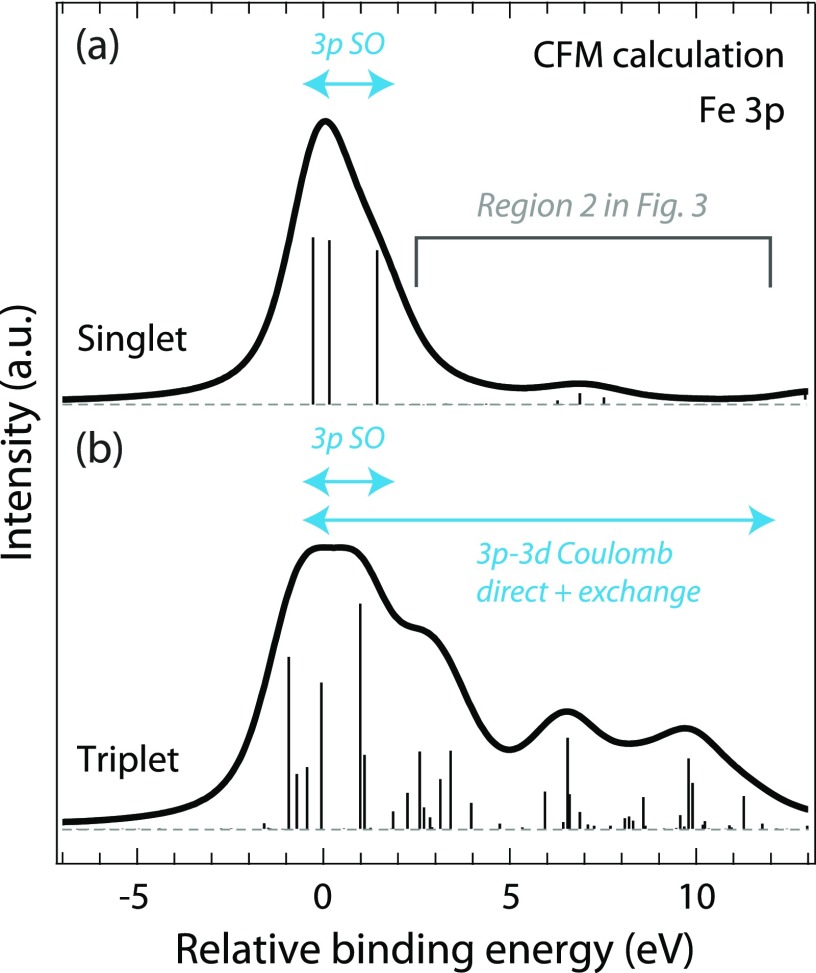
Fe 3p photoelectron spectra calculated within the crystal-field multiplet (CFM) model representing (a) singlet and (b) triplet states of, within the approximations of the CFM model, Fe(CO)₅, Fe(CO)₄, and Fe(CO)₃. Sticks are calculated binding energies and transition intensities of the final ionic 3p⁻¹ core-hole states. Spectra were aligned to 0 eV at maximum for an easier comparison of the shapes with intensities normalized at maximum.

Our approach for determining the spin state is based on using the localized 3p core hole on Fe and the induced local atomic multiplet effects to extract the multiplicity of Fe(CO)₄ and Fe(CO)₃. Fadley and co-workers established that the 3p photoelectron spectrum of 3d transition-metal atoms and ions in open-shell (high-spin) configurations exhibits atomic multiplet effects due to the strong core-valence 3p-3d Coulomb direct and exchange interactions in the final ionic states thus spreading the spectrum over more than 10 eV to the higher binding-energy side of the main 3p line.^39,40 Closed-shell (low-spin) configurations in contrast, such as in the Cu atom, show a single peak⁴¹ merely broadened by 3p spin-orbit interactions of 1–2 eV.^41,42 With our crystal-field multiplet (CFM) model calculations for Fe(CO)₅, Fe(CO)₄, and Fe(CO)₃ in Fig. 4, we extend this approach to infer the multiplicity of the transient intermediates, Fe(CO)₄ and Fe(CO)₃. For singlet states, the Fe 3p photoelectron spectrum exhibits one peak, thus well describing singlet-state Fe(CO)₅. In hypothetical triplet states, the 3p-3d core-valence interactions spread the multiplet to higher binding energies over more than 10 eV. Intensity in this region (region 2 in Fig. 3) is therefore a sensitive measure of the spin-state of Fe(CO)₄ and Fe(CO)₃. The absence of intensity in this region in our time-resolved core-level photoelectron spectra thus unambiguously proves that neither the transient intermediate Fe(CO)₄ nor Fe(CO)₃ on time scales up to 6 ps occurs in a triplet state. This directly validates the proposed singlet pathway for Fe(CO)₅ photodissociation.²¹ It also demonstrates the complementarity of time-resolved 3p photoelectron and K_β fluorescence spectroscopy⁴³ for determining the multiplicity of 3d transition-metal centers in inorganic and organometallic photoreactions^44,45 as both owe their sensitivity to the same 3p-3d core-valence interactions.

In summary, the photodissociation of the prototypical organometallic compound Fe(CO)₅ in the gas phase is investigated with optical pump and x-ray probe photoelectron spectroscopy at an x-ray free-electron laser. Our data prove successive dissociation to Fe(CO)₄ in a first step with subsequent dissociation to Fe(CO)₃ in a second step. We unambiguously find that neither the transient intermediate Fe(CO)₄ nor Fe(CO)₃ on time scales up to 6 ps occurs in their triplet ground states. This validates the proposed singlet pathway for Fe(CO)₅ photodissociation.²¹ Our time-resolved observation of singlet-state Fe(CO)₄ can guide future studies that aim at making use of the high reactivity of this coordinatively unsaturated intermediate. We define a time window of 3 ps during which further dissociation of Fe(CO)₄ as well as dissipative transition to its unreactive triplet state has to be prevented in order to make its excess energy accessible. Our results indicate that solute-solvent interactions possibly involving vibrational relaxation^12,13 may be necessary for the formation of triplet-state Fe(CO)₄. With time-resolved core-level photoelectron spectroscopy, we selectively probe and follow in time the evolution of the multiplicity of the Fe center thereby benchmarking time-resolved optical pump and x-ray probe photoelectron spectroscopy for extracting spin-density dynamics in organometallic photoreactions. Our results further extend the demonstrated capabilities of time-resolved photoelectron spectroscopy with optical and extreme ultraviolet (XUV) probe pulses,^24–31 thus complementing other time-resolved experimental techniques for the investigation of photochemical reactions.^46–56