Bayesian semiparametric variable selection with applications to periodontal data

Abstract

A normality assumption is typically adopted for the random effects in a clustered or longitudinal data analysis using a linear mixed model. However, such an assumption is not always realistic, and it may lead to potential biases of the estimates, especially when variable selection is taken into account. Furthermore, flexibility of nonparametric assumptions (e.g. Dirichlet process) on these random effects may potentially cause centering problems, leading to difficulty of interpretation of fixed effects and variable selection. Motivated by these problems, we proposed a Bayesian method for fixed and random effects selection in nonparametric random effects models. We modeled the regression coefficients via centered latent variables which are distributed as probit stick-breaking (PSB) scale mixtures. By using the mixture priors for centered latent variables along with covariance decomposition, we could avoid the aforementioned problems, and allow efficient selection of fixed and random effects from the model. We demonstrated the advantages of our proposed approach over other competing alternatives through a simulated example, and also via an illustrative application to a dataset from a periodontal disease study.

1. Introduction

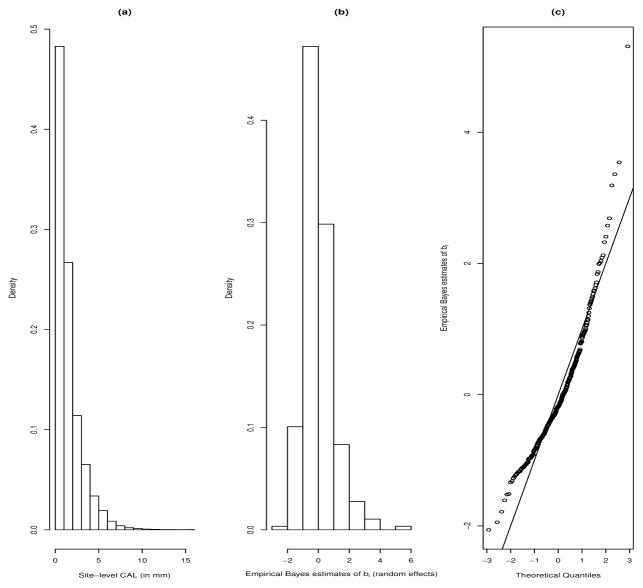
Linear mixed (effects) models are routinely used to analyze clustered and longitudinal data, where a common feature is the fidelity to the ‘Gaussian’ paradigm for the random effects and within subject random errors. Even though normality might be a reasonable model assumption, its violations may potentially impact the underlying estimation, prediction, etc of both the fixed and random effects. For example, consider the motivating data example from a clinical study conducted at the Medical University of South Carolina (MUSC) to determine periodontal health status of Gullah-speaking African American Type-2 diabetic (GAAD) subjects. One of the most important biomarkers to assess periodontal disease (PD), the clinical attachment level (or CAL, in mm), was measured for various pre-specified sites within a mouth/subject, giving rise to a typical clustered data framework. Figure 1 (Panel a) plots the density histogram of site-level CAL for the full data, while Panels b and c display the density histogram and Q-Q plots of the empirical Bayes’ estimates of the subject-level random effects, obtained after fitting a classical linear mixed model (LMM), controlling for some clinical covariables as fixed effects (such as Age, Gender, etc, more details in Section 5). These plots are indicative of the violation of the normality assumptions for the random effects, typically for a LMM analysis.

Figure 1.

Plots of density histogram for site-level CAL (Panel a); density histogram (Panel b) and Q-Q plots (Panel c) of empirical Bayes estimates of the subject-level random effects, obtained from fitting a LMM to the GAAD dataset.

To allow for flexibility of distributions of the random effect, several frequentist considerations are available [1, 2, 3]. Under the Bayesian framework, a vast majority of current research centers around the nonparametric Dirichlet process (DP) priors [4], DP mixtures [5], and other specifications, allowing unknown distributions for random effects [6, 7, 8, 9]. Under a LMM framework, inclusion of a covariate (say, age) only as a fixed effects component would quantify only the ‘average effect’ of age on the mean CAL (response), and leave out important information on how the age effect might vary across subjects. Hence, there is a need to also include a ‘random’ age effect to control for this with the ultimate goal to accommodate uncertainty of predictors and simultaneously achieve parsimony through variable selection and variance-covariance component selections. However, all of the methods described above do not accommodate this predictor uncertainty. One may potentially calculate AIC/BIC for each candidate model, yet this is infeasible unless the number of candidate predictors is modest. There does not exist any general consensus on the penalty for model complexity for a random effects model. Related frequentist propositions include score tests for random effect selection [10, 11, 12], a generalized likelihood ratio test [13], etc. However, these methods can not be directly utilized for the general subset selection problem. In a Bayesian context, a majority of work [14, 15, 16, 17, 18] focuses on variable/model selection in normal variance component models. Relaxing the normality assumption by a DP mixtures for the (unknown) random effects distribution, one may adopt the Basu and Chib [19] approach to compare the resulting semiparametric Bayesian model with the fully parametric linear model that excludes the random effect using marginal likelihoods and Bayes factors for DP mixtures. Such an approach is potentially feasible only when the number of competing random effect models is modest.

Under DP-related models for random effects, there is a difficulty in interpreting posterior inference for fixed effects and variance components of random effects due to the potential bias resulting from the unknown (distributional) specification of random effects. Under normality assumptions in the LMM, Chen and Dunson [17] proposed a Bayesian approach for random effects selection via a stochastic search variable selection algorithm [20] through a special decomposition of the random effects covariance. The Chen and Dunson’s model was extended [21] to fixed effects and random effects selection under linear and logistic mixed models. Unfortunately, it is not straightforward to modify these approaches to allow unknown random effects distributions due to difficulties in incorporating moment constraints. A center-adjusted approach was also proposed [22], however, it is difficult to incorporate random effects selection. The Chen and Dunson’s approach was also extended incorporating unknown distribution for random effects [23] using the centered stick-breaking mixtures [24]. A potential problem still remains because the variance of the latent variables related to random effects is not equal to one, resulting in non-unique decompositions of the covariance matrix for the random effects. Such decompositions may potentially affect the variance component selection and inferences. Cai and Dunson [25] developed a variable selection approach under the nonparametric random effects model with centered latent variables. However, the potential bias might still exist due to the nonparametric specification on the random effects.

In this article, we addressed some of the aforementioned limitations and developed a Bayesian approach for fixed and random effects selection with nonparametric distributions for random effects. By reparameterizing the random coefficients using centered latent variables relating to the fixed and random effects components, the proposed approach avoids the need for moment constraints, and the potential bias in estimation and variable selection. The centered latent variables were modeled by the probit stick-breaking (PSB) scale mixtures [24], allowing latent variables to be centered at the fixed effects. In addition, the centered reparametrization provided a way to incorporate variance-covariance components selection without violating the definition of decomposition of covariance matrix of the random effects. With these characteristics, the proposed method had more appropriate interpretation of the fixed effects and more efficient mixing behavior.

The paper proceeds as follows. Section 2 describes our Bayesian nonparametric specification of the LMM, the reparameterization of random coefficients, and the variable selection strategy. Section 3 outlines the posterior computational strategy, and related sampling procedures. Section 4 evaluates the performance of our method with existing alternatives using simulated data. Section 5 applies the methodology to the motivating PD dataset. Finally, Section 6 concludes, with some discussions.

2. Statistical Model

2.1. Nonparametric priors for random effects

We start with the definition of a typical LMM. Let y_ij be a response variable for the jth observation (j = 1, …, n_i) from subject i (i = 1, …, n), x_ij and z_ij be a p × 1 vector and a q × 1 vector of candidate predictors, respectively. The LMM for y_i can be written as

$${\mathbf{y}}_i={\mathbf{X}}_i\mathit{\beta }+{\mathbf{Z}}_i{\mathbf{b}}_i+{\mathit{\epsilon }}_i,$$ (1)

where y_i = (y_i1, …, y_ini)′, X_i = (x_i1, …, x_ini)′, Z_i = (z_i1, …, z_ini)′, β is a p × 1 vector of fixed effects regression coefficients, b_i = (b_i1, …, b_iq)′ ~ N_q(0, Σ) is a q × 1 vector of subject-specific random effects with covariance matrix Σ, and ε_i is a residual error vector, typically assumed to be ε_i ~ N(0, σ²I).

To allow for flexibility of the distributional assumption for the random effects, if all of the candidate predictors are included, one may choose b_i ~ G, where G is the unknown random effects distribution. Following the Bayesian approach [7], a prior distribution for G with support on the space of random probability measures can be chosen. A natural choice would be the DP prior which could be specified as G ~ DP(αG₀), where α is a precision parameter and G₀ is the base distribution of the DP. Under this specification, for any partition B = (B₁, …, B_k)′ of ℜ, we have {G(B₁), …, G(B_k)} ~ D(αG₀(B₁), …, αG₀(B_k)), where D(·) denotes the finite Dirichlet density. Under the stickbreaking representation of Sethuraman (1994) [26], we have

$$G=\sum _{h=1}^{\infty }{p}_h{\delta }_{{\mathit{\xi }}_h}(·),p_h=V_h\prod _{l<h}(1-V_l),V_h\stackrel{\mathit{iid}}{\sim }\text{beta}(1,\alpha ),{\mathit{\xi }}_h\stackrel{\mathit{iid}}{\sim }{G}_0,$$ (2)

with δ_ε denoting the degenerate distribution with all its mass at ε and V₀ = 0. Hence, the random distribution G can be represented as an infinite set of point masses at locations generated independently from the base distribution. In addition, we have E(G) = G₀, with a natural choice of G₀ being the N_q(0,Σ) distribution, so that the prior is centered at the LMM. Under this specification, the expected value of y_i (conditional on X_i and Z_i) is E(y_i |X_i,Z_i, β,G) = X_iβ + Z_iE(b_i). Now, under the nonparametric DP setting, the random effects distribution cannot guarantee that the mean of random effects is centered at 0 as the random mean of G, E(b_i) = ∫ b_idG(b_i), is typically non-zero. This leads to potential complications of interpretation and inference for the fixed effects corresponding to the random effects. In addition, the computational efficiency of Gibbs sampling algorithms for posterior computation in the LMM(and other hierarchical models) tends to depend strongly on the parameterization used [27]. For greater efficiency, one can focus on the centered parameterization: y_i = X_iβ_i + ε_i, with β_i ~ G, G ~ DP(αG₀), and G₀ = N_p(μ,Σ), assuming X_i = Z_i so p = q. In this case, the fixed effects can be expressed as β = ∫ β_idG(β_i) by integrating out the random effects. Li et al. [22]proposed a moment-adjustment procedure for inference on the fixed effects that are paired with the random effects and the variance components of the random effects with hierarchically centered DP prior. However, this approach assumes that all predictors are certainly included in the fixed and random effects components. In addition, it is not straightforward for this method to be extended to the case where fixed and random effects selection is taken into account. The reason is that the fixed and random effects must be paired in order to avoid the non-zero mean of random effect due to the DP setting. Yang [23] proposed a method for fixed and random effects selection with nonparametric distributions for the random effects. To avoid the potential biases caused by the nonparametric DP prior, the random effects are modeled nonparametrically by using the probit stick-breaking (PSB) scale mixtures [24].

The PSB approach [28, 29] was proposed for conditional distribution modeling with variable selection. Briefly, a probability measure G follows a PSB with base measure G₀ if it has a representation of the form

$$G=\sum _{h=1}^{\infty }{p}_h{\delta }_{{\mathit{\xi }}_h}(·),p_h=\mathrm{\Phi }({\eta }_h)\prod _{l<h}(1-\mathrm{\Phi }({\eta }_l)),{\eta }_h\stackrel{\mathit{iid}}{\sim }\mathrm{N}({\mu }_{\eta },{\sigma }_{\eta }^2),{\mathit{\xi }}_h\stackrel{\mathit{iid}}{\sim }{G}_0,$$ (3)

where Φ(·) denotes the cumulative standard normal distribution. [24] proposed priors for the residual density based on PSB scale mixtures and symmetrized PSB (sPSB) location-scale mixtures. Note that expression (3) is identical to the stick-breaking representation [26] of the DP, but the DP is obtained by replacing the stick-breaking weight Φ(η_h) with a beta(1, α) distributed random variable. Hence, the PSB process differs from the DP in using probit transformations of Gaussian random variables instead of betas for the stick lengths. In addition, η_h is not necessarily to be predictor-dependent, though it can be generalized as a predictor-dependent parameter. To allow the residuals of the linear regression model to follow an unknown distribution, a normal hierarchical structure was used with the proposed priors. For the scale PSB process mixture of Gaussian, the nonparametric distribution f(·) can be expressed as $f(·)={\sum }_{h=1}^{\infty }{p}_h\mathrm{N}(·;0,{\tau }_h^{-1})$, where p_h’s are defined as in (3), τ_h ~ 𝒢(a_τ, b_τ) and 𝒢(a, b) denote a gamma prior with mean of a/b and variance of a/b². Note that the unknown density f(·) is expressed as a countable mixture of Gaussians centered at zero but with varying variances. Observations will be automatically allocated to clusters, with outlying clusters corresponding to components having large variance. Similarly, the location-scale sPSB mixture of Gaussians can be expressed as $f(·)={\sum }_{h=1}^{\infty }{p}_h(\mathrm{N}(·;-{\mu }_h,{\tau }_h^{-1})+\mathrm{N}(·;{\mu }_h,{\tau }_h^{-1}))/2$, and remains centered at zero while allowing for multimodal densities. The resulting property of centering at zero from the PSB approach provides us a solution to the non-zero centering problem from the conventional DP setting.

2.2. Fixed and random effects selection

In this article, our focus is on selecting the predictors to be included in the fixed effects and random effects components of the model under nonparametric settings. The fixed effects and random effects components have p and q candidate predictors respectively. One of the methods on subset selection for the fixed effects predictors is based on mixture priors for the regression coefficients β [30, 31]. In particular, because β_l = 0 corresponds to the lth candidate predictor being effectively excluded from the fixed effects component, a prior that assigns positive probability to both H_0l : β_l = 0 and H_1l : β_l ≠ 0, for l = 1, …, p, allows for uncertainty in the subset of predictors to be included. In linear regression models, many choices of mixture priors have been proposed, and a variety of algorithms are available for posterior computation.

Compared to fixed effects selection, selection of random effects components is more challenging. One may intuitively follow the idea of fixed effects selection by inserting a vector of indicator variables, γ = diag(γ₁, …, γ_q) in the LMM specification resulting in Z_iγb_i. With γ_l = 1, the lth random effects is included and γ_l = 0 otherwise. One may then combine it with b_i ~ G with G ~ DP(αG₀). Although the steps are straightforward, this approach is not immune to flaws such as the uncentered parameterization resulting in potential estimation biases, modeling the covariance random effects indirectly through G₀ instead of G, and impossibility of selection of off-diagonal elements in the random effects covariance matrix. Chen and Dunson [17] proposed a modified Cholesky decomposition of Σ in developing a stochastic search variable selection algorithm, but their approach relies on introducing standard normal latent variables underlying the random effects. Here, the LMM takes the form y_i = X_iβ + Z_iΛΓε_i + ε_i, where the latent variables ε_i are constrained to follow N(0,1), Λ is a diagonal matrix, and Γ is a lower triangular matrix with 1’s in the diagonal entries. With the reparameterizations and constraints, E(b_i) = 0 and Var(b_i) = ΛΓΓ′Λ′. This Cholesky decomposition allows for selection of both diagonal elements (variances) and off-diagonal elements (covariances) through mixture priors. In the nonparametric case, one could instead model the latent variables as having an unknown distribution with mean 0 and variance 1. However, such constraints are non-trivial to include in nonparametric models. The approach by Yang [23] (described earlier) assumes the latent variables ε_i to follow the centered PSB and sPSB mixtures of Gaussians. Integrating out random effects results in the decomposition of the covariance matrix of the random effects, such that Var(b_i) = ΛΓΩΓ′Λ′ with Var(ε_i) = Ω. Selecting elements in Λ regardless of Ω in the approach may lead to potential biases in fixed effects and random effects selection.

2.3. Reparameterization and prior specification

To resolve the aforementioned drawbacks, we reparameterize the random effects with centered nonparametric distributions for the centered latent variables. In practice, it is typically unknown which covariates will be included/excluded in terms of fixed and random effects. To allow for selection of fixed and random effects for all covariates, we let X_i = Z_i. Then, model (1) can be expressed as

$${\mathbf{y}}_i={\mathbf{X}}_i{\mathit{\beta }}_i+{\mathit{\epsilon }}_i.$$ (4)

Instead of modeling β_i as the random effects centered at the fixed effects, we model β_i as

$${\mathit{\beta }}_i=\mathit{\beta }+\mathbf{\Gamma }({\mathit{\beta }}_i^{\ast }-\mathit{\beta }),$$ (5)

where ${\mathit{\beta }}_i^{\ast }={({\beta }_{i1}^{\ast },\dots ,{\beta }_{ip}^{\ast })}^{\prime }$ denotes a vector of independent latent variables underlying β_i, Γ denotes the lower triangular matrix with 1’s in the diagonal entries, and β denotes the fixed effects as in (1). In model (4), the candidate predictors included in the random effects are chosen as the candidate predictors included in the fixed effects, which allows all predictors to possibly vary across subjects. In addition, with the reparameterization of the random coefficients in (5), the proposed model allows for the nonparametric distributions of latent variables with possibility of avoiding the centering and scaling problems.

Let ${\beta }_{il}^{\ast }\stackrel{\mathit{iid}}{\sim }{G}_l$, for l = 1, …, p, where $G_l({\beta }_{il}^{\ast })=\int \mathrm{N}({\beta }_{il}^{\ast };{\beta }_l,{\lambda }_l)Q(d{\lambda }_l)$. The measure Q(·) is a random distribution of λ_l. To incorporate random effects selection into the model, we choose Q(·) as a mixture prior consisting of a point mass at zero (with probability π_l0) and a nonparametric PSB component:

$${\lambda }_l~{\pi }_{l0}{\delta }_0({\lambda }_l)+(1-{\pi }_{l0})P({\lambda }_l),P=\sum _{h=1}^{\infty }{p}_{lh}{\delta }_{{\lambda }_{lh}},{\lambda }_{lh}~\mathcal{I}\mathcal{G}(a_l,b_l),$$ (6)

where p_lh is defined as in (3), π_l0, a_l and b_l are hyperparameters. Typically, π_l0 is taken as 0.5 to reflect an equal preference of inclusion and exclusion. The prior probability that the lth predictor of the p candidate predictors is excluded from the random effects components is then π_l0 = Pr(λ_l = 0). Thus, the latent random coefficients ${\beta }_{il}^{\ast }$’s follow

$${\beta }_{il}^{\ast }\stackrel{\mathit{iid}}{\sim }\{\begin{array}{ll}{\delta }_{{\beta }_l}({\beta }_{il}^{\ast })\hfill & \text{with}{\pi }_{l0}\hfill \\ {\sum }_{h=1}^{\infty }{p}_{lh}\mathrm{N}({\beta }_{il}^{\ast };{\beta }_l,{\lambda }_{lh})\hfill & \text{with}1-{\pi }_{l0}\hfill \end{array}$$ (7)

With π_l0, the distribution of ${\beta }_{il}^{\ast }$’s reduces to a point mass distribution at β_l, implying that ${\beta }_{il}^{\ast }$’s, for i = 1, …, n, are replaced with β_l. In this case, the lth predictor only has no random effects. With 1 − π_l0, the resulting nonparametric distribution for ${\beta }_{il}^{\ast }$ implies that the latent variables are expressed as a countable mixture of Gaussians centered at the fixed effects β_l, but with varying variances. Under this scenario, there is heterogeneity of the effect of the lth predictor across subjects.

With the centering property of the PSB, it is obvious that the random coefficients β_i are centered at the fixed effects β with E(β_i) = β. In addition, it can be shown that Var(β_i) =ΓΨΨ′Γ′ which is the standard Cholesky decomposition of the covariance matrix with $\mathbf{\Psi }=\text{diag}({\psi }_1^{\frac{1}{2}},\dots ,{\psi }_p^{\frac{1}{2}})$, where ${\psi }_l=\text{Var}({\beta }_{il}^{\ast })$. When λ_l = 0 with probability π_l0, ψ_l = 0 and all the atoms in G_l are effectively generated from a point mass at β_l, such that there is no heterogeneity in the β_il coefficients among subjects. In this case, the corresponding off-diagonal elements γ_lr and γ_sl, for r = 1, …, l − 1, s = l + 1, …, p are removed by setting their values to 0. Note that γ_lr is only included in the model when both the lth and rth random effects are included, which occurs when ψ_l > 0 and ψ_r > 0. This procedure has no effect on the likelihood, but does impact posterior computation. We choose a prior for γ_ψ, the elements of γ that are included in the model. To facilitate posterior computation, we choose a conditionally conjugate N(γ_ψ; E_γψ, V_γψ) prior. In order to allow zero off-diagonal elements in the random effects covariance matrix, this prior can be easily modified to include a mass at zero. The overall prior probability of excluding all the random effects from the model is ${\prod }_{l=1}^p{\pi }_{l0}$. When ψ_l > 0 with 1 − π_l0, it is clear that ${\psi }_l={\sum }_{h=1}^{\infty }{p}_{lh}{\lambda }_{lh}$. [32] showed that with a truncated stick-breaking representation, ${\sum }_{h=1}^N{p}_h{\delta }_{{\mathit{\xi }}_h}(·)=1$ with ${\sum }_{h=1}^N{p}_h=1$ almost surely. For the choice of the truncation of the mixture, [33] suggested to use a reasonably large value such as 30, or the sample size.

To allow β_l to effectively drop out of the model, we choose a mixture prior consisting of a point mass at zero (with probability ν_l0) and a normal density:

$${\beta }_l~{\nu }_{l0}{\delta }_0({\beta }_l)+(1-{\nu }_{l0})\mathrm{N}({\beta }_l;{\beta }_{l0},{\sigma }_{l0}^2).$$ (8)

We refer to the prior (8) as a point-mass mixture prior, ${\mathrm{N}}_{{\delta }_0}({\beta }_{l0},{\sigma }_{l0}^2)$. The prior probability that the lth predictor of the p candidate predictors is excluded from the fixed effects component is then ν_l0 = Pr(β_l = 0). From the perspective of fixed effects and random effects selections, our specification can drop predictors by choosing mixture priors for the parameters β and Λ without being complicated by the nonparametric characterization. Following standard convention, we choose a conjugate gamma prior for the residual precision of the model, π(σ⁻²) 𝒢(c, d) with hyperparameters c and d.

3. Posterior computation

We choose priors for the parameters as described in Section 2.3. After initializing values for the parameters, the proposed Markov chain Monte Carlo (MCMC) algorithm proceeds through the following steps:

1. Following [32], we first update the cluster allocation parameter H_il, for i = 1, …, n and l = 1, …, p. The latent variable H_il indicates the cluster that β_il belongs to. Let ${\mathbf{z}}_i={\mathbf{y}}_i-{\mathbf{X}}_i{\mathbf{\Gamma }}^{\ast }\mathit{\beta }-{\mathbf{X}}_i{\mathbf{\Gamma }}_{-l}{\mathit{\beta }}_{i,-l}^{\ast }$, where Γ^* = I − Γ, Γ_−l denotes the submatrix of Γ excluding the lth column, and ${\mathit{\beta }}_{i,-l}^{\ast }$ denotes the subvector of ${\mathit{\beta }}_i^{\ast }$ with ${\beta }_{il}^{\ast }$ being excluded. Then H_il can be drawn from its full conditional posterior distribution, ${\sum }_{h=1}^{N_l}{\widehat{p}}_{\mathit{ilh}}{\delta }_h(·)$, where

   $${\widehat{p}}_{\mathit{ilh}}\propto p_{lh}{\mathrm{\sum }}_{il}^{\frac{1}{2}}{\lambda }_{lh}^{-\frac{1}{2}}{\sigma }^{-n_i}exp\left\{-\frac{1}{2}({\lambda }_{lh}^{-1}{\beta }_l^2+{\sigma }^{-2}{\mathbf{z}}_i^{\prime }{\mathbf{z}}_i-{\mathrm{\sum }}_{il}^{-1}{\mu }_{il}^2)\right\},$$

   with ${\mathrm{\sum }}_{il}={\{{\lambda }_{lh}^{-1}+{\sigma }^{-2}{({\mathbf{X}}_i{\mathbf{\Gamma }}_l)}^{\prime }({\mathbf{X}}_i{\mathbf{\Gamma }}_l)\}}^{-1},{\mu }_{il}={\mathrm{\sum }}_{il}\{{\lambda }_{lh}^{-1}{\beta }_l+{\sigma }^{-2}{({\mathbf{X}}_i{\mathbf{\Gamma }}_l)}^{\prime }{\mathbf{z}}_i\}$, and Γ_l being the lth column of Γ.

2. Under the current allocation {H_il = h : h ∈ (1, …, N_l)}, we update latent variable ${\beta }_{il}^{\ast }$, for i = 1, …, n and l = 1, …, p, from its full conditional posterior distribution given the data and other parameters, $\mathrm{N}({\beta }_{il}^{\ast };{\mu }_{il},{\mathrm{\sum }}_{il})$.

3. To update p_lh = Φ(η_lh)∏_r<h(1 − Φ(η_lr)), for h = 1, …, N_l and l = 1, …, p (following [24]), a latent variable ϕ_lh is introduced such that ϕ_lh ~ N(η_lh, 1). Thus, p_lh = P(ϕ_lh > 0, ϕ_lr < 0, for r < h). Then

   $${\varphi }_{lh}\mid ·~{\mathrm{N}}_{+}({\eta }_{lh},1)I(h=r)+{\mathrm{N}}_{-}({\eta }_{lh},1)I(h<r).$$

4. Updating η_lh, for h = 1, …, N_l and l = 1, …, p, is straightforward from its full conditional posterior distribution, $\mathrm{N}({\mathrm{\sum }}_{lh}({\sigma }_{\eta l}^{-2}{\mu }_{\eta l}+{\varphi }_{lh}),{\mathrm{\sum }}_{lh})$, where ${\mathrm{\sum }}_{lh}={({\sigma }_{\eta l}^{-2}+1)}^{-1}$ and ${\eta }_{lh}~\mathrm{N}({\mu }_{\eta l},{\sigma }_{\eta l}^2)$.

5. Following Geweke [30] and Kuo and Mallick [34], we update the variance component ψ_l, for l = 1, …, p, from the full conditional mixture distribution with point mass at 0. The conditional probability of ψ_l = 0 is calculated by integrating out λ_lh, for h = 1, …, N_l,

   $${\widehat{\pi }}_l=\frac{{\pi }_{l0}}{{\pi }_{l0}+(1-{\pi }_{l0})BF}$$
   with

   $$BF=\frac{\mathrm{L}({\mathit{\beta }}_l^{\ast },{\mathit{\beta }}_{-l}^{\ast },\mathit{\beta },\mathbf{\Gamma },{\sigma }^{-2};\mathbf{y})}{\mathrm{L}({\mathit{\beta }}_l^{\ast }={\beta }_l,{\mathit{\beta }}_{-l}^{\ast },\mathit{\beta },\mathbf{\Gamma },{\sigma }^{-2};\mathbf{y})}\prod _{h=1}^{N_l}\frac{\mathrm{\Gamma }({\widehat{a}}_{lh})b_l^{a_l}}{\mathrm{\Gamma }(a_l){\widehat{b}}_{lh}^{{\widehat{a}}_{lh}}},$$

   where L( ${\mathit{\beta }}_l^{\ast },{\mathit{\beta }}_{-l}^{\ast }$, β, Γ, σ⁻²; y) = ${\prod }_{i=1}^n$ N(z_i; X_iΓ_l ${\beta }_{il}^{\ast }$, σ²I_ni), ${\mathit{\beta }}_l^{\ast }$ = ( ${\beta }_{1l}^{\ast }$,…, ${\beta }_{nl}^{\ast }$)′, â_lh = a_l + $\frac{n_{lh}}{2}$, b̂_lh = b_l + $\frac{1}{2}$Σ_{i:Hil = h} ( ${\beta }_{il}^{\ast }$ − β_l)², and n_lh = ♯{i : H_il = h}. With π̂_l, we choose ψ_l from the degenerate distribution δ₀(·), which means that we have ψ_l = 0 and ${\beta }_{il}^{\ast }={\beta }_l$. Otherwise, we generate λ_lh from ℐ𝒢(â_lh, b̂_lh), for h = 1, …, N_l.

6. Similarly, Following [30, 34], we update the parameters related to the fixed effects and random effects selection. The fixed effects β_l, for l = 1, …, p, can be sampled from the mixture distribution with the point mass at 0, given by

   $${\widehat{\nu }}_l{\delta }_0({\beta }_l)+(1-{\widehat{\nu }}_l)\mathrm{N}({\beta }_l;{\widehat{E}}_l,{\widehat{V}}_l),$$
   where the probability of β_l = 0 is calculated by integrating out β_l,

   $${\widehat{\nu }}_l=\frac{{\nu }_{l0}{\sigma }_{l0}exp({\sigma }_{l0}^{-2}{\beta }_{l0}^2/2)}{{\nu }_{l0}{\sigma }_{l0}exp({\sigma }_{l0}^{-2}{\beta }_{l0}^2/2)+(1-{\nu }_{l0}){\widehat{V}}_l^{\frac{1}{2}}exp({\widehat{V}}_l^{-1}{\widehat{E}}_l^2/2)},$$

   where ${\widehat{V}}_l={({\stackrel{\sim }{V}}_l^{-1}+{\sigma }_{l0}^{-2})}^{-1},{\widehat{E}}_l={\widehat{V}}_l({\stackrel{\sim }{V}}_l^{-1}{\stackrel{\sim }{E}}_l+{\sigma }_{l0}^{-2}{\beta }_{l0}),{\stackrel{\sim }{V}}_l={\{{\sigma }^{-2}{\sum }_{i=1}^n{({\mathbf{X}}_i{\mathbf{\Gamma }}_l^{\ast })}^{\prime }({\mathbf{X}}_i{\mathbf{\Gamma }}_l^{\ast })+{\sum }_{h=1}^{N_l}{n}_{lh}{\lambda }_{lh}^{-1}\}}^{-1},{\stackrel{\sim }{E}}_l={\stackrel{\sim }{V}}_l\{{\sigma }^{-2}{\sum }_{i=1}^n{({\mathbf{X}}_i{\mathbf{\Gamma }}_l^{\ast })}^{\prime }{\mathbf{u}}_i+{\sum }_{h=1}^{N_l}{\lambda }_{lh}^{-1}{\sum }_{i:H_{il}=h}{\beta }_{il}^{\ast }\},{\mathbf{u}}_i={\mathbf{y}}_i-{\mathbf{X}}_i\mathbf{\Gamma }{\mathit{\beta }}_i^{\ast }-{\mathbf{X}}_i{\mathbf{\Gamma }}_{-l}^{\ast }{\mathit{\beta }}_{-l},{\mathbf{\Gamma }}_l^{\ast }$ denotes the lth column of Γ^*, ${\mathbf{\Gamma }}_{-l}^{\ast }$ denotes the submatrix of Γ^* excluding the lth column, and β_−l denotes the subvector of β with β_l excluded. When ψ_l = 0, ${\stackrel{\sim }{V}}_l={\sigma }^2{({\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{x}_{\mathit{ijl}}^2)}^{-1},{\stackrel{\sim }{E}}_l={\sigma }^{-2}{\stackrel{\sim }{V}}_l{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{x}_{\mathit{ijl}}{u}_{ij},u_{ij}=y_{ij}-{\mathbf{x}}_{ij,-l}^{\prime }{\mathit{\beta }}_{-l}-{\mathbf{x}}_{ij}^{\prime }{\mathbf{\Gamma }}_{-l}({\mathit{\beta }}_{i,-l}^{\ast }-{\mathit{\beta }}_{-l})$.

7. The non-zero lower triangular elements γ_ψ can be generated from

   $$\pi ({\mathit{\gamma }}_{\mathit{\psi }}\mid {\mathit{\beta }}_i^{\ast },\mathit{\beta },\mathbf{y},\mathbf{X})\propto \mathrm{N}({\widehat{E}}_{\mathit{\psi }},{\widehat{V}}_{\mathit{\psi }}),$$

   where V̂_ψ = (σ⁻² ${\sum }_{i=1}^n{\mathbf{V}}_i^{{\ast }^{\prime }}{\mathbf{V}}_i^{\ast }+V_{\mathit{\psi }}^{-1}$)⁻¹, Ê_ψ = V̂{σ⁻² ${\sum }_{i=1}^n{\mathbf{V}}_i^{{\ast }^{\prime }}$(y_i − X_i ${\mathit{\beta }}_i^{\ast }$) + $V_{\mathit{\psi }}^{-1}$E_ψ}, V_i = (V_i1,…,V_ini ${)}_{n_i\times P}^{\prime }$ with $V_{ij}={(x_{\mathit{ijr}}({\beta }_{il}^{\ast }-{\beta }_l):l=1,\dots ,p-1;r=l+1,\dots ,p)}^{\prime }$, and $P=\frac{1}{2}p(p-1)$, and ${\mathbf{V}}_i^{\ast }$ denotes V_i removing the elements corresponding to zeroes of ψ.

8. Finally, the variance of the error terms σ⁻² can be updated straightforwardly from the Gamma distribution

   $$\pi ({\sigma }^{-2}\mid {\mathit{\beta }}_i^{\ast },\mathit{\beta },\mathbf{y},\mathbf{X})\propto \mathcal{G}\left\{c+\frac{1}{2}\sum _{i=1}^n{n}_i,d+\frac{1}{2}\sum _{i=1}^n{({\mathbf{y}}_i-{\mathbf{X}}_i{\mathit{\beta }}_i)}^{\prime }({\mathbf{y}}_i-{\mathbf{X}}_i{\mathit{\beta }}_i)\right\}.$$

Relying on the above algorithm, we conduct a stochastic search through the fixed effects and random effects model spaces. For updating a single parameter from the non-conjugate distribution, we use adaptive rejection Metropolis sampling [35]. The algorithm was implemented in Matlab [36], with the respective MCMC iteration and burn-in sizes for simulation studies and real data application presented in Sections 4 and 5. After convergence of the samples for the parameters and latent variables, the posterior densities of the parameters and posterior probabilities for each of the different submodels can be straightforwardly calculated. Convergence of model parameters for both simulations and real data analysis were tested using the Geweke’s diagnostics [37] and Gelman-Rubin diagnostics [38], and good mixing behavior was observed.

4. A simulated study

A simulated data example was used to evaluate the performance of the proposed approach. In the simulation design, we combined the following scenarios: 1) the outcome only depends on some of the predictors in terms of fixed and random effects, which allows for selection of fixed and random effects based on the models; 2) the random effects were designed to follow various distributions, including the normal distribution, degenerate distribution, and the multi-modal distribution; 3) the covariance matrix of random effects reflects the varying correlations among the random effects. We generated 100 data sets, each with 200 subjects and 10 repeated measurements for each subject. Ten covariates, x_ij = (x_ij1, x_ij2, x_ij3, x_ij4, x_ij5, x_ij6, x_ij7, x_ij8, x_ij9, x_ij10)′, were included, where x_ij1 = 1 corresponding to the intercept, and the rest are generated from a standard uniform distribution. We chose ${\beta }_{i1}^{\ast }~\mathrm{N}(2,0.1),{\beta }_{i2}^{\ast }=2,{\beta }_{i3}^{\ast }~\mathrm{N}(1,0.4),{\beta }_{i4}^{\ast }~0.6\mathrm{N}(0.6,0.2)+0.4\mathrm{N}(-0.9,0.4)$, and ${\beta }_{i5}^{\ast }=\dots ={\beta }_{i10}^{\ast }=0$, implying β = (2, 2, 1, 0, 0, 0, 0, 0, 0, 0)′. We chose the off-diagonal elements of Γ as γ = (γ₂₁, γ₃₁, γ₃₂, γ₄₁, γ₄₂, γ₄₃, γ₅₁, …, γ_10,9)′ = (0, 0.9, 0, 0.5, 0, 0.6, 0, …, 0)′. Then, the designed covariance matrix for the first four random coefficients (the rest elements are zeros), ${\left\{{\sigma }_{lm}\right\}}_{l,m=1}^4$, is

$$\left(\begin{array}{cccc}0.10& 0& 0.09& 0.05\\ 0& 0& 0& 0\\ 0.09& 0& 0.48& 0.29\\ 0.05& 0& 0.29& 0.99\end{array}\right).$$

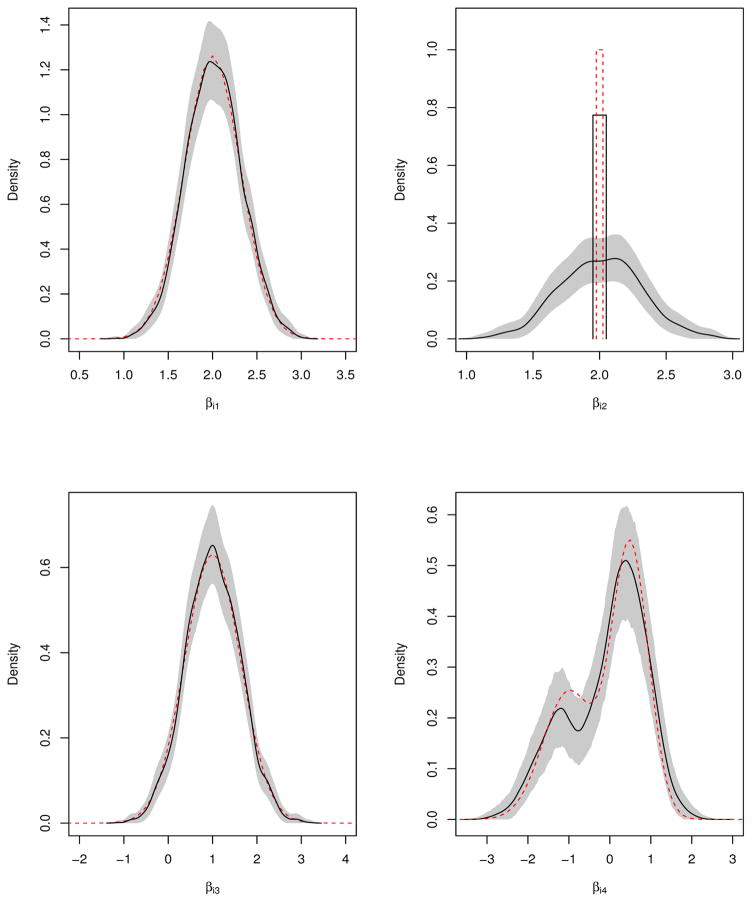
We choose σ² = 0.4. The response variable y_ij is sampled from (1). The true distributions of the first four elements of ${\mathit{\beta }}_i^{\ast }$ are displayed by the dashed lines in Figure 2.

Figure 2.

Posterior densities (solid lines) and true densities (dashed lines) of the first four parameters β_i in the simulated example. The shaded area indicates the 95% credible interval band. The vertical bars denote the probability of the point mass at 2.

Following the priors described in Section 2.3, we chose the prior distribution for σ⁻² as 𝒢(0.05, 0.05). The prior distributions for the elements of β were chosen as N_δ0(0, 10). The prior probability of inclusion of a predictor was chosen to be 0.5 to reflect equal weights on inclusion and exclusion. The elements of γ_ψ were chosen to follow independent N(0, 1). The prior for λ_lh was chosen as ℐ𝒢(1, 1). We ran the Gibbs sampling algorithm described in Section 3 for 10,000 iterations, after a burn-in of 1,000. Geweke’s convergence diagnostic [37] was conducted for the coefficients by calculating Z-scores and the corresponding p-values. The p-values were all larger than 0.35, implying the good mixing and convergence. In addition, the Gelman-Rubin convergence diagnostic test [38] was also applied based on multiple chains with over-dispersed starting values. The range of shrinkage reduction factors is between 1.01 and 1.08, indicating the good convergence. Posterior summaries, such as posterior probabilities of the selected submodels, estimated posterior means, and 95% credible intervals for each of the parameters were obtained based on the post burn-in samples. Sensitivity of the results to the prior specification was assessed by repeating the analyses with different hyperparameters. Although we do not show details, inferences for all models are robust to the prior specification. We noticed that different choices of hyperparameters in the prior for λ_lh could lead to the results with some variations in parameter estimates and probabilities of selected models. These variations were shown in Table 1 and Table 3. This is not unexpected, given the small sample size and the relatively large number of predictors. In terms of selection of hyperparameters, the bottom line is not to use too small values close to zero to obtain a diffuse prior, which typically yields an improper posterior density [39]. We suggest choosing the prior ℐ𝒢(a_l, a_l) for λ_lh with a_l value between 0.5 and 10.

Table 1.

Comparison of the estimates of the parameters for the first four covariates in the simulated example.

Parameter	True value	LMM	CD	Yang	NPME
β1	2	2.03(1.96,2.12)	2.03(1.97,2.13)	2.02(1.96,2.09)	2.01(1.98,2.07)
β2	2	2.02(1.93,2.11)	2.02(1.93,2.09)	1.98(1.94,2.05)	2.01(1.96,2.05)
β3	1	1.10(0.96,1.23)	1.08(0.95,1.19)	1.04(0.96,1.16)	1.03(0.96,1.11)
β4	0	0.03(−0.12,0.16)	0.05(−0.10,0.19)	0.02(−0.09,0.12)	0.01(−0.07,0.10)
σ11	0.1	0.12(0.07,0.16)	0.12(0.07,0.17)	0.08(0.03,0.12)	0.09(0.04,0.13)
σ21	0	0.01(−0.05,0.06)	0.003(−0.02,0.03)	0.003(−0.02,0.03)	0.002(−0.01,0.02)
σ22	0	0.30(0.25,0.38)	0.01(0.00,0.05)	0.004(0.00,0.05)	0.003(0.00,0.03)
σ31	0.09	0.07(0.03,0.15)	0.12(0.06,0.17)	0.08(0.03,0.14)	0.09(0.04,0.12)
σ32	0	−0.01(−0.07,0.06)	0.003(−0.03,0.04)	−0.00(−0.03,0.03)	0.00(−0.02,0.03)
σ33	0.48	0.43(0.33,0.54)	0.55(0.40,0.69)	0.44(0.35,0.52)	0.44(0.36,0.52)
σ41	0.05	0.02(−0.04,0.09)	0.02(−0.04,0.08)	0.03(−0.04,0.10)	0.03(−0.04,0.09)
σ42	0	0.002(−0.06,0.05)	0.002(−0.04,0.04)	0.002(−0.04,0.05)	0.001(−0.04,0.05)
σ43	0.29	0.32(0.26,0.34)	0.27(0.23,0.33)	0.27(0.23,0.32)	0.30(0.26,0.36)
σ44	0.99	1.08(0.97,1.18)	0.95(0.88,1.03)	0.96(0.89,1.03)	0.97(0.90,1.03)
σ2	0.4	0.38(0.34,0.43)	0.41(0.33,0.49)	0.43(0.36,0.49)	0.41(0.36,0.47)

Table 3.

Estimated model posterior probabilities of top five models in the simulated example. Methods used: LMM = R package MCMCglmm of Hadfield [40]; CD = Chen and Dunson (2003)[17]; Yang = Yang (2013)[23]; NPME = the proposed nonparametric mixed effects model.

Model	CD	Yang	NPME	DIC	BPIC
xij1, xij2, xij3, zij1, zij3, $z_{ij4}^a$	${0.738}_{{(0.672,0.761)}^c}^b$	0.736(0.677,0.775)	0.761(0.720,0.809)	4137.36	4584.62
xij1, xij2, xij3, zij1, zij2, zij3, zij4	0.125(0.076,0.140)	0.100(0.078,0.136)	0.111(0.088,0.130)	4215.06	4843.14
xij1, xij2, xij3, zij1, zij3, zij4, zij9	0.030(0.012,0.040)	0.025(0.016,0.041)	0.029(0.019,0.035)	4241.91	4775.53
xij1, xij2, xij3, zij1, zij3, zij4, zij8	0.026(0.014,0.044)	0.021(0.009,0.040)	0.013(0.008,0.033)	4247.80	4783.78
xij1, xij2, xij4, zij1, zij3, zij4, zij7	0.011(0.001,0.019)	0.009(0.000,0.017)	0.008(0.000,0.015)	4240.06	4790.50

^aTrue model

^bPosterior probability

^cRange

To compare the results from our proposed nonparametric mixed effects (NPME) model with other alternatives, we fitted a Bayesian LMM using the R package MCMCglmm [40], Chen and Dunson’s (CD) model [17] with modifications by adding the fixed effects selection, and Yang’s (Yang) [23] method with unimodal distribution. Table 1 presents the true values, posterior estimates, and 95% credible intervals of the parameters corresponding to the first four covariates from the four competing methods. It is shown that the NPME estimates are closer to the true values than those from the other models. The estimates of the parameters for the rest of the covariates are pretty close to zeros from all the methods, which are not shown due to the space limit. Table 2 shows the comparison of the results from the four methods over 100 simulated data sets. In Table 2, we calculated the average of the estimated standard errors (ESE), the sample standard deviation (SSD) of the 100 point estimates and the mean squared errors (MSEs). Although all of the MSEs are small for the estimates of β’s from the four methods, it is clear that the estimates from the proposed method have relatively smaller ESEs, SSDs and MSEs.

Table 2.

Comparison of the estimated standard errors (ESE), the sample standard deviation (SSD) and the mean squared errors (MSEs) of the estimates of β’s based on 100 simulated data sets. Methods used: LMM = R package MCMCglmm of Hadfield [40]; CD = Chen and Dunson (2003)[17]; Yang = Yang (2013)[23]; NPME = the proposed nonparametric mixed effects model.

Method	β1	β2	β3	β4	β5	β6	β7	β8	β9	β10
LMM
ESE	0.0073	0.0274	0.0068	0.0068	0.0073	0.0052	0.0080	0.0070	0.0060	0.0066
SSD	0.0075	0.0244	0.0076	0.0072	0.0069	0.0060	0.0073	0.0075	0.0063	0.0066
MSE	0.0021	0.0100	0.0075	0.0049	0.0061	0.0055	0.0066	0.0030	0.0049	0.0032
CD
ESE	0.0069	0.0039	0.0080	0.0071	0.0069	0.0058	0.0076	0.0065	0.0069	0.0061
SSD	0.0092	0.0043	0.0072	0.0054	0.0072	0.0064	0.0060	0.0060	0.0061	0.0065
MSE	0.0007	0.0005	0.0072	0.0068	0.0064	0.0050	0.0061	0.0041	0.0053	0.0032
Yang
ESE	0.0061	0.0043	0.0059	0.0030	0.0068	0.0056	0.0065	0.0057	0.0068	0.0061
SSD	0.0065	0.0042	0.0054	0.0038	0.0067	0.0063	0.0057	0.0055	0.0063	0.0063
MSE	0.0009	0.0012	0.0020	0.0012	0.0038	0.0042	0.0040	0.0017	0.0041	0.0025
NPME
ESE	0.0043	0.0026	0.0034	0.0031	0.0043	0.0039	0.0047	0.0025	0.0031	0.0037
SSD	0.0034	0.0039	0.0041	0.0032	0.0040	0.0035	0.0046	0.0030	0.0035	0.0034
MSE	0.0008	0.0008	0.0011	0.0010	0.0010	0.0008	0.0012	0.0007	0.0021	0.0008

Table 3 presents the posterior probabilities of top five models selected by the proposed mixed effect method and the other two Bayesian methods. We also calculated corresponding deviance information criterion (DIC) [41], obtained after running separate LMM analyses for each model in the list. Although each method chooses the true model as the best model, our NPME approach selected the true model with the higher posterior probability than the CD and the Yang methods. The DICs confirmed the selection based on the posterior probabilities. To avoid the potential overfitting problem when using DIC, we also considered the Bayesian predictive information criterion (BPIC) [42]. Due to the complexity of the proposed semiparametric model, computing the score required for BPIC could be complicated. Instead, we calculated the BPIC based on [43], where we included double of the model complexity in the criterion which provides more accurate penalty in the criterion. The BPICs in Table 3 confirmed the top selected model but there was some disparity among DIC, BPIC and the selection methods for the other models. As pointed out by [41, 43], the penalty term based on the model complexity in DIC and BPIC are not invariant to reparameterization, which may cause this problem. Figure 2 depicts the posterior densities of the random coefficient parameters β_i based on our NPME model, and the corresponding true densities. It appears that the proposed NPME successfully captured the right densities of β_i.

5. Application: Periodontal Data

We illustrate our approach through analysis of the motivating GAAD dataset (see Section 1) generated from a clinical study at the Medical University of South Carolina [44]. The relationship between PD and diabetes level has been previously studied in the dental literature [45, 46], and the objective of this analysis is to quantify the disease status of this interesting population, and to study the associations between PD status and diabetes level (determined by the popular marker HbA1c, or ‘glycosylated hemoglobin’) in the Type-2 diabetic African-American adults residing in the coastal sea-islands of South Carolina.

Our analysis focused on identifying predictors of one of the most popular bio-markers of PD, the clinical attachment level (CAL). CAL is the distance down a tooth’s root that is no longer attached to the surrounding bone by the periodontal ligament. During a full periodontal exam, CAL is usually measured at six pre-specified sites [47] for each tooth (excluding the third molars, i.e., the wisdom teeth). For a subject with no missing teeth, there are S = 168 measurements for CAL. The CAL measures for each subject are clustered and highly correlated. The subject-level covariates include age (in year), body mass index (BMI) (in kg/m²), gender (1=female, 0=male), HbA1c (1=high, 0=controled) and smoking status (1=smoker, 0=non-smoker). In addition, the total number of available teeth (cluster size) within each mouth/subject is varying, and we included the log(cluster size) for each subject as a predictor as it is highly associated with dental health [48].

In risk assessment studies involving PD, a linear relationship was considered between the response CAL and the associated risk factors in this data set [49, 50, 51]. We followed the same linearity assumption, and proceed by fitting our nonparametric LMM. Predictors included in the fixed effects component have an average effect on the mean CAL, while predictors included in the random effect component vary in their effects across subjects. Let x_ij = (x_ij1, x_ij2, x_ij3, x_ij4, x_ij5, x_ij6, x_ij7)′ denote the vector of candidate predictors with x_ij1 = 1, x_ij2=age, x_ij3 =BMI, x_ij4 =gender, x_ij5 =HbA1c, x_ij6 =smoking status, and x_ij7 =log(cluster size). We included 288 out of 360 patients, consisting of patients with at least one tooth (i.e. 6 measures) and complete covariate information. The cluster size (per subject) varied between 18 and 168.

The prior distributions for the elements of β are chosen as N_δ0 (0, 10) with ν_l0 = 0.5. The prior distributions for the free elements of γ are independent N(0, 1). The mixture prior distributions of the elements of λ_lh are chosen as independent ℐ𝒢(1, 1). We also chose 𝒢(0.05, 0.05) as the prior for σ⁻². We ran the MCMC algorithm described in Section 3 for 20,000 iterations, with a burn-in size of 10,000. The Geweke’s diagnostic tests [37] for regression coefficients based on Z-scores and the Gelman-Rubin diagnostic [38] demonstrated good mixing. Posterior probabilities for the possible submodels, estimated posterior means, and 95% credible intervals for each of the parameters are calculated thereafter. Sensitivity of the results to the prior specifications were assessed by repeating the analyses with varying choices of hyperparameters, similar to those in the simulated example. The results appeared stable.

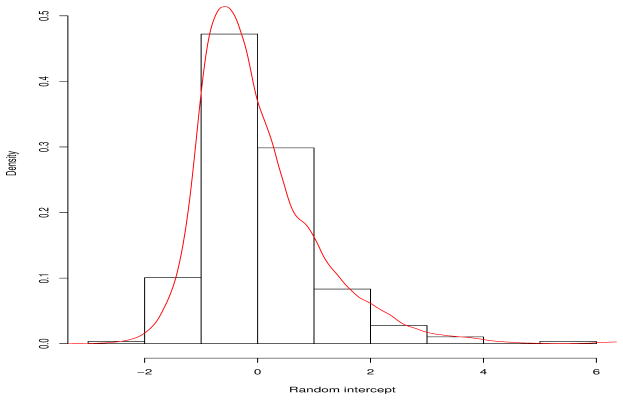
Table 4 presents the posterior means and 95% credible intervals for fixed effects, and the marginal posterior probability of inclusion of predictors in terms of fixed effects and random effects. From the proposed approach, we observe a significant negative effect of gender on CAL, indicating males more likely to be prone to PD than females. A significantly positive effect of HbA1c implies patients with uncontrolled glycemic level are more likely to experience PD. This result is consistent with previous findings [48]. In addition, the log of cluster size of teeth sites confirmed a significantly negative impact on the CAL, which is intuitive given that patients with larger number of available teeth (i.e., higher log cluster size) are expected to have a lower degree of PD. From the Bayesian LMM, only the log of cluster size is significantly and negatively affecting CAL. For comparison purpose, the means and 95% credible intervals for β₁, …, β₇ from the Bayesian LMM are also presented in Table 4. Although the estimates of the fixed effects from the two approaches are similar, the 95% credible intervals of estimates from the Bayesian LMM are wider than those based on our proposed approach. From the marginal posterior probabilities of inclusion, it is clear that for the fixed effects components, the predictors including gender, HbA1C and log(cluster size) are important in predicting CAL. On the other hand, our nonparametric random effects method suggests to include the random intercept and effects for the smoking status, implying heterogeneity of these effects across subjects, while the effects of the other predictors do not vary substantially. The proposed method selected the top model with the posterior probability of 0.35, including all predictors in fixed effects, and all predictors except age and log(cluster size) in random effects. In contrast, Chen and Dunson’s method and Yang’s method chose the same model with the posterior probability of 0.29 and 0.28, respectively. Based on the marginal probability, the Bayes factor can be calculated [52] as inclusion criterion for a single predictor in terms of fixed and random effects. Kass and Raftery [52] suggest the cutoff points for positive, strong and very strong evidence for a Bayes factor as 3, 20 and 150, respectively. Given the same prior probability for inclusion and exclusion (i.e. 0.5), the marginal posterior probability over 0.96 corresponds to the Bayes factor being over 20, indicating a strong evidence of inclusion. Figure 3 shows the histogram of empirical Bayes estimates of random intercept based on the LMM and the density curve of posterior estimates of the random intercept from the proposed method. In terms of model fits to the data, we calculated the DIC and BPIC for both the models. The DICs for the Bayesian LMM and our proposed model are 54,403.15 and 54,205.68, respectively, and the BPICs for the Bayesian LMM and our proposed model are 54,545.39 and 54,386.00, respectively, implying that the proposed model has a better fit to the data.

Table 4.

Estimates of fixed effects, 95% credible intervals, and marginal posterior inclusion probabilities of predictors in the fixed effects and random effects components in the GAAD dataset. Methods compared: LMM = R package MCMCglmm [40]; CD = Chen and Dunson’s method [17]; Yang = Yang’s method [23]; NPME = our proposed nonparametric mixed effects model.

Predictor	Fixed Effect Estimate (95% CI)				NPME Marginal Probability of Inclusion
	LMM	CD	Yang	NPME	Fixed Effect	Random Effect
Intercept	6.43(5.00,8.06)	6.61(4.88,8.45)	6.56(5.10,8.38)	6.21(5.01,7.34)	1.00	0.95
Age	−0.01(−0.21,0.24)	−0.02(−0.11,0.12)	−0.03(−0.08,0.14)	−0.02(−0.12,0.08)	0.80	0.66
BMI	−0.11(−0.33,0.12)	−0.10(−0.45,0.21)	−0.09(−0.28,0.14)	−0.12(−0.23,0.003)	0.72	0.75
Gender	−0.41(−0.89,0.09)	−0.43(−0.81,0.02)	−0.45(−0.80,0.03)	−0.44(−0.70,−0.18)	1.00	0.76
HbA1c	0.30(−0.06,0.68)	0.33(−0.01,0.64)	0.33(−0.03,0.76)	0.29(0.08,0.48)	0.98	0.79
Smoking Status	0.16(−0.26,0.60)	0.13(−0.23,0.51)	0.14(−0.30,0.56)	0.16(−0.10,0.40)	0.81	0.97
log(cluster size)	−1.03(−1.42,−0.56)	−1.00(−1.38,−0.61)	−0.99(−1.32,−0.61)	−0.92(−1.16,−0.63)	1.00	0.001

Figure 3.

Histogram of empirical Bayes estimates and the density of posterior estimates of the random intercept.

6. Conclusions

We develop a Bayesian approach to the problem of nonparametric random effects models where both the predictors to be included and distributions of their random effects are unknown. Relying on reparameterization of the random coefficients and the centered nonparametric distributions, our proposed approach avoids the potential biases in estimation, which may lead to difficulty in interpretation. Incorporating centered independent latent variables with the decomposition of the dependency of random coefficients allows the approach to be efficient and straightforward to implement. By using latent random coefficients which are centered at fixed effects, the proposed reparameterization allows for the random effects not necessarily being the subset of the fixed effects, resulting in the independent selection of the fixed and random effects. The simulation study shows that the performance of the proposed method is better than the other competing methods available. It is straightforward to extend the method to allow categorical outcomes by using data augmentation as in probit models. Although motivated by the random effects selection problem, the proposed approach provides a general strategy for dependency modeling in related unknown distributions. Future research may focus on analyzing multivariate responses with spatial information observed in datasets from dental epidemiology. In addition, it might be really interesting to analyze non-continuous responses, with variable selection under the similar nonparametric framework. Such methods are less developed and challenging, and will be pursued elsewhere.