Abstract
Factor analytic work on the Positive and Negative Syndrome Scale (PANSS) and Brief Psychiatric Rating Scale (BPRS) has yielded varied and conflicting results. The current study explored potential causes of these discrepancies. Prior research has been limited by small sample sizes and an incorrect assumption that the items are normally distributed when in practice responses are highly skewed ordinal variables. Using simulation methodology, we examined the effects of sample size, (in)correctly specifying item distributions, collapsing rarely endorsed response categories, and four factor analytic models. The first is the model of Van Dorn et al., developed using a large integrated data set, specified the item distributions as multinomial, and used cross‐validation. The remaining models were developed specifying item distributions as normal: the commonly used pentagonal model of White et al.; the model of Van der Gaag et al. developed using extensive cross‐validation methods; and the model of Shafer developed through meta‐analysis. Our simulation results indicated that incorrectly assuming normality led to biases in model fit and factor structure, especially for small sample size. Collapsing rarely used response options had negligible effects.
Keywords: BPRS, data integration, factor analysis, PANSS, psychopathology
1. INTRODUCTION
Given the widespread use of the Positive and Negative Syndrome Scale (PANSS; Kay, Fiszbein, & Opler, 1987) and the Brief Psychiatric Rating Scale (BPRS; Overall, 1974) in research and clinical settings, methodological understanding of their factor structure has a major impact on the interpretation of results. However, prior factor analytic work on the PANSS and BPRS has been limited in two ways. First, many studies are limited by small sample sizes, which may be underpowered to adequately detect the factor structure that underlies the PANSS and BPRS. Second, most studies assume data are normally distributed, when in reality the items are positively skewed ordinal data. Modeling positively skewed ordinal data as normally distributed can result in misestimated correlations, which in turn biases factor analytic results. Moreover, little is known about the effects of collapsing sparsely endorsed item categories on factor analytic results. Understanding the extent to which factor analyses are affected by the limitations of sample size and misspecified distributions, as well as the practice of collapsing categories, will aid in the estimation – and subsequent application – of the factor structure of these scales. The results also have application to any other scales that have similar properties.
Sample size is recognized as a critical aspect of factor analysis, though recommendations of minimum size vary in response to data aspects, such as strength of correlation, distribution, and measurement error variance (MacCallum, Widaman, Zhang, & Hong, 1999; Rouquette & Falissard, 2011; Schmitt, 2011). In a simulation study assessing the number of subjects required to achieve adequate parameter estimates and power with psychiatric scales, including the PANSS and BPRS, authors found that “a minimum of 300 subjects is generally acceptable but should be increased when the number of factors within the scale is large, when exploratory factor analysis (EFA) is used, and when the number of items is small” (Rouquette & Falissard, 2011, p. 235). Indeed, most attempts to identify the factor structure of the PANSS and BPRS have resulted in a relatively high number of factors extracted – most frequently, four‐ or five‐factor solutions (Shafer, 2005; Wallwork, Fortgang, Hashimoto, Weinberger, & Dickinson, 2012). Furthermore, the use of EFA, which would necessitate a larger sample, is recommended with these psychiatric scales, given that principal component analysis assumes measurement without error, which is not a realistic assumption with either the PANSS or the BPRS, and thus can result in inflated estimates (Costello & Osborn, 2005; Fabrigar, Wegener, MacCallum, & Strahan, 1999; Schmitt, 2011). Simulation results demonstrated that, when performing EFA using a four‐factor solution, a 20‐item scale (approximating the 18‐item BPRS) requires a sample size of 600; a 30‐item scale, such as the PANSS, requires at least 450 participants (Rouquette & Falissard, 2011).
Despite these recommendations, prior studies on the PANSS and BPRS have used sample sizes of 45 to 201 patients to identify four‐ or five‐factor solutions (see Biancosino, Picardi, Marmai, Biondi, & Grassi, 2010; Burger, Calsyn, Morse, Klinkenberg, & Trusty, 1997; Czobor & Volavka, 1996; Dingemans, Linszen, Lenior, & Smeets, 1995; Harvey et al., 1996; Jacobs, Ryba, & Zapf, 2008; Long & Brekke, 1999; Nakaya, Suwa, & Ohmori, 1999; Overall & Beller, 1984; Ownby & Seibel, 1994; Picardi et al., 2008; Rodriguez‐Jimenez et al., 2013; Shtasel et al., 1992; Stuart, Malone, Currie, Klimidis, & Minas, 1995; Ventura, Nuechterlein, Subotnik, Gutkind, & Gilbert, 2000; Willem Van der Does, Dingemans, Linszen, Nugter, & Scholte, 1995). For example, Stuart et al. (1995) used a sample of 70 patients to extract a five‐factor model with the 18‐item BPRS, whereas Willem Van der Does et al. (1995) extracted a four‐factor model using the 24‐item BPRS‐Expanded Version with only 45 patients in their sample. Small sample size has been shown to increase the standard errors of factor loadings, thus threatening the accuracy and stability of the factor solution (Archer & Jennrich, 1973; MacCallum et al., 1999).
In addition to inadequate sample size, distributional misspecifications may also result in biased estimates. Because the PANSS and BPRS are scored on a 7‐point scale, the correct assumption within EFA is to treat items as having a multinomial, rather than normal, distribution. This approach assumes underlying (multivariate) normality of the items, with thresholds that cut the underlying distribution, which results in the observed ordinal data. One recommended approach in the case of ordinal variables uses weighted least squares (WLS) or robust WLS to estimate polychoric correlation matrices and use these as input to standard EFA software (Muthén, 1984). To do otherwise, as in the case of using maximum likelihood (ML) estimation with skewed data, adversely affects “crucial elements of statistical estimation and testing” (Boomsma, 2009, p. 184). However, prior factor analytic work with the PANSS and BPRS has been inconsistent with the distributional specification of items. To our knowledge, the WLS/robust WLS approach proposed by Muthén (1984) and validated in subsequent simulation research (e.g. Flora & Curran, 2004) has been implemented in only a few studies on the PANSS and BPRS (see Kelley, White, Compton, & Harvey, 2013; Stochl et al., 2014, 2016; Van Dorn et al., 2016; Wallwork et al., 2012). Other studies report using ML estimation (e.g. Thomas, Donnell, & Young, 2004) or, more frequently, do not report distributional specifications et al.l. Although Rouquette and Falissard (2011) categorized their simulated data to be consistent with ordinal data in practice, they assumed normality when analyzing the data, calling into question their conclusions for factor extraction (though the current work reports similar conclusions for sample size requirements). Without correctly adjusting for the ordinal scale, results of model fit, parameters, and standard error estimates are likely to be biased (Beauducel & Herzberg, 2006; Flora & Curran, 2004; Lei, 2009; Savalei & Rhemtulla, 2013).
An additional consideration of ordinal variables in factor analysis is what to do with sparsely endorsed categories. Recent analyses of PANSS and BPRS items in a large, integrated data set correctly specified the distribution as ordinal, but found that the positive skew led to insufficient cell sizes in frequency tables (Van Dorn et al., 2016) leading to unstable estimates of polychoric correlations. Categories 7, 6, and sometimes 5, which characterize extreme, severe, and moderately severe symptoms, respectively, were collapsed to ensure that these more severe symptoms states were represented by at least 1% of the sample. Doing so improved model convergence and stability, but the practice of collapsing categories has received mixed reactions in the literature; some maintain that collapsing categories will not adversely affect results (Hsueh, Wang, Sheu, & Hsieh, 2004; Meulman & Heiser, 2001; Muthén & Kaplan, 1985), whereas others note potential limitations of the practice. Specifically, Savalei and Rhemtulla (2013) found that binary data were problematic (in terms of correctly accepting/rejecting the correct model) relative to data with three to seven response options. Although differences in rejection rates for six versus seven category data were trivial, the thresholds in the two conditions were sufficiently different that the six category condition did not approximate the seven category condition with the last two categories collapsed.
If factor solutions differ as a function of sample size, distributional assumptions, and collapsed categories, results are not comparable across patients or studies (Lyne, Kinsella, & O'Donoghue, 2012). This barrier to cumulative science slows the pace of discovery and creation of evidence‐based programs. For example, the National Institute of Mental Health's (NIMH's) Research Domain Criteria (RDoC) is an emerging framework intended to focus on dimensions of functioning that cross‐cut disorders (Barch et al., 2013; Insel et al., 2010). However, to assess the effectiveness and generalizability of this approach – as well as any interventions that target psychiatric symptoms, rather than categorical classifications of mental disorders – symptoms need to mean the same thing and be measured on a common metric. This also limits the assessment, and comparison, of changes in patients' symptoms over time, particularly across studies and interventions, and in cases where consistent total scores mask specific areas of exacerbated or stable symptoms (Thomas et al., 2004). Determining the roles of sample size, distributional specifications, and collapsed categories in psychiatric symptoms factor analyses is thus important for the establishment of an invariant factor structure for use in research and clinical practice.
The current work utilizes simulation methodology to examine how PANSS and BPRS factor analytic results are affected by the limitations of sample size, differentially specified distributions, and the practice of collapsing sparsely endorsed item categories. Specifically, we sought to answer three primary research questions:
How does sample size affect EFA factor extraction?
How do different distributional specificationss (normal versus ordinal) of seven‐category items affect (i) EFA factor extraction, (ii) model fit, (iii) external validity, (iv) determinant estimation, and (v) outcome estimation?
When specifying seven‐category items as ordinal variables, how does collapsing sparsely endorsed categories affect (i) EFA factor extraction, (ii) model fit, (iii) external validity, (iv) determinant estimation, and (v) outcome estimation?
To facilitate this exploration, we examined one four‐factor model (Van Dorn et al., 2016) and three five‐factor models, selected because of their widespread use as scoring systems for the PANSS and BPRS. First, we considered the model of White, Harvey, Opler, and Lindenmayer (1997), identified through large‐scale research and thus unlikely to be affected by concerns of small sample size, as noted earlier. Second, we used the model of van der Gaag, Hoffman, et al. (2006), which was developed using 10‐fold cross‐validation. Although this work represents some of the most extensive attempts to cross‐validate a factor structure for the PANSS, it is limited by the assumption that data were normally distributed and a misapplication of k‐fold cross validation (Efron & Tibshirani, 1994). Finally, we used the model of Shafer (2005), which was developed via meta‐analysis of 26 studies and over 17,000 observations. However, this study was limited by the fact that instead of correlation matrices, co‐occurrence matrices were factor analyzed, and the co‐occurrence matrices were derived from studies assuming that BPRS items are normally distributed.
2. METHODS
2.1. Data simulation
A simulation study, also called a parametric bootstrap (Efron & Tibshirani, 1994), simulates repeated data sets from model parameters estimated from existing data or from researcher‐selected parameters. The simulation study can have multiple experimental design conditions, such as varying the sample size or analyzing each simulated data set with multiple competing models. The results on which a simulation study may focus include parameter estimates, the number of factors extracted, factor structure, and model fit among others. In the current study, we used the correlation matrix estimated from the 30 PANSS and 18 BPRS items from data reported by Van Dorn et al. (2016). The correlation matrix was estimated assuming multinomial data and an underlying continuous normal distribution for each item using a probit link. Multivariate normal data were simulated from the correlation matrix using the mvrnorm function of the R (R Core Team, 2014) package MASS (Venables & Ripley, 2002). The correlation matrix, rather than the factor model of Van Dorn et al. (2016) was used. Each item was categorized into 7‐point ordinal items using the thresholds estimated by Van Dorn et al. (2016, p. 466). Thresholds are the points on the horizontal axis of the underlying normal distribution for each item. Categorizing the continuous underlying variable at these thresholds approximately reproduces the observed frequencies on each item (due to sampling error).
Six sample size conditions of 50, 100, 150, 300, 500, and 5000 were explored, and 500 data sets were simulated for each sample size. These sample sizes we selected to represent the range of sample sizes observed in prior factor analytic studies of the PANSS and BPRS. One four‐factor model (Van Dorn et al., 2016) and three five‐factor models (White et al., 1997; van der Gaag, Hoffman, et al., 2006; Shafer, 2005) were fit to the data. Each of the four models was fit to the simulated ordinal data twice: once assuming normally distributed data (using the ML estimator) and once assuming ordinal data (using the weighted least squares with means and variance adjustment [WLSMV] estimator). This was done to estimate the magnitude of bias due to the oft‐misused normality assumption. Each model‐distribution combination was fit to the data with and without collapsing rarely endorsed item categories (< 1%, using the approach described by Van Dorn et al., 2016). This leads to a 6 (sample sizes) × 4 (models) × 2 (distributions) × 2 (with/without collapsing) factorial simulation study design with 96 cells. Each cell was fit to the 500 data sets, resulting in 48,000 analyses. Models were fit using Mplus 7 (Muthén & Muthén, 1998–2012) automated using R (R Core Team, 2014) and the MplusAutomation package (Hallquist & Wiley, 2013).
3. ANALYSES
Several unique features of this simulation study design affected analysis decisions. First, none of the compared models were nested, precluding the use of chi‐square tests to compare models. Although ML estimation of ordinal models is possible, the run times were prohibitively long (up to two or more days per model per data set). Consequently, the least squares WLSMV estimator was used for ordinal models. WLSMV estimation does not provide likelihood‐based fit indices frequently used for comparing non‐nested models, such as the Bayesian Information Criterion (BIC; Schwarz, 1978). Regardless, the models of Shafer and White use less than the full set of 30 items, which also preclude the use of fit indices such as the BIC. Hence, we used the root mean square error of approximation (RMSEA) as the primary outcome for examining relative model fit. Although there is still ongoing research on cutoffs for the RMSEA (Chen, Curran, Bollen, Kirby, & Paxton, 2008), common practice is to require RMSEA to be less than 0.05 or 0.06 as an indication of good fit (Browne & Cudeck, 1992; Browne & Cudeck, 1993; Curran, Bollen, Chen, Paxton, & Kirby, 2003; Hu & Bentler, 1999; MacCallum, Browne, & Sugawara, 1996; Preacher, Zhang, Kim, & Mels, 2013).
Design effects (sample size, model, distribution, and item category collapsing) on model fit (RMSEA) were assessed using analysis of variance (ANOVA) (via SAS ROBUSTREG to address skewness =0.3 and kurtosis =4.2). All two‐way interactions were included except collapsing × model, which was not significant. All three‐way interactions were included except sample size × model × collapsing, which was not significant. The four‐way interaction was not significant and was also excluded from the results reported later.
Before interpreting the RMSEA or any other model result (such as parameter estimates), researchers must check whether each model converged to a proper solution. Failure to converge to a trustworthy solution is indicated by a warning in Mplus and should not be ignored even if parameter estimates are produced. In the current study, models that had these errors were excluded from analyses, which resulted in an imbalanced design (i.e. fewer than 500 complete in each cell of the design described earlier).
4. RESULTS
The proportions of data sets in each condition that converged to a proper solution are shown in the first row of Figure 1. Analyses with only 50 participants never converged when misspecifying the distribution as normal, a common practice in most prior research on the PANSS and BPRS (see Figure 1, first row, first column, left‐most edge of graph at n = 50). The Shafer model had substantial convergence problems across all other sample size conditions, reaching only 60% convergence at n = 5000 under the incorrectly specified normal distribution, and never exceeding 20% convergence under the correctly specified ordinal models. It is important to note that convergence for the Shafer model improved for increasing sample sizes only when misspecifying the distribution as normal. This points to the danger of assuming an incorrect distribution: failure to converge to a proper solution can be an indication of a poorly fitting model. Failing to observe non‐convergence by fitting the model with the incorrect distribution may lead to the naive interpretation of the incorrectly specified model. This phenomenon affects both the van der Gaag and White models, too, though to a lesser degree and only at sample sizes less than 300. Finally, the results shown in the first row of Figure 1 suggest that studies using data like that from the PANSS and BPRS should use at least 300 participants. In addition, results for conditions with fewer than 300 participants should be interpreted cautiously, except for the Van Dorn model, which had good convergence for n = 100 and n = 150 conditions.
Figure 1.
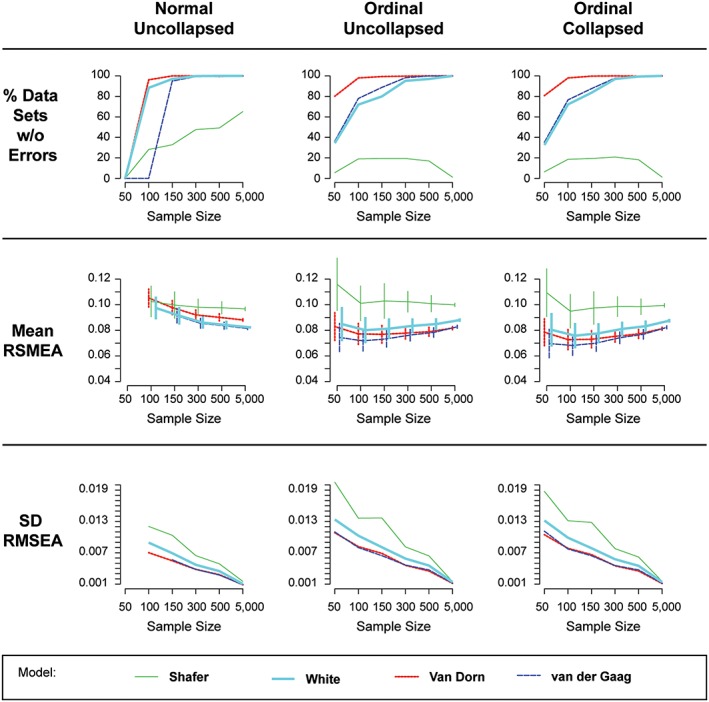
Percentage of models converging to proper solutions, average RMSEA (± 1 SD), and SD RMSEA in each simulation study condition (note. The normal, collapsed condition was nearly identical to the normal, uncollapsed condition (first column) and is excluded for simplicity)
Descriptive statistics for the RMSEA are visualized in the bottom two rows of Figure 1. Sample size is shown equally spaced (for simplicity) from left to right in each panel of Figure 1. The columns of Figure 1 delineate the distribution and item collapsing conditions. The four models are shown via separate lines. The center row shows the average RMSEA with ±1 standard deviation (SD) bars. To show the relative magnitude of the SD across conditions, these are presented in the bottom row.
The second row of Figure 1 shows the mean of the estimated RMSEA computed over converged data sets (see row 1) for each condition in the simulation design. The standard deviations of the RMSEA are used to construct error bars around the mean. As noted earlier, an RMSEA less than 0.06 is an indication of good model fit, indicating the fit for all compared models are marginal at best (though this is often the case in applied research). Three important patterns are immediately observed. First, the Shafer model had substantially higher RMSEA (worse fit) than the other three models. Second, specifying the model as having normal items yields an under‐estimation of model fit (i.e. higher RMSEA) relative to specifying a multinomial distribution for items, except at the largest sample size. Finally, when specified items as ordinal, the White, Van Dorn, and van der Gaag models were not consistently distinguishable using RMSEA except at n = 5000, where the Van Dorn and van der Gaag models were better fitting than the White model though indistinguishable from each other at large sample size. The third row of Figure 1 also shows the absolute value of the SD of the RMSEA for each condition. The decreasing lines for all conditions are as expected – sampling error in estimating the RMSEA decreases as sample size increases.
Results for the ANOVA model examining simulation design effects on RMSEA are shown in Table 1 (ANOVA effect sizes) and Table 2 (ANOVA parameter estimates). The effect sizes in Table 1 are sorted from largest to smallest. The two largest effects on RMSEA are model (i.e. Shafer, 2005; van der Gaag, Hoffman, et al., 2006; Van Dorn et al., 2016; White et al., 1997) and distribution (i.e. normal, ordinal). An unexpected result was that collapsing item categories had relatively small effects on RMSEA, suggesting that the practice of collapsing categories can be safely used to address potential problems with low incidence categories.
Table 1.
Effect sizes for ANOVA model with simulation study design factors predicting RMSEA
| Source | Total variation accounted for | Partial variation accounted for | ||
|---|---|---|---|---|
| Semipartial eta‐square | Semipartial omega‐square | Partial eta‐square | Partial omega‐square | |
| Model | 0.2338 | 0.2338 | 0.4186 | 0.4181 |
| Distribution | 0.1949 | 0.1949 | 0.3750 | 0.3746 |
| Sample size × Distribution | 0.1283 | 0.1282 | 0.2832 | 0.2827 |
| Model × Distribution | 0.0713 | 0.0712 | 0.1800 | 0.1796 |
| Sample size | 0.0174 | 0.0174 | 0.0509 | 0.0506 |
| Sample size × Model | 0.0136 | 0.0134 | 0.0401 | 0.0396 |
| Collapsing | 0.0072 | 0.0072 | 0.0218 | 0.0218 |
| Sample size × Model × Distribution | 0.0041 | 0.004 | 0.0124 | 0.0121 |
| Sample size × Collapsing | 0.0032 | 0.0032 | 0.0098 | 0.0096 |
| Distribution × Collapsing | 0.0010 | 0.0010 | 0.0032 | 0.0032 |
| Distribution × Collapsing | 0.0003 | 0.0002 | 0.0008 | 0.0007 |
| Model × Distribution × Collapsing | 0.0002 | 0.0002 | 0.0007 | 0.0005 |
Table 2.
Parameter estimates for ANOVA model with simulation study design factors predicting RMSEA
| Parameter | Estimate | Standard error | Chi‐square | Pr > chi‐square |
|---|---|---|---|---|
| Intercept | 0.0829 | 0.0002 | 159532 | <.0001 |
| n = 5000 | −0.0012 | 0.0003 | 19.72 | <.0001 |
| n = 500 | −0.0041 | 0.0003 | 235.18 | <.0001 |
| n = 300 | −0.0051 | 0.0003 | 371.79 | <.0001 |
| n = 150 | −0.0061 | 0.0003 | 513.85 | <.0001 |
| n = 100 | −0.0061 | 0.0003 | 517.86 | <.0001 |
| n = 50 | REF | |||
| Shafer | 0.0329 | 0.0007 | 2520.75 | <.0001 |
| White | 0.002 | 0.0003 | 40.1 | <.0001 |
| van der Gaag | −0.0073 | 0.0003 | 546.93 | <.0001 |
| Van Dorn | REF | |||
| Normal | 0.0282 | 0.0003 | 11599.4 | <.0001 |
| Ordinal | REF | |||
| Collapsed | −0.0042 | 0.0002 | 289.46 | <.0001 |
| Uncollapsed | REF | |||
| n = 5000 × Normal | −0.0218 | 0.0003 | 3901.1 | <.0001 |
| n = 500 × Normal | −0.0169 | 0.0003 | 2347.42 | <.0001 |
| n = 300 × Normal | −0.0139 | 0.0003 | 1590.38 | <.0001 |
| n = 150 × Normal | −0.0073 | 0.0004 | 427.71 | <.0001 |
| n = 5000 × Collapsed | 0.0037 | 0.0003 | 155.97 | <.0001 |
| n = 500 × Collapsed | 0.0025 | 0.0003 | 75.41 | <.0001 |
| n = 300 × Collapsed | 0.0018 | 0.0003 | 37.88 | <.0001 |
| n = 150 × Collapsed | 0.0005 | 0.0003 | 3.3 | 0.0692 |
| n = 100 × Collapsed | 0.0001 | 0.0003 | 0.22 | 0.6358 |
| n = 5000 × Shafer | −0.014 | 0.0015 | 86.93 | <.0001 |
| n = 5000 × White | 0.0042 | 0.0004 | 130.16 | <.0001 |
| n = 5000 × van der Gaag | 0.0082 | 0.0004 | 507.61 | <.0001 |
| n = 500 × Shafer | −0.0104 | 0.0007 | 199.72 | <.0001 |
| n = 500 × White | 0.0039 | 0.0004 | 110.3 | <.0001 |
| n = 500 × van der Gaag | 0.0067 | 0.0004 | 337.13 | <.0001 |
| n = 300 × Shafer | −0.0074 | 0.0007 | 102.7 | <.0001 |
| n = 300 × White | 0.0036 | 0.0004 | 91.79 | <.0001 |
| n = 300 × van der Gaag | 0.0058 | 0.0004 | 248.31 | <.0001 |
| n = 150 × Shafer | −0.0075 | 0.0007 | 104.76 | <.0001 |
| n = 150 × White | 0.0029 | 0.0004 | 59.65 | <.0001 |
| n = 150 × van der Gaag | 0.0039 | 0.0004 | 108.92 | <.0001 |
| n = 100 × Shafer | −0.0091 | 0.0007 | 154.91 | <.0001 |
| n = 100 × White | 0.0014 | 0.0004 | 13.12 | 0.0003 |
| n = 100 × van der Gaag | 0.0024 | 0.0004 | 40.3 | <.0001 |
| Normal × Collapsed | 0.0025 | 0.0003 | 66.29 | <.0001 |
| Shafer × Normal | −0.0254 | 0.0005 | 2275.35 | <.0001 |
| White × Normal | −0.0111 | 0.0003 | 1037.16 | <.0001 |
| van der Gaag × Normal | −0.0031 | 0.0003 | 87.73 | <.0001 |
| n = 5000 × Shafer × Normal | 0.0149 | 0.0015 | 103.34 | <.0001 |
| n = 5000 × White × Normal | −0.001 | 0.0004 | 5.56 | 0.0184 |
| n = 5000 × van der Gaag × Normal | −0.0044 | 0.0004 | 108.08 | <.0001 |
| n = 500 × Shafer × Normal | 0.0103 | 0.0007 | 233.39 | <.0001 |
| n = 500 × White × Normal | −0.0008 | 0.0004 | 3.76 | 0.0524 |
| n = 500 × van der Gaag × Normal | −0.0027 | 0.0004 | 41.83 | <.0001 |
| n = 300 × Shafer × Normal | 0.0058 | 0.0007 | 77.13 | <.0001 |
| n = 300 × White × Normal | −0.0006 | 0.0004 | 1.68 | 0.1945 |
| n = 300 × van der Gaag × Normal | −0.0019 | 0.0004 | 19.93 | <.0001 |
| n = 150 × Shafer × Normal | 0.0036 | 0.0007 | 27.86 | <.0001 |
| n = 150 × White × Normal | −0.0002 | 0.0004 | 0.12 | 0.7285 |
| n = 5000 × Normal × Collapsed | −0.0021 | 0.0004 | 34.53 | <.0001 |
| n = 500 × Normal × Collapsed | −0.0014 | 0.0004 | 15.68 | <.0001 |
| n = 300 × Normal × Collapsed | −0.0009 | 0.0004 | 6.12 | 0.0133 |
| n = 150 × Normal × Collapsed | −0.0003 | 0.0004 | 0.81 | 0.3683 |
| Shafer × Normal × Collapsed | 0.0006 | 0.0002 | 5.58 | 0.0182 |
| Shafer × Ordinal × Collapsed | −0.0014 | 0.0004 | 16.47 | <.0001 |
| White × Normal × Collapsed | 0 | 0.0002 | 0.06 | 0.803 |
| White × Ordinal × Collapsed | 0 | 0.0002 | 0.02 | 0.875 |
| van der Gaag × Normal × Collapsed | 0 | 0.0002 | 0.06 | 0.8135 |
| van der Gaag × Ordinal × Collapsed | 0.0003 | 0.0002 | 2.36 | 0.1247 |
Negative values in Table 2 indicate improvement in model fit relative to the reference levels. Because of missingness (especially n = 50 with normal data; see upper left panel of Figure 1), some design cells were missing from Table 1. Before describing the effects for each condition in the simulation design, we comment on the largest effects. The two largest effects (in terms of absolute value) were for the Shafer meta‐analytic model (relative to the Van Dorn model), which was beta =0.033 (a detriment to model fit), and specifying normality relative to correctly specifying a multinomial distribution, which was beta =0.028 (also a detriment to model fit). This is consistent with the relative magnitudes of the effect sizes shown in Table 1. The next largest effect was in the interaction between model and normality, where assuming normality substantially improved the Shafer meta‐analysis model, beta = −0.026. Consistent with these findings, the largest effect sizes in terms of eta squared (Cohen, 1973) and omega squared (Keren & Lewis, 1979) were for model and distribution as shown in Table 1.
4.1. Sample size
In the ANOVA model, the main effect of increasing sample size was to improve model fit, although improvements generally increased at a decreasing rate relative to the n = 50 reference category. The sample size by distribution interaction indicates that for normal data (relative to ordinal data) increasing sample size had an increasing positive effect on fit (i.e. larger reductions in RMSEA).
4.2. Model
Relative to the Van Dorn model, the Shafer meta‐analytic model and White models fit worse, although the latter effect was very small. The van der Gaag models fit slightly better than the Van Dorn model. However, interpreting this result should be tempered by the fact that until the sample size reaches n = 300, the White and van der Gaag models had much poorer proper convergence rates than the Van Dorn model.
Relative to n = 50 and the Van Dorn model, increasing sample size had small detrimental effects for the van der Gaag and White models, and small improvements for the Shafer meta‐analytic model. Figure 1, middle row, shows that under correctly specified ordinal‐item distributions (columns two and three), the White, van der Gaag, and Van Dorn models fit similarly. This was especially borne out by the amount of overlap in the SD bars for these three models. At sample sizes up to 500, the three competing hypotheses represented by the three models were not consistently distinguished. At n = 5000, the White model fit significantly more deficiently than the Van Dorn and van der Gaag models.
4.3. Distribution
The main effect of specifying a normal distribution was to have a large negative impact on RMSEA. This can be seen by comparing the first column in the middle row of Figure 1 with the second and third columns in that row. In addition, misspecifying the distribution as normal yielded downward biased SD values in the RMSEA as can be seen comparing the first column, bottom row of Figure 1 with the last two columns in the bottom row. However, this bias reduces as samples size increases.
4.4. Collapsing
Collapsing had a small positive main effect (beta =0.028) on RMSEA (i.e. RMSEA was lower for collapsed than uncollapsed models).
4.5. Model selection using RMSEA
Although the results of the ANOVA table are typical for a simulation study and are very useful for generalization, they do not mimic actual practice. Comparing multiple models fit with the same data set represents contrasting hypotheses about the data. In practice, researchers will usually determine which model fits their data the best. In the case of RMSEA, the model with lowest RMSEA would likely be determined the “best” fitting model. Models that did not converge to a proper solution would not be considered even if an RMSEA estimate was produced. Using this criterion, the best fitting model was determined for each data set across the four conditions obtained by crossing the two collapsing by two distribution conditions.
Table 3 summarizes the percentage of data sets for which each of the four models was observed to have the lowest estimated RMSEA. Consistent with the ANOVA results, collapsing had little effect, as can be seen by comparing the first and second columns of Table 3. The choice of distribution had a dramatic effect on model choice. Specifically, the van der Gaag model was selected much more often under incorrectly specified normality for items (relative to ordinal), whereas the White model was selected much more often under correctly specified ordinal items (relative to normal).
Table 3.
Percentage of data sets for which each of the four models had the lowest RMSEA at each sample size by distribution and item collapsing
| Distribution | Sample size | Uncollapsed | Collapsed | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Shafer | White | Van der Gaag | Van Dorn | Shafer | White | Van der Gaag | Van Dorn | ||
| Normal | 50 | NA | NA | NA | NA | NA | NA | NA | NA |
| 100 | 11.4% | 18.8% | 69.8% | 0.0% | 9.6% | 16.8% | 73.6% | 0.0% | |
| 150 | 4.8% | 3.6% | 10.6% | 81.0% | 3.6% | 3.2% | 9.0% | 84.2% | |
| 300 | 0.8% | 1.0% | 6.8% | 91.4% | 0.4% | 0.6% | 7.6% | 91.4% | |
| 500 | 0.2% | 0.2% | 5.0% | 94.6% | 0.2% | 0.0% | 3.4% | 96.4% | |
| 5000 | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 100.0% | |
| Ordinal | 50 | 12.4% | 40.4% | 31.2% | 16.0% | 13.2% | 39.2% | 33.4% | 14.2% |
| 100 | 0.6% | 12.2% | 27.2% | 60.0% | 0.4% | 13.0% | 28.2% | 58.4% | |
| 150 | 0.0% | 4.2% | 24.4% | 71.4% | 0.0% | 4.8% | 20.4% | 74.8% | |
| 300 | 0.0% | 0.6% | 5.6% | 93.8% | 0.0% | 0.2% | 5.0% | 94.8% | |
| 500 | 0.0% | 0.0% | 3.0% | 97.0% | 0.0% | 0.0% | 1.2% | 98.8% | |
| 5000 | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 100.0% | |
Note: NA, not available.
Overall, when items were specified as normal, the van der Gaag model fit best for n = 50, and the Van Dorn model fit best for the largest percentage of data sets for all larger sample sizes. When items were specified as ordinal, the White model fit best for the n = 50 condition, with the van der Gaag coming in second. For n = 100, this result reverses. The Van Dorn model fit best most of the time for n ≥ 100. It should also be noted that the van der Gaag and Van Dorn models often fit similarly. In practice the parsimony principle may be used to distinguish between models with very close fit, and the Van Dorn model has 180 parameters whereas the van der Gaag model has 196.
5. DISCUSSION
This simulation study provides insight into the role of three major components of factor analytic work with the PANSS and BPRS: sample size, distributional specification, and collapsed categories. Results indicate that both sample size and distributional specification affected model fit, such that smaller sample size and specifying item distributions as normal, rather than ordinal, were both associated with worse fit. Indeed, sample size and choice of distribution had notable impacts on model selection, particularly when concomitant. In contrast, item category collapsing to account for sparsely endorsed categories had negligible effects on model fit. These results suggest that sufficient sample size and correctly specifying item distributions as ordinal are necessary for establishing valid psychiatric symptom structures, whereas the practice of collapsing categories is a feasible option in the case of items that are rarely endorsed. Overall, RMSEA was only close to the recommended cutoff of 0.06, but that fit was similar among models for all but the worst fitting White model. This suggests that future research may need to explore non‐factor‐analytic criteria to distinguish between existing models.
In showing that sample size and distributional assumptions affect factor extraction of the PANSS and BPRS, findings highlight current barriers for research and clinical practice. Prior attempts to identify a psychiatric symptoms factor structure have often relied upon small sample sizes and distributional assumptions of normality. Our findings thus cast doubt on the estimation and subsequent application of these results. For example, the absence of a valid, reliable, and invariant factor structure slows the cumulative science necessary to achieve goals related to NIMH's RDoC, which focuses on dimensions of functioning across domains and patients. This also limits the evaluation of interventions targeting psychiatric symptoms, such as clinically‐ and research‐based psychopharmacological and psychosocial interventions (Mueser et al., 2002). Moreover, the variance of factor solutions across studies restricts clinicians' ability to effectively monitor and compare treatment outcomes and patients' illness trajectories over time.
Our findings inform research efforts to establish an invariant psychiatric symptoms factor structure. To our knowledge, this is the first empirical study of the effects of collapsing sparsely endorsed response categories. The findings show that this practice, which grew out of practical response to model non‐convergence, has negligible effects on model selection among the models used herein. Further simulation research, where the “correct” model is known, is required to assess whether this holds in general. Additionally, future research should take advantage of improving practices of making data publicly available. Had the data from which the White, Shafer, and van der Gaag models were developed been available, the current study would have been strengthened by having multiple real data correlation matrices from which to simulate data. Furthermore, these raw data could have been integrated with the data of Van Dorn et al. (2016), providing greater generalizability. Although the negative impact of incorrectly assuming data are normal was predicted by other methodological work (Beauducel & Herzberg, 2006; Flora & Curran, 2004; Lei, 2009; Savalei & Rhemtulla, 2013), the current study underscores the need for researchers to make adequate distributional assumptions, and report them in their manuscripts, especially for the small‐to‐moderate sample sizes that make up the majority of research reports. What was unexpected was the result that in very large sample sizes, the distributional assumption had relatively negligible impact on model fit (Lei, 2009), though it is unknown whether this finding will hold in other contexts such as regression or mediation modeling.
As with all simulation studies, the conditions selected (e.g. distribution, sample size) represent only a fraction of data aspects that may affect outcomes. However, the conditions selected for this study are especially pertinent to the study and use of the PANSS and BPRS. In addition, the data were simulated from the correlation matrix of a prior study (Van Dorn et al., 2016) and not from the data upon which the White, Shafer, and van der Gaag models were developed. Although it is likely that the results favor the Van Dorn model owing to this, it highlights practices that can improve cumulative science. These include making data publicly available for integrative data analysis (as was the sample from Van Dorn et al., 2016), or at a minimum reporting the estimated correlation matrix (from which data could be simulated for comparative simulations using the methods described herein) and estimated thresholds for each item.
6. CONCLUSIONS
Previous attempts to identify the factor structure of the PANSS and BPRS have relied upon small samples and untenable assumptions of normality. This simulation study demonstrates that model fit – and subsequently, factor selection – in fact differs as a function of sample size and distributional specifications, calling into question the validity of many prior factor solutions. Results suggest that the practice of collapsing categories that are rarely endorsed is a viable option in factor analyses. This work is an important step in establishing a valid factor structure that can be used to evaluate treatment outcomes and illness trajectories across different patients and studies, and eventually inform goals of the RDoC, including a better understanding of dimensions of functioning.
DECLARATION OF INTEREST STATEMENT
The authors declare that they have no conflict of interest.
Tueller SJ, Johnson KL, Grimm KJ, Desmarais SL, Sellers BG, Van Dorn RA. Effects of sample size and distributional assumptions on competing models of the factor structure of the PANSS and BPRS. Int J Methods Psychiatr Res. 2017;26:e1549 10.1002/mpr.1549
Footnotes
van der Gaag, Cuijpers, et al. (2006) indicates that their data were analyzed using robust maximum likelihood, which was developed to address issues of excess kurtosis, but is less effective in dealing with extremely skewed data such as the responses to PANSS items.
van der Gaag, Hoffman, et al. (2006) added stepwise model modification within their 10‐fold cross‐validation with the stated goal to “avoid capitalization on chance” despite it being well established that stepwise procedures do just that and in addition to causing bias and several other statistical problems (Copas, 1983; Hurvich & Tsai, 1990; Rencher & Pun, 1980; Roecker, 1991; Wilkinson & Dallal, 1981).
It is unknown whether the factor analyzing co‐occurrence matrices rather than correlation matrices yields valid factor‐analytic inferences. In addition, all primary and secondary factor loading were given equal weight, ignoring the sign and magnitude of factor loadings from the studies being meta‐analyzed.
Although the data generating process ensured that the distribution underlying the ordinal variables was normal, Flora and Curran (2004) have reported evidence to suggest that the “estimation of polychoric correlations is robust to modest violations of underlying normality.” Hence, we do not explore that condition herein.
The decrease in the SD of the RMSEA should not be misinterpreted as linear with sample size, although it appears this way in the last row of Figure 1. Note that the x‐axis is equally spaced across the sample size conditions, rather than spacing proportional to the sample size itself. This is done for convenience.
REFERENCES
- Archer, J. O. , & Jennrich, R. I. (1973). Standard errors for orthogonally rotated factor loadings. Psychometrika, 38(4), 581–592. doi: 10.1007/BF02291496 [DOI] [Google Scholar]
- Barch, D. M. , Bustillo, J. , Gaebel, W. , Gur, R. , Heckers, S. , Malaspina, D. , … Carpenter, W. (2013). Logic and justification for dimensional assessment of symptoms and related clinical phenomena in psychosis: relevance to DSM‐5. Schizophrenia Research, 150(1), 15–20. doi: 10.1016/j.schres.2013.04.027 [DOI] [PubMed] [Google Scholar]
- Beauducel, A. , & Herzberg, P. Y. (2006). On the performance of maximum likelihood versus means and variance adjusted weighted least squares estimation in CFA. Structural Equation Modeling, 13(2), 186–203. doi: 10.1207/s15328007sem1302_2 [DOI] [Google Scholar]
- Biancosino, B. , Picardi, A. , Marmai, L. , Biondi, M. , & Grassi, L. (2010). Factor structure of the Brief Psychiatric Rating Scale in unipolar depression. Journal of Affective Disorders, 124(3), 329–334. doi: 10.1016/j.jad.2009.11.019 [DOI] [PubMed] [Google Scholar]
- Boomsma, A. (2009). The robustness of maximum likelihood estimation in structural equation models In Cuttance P., & Ecob R. (Eds.), Structural Modeling by Example: Applications in Educational, Sociological, and Behavioral Research. (pp. 160–188). Cambridge: Cambridge University Press. [Google Scholar]
- Browne, M. W. , & Cudeck, R. (1992). Alternative ways of assessing model fit. Sociological Methods & Research, 21(2), 230–258. [Google Scholar]
- Browne, M. W. , & Cudeck, R. (1993). Alternative ways of assessing model fit In Bollen K., & Long J. (Eds.), Testing Structural Equation Models. (pp. 136–162). Newbury Park, CA: Sage. [Google Scholar]
- Burger, G. K. , Calsyn, R. J. , Morse, G. A. , Klinkenberg, W. D. , & Trusty, M. L. (1997). Factor structure of the expanded Brief Psychiatric Rating Scale. Journal of Clinical Psychology, 53(5), 451–454. doi: [DOI] [PubMed] [Google Scholar]
- Chen, F. , Curran, P. J. , Bollen, K. A. , Kirby, J. , & Paxton, P. (2008). An empirical evaluation of the use of fixed cutoff points in RMSEA test statistic in structural equation models. Sociological Methods & Research, 36(4), 462–494. doi: 10.1177/0049124108314720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen, J. (1973). Eta‐squared and partial eta‐squared in fixed factor ANOVA designs. Educational and Psychological Measurement, 33(1), 107–112. doi: 10.1177/001316447303300111 [DOI] [Google Scholar]
- Copas, J. B. (1983). Regression, prediction and shrinkage. Journal of the Royal Statistical Society: Series B, 45(3), 311–354. [Google Scholar]
- Costello, A. B. , & Osborn, J. W. (2005). Best practices in exploratory factor analysis: Four recommendations for getting the most from your analysis. Practical Assessment, Research & Evaluation, 10(7), 1–9. [Google Scholar]
- Czobor, P. , & Volavka, J. (1996). Dimensions of the Brief Psychiatric Rating Scale: An examination of stability during haloperidol treatment. Comprehensive Psychiatry, 37(3), 205–215. doi: 10.1016/S0010-440X(96)90037-1 [DOI] [PubMed] [Google Scholar]
- Curran, P. J. , Bollen, K. A. , Chen, F. , Paxton, P. , & Kirby, J. B. (2003). Finite sampling properties of the point estimates and confidence intervals of the RMSEA. Sociological Methods & Research, 32(2), 208–252. [Google Scholar]
- Dingemans, P. M. , Linszen, D. H. , Lenior, M. E. , & Smeets, R. M. (1995). Component structure of the expanded Brief Psychiatric Rating Scale (BPRS‐E). Psychopharmacology (Berlin), 122(3), 263–267. doi: 10.1007/BF02246547 [DOI] [PubMed] [Google Scholar]
- Efron, B. , & Tibshirani, R. J. (1994). An Introduction to the Bootstrap. Boca Raton, FL: CRC Press. [Google Scholar]
- Fabrigar, L. R. , Wegener, D. T. , MacCallum, R. C. , & Strahan, E. J. (1999). Evaluating the use of exploratory factor analysis in psychological research. Psychological Methods, 4(3), 272–299. doi: 10.1037/1082-989X.4.3.272 [DOI] [Google Scholar]
- Flora, D. B. , & Curran, P. J. (2004). An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychological Methods, 9(4), 466–491. doi: 10.1037/1082-989X.9.4.466 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallquist, M. , & Wiley, J. (2013). MplusAutomation: Automating Mplus model estimation and interpretation. R package version 0.6–2. http://CRAN.R-project.org/package=MplusAutomation
- Harvey, P. D. , Davidson, M. , White, L. , Keefe, R. S. , Hirschowitz, J. , Mohs, R. C. , & Davis, K. L. (1996). Empirical evaluation of the factorial structure of clinical symptoms in schizophrenia: Effects of typical neuroleptics on the brief psychiatric rating scale. Biological Psychiatry, 40(8), 755–760. doi: 10.1016/0006-3223(95)00486-6 [DOI] [PubMed] [Google Scholar]
- Hsueh, I. P. , Wang, W. C. , Sheu, C. F. , & Hsieh, C. L. (2004). Rasch analysis of combining two indices to assess comprehensive ADL function in stroke patients. Stroke, 35(3), 721–726. doi: 10.1161/01.STR.0000117569.34232.76 [DOI] [PubMed] [Google Scholar]
- Hu, L. T. , & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling, 6(1), 1–55. doi: 10.1080/10705519909540118 [DOI] [Google Scholar]
- Hurvich, C. M. , & Tsai, C. L. (1990). The impact of model selection on inference in linear regression. American Statistician, 44(3), 214–217. doi: 10.2307/2685338 [DOI] [Google Scholar]
- Insel, T. , Cuthbert, B. , Garvey, M. , Heinssen, R. , Pine, D. S. , Quinn, K. , … Wang, P. (2010). Research domain criteria (RDoC), toward a new classification framework for research on mental disorders. American Journal of Psychiatry, 167(7), 748–751. doi: 10.1176/appi.ajp.2010.09091379 [DOI] [PubMed] [Google Scholar]
- Jacobs, M. S. , Ryba, N. L. , & Zapf, P. A. (2008). Competence‐related abilities and psychiatric symptoms: An analysis of the underlying structure and correlates of the MacCAT‐CA and the BPRS. Law and Human Behavior, 32(1), 64–77. doi: 10.1007/s10979-007-9086-8 [DOI] [PubMed] [Google Scholar]
- Kay, S. R. , Fiszbein, A. , & Opler, L. A. (1987). The positive and negative syndrome scale (PANSS) for schizophrenia. Schizophrenia Bulletin, 13(2), 261–276. doi: 10.1093/schbul/13.2.261 [DOI] [PubMed] [Google Scholar]
- Kelley, M. E. , White, L. , Compton, M. T. , & Harvey, P. D. (2013). Subscale structure for the Positive and Negative Syndrome Scale (PANSS): A proposed solution focused on clinical validity. Psychiatry Research, 205(1–2), 137–142. doi: 10.1016/j.psychres.2012.08.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keren, G. , & Lewis, C. (1979). Partial omega squared for ANOVA designs. Educational and Psychological Measurement, 39(1), 119–128. doi: 10.1177/001316447903900116 [DOI] [Google Scholar]
- Lei, P. W. (2009). Evaluating estimation methods for ordinal data in structural equation modeling. Quality & Quantity, 43(3), 495–507. doi: 10.1007/s11135-007-9133-z [DOI] [Google Scholar]
- Long, J. D. , & Brekke, J. S. (1999). Longitudinal factor structure of the Brief Psychiatric Rating Scale in schizophrenia. Psychological Assessment, 11(4), 498–506. doi: 10.1037/1040-3590.11.4.498 [DOI] [Google Scholar]
- Lyne, J. P. , Kinsella, A. , & O'Donoghue, B. (2012). Can we combine symptom scales for collaborative research projects? Journal of Psychiatric Research, 46(2), 233–238. doi: 10.1016/j.jpsychires.2011.10.002 [DOI] [PubMed] [Google Scholar]
- MacCallum, R. C. , Browne, M. W. , & Sugawara, H. M. (1996). Power analysis and determination of sample size for covariance structure modeling. Psychological Methods, 1(2), 130–149. doi: 10.1037/1082-989X.1.2.130 [DOI] [Google Scholar]
- MacCallum, R. C. , Widaman, K. F. , Zhang, S. , & Hong, S. (1999). Sample size in factor analysis. Psychological Methods, 4(1), 84–99. doi: 10.1037/1082-989X.4.1.84 [DOI] [Google Scholar]
- Meulman, J. J. , & Heiser, W. J. (2001). SPSS Categories 11.0. Chicago, IL: SPSS. [Google Scholar]
- Mueser, K. T. , Corrigan, P. W. , Hilton, D. W. , Tanzman, B. , Schaub, A. , Gingerich, S. , … Herz, M. I. (2002). Illness management and recovery: A review of the research. Psychiatric Services, 53(10), 1272–1284. doi: 10.1176/appi.ps.53.10.1272 [DOI] [PubMed] [Google Scholar]
- Muthén, B. (1984). A general structural equation model with dichotomous, ordered categorical, and continuous latent variable indicators. Psychometrika, 49(1), 115–132. doi: 10.1007/BF02294210 [DOI] [Google Scholar]
- Muthén, B. , & Kaplan, D. (1985). A comparison of some methodologies for the factor analysis of non‐normal Likert variables. British Journal of Mathematical and Statistical Psychology, 38(2), 171–189. doi: 10.1111/j.2044-8317.1985.tb00832.x [DOI] [Google Scholar]
- Muthén, L. K. , & Muthén, B. O. (1998–2012). Mplus User's Guide (7th ed.). Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Nakaya, M. , Suwa, H. , & Ohmori, K. (1999). Latent structures underlying schizophrenic symptoms: A five‐dimensional model. Schizophrenia Research, 39(1), 39–50. doi: 10.1016/S0920-9964(99)00018-3 [DOI] [PubMed] [Google Scholar]
- Overall, J. E. (1974). The Brief Psychiatric Rating Scale in psychopharmacology research In Pichot P., & Olivier‐Martin R. (Eds.), Psychological Measurements in Psychopharmacology: Modern Problems in Psychopharmacology (pp. 67–78). Oxford: Karger. [Google Scholar]
- Overall, J. E. , & Beller, S. A. (1984). The Brief Psychiatric Rating Scale (BPRS) in geropsychiatric research: I. Factor structure on an inpatient unit. Journals of Gerontology, 39(2), 187–193. doi: 10.1093/geronj/39.2.187 [DOI] [PubMed] [Google Scholar]
- Ownby, R. L. , & Seibel, H. P. (1994). A factor analysis of the Brief Psychiatric Rating Scale in an older psychiatric population: Exploratory and confirmatory analyses. Multivariate Experimental Clinical Research, 10, 145–156. [Google Scholar]
- Picardi, A. , Battisti, F. , de Girolamo, G. , Morosini, P. , Norcio, B. , Bracco, R. , & Biondi, M. (2008). Symptom structure of acute mania: a factor study of the 24‐item Brief Psychiatric Rating Scale in a national sample of patients hospitalized for a manic episode. Journal of Affective Disorders, 108(1–2), 183–189. doi: 10.1016/j.jad.2007.09.010 [DOI] [PubMed] [Google Scholar]
- Preacher, K. J. , Zhang, G. , Kim, C. , & Mels, G. (2013). Choosing the optimal number of factors in exploratory factor analysis: A model selection perspective. Multivariate Behavioral Research, 48(1), 28–56. [DOI] [PubMed] [Google Scholar]
- R Core Team (2014). R: A language and environment for statistical computing. Vienna: . http://www.R-project.org/ R Foundation for Statistical Computing. [Google Scholar]
- Rencher, A. C. , & Pun, F. C. (1980). Inflation of R2 in best subset regression. Technometrics, 22(1), 49–54. doi: 10.2307/1268382 [DOI] [Google Scholar]
- Rodriguez‐Jimenez, R. , Bagney, A. , Mezquita, L. , Martinez‐Gras, I. , Sanchez‐Morla, E. M. , Mesa, N. , … Palomo, T. (2013). Cognition and the five‐factor model of the positive and negative syndrome scale in schizophrenia. Schizophrenia Research, 143(1), 77–83. doi: 10.1016/j.schres.2012.10.020 [DOI] [PubMed] [Google Scholar]
- Roecker, E. B. (1991). Prediction error and its estimation for subset – selected models. Technometrics, 33(4), 459–468. doi: 10.1080/00401706.1991.10484873 [DOI] [Google Scholar]
- Rouquette, A. , & Falissard, B. (2011). Sample size requirements for the internal validation of psychiatric scales. International Journal of Methods in Psychiatric Research, 20(4), 235–249. doi: 10.1002/mpr.352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savalei, V. , & Rhemtulla, M. (2013). The performance of robust test statistics with categorical data. British Journal of Mathematical and Statistical Psychology, 66(2), 201–223. doi: 10.1111/j.2044-8317.2012.02049.x [DOI] [PubMed] [Google Scholar]
- Schmitt, T. A. (2011). Current methodological considerations in exploratory and confirmatory factor analysis. Journal of Psychoeducational Assessment, 29(4), 304–321. doi: 10.1177/0734282911406653 [DOI] [Google Scholar]
- Schwarz, G. E. (1978). Estimating the dimension of a model. Annals of Statistics, 6(2), 461–464. doi: 10.1214/aos/1176344136 [DOI] [Google Scholar]
- Shafer, A. (2005). Meta‐analysis of the brief psychiatric rating scale factor structure. Psychological Assessment, 17(3), 324–335. doi: 10.1037/1040-3590.17.3.324 [DOI] [PubMed] [Google Scholar]
- Shtasel, D. L. , Gur, R. E. , Gallacher, F. , Heimberg, C. , Cannon, T. , & Gur, R. C. (1992). Phenomenology and functioning in first‐episode schizophrenia. Schizophrenia Bulletin, 18(3), 449–462. doi: 10.1093/schbul/18.3.449 [DOI] [PubMed] [Google Scholar]
- Stochl, J. , Jones, P. B. , Perez, J. , Khandaker, G. M. , Bohnke, J. R. , & Croudace, T. J. (2016). Effects of ignoring clustered data structure in confirmatory factor analysis of ordered polytomous items: A simulation study based on PANSS. International Journal of Methods in Psychiatric Research, 25(3), 205–219. doi: 10.1002/mpr.1474 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stochl, J. , Jones, P. B. , Plaistow, J. , Reininghaus, U. , Priebe, S. , Perez, J. , & Croudace, T. J. (2014). Multilevel ordinal factor analysis of the positive and negative syndrome scale (PANSS). International Journal of Methods in Psychiatric Research, 23(1), 25–35. doi: 10.1002/mpr.1429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart, G. W. , Malone, V. , Currie, J. , Klimidis, S. , & Minas, I. H. (1995). Positive and negative symptoms in neuroleptic‐free psychotic inpatients. Schizophrenia Research, 16(3), 175–188. doi: 10.1016/0920-9964(94)00083-K [DOI] [PubMed] [Google Scholar]
- Thomas, A. , Donnell, A. J. , & Young, T. R. (2004). Factor structure and differential validity of the expanded Brief Psychiatric Rating Scale. Assessment, 11(2), 177–187. doi: 10.1177/1073191103262893 [DOI] [PubMed] [Google Scholar]
- van der Gaag, M. , Cuijpers, A. , Hoffman, T. , Remijsen, M. , Hijman, R. , de Haan, L. , … Wiersma, D. (2006). The five‐factor model of the Positive and Negative Syndrome Scale I: Confirmatory factor analysis fails to confirm 25 published five‐factor solutions. Schizophrenia Research, 85(1–3), 273–279. doi: 10.1016/j.schres.2006.04.001 [DOI] [PubMed] [Google Scholar]
- van der Gaag, M. , Hoffman, T. , Remijsen, M. , Hijman, R. , de Haan, L. , van Meijel, B. , … Wiersma, D. (2006). The five‐factor model of the Positive and Negative Syndrome Scale II: A ten‐fold cross‐validation of a revised model. Schizophrenia Research, 85(1–3), 280–287. doi: 10.1016/j.schres.2006.03.021 [DOI] [PubMed] [Google Scholar]
- Van Dorn, R. A. , Desmarais, S. L. , Grimm, K. , Tueller, S. , Johnson, K. L. , Sellers, B. , & Swartz, M. (2016). The latent structure of psychiatric symptoms across mental disorders as measured with the PANSS and BPRS. Psychiatric Research, 245, 83–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venables, W. N. , & Ripley, B. D. (2002). Modern Applied Statistics with S. New York: Springer. [Google Scholar]
- Ventura, J. , Nuechterlein, K. H. , Subotnik, K. L. , Gutkind, D. , & Gilbert, E. A. (2000). Symptom dimensions in recent‐onset schizophrenia and mania: a principal components analysis of the 24‐item Brief Psychiatric Rating Scale. Psychiatry Research, 97(2–3), 129–135. doi: 10.1016/S0165-1781(00)00228-6 [DOI] [PubMed] [Google Scholar]
- Wallwork, R. S. , Fortgang, R. , Hashimoto, R. , Weinberger, D. R. , & Dickinson, D. (2012). Searching for a consensus five‐factor model of the Positive and Negative Syndrome Scale for schizophrenia. Schizophrenia Research, 137(1–3), 246–250. doi: 10.1016/j.schres.2012.01.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- White, L. , Harvey, P. D. , Opler, L. , & Lindenmayer, J. P. (1997). Empirical assessment of the factorial structure of clinical symptoms in schizophrenia. A multisite, multimodel evaluation of the factorial structure of the Positive and Negative Syndrome Scale. The PANSS Study Group. Psychopathology, 30(5), 263–274. doi: 10.1159/000285058 [DOI] [PubMed] [Google Scholar]
- Wilkinson, L. , & Dallal, G. E. (1981). Tests of significance in forward selection regression with an F‐to enter stopping rule. Technometrics, 23(4), 377–380. doi: 10.2307/1268227 [DOI] [Google Scholar]
- Willem Van der Does, A. J. , Dingemans, P. M. , Linszen, D. H. , Nugter, M. A. , & Scholte, W. F. (1995). Dimensions and subtypes of recent‐onset schizophrenia. A longitudinal analysis. Journal of Nervous and Mental Disease, 183(11), 681–687. doi: 10.1097/00005053-199511000-00002 [DOI] [PubMed] [Google Scholar]


