Estimation of Rank Correlation for Clustered Data

Abstract

It is well known that the sample correlation coefficient (R_xy) is the maximum likelihood estimator (MLE) of the Pearson correlation (ρ_xy) for i.i.d. bivariate normal data. However, this is not true for ophthalmologic data where X (e.g., visual acuity) and Y (e.g., visual field) are available for each eye and there is positive intraclass correlation for both X and Y in fellow eyes. In this paper, we provide a regression-based approach for obtaining the MLE of ρ_xy for clustered data, which can be implemented using standard mixed effects model software. This method is also extended to allow for estimation of partial correlation by controlling both X and Y for a vector U of other covariates. In addition, these methods can be extended to allow for estimation of rank correlation for clustered data by (a) converting ranks of both X and Y to the probit scale, (b) estimating the Pearson correlation between probit scores for X and Y, and (c) using the relationship between Pearson and rank correlation for bivariate normally distributed data. The validity of the methods in finite-sized samples is supported by simulation studies. Finally, two examples from ophthalmology and analgesic abuse are used to illustrate the methods.

1. Introduction

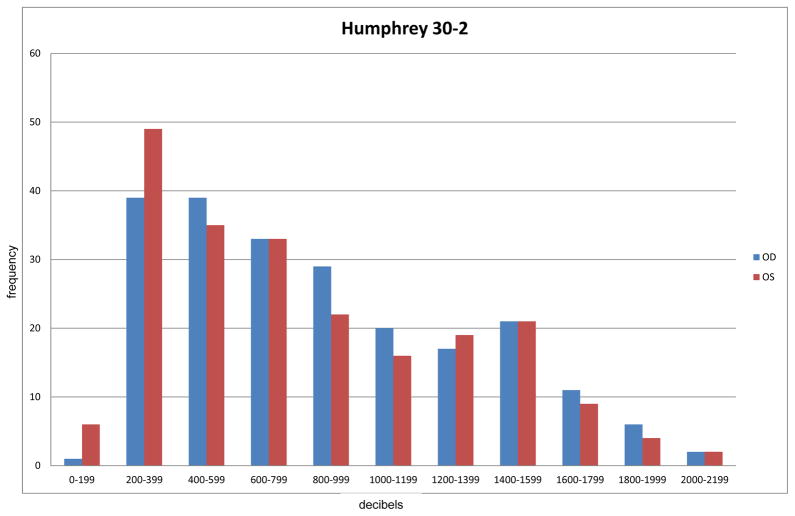
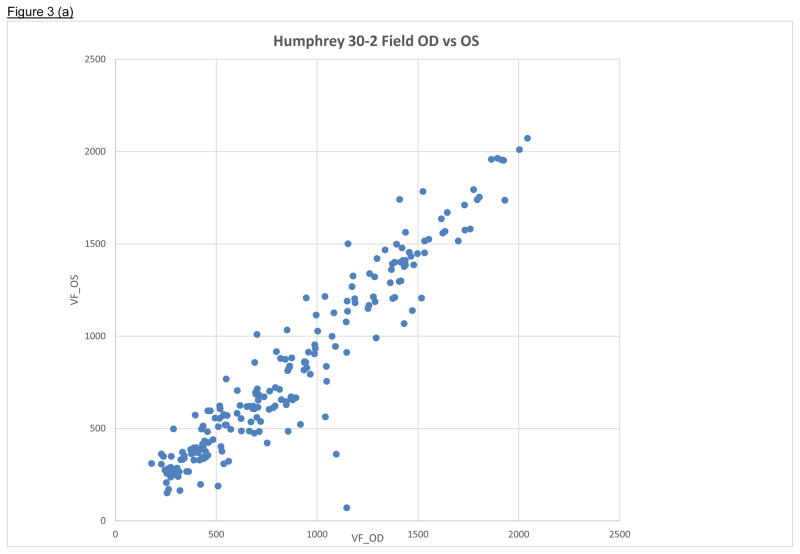
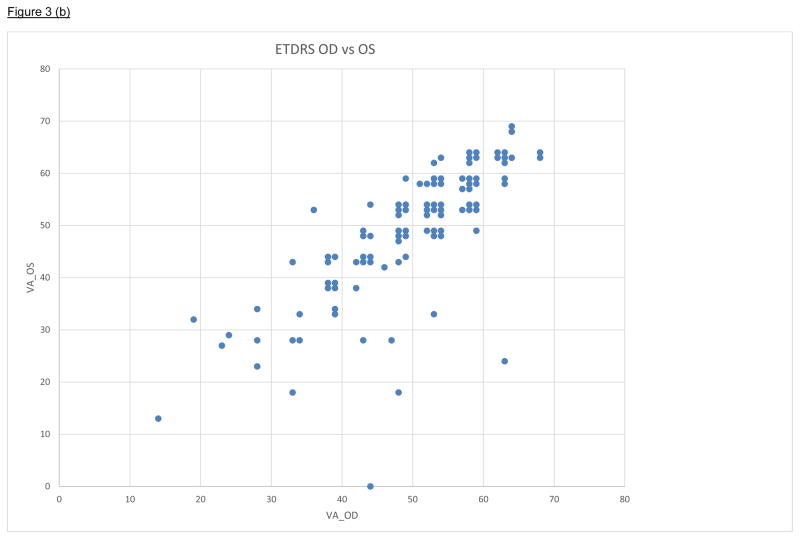
It is well known that the sample correlation coefficient (R_xy) is the maximum likelihood estimator (MLE) of the Pearson correlation coefficient (ρ_xy) for i.i.d. bivariate normally distributed data.[1] Also, there is an extensive literature on estimation of regression models for clustered normally distributed data.[2] However, estimation of Pearson correlation in the clustered data setting has received less attention. Furthermore, many outcome measures in ophthalmology are either continuous and not normally distributed or are ordinal. For example, the Humphrey visual field is often used to characterize visual field in retinitis pigmentosa (RP) patients. The Humphrey field is continuous, but is not normally distributed (see Figure 1). Similarly, Early Treatment Diabetic Retinopathy Study (ETDRS)[3] visual acuity, a measure of central vision, is also frequently not normally distributed (see Figure 2). Thus, the rank correlation is a natural measure of association between these two measures. However, both measures are correlated in fellow eyes which violates standard assumptions of inference regarding rank correlation (see Figure 3).

Figure 1.

Distribution of Humphrey 30-2 field (decibels) for right (OD) and left (OS) eyes among 220 retinitis pigmentosa (RP) patients

Figure 2.

Distribution of ETDRS visual acuity (number of letters correctly read) for right (OD) and left (OS) eyes among 220 retinitis pigmentosa (RP) patients

Figure 3.

Figure 3a Cross-classification of Humphrey 30-2 field (decibels) for right (OD) and left (OS) eyes among 220 retinitis pigmentosa (RP) patients

Figure 3bCross-classification of ETDRS visual acuity (number of letters correctly read) for right (OD) and left (OS) eyes among 220 retinitis pigmentosa (RP) patients

The subject of this paper is to provide methods for obtaining point and interval estimates of rank correlation for clustered data. We first develop methods for estimation of Pearson correlation and then extend these methods to estimation of rank correlation. Methods are first presented for the case of two subunits per cluster and extended to allow for more than two subunits per cluster. Extensions for unbalanced data (i.e., a variable number of subunits per cluster) are also provided.

2. Estimation of Pearson correlation for clustered data

(a) Clusters of size 2

We assume throughout this paper that subunits within a cluster are distinguishable (e.g., right eye (OD) and left eye (OS) scores). We also assume that the Pearson correlation between X and Y scores is the same for right and left eyes. We will begin with a discussion of maximum likelihood estimation of Pearson correlation for clusters of size 2 and will extend our inference to clusters of arbitrary size. Let X_ij = X score for the j^th subunit in the i^th cluster; i = 1, …, n; j = 1,2 and Y_ij defined similarly for the Y score. Our goal is to estimate corr(X_ij,Y_ij). For simplicity, we will use the notation (x_ij,y_ij) to denote both the random variable (X_ij,Y_ij) as well as its sample realization. Suppose we have the data

${\underset{\_}{z}}_i=\left(\begin{array}{c}{\underset{\_}{x}}_i\\ {\underset{\_}{y}}_i\end{array}\right)$, where x_i = (x_i1,x_i2)′, y_i = (y_i1,y_i2)′; i = 1, …, n.

Thus, x_i and y_i are 2 × 1 vectors and z_i is a 4 × 1 vector.

We assume that z_i is multivariate normal with mean μ = (μ_x,μ_x,μ_y,μ_y)′ and covariance matrix Σ given by

$$\sum =\left(\begin{array}{cccc}{\sigma }_x^2& {\rho }_{xx}{\sigma }_x^2& {\rho }_{xy}{\sigma }_x{\sigma }_y& {\rho }_{xy}^{\ast }{\sigma }_x{\sigma }_y\\ {\rho }_{xx}{\sigma }_x^2& {\sigma }_x^2& {\rho }_{xy}^{\ast }{\sigma }_x{\sigma }_y& {\rho }_{xy}{\sigma }_x{\sigma }_y\\ {\rho }_{xy}{\sigma }_x{\sigma }_y& {\rho }_{xy}^{\ast }{\sigma }_x{\sigma }_y& {\sigma }_y^2& {\rho }_{yy}{\sigma }_y^2\\ {\rho }_{xy}^{\ast }{\sigma }_x{\sigma }_y& {\rho }_{xy}{\sigma }_x{\sigma }_y& {\rho }_{yy}{\sigma }_y^2& {\sigma }_y^2\end{array}\right)\equiv \left(\begin{array}{cc}{\mathrm{\sum }}_x& {\mathrm{\sum }}_{xy}\\ {\mathrm{\sum }}_{yx}& {\mathrm{\sum }}_y\end{array}\right)$$

Thus, ρ_xy = corr(x_ij,y_ij) = inter-class Pearson correlation between visual acuity (VA) (x_ij) and visual field (VF) (y_ij) for the same eye, i = 1, n; j = 1,2.

${\rho }_{xy}^{\ast }=\mathit{corr}\left(x_{i{j}_1},y_{i{j}_2}\right)\equiv \text{cross-correlation}\text{between}X$ and Y = inter-class Pearson correlation between VA for the right eye (OD) and VF for the left eye (OS) and conversely, i = 1, …, n; j₁ ≠ j₂ = 1,2.

ρ_xx = corr(x_ij1,x_ij2) = intraclass correlation between VA for the left and right eyes, i = 1, …, n; j₁ ≠ j₂ = 1,2.

ρ_yy = corr(y_ij1,y_ij2) = intraclass correlation between VF for the left and right eyes, i = 1, …, n; j₁ ≠ j₂ = 1,2.

The likelihood for the i^th subject is given by

$$L_i=\frac{1}{{(2\pi )}^2{\mid \mathrm{\sum }\mid }^{1/2}}exp[-\frac{1}{2}{\left({\underset{\_}{z}}_i=\underset{\_}{\mu }\right)}^{\prime }{\mathrm{\sum }}^{-1}\left({\underset{\_}{z}}_i-\underset{\_}{\mu }\right)]$$

and the overall likelihood is given by:

$$L=\prod _{i=1}^n{L}_i$$

The goal is to obtain maximum likelihood estimates (MLE) of ρ_xy. Note that if ${\rho }_{xx}={\rho }_{yy}={\rho }_{xy}^{\ast }=0$, then the MLE of ρ_xy is the ordinary Pearson product-moment correlation [1] given by

$${\widehat{\rho }}_{xy,\mathit{Pearson}}=\sum _{i=1}^n\sum _{j=1}^2\left(x_{ij}-\overline{\overline{x}}\right)\left(y_{ij}-\overline{\overline{y}}\right)/{\left[\sum _{i=1}^n\sum _{j=1}^2{\left(x_{ij}-\overline{\overline{x}}\right)}^2\sum _{i=1}^n\sum _{j=1}^2{\left(y_{ij}-\overline{\overline{y}}\right)}^2\right]}^{1/2}$$

where

$$\overline{\overline{x}}=\sum _{i=1}^n\sum _{j=1}^2{x}_{ij}/(2n)$$

and

$$\overline{\overline{y}}=\sum _{i=1}^n\sum _{j=1}^2{y}_{ij}/2n$$

However, it is difficult to obtain closed form maximum likelihood estimates of ρ_xy using standard software if z_i1 = (x_i1,y_i1) and z_i2 = (x_i2,y_i2) are not independent. Instead, we consider an indirect approach. Specifically, if we factor L_i as follows:

$$L_i=L_{1i}\left({\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i\right)L_{2i}\left({\underset{\_}{x}}_i\right)$$

then the overall likelihood is given by

$$L\equiv L_1{L}_2=\prod _{i=1}^n{L}_{1i}\left({\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i\right)\prod _{i=1}^n{L}_{2i}\left({\underset{\_}{x}}_i\right)$$

Note that all the information concerning ρ_xy is contained in L₁ Hence, it will suffice to maximize L₁ rather than L. We can write L_1i as a conditional regression likelihood given by

$$L_{1i}=\frac{{\mid {\mathrm{\sum }}^{\ast }\mid }^{-1/2}}{2\pi }exp\left[-\frac{1}{2}{\left({\underset{\_}{y}}_i-{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}\right)}^{\prime }{\mathrm{\sum }}^{{\ast }^{-1}}\left({\underset{\_}{y}}_i-{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}\right)\right]$$

where

$$\begin{array}{c}{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}=\alpha \mathbf{1}+{\beta }_1{\underset{\_}{x}}_i+{\beta }_2{\underset{\_}{v}}_i\\ {\underset{\_}{x}}_i={(x_{i1}{x}_{i2})}^{\prime },{\underset{\_}{v}}_i={(x_{i2}{x}_{i1})}^{\prime },\mathbf{1}={(\begin{array}{cc}1& 1\end{array})}^{\prime }\\ {\mathrm{\sum }}^{\ast }\equiv {\mathrm{\sum }}_{\underset{\_}{y}\mid \underset{\_}{x}}={\sigma }_{y\mid \underset{\_}{x}}^2\left(\begin{array}{cc}1& {\rho }_{yy\mid \underset{\_}{x}}\\ {\rho }_{yy\mid \underset{\_}{x}}& 1\end{array}\right)\end{array}$$

Thus, marginally we have the model

$$\begin{array}{c}{y}_{ij}\mid {\underset{\_}{x}}_i~N\left(\alpha +{\beta }_1{x}_{ij}+{\beta }_2{x}_{i,3-j},{\sigma }_{y\mid \underset{\_}{x}}^2\right),i=1,\dots ,n;j=1,2\\ \mathit{corr}\left(y_{i1},y_{i2}\mid {\underset{\_}{x}}_i\right)={\rho }_{yy\mid \underset{\_}{x}}\end{array}$$ (1)

However, based on the properties of the multivariate normal distribution [1], the conditional distribution of y_i given x_i is multivariate normal (MVN) with mean and variance given by:

$${\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i~\text{MVN}({\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i},{\mathrm{\sum }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i})$$

where

$$\begin{array}{c}{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}=\left(\begin{array}{c}{\mu }_y\\ {\mu }_y\end{array}\right)+{\mathrm{\sum }}_{yx}{\mathrm{\sum }}_x^{-1}\left(\begin{array}{c}{x}_{i1}-{\mu }_x\\ x_{i2}-{\mu }_x\end{array}\right)\\ {\mathrm{\sum }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}={\mathrm{\sum }}_y-{\mathrm{\sum }}_{yx}{\mathrm{\sum }}_x^{-1}{\mathrm{\sum }}_{xy}\end{array}$$

In this case, it follows straightforwardly from (1) that

$$\begin{array}{c}\mathrm{E}\left(y_{ij}\mid {\underset{\_}{x}}_i\right)\equiv {\mathrm{\mu }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i,}\\ ={\mu }_y+\left({\sigma }_y/{\sigma }_x\right)\left(\frac{{\rho }_{xy}-{\rho }_{xy}^{\ast }{\rho }_{xx}}{1-{\rho }_{xx}^2}\right)\left(x_{ij}-{\mu }_x\right)+\left({\sigma }_y/{\sigma }_x\right)\left(\frac{{\rho }_{xy}^{\ast }-{\rho }_{xy}{\rho }_{xx}}{1-{\rho }_{xx}^2}\right)\left(x_{i,3-j}-{\mu }_x\right),j=1,2\\ V_{jj}\equiv {\mathrm{\sum }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i,jj}\equiv \mathit{Var}\left(y_{ij}\mid {\underset{\_}{x}}_i\right)={\sigma }_y^2\left[1-{\rho }_{xy}^2-\frac{{\left({\rho }_{xy}^{\ast }-{\rho }_{xy}{\rho }_{xx}\right)}^2}{1-{\rho }_{xx}^2}\right],j=1,2\\ V_{12}={\mathrm{\sum }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_{i,}12}\equiv \mathit{Cov}\left(y_{i1},y_{i2}\mid {\underset{\_}{x}}_i\right)={\sigma }_y^2\left[{\rho }_{yy}-\frac{\left(2{\rho }_{xy}{\rho }_{xy}^{\ast }-{\rho }_{xy}^{\ast 2}{\rho }_{xx}-{\rho }_{xy}^2{\rho }_{xx}\right)}{1-{\rho }_{xx}^2}\right]={\mathrm{\sum }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_{i,}21}\end{array}$$ (2)

Therefore, if we equate E(y_ij|x_i) in equations 1 and 2, we obtain:

$${\beta }_1=\frac{\left({\rho }_{xy}-{\rho }_{xy}^{\ast }{\rho }_{xx}\right)\left({\sigma }_y/{\sigma }_x\right)}{1-{\rho }_{xx}^2}$$ (3)

$${\beta }_2=\frac{\left({\rho }_{xy}^{\ast }-{\rho }_{xy}{\rho }_{xx}\right)\left({\sigma }_y/{\sigma }_x\right)}{1-{\rho }_{xx}^2}$$ (4)

Upon combining equations 3 and 4, and solving for ρ_xy and ${\rho }_{xy}^{\ast }$, we obtain:

$$\begin{array}{l}{\rho }_{xy}=\frac{{\sigma }_x}{{\sigma }_y}({\beta }_1+{\rho }_{xx}{\beta }_2)\\ {\rho }_{xy}^{\ast }=\frac{{\sigma }_x}{{\sigma }_y}({\beta }_2+{\rho }_{xx}{\beta }_1)\end{array}$$ (5)

We can obtain MLE’s of σ_x and ρ_xx based on x from L₂ denoted by σ̂_x and ρ̂_xx upon using standard mixed effects software (e.g., PROC MIXED of SAS) with a compound symmetry correlation structure. Similarly, we can obtain MLE’s of σ_y denoted by σ̂_y from the joint likelihood of y_i = (y_i1,y_i2) given by $L_3={\prod }_{i=1}^n{L}_y({\underset{\_}{y}}_i)$ upon using PROC MIXED based on y with a compound symmetry correlation structure.

Thus, we can use equation 5 to obtain MLE’s of ρ_xy and ${\rho }_{xy}^{\ast }$ given by:

$$\begin{array}{l}{\widehat{\rho }}_{xy,\mathit{MLE}}=\frac{{\widehat{\sigma }}_x}{{\widehat{\sigma }}_y}\left({\widehat{\beta }}_1+{\widehat{\rho }}_{xx}{\widehat{\beta }}_2\right)\\ {\widehat{\rho }}_{xy,\mathit{MLE}}^{\ast }=\frac{{\widehat{\sigma }}_x}{{\widehat{\sigma }}_y}\left({\widehat{\beta }}_2+{\widehat{\rho }}_{xx}{\widehat{\beta }}_1\right)\end{array}$$ (6)

However, an equivalent approach is to express equation 1 directly in terms of ρ_xy and ${\rho }_{xy}^{\ast }$. Specifically, if we substitute equations 3 and 4 into equation 1 and collect terms, we obtain

$$\begin{array}{c}{y}_{ij}\mid {\underset{\_}{x}}_i~N\left(\alpha +{\rho }_{xy}{s}_{ij,2}+{\rho }_{xy}^{\ast }{t}_{ij,2},{\sigma }_{\underset{\_}{y}\mid \underset{\_}{x}}^2\right),i=1,\dots ,n;j=1,2\\ \mathit{corr}\left(y_{i1},y_{i2}\mid {\underset{\_}{x}}_i\right)={\rho }_{yy\mid \underset{\_}{x}}\end{array}$$ (7)

where

$$\begin{array}{l}{s}_{ij,2}=\frac{{\sigma }_y}{{\sigma }_x}\left(\frac{1}{1-{\rho }_{xx}^2}\right)\left(x_{ij}-{\rho }_{xx}{x}_{i,3-j}\right)\\ t_{ij,2}=\frac{{\sigma }_y}{{\sigma }_x}\left(\frac{1}{1-{\rho }_{xx}^2}\right)\left(x_{i,3-j}-{\rho }_{xx}{x}_{ij}\right)\end{array}$$

Thus, MLE’s of ρ_xy and ${\rho }_{xy}^{\ast }$ can be obtained from equation 7 using PROC MIXED with a compound symmetry correlation structure, where σ_y,σ_x and ρ_xx are estimated using PROC MIXED in a similar manner as in equation 6.

(b) Clusters of size > 2

Suppose we have data ${\underset{\_}{z}}_i=\left(\begin{array}{c}{\underset{\_}{x}}_i\\ {\underset{\_}{y}}_i\end{array}\right)$, where

x_i = (x_i1, …, x_ik)′, y_i = (y_i1, …, y_ik)′ are (k×1) vectors and z_i is a 2k×1 vector, i = 1, …, n.

The overall likelihood L is given by:

$$\begin{array}{c}L={\prod }_{i=1}^n{L}_i,\text{where}\\ L_i=L\left({\underset{\_}{z}}_i\right)=L_{1i}({\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i)L_{2i}({\underset{\_}{x}}_i)\end{array}$$

Since $L_1\equiv L_1({\rho }_{xy},{\rho }_{xy}^{\ast },{\rho }_{yy},{\rho }_{xx},{\sigma }_y^2,{\sigma }_x^2)$ and $L_2\equiv L_2({\rho }_{xx},{\sigma }_x^2)$, it follows that all the information concerning ρ_xy is contained in L₁ Similar to the case of k = 2, we can write L_1i as a conditional regression likelihood given by:

$$L_{1i}=\frac{{\left|{\mathrm{\sum }}_{\underset{\_}{y}\mid \underset{\_}{x}}\right|}^{\raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{{(2\mathrm{\pi })}^{\raisebox{1ex}{$k$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\mathit{exp}\left[-\frac{1}{2}{\left({\underset{\_}{y}}_i-{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}\right)}^{\prime }{\mathrm{\sum }}_{\underset{\_}{y}\mid \underset{\_}{x}}^{-1}\left({\underset{\_}{y}}_i-{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}\right)\right]$$

where

$$\begin{array}{c}{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}=\alpha {\mathbf{1}}_k+{\beta }_1{\underset{\_}{x}}_i+{\beta }_2{\underset{\_}{v}}_i\\ {\mathbf{1}}_{\mathit{k}}={(1,\dots ,1)}^{\prime }\text{is}\mathrm{a}k\times 1\text{vector}\text{of}\text{ones};{\underset{\_}{v}}_i={(v_{i1},\dots ,v_{ik})}^{\prime }\end{array}$$

and

$$\begin{array}{c}{v}_{ij}=\sum _{\begin{array}{l}q=1\\ q\ne j\end{array}}^k{x}_{iq}\equiv x_{i+,-j},j=1,\dots ,k,i=1,\dots ,n\\ {\sum }_{\underset{\_}{y}\mid \underset{\_}{x}}={\sigma }_{\underset{\_}{y}\mid \underset{\_}{x}}^2\left[\left(1-{\rho }_{yy\mid \underset{\_}{x}}\right)I_{k\times k}+{\rho }_{yy\mid \underset{\_}{x}}{J}_{k\times k}\right]\end{array}$$

where I_k×k is the k×k identity matrix and J_k×k is a (k×k) matrix of one’s.

Thus, marginally, we have the regression model

$$\begin{array}{c}{y}_{ij}\mid {\underset{\_}{x}}_i~N\left(\alpha +{\beta }_1{x}_{ij}+{\beta }_2{x}_{i+,-j},{\sigma }_{y\mid \underset{\_}{x}}^2\right)\\ \mathit{corr}\left(y_{i{j}_1},y_{i{j}_2}\mid {\underset{\_}{x}}_i\right)={\rho }_{yy\mid \underset{\_}{x}},j_1\ne j_2=1,\dots ,k\end{array}$$ (8)

Similar to equation 2, based on the properties of the multivariate normal distribution [1], the conditional distribution of y_i given x_i is multivariate normal with mean and variance given by

$$\begin{array}{l}\hfill {\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i~\mathit{MVN}\left({\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i},{\mathrm{\sum }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}\right),\text{where}\hfill \\ {\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}={\mu }_y{\mathbf{1}}_k+{\mathrm{\sum }}_{yx}{\mathrm{\sum }}_x^{-1}\left({\underset{\_}{x}}_i-{\mu }_x{\mathbf{1}}_k\right)\\ \hfill {\mathrm{\sum }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}={\mathrm{\sum }}_y-{\mathrm{\sum }}_{yx}{\mathrm{\sum }}_x^{-1}{\mathrm{\sum }}_{xy}\hfill \end{array}$$ (9)

It follows straightforwardly from (9) that

$$\begin{array}{c}{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i}={\mu }_y{\mathbf{1}}_k+\frac{{\sigma }_y}{[{\sigma }_x(1-{\rho }_{xx})][1+(k-1){\rho }_{xx}]}\left\{\begin{array}{c}\left\{{\rho }_{xy}[1+(k-2){\rho }_{xx}]-(k-1){\rho }_{xy}^{\ast }{\rho }_{xx}\right\}\left({\underset{\_}{x}}_i-{\mu }_x{\mathbf{1}}_k\right)\\ +\left({\rho }_{xy}^{\ast }-{\rho }_{xy}{\rho }_{xx}\right)\left({\underset{\_}{v}}_i-{\mu }_x{\mathbf{1}}_k\right)\end{array}\right\}\\ V_{jj}={\mathrm{\sum }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i,jj}=\mathit{Var}\left(y_{ij}\mid {\underset{\_}{x}}_i\right)={\sigma }_y^2\left\{1-{\rho }_{xy}^2-\frac{(k-1){\left({\rho }_{xy}^{\ast }-{\rho }_{xy}{\rho }_{xx}\right)}^2}{(1-{\rho }_{xx})[1+(k-1){\rho }_{xx}]}\right\},j=1,\dots ,k\\ V_{j_1,j_2}={\mathrm{\sum }}_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i,j_1{j}_2}=\mathit{Cov}\left(y_{i{j}_1},y_{i{j}_2}\mid \underset{\_}{x}\right)={\sigma }_y^2\left\{{\rho }_{yy}-\frac{[2{\rho }_{xy}{\rho }_{xy}^{\ast }-(k-1){\rho }_{xy}^{\ast 2}{\rho }_{xx}-{\rho }_{xy}^2{\rho }_{xx}+(k-2){\rho }_{xy}^{\ast 2}]}{(1-{\rho }_{xx})[1+(k-1){\rho }_{xx}]}\right\},j_1\ne j_2\\ =1,\dots ,k\hfill \end{array}$$

Note that if k = 2, equation 9 reduces to equation 2.

Thus, from equations (8) and (9) we obtain

$${\beta }_1=\left({\sigma }_y/{\sigma }_x\right)\left\{\frac{{\rho }_{xy}[1+(k-2){\rho }_{xx}]-(k-1){\rho }_{xy}^{\ast }{\rho }_{xx}}{[1+(k-1){\rho }_{xx}](1-{\rho }_{xx})}\right\}$$ (10)

$${\beta }_2=\left({\sigma }_y/{\sigma }_x\right)\left\{\frac{{\rho }_{xy}^{\ast }-{\rho }_{xy}{\rho }_{xx}}{[1+(k-1){\rho }_{xx}](1-{\rho }_{xx})}\right\}$$

Upon combining equations 8 and 10 and factoring out ρ_xy and ${\rho }_{xy}^{\ast }$, we obtain

$$y_{ij}\mid {\underset{\_}{x}}_i~N\left(\alpha +{\rho }_{xy}{s}_{ij,k}+{\rho }_{xy}^{\ast }{t}_{ij,k},{\sigma }_{\underset{\_}{y}\mid \underset{\_}{x}}^2\right),i=1,\dots ,n;j=1,\dots ,k$$ (11)

where

$$\begin{array}{c}{s}_{ij,k}=\left(\raisebox{1ex}{${\sigma }_y$}\!\left/ \!\raisebox{-1ex}{${\sigma }_x$}\right.\right)\frac{\left\{x_{ij}[1+(k-2){\rho }_{xx}]-x_{i+,-j}{\rho }_{xx}\right\}}{[1+(k-1){\rho }_{xx}](1-{\rho }_{xx})}\\ t_{ij,k}=\left(\raisebox{1ex}{${\sigma }_y$}\!\left/ \!\raisebox{-1ex}{${\sigma }_x$}\right.\right)\frac{[x_{i+,-j}-(k-1)x_{ij}{\rho }_{xx}]}{[1+(k-1){\rho }_{xx}](1-{\rho }_{xx})}\end{array}$$

and σ_y,σ_x and ρ_xx are estimated in a similar manner as in equation 6.

(a) Interval Estimation

We could obtain interval estimates of ρ_xy by using se(ρ̂_xy) from equation 11 and assume asymptotic normality of ρ̂_xy. However, asymptotic normality is more quickly achieved for estimated correlation coefficients if one uses Fisher’s z transformation. If we let Z_xy = 0.5 ln[(1+ρ_xy)/(1−ρ_xy)] and Ẑ_xy = 0.5 ln[(1+ρ̂_xy)/(1−ρ̂_xy)], then from the delta method we have

$$\mathit{var}({\widehat{Z}}_{xy})\cong \mathit{var}({\widehat{\rho }}_{xy})/{(1-{{\widehat{\rho }}_{xy}}^2)}^2.$$

Thus, an approximate 100%×(1−α) CI for Z_xy based on Fisher’s z transformation is given by

$${\widehat{Z}}_{xy}\pm {\mathrm{\Phi }}^{-1}(1-\alpha /2)se({\widehat{\rho }}_{xy})/(1-{\widehat{\rho }}_{xy}^2)\equiv (Z_{xy,1},Z_{xy,2})$$

where Φ⁻¹ is the inverse normal distribution.

The corresponding 100%×(1−α) CI for ρ_xy is given by (ρ_xy,1,ρ_xy,2) where

$${\rho }_{xy,q}=\left[exp\left(2Z_{xy,q}\right)-1\right]/[exp\left(2Z_{xy,q}\right)+1],q=1,2.$$ (12)

1. Estimation of Rank Correlation for Clustered Data

We also consider the estimation of rank correlation for clustered data. For this purpose, we define F_Xj(x) ≡ Pr(X_j ≤ x) = c.d.f. of X_j, and similarly for F_Yj(y), j=1, …, k, where X_j and Y_j are continuous random variables. Pearson referred to F_Xj(x) and F_Yj(y) as grades of X_j and Y_j within a reference population[4].

Let H_Xj(x) = Φ⁻¹[F_Xj(x)], H_Yj(y) = Φ⁻¹[F_Yj(y)]. By definition, if X_j and Y_j are continuous random variables, then H_Xj and H_Yj are univariate normal. We also assume that H_Zj ≡ (H_Xj,H_Yj) is bivariate normal. Finally, we define P_i,Xj = F_Xj(x_ij) and P_iYj = F_Yj(y_ij); i = 1, …, n; j = 1, …, k.

We wish to estimate ρ_s,j = corr(P_i,Xj,P_iYj) which we define as the underlying rank correlation between X and Y for replicate j. It is customary to estimate ρ_s,j by the Spearman rank correlation coefficient ρ̂_s,j = corr[rank_j(X_ij),rank_j(Y_ij)] where the ranks are sample ranks of X_ij and Y_ij, j = 1, …, k within a sample of size n. However, we have previously shown that an alternative estimator of ρ_s,j exists which is both more efficient than ρ̂_s,j and allows one to directly estimate confidence limits for ρ_s,j [5]. Specifically, let H_i,Xj = Φ⁻¹(P_i,Xj) ≡ probit(P_i,Xj), H_i,Yj = Φ⁻¹(P_iYj) ≡ probit(P_iYj) and H_i,Zj = (H_i,Xj,H_i,Yj).

We note that the probit transformation is rank-preserving. Therefore, ρ_s,j is the same in both the original and probit scale. Let us define Ĥ_i,Xj,n = Φ⁻¹[rank_j(X_ij)/(n+1)], Ĥ_i,Yjn = Φ⁻¹[rank_j(Y_ij)/(n+1)] and Ĥ_i,Zjn = (Ĥ_i,Xj,n, Ĥ_i,Yj,n). In Theorem 2 in the Appendix, we show that if H_i,Zj is bivariate normal, then Ĥ_i,Zj,n is asymptotically bivariate normal as n→∞. Furthermore, Moran has shown a direct connection between a Pearson and rank correlation for bivariate normally distributed scales [6] whereby

$${\rho }_{s,j}=(6/\pi ){sin}^{-1}\left({\rho }_{H,j}/2\right)$$ (13)

where ρ_H,j = corr(H_i,Xj,H_i,Yj). We can estimate ρ_H,j by ρ̂_H,j = corr(Ĥ_i,Xj,Ĥ_i,Yj).

To incorporate clustering, we assume that ρ_s,j = ρ_s for all j = 1, …, k and use the regression model in equation 11 based on probit scores rather than raw scores to obtain an estimate of ρ_H,j = corr(H_i,Xj,H_i,Yj) which we assume is the same for all j and denote by ρ̂_H. Equation 11 assumes multivariate normality of z_i = (x_i,y_i). In Theorem 3 in the Appendix we show that if (H₁, …, H_L) is multivariate normal, then (Ĥ_1,n, …, Ĥ_L,n) is asymptotically multivariate normal as n → ∞. The corresponding estimator of Spearman rank correlation which is denoted by ρ̂_s,a is given by

$${\widehat{\rho }}_{s,a}=(6/\pi ){sin}^{-1}({\widehat{\rho }}_H/2)$$

Furthermore, a 100%×(1−α) CI for ρ_s is given by

$$[(6/\pi ){sin}^{-1}\left({\rho }_{H,1}/2\right),(6/\pi ){sin}^{-1}\left({\rho }_{H,2}/2\right)]$$ (14)

where ρ_H,1 and ρ_H,2 are obtained from equation 12 based on probit scores rather than raw scores.

Similarly, from equation 11 we can also obtain an estimate of the Spearman cross-correlation of ( ${\rho }_s^{\ast }$) given by

$${{\widehat{\rho }}_{s,a}}^{\ast }=(6/\pi ){sin}^{-1}({{\widehat{\rho }}_H}^{\ast }/2)$$

where

$${{\widehat{\rho }}_H}^{\ast }=\mathit{corr}\left({\widehat{H}}_{i,X_{j_1}},{\widehat{H}}_{i,Y_{j_2}}\right),j_1\ne j_2=1,\dots ,k,$$

and obtain a 100% × (1−α) CI for ${\rho }_s^{\ast }$ based on equations 12 and 13 given by

$$[(6/\pi ){sin}^{-1}\left({\rho }_{H,1}^{\ast }/2\right),(6/\pi ){sin}^{-1}\left({\rho }_{H,2}^{\ast }/2\right)]$$

2. Estimation of partial correlation for clustered data

It is likely that there is positive correlation between visual field area (VF) and visual acuity (VA). However, it is possible that this is partially due to the effect of age since older RP patients tend to have lower field and acuity measurements than younger RP patients. Also, in some datasets gender differences are found for visual function measures in RP patients [7]. Furthermore, there are different genetic types of RP and level of visual function is known to differ by genetic type [7]. Hence, it would be desirable to estimate the correlation between VF and VA in individual eyes, while controlling for age, gender and genetic type.

(a) Partial Pearson correlation

We assume that there are a set of L cluster-specific covariates denoted by u_i = (u_i1, …, u_iL)′ where u_i is an (L × 1) vector and u_il is the value of the l^th cluster-specific covariate for the i^th cluster. Let U_i be a k × L matrix, where U_i,jl = U_il, i = 1, …, n; j = 1, …, k; l = 1, …, L. In addition, we assume there are a set of M subunit-specific covariates w_ij = (w_ij1, …, w_ijM)′ where w_ij is an M × 1 vector and w_ijm is the value of the m^th subunit-specific covariate for the j^th subunit in the i^th cluster. Finally, let W_i be a k × M matrix where W_i,jm = w_ijm, i = 1, …, n; j = 1, …, k; m = 1, …, M.

We define the partial correlation between X and Y by ρ_xy,_partial = corr(x_ij,y_ij|u_i,W_i), i = 1, …, n; j = 1, …, k. Similarly, the partial cross-correlation between X and Y is defined by ${\rho }_{xy,\mathit{partial}}^{\ast }=\mathit{corr}\left(x_{i{j}_1},y_{i{j}_2}\mid {\underset{\_}{u}}_i,W_i\right)$, i = 1, …, n; j₁ ≠ j₂ = 1, …, k.

To estimate these correlations, we factor the likelihood of L_i as follows:

$$L_i=L\left({\underset{\_}{z}}_i\right)=L_{Ai}({\underset{\_}{z}}_i\mid {\underset{\_}{u}}_i,W_i)L_{Bi}({\underset{\_}{u}}_i,W_i)$$

Furthermore, we can factor L_Ai as follows:

$$L_{Ai}\left({\underset{\_}{z}}_i\mid {\underset{\_}{u}}_i,W_i\right)=L_{Ai1}\left({\underset{\_}{y}}_i|{\underset{\_}{x}}_i,{\underset{\_}{u}}_i,W_i\right)L_{Ai2}({\underset{\_}{x}}_i\mid {\underset{\_}{u}}_i,W_i)$$

All the information concerning ρ_xy,_partial and ${\rho }_{xy,\mathit{partial}}^{\ast }$ is contained in L_Ai1. Hence, it will suffice to maximize $L_{A1}={\prod }_{i=1}^n{L}_{Ai1}$ to obtain the MLE’s of ρ_xy,_partial and ${\rho }_{xy,\mathit{partial}}^{\ast }$. We can write L_Ai1 as a conditional regression likelihood given by

$$L_{Ai1}=\frac{{\left|{\mathrm{\sum }}_{\underset{\_}{y}\mid \underset{\_}{x},U,W}\right|}^{-1/2}}{{(2\pi )}^{k/2}}\mathit{exp}\left[-\frac{1}{2}{\left({\underset{\_}{y}}_i-{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i,{\underset{\_}{u}}_i,W_i}\right)}^{\prime }{\mathrm{\sum }}_{\underset{\_}{y}\mid \underset{\_}{x},U,W}^{-1}({\underset{\_}{y}}_i-{\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i,{\underset{\_}{u}}_i,W_i})\right]$$ (15)

where

$${\mu }_{{\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i,{\underset{\_}{u}}_i,W_i}=\alpha {\mathbf{1}}_k+{\beta }_1{\underset{\_}{x}}_i+{\beta }_2{\underset{\_}{v}}_i+U_i{\underset{\_}{\beta }}_3+W_i{\underset{\_}{\beta }}_4+W_i^{\ast }{\underset{\_}{\beta }}_5$$

$$W_{i,jm}^{\ast }=W_{i+,-j,m}=\sum _{\begin{array}{l}q=1\\ q\ne j\end{array}}^k{w}_{\mathit{iqm}},i=1,\dots ,n;j=1,\dots ,k;m=1,\dots ,M.$$

and

$${\mathrm{\sum }}_{\underset{\_}{y}\mid \underset{\_}{x},U,W}={\sigma }_{\underset{\_}{y}\mid \underset{\_}{x},U,W}^2\left[\left(1-{\rho }_{yy\mid \underset{\_}{x},U,W}\right)I_{k\times k}+{\rho }_{yy\mid \underset{\_}{x},U,W}{J}_{k\times k}\right]$$

β₃ is an L × 1 vector of regression coefficients for cluster-specific covariates and β_4,β₅ are M × 1 vectors of regression coefficients for subunit-specific covariates.

To estimate ρ_xy,_partial and ${\rho }_{xy,\mathit{partial}}^{\ast }$ we

1. Use mixed effects regression models to regress y_i and x_i respectively on U_i,W_i and $W_i^{\ast }$ and obtain residuals ${\underset{\_}{y}}_i^{\ast }$ and ${\underset{\_}{x}}_i^{\ast }$.

2. Obtain estimates of ${\sigma }_y^{\ast }$ using mixed effects models based on maximizing

   $$L_3^{\ast }=\prod _{i=1}^n{L}_y\left({\underset{\_}{y}}_i^{\ast }\right)$$ (16)

   where ${\sigma }_y^{2\ast }=\mathit{var}(y\mid U,W)\equiv \mathit{var}(y_i^{\ast })$

3. Obtain estimates of ${\sigma }_x^{\ast }$ and ${\rho }_{xx}^{\ast }$ using mixed effects models based on

   $$L_2^{\ast }=\prod _{i=1}^n{L}_{2i}\left({\underset{\_}{x}}_i^{\ast }\right)$$

   where ${\sigma }_x^{2\ast }=\mathit{var}\left(x\mid \underset{\_}{U},\underset{\_}{W}\right)\equiv var(x_i^{\ast }),{\rho }_{xx}^{\ast }=\mathit{corr}(x_{i1},x_{i2}\mid \underset{\_}{U},\underset{\_}{W})$

4. Obtain covariate-adjusted estimates $s_{ij,k}^{\ast }$ and $t_{ij,k}^{\ast }$ given by substituting $x_{ij}^{\ast },{\sigma }_y^{\ast },{\sigma }_x^{\ast }$ and ${\rho }_{xx}^{\ast }$ for x_ij,σ_y,σ_x and ρ_xx in equation 11.

5. Estimate ρ_xy,_partial and ${\rho }_{xy,\mathit{partial}}^{\ast }$ using mixed effects models given by $y_{ij}^{\ast }~N\left({\alpha }^{\ast }+{\rho }_{xy,\mathit{partial}}{s}_{ij,k}^{\ast }+{\rho }_{xy,\mathit{partial}}^{\ast }{t}_{ij,k}^{\ast }{\sigma }_{\underset{\_}{y}\mid \underset{\_}{x}}^{2\ast }\right)$ with a compound symmetry correlation structure.

6. Obtain interval estimates for ρ_xy,_partial and ${\rho }_{xy,\mathit{partial}}^{\ast }$ using the methods in equation 12.

(b) Partial Spearman rank correlation

Similarly, estimates of ρ_s,_partial and ${\rho }_{s,\mathit{partial}}^{\ast }$ can be obtained by computing sample probits ${\widehat{H}}_{i,X_j}^{\ast }$ and ${\widehat{H}}_{i,Y_j}^{\ast }$ using ranks based on $x_{ij}^{\ast }$ and $y_{ij}^{\ast }$ instead of x_ij and y_ij and using the methods in equation 13.

5. Unbalanced data

In ophthalmology there often are datasets where some subjects have data available for one eye and other subjects have data available for two eyes. Specifically, in the RP dataset, there were 7 patients with VA and VF available in one eye, but incomplete data in the fellow eye. Five of the patients with incomplete data were missing both VA and VF, while two of the patients were missing VF but not VA, in the incomplete eye. The missing data profile can get more complex if one wants to estimate partial correlation and there is missing covariate data.

In general, since replicates are distinguishable we treat unbalanced data as a type of missing data problem. One possible option is to use all available data, but allow k to vary for different clusters and use mixed effects software methods as provided in equation 11 to estimate ρ_xy However, as shown in equation 9, the variance-covariance matrix Σ_yi|xi will also depend on k which will not be taken into account using standard software.

If unbalanced data are considered missing data, then the best option is to use multiple imputation methods to analyze the data [8]. For clusters of size 2 using SAS software, this would proceed as follows:

1. use PROC MI of SAS to impute the missing data based on the data vector h_i = (x_i1,y_i1,x_i2,y_i2,u_i,w_i1,w_i2) based on M imputations,

2. analyze each imputed data set based on the methods in equation 7,

3. use PROC MIANALYZE to combine results over the M imputations.

This strategy can also be used where the maximum cluster size = k. We used this strategy in both of our examples each of which had small amounts of missing data and had max cluster size = 2 and 3, respectively.

6. Simulation Studies

We have conducted simulation studies to assess the finite sample properties of the estimators of ρ_xy both for clusters of 2 as given in Equation 7 and clusters of size > 2 (i.e., 3) as given in Equation 11. We generated z_i based on the multivariate normal distribution in Section 2 (separately for k=2,3). In addition to the MLE methods described in Equations 7 and 11, we also considered other ad hoc, but frequently used methods. Specifically, we looked at the situation where an investigator has data from 2 eyes available, but only uses a single eye in the analyses (e.g., the right eye, or the left eye) to avoid the correlated data problem. Similarly for k=3, where only 1 of 3 distinguishable replicates was used in the analysis. We then estimated ρ_xy from the ordinary Pearson product-moment correlation from the n (x,y) pairs and obtained confidence limits based on Fisher’s z statistic. We refer to this approach as the 1 subunit method. In addition, we estimated ρ_xy from the ordinary Pearson product-moment correlation based on kn (x,y) pairs and obtained confidence limits based on Fisher’s z statistic ignoring the correlated data. We refer to this approach as the all subunits method.

We generated multivariate normal data with parameters μ = 0, σ² = 1 and

1. ${\rho }_{xy}={\rho }_{xy}^{\ast }=0$, ρ_xx = ρ_yy = (0.2,0.5,0.8) to assess type I error.

2. $\left({\rho }_{xy},{\rho }_{xy}^{\ast }\right)=(0.2,0.1)$, ρ_xx = ρ_yy = (0.2,0.5,0.8) to assess power.

3. $\left({\rho }_{xy},{\rho }_{xy}^{\ast }\right)=(0.5,0.4)$, ρ_xx = ρ_yy = (0.5,0.8) to assess power.

Bias and coverage probability were determined for each method for each of (a) – (c). Separate simulations were performed for k=2 and k=3. Four thousand simulations were performed for each design in (a) – (c) and each k=2, 3. In addition, to assess the adequacy of the model for unbalanced data, we simulated multivariate normal data for k=3 subunits per cluster, but randomly deleted the 3^rd subunit for 20% of the clusters, thus creating a dataset where 80% of the clusters had 3 subunits and 20% had 2 subunits. The same approach was used to create a dataset where 95% of the clusters had 3 subunits and 5% of the clusters had 2 subunits. These unbalanced data simulations were performed for each of

• (b) ${\rho }_{xy}={\rho }_{xy}^{\ast }=0$, ρ_xx = ρ_yy = 0.5 to assess type I error.
• (c) $\left({\rho }_{xy},{\rho }_{xy}^{\ast }\right)=(0.2,0.1)$, ρ_xx = ρ_yy = 0.5 to assess power.

Finally, for each of the designs in (a) – (e) separate simulations were performed for n=50 and n=100. The results are summarized in Table 1.

Table 1.

Simulation Results

						n=50				n=100
k		ρxy	${\mathrm{\rho }}_{\text{xy}}^{\ast }$	ρxx(ρyy)	method	ρ̂xy	Type I error	coverage prob.	power	ρ̂xy	Type I error	coverage prob.	power
Balanced Designs
2		0	0	0.2	MLE	0.001	0.052	94.9	---	0.001	0.047	95.3	---
					1 subunit	−0.001	0.054	94.6	---	0.002	0.052	94.8	---
					all subunits	0.000	0.061	94.0	---	0.001	0.053	99.3	---
				0.5	MLE	0.001	0.056	94.4	---	0.001	0.050	95.2	---
					1 subunit	−0.001	0.054	94.6	---	0.002	0.052	94.8	---
					all subunits	0.001	0.091	90.9	---	0.001	0.077	98.7	---
				0.8	MLE	0.001	0.057	94.6	---	0.002	0.050	95.2	---
					1 subunit	−0.001	0.054	94.6	---	0.002	0.052	94.8	---
					all subunits	0.000	0.133	86.7	---	0.002	0.127	97.0	---
		0.2	0.1	0.2	MLE	0.200	---	95.0	49.3	0.200	---	95.3	79.9
					1 subunit	0.198	---	94.6	28.3	0.201	---	94.7	53.1
					all subunits	0.199	---	94.4	51.4	0.200	---	94.8	81.1
				0.5	MLE	0.201	---	94.7	43.3	0.200	---	95.3	72.0
					1 subunit	0.198	---	94.6	28.3	0.201	---	94.7	53.1
					all subunits	0.200	---	91.2	52.5	0.201	---	92.1	78.9
				0.8	MLE	0.201	---	94.9	33.2	0.202	---	95.2	61.1
					1 subunit	0.198	---	94.6	28.3	0.201	---	94.7	53.1
					all subunits	0.201	---	86.4	52.4	0.202	---	87.1	76.7
		0.5	0.4	0.5	MLE	0.499	---	94.6	99.8	0.500	---	94.6	100.0
					1 subunit	0.497	---	94.9	96.4	0.500	---	95.0	100.0
					all subunits	0.496	---	92.6	99.9	0.498	---	92.9	100.0
				0.8	MLE	0.500	---	95.5	99.0	0.502	---	95.3	100.0
					1 subunit	0.497	---	94.9	96.4	0.500	---	95.0	100.0
					all subunits	0.498	---	87.1	99.7	0.500	---	87.6	100.0
3		0	0	0.2	MLE	0.001	0.052	95.0	---	0.000	0.056	94.5	---
					1 subunit	−0.001	0.054	94.6	---	0.002	0.052	94.8	---
					all subunits	0.001	0.060	94.0	---	0.000	0.064	93.7	---
				0.5	MLE	0.003	0.052	95.2	---	0.001	0.057	94.6	---
					1 subunit	−0.001	0.054	94.6	---	0.002	0.052	94.8	---
					all subunits	0.003	0.113	88.7	---	0.001	0.120	88.0	---
				0.8	MLE	0.004	0.048	95.7	---	0.001	0.052	95.1	---
					1 subunit	−0.001	0.054	94.6	---	0.002	0.052	94.8	---
					all subunits	0.004	0.197	80.3	---	0.002	0.202	79.8	---
		0.2	0.1	0.2	MLE	0.201	---	95.1	66.6	0.200	---	94.4	92.0
					1 subunit	0.198	---	94.6	28.3	0.201	---	94.7	53.1
					all subunits	0.199	---	94.2	68.6	0.199	---	93.7	92.9
				0.5	MLE	0.203	---	95.2	52.4	0.202	---	94.6	81.7
					1 subunit	0.198	---	94.6	28.3	0.201	---	94.7	53.1
					all subunits	0.202	---	88.9	66.5	0.201	---	88.1	89.7
				0.8	MLE	0.205	---	95.4	32.4	0.202	---	95.1	63.7
					1 subunit	0.198	---	94.6	28.3	0.201	---	94.7	53.1
					all subunits	0.204	---	79.8	34.9	0.201	---	79.4	84.8
		0.5	0.4	0.5	MLE	0.500	---	94.6	100.0	0.500	---	93.6	100.0
					1 subunit	0.497	---	94.9	96.4	0.500	---	95.0	100.0
					all subunits	0.496	---	90.3	100.0	0.498	---	90.3	100.0
				0.8	MLE	0.503	---	95.9	99.3	0.501	---	95.2	100.0
					1 subunit	0.497	---	94.9	96.4	0.500	---	95.0	100.0
					all subunits	0.500	---	80.4	100.0	0.499	---	79.5	100.0
Unbalanced Designs
2	5%	0	0	0.5	MLE	0.002	0.055	95.2	---	0.000	0.058	94.7	---
3	95%	0.2	0.1	0.5	MLE	0.202	---	95.4	52.6	0.201	---	94.7	81.8
2	20%	0	0	0.5	MLE	−0.019	0.049	95.5	---	−0.008	0.056	94.8	---
3	80%	0.2	0.1	0.5	MLE	0.182	---	95.2	40.7	0.193	---	94.5	76.9

^*4000 simulations were run for each set of parameter combinations

For balanced designs, we see that bias is low for all 3 methods. For the MLE method type I error ranges from 0.047 to 0.057 (mean = 0.052), which is acceptable. Similarly, the 1 subunit method type I error ranges from 0.052 to 0.054 (mean = 0.053). However, type I error is not preserved for the all subunits method and ranges from 0.053 to 0.064 (mean = 0.061) for ρ_xx = 0.2, from 0.077 to 0.120 (mean = 0.100) for ρ_xx = 0.5 and from 0.127 to 0.202 (mean = 0.155) for ρ_xx = 0.8.

Coverage probability for the MLE method ranges from 93.6% to 95.9% (mean = 95.0%), which is acceptable. Similarly, coverage probability for the 1 subunit method ranges from 94.6% to 95.0% (mean = 94.8%), which is also acceptable. However, for the all subunits method coverage ranges from 93.7% to 99.3% (mean = 94.8%) when ρ_xx = 0.2, from 88.0% to 98.7% (mean = 93.4%) when ρ_xx = 0.5 and from 79.4% to 97.0% (mean = 84.3%) when ρ_xx = 0.8. In general, the high type I error when ρ_xx = 0.5 or 0.8 is due to an inappropriately low se and a corresponding low coverage probability.

Power for the MLE method is always greater than for the 1 subunit method, sometimes dramatically so, especially when ρ_xx = 0.2. For example, when ρ_xy = 0.2, ${\rho }_{xy}^{\ast }=0.1$ and n = 100, power is 79.9 for the MLE method and 53.1% for the 1 subunit method when k=2 and 92.0% for the MLE method and 53.1% for the 1 subunit method for k=3. Overall, the MLE method has appropriate type I error and coverage probability and improved power vs. the 1 subunit method. The all subunits method has inappropriate type I error especially when ρ_xx ≥ 0.5. Thus, overall the MLE method is the preferred method among the 3 approaches.

For unbalanced designs, with 5% of subjects missing a 3^rd replicate, bias is low and coverage probability ranges from 94.7% to 95.4%. With 20% of subjects missing a 3^rd replicate, there was slight negative bias both for n=50 and to a lesser extent n=100. Power in the 5% missing data design was 81.8% for n=100 and 52.6% for n=50, virtually the same as with no missing data (k=3, n=100, 81.7%; n=50, 52.4%). Power in the 20% missing data design was noticeably reduced (n=100, 76.9%; n=50, 40.7%). Overall, missing data methods are an effective approach to analyzing clustered data with unbalanced designs.

An assumption of the estimation procedure for rank correlation is that the distribution of both X and Y are continuous. We also performed simulation studies to assess the adequacy of estimation of rank correlation for clustered data based on (13,14) when the distribution of X and/or Y is discrete. For this purpose, we simulated (X,Y) scores from a bivariate normal distribution, computed the sample probits of X and Y scores, but then subdivided the sample probit scores into quintiles and replaced the individual sample probit scores by the median sample probit score within a quintile. We then obtained point and interval estimates of the rank correlation based on (13) and (14). We considered the following parameter combinations $({\rho }_{xy},{\rho }_{xy}^{\ast })=(0,0)$, (0.2,0.1); n = (50,100), (ρ_xx = ρ_yy = 0.5), k = 3. 4,000 simulations were conducted for each parameter combination. The results are given in Appendix Table 1.

We see that when $({\rho }_{xy},{\rho }_{xy}^{\ast })=(0,0)$, the type I error ranges from 0.054 to 0.055. Over the 4 parameter combinations the coverage probability ranges from 94.6% to 95.9%. Power ranges from 52.4% when n=50 and 76.8% when n=100, which is slightly lower than for continuous distributions with the same parameter combinations ( $({\rho }_{xy},{\rho }_{xy}^{\ast })=(0.2,0.1)$, (ρ_xx = ρ_yy = 0.5), k = 3, power = 81.7%, n=100; 52.4%, n=50). Overall, the approach in (13) and (14) for estimation of rank correlation seems adequate for discrete distributions based on these designs.

Another assumption of the procedure for estimation of rank correlation for clustered data is that the distribution of (H_X,H_Y) is bivariate normal. By definition H_X and H_Y are univariate N(0,1) random variables, but the assumption of bivariate normality may not hold. To assess the sensitivity of our rank correlation estimation procedures to this assumption we generated (H_X,H_Y) from a Kimeldorf-Sampson (KS) bivariate copula [9] of the form:

$$\begin{array}{l}F(a,b,\delta )=Pr(H_X\le a\text{and}{H}_Y\le \mathrm{b})\\ ={\left\{{[\mathrm{\Phi }(a)]}^{-\delta }+{[\mathrm{\Phi }(b)]}^{-\delta }-1\right\}}^{-1/\delta },\delta \ge 0.\end{array}$$ (17)

Note that the univariate margins of F are N(0,1) random variables. Also, if δ = 0, then H_X and H_Y are independent, i.e., F(a,b,0) = Φ(a) Φ(b).

To simulate data from this family we first obtained the conditional distribution of H_Y|H_X from (17) given by:

$$F_{H_Y\mid H_X}(b\mid a,\delta )={\left\{{[\mathrm{\Phi }(a)]}^{-\delta }+{[\mathrm{\Phi }(b)]}^{-\delta }-1\right\}}^{-\frac{1}{\delta }-1}{[\mathrm{\Phi }(a)]}^{-\delta -1}$$ (18)

We then generated two iid U(0,1) random variables (U₁, U₂) to correspond to Φ(a) and F_HY|HX(b|a,δ) respectively, and solved for a and b as follows:

$$\begin{array}{c}a={\mathrm{\Phi }}^{-1}(U_1)\\ b={\mathrm{\Phi }}^{-1}\left[{\left\{1-U_1^{-\delta }\left[1-U_2^{-\delta /(1+\delta )}\right]\right\}}^{-1/\delta }\right]\end{array}$$ (19)

To simulate clustered data from this family, we created a clustered KS copula by first generating (a,b) as in (19). We then generated iid (ea_q,eb_q),q = 1,2 with univariate N(0,g) margins from this copula based on

$$\begin{array}{c}{e}_{a_q}=g^{\frac{1}{2}}{\mathrm{\Phi }}^{-1}(U_{1q})\\ e_{b_q}=g^{1/2}{\mathrm{\Phi }}^{-1}\left[{\left\{1-U_{1q}^{-\delta }\left[1-U_{2q}^{-\delta /(1+\delta )}\right]\right\}}^{-1/\delta }\right],q=1,2\end{array}$$ (20)

where (U_1q, U_2q) are iid U(0,1), (U₁₁,U₂₁) is independent of (U₁₂,U₂₂) and (U_1q, U_2q), q = 1,2 are independent of (U₁, U₂). Finally, we created clustered data using

$$x_q=\left(a+e_{a_q}\right)/\sqrt{1+g},y_q=\left(b+e_{b_q}\right)/\sqrt{1+g},q=1,2.$$ (21)

Note that based on (17–21) x_q and y_q are univariate N(0,1), but F(x_q, y_q) is not bivariate normal,

$${\rho }_{xy}=\mathit{corr}\left(x_q,y_q\right),q=1,2;{\rho }_{xy}^{\ast }=\mathit{corr}\left(x_{q_1},y_{q_2}\right),q_1\ne q_2=1,2,\text{and}{\rho }_{xy}\ne {\rho }_{xy}^{\ast }$$

To determine the value of δ we refer to Joe [10], page 147 who shows by numerical integration that with copulas from the family in (17) for δ = 1.06, the Spearman rank correlation = 0.5. However, the clustered KS copula in (21) is a summation of two random variables from this family and does not correspond to the distribution of (H_X, H_Y) in (17). Hence, we simulated 100,000 random vectors (X₁,Y₁,X₂,Y₂) from (21) for g = 1/2 and g = 1, respectively, and empirically estimated ρ_xy,s and ${\rho }_{xy,s}^{\ast }$ from

$$\begin{array}{l}{\widehat{\rho }}_{xy,s}=\{\mathit{corr}[\mathit{rank}(X_1),\mathit{rank}(Y_1)]+\mathit{corr}[\mathit{rank}(X_2),\mathit{rank}(Y_2)]\}/2\\ {\widehat{\rho }}_{xy,s}^{\ast }=\{\mathit{corr}[\mathit{rank}(X_1),\mathit{rank}(Y_2)]+\mathit{corr}[\mathit{rank}(X_2),\mathit{rank}(Y_1)]\}/2\end{array}$$

Using δ = 1.06, this yielded $\left({\widehat{\rho }}_{xy,s},{\widehat{\rho }}_{xy,s}^{\ast }\right)=(0.497,0.328)$ for g = 1/2 and (0.497,0.246) for g = 1.

We then assumed these were the true values of ρ_xy,s and ${\rho }_{xy,s}^{\ast }$ and performed the estimation procedure in (13) and (14) to obtain point and interval estimates of ρ_xy,s based on 4,000 samples of size 50 and 100, respectively, thus obtaining empirical estimates of bias and coverage probability. The results are provided in Appendix Table 2.

We see that the median estimated value is slightly lower than the true value for both ρ_xy,s and ${\rho }_{xy,s}^{\ast }$, although the absolute bias is small (≤ 0.011). The coverage probability ranges from 94.1% to 96.6% for g = 1/2 and 91.4% to 96.7% for g = 1 (overall mean = 94.8%) which is acceptable. In summary, the estimation procedure for rank correlation in (13) and (14) performs well for probit scores (H_X,H_Y) whose distribution is not bivariate normal, but instead comes from the clustered KS copula in (21).

5. Examples

(a) Estimating the correlation between visual field and visual acuity in RP patients

We have a sample of 220 RP patients who were enrolled in a clinical trial assessing the effects of docosahexaenoic acid (DHA) supplementation vs. placebo on the rate of decline of visual function over a 4-year period [11]. For this analysis we assess the correlation between Humphrey 30-2 visual field (VF) and ETDRS visual acuity (VA) in individual eyes at the initial (screening) visit. Two hundred thirteen of the patients had VF and VA available in both eyes; five patients had (VA, VF) available in a single eye, but neither available in the fellow eye; two patients had (VA, VF) available in one eye and VA, but not VF available in the fellow eye. Covariate values (i.e., age, gender and genetic type) were complete for all subjects. We used multiple imputation methods as described in Section 5 to impute the missing VF and VA values and perform the analyses described in sections 2, 3 and 4.

We first provide descriptive statistics of VA and VF in Table 2. We see that the mean ETDRS score (VA) = 51.5 ± 0.6 (mean ± se) letters while the mean Humphrey 30-2 visual field (VF) = 848.9 ± 31.7 db. For reference purposes, a person with 20/20 vision has an ETDRS score of 85 letters; an ETDRS score of 50 letters corresponds roughly to a visual acuity of 20/100 [12]. A normal Humphrey 30-2 visual field is about 2500 db. We see that VF but not VA is lower for older subjects and lower for males vs. females. Furthermore, both VA and VF vary substantially by genetic type with the best function among dominant patients and the worst function among sex-linked patients. Other genetic types had intermediate levels of function. We now provide estimates of the Pearson correlation between VF and VA for individual eyes using the eye as the unit of analysis based on the model in equation 7. The results are given in Table 3. We see that the estimated Pearson correlation between VF(y) and VA(x) in the same eye = 0.212 (95% CI=0.088, 0.329), p<0.001, while the Pearson cross-correlation (correlation between VF in the right eye and VA in the left eye, and conversely) = 0.177 (95% CI = 0.054, 0.295), p=0.004. We also computed a partial Pearson correlation, adjusting for age, gender, and genetic type (person-specific covariates) and right vs. left eye (eye-specific covariate) based on equation 16. The partial Pearson correlation = 0.195 and the partial Pearson cross-correlation = 0.156 which are lower than the crude correlations, although still statistically significant (p=0.002, 0.012, respectively).

Table 2.

Descriptive Statistics for the RP Data Set (220 patients)^*

Variable	Category	VA**			VF***
		mean (se)	Neyes (Neyes,obs†)	(95% CI)	mean (se)	Neyes (Neyes,obs†)	(95% CI)
	overall	51.5 (0.6)	440 (435)	(50.3, 52.8)	848.9 (31.7)	440 (433)	(786.7, 911.1)
age (yrs)
	< 35	50.3 (1.0)	166 (166)	(48.3, 52.3)	934.3 (51.2)	166 (165)	(833.9, 1034.6)
	≥ 35	52.3 (1.0)	274 (269)	(50.7, 53.8)	797.2 (39.9)	274 (268)	(719.0, 875.4)
gender
	M	51.0 (0.9)	218 (217)	(49.2, 52.7)	798.4 (44.9)	218 (216)	(710.4, 886.3)
	F	52.1 (0.9)	222 (218)	(50.3, 53.8)	898.5 (44.5)	222 (217)	(811.3, 985.7)
genetic type+
	DOM	54.4 (1.3)	102 (100)	(51.9, 56.9)	1005.6 (65.1)	102 (99)	(878.0, 1133.2)
	AR	51.3 (1.7)	60 (60)	(48.1, 54.6)	849.6 (84.9)	60 (59)	(683.3, 1015.5)
	XL	44.1 (2.3)	30 (30)	(39.5, 48.7)	670.6 (119.9)	30 (30)	(435.5, 905.7)
	ISO	52.2 (0.9)	214 (211)	(50.5, 53.9)	812.1 (45.0)	214 (211)	(724.0, 900.2)
	UND	45.4 (2.2)	34 (34)	(41.0, 49.7)	766.3 (112.7)	34 (34)	(545.4, 987.1)
eye
	right eye (OD)	51.5 (0.6)	220 (219)	(50.3, 52.7)	873.0 (31.7)	220 (217)	(810.4, 935.5)
	left eye (OS)	51.6 (0.7)	220 (216)	(50.1, 53.0)	824.8 (32.6)	220 (216)	(760.6, 889.0)

^*VA is available for 219 patients for the right eye (OD) and 216 patients for the left eye (OS); VF is available for 217 patients for the right eye (OD) and 216 patients for the left eye (OS); age, gender and genetic type are available for all 220 patients; missing data are accounted for using multiple imputation.

^**VA = visual acuity (ETDRS letter score)

^***VF = Humphrey visual field (db)

⁺DOM = dominant; AR = recessive; XL = sex-linked; ISO = isolate; UND = undetermined

^†N_eyes,obs = number of eyes observed for the characteristic; N_eyes = number of eyes observed + number of eyes imputed for the characteristic

computer run:

• :/proj/stross/stros0a/rankcorrelation/correlation.proc.mi.age.sas 11/24/15
• :/proj/stross/stros0a/rankcorrelation/correlation.ranked.proc.mi.sexddm 11/30/15
• :/proj/stross/stros0a/rankcorrelation/correlation.ranked.proc.mi.overall 12/1/15
• :/proj/stross/stros0a/rankcorrelation/correlation.ranked.ns.sas 11/7/16

Table 3.

Correlation Estimates for the RP Data Set (220 patients, 440 eyes)^*

		Crude				Adjusted
Type of correlation	Parameter	Point estimate	95% CI	P-value	Neyes (Neyes,obs**)	Point estimate	95% CI	P-value	Neyes (Neyes,obs**)
Pearson	ρxy	0.212	(0.088, 0.329)	<0.001	440 (433)	0.195	(0.071, 0.312)	0.002	440 (433)
	${\mathrm{\rho }}_{\text{xy}}^{\ast }$	0.177	(0.054, 0.295)	0.004	440 (433)	0.156	(0.033, 0.274)	0.012	440 (433)
	ρxx	0.787				0.766
	${\mathrm{\sigma }}_{\mathrm{x}}^2$	100.2				91.1
	ρyy	0.944				0.943
	${\mathrm{\sigma }}_{\mathrm{y}}^2$	227, 330				201, 710
Rank	ρxy,s	0.229	(0.110, 0.341)	<0.001	440 (433)	0.221	(0.103, 0.333)	<0.001	440 (433)
	${\mathrm{\rho }}_{\text{xy},\mathrm{s}}^{\ast }$	0.200	(0.082, 0.312)	<0.001	440 (433)	0.189	(0.072, 0.301)	0.001	440 (433)
	ρxx,s	0.819				0.807
	${\mathrm{\sigma }}_{\mathrm{x},\mathrm{s}}^2$	0.946				0.891
	ρyy,s	0.909				0.900
	${\mathrm{\sigma }}_{\mathrm{y},\mathrm{s}}^2$	0.962				0.884

^*VA is available for 219 patients for the right eye (OD) and 216 patients for the left eye (OS); VF is available for 217 patients for the right eye (OD) and 216 patients for the left eye (OS); age, gender and genetic type are available for all 220 patients; missing data are accounted for using multiple imputation.

^**N_eyes,obs = number of eyes where both VA and VF are observed; N_eyes = number of eyes observed + number of eyes imputed for the characteristic

computer run:

• :/proj/stross/stros0a/rankcorrelation/correlation.ranked.proc.mi3a.sas 11/23/15
• :/proj.stross/stros0a/rankcorrelation/correlation.ranked.proc.mi.residual.probit.sas 12/04/15
• :/proj/stross/stros0a/rankcorrelation/correlation.ranked.proc.mi.residual.sas 12/04/15

Because both VF and VA are not normally distributed, we also computed the corresponding crude and partial rank correlations based on equation 13. The rank correlation coefficients are slightly larger than the corresponding Pearson correlations (ordinary rank correlation = 0.229, p<0.001; partial rank correlation = 0.221, p<0.001; ordinary rank cross-correlation = 0.200, p<0.001; partial rank cross-correlation = 0.189, p = 0.001).

Note that for both Pearson and rank correlation, the cross-correlations ( ${\rho }_{xy}^{\ast },{\rho }_{xy,s}^{\ast }$) are almost as large as the corresponding inter-class correlations (ρ_xyρ_xy,s) indicating likely efficiency gains in estimation of ρ_xy and ρ_xy,s by ρ̂_xy,MLE as presented in equation 7 vs. the ordinary Pearson product-moment correlation given by ρ̂_xy,Pearson since ${\sigma }_{\underset{\_}{y}\mid \underset{\_}{x}}^2$ will be reduced if t_ij,₂ is included as a predictor of y_ij in equation 7.

To check the assumption of bivariate normality, we note that if H_X is univariate normal, then (H_X,H_Y) will be bivariate normal if H_Y|H_X ~ N(α + βH_X,σ²). To test this assumption we (1) ran a linear regression of Ĥ_i,Yj,n on Ĥ _i,Xj,n, (2) obtained studentized residuals from the regression and (3) performed the Shapiro-Wilk test of normality on the distribution of studentized residuals (available in PROC UNIVARIATE of SAS). This was done separately for right (j=1) and left (j=2) eyes, where Y = VF and X = VA. The Shapiro-Wilk test statistic was W = 0.98, p > 0.05 for right eyes and W = 0.98, p > 0.05 for left eyes indicating that the assumption of bivariate normality is appropriate for these data.

(b) Estimating the correlation between biomarkers of phenacetin and aspirin intake in a study of analgesic abuse among Swiss women

The Swiss Analgesic Study started in 1967/1968 [13]. There were 1244 Swiss women participating in the study. The goal was to evaluate the association between the use of phenacetin-containing analgesics and the prevalence and incidence of kidney disorders. NAPAP (N-acetyl-P-aminophenol) is a urinary metabolite associated with recent use of phenacetin-containing analgesics. NAPAP was initially measured in a urine sample at the baseline clinic visit. There were two additional urine samples collected at home on 2 separate days within 1 week of the baseline clinic visit. One issue is that some analgesics contain both phenacetin and aspirin and it is important to determine the correlation between biomarkers that reflect recent phenacetin and aspirin intake. Salicylate concentrations in urine may be increased after recent intake of aspirin-containing analgesics, but the amount of increase depends on the pH level in urine with alkaline urine (pH > 7.0) resulting in increased secretion in urine [14]. Urinary salicylates may also increase after ingestion of other substances (e.g., cranberry juice) [15].

For this analysis, concentrations of NAPAP and salicylates were determined from the same 3 urine specimens for each woman. NAPAP values were represented as continuous variables and expressed in units of optical density (o.d.), but its distribution is highly skewed and non-normal. Urinary salicylates (mg %) were measured in four categories (0-19 mg% / 20-49 mg% / 50-99 mg% / 100+ mg%) and converted to a continuous scale by using the median value within each category (10 mg% / 35 mg% / 75 mg% / 100 mg%). Since the distributions of both NAPAP and salicylates were non-normal, the rank correlation is a natural measure of association. Descriptive data for this study are provided in Table 4.

Table 4.

Descriptive Statistics for the Swiss Study Data Set, (1244 women)^*

	NAPAP (o.d.)			Salicylates (mg%)
	mean(se)	Nvis(Nvis,obs)**	(95% CI)	mean(se)	Nvis(Nvis,obs)**	(95% CI)
overall	0.162 (0.008)	3732 (3680)	(0.147, 0.178)	15.0 (0.4)	3732 (3600)	(14.2, 15.7)
age
<40	0.146 (0.013)	1311 (1292)	(0.120, 0.172)	15.2 (0.7)	1311 (1265)	(13.9, 16.5)
≥40	0.171 (0.010)	2421 (2388)	(0.152, 0.191)	14.8 (0.5)	2421 (2335)	(13.9, 15.8)
weight (kg)
≤57.0	0.202 (0.016)	912 (898)	(0.171, 0.233)	16.4 (0.8)	912 (880)	(14.9, 18.0)
57.1 – 63.9	0.134 (0.017)	840 (832)	(0.102, 0.167)	13.2 (0.8)	840 (813)	(11.6, 14.8)
64.0 – 72.9	0.142 (0.014)	1113 (1098)	(0.114, 0.170)	14.6 (0.7)	1113 (1075)	(13.2, 16.1)
≥73.0	0.174 (0.016)	867 (851)	(0.142, 0.206)	15.6 (0.8)	867 (832)	(14.0, 17.2)
Number of cigarettes currently smoked per day
0	0.134 (0.010)	2295 (2266)	(0.117, 0.156)	14.5 (0.5)	2295 (2222)	(13.5, 15.5)
1 – 9	0.157 (0.017)	759 (745)	(0.123, 0.191)	15.4 (0.9)	759 (725)	(13.7, 17.1)
≥10	0.258 (0.018)	678 (669)	(0.222, 0.294)	16.1 (0.9)	678 (653)	(14.4, 17.9)
location of urine collection
clinic visit	0.175 (0.010)	1244 (1244)	(0.155, 0.194)	15.6 (0.5)	1244 (1202)	(14.5, 16.6)
1st home urine	0.153 (0.009)	1244 (1217)	(0.136, 0.170)	14.6 (0.5)	1244 (1191)	(13.7, 15.6)
2nd home urine	0.160 (0.009)	1244 (1219)	(0.142, 0.177)	14.7 (0.5)	1244 (1207)	(13.7, 15.7)

^*NAPAP is available for 1244 women at the clinic visit, 1217 women at the 1^st home urine and 1219 women for the 2^nd home urine; Salicylates are available for 1202 women at the clinic visit, 1191 women at the 1^st home urine and 1207 women at the 2^nd home urine; age, weight and number of cigarettes currently smoked are available for all 1244 women; missing data are accounted for using multiple imputation.

^**N_vis,obs = number of visits where the characteristic was observed; N_vis = number of visits where the characteristic was observed + number of visits where the characteristic was imputed.

• :/proj/stross/stros0a/rankcorrelation/swiss.proc.mi.age.sas 01/22/16
• :/proj/stross/stros0a/rankcorrelation/swiss.proc.mi.overall.sas 01/22/16
• :/proj/stross/stros0a/rankcorrelation/swiss.proc.mi.weight.smoke.sas 02/02/16
• :/proj/stross/stros0a/rankcorrelation/swiss.age.wgt.smk.ns.sas 11/7/16

There were 90 women (7.2%) who had missing data for at least one NAPAP replicate and/or one salicylate replicate. We used multiple imputation methods with 5 imputations to impute the missing data (using PROC MI of SAS) and to perform the analyses in equation 11 (using PROC MIANALYZE of SAS).

We see that mean NAPAP was higher for women age 40 or older vs. women < 40 years of age, while mean salicylates were comparable in the two age groups. Mean NAPAP was higher for both light (≤57.0kg) and heavier (≥73.0kg) women and was much higher for women who currently smoke ≥10 cigarettes/day vs. non-current smokers. The trends for salicylates were in the same direction. Both NAPAP and salicylates were somewhat higher at the clinic visit than at the two home urines.

The correlation analyses based on equation 11 are reported in Table 5. The intraclass correlation (ICC) was higher for NAPAP (ρ_yy = 0.611) than for salicylates (ρ_xx = 0.402). The Pearson correlation between NAPAP and salicylates was 0.391 (p<0.001) when measured at the same visit (ρ_xy ) and 0.248 when measured at different visits ( ${\rho }_{xy}^{\ast }$). After adjusting for age, weight, smoking and location of urine collection, the estimated Pearson correlation between NAPAP and salicylates remained about the same when measured at the same visit (i.e., ρ_xy = 0.390) and when measured at different visits (i.e., ${\rho }_{xy}^{\ast }=0.246$).

Table 5.

Correlation Estimates for the Swiss Study Data Set (1244 women)^*

		Crude†				Adjusted‡
Type of correlation	Parameter	Point estimate	95% CI	P-value	Nvis(Nvis,obs)**	Point estimate	95% CI	P-value	Nvis(Nvis,obs)**
Pearson	ρxy	0.391	(0.355, 0.426)	<0.001	3732 (3597)	0.390	(0.354, 0.425)	<0.001	3732 (3597)
	${\mathrm{\rho }}_{\text{xy}}^{\ast }$	0.248	(0.213, 0.282)	<0.001	3732 (3597)	0.246	(0.212, 0.280)	<0.001	3732 (3597)
	ρxx	0.402				0.401
	${\mathrm{\sigma }}_{\mathrm{x}}^2$	313.2				312.5
	ρyy	0.611				0.602
	${\mathrm{\sigma }}_{\mathrm{y}}^2$	0.105				0.102
Rank	ρxy,s	0.290	(0.250, 0.328)	<0.001	3732 (3597)	0.288	(0.247, 0.328)	<0.001	3732 (3597)
	${\mathrm{\rho }}_{\text{xy},\mathrm{s}}^{\ast }$	0.197	(0.162, 0.231)	<0.001	3732 (3597)	0.194	(0.159, 0.229)	<0.001	3732 (3597)
	ρxx,s	0.329				0.329
	${\mathrm{\sigma }}_{\mathrm{x},\mathrm{s}}^2$	0.426				0.426
	ρyy,s	0.538				0.528
	${\mathrm{\sigma }}_{\mathrm{y},\mathrm{s}}^2$	0.952				0.932

^*NAPAP is available for 1244 women at the clinic visit, 1217 women at the 1^st home urine and 1219 women for the 2^nd home urine; Salicylates are available for 1202 women at the clinic visit, 1191 women at the 1^st home urine and 1207 women at the 2^nd home urine; age, weight and number of cigarettes currently smoked are available for all 1244 women; missing data are accounted for using multiple imputation.

^**N_vis,obs = number of visits where both urinary NAPAP and salicylates were available; N_vis = number of visits where both urinary NAPAP and salicylates were available + number of visits where either was imputed

^†y=NAPAP, x=salicylates

^‡adjusted for age, weight, smoking and location of urine collection

computer run:

• :/proj/stross/stros0a/rankcorrelation/swiss.proc.mi2.sas 1/21/16
• :/proj.stross/stros0a/rankcorrelation/swiss.proc.mi.probit.sas 1/21/16
• :/proj/stross/stros0a/rankcorrelation/swiss.proc.mi.residual3.sas 2/2/16
• :/proj/stross/stros0a/rankcorrelation/swiss.proc.mi.probit.residual3.sas 2/4/16

Since the distribution of NAPAP was highly skewed and the distribution of salicylates represented in 4 broad ordered categories, it was reasonable to also consider rank correlation as a measure of association. The estimated rank correlation was 0.290 when NAPAP and salicylates were measured at the same visit (ρ_xy,s) and 0.197 when measured at different visits ( ${\rho }_{xy,s}^{\ast }$). After adjusting for age, weight, smoking and location of urine collection, the rank correlations decreased slightly when measured at the same visit (ρ_xy,s = 0.288) and at different visits ( ${\rho }_{xy,s}^{\ast }=0.194$).

This example shows that there is a considerable difference between ρ̂_xy vs. ${\widehat{\rho }}_{xy}^{\ast }$ and similarly between ρ̂_xy,s vs. ${\widehat{\rho }}_{xy,s}^{\ast }$ indicating that NAPAP and salicylate values at different visits are best modeled as distinguishable replicates.

We also performed the Shapiro-Wilk test of normality for the distribution of studentized residuals of Ĥ_i,Yj,n given Ĥ_i,Xj,n as described in the RP example. The Shapiro-Wilk test statistic was W = 0.99, p < 0.05 at the clinic visit, W = 0.99, p < 0.05 at the 1^st home urine, and W = 0.99, p < 0.05 at the 2^nd home urine. The reference value for the W test statistic under normality is W = 1.0. Thus, there was only a mild departure from the null value of W and the significance of the W test is due to the large sample size.

6. Discussion

In this paper we have presented methods for maximum likelihood estimation of Pearson correlation in the clustered data setting. The methods are applicable to clustered data based on distinguishable replicates and can be used both for clusters of size 2 (Equation 7) and clusters of size > 2 (Equation 11). They are based on a population-average type of model. A simpler approach to this problem from a population-average perspective is based on the regression model

$$y_{ij}=\alpha +\beta x_{ij}+e_{ij},i=1,\dots ,n;j=1,\dots ,k$$ (22)

where

$$e_{ij}~\mathit{MVN}(\underset{\_}{0},\mathrm{\sum })$$

and

$$\mathrm{\sum }={\sigma }_{\underset{\_}{y}\mid \underset{\_}{x}}^2\left[\left(1-{\rho }_{yy\mid \underset{\_}{x}}\right)I_{k\times k}+{\rho }_{yy\mid \underset{\_}{x}}{J}_{k\times k}\right]$$

The corresponding estimator of ρ_xy denoted by ρ̂_xy,standard is given by:

$${\widehat{\rho }}_{xy,\mathit{standard}}=\widehat{\beta }{\widehat{\sigma }}_x/{\widehat{\sigma }}_y$$ (23)

The model in (22) and the corresponding estimator in (23) are actually a special case of Equation 11 when ${\rho }_{xy}^{\ast }={\rho }_{xy}{\rho }_{xx}$. In words, ${\rho }_{xy}^{\ast }={\rho }_{xy}{\rho }_{xx}$ if the correlation between y_ij1and _xij2 is completely mediated by the correlation between y_ij and x_ij and between x_ij1and x_ij2. In general, this will not always be the case and the estimator in (23) is not the MLE of ρ_xy under the model in (8).

Bland and Altman [16] have also considered a population-average approach to estimation of ρ_xy. With their approach, a pseudo-data set is created where pairs (x̄_i, ȳ_i) are repeated k_i times and k_i = # replicates for the i^th subject. Their estimator can be expressed in the form:

$${\widehat{\rho }}_{xy,BA}=\sum _{i=1}^n{k}_i({\overline{x}}_i-\overline{\overline{x}})({\overline{y}}_i-\overline{\overline{y}})/{\left\{\left[\sum _{i=1}^n{k}_i{({\overline{x}}_i-\overline{\overline{x}})}^2\right]\left[\sum _{i=1}^n{k}_i{({\overline{y}}_i-\overline{\overline{y}})}^2\right]\right\}}^{1/2}$$

where

$$\overline{\overline{x}}=\sum _{i=1}^n{k}_i{\overline{x}}_i/K,\overline{\overline{y}}=\sum _{i=1}^n{k}_i{\overline{y}}_i/K,K=\sum _{i=1}^n{k}_i$$

The ordinary Pearson correlation is then computed based on the K observations in the pseudo-data set and is tested for significance using a t distribution with n - 2 df as the reference distribution.

Lorenz, Datta and Harkema [17] also consider a population-average approach, but based on observations from individual cluster-members rather than cluster averages. Their estimator takes the form:

$${\widehat{\rho }}_{xy,\mathit{LDH}}=\sum _{i=1}^n\left[\sum _{j=1}^{k_i}\left(x_{ij}-\overline{\overline{x}}\right)\left(y_{ij}-\overline{\overline{y}}\right)/k_i\right]/{\left\{\left[\sum _{i=1}^n\sum _{j=1}^{k_i}{\left(x_{ij}-\overline{\overline{x}}\right)}^2/k_i\right]\left[\sum _{i=1}^n\sum _{j=1}^{k_i}{\left(y_{ij}-\overline{\overline{y}}\right)}^2/k_i\right]\right\}}^{1/2}$$

Large sample asymptotic normality of ρ̂_xy,LDH is assumed and significance testing is based on z_LDH = ρ̂_xy,LDH/[var(ρ̂_xy,LDH)^1/2] and compared with a N(0,1) distribution. The delta method is used to estimate var(ρ̂_xy,LDH). The LDH approach is also applied to estimation of Kendall’s τ for clustered data.

Both the BA and LDH approaches assume that replicates are indistinguishable and allow for a variable number of replicates per cluster. With the BA estimator, the i^th cluster-mean is weighted k_i times. With the LDH estimator each cluster gets equal weight regardless of cluster-size. If either ρ_xx > 0 or ρ_yy > 0, the optimal weighting for the ith cluster will be between 1 and k_i.

The estimators in equations 7 and 11 of this paper assume replicates are distinguishable and use multiple imputation methods to estimate missing (x, y) replicate scores based on (x, y) scores for other cluster members as well as values of other covariates and performs the analysis based on n_IMP imputed data sets using Rubin’s rules. The estimators are maximum likelihood, can be implemented with standard software, are extended to the rank correlation setting and allow one to control for other covariates.

The distinguishing feature of ML estimation is that for clustered data the likelihood is based on

$$L=\prod _{i=1}^n{L}_i,$$

where $L_i={\prod }_{i=1}^n{L}_{1i}\left({\underset{\_}{y}}_i\mid {\underset{\_}{x}}_i\right)L_{2i}\left({\underset{\_}{x}}_i\right)$ and $L_1={\prod }_{i=1}^n{L}_{\underset{\_}{1}i}$ is maximized to estimate ρ_xy.

In the LDH approach the likelihood is based on

$$L_1^{\ast }=\prod _{i=1}^n\prod _{j=1}^{k_i}L\left(y_{ij}\mid x_{ij}\right)$$

Under $L_1^{\ast }$, y_ij is expressed as a function of x_ij, while under L₁, y_ij is expressed as a function of both x_ij and x_i+,−j. $L_1^{\ast }$ is a special case of L₁ when ${\rho }_{xy}^{\ast }={\rho }_{xy}{\rho }_{xx}$. $L_1^{\ast }$ is the likelihood in the i.i.d. situation when ρ_xx = ρ_yy = 0 [1], but not in the clustered data situation.

Another approach is to consider a subject-specific type of model [18]. Under this approach, we consider the random intercept model

$$y_{ij}=\mu +q_i+\beta x_{ij}+e_{ij},i=1,\dots ,n;j=1,\dots ,k_i$$ (24)

where

$$q_i~N\left(0,{\sigma }_q^2\right),e_{ij}~N(0,{\sigma }^2)$$

Under this model, the estimator β has a subject-specific interpretation (i.e., are changes in X between 2 replicates for an individual correlated with corresponding changes in Y). For example, do changes in visual field between 2 eyes of a subject correspond to changes in visual acuity. Bland and Altman [18] consider a slight variation of (24) where q is a fixed effect instead of a random effect.

Finally, we have extended our results to the estimation of Spearman rank correlation for clustered data. To our knowledge, this is the first time this has appeared in the literature. We also extend the Pearson and rank correlation results to the setting of partial correlation, where one can control for both cluster-specific and subunit-specific covariates. For rank correlation this is different from the partial Spearman correlation available in some statistical packages where one calculates covariate-adjusted residuals for both Y and X based on the raw data and then computes the Spearman correlation based on the residuals. With our approach, probit scores are first computed for X and Y variables and residuals are computed by regressing X and Y probit scores respectively, on covariates. Rank correlations are then obtained based on Spearman correlations between the probit residuals. This should provide a more nonparametric estimate of partial Spearman correlation.

The relationship between Pearson and Spearman correlation given in (13), assumes that H_Z = (H_X, H_Y) is bivariate normal. If X and/or Y are categorical, such as for salicylates in the second example, then this assumption will be violated. However, if we assume that there is a latent continuous scale but the continuous scale is divided into categories and the actual rank of an observation on the latent continuous scale is replaced by the average rank within a category, then this assumption may be more plausible. Also, in the simulation studies where we replaced the actual rank on the continuous scale by the average rank within a category (see Appendix Table 1), the type I error and coverage were preserved.

We also assessed the validity of the estimation procedure in (13) and (14) when H_X and H_Y are each univariate normal, but (H_X, H_Y) is not bivariate normal. The clustered KS copula in (21) was introduced for this purpose. Simulation studies indicate that bias and coverage probability associated with the estimators of ρ_xy,s and ${\rho }_{xy,s}^{\ast }$ in (13) and (14) are acceptable in this setting for n ≥ 50 (see Appendix Table 2). We also proposed a diagnostic procedure to test the assumption of bivariate normality of replicate probit scores which was applied and satisfied for both of the examples in this paper.

Appendix – Proofs

Theorem 1

Let X be a continuous random variable and let {x₁,…,x_n} be an i.i.d. sample from X. Define ${\widehat{H}}_{x,n}={\mathrm{\Phi }}^{-1}\left[R_{X,n}^{(x)}/(n+1)\right]$, where Φ⁻¹ is the inverse normal distribution, $R_{X,n}^{(x)}=1+{\sum }_{i=1}^{n}U(x-x_i)$, and U(a) = 1 if a > 0, = 0 otherwise. If H_x = Φ⁻¹[F_X(x)] where F_X is the c.d.f. of X, then Ĥ_x,n converges in probability to H_x as n → ∞.

Proof

From (A.110), p. 346 of Lehmann [19] if E (Ĥ_x,n – H_x)² → 0 as n → ∞, then Ĥ_x,n converges in probability to H_x as n → ∞.

Let P_x = Φ(H_x) = F_X(x) and ${\widehat{P}}_{x,n}=\mathrm{\Phi }\left({\widehat{H}}_{x,n}\right)=R_{X,n}^{(x)}/(n+1)$

We have that

$$E{\left({\widehat{H}}_{x,n}-H_x\right)}^2={\left[E\left({\widehat{H}}_{x,n}\right)-H_x\right]}^2+\mathit{var}({\widehat{H}}_{x,n})$$ (A1)

To assess the 1^st component of (A1) we use a Taylor series expansion of Ĥ_x,n about H_x, yielding

$${\widehat{H}}_{x,n}=H_x+\sqrt{2\pi }\mathit{exp}(H_x^2/2)\left({\widehat{P}}_{x,n}-P_x\right)+\pi H_x\mathit{exp}(H_x^2){\left({\widehat{P}}_{x,n}-P_x\right)}^2+\sum _{r=3}^{\infty }{a}_r{\left({\widehat{P}}_{x,n}-P_x\right)}^r$$ (A2)

where |a_r| < ∞, r ≥ 3. if we take expectations of both sides of (A2) we obtain:

$$E\left({\widehat{H}}_{x,n}\right)=H_x+\sqrt{2\pi }\mathit{exp}(H_x^2/2)E\left({\widehat{P}}_{x,n}-P_x\right)+\pi H_x\mathit{exp}(H_x^2)E{\left({\widehat{P}}_{x,n}-P_x\right)}^2+\sum _{r=3}^{\infty }{a}_{r}E{\left({\widehat{P}}_{x,n}-P_x\right)}^r$$ (A3)

Since E(P̂_x,n – P_x)^q → 0 as n → ∞ for q ≥ 1 it follows that E(Ĥ_x,n) – H_x → 0 as n → ∞

To assess the 2^nd component of (A1) we use the delta method, whereby

$$\begin{array}{l}\mathit{var}\left({\widehat{H}}_{x,n}\right)=2\pi \mathit{exp}(H_x^2)\mathit{var}\left({\widehat{P}}_{x,n}\right)+O(1/n)\\ =2\pi \mathit{exp}(H_x^2)n{P}_x(1-P_x)/{(n+1)}^2+O(1/n)\to 0\text{as}n\to \infty \end{array}$$ (A4)

Thus, based on (A1), (A3) and (A4), E(Ĥ_x,n – H_x)² → 0 as n → ∞, whereby Ĥ_x,n converges in probability to H_x as n → ∞.

Corollary 1

Let Ĥ_x,n be defined as in Theorem 1, H_X = {Ĥ_x, xεX} and Ĥ_X,n = {Ĥ_x,n, xεX}. Ĥ_X,n converges in law to a N(0,1) distribution as n → ∞.

Proof

We have that

$$\underset{n\to \infty }{lim}Pr({\widehat{H}}_{X,n}\le z)=Pr(H_X\le z)=\mathrm{\Phi }(z).$$

Hence, Ĥ_X,n is asymptotically normal as n → ∞.

Theorem 2

Let Ĥ_X,n and Ĥ_Y,n be defined as in Corollary 1. Let H_Z = (H_X,H_Y), ρ_XY = cov(H_X,H_Y) and Ĥ_Z,n = (Ĥ_X,n, Ĥ_Y,n) If H_Z is bivariate normal, then Ĥ_Z,n is asymptotically bivariate normal as n → ∞.

Proof

From Theorem 2.6.2, p. 37 of Anderson [1], H_Z is bivariate normal if and only if aH_X + bH_Y is univariate normal for all a, b, where min(|a|,|b|) > 0. We have from Corollary 1 that aĤ_X,n + bĤ_Y,n converges in law to aH_X + bH_Y as n → ∞. Thus, since var(H_X) = var(H_Y) = 1 and cov(H_X,H_Y) = ρ_XY then

$$\underset{n\to \infty }{lim}Pr\left(a{\widehat{H}}_{X,n}+b{\widehat{H}}_{Y,n}\le z\right)=\mathrm{\Phi }\left(z/\sqrt{a^2+b^2+2ab{\rho }_{XY}}\right)$$

Therefore, aĤ_x,n + bĤ_y,n is asymptotically univariate normal for all a, b. It follows that H_Z,n is asymptotically bivariate normal as n → ∞.

Theorem 3

Let X₁,…,X_L be continuous random variables and define H_Xl(x) = Φ⁻¹[F_Xl(x)], l =1,…,L. Let ρ_l1l2 = cov(H_Xl1,H_Xl2), l₁ ≠ l₂ = 1,…,L: Define Ĥ_Xln(x) = Φ⁻¹ [R_Xln(x)/(n+1)], where $R_{X_l,n}(x)=1+{\sum }_{i=1}^{n}U(x-x_{il})$ and x_il = value of X_l for the i^th subject, i = 1,…,n; l = 1,…,L.

If H_X ≡ (H_X1,… H_XL,) is multivariate normal, then Ĥ_Xn ≡ (Ĥ_X1,n,…, Ĥ_XL,n) will be asymptotically multivariate normal as n → ∞.

Proof

From Theorem 2.6.2, p. 37 of Anderson [1] H_x will be multivariate normal if and only if $Z={\sum }_{l=1}^L{a}_l{H}_{X_l}$ is univariate normal for all a = (a₁,…,a_L) where min(|a_l|, l = 1,…,L) > 0. We have from Corollary 1 that ${\widehat{Z}}_n={\sum }_{l=1}^L{a}_l{\widehat{H}}_{X_l,n}$ converges in law to Z as n → ∞ Thus, since var(H_Xl) = 1, l = 1,…,L, and cov(H_Xl1,H_Xl2) = ρ_l1l2, l₁ ≠ l₂ = 1,…,L, then $\underset{n\to \infty }{lim}Pr\left({\widehat{Z}}_n\le z\right)=\mathrm{\Phi }\left(z/\sqrt{{\sum }_{l=1}^L{a}_l^2+{\sum }_{l_1\ne l_2=1}^L{a}_{l_1}{a}_{l_2}{\rho }_{l_1{l}_2}}\right)$. Therefore, Ẑ_n is asymptotically univariate normal for all a where min(|a_l|, l = 1,…,L) > 0. It follows that Ĥ_Xn is asymptotically multivariate normal as n → ∞

Appendix Table 1.

Simulation Results for Rank Correlation Based on Discrete Data, MLE method

k	ρxy	${\mathrm{\rho }}_{\text{xy}}^{\ast }$	ρxx(ρyy)	n	ρ̂xy	Type I error	coverage probability (%)	power
3	0	0	0.5	50	0.028	0.055	94.7	---
	0	0	0.5	100	0.010	0.054	94.8	---
	0.2	0.1	0.5	50	0.194	---	95.9	52.4
	0.2	0.1	0.5	100	0.184	---	94.6	76.8

Computer runs:

• :/proj/stross/stros0a/rankcorrelation/simulation.3rep.4000.n100.5.probit.sas 9/15/16
• :/proj/stross/stros0a/rankcorrelation/simulation2.3rep.4000.n100.5.probit.sas 9/15/16
• :/proj/stross/stros0a/rankcorrelation/simulation.3rep.4000.n50.5.probit.sas 9/15/16
• :/proj/stross/stros0a/rankcorrelation/simulation2.3rep.4000.n50.5.probit.sas 9/15/16

Appendix Table 2.

Bias and coverage probability of (ρ̂_xy,s, ${\widehat{\mathrm{\rho }}}_{\text{xy},\mathrm{s}}^{\ast }$) based on (13) and (14) when the data are generated from the clustered KS^* copula in (21)

g	n	parameter	true value**	median estimated value+	bias	coverage probability (%)
0.5	50	ρxy,s	0.497	0.488	−0.009	96.6
		${\mathrm{\rho }}_{\text{xy},\mathrm{s}}^{\ast }$	0.328	0.327	−0.001	94.4
	100	ρxy,s	0.497	0.491	−0.006	96.6
		${\mathrm{\rho }}_{\text{xy},\mathrm{s}}^{\ast }$	0.328	0.325	−0.003	94.1
1.0	50	ρxy,s	0.497	0.486	−0.011	96.4
		${\mathrm{\rho }}_{\text{xy},\mathrm{s}}^{\ast }$	0.246	0.246	0	92.1
	100	ρxy,s	0.497	0.491	−0.006	96.7
		${\mathrm{\rho }}_{\text{xy},\mathrm{s}}^{\ast }$	0.246	0.244	−0.002	91.4

^*Kimeldorf-Sampson

^**based on simulating 100,000 random vectors (X₁, Y₁, X₂, Y₂) from the clustered KS copula in (21) and estimating ρ_xy,s from mean [Spearman correlation (X₁,Y₁ )+Spearman correlation (X₂,Y₂ )] and ${\mathrm{\rho }}_{\text{xy},\mathrm{s}}^{\ast }$ from mean [Spearman correlation (X₁, Y₂ )+Spearman correlation (X₂, Y₁)].

⁺based on 4,000 simulated datasets consisting of n (X₁, Y₁, X₂, Y₂) vectors from the clustered KS copula in (21).

Computer runs:

• :/proj/stross/stros0a/rankcorrelation/simulation.new.n100000.sas 9/29/16
• :/proj/stross/stros0a/rankcorrelation/simulation.new2.n100000.sas 10/13/16
• :/proj/stross/stros0a/rankcorrelation/simulation.new.4000.n50.sas 10/13/16
• :/proj/stross/stros0a/rankcorrelation/simulation.new.4000.n100.sas 10/13/16
• :/proj/stross/stros0a/rankcorrelation/simulation.new2.4000.n50.sas 10/14/16
• :/proj/stross/stros0a/rankcorrelation/simulation.new2.4000.n100.sas 10/14/16