Demystifying the cytokine network: Mathematical models point the way

Abstract

Cytokines provide the means by which immune cells communicate with each other and with parenchymal cells. There are over one hundred cytokines and many exist in families that share receptor components and signal transduction pathways, creating complex networks. Reductionist approaches to understanding the role of specific cytokines, through the use of gene-targeted mice, have revealed further complexity in the form of redundancy and pleiotropy in cytokine function. Creating an understanding of the complex interactions between cytokines and their target cells is challenging experimentally. Mathematical and computational modeling provides a robust set of tools by which complex interactions between cytokines can be studied and analyzed, in the process creating novel insights that can be further tested experimentally. This review will discuss and provide examples of the different modeling approaches that have been used to increase our understanding of cytokine networks. This includes discussion of knowledge-based and data-driven modeling approaches and the recent advance in single-cell analysis. The use of modeling to optimize cytokine-based therapies will also be discussed.

1. Introduction

Cytokines allow immune cells to communicate with each other and with parenchymal cells. Cytokines include interleukins, interferons, chemokines and growth factors that are released by immune cells in response to a variety of stimuli and they induce complex transcriptional responses resulting in cellular proliferation, differentiation, and migration. These responses are mediated by the binding of cytokines to specific receptors expressed on responding cells. There are over one hundred cytokines and many exist in families that share receptor components and signal transduction pathways. Reductionist approaches to understanding the role of specific cytokines, through the use of gene-targeted mice, have revealed further complexity in the form of redundancy and pleiotropy in cytokine function [1,2].

Many diseases are characterized by complex cytokine networks that have either positive or negative impacts on disease. For example, in colorectal cancer cytokines can either lead to tumor rejection through the induction of anti-tumor immunity or can promote tumor growth through chronic inflammation [3]. In addition, there are temporal effects such that cytokines, e.g. TNF and IL-17, may play a useful anti-tumor role early in the disease but become pro-tumorigenic later as the tumor progresses [3]. Similarly complex networks play an important role in autoimmune diseases such as rheumatoid arthritis (RA) [4] and inflammatory bowel disease (IBD) [5]. Therapies for inflammatory diseases such as RA and IBD have targeted the cytokines thought to play a key role in disease pathogenesis, TNF and IL-17 [6,7]. While these therapies have been very successful for many patients not all individuals with IBD, for example, respond to anti-TNF therapy [8]. Some of these patients have benefited from therapies that target other cytokines such as IL-12, IL-13 and IL-6 [5].

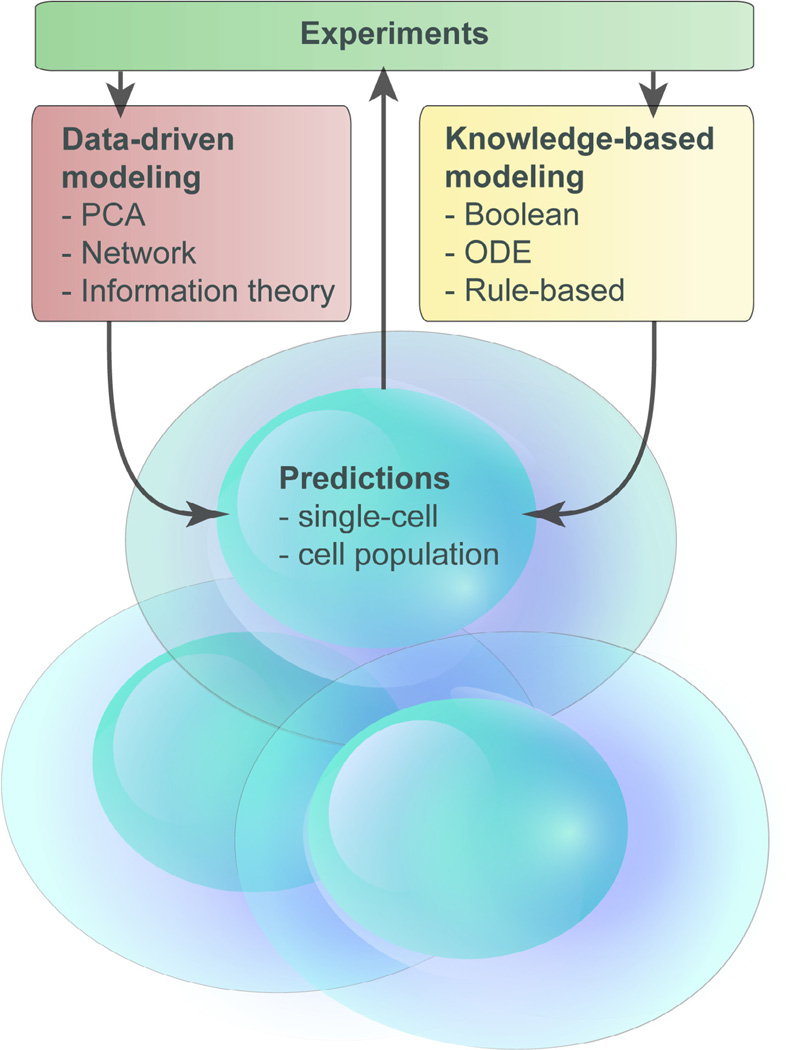
Advances in multiplex technology allow cytokine measurements in a wide variety of settings. These technologies generate large datasets that can include proteomic, genomic and epigenomic information. New analytic techniques are being developed to analyze these datasets [9], but there is a further need to place these data in a biological framework. Systems biology approaches allow the development of mathematical models that not only explain how a network of cytokines may be influencing a disease process, but may provide testable predictions concerning possible therapeutic interventions [10]. Several modeling approaches have been developed for biological systems and two main types of modeling are used; one is knowledge or theory-based in which prior knowledge is used to construct a mathematical model and the other is data-driven in which complex experimental datasets are analyzed mathematically to generate new hypotheses (Fig. 1) [11]. Both approaches have been successfully applied to the immune system and have generated novel insights into many immune processes including vaccine responses [12,13], IL-2 and Tregs [14], IL-7 receptor signaling [15] IgE receptor [16] and TCR signaling pathways [17,18]. This review will discuss recent examples in which each of these modeling approaches have shed light on the complex world of cytokines and their functions in the immune response.

Fig. 1.

Modeling approaches used to study cytokine interactions. Two main modeling approaches are used; knowledge-based approaches that may utilize Boolean logic, ordinary differential equations (ODE) or rule-based techniques or data-driven approaches in which large experimental datasets are analyzed using principal component analysis (PCA), network or information theory. This is an iterative process with experimental data used to create and validate models, models analyzed to generate predictions which are then tested in further experiments.

2. Differentiation of cytokine-producing cells and the control of cytokine production

The adaptive immune response is orchestrated by CD4⁺ T cells through the secretion of cytokines that drive the activation and differentiation of effector cells such as B cells, cytotoxic T cells and cells of the innate immune system. Naïve CD4⁺ T cells are induced to differentiate into T helper (Th) cell subsets following recognition of peptide (p)MHC complexes presented by dendritic cells (DC) in the context of a particular cytokine microenvironment. At least 6 major Th subsets are recognized today: Th1, Th2, Th17, Th9, T follicular helper (Tfh), and regulatory (Treg) cells [19,20] and this number is likely to keep increasing. Th cell subsets are distinguished by the expression of specific transcription factors that regulate the distinct patterns of cytokine secretion characteristic of each Th cell subset. Th cell differentiation has been the topic of many mathematical models [21]. Early mathematical models of this differentiation process utilized ordinary differential equations (ODE) and were developed from existing knowledge [22,23]. More recently different modeling techniques have been used, including logical network models [24,25], and increasingly, experimental data have been used to drive the models [26,27].

Th1 and Th2 cells were first described in the 1980s [28] and Th1 differentiation requires the presence of IFN-γ and IL-12 [29], whereas Th2 cells arise in the presence of IL-4 [30]. In addition, there are inhibitory interactions between cytokines such that IFN-γ inhibits the action of IL-4 on Th2 differentiation and vice versa [31]. Th1/Th2 differentiation has been the subject of many mathematical models over the years. Many of these models treated Th1/Th2 differentiation as a binary cell fate decision controlled by specific gene regulatory networks, in this case T-bet and GATA-3 [32–34]. However recent single-cell analyses have cast doubt on the binary cell fate model by revealing that cells adopt a continuum of states [35,36]. A recent study examined this question in more detail using a combination of experimental and modeling approaches [26]. By stimulating CD4 T cells in the presence of increasing amounts of both IL-12 and IL-4, it was shown that expression of T-bet and GATA-3 occurs continuously and is tuned by the input signals. The authors show using a model of the gene regulatory network describing Th1/Th2 differentiation [32,37], that autoregulation of transcription factor expression must dominate over cross-inhibitory effects for the continuum to exist [26]. Further, they show that production of IFN-γ or IL-4 by individual cells is determined in a stochastic way, and that individual cells retain the ability to make one or both cytokines independently [26]. The final model describes a two stage differentiation process involving continuous tunable transcription factor expression that then drives binary stochastic cytokine secretion [26]. Thus, this study demonstrates, using a combination of modeling and experimental validation, that Th1 or Th2 cells retain the ability to tune their cytokine responses depending on the external conditions.

The differentiation of naïve CD4⁺ T cells into Th17 and induced (i)Treg both require TGF-β but the addition of IL-6 will favor Th17 over iTreg differentiation, whereas the presence of retinoic acid favors iTreg development [38]. Th17 cells play important roles in the defense against extracellular pathogens and fungi but also have immunopathological roles in some autoimmune diseases such as multiple sclerosis and RA [39]. Treg cells, on the other hand play an important role in preventing autoimmunity and minimizing immunopathology following an infection [40,41]. TGF-β and IL-6 induce the Th17 master regulator RORγt [42], whereas the presence of TGF-β with retinoic acid will induce the expression of the iTreg-specific transcription factor Foxp3 [43,44]. Several models have been developed to explore these interactions and to shed light on the factors driving the differentiation outcome. In one approach [45], an ODE model described the reciprocal differentiation of Th17 and iTreg, was able to recapitulate the key features of Th17 and iTreg differentiation and, in addition provided new insights into the existence of cells that express both RORγt and Foxp3 [45]. The model suggested that double-expressing cells do not represent an intermediate step in differentiation but rather that they appeared in conditions of high TGF-β concentration at later stages of differentiation. This is in agreement with reports that describe the existence of iTreg that co-express Foxp3 and RORγt and have suppressive function [46].

In another approach aimed at investigating Th17 differentiation the authors used a RNASeq dataset generated over a detailed time course to explore the validity of several potential models [27]. In this study a dynamic ODE model of Th17 differentiation was used as a framework and four hypothetical mechanisms were identified that resulted in 12 alternative models for the molecular interactions important for Th17 differentiation. A statistical approach was applied to the time course RNASeq data and used to select which of the 12 alternative models best fit the data. This approach identified three models that best fit the RNASeq data, and by incorporating additional protein data on the dose response relationship between TGF-β and Foxp3 expression a single model was identified. The most robust model was one that incorporated the mechanisms of RORγt inhibition by Foxp3 and the inhibition of Foxp3 by STAT3 signaling downstream of IL-6 [27]. This study is a good example of combining modeling with detailed time course experimental data to provide important new insights into the complexities of Th17 differentiation.

Recent studies have examined the control of IFN-γ production in differentiated Th1 cells [47]. In the case of IFN-γ production by T cells the authors used a combination of single-cell assays and mathematical modeling to determine whether the observed heterogeneity in production level of IFN-γ is stably maintained in an individual T cell, such that cells are either producers or non-producers, or whether every cell can be a cytokine producer or non-producer depending on the timing or circumstance. The experiments showed that individual T cells make a stable decision to produce IFN-γ or not and that this is correlated with several factors including the expression level of T-bet and the methylation status of the IFN-γ and Tbx21 loci [47]. The mathematical model of the population heterogeneity was best able to fit the data when each cell was given an inherent ability to produce a certain level of IFN-γ, rather than being the consequence of gene-expression noise [47]. Interestingly T cells retained a quantitative memory of IFN-γ production levels for as long as one month in vivo. Similar results were obtained for IL-17 production [47].

Another study has examined the control of TNF production by macrophages stimulated with various TLR ligands [48]. In this study ODE models of the three stages of TNF production, transcription, RNA stabilization and translation, were combined and used to simulate macrophage response to various TLR signals. This model could accurately simulate the responses to LPS and poly I:C, but failed in the case of CpG. In order to accurately simulate CpG-induced TNF production it was necessary to add a model component of autocrine signaling by TNF in order to promote optimal NFκB-mediated TNF production [48]. Experiments were performed to confirm that optimal NFκB activation in response to CpG required the presence of TNF, whereas this was not required for the LPS response [48].

3. Cytokine signaling

Cytokines bind to specific receptors on cells, which trigger a signaling cascade ultimately leading to gene transcription and a cellular response. Many cytokines share receptor components and signaling intermediates but yet induce distinct responses in individual cells. Examples include the common γ-chain cytokines [49], the IL-12 and IL-6 family of cytokines [50]. IL-12 and IL-23 share the same signaling chain, IL-12Rβ2, and signal via JAK2 and STAT4 [51]. IL-2, IL-4, IL-9, IL-7, IL-15 and IL-21 all share the common γ chain important for signaling [52]. IL-2 and IL-15 not only share the common γ-chain but also share the IL-2Rβ chain, and specificity is conferred by an α chain that is unique for each cytokine [53,54]. Recent studies examining the signaling pathways induced by both cytokines in T cells have revealed that these are quite similar and that distinct cellular responses induced by IL-2 or IL-15 are influenced by differential signal strength, caused by differences in the binding affinity and in the expression levels of the unique α chains as well as the dynamics of receptor internalization [55].

Cytokines may also have more than one effect on the same cell. For example, IL-2 can induce both proliferation and death in T cells depending on the circumstance. A simple ODE model of this paradoxical signaling [56] demonstrated that these events were important in the homeostasis of cell populations. The proliferative and death inducing effects of IL-2 were both positively correlated with the production of IL-2 by T cells but the dynamics were distinct. The proliferation rate was correlated with IL-2 secretion in a cooperative manner whereas there was a linear relationship between IL-2 production and death [56]. The model predicted that if the cells were diluted during the proliferative phase the death function would dominate and this was confirmed experimentally [56]. Additionally, the model demonstrated that it was important for robust homeostasis for the same cytokine to have these paradoxical effects rather than allowing two separate cytokines to either increase proliferation or increase the death rate. A modified model that allowed for two cytokines to have the proliferative and death-inducing effects created unstable dynamics which were much more sensitive to the parameter values. There was only a very narrow range of parameters in which the two cytokine model could achieve homeostasis whereas the one cytokine model was robust over a wide range of parameters [56].

Cytokines such as TNF-α or TGF-β can bind to more than one receptor which leads to increased complexity in the cellular response. TGF-β binds to type I and type II receptors which work in concert to activate the TGF-β signaling pathway. TGF-β has multiple functions, and, in addition, a family of related cytokines can bind to these receptors. This signaling pathway has been extensively modeled [57] and these models have provided important insights into the biology of TGF-β in multiple settings. Several recent studies have examined the effects of sustained versus pulsed TGF-β signaling using combined experimental and mathematical approaches [58–60].

A cautionary tale is provided by two recent studies of pulsatile signals that appear to result in opposite conclusions. In one study cells treated to a short pulse of TGF-β became unresponsive to subsequent ligand stimulation [59]. This behavior was associated with a rapid internalization and degradation of TGF-β receptors followed by slow re-expression of these receptors. A mathematical model of the receptor dynamics and refractory state was constructed and this model identified important determinants of the refractory state, namely the rate of receptor turnover and the ratio of the ligand-induced to constitutive receptor turnover [59]. Further, the model predicted that the ability of tumor cells to respond to TGF-β would be dependent on the level of autocrine TGF-β production and this was confirmed experimentally [59]. An earlier paper [60] using the same cell line failed to show the development of a refractory state, but rather showed that multiple short pulses of TGF-β led to sustained signaling. A mathematical model was developed and this reproduced the experimental results and was able to explain the switch like behavior seen for several readouts [60]. These two papers used slightly different experimental approaches to interrupt the TGF-β signal with one study using an inhibitor of the TGF-β signal or a neutralizing anti-TGF-β antibody [59], whereas the other study washed the excess TGF-β out from the cells [60]. It is possible that these experimental differences could be responsible for the contradictory results reported in these two studies, and this has yet to be resolved. In both cases the models were able to reproduce the experimental results and provide predictions that were experimentally validated. These studies highlight that care must be taken when choosing biological conditions, and interpreting the results of a mechanistic model. However, since these two studies focus on slightly different aspects of the signaling pathway it is possible that careful analysis of both systems will reveal a unified understanding of TGF-β signaling.

Differences in the relative abundance of receptors or signaling intermediates can dictate how a cell responds to a cytokine. A prime example of how levels of receptor expression induce differential cellular responses is the high affinity (HA) IL-2R. Naïve T cells only express HA-IL-2R following activation and upregulation of CD25. In contrast, Treg constitutively express HA-IL-2R and thus can sequester IL-2 produced by activated T cells. Modeling of the IL-2R-induced signals in T cell populations, combined with detailed single-cell measurements revealed the complex dynamics of the ‘‘tug of war” between Th and Treg cells for IL-2 [61]. The wide variability in IL-2R expression between different T cells influences their ability to produce and consume IL-2 and to initiate signaling via the IL-2R [61]. This has been substantiated in several in vivo models in which it was shown that IL-2 produced early in an immune response is utilized by resident Treg cells [62].

Another example of the effects of the abundance of signaling intermediates was examined in a detailed data-driven model of IL-13 signaling in two B cell lymphoma lines. These cell lines are representative of two distinct tumor types, Hodgkin lymphoma and primary mediastinal B cell lymphoma, that differ in their clinical outcome and response to therapy. Both cell types exhibit a hyperactive IL-13 signaling pathway that is thought to contribute to their growth. Detailed analysis of the abundance of the signaling components revealed altered stoichiometry related to the relative abundance of positive (JAK2) and negative (SHP1) signaling intermediates. Exposure of these cells lines to IL-13 identified differences and similarities in the signaling pathways in these two cell lines [63]. Structurally similar models were developed and calibrated for both cell lines and parameters were defined for each cell line based on detailed quantitative measurements. These models reproduced experimental data and revealed distinct therapeutic targets in each of the cell lines that could be tested clinically [63].

4. Cytokine networks

Cytokines do not act in isolation and, frequently, cells are exposed to multiple cytokines at the same time or sequentially. These interactions may change how a cell responds to any given cytokine. IL-2 and IL-4 were first described as growth factors for T and B cells respectively. Interestingly, IL-2 and IL-4 synergize when inducing proliferation of T cells [64,65] but they are antagonistic when inducing B cell proliferation, which was associated with the down-regulation of high affinity IL-2R when B cells were pretreated with IL-4 [66]. An ODE model that would explain these apparently contradictory actions of IL-2 and IL-4 on the proliferation of B and T cells was developed [67]. The model predicted that synergy or antagonism depended on the dynamics of the IL-2 and IL-4 receptor numbers. In activated T cells, because the number of high affinity IL-2R is large the threshold is reached before the reduction of receptor numbers by IL-4 can impact the proliferative response, and thus the synergy term dominates. In B cells the number of IL-2R is much lower and thus the presence of IL-4 will reduce this number such that there is apparent antagonism between the cytokines [67]. The model was calibrated to experimental data and, in T cells, the threshold number for IL-2 was approximately 10 fold less than that required for IL-4 to induce proliferation [68]. As discussed below single-cell analysis has shed important new light on this phenomenon.

More recently the response of macrophages to a wide array of cytokines and TLR ligands was examined in single or double ligand combinations as collected by the Alliance for Cell Signaling [69]. These datasets consisted of phosphoproteins, measured by Western blot and cytokine secretion measured at various time points following stimulation. This study describes a novel methodology for the reconstruction of the phosphoprotein networks following macrophage stimulation, termed an information theoretic approach [69]. This approach is based on the estimation of mutual information [70] of interactions by using kernel density estimators. This provides a novel method to analyze large signaling datasets and, in the case of macrophage response, known signaling networks were identified and some novel interactions were found [69]. For example, this study revealed that TNF secretion was regulated by the largest number of phosphoproteins and identified ribosomal 6 kinase as a novel regulator of TNF production [69].

Another study used discrete logic modeling to examine the response of human cells to combinations of 7 cytokines [71]. This study used extensive datasets available in the literature to build and train the model. Subsequent model testing against new data showed increased predictive power and identified new interactions between signaling molecules that were validated experimentally [71]. Thus, the use of Boolean logic was able to generate a model of complex signaling pathways that yielded testable predictions.

A recent study examined the profiles of cytokines produced by PBMC from healthy or HIV⁺ individuals in response to three different stimuli [72]. Using partial least-squares discriminant analysis of these datasets they identified differences in the pattern of cytokine responses that depended on the stimulus and donor type. In addition, a decision tree analysis revealed that HIV⁺ donors had an early defect in the production of IFN-γ in response to innate stimuli. Further experiments revealed that this was an NK cell defect and that it had an impact on later production of cytokines by other immune cells [72].

Increasing complexity arises when attempting to model an entire immune response involving several cell types and the cytokines they produce. This has resulted in the generation of multi-scale models in which multiple layers such as intracellular signaling pathways, secretion and diffusion of cytokines and the response of multiple cell types are included [73,74]. One such model examined how the response to TNF-induced apoptosis in the intestine was influenced by the presence of lymphocytes [75]. Using a data-driven multi-scale model this study found that the presence of lymphocytes abrogated the negative impact of TNF signaling in the intestine through the secretion of the chemokine MCP-1 and recruitment of plasmacytoid DCs [75]. Another study examined the role of IL-21 in maintaining the CD4 T cell response in the gut to Helicobacter Pylori infection [76].

5. Single-cell analysis

Heterogeneity is ubiquitous in biological systems. Even when studying cultured cell lines, there is natural cell-to-cell variability in the activity or abundance of regulators for cytokine-dependent signals. Non-genetic differences between cells that result from morphological, asynchronous cell-cycle state, microenvironment, or stochastic sources can lead to diverse responses from subpopulations of single cells in otherwise homogeneous conditions [36,77,78]. Because the goal of many mathematical models is to understand how cells process information and respond to stimuli, it is important to parameterize models to single-cell data when it is available. Recent technological advances in single-cell analysis makes it possible to address some of these issues and understand how variability in cytokine-induced signals leads to different cell fates. These include advances in single-cell analysis, imaging, and ‘omics’ techniques [35,79–81].

Although many useful predictions can be made from observations that measure ‘bulk’ properties from cell populations, such as the biochemical average in a lysate from many thousands of cells, these measurements often miss important principles of signal transduction. For example, although an EC50 from a doseresponse curve can be used to characterize the potency of a drug, this is also the precise concentration that produces the greatest heterogeneity of single-cell responses. How does heterogeneity in the biochemical state of a cell lead to different responses to a cytokine or drug? Cotari et al. recently developed a hybrid computational and experimental methodology called cell-to-cell variability analysis (CCVA) to dissect these quantitative relationships [82]. Using flow cytometry to simultaneously measure IL-2Rα receptor abundance and pSTAT5 as a downstream effector in the same cell, they used CCVA to determine how cell-to-cell variation in IL2-Rα abundance influences sensitivity to cytokines whose receptor shares the common γ-chain. Comparing cell subpopulations from a cultured cell line showed that the EC50 for IL-2 and other γ-chain cytokines can vary by orders of magnitude depending on IL2-Rα abundance. Using a Bayesian strategy to parameterize a thermodynamic model of receptor complexes to single-cell data revealed that IL-2Rα competes with other pre-formed receptor complexes for binding the common γ-chain, and γ-chain depletion by abundant complexes can alter the EC50 for other γ-chain cytokines in the same cell. Their model predicts that the relative abundance of each α-chain complex, and their relative affinity for the γ-chain, are key parameters determining each cell’s sensitivity to a cytokine.

In a related single-cell study, Voisinne et al. showed that weakly activated CD8⁺ T cells can be co-opted to proliferate by paracrine signals from strongly activated T cells in their microenvironment [83]. Variability between single cells in the abundance of receptors or other signaling regulators lead to cell-specific thresholds for antigen discrimination, and even though some cell subpopulations were insensitive to low quality or low quantity of antigen in isolation, they could still become activated when grown in a mixed-culture. Using a hybrid deterministic/stochastic framework to model single-cell responses, an IL-2-mediated positive feedback loop was shown to provide additional PI3K activation sufficient for cell cycle entry in some cells despite weak TCR activation. Their experiments and model suggest that IL-2 secreted by subpopulations of strongly responding cells provide a synergistic signal, effectively reducing the threshold of activation for weak responders in their vicinity.

The system used a co-culture of transgenic cells, and one may ask: Is natural cell-to-cell variability in an isogenic system sufficient for ‘sender’ and ‘responder’ cells to simultaneously co-exist in the same culture? This question is partially answered in another study of monocyte-derived cells that compares cytokine secretion between isolated single cells and cell populations [84]. Using a microwell-based culture system to multiplex measurements of cytokines, Xue et al. showed that paracrine signals within a cell population contribute significantly to the LPS-stimulated secretome, and are attenuated when cells are grown in isolation. By developing a Graphical Gaussian Model of the extracellular regulatory network, they identified critical paracrine dependencies that differentiate cytokine secretion profiles for cell populations and isolated single cells. The distributions of single cell cytokine secretion also revealed significant cell-to-cell variability. For the case of TNF, the top 5% of TNF-secreting single cells were estimated to account for 60% of total TNF secretion, indicating the presence of a small population of ‘high TNF-producing cells’ that may share paracrine signals with nearby cells to amplify the local response. Together, these observations suggest that heterogeneity may be favored by the immune system, to fine-tune cell behaviors through communicating subpopulations of ‘sender’ and ‘responder’ cells that share noisy signals.

Patil et al. [85] examined IFN-β production by DC infected with Newcastle disease virus (NDV) in order to determine the source of observed cell-to-cell variability. In this case they counted the molecules of Ifnb1 and NDV RNA in individual cells to quantitate cytokine production. They found that fewer than 35% of NDV-infected cells produced Ifnb1 RNA at early time points and that this increased over time. In addition, there was no correlation between the levels of NDV RNA and Ifnb1 RNA in the cells. This was in contrast to LPS treatment when the majority of DC produced Ifnb1 at the early time point. The computational approach of stochastic feature screening [86] was used to characterize the factors driving this cell to cell variability. The stochastic features screened included the infectivity of the cell, whether an infected cell would respond. Cell-to-cell variability in the amount of Ifnb1 RNA produced and the time for the response to be initiated. Results of propagation simulations suggested that all four features were needed to reproduce the experimental variability in Ifnb1 expression after NDV infection, but not for the LPS response [85].

In response to cytokines and other environmental stimuli, cells must precisely coordinate spatiotemporal dynamics of signal transduction networks. For many signaling systems, specificity of a stimulus is encoded through dynamic ‘features’ of activation or subcellular localization for signaling mediators, such as time-varying changes in their amplitude, duration, or frequency [87,88]. Live-cell imaging experiments using cells that express fluorescent biosensors have revealed many principles of information encoding and decoding in single cells that would be impossible to observe using population-level assays. For example, dynamic ‘features’ for pulses of activated ERK encode responses to extracellular EGF and NGF that regulate cellular decisions to proliferate or differentiate [89,90]. Stochastic variability between cells in protein expression leads to differences in the rate and timing of caspase activation in cellular responses to TRAIL, leading to cell-to-cell variability in cell death and a phenomenon called fractional killing [91,92]. Live-cell data were also essential to develop temporally resolved models of the canonical NF-κB pathway, leading to detailed understanding of critical feedback motifs that regulate inflammatory signal transduction [26,80,93,94]. In a related study, quantitative single-cell methods that simultaneously measure time courses for nuclear localization of NF-κB were combined with gene expression in the same cell to determine how the transcriptional system decodes NF-κB dynamics [95]. The NF-κB transcriptional system was shown to be capable of fold-change detection, and some genes showed qualitative differences in their response to the same ‘feature’ of NF-κB dynamics. By adapting an ODE-based model, a type 1 incoherent feed-forward network motif in the NF-κB system was found to be essential for fold-change detection. The model predicts that changes in the cellular abundance of proteins that compete for binding to NF-κB promoters can tune diverse patterns of gene expression in response to inflammatory cytokines. Further efforts to integrate dynamics with other single-cell assays, such as combined measurement of genome and transcriptome in the same cell [96], will undoubtedly lead to more sophisticated models of single-cell behavior with greater predictive capabilities.

6. Clinical applications of modeling approaches

Cytokines contribute to the pathogenesis of many diseases including autoimmune [4], inflammatory [5] and allergic [97] diseases. Several new therapeutics for these diseases target cytokines and have shown promise in a wide variety of conditions [6,7]. While these new therapies are proving successful in many patients there are still questions concerning who would best respond to the therapy and what is the best regimen for delivery. Several recent studies have examined these questions [98–104]. In a study of patients with asthma bipartite network analysis of patients and cytokines allowed the assignment of specific pathogenic mechanisms and cytokines to particular clinical subgroups [102]. Bipartite networks use two sets of nodes and the edges can only connect nodes from different sets. In this study [105] data from the measurement of 18 cytokines in bronchoalveolar lavage fluid in 83 asthma patients was visualized using a bipartite network created with the Kamada–Kawai algorithm [106]. This analysis revealed three main clusters of patients that could be distinguished by cytokine pattern and also clinical parameters. These corresponded to a patient cluster with high levels of Th2 cytokines, a cluster with high Th2 and innate cytokines and a third cluster with low cytokine levels. The third cluster also identified patients with more preserved lung function. Interestingly, this classification does not match the standard clinical classification of severe versus nonsevere asthma. These results suggest that novel approaches to classify clinical conditions using modeling and cytokine profiles will provide novel insights important for patient management and disease pathogenesis.

Models have been used to determine optimal dosage and timing of cytokine-targeted treatments in various settings. In one study an ODE model was used to optimize the treatment protocol of IL-21 given as an anti-tumor therapeutic [98], demonstrating that lower doses given twice a day just as effective and less toxic than higher doses given once a day [98]. Another model examined the tumor-promoting effects of IL-35 [107] and also studied the effects of administering an anti-IL-35 reagent as a therapeutic. This study suggested that continuous administration of the anti-IL-35 would be most efficacious in reducing the tumor load [107]. Another therapeutic approach in cancer has been the coupling of inflammatory cytokines, such as IL-2, to antibodies specific for tumor-associated antigens; so called immunocytokines [108]. A recent study [104] found that the immunocytokines did not necessarily accumulate in the tumor but rather bound to IL-2R positive cells. This, however, did not appear to impede the therapeutic effect. An ODE model examining the effect of immunocytokine size on biodistribution revealed that the while small immunocytokines are more rapidly cleared from the blood they accumulate better in the tumor and thus have increased effectiveness [104].

Another study has examined the development of resistance to IFN treatment in patients infected with HCV [101]. A detailed ODE model of the IFN signaling pathway and viral kinetics revealed a mechanism by which HCV subverts the IFN response thus allowing for viral persistence and resistance to further IFN treatment. The study further showed that direct-acting anti-virals can over-come this state allowing for the virus to be cleared, and this has shown promise clinically [101].

7. Conclusions

Computational modeling of cytokine networks is being increasingly integrated into studies of cytokine mechanisms and network dynamics. Mechanistic models have been used to identify novel interactions and to optimize therapeutic protocols. Data-driven models have been used to find novel components and interactions in large cytokine networks and signaling pathways. Studies at the single-cell level demonstrate how the immune system harnesses heterogeneity to achieve optimal function. These studies are likely to bring new insights to the field and will aid in the development and optimization of new cytokine-based therapies in a wide variety of diseases.