Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Jun 4.
Published in final edited form as: J Am Chem Soc. 2016 Aug 9;138(33):10402–10405. doi: 10.1021/jacs.6b06216

Quantification of the Electrophilicity of Benzyne and Related Intermediates

Noah F Fine Nathel †,§, Lucas A Morrill †,§, Herbert Mayr ‡, Neil K Garg †,*
PMCID: PMC5457803  NIHMSID: NIHMS862689  PMID: 27480639

Abstract

The determination of reactivity parameters for short-lived intermediates provides an indispensable tool for synthetic design. Despite that electrophilicity parameters have now been established for more than 250 reactive species, the corresponding parameters for benzyne and related intermediates have not been uncovered. We report a study that has allowed for the quantification of benzyne’s electrophilicity parameter. Our approach relies on the strategic use of the diffusion-clock method and also provides electrophilicity parameters E for other substituted arynes.

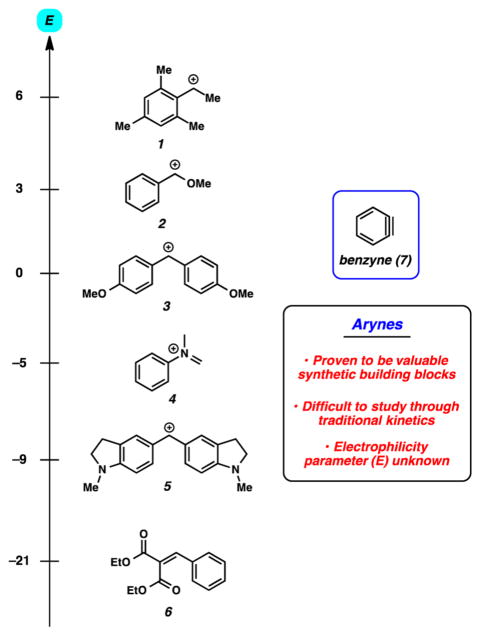
A critical aspect of successful synthetic design plans is the ability to reliably predict chemical reactivity. Accordingly, over decades of research, chemists have developed reactivity profiles that account for a variety of functional groups. Early breakthroughs, such as the Swain and Scott parameters,1 paved the way for the established reactivity scales now available.2–4 Most commonly used today is the benzhydrylium-based reactivity scale, which includes nucleophilicity and electrophilicity parameters for more than 1,200 compounds, including reactive intermediates (Figure 1, e.g., 1–6).2,5 Notably missing from the many species studied thus far is benzyne (7). Since its validation in the 1950s,6 benzyne (7) has proven to be an indispensable synthetic building block. Benzyne (7) and related species have been used to construct decorated arenes and heterocycles and assemble intricate natural product scaffolds.7 Moreover, attempts to observe arynes by microwave and infrared spectroscopy8 and atomic force microscopy,9 along with computational studies of arynes,10,11 have provided a wealth of knowledge about aryne structure and regioselectivities in trapping experiments. One notable question has remained: Just how electrophilic is benzyne?

Figure 1.

Figure 1

Open in a new tab

Sampling of the benzhydrylium-based electrophilicity scale showing compounds 1–6 and benzyne (7).

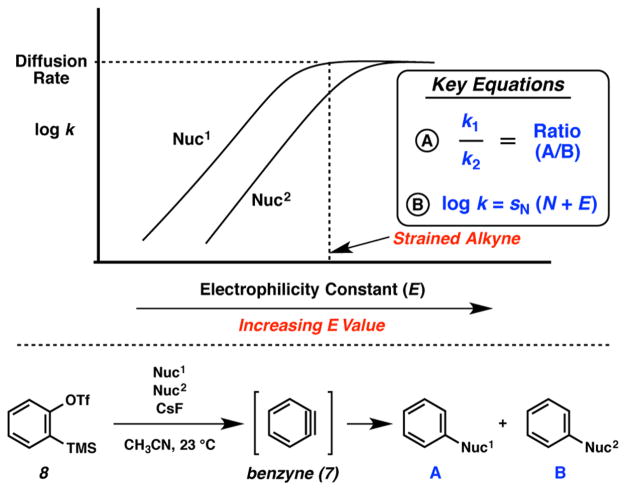
This question has gone unanswered because of the fleeting nature of benzyne (7). We reasoned that the elucidation of benzyne’s electrophilicity parameter could be made possible by utilization of the diffusion-clock method, which has previously been used to determine the electrophilicity of highly reactive carbocations.12,13 In prior kinetic studies, the fastest reactions of carbocations (generated using laser-flash photolysis) with neutral nucleophiles in organic solvents were found to proceed with second-order rate constants of 2–4 × 109 L mol−1 s−1, due to diffusion control.14 As depicted in Figure 2, nucleophiles that differ in reactivity toward weak electrophiles become equally reactive toward strong electrophiles as the diffusion limit is reached.15

Figure 2.

Figure 2

Open in a new tab

Diffusion-clock method and planned application to determine the E parameter for benzyne (7).

Assuming that the relative reactivities of nucleophiles toward carbocations and typical Michael acceptors (reference electrophiles) also hold for reactions with arynes, we reasoned that the diffusion-clock method could be used to determine the electrophilic reactivities of arynes. Specifically, if benzyne (7) was generated (from precursor 8) in the presence of equal concentrations of trapping nucleophiles (Nuc1 and Nuc2, both used in large excess), the resulting A/B ratio could be used to calculate k1/k2 as suggested in Equation A (Figure 2). If Nuc1 reacts with diffusion control (i.e., k1 ≈ 3 × 109 L mol−1 s−1)16 the rate constant k2 can be calculated from the k1/k2 ratio. Armed with this rate constant, the electrophilicity of benzyne could then be determined using the previously derived equation for the reactions of electrophiles with nucleophiles (Equation B, Figure 2).2 In this key equation, electrophiles are characterized by one parameter (electrophilicity E) and nucleophiles are characterized by two solvent-dependent parameters (nucleophilicity N and nucleophile-specific susceptibility sN). With the experimentally determined rate constant and the previously established nucleophilicity parameters (N and sN), solving the equation for E would be straightforward. Herein, we demonstrate the success of this approach to determine the elusive E parameter for benzyne (7) and several other related species.

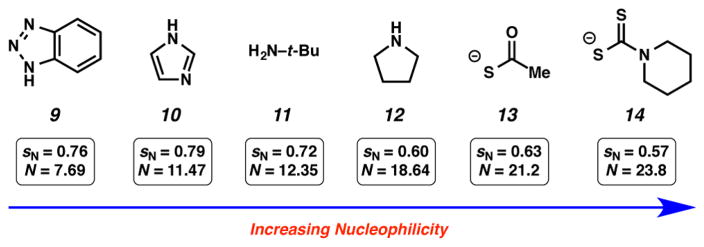
To initiate our studies, we selected a series of nucleophiles to be used in trapping experiments. Nucleophiles 9–14 (Figure 3) were chosen because (a) their nucleophilicity parameters in CH3CN had already been established and (b) they were likely to undergo efficient reaction with the highly reactive intermediates we planned to study.17 Table 1 highlights the experiments that were used to determine the E parameter for benzyne (7) and related reactive intermediates 18–20. Beginning with benzyne (7), the appropriate silyl triflate precursor was treated with CsF in acetonitrile in the presence of two competing nucleophiles that have known and varying nucleophilicity parameters. After consumption of the silyl triflate and workup, the crude mixture was analyzed by supercritical fluid chromatography (SFC) to provide the ratio of products A/B. The competition experiment between pyrrolidine (12) and thioacetate (13) led to a 2.89 to 1 ratio of products (entry 1a). Given that thioacetate (13) and pyrrolidine (12) have significantly different nucleophilicity parameters, the low selectivity indicates that both nucleophiles react under diffusion control with benzyne (7). Next, we studied the competition between pyrrolidine (12), a nucleophile that reacts with diffusion control, and less reactive nucleophiles. The utilization of t-butylamine (11) gave a 21.5 to 1 ratio of products (entry 1b), whereas the use of imidazole (10) led to a 37.7 to 1 ratio of adducts (entry 1c). Based on these results (i.e., entries 1a–1c), the E parameter for benzyne (7) was calculated to be −1.18 For comparison, benzyne (7) is 1 order of magnitude less electrophilic compared to the bis(4-methoxyphenyl)methylium ion (3, Figure 1).

Figure 3.

Figure 3

Open in a new tab

Nucleophiles used in this study and their N and sN values in acetonitrile.

Table 1.

Determination of Electrophilicity Parameter (E) for Strained Intermediates 7 and 18–20

graphic file with name nihms862689u1.jpg
Entrya Reactive Intermediate Nuc1 Nuc2 Ratio (A/B) = k1/k2b E
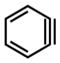1a graphic file with name nihms862689t1.jpg
7 		12 13 2.89 N/A
1b 12 11 21.5 −1
1c 12 10 37.7 −1
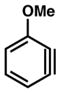2a graphic file with name nihms862689t2.jpg
18 		14 13 4.40 N/A
2b 14 10 13.0 −1
2c 14 11 17.5 −1
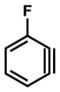3a graphic file with name nihms862689t3.jpg
19 		12 10 1.60 N/A
3b 14 9 5.61 ≈ +4
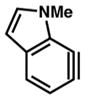4a graphic file with name nihms862689t4.jpg
20 		14 12 3.77 N/A
4b 14 10 15.6 −1
4c 14 11 23.8 −1
Open in a new tab
a

Conditions: silyl triflate (1.0 equiv), Nuc1 (5.0 equiv), Nuc2 (5.0 equiv), CsF (5.0 equiv) in CH3CN (0.2 M) at 23 °C.

b

Ratio (A/B) determined by SFC or 1H NMR analysis.

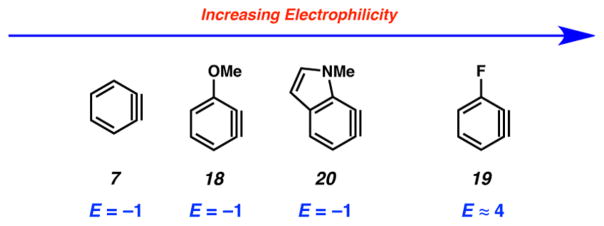
Having determined the E parameter for benzyne (7), we performed a series of competition experiments in order to establish the E parameter for other useful strained intermediates (18–20, Table 1). In the case of methoxybenzyne 18, the competition experiment using dithioate (14) and thioacetate (13) gave a 4.40 to 1 ratio (entry 2a), indicating that both nucleophiles react with 18 close to diffusion control. Competition between dithioate 14 and imidazole (10) gave a 13.0 to 1 ratio of adducts (entry 2b). Further competition experiments with dithioate (14) and t-butylamine (11) gave a 17.5 to 1 ratio of products (entry 2c).19 Thus, the E parameter for 18 was determined to be −1, like benzyne (7). In the case of fluorobenzyne 19, it was necessary to employ a nucleophile that was significantly less reactive than t-butylamine (11) because the use of anything more reactive led to diffusion control. For example, a competition experiment between pyrrolidine (12) and imidazole (10), which is less reactive than t-butylamine (11), gave a 1.60 to 1 ratio of adducts (entry 3a). The only suitable nucleophile tested that did not react under diffusion control was benzotriazole (9). The competition experiment between dithioate (14) and benzotriazole (9) gave a ratio 5.61 to 1. As k2 derived from this ratio was in the nonlinear part of the log k2 vs E correlations, only an approximate value of E(19) ≈ +4 could be estimated (entry 3b). It is interesting to note that 19 is 5 orders of magnitude more electrophilic than 7 or 18 and shares similar reactivity to that of a benzylic carbocation (2 and 1, Figure 1). We also determined the E value for 6,7-indolyne 20, a versatile heterocyclic building block that is known to react regioselectively with nucleophiles,11c by performing three competition experiments. We first used dithioate (14) and pyrrolidine (12). The small reactivity ratio showed that nucleophile (14) reacted under diffusion control. However, competition experiments between dithioate (14) and imidazole (10) and between dithioate (14) and t-butylamine (11) (entries 4b and 4c) gave reactivity ratios of 15.6 and 23.8, respectively,18 which allowed us to determine the E value for 20 to be approximately −1.

A summary of the E parameters for the strained intermediates studied herein is shown in Figure 4. Benzyne (7), methoxybenzyne (18), and 6,7-indolyne (20) all have E values close to −1. Fluorobenzyne (19) is several orders of magnitude more electrophilic, with an E value close to 4. The extreme electron-withdrawing nature of the fluoride substituent presumably contributes to the greater electrophilicity. It should be noted, however, that the electrophilicity parameters derived in this work hold only for additions of nucleophiles to the triple bond that proceed with rate-determining formation of one new σ-bond.20

Figure 4.

Figure 4

Open in a new tab

Summary of E parameters determined.

In summary, we have performed a study to quantify the electrophilicity parameter (E) for benzyne (7) and several substituted arynes (18–20). To achieve this, we strategically employed the diffusion-clock method as a means to overcome the inherent challenge of performing kinetic experiments of a fleeting intermediate. These efforts expand the growing database of reactivity parameters for synthetic intermediates and allow, for the first time, the quantification of aryne electrophilicities.

Acknowledgments

The authors are grateful to the NIH-NIGMS (R01 GM090007 for N.K.G.), Bristol-Myers Squibb, the Dreyfus Foundation, the UCLA Gold Shield Alumnae, and the University of California, Los Angeles, for financial support. We are grateful to the NIH-NIGMS (F31-GM101951-02 to N.F.F.N.) and the Foote Family (L.A.M.). These studies were supported by shared instrumentation grants from the NSF (CHE-1048804) and the National Center for Research Resources (S10RR025631).

Footnotes

Notes

The authors declare no competing financial interest.

Supporting Information

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.6b06216.

Detailed experimental procedures and compound characterization data (PDF)

References

  • 1.Swain CG, Scott CB. J Am Chem Soc. 1953;75:141–147. [Google Scholar]
  • 2.(a) Mayr H, Patz M. Angew Chem, Int Ed Engl. 1994;33:938–957. [Google Scholar]; (b) Mayr H, Bug T, Gotta MF, Hering N, Irrgang B, Janker B, Kempf B, Loos R, Ofial AR, Remennikov G, Schimmel H. J Am Chem Soc. 2001;123:9500–9512. doi: 10.1021/ja010890y. [DOI] [PubMed] [Google Scholar]; (c) Lucius R, Loos R, Mayr H. Angew Chem, Int Ed Engl. 2002;41:91–95. doi: 10.1002/1521-3773(20020104)41:1<91::aid-anie91>3.0.co;2-p. [DOI] [PubMed] [Google Scholar]; (d) Mayr H, Kempf B, Ofial AR. Acc Chem Res. 2003;36:66–77. doi: 10.1021/ar020094c. [DOI] [PubMed] [Google Scholar]; (e) Mayr H, Ofial AR. Pure Appl Chem. 2005;77:1807–1821. [Google Scholar]; (f) Richter D, Hampel N, Singer T, Ofial AR, Mayr H. Eur J Org Chem. 2009:3203–3211. [Google Scholar]; (g) Mayr H, Ofial AR. J Phys Org Chem. 2008;21:584–595. [Google Scholar]; (h) Mayr H, Lakhdar S, Maji B, Ofial AR. Beilstein J Org Chem. 2012;8:1458–1478. doi: 10.3762/bjoc.8.166. [DOI] [PMC free article] [PubMed] [Google Scholar]; (i) Corral-Bautista F, Klier L, Knochel P, Mayr H. Angew Chem. 2015;127:12676–12680. doi: 10.1002/anie.201501385. [DOI] [PubMed] [Google Scholar]
  • 3.(a) Ritchie CD. Acc Chem Res. 1972;5:348–354. [Google Scholar]; (b) Ritchie CD. J Am Chem Soc. 1975;97:1170–1179. [Google Scholar]; (c) Ritchie CD, Sawada M. J Am Chem Soc. 1977;99:3754–3761. [Google Scholar]; (d) Ritchie CD, Van Verth JE, Virtanen POI. J Am Chem Soc. 1982;104:3491–3497. [Google Scholar]; (e) Ritchie CD. J Am Chem Soc. 1984;106:7187–7194. [Google Scholar]; (f) Ritchie CD. Can J Chem. 1986;64:2239–2250. [Google Scholar]
  • 4.(a) Kane-Maguire LAP, Honig ED, Sweigart DA. Chem Rev. 1984;84:525–543. [Google Scholar]; (b) Pike RD, Sweigart DA. Coord Chem Rev. 1999;187:183–222. [Google Scholar]
  • 5. [accessed June 1, 2016];Mayr’s Database of Reactivity Parameters. http://www.cup.lmu.de/oc/mayr/reaktionsdatenbank/
  • 6.(a) Roberts JD, Simmons HE, Jr, Carlsmith LA, Vaughan CW. J Am Chem Soc. 1953;75:3290–3291. [Google Scholar]; (b) Wittig G, Pohmer L. Angew Chem. 1955;67:348. [Google Scholar]; (c) Huisgen R, Rist H. Justus Liebigs Ann Chem. 1955;594:137–158. [Google Scholar]
  • 7.For reviews regarding benzyne and related reactive intermediates, see: Pellissier H, Santelli M. Tetrahedron. 2003;59:701–730.Wenk HH, Winkler M, Sander W. Angew Chem, Int Ed. 2003;42:502–528. doi: 10.1002/anie.200390151.Sanz R. Org Prep Proced Int. 2008;40:215–291.Bronner SM, Goetz AE, Garg NK. Synlett. 2011;2011:2599–2604.Tadross PM, Stoltz BM. Chem Rev. 2012;112:3550–3557. doi: 10.1021/cr200478h.Gampe CM, Carreira EM. Angew Chem, Int Ed. 2012;51:3766–3778. doi: 10.1002/anie.201107485.Bhunia A, Yetra SR, Biju AT. Chem Soc Rev. 2012;41:3140–3152. doi: 10.1039/c2cs15310f.Yoshida H, Takaki K. Synlett. 2012;23:1725–1732.Dubrovskiy AV, Markina NA, Larock RC. Org Biomol Chem. 2013;11:191–218. doi: 10.1039/c2ob26673c.Wu C, Shi F. Asian J Org Chem. 2013;2:116–125.Hoffmann RW, Suzuki K. Angew Chem, Int Ed. 2013;52:2655–2656. doi: 10.1002/anie.201209041.Goetz AE, Garg NK. J Org Chem. 2014;79:846–851. doi: 10.1021/jo402723e.Goetz AE, Shah TK, Garg NK. Chem Commun. 2015;51:34–45. doi: 10.1039/c4cc06445c.
  • 8.(a) Radziszewski JG, Hess BA, Jr, Zahradnik R. J Am Chem Soc. 1992;114:52–57. [Google Scholar]; (b) Godfrey P. Aust J Chem. 2010;63:1061–1065. [Google Scholar]
  • 9.Pavlicek N, Schuler B, Collazos S, Moll N, Pérez D, Guitián E, Meyer G, Peña D, Gross L. Nat Chem. 2015;7:623–628. doi: 10.1038/nchem.2300. [DOI] [PubMed] [Google Scholar]
  • 10.For examples of the charge-controlled model see: Ikawa T, Nishiyama T, Shigeta T, Mohri S, Morita S, Takayanagi S-I, Terauchi Y, Morikawa Y, Takagi A, Ishikawa y, Fujii S, Kita Y, Akai S. Angew Chem, Int Ed. 2011;50:5674–5677. doi: 10.1002/anie.201100360.Ikawa T, Tokiwa H, Akai S. Yuki Gosei Kagaku Kyokaishi. 2012;70:1123–1133.Ikawa T, Takagi A, Goto M, Aoyama Y, Ishikawa Y, Itoh Y, Fujii S, Tokiwa H, Akai S. J Org Chem. 2013;78:2965–2983. doi: 10.1021/jo302802b.Takagi A, Ikawa T, Kurita Y, Saito K, Azechi K, Egi M, Itoh Y, Tokiwa H, Kita Y, Akai S. Tetrahedron. 2013;69:4338–4352.Takagi A, Ikawa T, Saito K, Masuda S, Ito T, Akai S. Org Biomol Chem. 2013;11:8145–8150. doi: 10.1039/c3ob41787e.
  • 11.For our laboratories’ studies of arynes, heterocyclic arynes, strained alkynes and allenes, and the aryne distortion model, see: Bronner SM, Bahnck KB, Garg NK. Org Lett. 2009;11:1007–1010. doi: 10.1021/ol802958a.Cheong PHY, Paton RS, Bronner SM, Im GYJ, Garg NK, Houk KN. J Am Chem Soc. 2010;132:1267–1269. doi: 10.1021/ja9098643.Im GYJ, Bronner SM, Goetz AE, Paton RS, Cheong PHY, Houk KN, Garg NK. J Am Chem Soc. 2010;132:17933–17944. doi: 10.1021/ja1086485.Bronner SM, Goetz AE, Garg NK. J Am Chem Soc. 2011;133:3832–3835. doi: 10.1021/ja200437g.Goetz AE, Bronner SM, Cisneros JD, Melamed JM, Paton RS, Houk KN, Garg NK. Angew Chem, Int Ed. 2012;51:2758–2762. doi: 10.1002/anie.201108863.Bronner SM, Mackey JL, Houk KN, Garg NK. J Am Chem Soc. 2012;134:13966–13969. doi: 10.1021/ja306723r.Goetz AE, Garg NK. Nat Chem. 2013;5:54–60. doi: 10.1038/nchem.1504.Medina JM, McMahon TC, Jiménez-Osés G, Houk KN, Garg NK. J Am Chem Soc. 2014;136:14706–14709. doi: 10.1021/ja508635v.Medina JM, Mackey JL, Garg NK, Houk KN. J Am Chem Soc. 2014;136:15798–15805. doi: 10.1021/ja5099935.McMahon TC, Medina JM, Yang YF, Simmons BJ, Houk KN, Garg NK. J Am Chem Soc. 2015;137:4082–4085. doi: 10.1021/jacs.5b01589.Barber JS, Styduhar ED, Pham HV, McMahon TC, Houk KN, Garg NK. J Am Chem Soc. 2016;138:2512–2515. doi: 10.1021/jacs.5b13304.Shah TK, Medina JM, Garg NK. J Am Chem Soc. 2016;138:4948–4954. doi: 10.1021/jacs.6b01986.
  • 12.Richard JP, Rothenberg ME, Jencks WP. J Am Chem Soc. 1984;106:1361–1372.See also subsequent articles in this issue Roth M, Mayr H. Angew Chem, Int Ed Engl. 1995;34:2250–2252.Roth M, Mayr H. Macromolecules. 1996;29:6104–6109.
  • 13.The diffusion-clock method for determining carbocation reactivities in aqueous solution is based on the fact that the reaction of the tritylium ion with the azide ion in aqueous solution is diffusion-controlled (k2 ≈ 5 × 109 L mol−1 s−1). All carbocations that are more reactive than the tritylium ion can therefore be expected to react with the azide ion with equal rates. Thus, the ROH/RN3 ratio, which was obtained by solvolytic generation of carbocations from alkyl halides in aqueous azide solution, was used to calculate the rate constant for the reaction of R+ with water; see ref 12a.
  • 14.(a) Bartl J, Steenken S, Mayr H. J Am Chem Soc. 1991;113:7710–7716. [Google Scholar]; (b) Ammer J, Nolte C, Mayr H. J Am Chem Soc. 2012;134:13902–13911. doi: 10.1021/ja306522b. and references cited therein. [DOI] [PubMed] [Google Scholar]
  • 15.Small differences in reactivity (i.e., factors of 2–3) may be due to the differences in diffusion coefficients of the reactants.
  • 16.If two nucleophiles, which differ strongly in their reactivities toward reference electrophiles, show equal or similar reactivity toward an aryne, one can conclude that they react with diffusion control (≈3 × 109 L mol−1 s−1).
  • 17.For the reaction of arynes with 9, 10, 11, and 12, see: Liu Z, Larock RC. J Org Chem. 2006;71:3198–3209. doi: 10.1021/jo0602221.For the reaction of arynes with sulfur nucleophiles, see: García-López JA, Çetin M, Greaney MF. Angew Chem, Int Ed. 2015;54:2156–2159. doi: 10.1002/anie.201410751.García-López JA, Çetin M, Greaney MF. Org Lett. 2015;17:2649–2651. doi: 10.1021/acs.orglett.5b01115.
  • 18.k1 is assumed to be 3 × 109 M−1 s−1. Calculated k2 values are provided in the Supporting Information.
  • 19.In several competition experiments, imidazole is more reactive than t-butylamine. Though this may seem surprising, the observed ratios are within reasonable and expected error.
  • 20.Whereas rate constants for cycloadditions or ene-reactions can analogously be determined by the diffusion-clock method described herein, these rate constants will not follow the equation: log k(20 °C) = sN(N + E), a prerequisite for the use of the electrophilicity parameters E.

RESOURCES