Independency of the cardio-ankle vascular index from blood pressure at the time of measurement

In the recent article by Spronck et al.[1], the authors concluded that β and cardio-ankle vascular index (CAVI) are inherently blood pressure (BP)-dependent, potentially leading to erroneous conclusions in arterial stiffness trials.

There are some useful insights in the article, and these might contribute to a deeper understanding of the concept of measuring arterial stiffness, but the title of the article and the conclusions reached are ultimately inaccurate and misrepresent the concept of the CAVI. We would like to explain our reasoning behind why we reached this conclusion.

First, as the authors point out, there is a difference between Hayashi's beta (described as β_o in this article) [2] and Kawasaki's beta (β) [3]. Hayashi's beta is based on a reference BP at 100 mmHg, whereas Kawasaki's beta is based on DBP. It is not possible to measure the diameter change around a reference value of 100 mmHg clinically in each patient. Therefore, for practical reasons, Kawasaki's method has been employed. The difference between β and β_o has already been referred to by Kawasaki et al.[3]. He reported that this difference is not clinically significant. Kawasaki's β arterial mathematical model has been generally accepted and has prevailed. This is one reason why CAVI was developed based upon Kawasaki's β.

Even though there are differences between β_o and β, both are mathematical models reflecting proper arterial stiffness independently from BP at measurement time. However, in their article, the authors assumed β_o as a ‘ground truth’ and only demonstrated that β changed with BP in comparison with β_o. They provided no evidence or logical arguments to assess which method is superior to the other.

Therefore, the statement that ‘Arterial stiffness index beta inherently depends on blood pressure’ is incorrect.

Second, the authors presented the equation cardio-ankle vascular index o (CAVI_o) = 2ρPWV²/P_d − ln(P_d/P_ref) [Eq. (9)] and compared it with CAVI using simulation data. They demonstrated that CAVI_o is not dependent on BP, whereas CAVI does change with BP.

CAVI and CAVI_o are based on stiffness index β and a wave equation derived from Newton's second law (Bramwell–Hill's equation in the case of the artery). The difference between CAVI and CAVI_o is that CAVI employs β over a range of diastolic to systolic pressures and CAVI_o employs β at diastolic pressure. Bramwell–Hill's equation is then applied to the β or β_o equation.

We employed SBP and DBP in the measurement of CAVI [4].

CAVI_o uses diastolic pressure as the standard reference value. If the length of the arterial pathway being measured is short enough, diastolic pressure would not significantly change. However, it is known that diastolic pressure decreases, and systolic pressure increases from the origin of the aorta to the peripheral arteries [5].

Therefore, in case of the long arterial pathway, adoption of one point of DBP only becomes less accurate as a reference value representing the entire length of the pathway. In this way, there is a concern that CAVI_o along a long pathway becomes less accurate. In the case of CAVI, both SBP and DBP are used. Although both methods are mathematically different and each have rational basis, both also have their limitations. The clinical utilities of both equations will be important, and those are presented later.

Third, the authors compiled Table 1 based upon a virtual calculation. At a glance, it seems that the authors tested both arterial stiffness indexes when BP changed, and that CAVI_o did not change, whereas CAVI did change. However, upon closer scrutiny, it seems that the simulation was designed not to change the CAVI_o value between baseline and follow-up, and clinical data were generated using normally distributed random numbers simulating biological variation. As there is a mathematical difference between CAVI and CAVI_o, it is natural that CAVI would change in relation to CAVI_o, when BP changed.

Therefore, the results of the simulation only showed that there are some differences between CAVI and CAVI_o when BP changes, but no evidence or logic was presented to show which method is more accurate than the other.

No clinical data of any kind were included in this simulation, though the terms ‘young subject’ and ‘older subject’ are included in the text, which may cause some misunderstanding.

As for the relationship between CAVI and BP at the time of measurement, the independency of CAVI from BP was confirmed experimentally in man in vivo in Shirai et al. [6]. In this article, we demonstrated that by administration of metoprolol, β1 selective blocker, BP decreased, but CAVI did not significantly change, indicating that CAVI is independent from BP at measuring time.

Fourth, we tried to find out the actual difference between both CAVI and CAVI_o in two clinical studies.

At first, we reanalyzed part of the data of the article in Shirai et al. [6] as shown in Fig. 1. When metoprolol was administered, BP decreased, and both CAVI and CAVI_o did not change significantly. When doxazosin was administered, BP decreased. At this time, CAVI and CAVI_o decreased in the same way. The tendency of both values was parallel and essentially the same. The significance in statistical analysis was almost the same.

FIGURE 1.

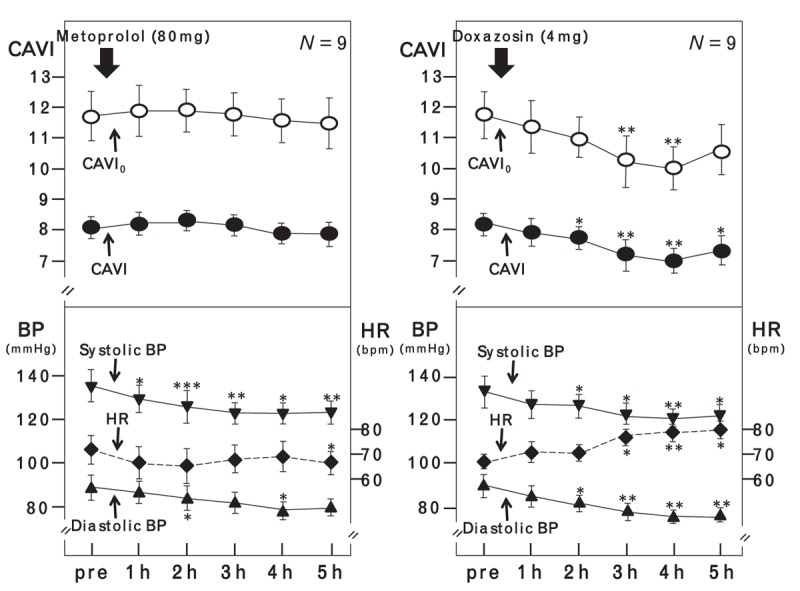
The comparison between cardio-ankle vascular index and cardio-ankle vascular index o during administration of metoprolol and doxazosin. Data are presented as the mean ± standard error. Paired t test was used to compare preadministration and postadministration value. ^∗P < 0.05, ^∗∗P < 0.01, ^∗∗∗P < 0.001. BP, blood pressure; CAVI, cardio-ankle vascular index; CAVIo, cardio-ankle vascular index o; HR, heart rate.

Next, we reanalyzed the epidemiologic data reported by Suzuki et al.[7]. The number of patients was 3665 in the healthy group and 4988 in the hypertensive group. Patients were also divided by sex and age (elderly or working age). CAVI and CAVI_o values of the hypertensive group were significantly higher than those in the healthy group in all sex and age categories (Fig. 2). The significance in statistical analysis of both indexes was the same.

FIGURE 2.

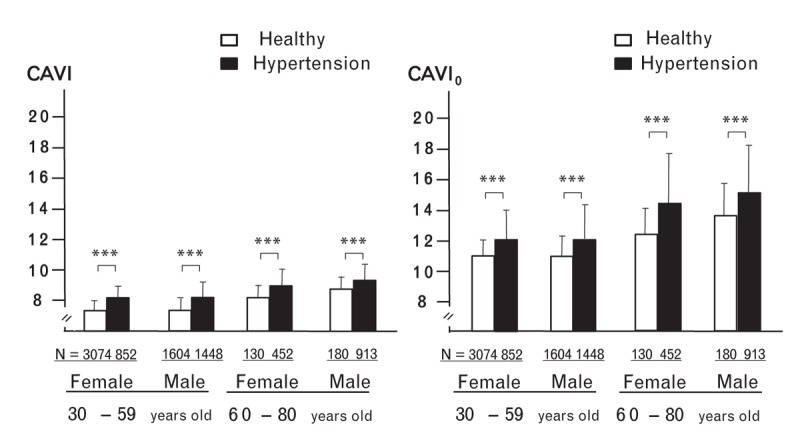
The comparison between cardio-ankle vascular index and cardio-ankle vascular index o in a hypertensive group and a healthy group. Data are presented as the mean ± SD. Unpaired Student's t test was used in comparisons with two groups. ^∗P < 0.001. CAVI, cardio-ankle vascular index; CAVIo, cardio-ankle vascular index o.

These results suggested that the claim that the existing implementation of CAVI could lead to erroneous conclusions in arterial stiffness trials is not at all the case.

In summary, the beta theory-derived index, which the authors presented in Eq. (9), is elegantly presented and has some merit in mathematical terms. However, the equation used by CAVI is perfectly valid as a tool for measuring arterial stiffness in a real-world setting.

The difference between the two arterial mathematical methods has been shown not to be significant. Even though there is some difference between the two methods, both are mathematical models that represent actual arterial stiffness, and as such, both can be considered valid for use. In practice, there is no possibility that CAVI could lead to erroneous conclusions in arterial stiffness trials.

These results suggest that the title of this article and its conclusions should be amended as they misrepresent the essence and effectiveness of CAVI.

ACKNOWLEDGEMENTS

Conflicts of interest

There are no conflicts of interest.