Statistical coevolution analysis and molecular dynamics: Identification of amino acid pairs essential for catalysis

Abstract

Molecular dynamics (MD) simulations of HhaI DNA methyltransferase and statistical coupling analysis (SCA) data on the DNA cytosine methyltransferase family were combined to identify residues that are coupled by coevolution and motion. The highest ranking correlated pairs from the data matrix product (SCA·MD) are colocalized and form stabilizing interactions; the anticorrelated pairs are separated on average by 30 Å and form a clear focal point centered near the active site. We suggest that these distal anti-correlated pairs are involved in mediating active-site compressions that may be important for catalysis. Mutants that disrupt the implicated interactions support the validity of our combined SCA·MD approach.

The proposal that protein dynamics contributes significantly to enzyme catalysis is intriguing (1–4) yet is supported by limited experimental evidence. Previous studies have shown that correlated and anticorrelated motions within an enzyme's active site enhance the reaction rate by various mechanisms that increase the relative amounts of reactive orientations (5). These active-site fluctuations are proposed to result from motions involving distal structural elements and interconnecting networks (1–4). This hypothesis is indirectly supported by emerging molecular dynamics (MD) (1, 2), NMR (6, 7), and hybrid approaches (8–12). The MD studies, although difficult to verify experimentally, have provided highly suggestive results relating dynamics to catalysis. Ultimately, the quantitative contribution to catalysis of various dynamic mechanisms requires direct experimental testing. We combined MD simulations and a coevolution analysis [statistical coupling analysis (SCA); ref. 13] to identify residues that are coupled by coevolution and motion.

Although MD simulations reveal active-site correlated and anticorrelated motions, the identity and role of specific structural elements outside the active site in mediating such motions is difficult to assign. For example, MD cross-correlation analyses are dominated by anticorrelated motions occurring between the most distal regions of protein, often residing in distinct domains (5). Although MD simulations implicate regions of allowed motion, the identity of single amino acids that facilitate these motions is not forthcoming and hence difficult for protein engineers to test. SCA identifies the functional coupling of specific residue pairs that in many cases are distal in the three-dimensional structure. The coupling of such residues leads to their coevolution and is revealed by the statistical analysis of hundreds of related sequences; this approach recently was validated by NMR and protein engineering studies (13–16). These applications of SCA have been focused on protein–ligand interactions, and here we apply SCA toward protein dynamics and catalysis.

M.HhaI is one of many S-adenosylmethionine (AdoMet)-dependent DNA-modifying enzymes found in bacteria, plants, and animals (17). These enzymes decorate the DNA major groove with a methyl group at cytosine (C⁵ or N⁴) or adenine (N⁶), thereby providing an epigenetic signature with diverse biological consequences. The bacterial and human enzymes are the targets of novel antibiotics (18) and cancer drug development efforts (19), respectively. M.HhaI is representative of many DNA methyltransferases because it retains highly conserved motifs associated with substrate recognition and catalysis (20). M.HhaI was the first AdoMet-dependent enzyme whose structure was determined by x-ray crystallography (21) and the first nucleic acid-modifying enzyme shown to use a base-flipping mechanism (22). Base flipping involves the stabilization of the target DNA base into an extrahelical position that facilitates nucleophilic attack onto the pyrimidine ring and methyl transfer by positioning the cytosine in close proximity to the methyl donor, AdoMet. Cognate DNA binding induces a large-scale domain compression, ≈26 Å movement of the catalytic loop (residues 80–99), and is believed to follow an induced-fit model (Fig. 1) (22, 23). Catalysis is initiated by the reversible attack of Cys-81 onto the cytosine C⁶ position, followed by a slower transfer of the methyl group from AdoMet to the C⁵ position (22, 24). β-elimination regenerates the active enzyme, and product release dominates k_cat. Kinetic isotope studies and MD simulations have shown that AdoMet-dependent methyltransferases use active-site compressions to facilitate catalysis (25–27). The abundance of structural and kinetic data for M.HhaI and the biomedical relevance of DNA methyltransferases make this an ideal system for our analysis.

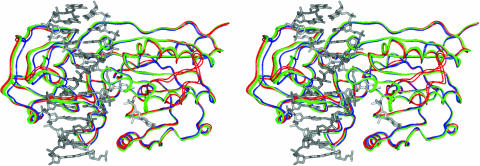
Fig. 1.

Domain and loop motions in M.HhaI. The backbone atoms of the large domain (residues 1–190 and 304–327) for nine ternary (with various forms of DNA and cofactor) and two binary (with AdoMet) structures were superimposed onto the 6MHT structure. The DNA and cofactor are shown as gray sticks with the open group of M.HhaI structures (5MHT, 6MHT, 7MHT, 8MHT, 9MHT, and 10MH) as green and a more closed group (1MHT, 3MHT, and 4MHT) as blue. The binary complexes shown in red (1HMY and 2HMY) adopt an even more open conformation. The catalytic loop (residues 80–99) of the binary complexes moves up to 26 Å from its position in the ternary complexes and was left out of the superimpositions. These superimpositions reveal the changes in domain orientation and catalytic loop conformation upon substrate binding.

Methods

MD simulations of the M.HhaI–DNA–AdoMet complex [with 12-mer DNA d(CCATGCGCTGAC), AdoMet, and 2.05 Å crystal structure from Protein Data Bank (PDB) ID code 6MHT] (28) were carried out for 7 ns by using charmm (29, 30) and the charmm27 residue topology and parameter files on a linux cluster with 356 processors at the University of Michigan (National Partnership for Advanced Computational Infrastructure, National Science Foundation). Because a modified sugar containing a 4′ sulfur was used to obtain the 6MHT structure, this atom was converted to a 4′ oxygen. Cys-81 and Glu-119 were modeled as neutral and ionized residues, respectively (26). A total of 20 Na⁺ counterions were placed 5 Å from the DNA phosphates not involved in salt bridges with either arginine or lysine side chains. The solvent-exposed His-148 and His-204 were treated as protonated residues to allow modeling of a neutral system. This system was placed into a periodic box of transferable intermolecular potential 3 point water (31). Water molecules within 2.8 Å of an atom of the enzyme, DNA, AdoMet, or counterions were deleted to prevent initial steric clashes, resulting in a total of 39,907 atoms (11,144 water molecules). Verlet integration at a time step of 0.001 ps (1,000 steps per ps) was used. Then, 100 steps of steepest-descent algorithm minimization with a force criterion of 0.001 kcal per 10 steps were followed by the adopted basis Newton–Raphson algorithm minimization for 2,000 steps (tolerance 1 × 10^–9 kcal per 10 steps). Non-bonded interactions were cut off at 14.0 Å and were updated every 25 steps. The system was heated to 300 K, followed by equilibration. Coordinates were saved every 0.1 ps, giving a total of 70,000 structures. Structural visualization and manipulation was performed by using midasplus (University of California, San Francisco) and quanta (Version 4.0, MSI, Biosym/Micron Separations, San Diego). rms deviation (rmsd) analysis of the calculated MD structures established that the system was equilibrated at ≈2.0 Å at ≈2.0 ns.

We carried out a cross-correlation analysis of the atomic fluctuations from the simulations (5, 32–35). For the displacement vectors Δr_i and Δr_j for atoms i and j, respectively, the cross-correlation C (i, j) is given by

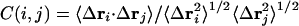[1]

The angle brackets denote an ensemble average. The elements C (i, j) can be collected in matrix form and displayed as a two-dimensional dynamical cross-correlation map (34). There is a time scale implicit in the C (i, j). The cross-correlation was calculated as block averages over time from 500 ps to 7 ns from the MD trajectory. The first coordinate set of the analysis portion of the simulation (at 500 ps) was used as a reference. Each subsequent coordinate set was translated and then rotated to obtain the minimum rmsd of the α-carbon atoms from the reference coordinate set. Positive (correlated) residues moved in the same direction, whereas negative (anticorrelated) residues moved in the opposite direction. A completely correlated or anticorrelated motion, C (i, j) = 1 or C (i, j) =–1, means the motions have the same phase and period. The extent of correlation between motions of backbone α-carbon atoms was calculated by using charmm27 and plotted with the program gmt (36).

SCA on M.HhaI was conducted as described in refs. 13 and 37. An alignment of 389 DNA cytosine C⁵ methyltransferases was obtained from the Pfam database (www.sanger.ac.uk/Software/Pfam). Partial sequences containing <200 residues were eliminated, and the alignment was truncated to include only positions present in M.HhaI. The final alignment of 234 sequences is available on request. To conservatively examine only those evolutionary correlations that are likely to indicate functional (rather than historical) interactions, we included only perturbations at amino acids that are present in 100–200 sequences in the alignment. Excluding the variable region (171–271, M.HhaI numbering), the mean of the ΔΔG^STAT values for all residue pairs is 0.19 kT* [± 0.19 kT* standard deviation (SD)], where kT* is an arbitrary energy unit (13). To set a very high standard for identifying the pairs of residues showing the greatest coevolution, we chose 0.75 kT* (mean plus 3 SDs) as the initial threshold of significance for ΔΔG^STAT values.

The SCA·MD matrix was created by multiplying the individual elements of the SCA matrix with the corresponding elements of the truncated MD matrix. The resulting matrix and parental matrices were analyzed and graphed by using excel (Microsoft) and mathematica (Wolfram Research, Champaign, IL), respectively. Lines for anticorrelated pairs were created by using PDB coordinates for α-carbons from the 3MHT structure. The yellow 3.0-Å sphere, which encompassed all red line segments between anticorrelated pairs, was found with mathematica by minimizing the function defined by the magnitude of the vectors to the line segments.

All stereoviews of M.HhaI were generated on insightii (Accelrys, San Diego) and pymol (http://pymol.sourceforge.net). Superimposition of all structures (38) and rmsd calculations shown in Fig. 1 used insightii. The colors and PDB codes are as follows: green, 5MHT, 6MHT, 7MHT, 8MHT, 9MHT, and 10MH, rmsd 0.20–0.26 Å for the atoms superimposed onto 6MHT; blue, 1MHT, 3MHT, and 4MHT, rmsd 0.55–0.59 Å; and red, 1HMY and 2HMY, rmsd 0.64 and 0.52 Å, respectively. The MD plot shown in Fig. 2A was generated by using gmt (36), the SCA plot was generated by using matlab 6.1 (Mathworks, Natick, MA), and the SCA·MD plot was generated by using mathematica.

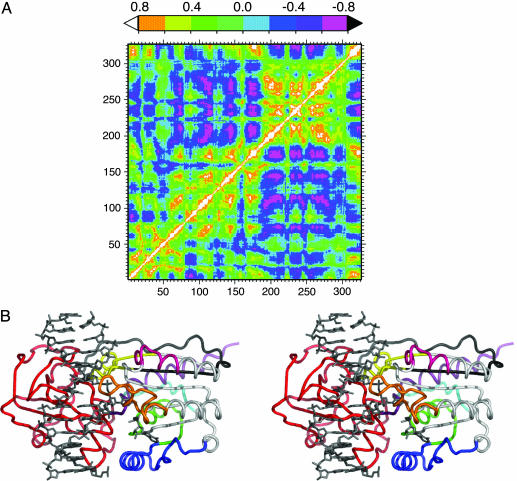
Fig. 2.

MD cross-correlation analysis. (A) Cross-correlation map from 500 ps to 7 ns for M.HhaI with cognate DNA and AdoMet. Correlated motion is shown by positive values up to 1 (white to green), and anticorrelated motion is shown by negative values up to –0.8 (cyan to pink). (B) Regions of anticorrelated motion derived from MD simulations of M.HhaI are shown in stereo with the DNA and AdoMet shown as gray sticks. The red peptide (191–303) is the small domain and hinge region, which is essentially anticorrelated to all regions not colored red and reflects domain motion. Examination of the large domain reveals anticorrelated motion between the most distal regions. Regions within the large domain that did not show much anticorrelated motion (11–19, 66–79, 101–124, and 136–149) are colored white. Colored regions for M.HhaI, cyan (1–10), green (20–40), blue (40–65), orange (80–99), pink (125–135), yellow (150–165), black (166–190), and purple (304–327), were shown to be anticorrelated in the following manner: blue with purple, orange, pink, yellow, black, and cyan; cyan with orange and pink; green with orange and pink; orange with purple; and, finally, pink with yellow.

Results

By combining MD data with an SCA study, we were able to identify specific amino acids responsible for predicted motions in M.HhaI. First, a 7-ns MD simulation of an M.HhaI–DNA–AdoMet model complex was carried out, and cross-correlation analyses were performed from 500 ps to 7 ns (Fig. 2 A). A truncated form of this same plot is shown in Fig. 3A. The diagonally symmetric map quantifies allowed anticorrelated (cyan to pink; 0 to –0.81) and correlated (green to white; 0 to 1) motions for the entire protein and is dominated by anticorrelated motion between the domains (Fig. 2B) (1, 5, 29). This extensive anticorrelated motion is related to the domain motion identified in the various crystal structures (Fig. 1) (20–22). Within the catalytic domain, regions of anticorrelated motion appear to make a compression (Fig. 2B). Although the MD clearly identifies protein segments engaged in correlated and anticorrelated motion, the identity of specific residues important for such motions is not provided.

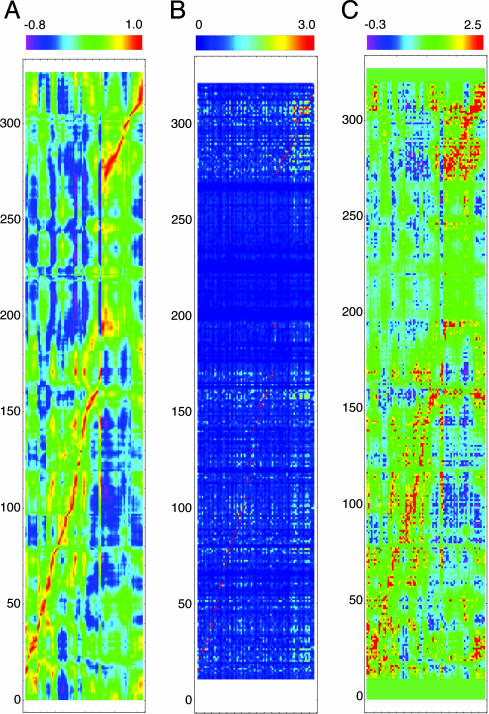
Fig. 3.

SCA·MD analysis. (A) Truncated MD cross-correlation plot for the 7-ns simulation, formed by inclusion of only those columns present in the SCA. Values range from 1 (highly correlated) to –0.8 (highly anticorrelated). (B) SCA plot from the coevolution study on the DNA cytosine methyltransferase family. Because of statistical cutoffs, many amino acids are excluded and only 79 perturbations are shown. Amino acids 1–12 and 320–327 were omitted because of variance in sequence lengths for all enzymes in the alignment; the columns have 308 rows, whereas the rows have 79 columns. Values range from 0 (uncoupled) to 3.0 (coupled). (C) SCA·MD plot from our multiplication. Although the image appears very similar to the MD, it has some clear and unique differences as follows: its peaks and valleys are much sharper, there are many points that are much higher than all of the surrounding values, and many regions have gone to near-0 values. Values range from –0.3 (anticorrelated and coupled) to 2.5 (correlated and coupled) with near-0 values showing no coupling.

We performed SCA on an alignment of 234 protein sequences of the DNA cytosine C⁵ methyltransferase family (13, 37). SCA examines how alterations in the amino acid distributions at a given position of the alignment affect the distribution for a second site and quantifies this coevolution between pairs of positions as a statistical energy value, ΔΔG^STAT_. The SCA was performed by systematically perturbing each position where a specific amino acid was present in 100–200 sequences of the alignment; hence, highly conserved or variable positions that do not provide statistically relevant measurements were omitted. The resulting 79 perturbations are represented as columns in Fig. 3B, with the rows reflecting all alignment positions and the colors corresponding to the response to perturbation (13, 37). The highly variable region of this enzyme family (171–271, M.HhaI numbering), which includes the DNA recognition domain, yielded uniformly low coupling values (Fig. 3B).

We constructed our SCA·MD matrix by element multiplication. The eight highest-ranking correlated pairs distal in sequence, Leu-28–Ala-315, Lys-114–Asp-73, Val-116–Cys-170, Gly-284–Asn-309, Val-291–Phe-302, Arg-281–Asp-287, Val-310–Tyr-157, and His-127–Gly-92, were found to all be within van der Waals contact. More specifically, we believe these contacts are critical structural elements responsible for maintaining specific enzymatic functions. In contrast, the highest-ranking anticorrelated pairs, Gly-158–Phe-79, Pro-160–Ile-61, Pro-160–Arg-97, Gln-161–Pro-70, Ile-308–Gly-92, Ile-308–Ala-83, Asp-95–Val-282, Ala-149–Pro-293, Tyr-145–Arg-277, and Val-307–Phe-101, were found to all lie on opposing sides of the active site. We believe these pairs are partly responsible for facilitating an active-site compression.

Discussion

A predictive approach for identifying specific amino acids is required to validate and quantify the importance of protein motions that may contribute to catalysis. The identification of residues or protein structural elements that mediate correlated and anticorrelated motions is a formidable challenge (1–7, 11, 12, 25). Such motions include, but are not limited to, domain and loop motions (Fig. 1). We sought to develop a predictive approach to enable the direct experimental testing of the relationship of dynamics and catalysis. The MD and SCA are independent covariation analyses that have several similarities: they reveal couplings between any one amino acid and every other amino acid within a given protein, produce matrixes with pronounced diagonal elements, and relate peptide regions that can be spatially distant. We combined the SCA and MD data by determining the product of the elements within the two sets. This technique weights correlated motion by evolutionary conservation, a process that we hypothesize will provide an improved measure of functionally relevant protein motions. We note that this method is distinct from MD or SCA alone; both evolutionary important interactions that do not manifest as dynamic couplings and MD correlations that are not conserved will be eliminated. In essence, the SCA·MD reveals the subset of residues that display conserved and coupled protein motions. Our multiplication matrix, SCA·MD (Fig. 3C), appears similar to the MD matrix (Fig. 3A) with sharper features, reminiscent of the SCA matrix (Fig. 3B).

Our SCA alignment identified a core set of residues, each of which shows a highly significant ΔΔG^STAT value between itself and four or more other residues. Identified are 17 positions, and they all reside in regions associated with motion, at the domain interface and within the catalytic loop (residues 80–99) (Fig. 1 and ref. 20). Only two of the SCA core residues, Phe-79 and Ser-305, are directly involved in the active site, and the majority form a semicontiguous network near the domain interface. Seven residues of the SCA core lie in the hinge region between the two domains (23) and are shown in red in Fig. 4A. Another set is found at the large domain–hinge interface or as neighbors of residues at the interface and are shown in green in Fig. 4A. A small group of SCA core residues (Phe-79, Gly-92, Gly-98, and Phe-101), shown in orange in Fig. 4A, coevolve with those near the domain interface while positioned on the opposite side of the catalytic domain. This set appears important for positioning the catalytic loop (residues 80–99) (Fig. 1), with Phe-79 and Phe-101 anchoring the loop ends and Gly-92 and Gly-98 enabling loop flexibility. Our SCA has identified a set of core residues that are positioned in regions critical for the known motions of M.HhaI, domain compression and catalytic loop movement. This result is distinct from prior applications of SCA because all of the core residues are within peptide regions shown to be important for protein dynamics and catalysis (13, 15, 16, 37). Further, the positioning of the SCA core within regions that undergo conformational changes supports protein dynamics as a possible mechanism for coupling the coevolving residues identified in the SCA. A correlation between protein motions and SCA-identified residues was observed previously in a NMR experiment (14); our results here provide additional evidence for a relationship between the SCA and the MD simulations.

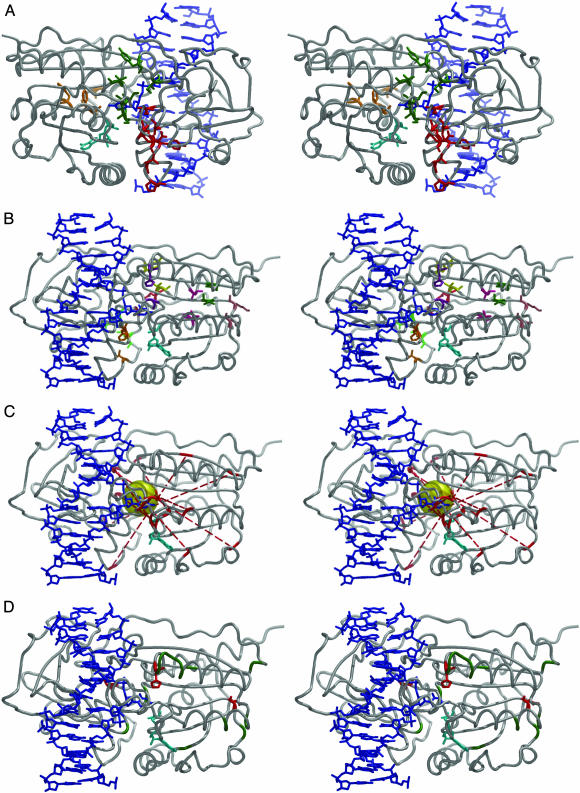
Fig. 4.

Stereoviews of M.HhaI showing protein (gray), DNA (blue), and AdoMet (cyan). (A) Core SCA residues are shown grouped by location. This image is rotated 180° from all other stereo images. Residues are as follows: catalytic loop (orange), Phe-79, Gly-92, Gly-98, Phe-101; hinge region (red), Ala-280, Met-283, Asp-287, Val-291, Pro-293, Tyr-299, and Phe-302; and large domain-hinge interface (green), Tyr-157, Ile-159, Ser-305, Val-307, Ile-308, and Val-310. (B) The top eight sequentially distal correlated pairs derived from our SCA·MD analysis as follows: Leu-28–Ala-315 (hot pink), Lys-114–Asp-73 (salmon), Val-116–Cys-170 (dark green), Gly-284–Asn-309 (red), Val-291–Phe-302 (orange), Arg-281–Asp-287 (light green), Val-310–Tyr-157 (yellow), and His-127–Gly-92 (purple). (C) The α-carbons of the top 10 anticorrelated pairs derived from our SCA·MD analysis (red) are connected by dotted lines as follows: Gly-158–Phe-79, Pro-160–Ile-61, Pro-160–Arg-97, Gln-161–Pro-70, Ile-308–Gly-92, Ile-308–Ala-83, Asp-95–Val-282, Ala-149–Pro-293, Tyr-145–Arg-277, and Val-307–Phe-101. The yellow 3.0-Å-radius sphere near the active site encompasses all of the lines and includes part of the extrahelical cytosine. (D) M.HhaI mutants discussed in the text. Asn-39 → Ala, Asp-71 → Ala, Arg-106 → Ala, Lys-111 → Ala, Asp-128 → Ala, Asn-129 → Ala, Gly-130 → Ala, Asn-131 → Ala, Thr-132 → Ala, Met-168 → Ala, Asn-173 → Ala, Gln-301 → Ala, and Val-306 → Ala mutants (green) were not highlighted by the SCA·MD analysis and showed no impact on M.HhaI function. Asp-73 → Ala, His-127 → Ala, and Val-282 → Ala mutants (red) were identified by SCA·MD and showed significant changes in kinetic parameters.

The top 34 correlated pairs identified by our SCA·MD approach includes 8 pairs that are distal in sequence (n > 4 residues) and 26 pairs that are proximal (n ≤ 4 residues). Each of the eight sequentially distal pairs are within van der Waals contact and appear to be critical for maintaining key structural scaffolds in various contexts (Fig. 4B), and, most notably, the majority do not occur within or between well formed secondary structures. Mutation of one such residue to alanine, His-127 → Ala, which is positioned on the protein surface ≈15 Å from the active site, results in a 10-fold decrease in methyl transfer rates (39). Furthermore, adjacent alanine mutants that were not highlighted by our SCA·MD approach (Asp-128 → Ala, Asn-129 → Ala, Gly-130 → Ala, Asn-131 → Ala, and Thr-132 → Ala) show no change in methyl transfer (Fig. 4D) (39). Remarkably, mutation of Asp-73, which is ≈21 Å away from the AdoMet cofactor, to alanine (Asp-73 → Ala) results in a 24-fold increase in AdoMet affinity (40). Other positions near Asp-73 and the AdoMet cofactor, upon mutation to alanine (Asn-39 → Ala, Asp-71 → Ala, Arg-106 → Ala, and Lys-111 → Ala), cause no detectable changes in AdoMet affinity (40); none of these other positions were identified by the SCA·MD approach (Fig. 4D). These results suggest that the SCA·MD approach successfully identified the residues and interactions important for function because adjacent or more proximal mutations showed no evidence of the same phenotype. The importance of correlated motions has received relatively little attention, in part because of the difficulty in relating this mechanistically to catalysis. Nevertheless, such motions may work in concert with other motions to facilitate catalysis, and we believe our SCA·MD approach has identified the most critical positions for maintaining M.HhaI structure.

Ten of the highest 14 anticorrelated pairs derived from our SCA·MD multiplication traverse the active site to form a focal point, defined by connecting the α-carbons of the pairs. This focal point forms a 3.0-Å radius sphere that contacts each of the lines and encompasses part of the extrahelical cytosine (Fig. 4C). The four pairs not shown span the two domains. This spatial arrangement of evolutionarily coupled anticorrelated pairs is consistent with previous proposals that methyltransferases use some form of active-site compression to facilitate catalysis (25–27). The focal point encompasses the target cytosine such that the χ-angle defined by the glycosidic bond could readily be altered, and prior studies have shown this angle to be highly correlated to catalysis (25, 26, 39). Also, the focal point is located on the periphery of the large domain, ≈10 Å away from its center of mass. The presence and location of this focal point is significant because it is not observed with the MD analysis alone. One residue identified as anticorrelated by this SCA·MD analysis, Val-282, upon mutation to alanine (Val-282 → Ala), results in a ≈4-fold increase in k_cat and is ≈17 Å from the active site (40). Although the protein dynamic contribution to this change in k_cat is not presently understood, Val-282 is flanked by other residues that were not identified by the SCA·MD analysis (Gln-301 and Val-306), which, upon conversion to alanine, do not show the same phenotype (40) (Fig. 4D). This finding further supports the ability of the SCA·MD approach to identify residues located some distance from the active site that appear to be functionally important.

A mechanistic understanding of how correlated and anticorrelated dynamics impact enzyme catalysis requires assigning quantitative functional and dynamic contributions from individual residues within an enzyme's architecture. The SCA·MD approach identifies specific residues that, although distal from the active site, are involved in protein dynamics and are coconserved. Further, we suggest that a subset of such dynamically and evolutionary coupled residues is likely to be involved in substrate binding and/or catalysis. The application of this combined SCA·MD approach to other proteins may lead to a deeper understanding of protein dynamics and enzyme catalysis. Our SCA·MD approach identifies specific residues that show dynamic and evolutionary couplings at a distance, thereby setting the stage for experiments that provide the necessary basis for testing the underlying hypothesis.