Abstract
Understanding the heterogeneity in health of older adults is a compelling question in the biology of aging. We analyzed the performance of five measures of health heterogeneity, judging them by their ability to predict mortality. Using clinical and biomarker data on 1,013 participants of the Canadian Study of Health and Aging who were followed for up to 6 years, we calculated two indices of biological age using the Klemera and Doubal method, which controversially includes using chronological age as a “biomarker,” and three frailty indices (FIs) that do not include chronological age: a standard clinical FI, an FI from standard laboratory blood tests and blood pressure, and their combination (FI-combined). Predictive validity was tested using Cox proportional hazards analysis and discriminative ability by the area under the receiver-operating characteristic curves. All five measures showed moderate performance that was improved by combining measures to evaluate larger numbers of items. The greatest addition in explanatory power came from the FI-combined that showed the best mortality prediction in an age-adjusted model. More extensive comparisons across different databases are required, but these results do not support including chronological age as a biomarker.
Keywords: Biological aging, Biomarkers, Frailty indices, Biological age, Health heterogeneity
Introduction
Chronological age (CA) is an excellent predictor of mortality in populations. Its relationship with mortality, known as the Gompertz law, has been widely used to describe the distribution of adult lifespan by both demographers and actuaries (1). Among individuals, however, the relationship between age and mortality is highly variable, reflecting genetic, environmental, and socioeconomic factors (2,3). The role of stochastic component in aging is fundamental (4) and cannot be underestimated. As some people appear to age faster than do others, the metaphor of “biological aging” (in contrast to “chronological aging”) is widely employed.
Different approaches to quantify biological age (BA) in individuals have been proposed. An early effort used a test battery to measure the rate of aging (5). This approach is now referred to as employing “biomarkers of aging” (6) and has been applied not only to humans but also to animals (7,8). For many years, biomarkers of aging were defined as specific, nondisease traits (the possibility of the latter sometimes disputed (9)), in multiple physiological domains, that predict mortality in an age-coherent way, and do so better than does CA (10–13).
The many attempts to quantify BA with biomarkers over the decades (5,13) show increasing use of multivariate statistical techniques (14–17). A 2013 study (18) compared 5 multivariate algorithms to calculate BA from a set of 7–10 biomarkers in the National Health and Nutrition Examination survey (NHANES) and favored an algorithm proposed by Klemera and Doubal (17). Their algorithm was also recently used to quantify BA in younger adults (19). Interestingly, an essential part of the Klemera–Doubal algorithm is that CA is added to the battery of biomarkers as itself a biomarker of aging (17). Not counter intuitively, including CA in the calculation of BA improved its ability to predict mortality (17). Klemera and Doubal (17) anticipated that labeling CA as a biomarker would be controversial. It leaves unanswered whether a robust estimate of BA can be obtained from biomarkers without including CA.
One way to consider the relationship between CA and BA is to recognize that contemporary definitions of BA, for all their diversity, are empirical measures of the heterogeneity of health in people of the same age, a feature also known as frailty (20,21). Heterogeneity in health can be measured using a deficit accumulation approach (22). Our group has introduced the concept of a frailty index (FI) to quantify the susceptibility of people of the same age to adverse outcomes (23). Any FI counts a range of clinically apparent health deficits of varying types and divides that count by the total number of items measured (23,24). The approach has also been extended to animal models (25–27). An FI can also be created exclusively from biomarkers, including values from common laboratory tests (eg, serum urea, thyroid-stimulating hormone, electrolytes) and physiological measures (eg, blood pressure) (28,29). How this approach to measuring heterogeneity in health compares with a biomarker-based BA selected by multivariable regression analysis is not known. This is an important question because it allows a means of understanding how to incorporate CA and BA age in mortality prediction. For example, is it better seen as a biomarker or a covariate?
Here, we compared the performance of the FI with two biomarker-based measures of BA that employed the Klemera–Doubal algorithm (one with and one without CA) in predicting mortality. Building on recent work (28,30) in the Canadian Study of Health and Aging (CSHA), in people in whom both clinical and biomarker data were available, our objectives were to compare these empirical estimates and to consider whether including CA was of sufficient benefit to the performance of the models that its theoretical implications should be evaluated.
Methods
Study Population
Our sample is drawn from the first wave of data from the CSHA. As detailed elsewhere, in 1991–1992, a cohort of 10,263 older adults (aged 65 and older at baseline) was assembled from an age-stratified, national random sample, clustered by area, with oversampling of older people (75–84 and 85 and older strata) and those in institutions (1,255; 9,008 in the community) to study cognitive impairment and other health conditions (31,32). Of the 2,914 participants who had a clinical examination, here we used a subset of both community-dwelling and institutionalized participants (n = 1,375), who had laboratory test data. Of these 1,375 participants, 1,013 participant had sufficient data (without missing data (28)) to construct one version of the FI based only on routine physical and laboratory tests (FI-LAB) as detailed elsewhere (28). Decedent data were obtained from the Vital Statistics Registry in each province and from interviews with the household members (eg, spouses or next kin of deceases study participants). Mortality data were available up to the 6-year follow-up. Briefly, their mean age was 80.8 years (SD = 7.2), 61.6% were women; 67.4% of the participants lived in the community.
Frailty Indices
A standard FI (FI-CSHA) was previously constructed from 38 variables used in the CSHA clinical examination sample (28) (Supplementary Figure S1). In short, these variables included disease history, symptoms, and health rating variables (eg, functional limitations) and satisfied the criteria for being a deficit as previously described (33).
The FI-LAB was calculated earlier from 23 variables based on 21 routine blood tests plus systolic and diastolic blood pressure (28) dichotomized using the “normal” cutoff points, that is, represented by 0 or 1, where 0 indicates the values are within the normal cut off values and “1” otherwise (28). Following Howlett and coworkers (28), we also considered the FI-combined, which simply is the sum of the deficits in FI-LAB and FI-CSHA and divided by the new total.
Selection of Biomarkers
Of 22 biomarkers used to calculate the FI-LAB, following Klemera and Doubal (17), we selected those biomarkers in which their values (or their logarithms) were significantly correlated with age. The various versions of BA were calculated from those 10 selected biomarkers.
BA Estimates
All estimates of BA considered here are based on calculating regression parameters of the individual biomarkers on CA:
| (1) |
where represents estimated age-specific average of the jth biomarker at each CA. Using the same notation as Klemera and Doubal (17), we indicate qj and kj as the intercept and the slope, respectively.
Klemera–Doubal algorithms are based on calculating the two versions of BA. The first algorithm calculates BA without inclusion of CA (BAE) from the list (battery) of selected biomarkers:
| (2) |
Here, we use a notation that is slightly different from that used by Klemera and Doubal (16) when they introduced the weights, wj (j = 1,…, m) as the ratios of the squared slope kj to the residual variance, vj,
The second version of their algorithm calculates BA that takes into account CA as an additional biomarker (BAEC) (17). In their formula, the weight coefficient wCA (our notation) is the inverse variance . This they defined using the residual variance between BAE (equation 2) and CA, and taking into account the correlation coefficients between the individual biomarkers (for details see ref. 17):
| (3) |
Klemera and Doubal (17) and others (18,19,30) preferred the latter algorithm (equation 3) largely because it has been suggested to give a narrower estimate of BA, as illustrated by simulations (17).
It can be demonstrated, after elementary transformations, that equation (3) can be rewritten as follows:
| (4) |
where .
In other words, the term ε characterizes the relative weight of CA, compared with the sum of the weights of the biomarkers. The difference between the value of BA with and without CA (ie, the difference between BAE and BAEC) depends, therefore, exclusively on ε. From this, it should be clear that, as we have presented it, the Klemera–Doubal algorithm in effect assigns a weight for CA (the standard error ), which as it varies gives different values for BA. For example, we can consider two extreme cases, when ε << 1; (biomarkers overweight CA, is relatively large). In this case, that is, BAEC is close to BAE. In the other extreme case, when ε >> 1 (CA suppresses biomarkers, ie, is relatively small), In this case, BAEC is near CA. Note further that it is not clear how these maneuvers are related to an important basic presumption that the paper makes explicit, which is that the differences between BA and CA must reflect the individual degree of aging (17). As is evident above, BA is CA ± some value, but that value depends on CA, that is, BAEC will vary, depending on the weight given to CA, so that older people will have higher BAEC than younger people, other things being equal.
Modified Klemera–Doubal Algorithm
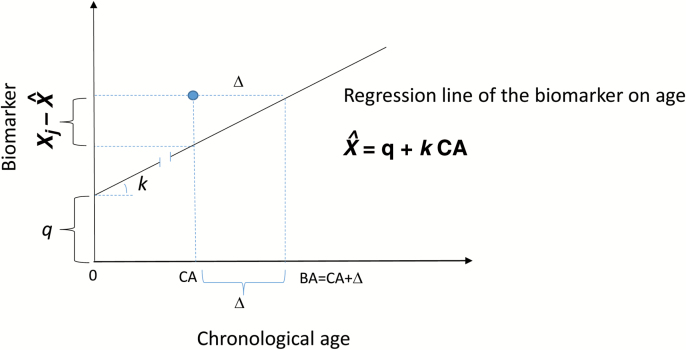
Here, we suggest a minor modification of the Klemera–Doubal algorithm to directly calculate the difference between BA and CA. In this way, the observed sum value of the biomarkers of an individual are compared with the expected value at this CA, based on the CA-biomarker regression equation (5), as illustrated in Figure 1:
Figure 1.
Definition of the difference Δ between the estimated biological age and chronological age (CA) of a person (indicated by the solid circle), illustrated for the jth biomarker Xj. These differences Δj obtained for biomarkers significantly correlated with CA (j = 1,…, m) are averaged (equation 5) with the weights depending on the slopes and residual variances.
| (5) |
This equation is similar to equation (2) with the substitution of the intercept by the value of the age-specific norm, . The BA can be calculated by adding Δ to the CA:
| (6) |
The last formula gives the value of BAE (after substitution of equation 1 into equation 2). The difference, however, is that equation (2) calculates BA directly. By contrast, we stress calculating Δ, which can be added to CA to estimate BA if necessary. This is important, as quite often, it is more useful to know whether the person’s BA is higher or lower than his/her CA rather than to know the estimate of their BA.
Data Analysis
We compared the following five measures of BA: BA obtained with the Klemera and Doubal method derived from 10 biomarkers with (i) and without (ii) CA (ie, BAE and BAEC); BA estimated with a standard FI-CSHA from data obtained in clinical evaluation (iii); an FI-LAB (iv); and an FI-combined that included both clinical and laboratory data (v).
Linear least squares regression techniques were used to estimate the parameters of the individual biomarkers of regression with age, either in their natural scale or using the log-transformed values, as appropriate.
To investigate the impact of these estimates of five methods on mortality, Kaplan–Meier survival and Cox proportional hazard regression models were used to estimate the probability of survival. The FI values were converted to integers between 0 and 100 by rounding them after multiplying by 100, giving equal percent increments. To compare the performance of models with different combinations of variables, the log likelihood test was used.
Receiver-operating characteristic analysis was used to assess the discriminative ability of the FIs and BA (assessed by different algorithms) separately and in combination, in relation to mortality. The confidence intervals for the receiver-operating characteristic were calculated using bootstrapping, with 1,000 replications. Data analysis was conducted using Matlab Version 8.5 (Mathworks) and SPSS (IBM SPSS Statistics Version 22). The statistical significance level was set at p < .05.
Results
Ten of the 22 available biomarkers were significantly correlated with CA (Table 1). These biomarkers (albumin, calcium, creatinine, diastolic blood pressure, hemoglobin, alkaline phosphatase, inorganic phosphorous, total protein, thyroid-stimulating hormone, and urea) were used to calculate BA, using different algorithms (equations 2,3,5, and 6).
Table 1.
Pearson Correlation Coefficient Between CA and Biomarkers
| Correlation With CA | Correlation of the Log Biomarker With CA | p Value | |
|---|---|---|---|
| Albumin (g/L) | −0.236 | −0.234 | <.0001 |
| AST (SGOT; IU/L) | −0.007 | −0.059 | .821 |
| BP, supine systolic (mmHg) | −0.008 | −0.012 | .800 |
| BP, supine diastolic (mmHg) | −0.130 | −0.131 | <.0001 |
| Calcium (mM) | −0.121 | −0.120 | .0001 |
| Creatinine (mM) | 0.142 | 0.142 | <.0001 |
| Folate (nM) | −0.005 | −0.008 | .869 |
| Folate, RBC (nM) | −0.042 | −0.024 | .469 |
| Glucose, fasting (mM) | 0.041 | 0.053 | .200 |
| Hemoglobin (g/L) | −0.246 | −0.243 | <.0001 |
| Mean corpuscular volume (fL) | 0.036 | 0.035 | .259 |
| Phosphatase, alkaline (IU/L) | 0.081 | 0.066 | .01 |
| Phosphorus, inorganic (mM) | 0.110 | 0.118 | .004 |
| Potassium (mM) | −0.010 | −0.120 | .728 |
| Protein, total (g/L) | −0.146 | −0.147 | <.0001 |
| Sodium (mM) | 0.039 | 0.038 | .209 |
| TSH (mIU/L) | 0.075 | — | .020 |
| T4, Free (pM) | −0.026 | −0.01 | .476 |
| Urea (mM) | 0.240 | 0.252 | <.0001 |
| Urine cg | −0.060 | — | .154 |
| Vitamin B12 (pg/L) | −0.041 | −0.059 | .196 |
| White blood cells (number/L) | 0.021 | 0.015 | .495 |
Notes: AST = aspartate aminotransferase; BP = blood pressure; CA = chronological age; RBC = red blood cell; TSH = thyroid-stimulating hormone.
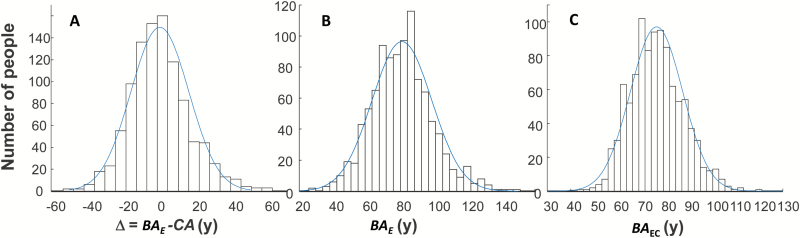
The frequency distribution for the estimated difference (Δ) between BAE and CA using equation (5) is presented in Figure 2A; the distribution of BAE (equation 6) is shown in Panel B. BAEC estimated using Klemera–Doubal algorithm using the is shown in Panel C. The histograms are overlaid with normal curves with the following parameters: for Δ, mean = 0.24 (SD = 16.39); for BAE, mean = 80.89 (SD = 17.83), and for BAEC, mean = 80.8 (SD = 11.1). The latter distribution is narrower than the former.
Figure 2.
(A) The histogram of the difference (Δ) between estimated biological age BAE from equations (1), (5), and (6) and CA; (B) BAE estimated using equations (1), (5), and (6). (C) BAEC estimated using equation (3) with wCA corresponded to the . The histograms are overlaid with the normal curves with the parameter: for Δ: mean = 0.24 (SD = 16.39); for BAE: mean = 80.9 (SD = 17.83), and for BAEC: mean = 80.8 (SD = 11.1).
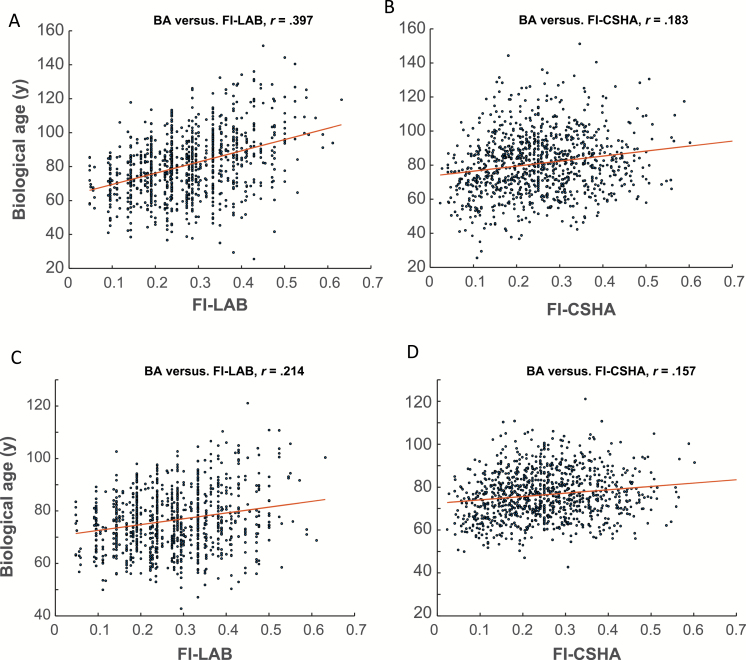
We investigated the relationship between BA and CA as a function of (or the relative weight, ε). As decreased, BA approached CA as illustrated in Supplementary Figure S1. Both FIs (FI-LAB and FI-CSHA) were significantly correlated with BAE (Figure 3A and B). The FI-LAB was moderately correlated with BAE (r = .397, p < .0001), whereas the FI-CSHA was weakly, but significantly correlated with BAE (r = .183, p < .001). BAEC was only weakly correlated with either FI (Figure 3C and D).
Figure 3.
BAE is strongly associated with the FI-LAB (A) than with the FI-CSHA (B). Similarly, BAEC is strongly associated with FI-LAB (C) than with the FI-CSHA (D) although BACE relationships with CA weaker than with BAE. The dots represent individuals’ values of the BA and FI-LAB; solid lines are the least squares regressions of BA on FI-LAB (A and C) and FI-CSHA (B and D).
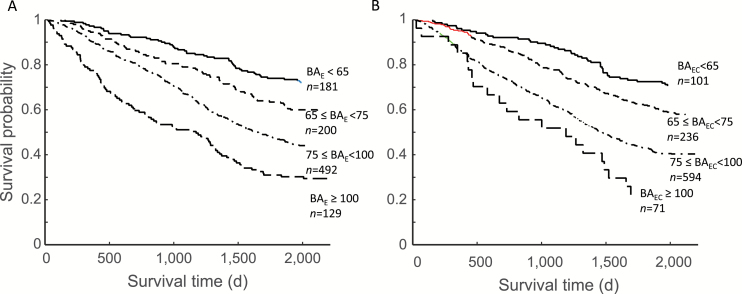
Mortality increased significantly with BA when BAE (Figure 4A) was stratified in to four groups. Similar results were seen when BAEC was divided into four strata (Figure 4B). The association of the BAs with mortality was also demonstrated using Cox regression (Table 2). In unadjusted models, including CA in estimates of BA gave the best fit (see log likelihood in the right column) and this was followed by CA. The latter had the highest hazard ratio (HR), followed by the FI-combined. In the model adjusted for age and sex, the betas for BAEC and the HRs were higher than for BAE, but the log likelihoods were the same. The log likelihood was the highest for the model that included FI-combined.
Figure 4.
Kaplan–Meier survival curves for grades of the BAE (A) and BAEC (B). The cut-points for the strata are as follows: <65, 65–75, 75–100, and >100.
Table 2.
Cox Proportional Hazards Regression Model
| Beta | Standard Error | Z Score | Hazard Ratio | 95% Confidence Interval | −Log L × 1,000 | |
|---|---|---|---|---|---|---|
| Unadjusted | ||||||
| Age (CA) | 0.076 | 0.007 | 10.878 | 1.079 | 1.074–1.094 | 3.2464 |
| BAE | 0.025 | 0.002 | 10.650 | 1.025 | 1.021–1.030 | 3.2560 |
| BAEC | 0.038 | 0.003 | 11.792 | 1.039 | 1.032–1.046 | 3.2444 |
| FI-LAB | 0.032 | 0.004 | 7.607 | 1.032 | 1.024–1.041 | 3.2819 |
| FI-CSHA | 0.028 | 0.004 | 7.410 | 1.029 | 1.021–1.037 | 3.2819 |
| FI-combined | 0.051 | 0.005 | 9.873 | 1.051 | 1.041–1.063 | 3.2616 |
| Adjusted | ||||||
| Sex | −0.296 | 0.093 | −3.186 | 0.744 | 0.617–0.896 | 3.2199 |
| Age | 0.062 | 0.008 | 8.11 | 1.063 | 1.048–1.080 | |
| BAE | 0.018 | 0.003 | 6.817 | 1.018 | 1.012–1.023 | |
| Sex | −0.296 | 0.093 | −3.186 | 0.744 | 0.617–0.896 | 3.2199 |
| Age | 0.053 | 0.008 | 6.481 | 1.054 | 1.037–1.072 | |
| BAEC | 0.026 | 0.004 | 6.817 | 1.027 | 1.019–1.035 | |
| Sex | 0.221 | 0.094 | −2.352 | 0.892 | 0.665–0.967 | 3.2282 |
| Age | 0.072 | 0.007 | 9.926 | 1.074 | 1.059–1.090 | |
| FI-LAB | 0.025 | 0.004 | 5.286 | 1.028 | 1.014–1.031 | |
| Sex | −0.303 | 0.093 | −3.2252 | 0.738 | 0.613–0.890 | 3.2258 |
| Age | 0.074 | 0.007 | 10.240 | 1.077 | 1.062–1.093 | |
| FI-CSHA | 0.024 | 0.004 | 5.774 | 1.023 | 1.015–1.031 | |
| Sex | 0.239 | 0.093 | −2.556 | 0.785 | 0.653–0.949 | 3.2156 |
| Age | 0.068 | 0.007 | 9.360 | 1.071 | 1.055–1.086 | |
| FI-combined | 0.040 | 0.005 | 7.375 | 1.041 | 1.030–1.052 | |
Notes: BA = biological age; CA = chronological age; CSHA = Canadian Study of Health and Aging; FI = frailty index.
The impact on the discriminative ability of either method to calculate BA to predict mortality was moderate but lower for the BAE (area under the receiver-operating characteristic, AUC = 0.679) compared with the BAEC (AUC = 0.699); these were equal after adjusting for age and sex (AUC = 0.726) but still lower than with FI-combined (AUC = 0.735; Table 3). We also investigated how the discriminative ability of the BAEC to predict mortality depended on the relative weight of the CA, ε, which inversely corresponds to the BA variance, . The results (Table 4) show that when ε increased (ie, meaning that the variance decreased) the ability of the BAEC to accurately predict mortality increased (column 5). Even so, using the value of BA that gave the greatest weight to CA was still inferior if the model was adjusted for age. In that case, the variance made no difference to the value of the AUC (column 3).
Table 3.
The AUC With 95% Confidence Intervals for Different Combinations of Variables and Their Combinations*
| AUC | 95% Confidence Interval | |
|---|---|---|
| Age + sex | 0.698 | 0.665–0.730 |
| BAE + sex | 0.679 | 0.646–0.712 |
| BAEC + sex | 0.699 | 0.667–0.731 |
| Age + sex + BAE | 0.726 | 0.695–0.757 |
| Age + sex + BAEC | 0.726 | 0.695–0.757 |
| Age + sex + FI-LAB | 0.715 | 0.684–0.747 |
| Age + sex + FI-CSHA | 0.725 | 0.694–0.756 |
| Age + sex + FI-combined | 0.735 | 0.705–0.766 |
Notes: AUC = area under the receiving-operating characteristic; BA = biological age; CSHA = Canadian Study of Health and Aging; FI = frailty index.
*BAEC was calculated with ε = 0.5
Table 4.
The AUC With 95% Confidence Intervals for BAEC Adjusted for Age and Sex for Different Relative Weight of CA, ε (Compared With the Weights of Biomarkers)
|
|
|
Age + Sex + BAEC | Sex + BAEC | ||||
|---|---|---|---|---|---|---|---|
| AUC | 95% Confidence Interval | AUC | 95% Confidence Interval | ||||
| 0 | Infinity | 0.726 | 0.695–0.757 | 0.679 | 0.646–0.712 | ||
| 0.05 | 3,500 | 0.726 | 0.695–0.757 | 0.681 | 0.646–0.712 | ||
| 0.1 | 1,750 | 0.726 | 0.695–0.757 | 0.684 | 0.651–0.716 | ||
| 0.2 | 900 | 0.726 | 0.695–0.757 | 0.688 | 0.659–0.720 | ||
| 0.5 | 350 | 0.726 | 0.695–0.757 | 0.699 | 0.667–0.731 | ||
| 1.0 | 175 | 0.726 | 0.695–0.757 | 0.713 | 0.690–0.707 | ||
| 10.0 | 17 | 0.726 | 0.695–0.757 | 0.716 | 0.691–0.708 | ||
Notes: AUC = area under the receiving-operating characteristic; BA = biological age; CA = chronological age. When the variance increases, its ability to accurately predict mortality decreases.
Discussion
We investigated the properties of two estimates of BA and analyzed their relationships with three FIs (FI-LAB, FI-CSHA, and the FI-combined). We compared how each of these five estimates discriminated people in relation to mortality and how this could be modified by accounting for CA. We found that both BA measures were moderately correlated with the FI-LAB and weakly with the FI-CSHA. That is not surprising, as the FI-LAB is composed of dichotomized biomarkers, half of which were used to calculate the BAs, whereas the FI-CSHA contains more clinically evident information about health status. Of the two versions of the BA, BAE (based exclusively on biological measures) was more strongly correlated with the FIs than was the BAEC that took into account CA. Both BAs had comparable performances in the adjusted Cox proportional hazards regressions and the receiver-operating characteristic analyses, although both were inferior to the FI-combined.
Both versions of the BA estimates were suggested by Klemera and Doubal (17) who, however, favored the second version, BAEC that treats CA as a “biomarker.” This BAEC has also been used by others (18,19,34). The major practical argument of Klemera and Doubal (16) in favor of using BAEC was that it gave a narrower range of estimated BA than did BAE. This, they argued, allowed them to guard against overestimating the age of people who had extreme biomarker values, who otherwise might be estimated to have a BA much beyond the known human lifespan (compare Figure 2B and C). Perhaps an even more important advantage of using BAEC might be if it were to provide a more accurate prediction of mortality than does BAE. Although this has been reported previously (18), the difference between BAEC and BAE was not specified, and the comparisons they reported with other candidate BA measures showed only small differences in predicting mortality (18). In short, it was not clear whether the above advantages were important. Here, in the Cox regression model, the HRs were lower for BAE (HR = 1.018, 95% confidence interval = 1.012–1.023) than for BAEC (HR = 1.027, 95% confidence interval = 1.019–10.035). Even so, the Z scores were the same (Z = 6.817) for both BAEC and BAE. In other words, there was no advantage to using the more complicated version of BAEC than simply using BAE in a model that adjusted for CA.
Furthermore, in our view, embedding CA in BA estimation risks not just lack of transparency of its effect, but more importantly, tautology. If the idea of BA is to quantify heterogeneity in health of people of the same CA, it is not clear to us what is gained by empirically optimizing the weight of CA to achieve a tighter correlation between BA and CA. This seems self-defeating, even if it avoids having some elderly people with adolescent BAs on the one hand or Methuselah-like estimates on the other hand. The BAEC lies within the boundaries (CA, BAE) approaching the limits on the left or on the right depending on the relative weight ε. It is also clear that adding CA to the battery of biomarkers drags down the estimates of BA closer to CA preventing the estimates of BA being too high (eg, >120 years). Whereas this might be considered by some as an advantage of the BAE, this happens, however, at the expense of its clarity. We have demonstrated that including CA in the list of biomarkers is unnecessary—CA is almost always known.
Klemera and Doubal (17) anticipated such skepticism, but their explanation, in our view, is based more on a strategy to avoid extreme values than it is on an attempt to address the systems biology. In contrast, for example, the FI robustly demonstrates an empirical limit to deficit accumulation at 0.7, which, without any additional manipulation, appears not to vary even in circumstances of extreme old age (35,36) or critical illness (37,38) and which likewise is not exceeded in a naturally aging animal model (26). The physical basis for how this limit comes about is now a matter of active investigation (39).
In this article, we demonstrated that there is a simple analytical relationship between the two measures of BA (equations 3 and 4). When CA is included in the model, it brings the BA estimate down toward CA. This effect is stronger if the relative weight of CA increases (or the variance decreases). Where any biomarker shows only small variability across individuals, its ability to inform us about biological aging is low. That is an additional argument against using CA as a (bio)marker and therefore against using BAEC in assessing biological aging. CA, however, could be used in addition to BAE in outcome prediction models as well known and almost always done. Belsky and coworkers (19) used BAEC to quantify biological aging in young adults. It is possible that similar results would be obtained if they have used BAE instead of BAEC, although the margins of the estimates would have been broader. Even so, replicating these analyses with a younger sample would be a useful next step, as well as incorporating information from multiple time points (40).
Perhaps even more important, instead of first calculating BA and then comparing that value with CA, we could first calculate the difference (Δ) between BA and CA (equation 5). In assessing an individuals’ vulnerability, this difference makes more sense than the absolute value of BA. Those who are at greater risk will have a greater value of this difference than those with low or negative values of Δ. In essence, Δ defines the difference between the state of the individual (defined by the m-dimensional vector of biomarkers) and an age-specific norm (here the regression line). Such norms could be age, sex, and even population specific (41).
The difference between the individual and the “norm” can be assessed in different ways, for example, using a FI as a general indicator of health, aging, and well-being (42–44) where the norm means the absence of deficits, although the norm could be defined on the basis of minimizing mortality risk (44). Note that BA can be also estimated from the FI (45–47) by expressing the differences in health status in the timescale. Interestingly, the FI consistently shows a limit of about 0.7 (ie, 70% of deficits present in the individual), the higher level is incompatible with life (35,48). We observed no such a limit with BAE and BAEC estimates. Note however that when an estimate of BA was produced from the FI it did not exceed the maximally observed life span (47).
Our data too should be interpreted with caution. Our sample was not representative as discussed in ref. (28). The biomarker sample size was relatively small, preventing us from performing the analyses separately in men and women. Some results of our analyses were different from what has been reported previously using the NHANES data (17). Both the list of biomarkers and the age of the samples were different (65 years and older in CSHA and 30–75 years in NHANES), which might explain the differences in the AUC we presented here and what was reported by Levine (17). For example, Levine reported that BA most accurately predicted mortality although, similarly to our report, the differences were marginal. The higher level of the AUC in the receiver-operating characteristic analysis obtained by Levine can be likely attributed to the larger sample size used in that study (17).
One advantage of using a FI to measure heterogeneity is that its calculation does not require any imputation—the FIs are generally robust in respect to the variables that make them up. In other words, an FI allows for some missing information to be dealt with (eg, if in the individual 4 out of 40 deficits were missing, the FI can be calculated by dividing the number of deficits present in this individual to 36, see also ref. 33). In this sense, the FI might be more appropriate for assessing the predictive models than the BA measures, although testing this hypothesis would require more head-to-head comparisons in other data sets.
An important aspect of this study is that we were able to present head-to-head comparisons of two measures of BA with three FI measures. Here, we compared three FIs with two versions of BA and in this way can understand the advantage of using each of them to evaluate the complexity of health and aging. In our data, none of these measures, considered separately, predict mortality as well as does CA, but each adds substantially to predicting mortality using CA. This is especially true for the FI-combined, which showed an impact on mortality prediction equal to CA. It has been pointed out that even though “the problems of old age come as a package,” most studies of the diseases of old age do not take this into account (49). In consequence, measures that can quantify the package in which these problems come, estimate their collective impact, and expose characteristic systems features are a necessary area of investigation (46). This speaks about the need for a collaborative, multidisciplinary approach to aging research (50–52). These considerations are motivating the additional inquires by our group, including understanding the physical basis of age-related variability in health.
Supplementary Material
Supplementary data is available at The Journals of Gerontology, Series A: Biomedical Sciences and Medical Sciences online.
Funding
This work was supported by the Canadian Institutes of Health Research (MOP 126018 to S.E.H. and MOP 209888 to K.R.).
Conflict of Interest
The authors report no conflict of interest.
Supplementary Material
Acknowledgments
K.R. receives career support from the Dalhousie Medical Research Foundation as the Kathryn Allen Weldon Professor of Alzheimer Research. A.M. is recipient of a University Research Professor.
References
- 1. Kirkwood TBL. Deciphering death: a commentary on Gompertz (1825) ‘On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies’. Philos Trans R Soc Lond B Biol Sci. 2015;370 doi:10.1098/rstb.2014.0379 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Yashin AI, Arbeev KG, Arbeeva LS, et al. How the effects of aging and stresses of life are integrated in mortality rates: insights for genetic studies of human health and longevity. Biogerontology. 2016;17:89–107. doi:10.1007/s10522-015-9594-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Andrew MK. Frailty and social vulnerability. Interdiscip Top Gerontol Geriatr. 2015;41:186–195. doi:10.1159/000381236 [DOI] [PubMed] [Google Scholar]
- 4. Martin GM. Stochastic modulations of the pace and patterns of ageing: impacts on quasi-stochastic distributions of multiple geriatric pathologies. Mech Ageing Dev. 2012;133:107–111. doi:10.1016/j.mad.2011.09.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Comfort A. Test-battery to measure ageing-rate in man. Lancet. 1969;2:1411–1414. [DOI] [PubMed] [Google Scholar]
- 6. Kirkwood TB. Alex Comfort and the measure of aging. Exp Gerontol. 1998;33:135–140. [DOI] [PubMed] [Google Scholar]
- 7. Ingram DK. Key questions in developing biomarkers of aging. Exp Gerontol. 1988;23:429–434. [DOI] [PubMed] [Google Scholar]
- 8. Nakamura E, Lane MA, Roth GS, Ingram DK. A strategy for identifying biomarkers of aging: further evaluation of hematology and blood chemistry data from a calorie restriction study in rhesus monkeys. Exp Gerontol. 1998;33:421–443. [DOI] [PubMed] [Google Scholar]
- 9. Butler RN, Sprott R, Warner H, et al. Biomarkers of aging: from primitive organisms to humans. J Gerontol A Biol Sci Med Sci. 2004;59:B560–B567. [DOI] [PubMed] [Google Scholar]
- 10. Miller RA. Biomarkers of aging. Sci Aging Knowledge Environ. 2001;2001:pe2. [DOI] [PubMed] [Google Scholar]
- 11. Arking R.The Biology of Aging: Observations and Principles. 3rd ed. New York, NY: Oxford University Press; 2006. [Google Scholar]
- 12. Sprott RL. Biomarkers of aging and disease: introduction and definitions. Exp Gerontol. 2010;45:2–4. doi:10.1016/j.exger.2009.07.008 [DOI] [PubMed] [Google Scholar]
- 13. Takeda H, Inada H, Inoue M, Yoshikawa H, Abe H. Evaluation of biological age and physical age by multiple regression analysis. Med Inform (Lond). 1982;7:221–227. [DOI] [PubMed] [Google Scholar]
- 14. Hochschild R. Improving the precision of biological age determinations. Part 1: a new approach to calculating biological age. Exp Gerontol. 1989;24:289–300. [DOI] [PubMed] [Google Scholar]
- 15. Karasik D, Demissie S, Cupples LA, Kiel DP. Disentangling the genetic determinants of human aging: biological age as an alternative to the use of survival measures. J Gerontol A Biol Sci Med Sci. 2005;60:574–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Kimura M, Mizuta C, Yamada Y, Okayama Y, Nakamura E. Constructing an index of physical fitness age for Japanese elderly based on 7-year longitudinal data: sex differences in estimated physical fitness age. Age (Dordr). 2012;34:203–214. doi:10.1007/s11357-011-9225-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Klemera P, Doubal S. A new approach to the concept and computation of biological age. Mech Ageing Dev. 2006;127:240–248. [DOI] [PubMed] [Google Scholar]
- 18. Levine ME. Modeling the rate of senescence: can estimated biological age predict mortality more accurately than chronological age? J Gerontol A Biol Sci Med Sci. 2013;68:667–674. doi:10.1093/gerona/gls233 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Belsky DW, Caspi A, Houts R, et al. Quantification of biological aging in young adults. Proc Natl Acad Sci USA. 2015;112:E4104–E4110. doi:10.1073/pnas.1506264112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Vaupel JW, Manton KG, Stallard E. The impact of heterogeneity in individual frailty on the dynamics of mortality. Demography. 1979;16:439–454. [PubMed] [Google Scholar]
- 21. Clegg A, Young J, Iliffe S, Rikkert MO, Rockwood K. Frailty in elderly people. Lancet. 2013;381:752–762. doi:10.1016/S0140-6736(12)62167-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Rockwood K, Mitnitski A. Frailty in relation to the accumulation of deficits. J Gerontol A Biol Sci Med Sci. 2007;62:722–727. [DOI] [PubMed] [Google Scholar]
- 23. Mitnitski AB, Mogilner AJ, Rockwood K. Accumulation of deficits as a proxy measure of aging. Sci World J. 2001;1:323–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Mitnitski AB, Mogilner AJ, MacKnight C, Rockwood K. The mortality rate as a function of accumulated deficits in a frailty index. Mech Ageing Dev. 2002;123:1457–1460. [DOI] [PubMed] [Google Scholar]
- 25. Parks RJ, Fares E, Macdonald JK, et al. A procedure for creating a frailty index based on deficit accumulation in aging mice. J Gerontol A Biol Sci Med Sci. 2012;67:217–227. doi:10.1093/gerona/glr193 [DOI] [PubMed] [Google Scholar]
- 26. Whitehead JC, Hildebrand BA, Sun M, et al. A clinical frailty index in aging mice: comparisons with frailty index data in humans. J Gerontol A Biol Sci Med Sci. 2014;69:621–632. doi:10.1093/gerona/glt136 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Kane AE, Hilmer SN, Boyer D, et al. Impact of longevity interventions on a validated mouse clinical frailty index. J Gerontol A Biol Sci Med Sci. 2016;71:333–339. doi:10.1093/gerona/glu315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Howlett SE, Rockwood MR, Mitnitski A, Rockwood K. Standard laboratory tests to identify older adults at increased risk of death. BMC Med. 2014;12:171 doi:10.1186/s12916-014-0171-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Mitnitski A, Collerton J, Martin-Ruiz C, et al. Age-related frailty and its association with biological markers of ageing. BMC Med. 2015;13:161 doi:10.1186/s12916-015-0400-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Rockwood K, McMillan M, Mitnitski A, Howlett SE. A frailty index based on common laboratory tests in comparison with a clinical frailty index for older adults in long-term care facilities. J Am Med Dir Assoc. 2015;16:842–847. doi:10.1016/j.jamda.2015.03.027 [DOI] [PubMed] [Google Scholar]
- 31. Canadian study of health and aging: study methods and prevalence of dementia. CMAJ. 1994;150:899–913. [PMC free article] [PubMed] [Google Scholar]
- 32. Canadian study of health and aging: study methods and prevalence of dementia. Int Psychogeriatr. 2001;(suppl 1):1–237. [Google Scholar]
- 33. Searle SD, Mitnitski A, Gahbauer EA, Gill TM, Rockwood K. A standard procedure for creating a frailty index. BMC Geriatr. 2008;8:24. doi:10.1186/1471-2318-8-24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Cho IH, Park KS, Lim CJ. An empirical comparative study on biological age estimation algorithms with an application of Work Ability Index (WAI). Mech Ageing Dev. 2010;131:69–78. doi:10.1016/j.mad.2009.12.001 [DOI] [PubMed] [Google Scholar]
- 35. Bennett S, Song X, Mitnitski A, Rockwood K. A limit to frailty in very old, community-dwelling people: a secondary analysis of the Chinese longitudinal health and longevity study. Age Ageing. 2013;42:372–377. doi:10.1093/ageing/afs180. [DOI] [PubMed] [Google Scholar]
- 36. Armstrong JJ, Mitnitski A, Launer LJ, White LR, Rockwood K. Frailty in the Honolulu-Asia Aging Study: deficit accumulation in a male cohort followed to 90% mortality. J Gerontol A Biol Sci Med Sci. 2015;70:125–131. doi:10.1093/gerona/glu089 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Heyland D, Cook D, Bagshaw SM, et al. ; Canadian Critical Care Trials Group; Canadian Researchers at the End of Life Network The very elderly admitted to ICU: a quality finish? Crit Care Med. 2015;43:1352–1360. doi:10.1097/CCM.0000000000001024. [DOI] [PubMed] [Google Scholar]
- 38. Zeng A, Song X, Dong J, et al. Mortality in relation to frailty in patients admitted to a specialized geriatric intensive care unit. J Gerontol A Biol Sci Med Sci. 2015;70:1586–1594. doi:10.1093/gerona/glv084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Taneja S, Mitnitski AB, Rockwood K, Rutenberg AD. A dynamical network model for age-related deficits and mortality. Phys Rev E. 2016;93:022309. [DOI] [PubMed] [Google Scholar]
- 40. Zhang WB, Pincus Z. Predicting all-cause mortality from basic physiology in the Framingham Heart Study. Aging Cell. 2016;15:39–48. doi:10.1111/acel.12408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Yashin AI, Ukraintseva SV, Arbeev KG, Akushevich I, Arbeeva LS, Kulminski AM. Maintaining physiological state for exceptional survival: what is the normal level of blood glucose and does it change with age? Mech Ageing Dev. 2009;130:611–618. doi:10.1016/j.mad.2009.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Mitnitski A, Song X, Skoog I, et al. Relative fitness and frailty of elderly men and women in developed countries and their relationship with mortality. J Am Geriatr Soc. 2005;53:2184–2189. [DOI] [PubMed] [Google Scholar]
- 43. Kulminski AM, Ukraintseva SV, Akushevich IV, Arbeev KG, Yashin AI. Cumulative index of health deficiencies as a characteristic of long life. J Am Geriatr Soc. 2007;55:935–940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Yashin AI, Arbeev KG, Kulminski A, Akushevich I, Akushevich L, Ukraintseva SV. Cumulative index of elderly disorders and its dynamic contribution to mortality and longevity. Rejuvenation Res. 2007;10:75–86. [DOI] [PubMed] [Google Scholar]
- 45. Mitnitski AB, Graham JE, Mogilner AJ, Rockwood K. Frailty, fitness and late-life mortality in relation to chronological and biological age. BMC Geriatr. 2002;2:1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Mitnitski A, Rockwood K. Biological age revisited. J Gerontol A Biol Sci Med Sci. 2014;69:295–296. [DOI] [PubMed] [Google Scholar]
- 47. Mitnitski A, Rockwood K. Aging as a process of deficit accumulation: its utility and origin. Interdiscip Top Gerontol. 2015;40:85–98. doi:10.1159/000364933 [DOI] [PubMed] [Google Scholar]
- 48. Rockwood K, Mitnitski A. Limits to deficit accumulation in elderly people. Mech Ageing Dev. 2006;127:494–496. doi:10.1016/j.mad.2006.01.002 [DOI] [PubMed] [Google Scholar]
- 49. Fontana L, Kennedy BK, Longo VD, Seals D, Melov S. Medical research: treat ageing. Nature. 2014;511:405–407. doi:10.1038/511405a [DOI] [PubMed] [Google Scholar]
- 50. Hilmer SH, Le Couteur DG. Standardized, multidisciplinary approaches for the study of aging biology for translation of aging interventions. J Gerontol Biol Sci. 2016;71:425–406. doi:10.1093/gerona/glv310. [DOI] [PubMed] [Google Scholar]
- 51. Ladiges W, Ikeno Y, Niedernhofer L, et al. The Geropathology Research Network: an interdisciplinary approach for integrating pathology into research on aging. J Gerontol Biol Sci. 2016;71:431–434. doi:10.1093/gerona/glv079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Nikolich-Žugich J, Goldman DP, Cohen PR, et al. Preparing for an aging world: engaging biogerontologists, geriatricians and the society. J Gerontol Biol Sci. 2016;71:435–446. doi:10.1093/gerona/glv164 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.