Planar-to-tubular structural transition in boron clusters: B₂₀ as the embryo of single-walled boron nanotubes

Abstract

Experimental and computational simulations revealed that boron clusters, which favor planar (2D) structures up to 18 atoms, prefer 3D structures beginning at 20 atoms. Using global optimization methods, we found that the B₂₀ neutral cluster has a double-ring tubular structure with a diameter of 5.2 Å. For the anion, the tubular structure is shown to be isoenergetic to 2D structures, which were observed and confirmed by photoelectron spectroscopy. The 2D-to-3D structural transition observed at B₂₀, reminiscent of the ring-to-fullerene transition at C₂₀ in carbon clusters, suggests it may be considered as the embryo of the thinnest single-walled boron nanotubes.

Small atomic clusters often exhibit structures and properties remarkably different from those of their bulk counterparts. For example, the most stable form of carbon is graphite, consisting of layers of two-dimensional (2D) graphene sheets. Yet small carbon clusters form chains, rings, and fullerenes (1–5). Boron, carbon's lighter neighbor, is also a strongly covalent material consisting of B₁₂ icosahedral cages (6–8). But small boron clusters were predicted to be planar (9–11), in stark contrast to the bulk three-dimensional (3D) cages. Planar boron clusters have been recently produced in the gas phase and experimentally confirmed up to B₁₅ (12–14). However, it is still unclear at what critical size the 2D-to-3D structural transition occurs. We show from concerted photoelectron spectroscopy (PES) and global geometry optimization theoretical studies (15–17) that the transition occurs at the size of 20 atoms. The B₂₀ neutral cluster is found to overwhelmingly favor a double-ring tubular-type structure over any 2D isomers, whereas in the anion the tubular and several 2D structures are close in energy. The 2D-to-3D transition at B₂₀ is reminiscent of the ring-to-cage transition at C₂₀, which forms the smallest fullerene (5). The tubular B₂₀ is the smallest stable 3D boron cluster and can be viewed as the embryo of the thinnest boron nanotube, with a diameter of 5.2 Å.

Methods

PES. The experiments were carried out by using a magnetic-bottle time-of-flight PES apparatus equipped with a laser vaporization supersonic cluster source (15, 17). 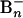cluster anions were produced by laser vaporization of a disk target made of enriched ¹⁰B isotope (99.75%) in the presence of a helium carrier gas and were analyzed with a time-of-flight mass spectrometer. The 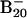clusters were mass-selected and decelerated before irradiation by a photodetachment laser beam. Photoelectrons were collected at nearly 100% efficiency by the magnetic bottle and analyzed in a 3.5-m-long electron flight tube. The photoelectron spectra were calibrated by the known spectrum of Rh^–, and the energy resolution of the apparatus was ΔE_k/E_k ∼ 2.5%, i.e., 25 meV for 1-eV electrons. Effort was devoted to control the cluster temperatures (Fig. 4, which is published as supporting information on the PNAS web site), which was vital for the well resolved photoelectron data (12).

Theoretical Calculations. The unbiased search for global minimum was carried out by using the basin-hopping algorithm (18, 19) coupled with ab initio density functional technique (20), where the potential energy transformation is combined with the Monte Carlo (MC) sampling method. After each accepted MC move a geometry minimization was carried out. Plane-wave pseudopotential density functional theory (19, 20) with a gradient corrected functional (blyp as implemented in the cpmd code) (21) was adopted to carry out the minimization. In essence, the basin-hopping method converts the potential energy surface to a multidimensional staircase with each accepted MC step to a basin of attraction. A vast variety of 2D isomeric structures were readily identified. To locate the tubular B₂₀ structure, which turned out to be separated by huge energy barriers from the vast majority of 2D structures, we started the search at a relatively high temperature of 0.05 hartree (1 hartree = 4.36 aJ). Once a non-2D structure emerged, the temperature was then brought down to 0.009 hartree and kept constant for further potential energy surface exploration. The tubular global minimum was reached after another 10³ MC moves. The global minimum search was repeated with several starting geometries. Regardless of the initial geometries, the final lowest-energy structures were always the same. To gain further confidence, we also performed ab initio simulated annealing with PBE96 exchange-correlational functional on the 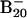starting with random geometries. We observed that the lowest-energy structures were dominated by the planar isomers. Of more than 200 local minima identified, the top 10 candidates were further relaxed by using all-electron density functional theory (22). All final calculations (Figs. 2, 3, and 5 and Tables 1 and 2; see also Fig. 5 and Table 2, which are published as supporting information on the PNAS web site) were carried out at B3LYP/6–311+G* all-electron basis set with the gaussian 03 software (23).

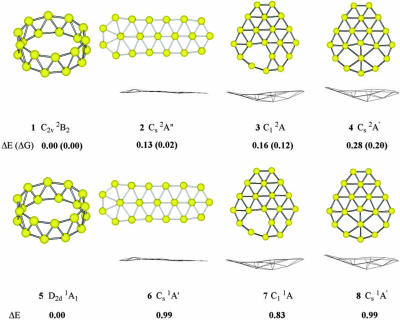
Fig. 2.

Low-lying structures of 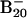(1–4) and B₂₀ (5–8) along with their relative energies (in eV) at B3LYP/6–311+G* level.

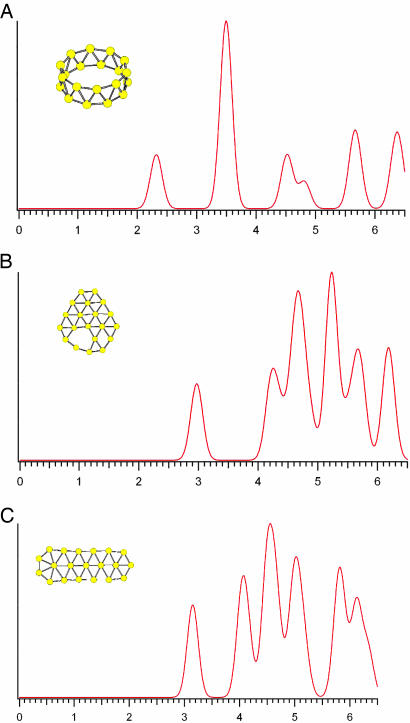
Fig. 3.

Simulated photoelectron spectra for three 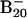low-lying isomers: isomer 1 (A), isomer 3 (B), and isomer 2 (C). The spectra were constructed by fitting the distribution of the calculated VDEs with unit-area Gaussian functions of 0.2 eV full width at half maximum (17).

Table 1.

Observed vertical detachment energies (VDE) from the photoelectron spectra of 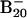and comparison with theoretical data at B3LYP/6–311+G* level for the lowest-energy isomers of 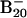(see Fig. 2)

Observed feature		VDE (theoretical), eV
	VDE (experimental), eV	Structure 1	Structure 2	Structure 3
X†	3.11(2)/3.02(2)	2.32/2.17	3.15/3.03	2.97/2.88
A‡	4.20(3)	3.49/3.52	4.04/4.14
B	4.40(3)	4.52/4.81	4.49/4.54	4.22/4.37
C	4.71(4)		4.66/4.94	4.59/4.71
D	4.92(4)		5.03/5.17	4.70/4.87
E	5.35(4)			5.21/5.27
F	5.46(4)			5.23/5.49
G	5.84(3)	5.65/5.70	5.79/5.87	5.66/5.75
H	6.33(3)	6.35/6.42	6.12/6.33	6.17/6.21

All energies are in eV. The theoretical VDEs in italic represent transitions to the singlet final states, whereas the remaining theoretical VDEs represent transitions to triplet final states. Numbers in parentheses indicate the experimental uncertainties in the last digit. Numbers in boldface represent the adiabatic detachment energy (ADE, in eV), which also defines the electron affinity of the neutral cluster.

^†The X—B energy separation of 1.3 eV defines the experimental HOMO—LUMO gap (excitation energy to the first triplet excited state) of the B₂₀ neutral (corresponding to the dominant isomer in the 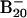beam). For comparison, the corresponding theoretical values are 1.17, 0.89, and 1.25 eV for structures 1, 2, and 3, respectively.

^‡Feature ascribed to a minor isomer populated in the 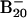cluster beam.

Results and Discussion

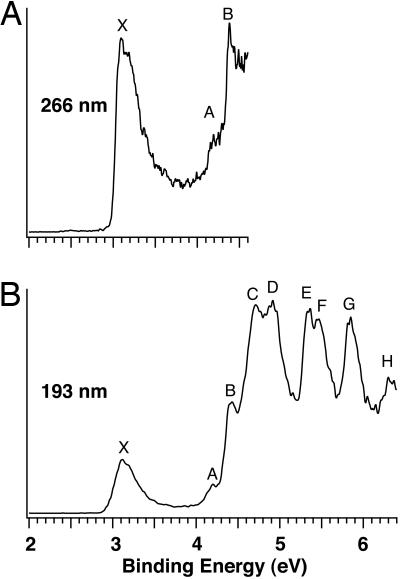
Fig. 1 shows the PES spectra of 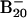at two photon energies. Numerous well resolved electronic transitions (X and A–H) were observed, and their electron-binding energies are given in Table 1, where they are also compared with theoretical data. The vertical detachment energy (VDE) of feature X was measured from the peak maximum to be 3.11 eV. The electron affinity (EA) of neutral B₂₀, evaluated from the well defined sharp onset of band X, is 3.02 eV. The intensity of feature A was much weaker, implying that it was likely due to a weakly populated isomer of 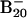in the cluster beam. A large energy separation of ≈1.3 eV was observed between features X and B. This spectral pattern suggested that neutral B₂₀ is a closed-shell molecule with a large gap between its highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). It is noted that among all B_n clusters in the size range n = 3–25 large HOMO–LUMO gaps were observed only for B₁₂ and B₂₀. B₁₂ was previously characterized to possess a quasiplanar C_3ν geometry and was found to be the most prototypical aromatic boron cluster with six π electrons (14), analogous to benzene in the aromatic hydrocarbons. The current observation of B₂₀ with the large HOMO–LUMO gap stimulated our interest for a thorough investigation of its structural and electronic properties.

Fig. 1.

Photoelectron spectra of 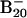at 266 nm (4.661 eV) (A) and at 193 nm (6.424 eV) (B).

Locating the global minimum for a 20-atom cluster is a demanding task (16, 17). Fig. 5 displays a selected set of structures considered. We further used the basin-hopping global optimization method (18, 19) coupled with ab initio density functional theory (DFT) technique (20). More than 200 low-energy minima (with energy difference <0.1 hartree from the global minimum) were identified for B₂₀. For the top 10 lowest-energy isomers we performed further optimization and vibration frequency calculations using all-electron DFT methods. The four lowest-energy isomers are shown in Fig. 2, along with their relative energies at the B3LYP/6–311+G* level of theory (23). We applied the same search methods for both the anion and neutral clusters. However, the two potential energy surfaces are different, although both are dominated by 2D structures. In the anion potential energy surface there exist several isomers that are close in energy. The double-ring tubular structure 1 is the most stable, followed by the elongated 2D structure 2 and the quasiplanar bowl-like structures 3 and 4. To include entropy and temperature effects, we also carried out free-energy calculations at room temperature (298 K). After this correction, both the tubular and elongated isomers become virtually equal in energy, closely followed by the bowl isomers. At the theoretical methods used all these anion isomers should be considered isoenergetic. It should be noted that structures 3 and 4 are nearly identical except for the displacement of a single boron atom. Therefore, most of the properties of these two isomers are nearly identical.

However, in the neutral potential energy surface, the most stable isomer is the double-ring tubular structure 5, which is favored by ≈1.0 eV relative to the lowest-energy 2D structures 6, 7, and 8. The current observations that the 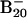anion favors 2D structures and the B₂₀ neutral favors the tubular structure suggest that the extra electron destabilizes the double-ring tubular isomer, whereas it stabilizes the 2D isomers. We also calculated the most stable structures for the 16- to 19-atom boron clusters and found that they all preferred 2D structures in both their anions and neutrals, and these structures are experimentally confirmed by PES data (not shown). It should be noted, however, that it is difficult to locate the tubular B₂₀ structure, which appears as a deep and narrow well in the potential energy surface separated by huge energy barriers from the vast majority of easily accessible 2D structures. To gain further confidence, we also performed ab initio simulated annealing with PBE96 exchange-correlational functional on 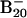starting with random geometries. We observed that the lowest-energy structures were dominated by the 2D isomers (23).

To confirm the computational results and facilitate comparison with the experimental data, we calculated the VDEs and EA (Table 1) and simulated the PES spectra from our density functional theory computations (Fig. 3) (17). The energy difference between the anion and neutral at the anion geometry gives the first VDE, and relaxing the neutral geometry to its equilibrium defines the EA. Only the 2D isomers compare favorably with the experimental values. The VDE and EA of both the elongated structure (2, VDE 3.15 eV, EA 3.03 eV) and the bowl isomer (3, VDE 2.97 eV, EA 2.88 eV; 4, VDE 3.04 eV, EA 2.89 eV) agree well with the experimental values of 3.11 and 3.02 eV, respectively. However, the tubular structure 1 gives binding energies (VDE 2.32 eV, EA 2.17 eV) much lower than the experiment. Closer comparison between the experimental and theoretical data (Table 1 and Figs. 1 and 3) clearly shows that isomer 3 agrees best with the experiment: the simulated spectrum of isomer 3 (Fig. 3B) has a remarkable one-to-one correspondence to the experimental spectrum. Isomer 2 gives a smaller HOMO–LUMO gap (Fig. 3C and Table 2) and is likely to be the minor isomer responsible for the weak feature A (Fig. 1B); the remaining electronic transitions of isomer 2 were buried in the spectra of the dominant isomer 3. Isomer 1 did not appear to be populated at all in the B^–₂₀ beam, which would have yielded a characteristic transition at lower binding energies (≈2.3 eV) in the experimental spectrum. The absence of isomer 1 was likely due to the kinetic control of cluster formation. Because clusters smaller than B₂₀ all have planar structures in their ground state, the planar B₂₀ cluster is expected to form with the highest probability. For example, the bowl isomers 3 and 4 can be derived from B₁₂ by adding seven boron atoms to the rim and one in the middle. Similarly, the elongated isomer (2) can be directly constructed by adding six additional boron atoms to one end of B₁₄. The situation of 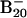is remarkably similar to the case of 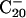, where the bowl and fullerene isomers cannot be produced by laser vaporization of graphite (5). The latter method can produce only the ring isomer, which is similar to the structures of smaller carbon clusters (2–4).

Heretofore we established that the tubular isomer is almost isoenergetic to the lowest-energy 2D isomers for the anion, whereas it is clearly the global minimum for the B₂₀ neutral. Because we have confirmed that all smaller clusters prefer 2D structures, the tubular B₂₀ cluster represents exactly the onset of 3D structures for the boron clusters, analogous to the onset of the fullerene structure at C₂₀. The B₂₀ tubular structure can be viewed as rolling up a two-row strip of 20 B atoms: it is stabilized by the strong sp² hybridized σ bonds within the wall and further enhanced by delocalized π bonds covering the inner and outer surfaces of the wall. As a result the tubular structures are also highly aromatic, analogous to the aromaticity in the planar boron clusters (14). Despite the strain imposed by the curvature, the preference of the tubular over 2D isomers is due to the stronger σ-bonding and the more uniform π-bonding in the former. As we showed previously (13, 14), in the planar boron clusters the peripheral boron atoms have very strong σ-bonding, whereas the inner boron atoms are connected by weaker multicenter bonding. The tubular structure gives rise to 20 strong peripheral B–B bonds, more than any planar isomers. Furthermore, although π-bonding in smaller B clusters indeed provides additional stability to the planar structure, our previous work on B₁₀ to B₁₅ revealed that in larger clusters the π orbitals tend to fragment (localize) in different parts of the 2D structures (14), weakening the contributions of the π-bonding to the stability of planar isomers and hinting possible 2D-to-3D transitions with increasing cluster sizes. On the other hand, despite the curvature there is still considerable π-bonding in the tubular structure, similar to that in fullerenes or carbon nanotubes.

The current work indicates that planar-to-tubular switch-over takes place at B₂₀. The tubular B₂₀ suggests a mechanism for forming the thinnest boron nanotube by extending the B₂₀ structure along the fivefold axis. In fact, larger diameter double-ring and multiple-ring tubular boron structures (such as B₂₄ and B₃₆), among a variety of other chosen structures, have been explored computationally (24–27). Very interestingly, a successful synthesis of single-walled boron nanotubes with a diameter of 3 nm has been reported recently (28). Our current work represents a systematic experimental and theoretical search for the smallest stable 3D boron clusters. The high stability of the tube-like B₂₀ suggests the existence of a whole new class of nanotubes made of boron atoms. Indeed, the tubular B₂₀ cluster may be viewed as the embryo of the thinnest boron nanotube, with a diameter of 5.2 Å.