A partial atomic structure for the flagellar hook of Salmonella typhimurium

Abstract

The axial proteins of the bacterial flagellum function as a drive shaft, universal joint, and propeller driven by the flagellar rotary motor; they also form the putative protein export channel. The N- and C-terminal sequences of the eight axial proteins were predicted to form interlocking α-domains generating an axial tube. We report on an ≈1-nm resolution map of the hook from Salmonella typhimurium, which reveals such a tube made from interdigitated, 1-nm rod-like densities similar to those seen in maps of the filament. Atomic models for the two outer domains of the hook subunit were docked into the corresponding outermost features of the map. The N and C termini of the hook subunit fragment are positioned next to each other and face toward the axis of the hook. The placement of these termini would permit the residues missing in the fragment to form the rod-like features that form the core domain of the hook. We also fit the hook atomic model to an ≈2-nm resolution map of the hook from Caulobacter crescentus. The hook protein sequence from C. crescentus is largely homologous to that of S. typhimurium except for a large insertion (20 kDa). According to difference maps and our fitting, this insertion is found on the outer surface of the hook, consistent with our modeling of the hook.

The bacterial flagellum is the organ of motility for many species of bacteria. About 40 genes are needed to assemble the structure; ≈22 of the genes contribute structural proteins found in the completed flagellum. Of these 22 proteins, six appear to be key components of the rotary motor. An additional protein is likely to function as an adaptor connecting the motor to the axial component (1). Nine more proteins make up the axial component consisting of a rod (drive shaft), hook (universal joint), junction, filament (propeller), and cap. Two of the remaining proteins make up rings, which serve as a bushing that allows passage of the drive shaft through the cell wall and outer membrane. The rest of the proteins are associated with the flagellar-specific protein export.

The rotary motor, powered by the proton-motive gradient across the cell membrane, turns the filament, which converts torque into thrust. The helical hook of the bacterial flagellum acts as a universal joint, allowing the motor to drive the filament off-axis. The hook connects the rod to the hook–filament junction, which in turn is connected to the filament. The hook, which is assembled before the more distal segments of the axial component, plays a role in the assembly of the filament. The flagellar filament elongates by subunit addition at its distal tip (2, 3). Subunits exported by the cell are thought to diffuse along a channel in the hook (and also the rod within the basal body and partially assembled filament). Three-dimensional reconstructions reveal a 3-nm channel running along the axis of the rod (D.R.T., D. G. Morgan, and D.J.D., unpublished data), hook (4), and filament (5), although higher-resolution maps of the filament reveal a smaller, 2-nm channel (6).

The helical symmetry operator of the rod (D.R.T., D. G. Morgan, and D.J.D., unpublished data), hook (7, 8), and filament (9) involves a rotation of ≈65° and an axial translation of ≈0.5 nm. At both their N and C termini, eight of the nine axial proteins have heptad repeats, which suggests the presence of α-helical bundles. Indeed, x-ray fiber diffraction (10), optical rotatory dispersion (11), and circular dichroism (12) of the filament indicate α-helical structures lying roughly parallel to the helical axis. The N- and C-terminal sequences, which are un-folded in monomeric hook and filament subunits, fold into α-helices upon polymerization (13, 14). In the case of the filament, these terminal sequences are necessary for filament assembly in vivo and for generation of the superhelical corkscrew shape (15).

Three-dimensional maps of the filament (6, 16, 17) reveal densities consistent with an inner tubular ring of α-helices, which orient approximately parallel to the axis. This ring forms a wall around a 2- to 3-nm central channel. Filaments made from proteolytic fragments lacking the N- and C-terminal heptad repeats lack this ring and have a channel of larger diameter (18, 19). Given the shared helical symmetry, common heptad repeats of the axial proteins, and the presence of putative α-helices in the filament, a reasonable hypothesis is that this tubular α-helical design is the common feature in the axial proteins.

Methods

Polyhooks were isolated as described in ref. 20. We used a polyhook strain of Salmonella typhimurium, SJW880 (Protein Data Bank ID code 28GZ) (21). Whereas normal hooks are ≈55 nm in length, hooks from this strain can be many times longer. SJW880 carries a mutation in FliK, a hook-length control protein, not in the hook protein itself, FlgE, and the polyhook structure appears identical to that of the wild-type hook (8). Grids were prepared for electron cryomicroscopy by using protocols for flagellar filaments (17), except that grids were prepared at 4°C, where almost 100% of the normally curly hooks are straightened. EM was carried out at 200 kiloelectron volts by using a field emission gun at ≈×66,000, an underfocus range from 1.3 to 2.7 μm, and a dose of 1,000 electrons per square nm.

We cut digitized images (0.32 nm per pixel) of frozen-hydrated polyhooks into 420 total polyhook segments of ≈800 hook subunits. Sixty-six such segments were subsequently rejected because their Fourier transforms failed to reveal at least three layer lines. Layer-line data sets from the remaining 354 images were aligned and merged by using cross-correlation methods. In the first round of alignment, we aligned data sets by using Fourier coefficients that were within the first node of the contrast transfer function (CTF), which was at ≈1/2.5-nm^–1 resolution. For subsequent rounds of alignment and averaging, we first performed a phase-only CTF correction. If the difference in phase residual between the up/down orientations was >10°, we included that data set. A total of 262 data sets met this criterion. The average amplitude-weighted phase residual was 60°, and the up/down phase difference was 20°.

We performed an amplitude-and-phase correction for the final average by using a Wiener filter (22). A value of 0.07 was used for amplitude contrast (23, 24). The amplitudes at low resolution, however, are larger than those predicted by the calculated CTF. In order not to overweight the low spatial frequencies, we altered the low-resolution part of the CTF correction, as was done on the flagellar filament: namely, for R < 1/3.2 nm^–1, the CTF was set to –1.0 (17). The denominator of the Wiener filter, which is equal to the sum of the squares of the individual CTFs, had a minimum of 62.0 (data not shown). The noise-to-signal ratio, which is the other term in the denominator, was set to 1.0, as was done on the filament (17). This minimum of the Wiener-filter denominator was about one-fourth of the maximum (262.0), showing that the defocus range we used (1.3–2.7 μm underfocus) sampled reciprocal space reasonably well. The position of the minimum was at 1/2.3 nm^–1, as would be expected for a median value of defocus of 1.9 μm.

The initial CTF corrections assumed that the level of defocus measured on a nearby area of the carbon foil could be applied to the hook itself. We confirmed the assumption by looking at the phase differences between the values for the layer-line data of the Wiener-filtered average and those of individual particles that were aligned but not CTF-corrected. To do so, we summed the amplitude-weighted cosines of the phase differences as a function of resolution. As expected, the product reversed sign near the nodes of the CTF (data not shown).

Before combining the near- and far-side data sets, we determined that the two sets were the same within experimental error. To do so, we subtracted a three-dimensional map derived from the near-side data set from that of the far-side data set. We then determined which voxels had statistically significant differences at the 5.2% confidence level. At this cutoff, 4.6% of the expected 5.2% voxel difference densities were found to be statistically significant; these densities were scattered throughout the map (data not shown). Thus, the near and far sides are not different in a statistical sense. We therefore combined the two data sets, eliminating the 38 of 84 layer lines collected that did not show a positive correlation when comparing the near- and far-side data. The near-equatorial first layer line (n = –11) is the layer line of most interest when considering the visualization of approximately axial rod-like features. A comparison of the near- and far-side data for this layer line showed good agreement out to ≈2.2-nm resolution and then an additional peak of agreement at 1-nm resolution. This result is similar to that of the filament (17). In combining the near- and far-side data sets, a cutoff of 0.9 nm was used, although the true resolution may not be as good as that.

As part of our fitting of the atomic model to the density map of the hook, we generated a map of the Caulobacter crescentus hook (Protein Data Base ID code 2BGY). The images were those used by Wagenknecht et al. (7). We processed the images, which were of negatively stained polyhooks, and a generated three-dimensional map of the C. crescentus hook at ≈2-nm resolution. We prepared a difference map by subtracting the S. typhimurium map, filtered to 2-nm resolution, from the C. crescentus map.

The docking of atomic models into the hook maps of the two species was done by using the real-space refinement program rsref (25, 26) based on x-plor (27).

Results

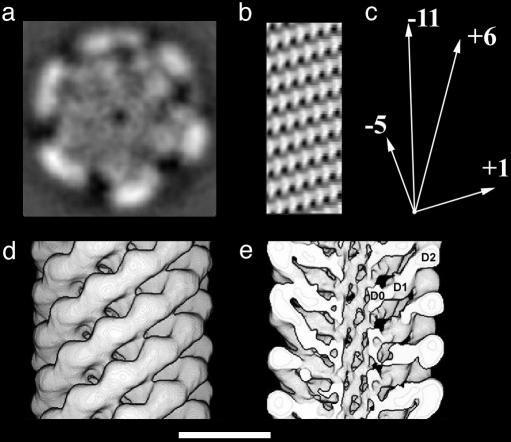
Fig. 1 shows the averaged layer-line data (b) for the set of images and a projection (a) calculated from these data. Fig. 2a shows a transverse section through the three-dimensional map of the hook. Fig. 2 d and e shows surface representations of the whole hook and one in which the front half has been cut away. The hook has three domains (Fig. 2e). Domain D2 lies at a radius of 7.5 nm and corresponds to the outermost feature on the surface of the hook, domain D1 is just inside domain D2 and lies between radii of 5 and 6 nm, and domain D0 forms a tube with a 1-nm-thick wall and a 3-nm axial lumen. Fig. 2b shows a cylindrical section through innermost (D0) rod-shaped domains. Each rod-shaped domain, which is ≈1 nm in diameter by ≈2.5 nm in length, is staggered relative to those above and below it to generate an interdigitating pattern.

Fig. 1.

EM and image analysis of the hook. The average of all of the hook data sets seen as a projection of the three-dimensional map is shown in Left. Such a projection is equivalent to the average hook image as it would be seen in the electron microscope. (Scale bar: 10 nm.) A display of the layer-line data [G_n(R, Z)] for the data included in the average is shown in Right. The logarithm of the amplitude is displayed to make the weaker layer lines visible. The cutoff in resolution is 0.9 nm.

Fig. 2.

Three-dimensional maps of the hook. (a) A section taken perpendicular to the helical axis. (b) A cylindrical section through the wall of the central tube. The rod-like features lining the central putative protein channel are spaced about 1 nm apart in the azimuthal (horizontal) direction. (c) A vector diagram showing the directions that the 5, 11, 6, and 1 start helices in b. (d) A surface representation of the hook density map. (e) A surface representation with the front half of the structure removed to reveal domain D0. The three domains of the hook subunit are labeled D0, D1, and D2. (Scale bar: 10 nm.)

The outer domain, D2, hangs out off the middle domain, D1. There is an axial gap between the D2 domains, which provides freedom for the hook to curve. This aspect of the hook structure is put forth in some detail in Samatey et al. (28). On the inside end of D1 are the rod-like features that form a narrow tube. This design is in some sense similar to the design of the Buddhist gojū-no-tō, or five-storied pagoda, which has floors hanging off a central support beam. This design allows the structure to bend without breaking, as might happen, for example, in an earthquake. In the case of the hook, the design represents a way to maintain structural integrity while still permitting a more flexible and more highly curved structure than the filament, which has a more rigid, double-tube design.

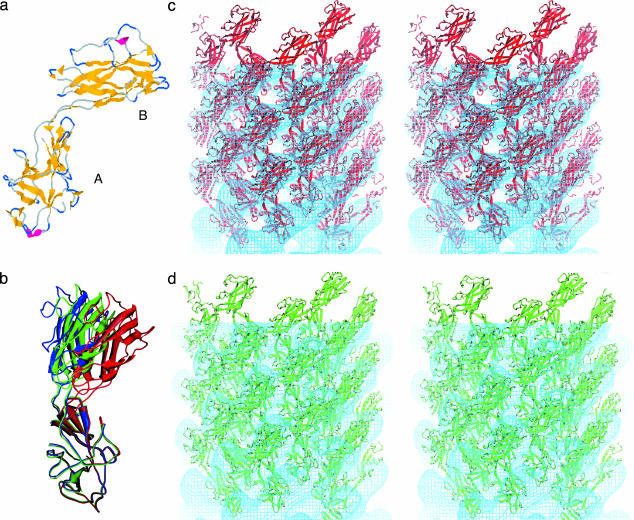
Fig. 3a shows the atomic model for a major fragment (FlgE31) of the hook subunit obtained by x-ray crystallography (28). To carry out the docking and conformational adjustment, we determined how to place the atomic model into the map. The innermost (D0) domain was left unoccupied; we argue that it corresponds to the missing N- and C-terminal sequences removed before crystallization. This interpretation is analogous to the situation in the filament, in which the N- and C-terminal sequences were removed to obtain crystals rather than filaments. These terminal sequences, which are unfolded in the monomer, form the walls of the tube of the filament. We suggest that these similar terminal sequences missing in the hook subunit form the similar inner domain in the hook structure. Moreover, neither of the two β-folds can fit into the D0 domain.

Fig. 3.

The atomic model of the outer two domains of the hook. (a) The structure of a major fragment of the hook subunit as determined by x-ray crystallography (28). β-Sheet is shown in yellow and α-helical segments in red. The lower domain (A) contains both N- and C-terminal regions, has the more evolutionarily conserved amino acid sequence, and corresponds to domain D1. The upper domain (B) corresponds to D2. (b) The change in domain arrangement involved in the docking and refinement. Three models are superimposed by fitting the D1 domains to one another. The figure shows the difference in the angle between domains D1 and D2 after refinement. The crystal structure model is shown in blue; the model refined against the C. crescentus map, green; the model refined against the S. typhimurium map, red. (c) A stereo pair of the atomic structure docked into the S. typhimurium map. Some of the subunits are shown outside the map. (d) A stereo pair showing the atomic structure docked into the C. crescentus map.

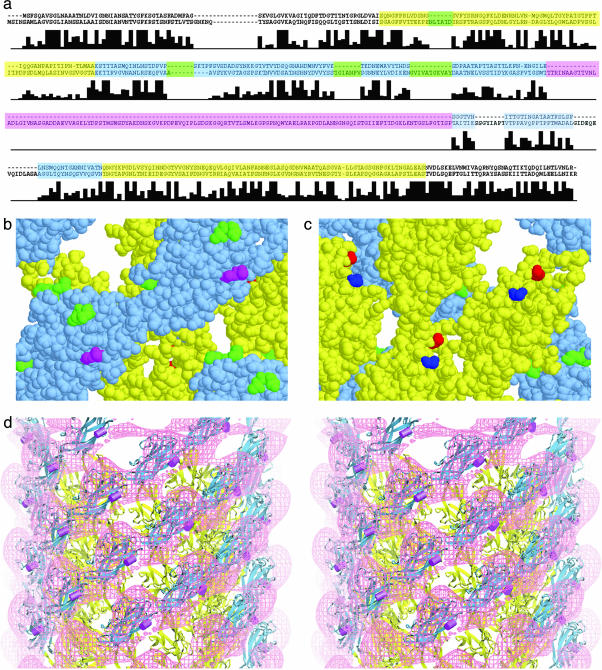
Deciding which of the two folds to place into domain D1 was straightforward. One of the two β-folds, denoted as A in Fig. 3a, contains the N and C termini of the peptide. It is plausible that fold A should be placed in D1 so that the N and C termini would be near domain D0. A further consideration was the degree of sequence conservation of domains among bacterial species. The idea is that sequences in the outer (D2) domain are less constrained by interdomain interactions. The same situation is found for the filament, in which sequences corresponding to the outer domain are less well conserved than those of the other domains. We used clustalw (29) to align the sequences of hook proteins for 13 species of bacteria (Fig. 4a). The sequences that make up fold A are better conserved, having fewer inserts among different species than those corresponding to fold B. Thus, we concluded that fold A must correspond to D1 and fold B to D2. The crystal structure of the FlgE fragment molecule was thus placed into the map as a rigid body followed by a manual adjustment (a hinged rotation) to better fit the domains onto the features in the map.

Fig. 4.

A comparison of the sequences of hook proteins. (a) Shown are the sequences corresponding to the proteins FlgE of S. typhimurium (upper sequence) and C. crescentus (lower sequence). The residues corresponding to domain D1 (or A in Fig. 3a) are shown in yellow, and those corresponding to domain D2 (or B in Fig. 3a) are shown in blue. The large insert found in C. crescentus but not S. typhimurium is shown in magenta. The other four inserts mapped in b and c are shown in green. Below the sequences is a bar graph showing sequence identity in FlgE for 13 bacterial species. (The height of the tallest bar corresponds to 13.) Note that the sequence assigned to domain D2 has more inserts than that of D1. (b) Space-filling model of hook subunits as seen from the outside. The sites of the small inserts are shown in green, and the site of the large insert in the hook of C. crescentus is shown in magenta. The yellow and blue portions correspond to domains D1 and D2, respectively, and the yellow and blue sequences in a.(c) Space-filling model of the hook subunits as seen from the inside the hook. The N and C termini, shown in blue and red, respectively, lie close to one another. The axis of the hook is vertical with the cell-proximal side at the bottom. (d) A stereo pair showing a surface representation of the difference map in which the S. typhimurium map is subtracted from the C. crescentus map. The atomic model derived by docking is shown with the site of the insert in C. crescentus marked by a magenta rod.

The refinement of the docking was done by using rsref (25, 26) based on x-plor (27). The manual modeling improved the overall fit, reducing the pseudoenergy term from 167.0 to 161.8. However, the molecular mechanical energy calculation indicated bad contacts between the two domains of the monomer and among the neighboring molecules in the hook structure. To apply the real-space molecular dynamics refinement in x-plor, the two domains of the FlgE fragment molecule were defined as individual rigid bodies connected by flexible peptide chains. Local symmetry operators were introduced to include the neighboring subunits in the simulation. The resulting refinement further improved the model-density match, resulting in a pseudoenergy score of 155.8, and significantly reduced the bad Van der Waals contacts, both within and between the molecules. The bending-angle difference between the initial crystal structure and the refined EM model is ≈8°. Fig. 3b shows the original fold from the crystallographic studies (red) and the fold after docking (blue). The fold shown in green best fits the C. crescentus map; the docking was carried out in the same manner as that for the S. typhimurium map. As is evident from the figure, adjustment of the model to fit the two maps involves bending, but only a 4° bend is needed in the case of the fit to the C. crescentus map. Fig. 3 c and d shows the atomic models docked into the hook map of S. typhimurium and C. crescentus, respectively.

As a simple check on our assignment of domains to morphological features, we reversed the assignment (i.e., we put domain A into D2 and domain B into D1) and again carried out real-space refinement using only the S. typhimurium hook map, which is the higher-resolution map. The pseudoenergy term, compared with that from our earlier assignment, increased from 155.8 to 203.6, and the model-density correlation decreased from 57.0% to 39.1%. A more compelling check on the assignment is presented in Discussion.

Discussion

The domain shapes and organization of the hook of S. typhimurium do not differ appreciably from those of C. crescentus (compare Fig. 3 c and d) except for the additional outer domain present in the latter. The three domains seen in the maps of the S. typhimurium are consistent with the three domains deduced from calorimetry experiments on the hook (30). The D2 domain in the hook in C. crescentus is larger (7), consistent with its having a large insert in the amino acid sequence for domain D2 (Fig. 3).

Because there is little sequence identity between the hook and filament proteins, we would expect the folds to be different except for the coiled-coils arising from the N- and C-terminal sequences. Indeed, the outer domains of the two structures do look different both in the low-resolution maps and in their atomic structures. In flagellin, there are three outer domains: an α-domain near the center, a mostly β-(or β-hairpin-rich) domain at slightly higher radius, and a β-domain at the outside (31). The hook has two outer domains, both having β-folds (28) as predicted (30). Even though the outer domains of the hook and filament can be classified as β-barrel folds, the β-folds of the hook domains are different from those of the two outer domains of the filament. The common feature of the hook and filament structures is the central tube with its 11 1-nm-diameter, rod-shaped densities.

The correctness of the docking can be confirmed from the sites of insertions into the hook protein. If the docking is correct, then these sites should be facing into regions empty of protein. From the alignment of the hook proteins sequences (Fig. 4a), we found three insertions in the more variable D2 domain and one insertion in the more conserved D1 domain. (In the alignment, there are two additional, apparent inserts, but because we were less sure that these might be due to poor alignment, we did not include them.) These sites of insertion all point into empty regions of the map (Fig. 4 b and c), as expected. The sites of insertions in D1 appear to have less space than those in D2, and indeed the insertions at this locus are small, only of six or so amino acids. Comparing the structure of the S. typhimurium hook with that of C. crescentus, Morgan et al. (4) found that there is an extra domain in the latter that extends outward from the right-hand edge of D2. In the sequence alignment, the site of the insertion (Fig. 4a) is approximately at residue 239. This location is shown in magenta in Fig. 4b. Fig. 4d shows the atomic model derived by the docking of the atomic model for the S. typhimurium hook subunit into the C. crescentus map. The site of the insert is shown as a magenta rod. The atomic model is superimposed on the difference-density map, which reveals, in magenta, the additional density present in the C. crescentus hook, compared with that in the S. typhimurium hook. The site of the insert is adjacent to the additional domain.

Domain D1 from one subunit underlies domain D2 from the adjacent subunit on the cell-proximal side along the 11-start family of lattice lines. This arrangement interlocks these subunits into rows, which are known as protofilaments in the filament. The protofilaments play an important role in generating the superhelical or corkscrew shape of the filament. It is less clear what role they might play in the hook; a possible model for the curvature is presented by Samatey et al. (28).

The sequence motifs common to the axial proteins are the heptad repeats in the N- and C-terminal sequences (32). Heptad repeats suggest a common α-helical design in the axial proteins. In the filament, a set of 11 rod-like densities formed a central cylinder or tube. The 1.1-nm interrod spacing is consistent with an α-domain (16, 17). The hook and rod also have a similar tube-shaped domain. The presence of these rod-like features (Fig. 1c) supports the hypothesis that all of the axial proteins of the flagellum share this structural motif.

The 11 rod-like densities in the hook, however, are more tilted with respect to the helical axis than those in the filament. In both structures, however, these rods lie along the n =–11 lattice lines (the direction of the protofilaments in the filament). The rod-like densities in the hook are about 2.5 nm in length, compared with 3.5 nm in the filament (17). Flagellin has an additional N-terminal 26 aa preceding the region homologous to the hook (32); the increased length of the N-terminal sequences might account for part of this discrepancy. The N- and C-terminal segments of hook protein, if extended from the N and C termini of the FlgE fragment toward domain D0, are likely to lie close to one another and face in toward the axis of the hook. As such, these segments are well positioned to form a coiled-coil domain like that found in the filament (6).

The reconstruction of the hook confirmed that the central channel in the hook has about the same diameter as that found in comparable maps of the filament. If, as hypothesized, hook assembly proceeds by export of subunits through the channel, can a hook subunit fit? The diameter of the channel is too small for a fully folded hook subunit to pass through, so the subunit must be unfolded, at least partially. These unfolded hook subunits would attain their final, folded conformation upon deposition at the growing tip, capped by FlgD (33), in the same way that flagellin is exported and refolded at the growing end of the filament, capped by FliD (34).