A Kinetic Signature for Parallel Pathways: Conformational Selection and Induced Fit. Links and Disconnects between Observed Relaxation Rates and Fractional Equilibrium Flux under Pseudo-First-Order Conditions

Abstract

Molecular association plays a ubiquitous role in biochemistry and is often accompanied by conformational exchange in one or both binding partners. Traditionally, two limiting mechanisms are considered for the association of two molecules. In a conformational selection (CS) mechanism, a ligand preferentially binds to a subset of conformations in its binding partner. In contrast, an induced fit (IF) mechanism describes the ligand-dependent isomerization of the binding partner in which binding occurs prior to conformational exchange. Measurements of the ligand concentration dependence of observed rates of relaxation are commonly used to probe whether CS or IF is taking place. Here we consider a four-state thermodynamic cycle subject to detailed balance and demonstrate the existence of a relatively unexplored class of kinetic signatures where an initial decrease in the observed rate is followed by a subsequent increase under pseudo-first-order conditions. We elucidate regions of rate space necessary to generate a nonmonotonic observed rate and show that, under certain conditions, the position of the minimum of the observed rate correlates with a transition in equilibrium flux between CS and IF pathways. Furthermore, we demonstrate that monotonic trends in the observed rate can occur when both CS and IF mechanisms are taking place, suggesting that caution must be taken not to overinterpret monotonic trends as evidence of the absence of either CS or IF. Lastly, we conclude that a nonmonotonic kinetic signature is uniquely unambiguous in the sense that when this trend is observed, one may conclude that both CS and IF mechanistic paths are utilized.

Graphical abstract

Macromolecular association underlies the reactions that create life and allow organisms to enact complicated developmental and metabolic programs, to sense and react to their environment, and to maintain the integrity of their genomic material. Examples are widespread and include the binding of oxygen to hemoglobin, the interaction of small molecules with cell surface receptors, the binding of metabolic intermediates to processing enzymes, the recruitment of RNA polymerases to their promoter sequences, and the binding of DNA repair factors to damaged base pairs or double-stranded breaks. The simple model of lock and key binding postulates that both binding partners exhibit single conformations that are negative images of each other, leading to a natural affinity.¹ However, in the most general case, molecules are dynamic and exist in multiple inter-converting conformations. Thus, one may pose the classic question about the mechanism of binding, as originally tackled by Monod, Wyman, and Changeux,² Koshland, Nemethy, and Filmer,^3,4 Eigen,⁵ and many others. More specifically, do particular conformations promote binding, or does binding promote the formation of specific conformations? Put another way, which happens first, binding or conformational change? The question of binding mechanism is often presented as a choice between two extreme cases: conformational selection (CS) or induced fit (IF).^6,7

Conformational selection describes preferential binding to, and stabilization of, a subset of molecular states that are populated in the absence of the ligand. Induced fit describes a conformational change that is produced after ligand binding. To examine this question experimentally, kinetic studies must be performed because the essence of the question lies in the order of events. These experiments typically perturb the equilibrium of an ensemble of molecules and measure the rates of relaxation of the system to a new equilibrium.⁸ These observed rates arise from combinations of microscopic rate constants dictated by the topology of the kinetic mechanism. Thus, the manner in which the observed rates change as a function of experimental variables can be used to test hypothetical molecular mechanisms. However, the interpretation of trends in observed rates can be model-dependent and does not always allow a clear conclusion to be drawn.⁹ For example, while a monotonically decreasing trend as a function of ligand concentration under pseudo-first-order conditions serves as a clear signal of conformational selection, a monotonically increasing trend does not allow one to unambiguously conclude whether an induced fit or conformational selection mechanism is at work.^7,10,11 In this case, additional experiments are required to distinguish between the two mechanisms by performing a titration of the binding partner in the presence of high ligand concentrations.^10,11

This study was motivated by our observation of a nonmonotonic observed rate in recent work on the stabilization of transcription initiation open complexes by the essential Mycobacterium tuberculosis transcription factor, CarD.¹² By monitoring open complex with a fluorescent reporter, we showed that as a function of increasing CarD concentration, the slowest observed rate during the approach to equilibrium of this system initially decreases but then reaches a minimum and begins to increase hyperbolically. Other examples of nonmonotonic observed rates as a function of ligand concentration have previously been reported for binding of single-stranded DNA (ssDNA) to single-stranded binding protein, binding of substrate to indole ligase¹⁴ and glucokinase,¹⁵ and binding of an effector to phosphoglycerate dehydrogenase.¹⁶ As described in each of these examples, the trend in observed rates can be captured in the context of a cyclic four-state kinetic model.

We consider this relatively unexplored class of ligand dependence and delineate the kinetic and thermodynamic properties required for nonmonotonicity. Previous work has shown that either conformational selection or induced fit can produce a nonmonotonic observed rate under non-pseudo-first-order conditions.^17,18 Here, we focus on pseudo-first-order conditions using a four-state thermodynamic cycle subject to detailed balance and show that a nonmonotonic observed rate indicates a transition in the mechanism of binding. This shift between conformational selection and induced fit has recently been experimentally and theoretically described by several groups;^14,19–25 however, a nonmonotonic observed rate has yet to be explored as a general kinetic signature for a pathway switch. Here we expand the analysis of the observed rates of a mixed mechanism system by deriving the observed rate dependence directly from the eigenvalues of a rate matrix that satisfies detail balance. In addition, we explore the dependence of the nonmonotonicity on the values of the microscopic rate constants. We define regions of rate space in which one may expect a nonmonotonic observed rate, and we highlight the importance of performing well-spaced titration experiments over a range of conditions and concentrations to maximize the probability of observing this behavior in real experimental systems. We also demonstrate that a wide range of qualitatively distinct trends in the observed rate can be generated by systems with identical ligand-dependent fractional fluxes. We stress that one must be cautious in interpreting monotonically increasing or decreasing observed rates as kinetic signatures that exclude a particular pathway, as these signatures can arise from kinetic models that include both mechanisms. We suggest that the nonmonotonic kinetic signature is the only unambiguous kinetic signature and allows one to conclude that both CS and IF mechanisms are being utilized and, more specifically, that a transition in mechanism from CS to IF occurs as a function of ligand concentration.

RESULTS AND DISCUSSION

A Nonmonotonic Observed Rate (Eigenvalue) Is a Kinetic Signature for a Pathway Switch

We constructed a four-state thermodynamic cycle linking the unimolecular conformational isomerization of a molecule, A (A ↔ A* and AL ↔ A*L), with the binding of a ligand, L (A ↔ AL and A* ↔ A*L) (Figure 1A). Within this scheme, a conformational selection mechanism for ligand binding is represented by the pathway of states (A ↔ A* ↔ A*L) and induced fit is captured by the A ↔ AL ↔ A*L pathway. Transitions between all sets of states are reversible, and the defined rates are labeled by the direction of the transition [i.e., the rate of the transition from state 1 to state 2 (A → A*) is given by k₁₂, while the reverse rate of transition from state 2 to state 1 (A* → A) is given by k₂₁]. The ligand dissociation rates and unimolecular isomerization rates are concentration-independent. The on-rates of ligand binding that naturally depend on ligand concentration are treated as pseudo-first-order as we assume that the concentration of A is significantly lower than that of L (non-pseudo-first-order conditions are considered toward the end of this section). Importantly, we require our system to satisfy detailed balance so that k₁₂k₂₃k₃₄k₄₁ = k₂₁k₁₄k₄₃k₃₂ and the laws of thermodynamics are not violated. Lastly, while we arbitrarily choose A*L to be the most stable state, this choice simply fixes the directionality of the scheme and does not affect the generality of the analysis. All calculations were performed using MATLAB.

Figure 1.

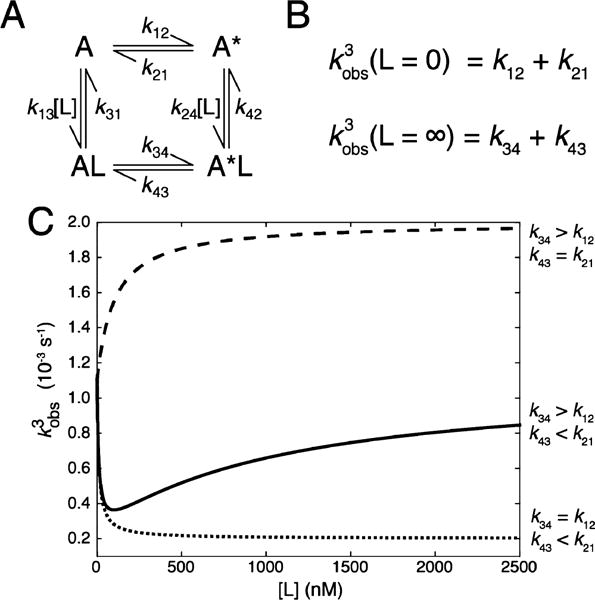
Third observed rate of a thermodynamic cycle. (A) Four states representing ligand-unbound (A and A*) and ligand-bound (AL and A*L) conformers are linked by rate constants, where k_ij represents the rate of going from state i to state j. Ligand on-rates are dependent on ligand concentration, while ligand off-rates and the rates of conformational exchange are first-order. (B) Third observed rate (k_obs,3) for the system in the limits of zero and infinite ligand concentrations. (C) Dependence of the third observed rate (k_obs,3)on ligand concentration for three sets of rates where the rates of conformational switching are slower than the rates of binding: (1) where the rate of isomerization to A* increases upon ligand binding (---), (2) where the rate of isomerization to A decreases upon ligand binding (⋯), and (3) where the rate of isomerization to A* increases and the rate of isomerization to A decreases upon ligand binding (—).

This system has three non-zero eigenvalues corresponding to three non-zero observed rates. Under pseudo-first-order conditions, two eigenvalues describe the relaxation of ligand binding to A and A* and increase linearly with ligand concentration. The third eigenvalue (i.e., observed rate) is a complex function of all the rates (Supporting Information) but in the limits of zero and infinite ligand concentrations is simply the sum of the rates of conformational exchange in the unbound and bound states, respectively⁹ (Figure 1B). The full ligand concentration dependence can be calculated either numerically or analytically and can exhibit a variety of dependencies on ligand concentration when isomerization is much slower than dissociation (Figure 1C and the Supporting Information). For example, if the A*L → AL transition (k₄₃)is slower than the A* → A transition (k₂₁) and the forward rates do not change upon ligand binding, one can observe a hyperbolically decreasing third observed rate. Alternately, if the AL → A*L transition (k₃₄) is faster than the A → A* transition (k₁₂) and the reverse rates do not change upon ligand binding, one observes a hyperbolically increasing third observed rate. However, if upon ligand binding the forward rate increases (k₃₄/k₁₂ > 1) and the reverse rate decreases (k₄₃/k₂₁ < 1), one may observe a nonmonotonic dependence of k_obs,3 on ligand concentration (Figure 1C, solid line).

To better understand how a nonmonotonic curve depends on the parameters of the four-state model, we produced series of plots in which pairs of rate constants were varied by the same factor to maintain detailed balance. The starting point for this analysis uses the following set of rate constants: k₁₂ = 10⁻⁴ s⁻¹, k₂₁ = 10⁻³ s⁻¹, k₁₃ = k₂₄ = 10⁸ M⁻¹s⁻¹, k₃₁ = 100 s⁻¹, k₄₂ =1 s⁻¹, k₃₄ =10⁻³ s⁻¹, and k₄₃ = 10⁻⁴ s⁻¹. First, we considered how the observed rate would depend on the affinities of the ligand for each conformational state. By multiplying the rates of dissociation of the ligand from both A and A* by factors between 0.125 and 8, we produced a family of curves where the absolute affinities of the ligand for A and A* vary but the relative affinities of the ligand for A and A* remain fixed (Figure 2A). When these curves are plotted on a logarithmic x-axis, the effect can clearly be observed (Figure 2B). Each factor of 2 in the off-rates leads to a shift in the minimum of the curve by a factor of exactly 2. To explore this dependence further, we used a zero-finding algorithm (MATLAB) and the expression for the derivative of the third eigenvalue (Supporting Information) to determine the position of the minimum. The relative position of the minimum depends hyperbolically on the on-rates and linearly on the off-rates as would be expected for an affinity as K_d = k_off/k_on (Figure 2C). This demonstrates how the inflection point between the initial decrease and subsequent increase in the observed rate depends on the affinities of the ligand for each conformational state of its binding partner. In contrast, the position of the minimum does not sensitively depend on the magnitude of the binding and dissociation rate constants as long as binding remains faster than conformational switching (i.e., a rapid equilibrium assumption¹⁴) and the ratio of off- to on-rates (i.e., the affinity) is preserved (Supplemental Figure 1). This can be contrasted with changes in the rates of isomerization that preserve the equilibrium between A and A* or AL and AL* but also change the shape of the observed rate curves (Supplemental Figure 2).

Figure 2.

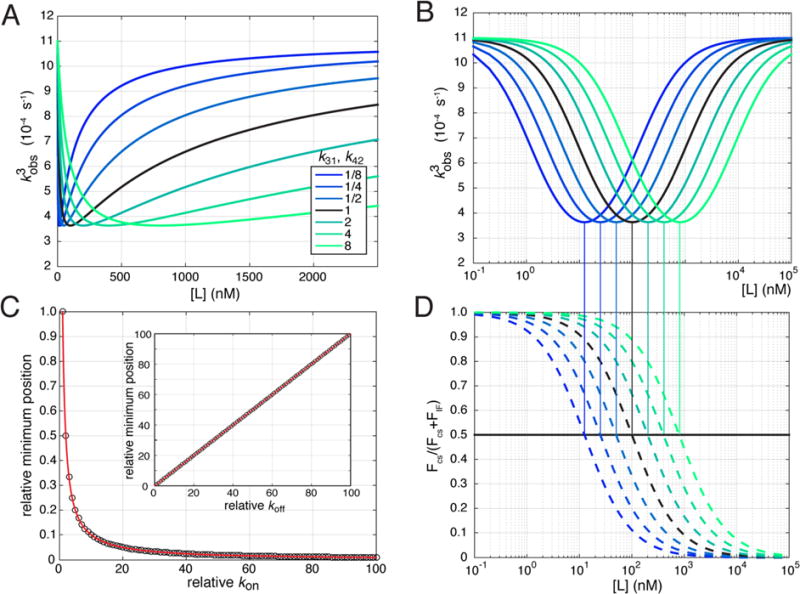
Single eigenvalue that describes a nonmonotonic third observed rate. (A) Third eigenvalue or observed rate (k_obs,3) as a function of ligand concentration. The family of curves contains the original rate set described in the text (black) and rate sets where both the ligand dissociation rates have been increased (green) or decreased (blue) according to the factors in the legend. (B) Same as panel A plotted on a logarithmic concentration scale. (C) Minimum position relative to the original rate set as described in the text as a function of either the relative ligand on-rates (k₁₃ and k₂₄)or the relative ligand off-rates (inset, k₃₁ and k₄₂). (D) Fractional flux [F_CS/(F_CS + F_if)] through the conformational selection arm of the cycle plotted as a function of ligand concentration for the rate sets plotted in panels A and B. The vertical lines connecting panels B and D indicate the coincidence of the ligand concentrations of 50% fractional flux and the position of the minima in panel B.

By calculating the equilibrium flux through the conformational selection (CS) mechanism (A → A* → A*L) and the induced fit (IF) mechanism (A → AL → A*L), Hammes et al.¹⁹ elegantly showed that the dominant mechanism depends on ligand concentration. In particular, while CS dominates at low ligand concentrations, IF dominates at high ligand concentrations. In analogy, we hypothesized that a minimum in the observed rate reveals a ligand concentration where the mechanism is undergoing a transition between CS and IF mechanisms. To test this hypothesis, we calculated the fractional equilibrium flux for the conformational selective mechanism [F_CS/(F_CS + F_IF)] as a function of ligand concentration for the rate sets used above¹⁹ (Figure 2D and Supplemental Methods). As predicted, the ligand concentrations at which the fractional flux equals 50% coincide with the ligand concentration of the minima (Figure 2B,D and Supplemental Figure 3). Importantly, the exact correspondence between 50% flux and the minimum observed rate does not hold generally and is true for only a symmetric cycle where the forward and reverse rates interchange in the bound state (i.e., the forward rate in the unbound state equals the reverse rate in the bound state and vice versa, or k₁₂ = k₄₃ and k₂₁ = k₃₄). Nonetheless, this illustrates that the appearance of a minimum observed rate in this system is indicative of mixed CS and IF mechanisms, even if they are not in equal flux. This observation provides a link between the existence and position of a minimum in the third observed rate with the equilibrium fluxes through the cycle.

Mechanisms That Generate the Same Equilibrium Fractional Flux Can Result in Qualitatively Different Kinetic Signatures

We stress that the link between the minimum observed rate and 50% flux does not exist in general. A transition in flux between CS and IF does not always reveal itself in the trends of the third observed rate. In particular, while a decreasing observed rate is correctly taken as evidence of a conformational selective mechanism, it does not exclude the possibility that an IF mechanism is also taking place. In fact, depending on the values of the forward and reverse isomerization rates, the behavior of the observed rate as a function of ligand concentration can be hyperbolically increasing, hyperbolically decreasing, or nonmonotonic all while preserving an identical flux dependence (Figure 3). These results can be taken as a demonstration that the same equilibrium flux may result in qualitatively distinct trends in observed rates.

Figure 3.

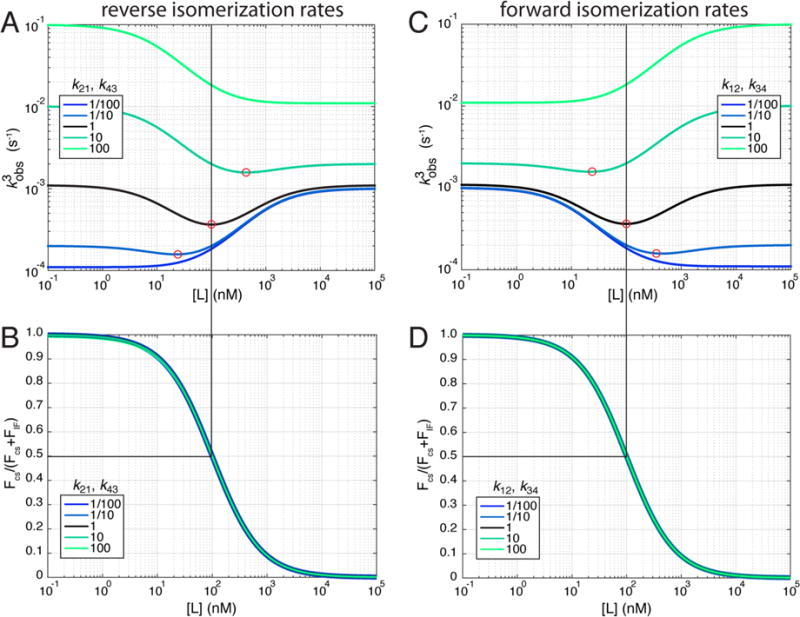
Third observed rate and fractional flux as a function of ligand concentration for different isomerization rates. (A) The reverse isomerization rates (k₂₁ and k₄₃) from the original rate set (black) were increased (green) or decreased (blue) by the factors indicated in the legend. Red circles indicate the approximate positions of the minimum observed rate for each curve. (B) Equilibrium fractional flux through the conformational selection pathway as a function of ligand concentration for the rate sets in panel A. (C) The forward isomerization rates (k₁₂ and k₃₄) from the original rate set (black) were increased (green) or decreased (blue) by the factors indicated in the legend. Red circles indicate the approximate positions of the minimum observed rate for each curve. (D) Equilibrium fractional flux through the conformational selection pathway as a function of ligand concentration for the rate sets in panel B.

As shown in Figure 2, if a minimum exists with a given set of rates, changing the absolute affinities for A and A* maintains the existence of the minimum, albeit in a shifted position. However, when the absolute values of the forward and reverse isomerization rates in the presence and absence of a ligand are varied, different trends emerge. For example, increasing the magnitude of both reverse rates (k₂₁ and k₄₃) 100-fold leads to the complete disappearance of a minimum. This can be seen in the curve itself (Figure 3A, green) and in the lack of a zero in the derivative (Supplemental Figure 4A). With these parameters, the eigenvalue decreases as a function of ligand concentration, which would be interpreted as indicative of conformational selection. However, the equilibrium fractional flux shows a transition between conformational selection and induced fit, just as is observed with the system that exhibits a minimum in the observed rate. Similarly, decreasing the magnitude of the reverse rates 100-fold also leads to the disappearance of a minimum. Again, this can be seen in the curve itself (Figure 3A, blue) and by the lack of a zero in the derivative (Supplemental Figure 4A). In this case, the eigenvalue now increases as a function of ligand concentration, but the fractional flux behaves in a manner identical to that of the other curves. Importantly, while the increasing curves completely lack minima, the apparently decreasing curves can possess minima at higher ligand concentrations. Thus, the cutoff at which decreasing curves have minima can be arbitrary and dependent on the maximum concentration tested (Supplemental Figure 4).

The same exercise performed with the forward isomerization rates (k₁₂ and k₃₄) leads to similar results (Figure 3C,D). Specifically, changing the magnitude of both forward rates by the same factor can eliminate the minimum. In this case, the dependency is the opposite of that of the reverse rates as one might expect. Increasing the magnitude of the forward rates by 100-fold results in an eigenvalue that only increases with ligand concentration (Figure 3C, green), and decreasing the magnitudes by 100-fold results in an eigenvalue that only decreases with ligand concentration (Figure 3C, blue). As before, while the observed rate trends vary dramatically, the fractional flux plots remain constant, illustrating that a variety of kinetic trends can be generated by a single flux-defined mechanism. In fact, 12 of the 28 possible pairs of rate constants that may be varied together to preserve detailed balance do not change the fractional flux as a function of ligand concentration when varied in the context of our initial rate set (Supplemental Figure 5). These results demonstrate that monotonic trends in observed rates can easily result from mechanisms in which both pathways are used and therefore cannot be used as evidence to exclude conformational selection or induced fit. This highlights the importance of considering the cycle as a potential mechanism. We conclude that a nonmonotonic trend in observed rate is a uniquely unambiguous kinetic signature in the sense that it only results from a mixed CS—IF mechanism.

Non-Pseudo-First-Order Conditions Also Produce Nonmonotonic Eigenvalues

The analyses described above have all been calculated assuming pseudo-first-order conditions. Specifically, the concentration of ligand was assumed to be much higher than the concentration of A, and curves were calculated via the matrix eigenvalue method. Under this assumption, the concentration of free ligand is essentially constant ([L]_free ≃ [L]_tot), and thus, binding on-rates are constant over time. However, in the most general case, this need not be true. Interestingly, it has been shown that even in the absence of the thermodynamic cycle, non-pseudo-first-order conditions may lead to nonmonotonic observed rates for three-state models of conformational selection or induced fit in isolation.^17,18 In fact, even a simple one-step (two-state) binding reaction can produce a nonmonotonic observed rate if studied in the range of [L]_tot near L_o = [A]_tot — K_d while [L]_tot varies from concentrations greater than L_o that are pseudo-first-order to concentrations less than L_o that are non-pseudo-first-order (see eq 7a in ref 26) (A. Kozlov and T. Lohman, personal communication).

We wanted to see how the nonmonotonic observed rates generated by the four-state thermodynamic cycle under pseudo-first-order conditions change when this assumption is not valid. Because the matrix eigenvalue formalism cannot be applied in this case, we performed simulations of the rate equations and updated the free ligand concentration (and thus the effective binding rate) after each time step. The effective observed rate for a given total ligand or total A concentration was estimated by fitting the simulated relaxation curves with a single exponential. Although in general, non-pseudo-first-order conditions lead to nonexponential relaxation curves, a single-exponential fit captured the observed kinetics (Supplemental Figure 6).

Using the rates of our original model system, when the [L]_tot concentration is being titrated, the minimum is most pronounced under conditions approaching pseudo-first-order. As the concentration of A increases, the minimum moves to higher concentrations of L and becomes less pronounced (Figure 4A). Interestingly, when [A]_tot is being titrated, a minimum can also be observed, but only at relatively high concentrations of ligand (Figure 4B). Therefore, depending on the actual rates of a given system and the concentration ranges used in the experiments, a nonmonotonic observed rate may be more or less likely to be observed. This analysis highlights the need to perform titrations over a range of concentrations of both binding partners to maximize the probability of observing a nonmonotonic observed rate. However, we stress that the observation of nonmonotonicity per se does not allow one to conclude that a mechanistic transition is occurring unless it is observed under pseudo-first-order conditions where the ligand is in significant excess of the macromolecule undergoing conformational exchange.

Figure 4.

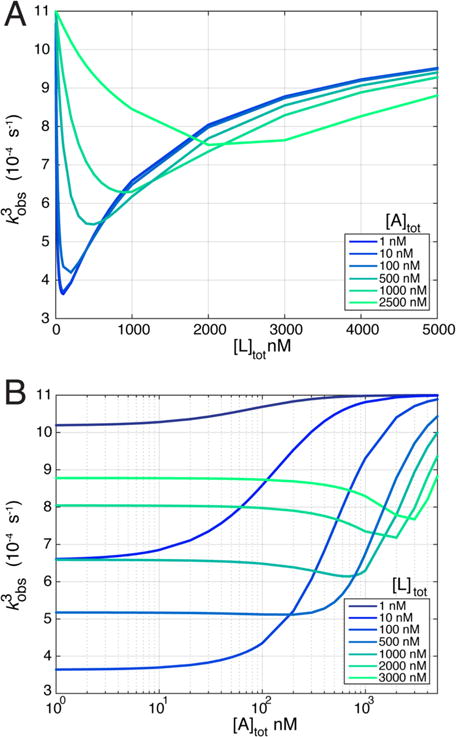
Non-pseudo-first-order conditions. The free ligand concentration was tracked during simulations, and relaxation curves were fit with single exponentials to estimate an observed rate for non-pseudo-first-order conditions. (A) Observed rate as a function of total ligand concentration with different concentrations of binding partner, A (shown in the legend). (B) Observed rate as a function of total A concentration in the presence of different concentrations of total internal ligand, L (shown in the legend).

Kinetic Requirements for Nonmonotonicity

To identify constraints on the combinations of rates that lead to nonmonotonic observed rates, we randomly chose rate constants log-distributed within a range of 3 orders of magnitude from their starting model values that satisfied detailed balance. The presence of a nonmonotonic observed rate was assessed by searching for a zero in the derivative of the third observed rate as a function of concentration (Supporting Information). Sets were scored as either always increasing or always decreasing when the derivatives were always positive or always negative, respectively. The rate sets were plotted using the ratio of forward rates in the presence and absence of ligand and the ratio of reverse rates in the presence and absence of ligand as y- and x-axes, respectively (Figure 5). Each point represents one rate set and is color-coded according to whether the set displays a nonmonotonic trend (blue), is monotonically increasing (green), or is monotonically decreasing (red) as a function of ligand concentration. The black horizontal and vertical lines represent ratios of 1 and thus delineate where the rate constant for that axis is identical in the presence and absence of ligand. For example, points to the left of the vertical line have k₄₃ < k₂₁ and points above the horizontal line have k₃₄ > k₁₂. The diagonal dashed lines represent a constant ΔΔG between the A ↔ A* and AL ↔ A*L equilibria. Only rate sets that stabilized A*L were considered, resulting in a restriction of rate space above the dashed line through (1,1) representing a ΔΔG of 0 (i.e., no relative stabilization of A*L). The dark gray and light gray dashed diagonal lines represent contours of equal relative stability of A*L versus A* with ΔΔG = RT ln(10²) = 2.7 kcal/mol and ΔΔG = RT ln(10⁴) = 5.5 kcal/mol, respectively.

Figure 5.

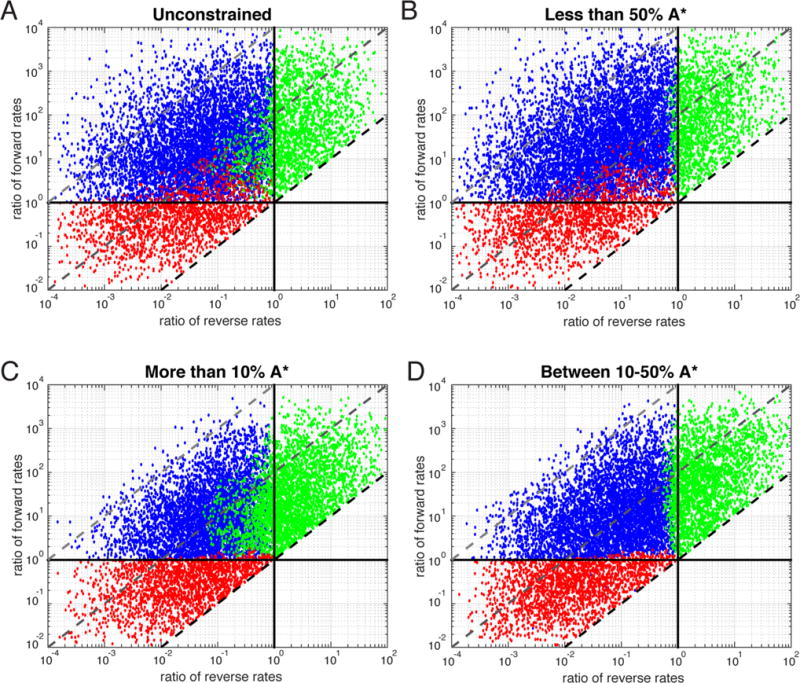
Exploration of rate space. Random sets of rates satisfying detailed balance were selected. Each rate was picked from a log-random distribution centered on the original rate set and covering 3 orders of magnitude. Each rate set is represented as a single point on the graphs where the x-axis is the ratio of the reverse rates in the presence and absence of ligand (k₄₃/k₂₁) and the y-axis is the ratio of the forward rates in the presence and absence of ligand (k₃₄/k₁₂). The vertical and solid horizontal lines represent ratios of 1 for the reverse and forward rates, respectively. The dashed diagonal lines represent contours of constant ΔΔG or degrees of stabilization of A*L. The conformational equilibrium (A ↔ A*) was subject to the following constraints: (A) unconstrained, (B) <50% A*, (C) >10% A*, and (D) between 10 and 50% A*. The distribution is subdivided into rate sets that exhibit a nonmonotonic (blue), decreasing (red), and increasing (green) third observed rate.

The top left quadrant of these plots is dominated by rate sets in which a minimum can be detected in the third observed rate as a function of ligand concentration (Figure 5A). In fact, the reduction of the reverse rate and the increase in the forward rate in the presence of ligand appear to be necessary for a minimum to exist as there are no blue rate sets in other regions of the plot. In contrast, if both forward and reverse rates are decreased in the presence of ligand (the bottom left quadrant), this eigenvalue only decreases as a function of ligand concentration (red), and if both rates increase (top right quadrant), the eigenvalue only increases as a function of ligand concentration (green). We stress that the rates of conformational exchange must be slower than the rates of binding for either nonmonotonic (blue) or decreasing monotonic (red) to be observed at all. When the forward rate of conformational isomerization (k₁₂) is significantly faster than the off-rate of binding to A* (k₄₂), all random sets generated show monotonically increasing observed rates regardless of the ratios of the forward and reverse rates (Supplemental Figure 7). This is consistent with the fact that conformational selection mechanisms result in observed rates that increase as a function of ligand concentration when k₁₂ > k₄₂.^7,10

However, some rate sets with only increasing eigenvalues (green) can be observed in the top left quadrant with the sets that produce minima (blue). These sets can be minimized by only considering rate sets that, at equilibrium, produce no more than 50% A* in the absence of ligand (Figure 5B). Furthermore, some sets with only decreasing eigenvalues (red) can be observed in the top left quadrant commingling with the sets that produce nonmonotonicity (blue). These sets can be minimized by considering only rate sets that produce at least 10% A* in the absence of ligand (Figure 5C). The combination of these requirements results in a relatively sharp distinction among the regions of rate space that lead to the three distinct behaviors (Figure 5D).

Overall, irrespective of the initial A ↔ A* equilibrium, as the ΔΔG between A ↔ A* and AL ↔ A*L equilibria increases (i.e., A*L becomes more stabilized), the presence of both a decrease in reverse rates and an increase in forward rates becomes more predictive of the presence of a minimum. This can be seen by the reduced presence of red and green sets past the dark dashed lines (ΔΔG = 2.7 kcal/mol) and the complete lack of red and green sets beyond the light dashed lines (ΔΔG = 5.5 kcal/mol) (Figure 5A).

As constraining the equilibrium between A and A* influenced the presence of rate sets that generate monotonic observed rates (Figure 5D), we replotted the rate sets using an axis that represented the fractional occupancy of A* relative to that of A. When the data are visualized using [A*]/([A] + [A*]), or equivalently k₁₂/(k₁₂ + k₂₁), as the y-axis, there exists a clear separation of monotonically increasing (green) and nonmonotonic (blue) sets (Figure 6A). As the relative stability of A* increases, more monotonically increasing rate sets can be observed invading the region of rate space necessary for a nonmonotonic trend. Analogously, as the relative stability of A* decreases, more monotonically decreasing rate sets can be observed in the same region (Figure 6B). In this case, the separation between regions of the rate space occupied by the two qualitative types of observed rate trends is not as obvious, but a three-dimensional representation that includes the ratio of reverse rates as a third axis clearly shows separation of the monotonic (red) and nonmonotonic (blue) sets (Supplementary Figure 8).

Figure 6.

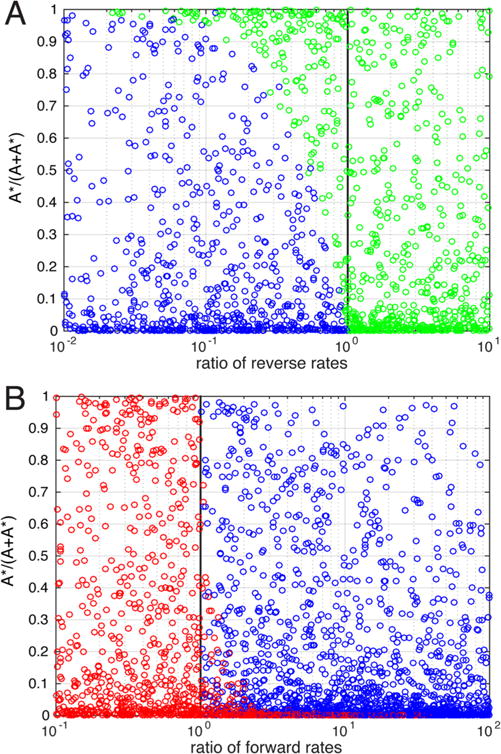
Effect of initial stability on observed rate trends. Rate sets are plotted as in Figure 5 using the fractional occupancy of A* with no ligand present and (A) the ratio of the reverse rates or (B) the ratio of the forward rates.

The relationship between the A ↔ A* equilibrium and the observation of monotonically increasing or decreasing observed rates in the region of rate space dominated by nonmonotonic-generating sets may appear counterintuitive. One might have expected that limiting the concentration of A* would push the system toward an induced fit mechanism that would result in monotonically increasing observed rates. Instead, a low A* concentration actually promotes the observation of monotonically decreasing observed rates (Figures 5A,C and 6B). Along the same lines, one might have expected that limiting the concentration of A would push the system toward conformational selection, which would result in monotonically decreasing observed rates. Instead, a low A concentration promotes the observation of monotonically increasing observed rates (Figures 5A,B and 6A). These results further stress the potential disconnect between the behavior of the observed rates of relaxation and the equilibrium flux through different pathways in a kinetic mechanism.

CONCLUSIONS

We have described the existence of a unique kinetic signature within the context of a four-state thermodynamic cycle describing ligand binding, specifically, a nonmonotonic trend in the third observed rate. This behavior is captured in the third eigenvalue of the rate matrix and naturally depends on all the microscopic rate constants of the system. Theoretically, this study adds to the richness of possible behaviors of a relatively simple kinetic mechanism that can be used to describe the fundamental molecular interactions that underlie biological function. We have explored the dependence of the minimum position and existence on multiple rate constants and have shown that the minimum position in ligand concentration depends on the affinities of the ligand for each of the two conformations of its binding partner. Furthermore, when certain pairs of rate constants are titrated, the minimum can be made to vanish, leading to the well-known increasing or decreasing trends in the observed rate. However, 12 of the possible 28 pairs of rates that can be covaried in the context of detailed balance conserve the fractional flux through the conformational selection and induced fit pathways (Supprlemental Figure 5). Thus, while the observation of a minimum under pseudo-first-order conditions can be taken as evidence of a ligand-dependent pathway switch (and, therefore, the existence of the induced fit mechanism), the absence of a minimum cannot alone be used to exclude this mechanism. More specifically, while the observation of a decreasing third observed rate is correctly taken as evidence of the presence of a conformational selection pathway, it should not be interpreted as proof of the lack of an induced fit path. This is especially important as the kinetically unobserved induced fit path may carry the bulk of the equilibrium flux under conditions of relatively high ligand concentrations (Figure 4).

Interestingly, an even simpler kinetic model consisting of a cycle of three states with two ligand-dependent rates may also generate nonmonotonic observed rates with minima (Supplementarl Figure 9). This model captures what Koshland and colleagues described as induced fit where association and conformational change occur concomitantly in a single kinetic step.^3,4,27 Conveniently, the three-state and four-state cyclic models may be distinguished from each other under conditions of high ligand concentrations. The observed rate increases linearly at high ligand concentrations in the three-state model (Supplemental Figure 9) and saturates at high ligand concentrations in the four-state model (Figures 1–3).

The question of why a nonmonotonic trend is not often reported in the literature is an interesting one. Whether the requirements for the presence of a readily observable minimum are rarely present in real systems or whether experimental titrations are too sparse or not performed in the appropriate concentration ranges remains to be seen. Practically, to increase the probability of observing a minimum in a real system, one should perform titrations of both binding partners over different concentration ranges. Regardless, the observation of the nonmonotonic trend is a powerful constraint for determining the mechanism of ligand binding. In particular, its observation indicates that both mechanistic extremes are contributing to binding and that there exists a relative balance between conformational selection and induced fit pathways.

ABBREVIATIONS

CS

conformational selection

IF

induced fit