Bayesian regression models outperform partial least squares methods for predicting milk components and technological properties using infrared spectral data

Abstract

The aim of this study was to assess the performance of Bayesian models commonly used for genomic selection to predict “difficult-to-predict” dairy traits, such as milk fatty acid (FA) expressed as percentage of total fatty acids, and technological properties, such as fresh cheese yield and protein recovery, using Fourier-transform infrared (FTIR) spectral data. Our main hypothesis was that Bayesian models that can estimate shrinkage and perform variable selection may improve our ability to predict FA traits and technological traits above and beyond what can be achieved using the current calibration models (e.g., partial least squares, PLS). To this end, we assessed a series of Bayesian methods and compared their prediction performance with that of PLS. The comparison between models was done using the same sets of data (i.e., same samples, same variability, same spectral treatment) for each trait. Data consisted of 1,264 individual milk samples collected from Brown Swiss cows for which gas chromatographic FA composition, milk coagulation properties, and cheese-yield traits were available. For each sample, 2 spectra in the infrared region from 5,011 to 925 cm⁻¹ were available and averaged before data analysis. Three Bayesian models: Bayesian ridge regression (Bayes RR), Bayes A, and Bayes B, and 2 reference models: PLS and modified PLS (MPLS) procedures, were used to calibrate equations for each of the traits. The Bayesian models used were implemented in the R package BGLR (http://cran.r-project.org/web/packages/BGLR/index.html), whereas the PLS and MPLS were those implemented in the WinISI II software (Infrasoft International LLC, State College, PA). Prediction accuracy was estimated for each trait and model using 25 replicates of a training-testing validation procedure. Compared with PLS, which is currently the most widely used calibration method, MPLS and the 3 Bayesian methods showed significantly greater prediction accuracy. Accuracy increased in moving from calibration to external validation methods, and in moving from PLS and MPLS to Bayesian methods, particularly Bayes A and Bayes B. The maximum R² value of validation was obtained with Bayes B and Bayes A. For the FA, C10:0 (% of each FA on total FA basis) had the highest R² (0.75, achieved with Bayes A and Bayes B), and among the technological traits, fresh cheese yield R² of 0.82 (achieved with Bayes B). These 2 methods have proven to be useful instruments in shrinking and selecting very informative wavelengths and inferring the structure and functions of the analyzed traits. We conclude that Bayesian models are powerful tools for deriving calibration equations, and, importantly, these equations can be easily developed using existing open-source software. As part of our study, we provide scripts based on the open source R software BGLR, which can be used to train customized prediction equations for other traits or populations.

INTRODUCTION

Infrared spectroscopy (IRS) is based on using different waves of the infrared region of the electromagnetic spectrum to excite molecules in relation to their rotational-vibrational structure (Karoui et al., 2010). The infrared spectrum of a sample is recorded after passing a beam of infrared light through it. When the frequency of the infrared wave is the same as the vibrational frequency of a chemical bond, absorption occurs; the spectrum therefore reflects the quantities and proportions of the various chemical bonds within the sample and hence its composition.

Infrared spectroscopy is often used to predict the chemical composition of food and feed (Karoui et al., 2010), but it is a secondary method needing prior calibration based on a training data set and validation based on a different data set, both obtained using samples analyzed according to reference methods. The Fourier-transform infrared (FTIR) spectroscopy, which measures transmission of a spectrum consisting of more than 1,000 different waves in the short-wave infrared region (SWIR, or near-infrared), the mid-wave IR (MWIR, or mid-infrared), and the long-wave IR (LWIR), is often used to predict the chemical composition of milk (Barbano and Lynch, 2006; Karoui and Baerdemaeker, 2007). Fourier-transform infrared spectroscopy has important advantages compared with traditional laboratory-based analysis techniques. Some advantages include the low time requirements, inexpensive except for the cost of the apparatus, ability to predict a large number of phenotypes for one sample carrying out only one analysis, ability to predict new phenotypes from stored spectra when a new prediction equation becomes available, and the feasibility of obtaining individual phenotypes for selection. In addition, FTIR spectroscopy is an accurate tool for predicting major milk component contents and is used internationally for the analysis of the fat, protein, casein, and lactose contents of cow milk from routine recording samples (ICAR, 2012). The prediction of milk components and technological traits (especially those that are difficult to analyze) is of particular interest in many areas, including milk payment systems, assessing technological properties of milk by the dairy industry, and direct (in relation to human health) or indirect (animal welfare, reproduction, methane production) prediction of some traits through milk FA content. All of these traits could be used in selection programs.

In recent years, several studies have used FTIR spectroscopy to predict the FA content of milk (Soyeurt et al., 2006; De Marchi et al., 2011). The FA show different prediction accuracy based on, for example, the amount of the individual FA in milk and the way of expressing that amount (on a milk or milkfat basis); for these reasons, these traits are considered to be difficult to predict and the level of accuracy is lower than when predicting major milk components (e.g., protein or fat). In part, this is because FA make up a smaller fraction of milk and many compounds with similar chemical composition are present (Stefanov et al., 2013; De Marchi et al., 2014). Calibration FTIR is even more difficult if an FA profile (i.e., each FA as a proportion of the sum of all FA) is to be predicted. Few studies have attempted to predict the FA profile of milk fat using FTIR spectroscopy, and the results are less accurate than those for the total FA content of milk (Soyeurt et al., 2006; Rutten et al., 2009).

Infrared spectroscopy technology is not very precise when used to predict the technological properties of food that only indirectly depend on the sample’s chemical composition. In the case of milk, FTIR spectroscopy has been used to predict new phenotypes of significant economic interest to the dairy industry, such as milk coagulation properties (MCP; Cecchinato et al., 2009), cheese yield (CY) and curd recovery (REC) or whey loss of milk nutrients (Ferragina et al., 2013).

The IRS prediction of new phenotypes is of particular interest for its potential use in the selection of farm animal populations using existing samples and spectrometers, such as milk recordings for the genetic improvement of milk fat and protein. Several studies have estimated the genetic parameters of infrared-predicted phenotypes, such as FA content (Rutten et al., 2010; Bastin et al., 2011; Cecchinato et al., 2012a), MCP (Bittante et al., 2012), and CY and REC of different nutrients (Cecchinato et al., 2015). Heritability estimates of measured phenotypes are similar to, or lower than, the heritabilities of the predicted traits such as milk technological properties (e.g., RCT; Cecchinato et al., 2009, 2011b; Bittante et al., 2014). In the case of FA profiles, there is a higher variation of heritability estimates (Rutten et al., 2010). Importantly, the estimated genetic correlations between measured and FTIR-predicted values for all traits studied were greater than the phenotypic correlations between the same values. The biological basis of the potential of FTIR spectra for genetic improvement of farm animals lies in the fact that the absorbance of many individual waves (Bittante and Cecchinato, 2013) or their principal components (Soyeurt et al., 2010; Dagnachew et al., 2013) have been proven to be heritable.

The accuracy of predictions obtained with IRS is influenced by many factors, including the trait to be predicted, the quality of the reference data set and the spectra, the number of samples used to develop the prediction equations, and the amount of the analyzed substance in the samples (Rutten et al., 2009; Karoui et al., 2010). A distinction is needed between direct and indirect predictions, and this distinction plays an important role in the prediction accuracy. One trait can be considered directly predicted when it has a significant signal in the spectral data (e.g., protein content); otherwise, in the indirect prediction of one trait, the signal in the spectral data is related to traits having a relationship with the studied trait (e.g., cheese yield), and a greater number of samples in calibration set is needed for high prediction accuracy. A special role, however, is played by mathematical techniques known collectively as chemometrics, including the selection of wavelengths, the pretreatment of spectra data, and the choice of statistical model used to develop the calibration equation. Infrared spectral data are high dimensional and therefore require special modeling techniques, such as dimension reduction regression, shrinkage estimation, and variable selection methods.

Partial least squares regression (PLS), a dimension-reduction method, is the most commonly used technique for developing calibration equations, and principal component analysis is a useful technique to carry out qualitative analysis of spectra and of their information (Tsenkova et al., 2000). Partial least squares regression is implemented in commercial software, such as WinISI (Infrasoft International LLC, State College, PA) or Unscrambler (Camo ASA, Oslo, Norway). These software programs provide multiple user-friendly tools for analyzing spectral data, although few regression models are implemented in them and the user has little control over many of the parameters controlling the algorithm.

Principal component regression and PLS are comparable methods (Luinge et al., 1993); PLS has some important advantages over principal component regression (Soyeurt et al., 2006) and performs well in predicting major milk components. Although the prediction accuracy of both PLS and principal components is much lower for qualitative traits, such as milk FA profiles and technological properties, this highlights the need to develop more efficient chemometric methods to analyze spectral data.

In recent years, important advances have been made in developing penalized and Bayesian models for high-dimensional regressions, and many of these methods have been adopted for regression on high-dimensional genotypes (e.g., genomic selection, Meuwissen et al., 2001). The Bayesian method is extremely flexible in that, with the choice of prior density assigned to marker effects, it allows implementation of models that estimate shrinkage and perform variable selection. Evidence from genomic selection suggests that these Bayesian models may have higher predictive power than dimension-reduction methods (de los Campos et al., 2013). We hypothesize that these methods can help us improve our ability to predict milk properties that are difficult to predict using dimension reduction methods such as PCR and PLS.

Therefore, the main goal of this study was to assess the performance of Bayesian models commonly used for genomic selection in predicting problematic traits, such as milk FA profiles and technological properties, from FTIR spectral data. We assessed the performance of several methods not used before in this context, which perform either shrinkage of variables (e.g. Bayesian ridge regression) or both shrinkage and variable selection (e.g., Bayes B), and compared their performance with that of the current industry standard method based on PLS. We also provide scripts based on the open source R software BGLR (de los Campos and Pérez-Rodriguez, 2014; Pérez and de los Campos, 2014) that can be used to develop calibration equations for other traits and data sets.

MATERIALS AND METHODS

Field Data

Data came from the Cowplus projects of the Autonomous Province of Trento, Italy. Samples were obtained from 1,264 Brown Swiss cows from 85 herds located in Trento with parities of 1 to 5, DIM ranging from 5 to 449, and production levels of 24.3 ± 7.9 kg/d. The samples were collected between April 2010 and February 2011; on a given day, only 1 herd was sampled during the evening milking; 2 milk subsamples per cow were collected and immediately refrigerated at 4°C without any preservative. One subsample (50 mL) was taken to the milk quality laboratory of the Breeders Federation of the Province of Trento (Trento, Italy) for composition analysis. The other subsample (2,000 mL) was taken to the cheese-making laboratory of the Department of Agronomy, Food, Natural Resources, Animals and Environment of the University of Padua; there, a subsample was used for model cheese fabrication and MCP analysis, whereas the remaining sample was frozen for further analysis (e.g., FA). Further details regarding the sampling procedure can be found in Cipolat-Gotet et al. (2012), and Cecchinato et al. (2013a). All samples were processed for analysis and model cheese fabrication within 20 h of collection. Data on the cows, herds, and individual test-day milk yields were provided by the Superbrown Consortium of Bolzano and Trento (Italy).

FTIR Spectral Acquisition

All individual milk samples were analyzed using a MilkoScan FT6000 (Foss, Hillerød, Denmark) over the spectral range from wavenumber 5,011 to 925 cm⁻¹ (from SWIR to LWIR). Spectra were stored as absorbance (A) using the transformation A = log(1/T), where T is the transmission (Figure 1). Two spectral acquisitions were carried out for each sample, and the results were averaged before data analysis.

Figure 1.

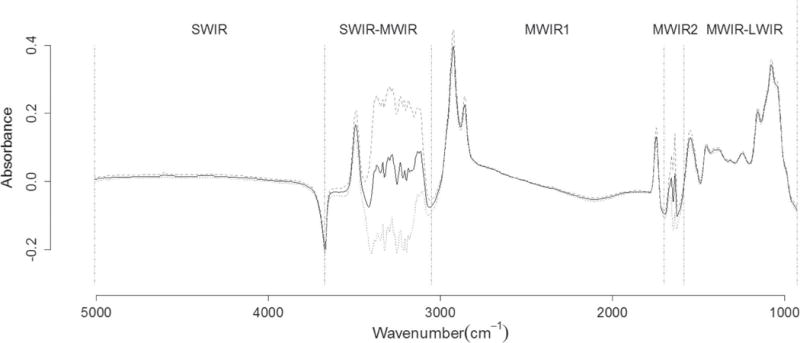
Absorbances of milk samples (Log T⁻¹; solid black line represents the average, whereas the 2 gray lines represent the mean ± SD). The vertical dashed lines define the 5 infrared regions (SWIR = short-wavelength infrared or near-infrared; MWIR = mid-wavelength infrared; LWIR = long-wavelength infrared).

Milk FA and Technological Properties

Forty-seven FA were analyzed by GC on a frozen aliquot of each individual milk sample and expressed as a percentage of total FA in the sample. We selected 4 FA for the prediction models: decanoic (or capric) acid (C10:0), 9-tetradecenoic (or myristoleic) acid (C14:1 cis-9; C14:1c9), hexadecanoic (or palmitic) acid (C16:0), and octadecanoic (or stearic) acid (C18:0). These 4 FA are highly representative of the variation in all 47 FA in terms of effect of diet, physiology, length of the carbonated chain (small, medium, and long), presence or absence of double bonds in the FA structure, proportion of the total FA, and heritability (Cecchinato et al., 2013b).

For every cow sampled, we produced an individual model cheese in accordance with the cheese-making procedure described by Cipolat-Gotet et al. (2013) and Bittante et al. (2013a). Briefly, 1,500 mL of milk from each individual cow was heated to 35°C in a stainless steel microvat, supplemented with thermophilic starter culture, mixed with rennet, and controlled for coagulation time. The resulting curd from each vat was cut, drained, shaped in wheels, pressed, salted, weighed, sampled, and analyzed. The whey collected from each vat was also weighed, sampled, and analyzed. All traits were derived from measures of the weights (g) and chemical compositions of the milk and whey. The traits considered here were cheese yield (CY_CURD) as grams of curd per 100 g of milk; protein recovery (REC_PROTEIN) as (grams of milk protein – grams of whey protein) × 100 g of milk protein; and fat recovery (REC_FAT) as (grams of milk fat – grams of whey fat) × 100 g of milk fat.

Milk coagulation properties of each individual milk sample were measured using a Formagraph (Foss Electric A/S) as described in Cipolat-Gotet et al. (2012). A rack containing 10 cuvettes was prepared, milk samples (10 mL) were heated to 35°C, and 200 μL of a rennet solution [Hansen Standard 160, with 80 ± 5% chymosin and 20 ± 5% pepsin, 160 international milk clotting units (IMCU)/mL; Pacovis Amrein AG, Bern, Switzerland] diluted to 1.6% (wt/vol) in distilled water was added at the beginning of the analysis to a final concentration of 0.051 IMCU/mL. Rennet coagulation time (RCT, min), defined as the time from addition of the enzyme to milk gelation, was used in this work as a trait representative of MCP.

Editing of the Spectra and Outlier Detection

The absorbance values of every wave in the FTIR spectra were centered and standardized to a null mean and a unit sample variance. Next, we calculated Mahalanobis distances using the standardized spectra data for outlier spectra detection. Looking at the plot of the Mahalanobis distances and deciding to exclude only the spectra with a very high probability to be outliers, we discarded the observations with a Mahalanobis distance greater than 5 times the standard deviation. All data editing was done in the R environment (R Core Team, 2013). The first derivative was also applied as mathematical pretreatment of the spectra. The results obtained using the pretreatment showed that all models we implemented fitted the data better using the first derivatives, but the ranking of the models did not change. For this reason, and to simplify interpretation, only the results of the “nonpretreatment” procedure are shown.

Statistical Analysis

Separate models were fitted to RCT, CY_CURD REC_PROTEIN, REC_FAT, C10:0, C14:1c9, C16:0, and C18:0. Here, we describe the statistical models for a generic phenotype (y_i; i = 1,…, n). Three Bayesian models, Bayesian ridge regression (Bayes RR), Bayes A and Bayes B (Meuwissen et al., 2001; see details below), and 2 reference models, PLS and modified partial least squares (MPLS), were fitted to each of the outcomes. Although PLS is one of the most commonly used in the literature for analysis of FTIR data, the MPLS method was also implemented, as there has been recent interest in using this model for FTIR analysis. Each of these methods is briefly described below.

Bayesian Models

Phenotypes were regressed on standardized spectra covariates using the linear model

$${\mathbf{y}}_i={\mathit{\beta }}_0+{\displaystyle \sum _{j=1}^{1,060}{\mathbf{x}}_{ij}}{\mathrm{\beta }}_j+{\epsilon }_i,$$

where β₀ is an intercept, {x_ij} are standardized FTIR spectra-derived wavelength data (j = 1,…, 1,060), β_j are the effects of each of the wavelengths, and ε_i are model residuals assumed to be independent and identically distributed (iid) with normal distribution centered at zero with variance ${\sigma }_{\epsilon }^2$. Given the above assumption, the conditional distribution of the data given effects and variance parameters is

$$P\left(\mathbf{y}|\mathrm{\theta }\right)={\displaystyle \prod _{i=1}^{n}N\left({\mu }_i,{\sigma }_{\epsilon }^2\right)},$$

where y = {y_i}, θ represents the collection of model parameters $\mathrm{\theta }=\left\{{\mathrm{\beta }}_0,\mathbf{\beta },{\sigma }_{\epsilon }^2\right\}$ N $\left({\mu }_i,{\sigma }_{\epsilon }^2\right)$ is a normal distribution centered at ${\mu }_i={\mathrm{\beta }}_0+{\displaystyle \sum _{j=1}^{1,060}{\mathrm{x}}_{ij}}{\mathrm{\beta }}_j$ and with variance ${\sigma }_{\epsilon }^2$, and β = {β_j} is a vector containing the effects of the individual spectra-derived wavelengths. Specification of the Bayesian model is completed by assigning prior distribution to the unknowns, θ. In the Bayesian models considered here, the prior density was as follows:

$$p\left(\mathrm{\theta }\right)=N\left({\mathrm{\beta }}_0|0,1\times {10}^5\right){\mathrm{\chi }}^{-2}\left({\sigma }_{\epsilon }^2|d{f}_{\epsilon },S_{\epsilon }\right)\left\{{\displaystyle \prod _{j=1}^{1,060}p\left({\mathrm{\beta }}_j|\Omega \right)}\right\}p\left(\Omega \right)$$

Here, the intercept is assigned a normal prior with a very large variance, which amounts to treating the intercept as a “fixed” effect, the residual variance is assigned a scaled-inverse chi-squared density (χ⁻²) with degree of freedom df_ε and scale parameters S_ε, and the effects of wavelengths are assigned iid priors, p(βj|Ω), indexed by a set of hyperparameters Ω, which are also treated as random. Finally, p(Ω) represent the prior distribution assigned to the hyperparameters; p(βj|Ω) and p(Ω) are different depending on the model implemented as it is described herein.

The Bayes RR, Bayes A, and Bayes B models differ in the form of the prior density assigned to the effects. In Bayes RR, effects are assigned Gaussian priors; that is, ${\left({\mathrm{\beta }}_j|\Omega \right)}^{\mathit{\text{iid}}}\sim N\left({\mathrm{\beta }}_j|0,{\sigma }_{\mathrm{\beta }}^2\right)$, $\Omega ={\sigma }_{\mathrm{\beta }}^2$ and $p\left(\Omega \right)={\mathrm{\chi }}^{-2}\left({\sigma }_{\mathrm{\beta }}^2|d{f}_{\mathrm{\beta }},S_{\mathrm{\beta }}\right)$. This specification shrinks the estimate toward zero, as also happens for Bayes A and Bayes B; the extent of shrinkage is homogeneous across effects and the method does not perform variable selection (de los Campos et al., 2013; Gianola, 2013). In Bayes A, ${\left({\mathrm{\beta }}_j|\Omega \right)}^{\mathit{\text{iid}}}\sim t\left({\mathrm{\beta }}_j|d{f}_{\mathrm{\beta }},S_{\mathrm{\beta }}\right)$ is a scaled-t density, which is indexed by 2 hyperparameters {df_β, S_β}: we fixed df_β = 5 and treated the scale as random; that is, Ω = S_β, and p(Ω) = Gamma (S_β| rate, shape). The scaled-t density has greater mass at zero and thicker tails than the Gaussian prior, and induces differential shrinkage of estimates of effects, whereas the estimated effects of predictors weakly correlated with the phenotype are shrunk toward zero strongly and those of predictors with strong association with the response are shrunk to a lesser extent (de los Campos et al., 2013; Gianola, 2013).

Finally, in Bayes B, p(β_j|Ω) is a mixture of a point of mass at zero and a scaled-t density, that is, ${\left({\mathrm{\beta }}_j|\Omega \right)}^{\mathit{\text{iid}}}\sim \pi \times t\left({\mathrm{\beta }}_j|d{f}_{\mathrm{\beta }},S_{\mathrm{\beta }}\right)+\left(1-\pi \right)\times 1\left({\mathrm{\beta }}_j=0\right)$; therefore, a priori, with probability π, β_j is drawn from the t-density and with probability (1 − π) β_j = 0. As with Bayes A, we set df_β = 5, and the other hyperparameters were treated as random; specifically, S_β ~ Gamma (S_β| rate, shape) and π ~ Beta (π|shape₁, shape₂).

The Bayesian models described above were implemented in BGLR (de los Campos and Pérez-Rodriguez, 2014). A detailed description of the models and algorithms implemented in BGLR, as well as a comprehensive list of examples can be found in Peréz and de los Campos (2014). All the above models have high-order hyperparameters that need to be specified, which include df_ε, S_ε, df_β, rate, shape, shape₁, and shape₂. All these parameters were specified using built-in BGLR rules that select default values for these unknowns and are fully explained in Peréz and de los Campos (2014). The rules were designed to yield proper but relatively uninformative priors. In all the Bayesian models, inferences were based on 30,000 samples collected after discarding the first 10,000 samples.

Simplified scripts showing how the predictive equations for Bayes A, Bayes B, and Bayes RR models can be implemented in BGLR are freely available along with data files relative to milk spectra and reference data by requesting them from the corresponding author of this paper.

Reference Models

We compared the performance of the Bayesian models with 2 commonly used methods: PLS and MPLS, both as implemented in the WinISI II software (Infrasoft International LLC). The following program settings were used to implement the reference models: no spectra pretreatments or outlier elimination stage; 4 groups for the cross-validation procedure (internal to the training data sets); a maximum of 16 MPLS and PLS terms.

Data Analysis

First, we fitted the models described above to each of the traits separately using the entire data set as training. We used this analysis to derive estimates of error variance $\left({\sigma }_g^2\right)$, the R² between phenotypes and predictions in the entire training data set, and the correlations among the predictions made by the different models. For the Bayesian models, we also reported the deviance information criterion (DIC) and the effective number of parameters (pD; Spiegelhalter et al. 2002). For the PLS and MPLS models, we reported the effective number of terms used. In addition, we provide the marginal correlation between the traits and the absorbances for each wave and the estimated coefficients for each model to shed light on how the different Bayesian models and MPLS and PLS models work.

Assessment of Prediction Accuracy

Most of the literature on calibration equations has assessed prediction accuracy using validation methods where individual records are randomly assigned to either training or testing sets, or folds of a cross-validation procedure. When this is done, records from the same herd are likely to appear in both training and validation data sets. In industry practice, calibration equations are derived using data from a restricted number of herds, which is problematic because it means predicting from FTIR traits (e.g., FA content or profiles) in herds that were not used to derive the prediction equations. This is clearly a much more difficult, but perhaps more realistic, prediction scenario. Therefore, in this study, we assigned herds and not individual records to training and testing data sets. In total, we generated 25 training-testing experiments, in each of which the data set was split into training (TRN) and testing (TST) subsets. The training subset was used to fit the models and to develop the calibration equation for predicting individual phenotypes in the testing subset as validation. Partition of the data set into TRN and TST subsets was done as follows: we sampled random herds and assigned all cows in the selected herds to the TST data set until we had at least 200 complete records. The remaining records were assigned to the TRN subset. This procedure guaranteed that the records from all cows in a given herd are in either the TRN or the TST subset, so that our setting assessed the “across-herd” predictive power of the calibration equations.

The numbers of cows per herd were similar for all traits measured. The mean, SD (minimum; maximum) herd size was as follows: 14.20, 1.33 (8; 15) in the FA traits; 14.61, 0.96 (8; 15) for RCT; 14.65, 0.83 (10; 15) for CY_CURD; 14.58, 0.92 (10; 15) for REC_PROTEIN; and 14.45, 0.95 (10; 15) for REC_FAT.

The TRN-TST procedure described above was replicated 25 times for each trait. The average numbers of samples (out of the 25 TRN-TST partitions) in TRN (TST) were 973 (206), 1,036 (206), 1,040 (205), 1,035 (205), and 1,023 (206) for FA, RCT, CY_CURD, REC_PROTEIN, and REC_FAT, respectively. The average numbers of herds in TRN (TST) were 68 (15) for FA, and 71 (14) for RCT, CY_CURD, REC_PROTEIN, and REC_FAT.

Prediction accuracy was measured using the coefficient of determination between predictions and observed traits in the TST data sets, the square root of the mean squared prediction error (RMSE), and the regression (estimated intercept and slope) of observed phenotype in the TST data set and predictions. In addition, we conducted pair-wise comparisons by counting the number of times (out of 25 replicates) in which the R² of a model was higher than that of another model, and conducted paired t-tests to compare the R² of pairs of models.

RESULTS

Table 1 shows descriptive statistics for the 4 FA (C10:0, C14:1c9, C16:0, and C18:0) and technological traits RCT, CY_CURD, REC_PROTEIN, and REC_FAT. The number of samples shown in the table differs among traits because phenotypes were not available for all the samples, and the number of samples shown refers to those remaining after elimination of outlier spectra. All traits had distributions in the expected ranges of values. Parameter estimates by trait and model using the full data set are presented in Table 2 for milk FA and Table 3 for technological traits. The calibration R² values (in the entire training data set) were high (about 0.50 on average for all models) for RCT, CY_CURD, REC_PROTEIN, C10:0, and C16:0 and lower for REC_FAT, C14:1c9, and C18:0. The model for PLS had the smallest R² and largest residual variance across traits. The Bayesian methods had higher calibration R² and smaller residual variance than the MPLS for all of the traits; however, the goodness of fit of the calibration equations to the calibration data set obtained with MPLS were those more similar to the fit obtained with the Bayesian methods. The DIC tended to favor Bayes A and Bayes B over Bayes RR, particularly in the case of the 4 FA. The effective number of terms used was, on average similar, for PLS and MPLS.

Table 1.

Descriptive statistics of 4 milk FA and selected technological traits

Trait	No. of samples	Mean	SD	Minimum	Maximum
FA,1 %
C10:0	1,179	3.17	0.63	0.61	5.65
C14:1 cis-9	1,179	1.08	0.32	0.22	2.56
C16:0	1,179	30.54	3.68	18.92	46.73
C18:0	1,179	8.97	1.89	3.38	16.31
Technological trait2
RCT, min	1,242	19.88	5.71	6.00	43.00
CYCURD, %	1,245	15.04	1.89	10.23	20.58
RECPROTEIN, %	1,240	78.08	2.41	70.51	85.25
RECFAT, %	1,229	89.88	3.58	76.77	98.12

¹C10:0 = decanoic (capric) acid; C14:1 cis-9 = 9-tetradecenoic (myristoleic) acid; C16:0 = hexadecanoic (palmitic) acid; C18:0 = octadecanoic (stearic) acid; each FA is expressed as a percentage of the total FA by weight.

²RCT = rennet coagulation time, min; CY_CURD = cheese yield, weight of fresh curd as a percentage of the milk processed by weight; REC_PROTEIN = recovery of protein, protein of the curd as a percentage of the protein of the milk processed; REC_FAT = recovery of fat, fat of the curd as a percentage of the fat of the milk processed.

Table 2.

Parameter estimates, goodness of fit statistics, and correlations between predictions made by different methods obtained for 4 milk FA when models were fitted to the entire data set, by trait and model¹

Trait2 and model	Variance		R2	DIC	pD/Terms	Correlations between predictions of different models
	Phenotypic	Residual				MPLS	Bayes RR	Bayes A	Bayes B
C10:0	0.40
PLS		0.21	0.48	—	15	0.90	0.89	0.86	0.83
MPLS		0.17	0.58	—	15	—	0.93	0.91	0.91
Bayes RR		0.10	0.76	971	184	—	—	0.98	0.97
Bayes A		0.10	0.75	889	135	—	—	—	0.98
Bayes B		0.10	0.76	729	73	—	—	—	—
C14:1 cis-9	0.10
PLS		0.07	0.33	—	11	0.94	0.95	0.89	0.82
MPLS		0.07	0.35	—	10	—	0.94	0.90	0.85
Bayes RR		0.05	0.50	80.3	109	—	—	0.96	0.90
Bayes A		0.04	0.57	−104	104	—	—	—	0.96
Bayes B	0.04		0.59	−244	71	—	—	—	—
C16:0	13.56
PLS		7.70	0.44	—	14	0.88	0.88	0.87	0.81
MPLS		5.75	0.58	—	14	—	0.94	0.94	0.92
Bayes RR		3.72	0.73	5,275	182	—	—	0.98	0.96
Bayes A		3.90	0.71	5,249	144	—	—	—	0.97
Bayes B		3.68	0.73	5,035	75	—	—	—	—
C18:0	3.56
PLS		2.68	0.27	—	11	0.85	0.82	0.77	0.71
MPLS		2.41	0.35	—	14	—	0.87	0.85	0.81
Bayes RR		1.37	0.62	4,071	171	—	—	0.98	0.93
Bayes A		1.27	0.65	3,945	152	—	—	—	0.96
Bayes B		1.27	0.65	3,750	62	—	—	—	—

¹R² = coefficient of determination calculated as the square of the correlation between observed and predicted values; DIC = deviance information criterion; pD/Terms = effective number of parameters/number of MPLS or PLS terms; PLS = partial least squares regression; MPLS = modified partial least squares regression, Bayes RR = Bayes ridge regression.

²C10:0 = decanoic (capric) acid; C14:1 cis-9 = 9-tetradecenoic (myristoleic) acid; C16:0 = hexadecanoic (palmitic) acid; C18:0 = octadecanoic (stearic) acid; each FA is expressed as a percentage of the total FA by weight.

Table 3.

Parameter estimates, goodness of fit statistics, and correlations between predictions made by different methods obtained for milk technological properties when models were fitted to the entire data set, by trait and model¹

Trait2 and model	Variance		R2	DIC	pD/Terms	Correlations between predictions of different models
	Phenotypic	Residual				MPLS	Bayes RR	Bayes A	Bayes B
RCT	32.57
PLS		15.49	0.53	—	14	0.92	0.92	0.92	0.87
MPLS		12.69	0.61	—	15	—	0.96	0.96	0.94
Bayes RR		8.35	0.75	6,534	179	—	—	0.99	0.97
Bayes A		8.82	0.73	6,513	138	—	—	—	0.98
Bayes B		8.71	0.73	6,333	60	—	—	—	—
CYCURD	3.57
PLS		1.00	0.72	—	14	0.97	0.98	0.98	0.96
MPLS		0.92	0.74	—	11	—	0.98	0.99	0.98
Bayes RR		0.74	0.79	3,405	118	—	—	1.00	0.98
Bayes A		0.72	0.80	3,335	107	—	—	—	0.99
Bayes B		0.67	0.81	3,175	72	—	—	—	—
RECPROTEIN	5.81
PLS		2.69	0.54	—	15	0.89	0.87	0.87	0.84
MPLS		1.85	0.68	—	16	—	0.95	0.95	0.94
Bayes RR		1.06	0.82	4,029	210	—	—	0.99	0.98
Bayes A		1.14	0.81	4,050	179	—	—	—	0.98
Bayes B		1.08	0.81	3,844	110	—	—	—	—
RECFAT	12.84
PLS		9.44	0.27	—	10	0.89	0.95	0.91	0.88
MPLS		8.79	0.32	—	9	—	0.93	0.93	0.94
Bayes RR		7.71	0.41	6,209	104	—	—	0.97	0.95
Bayes A		7.57	0.42	6,152	88	—	—	—	0.96
Bayes B		7.48	0.42	6,079	59	—	—	—	—

¹PLS = partial least squares regression; MPLS = modified partial least squares regression, Bayes RR = Bayes ridge regression; R² = coefficient of determination calculated as the square of the correlation between observed and predicted values; DIC = deviance information criterion; pD/Terms = effective number of parameters/number of MPLS or PLS terms.

²RCT = rennet coagulation time, min; CY_CURD = cheese yield, weight of fresh curd as a percentage of the milk processed by weight; REC_PROTEIN = recovery of protein, protein of the curd as a percentage of the protein of the milk processed; REC_FAT = recovery of fat, fat of the curd as a percentage of the fat of the milk processed.

Tables 2 and 3 include correlations between the predictions derived from the models. In general, these correlations were high for all pairs of models, although the correlations between the predictions obtained with the Bayesian methods were higher, whereas they were slightly lower between the predictions obtained using PLS and MPLS.

Figures 2 and 3 show the absolute values of marginal correlations between the absorbances at each wave and the phenotypes (FA in Figure 2, and technological traits in Figure 3), together with the estimated absolute value of effect of each wavelength by model. The coefficients of the individual waves of the calibration equations were expressed as the absolute ratio with respect to the greatest one, so that they included values in the [0, 1] range. All wavelengths in the SWIR region were positively correlated with the FA C10:0, C14:1c9, and C18:0 (about 0.3) and RCT (about 0.2), whereas within the same region, the correlations with C16:0, REC_FAT, and REC_PROTEIN were considerably lower. The marginal correlations in the SWIR-MWIR region were very low for all traits except CY_CURD. The MWIR and LWIR regions showed different correlation patterns across traits. Many waves were correlated with the traits of interest and, in most cases, the individual correlations were <0.3, the only notable exception being CYCURD, characterized by many waves with correlations >0.5.

Figure 2.

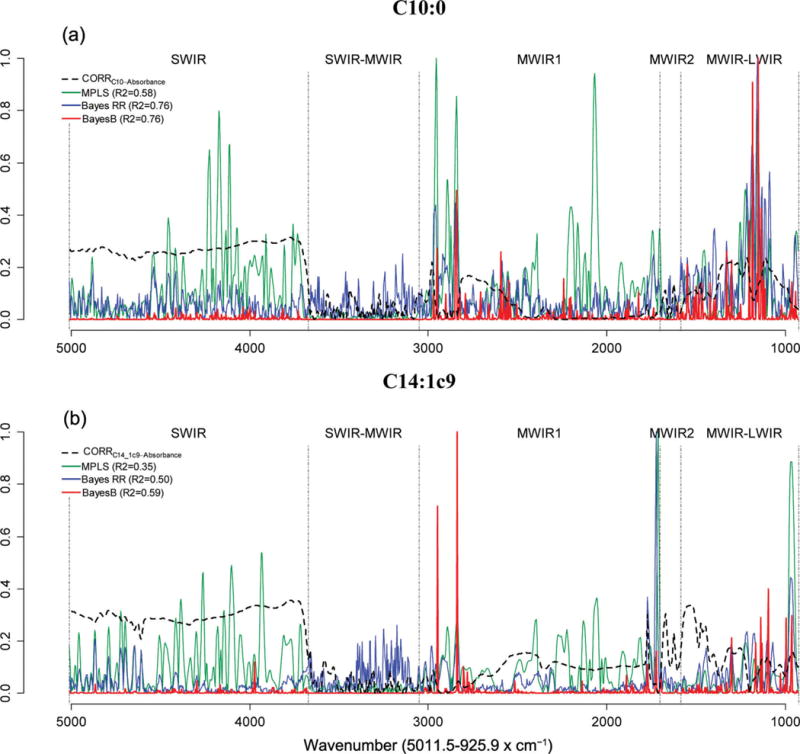
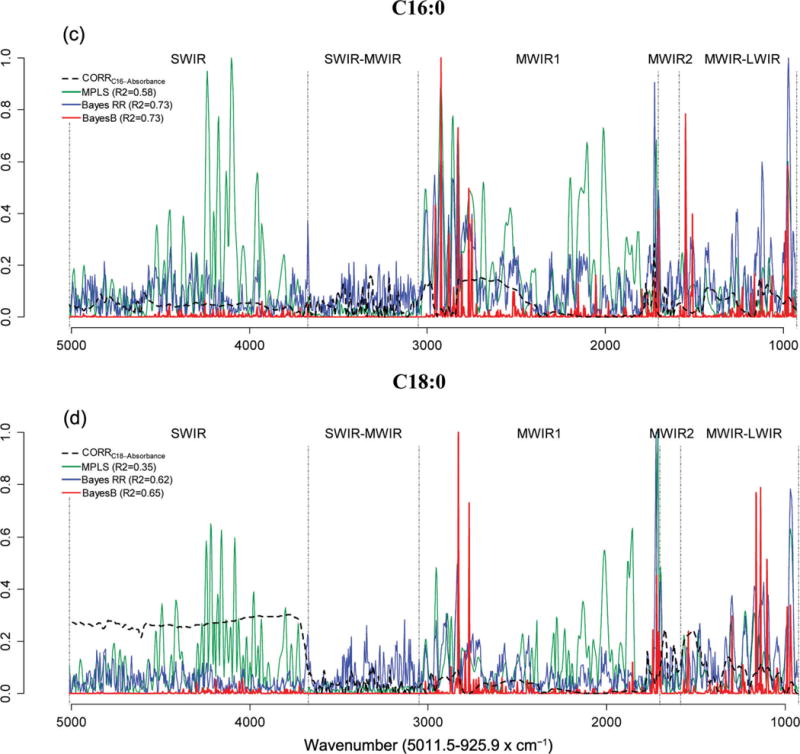
Absolute values of estimated effects (solid curves) and marginal correlations (CORR) with phenotype (dashed curve) by wavelength (horizontal axis). C10:0 = decanoic (capric) acid; C14:1 cis-9 = 9-tetradecenoic (myristoleic) acid; C16:0 = hexadecanoic (palmitic) acid; C18:0 = octadecanoic (stearic) acid; SWIR = short-wavelength infrared or near-infrared; MWIR = mid-wavelength infrared; LWIR = long-wavelength infrared; MPLS = modified partial least squares regression; Bayes RR = Bayes ridge regression. Color version available online.

Absolute values of estimated effects (solid curves) and marginal correlations (CORR) with phenotype (dashed curve) by wavelength (horizontal axis). C10:0 = decanoic (capric) acid; C14:1 cis-9 = 9-tetradecenoic (myristoleic) acid; C16:0 = hexadecanoic (palmitic) acid; C18:0 = octadecanoic (stearic) acid; SWIR = short-wavelength infrared or near-infrared; MWIR = mid-wavelength infrared; LWIR = long-wavelength infrared; MPLS = modified partial least squares regression; Bayes RR = Bayes ridge regression. Color version available online.

Figure 3.

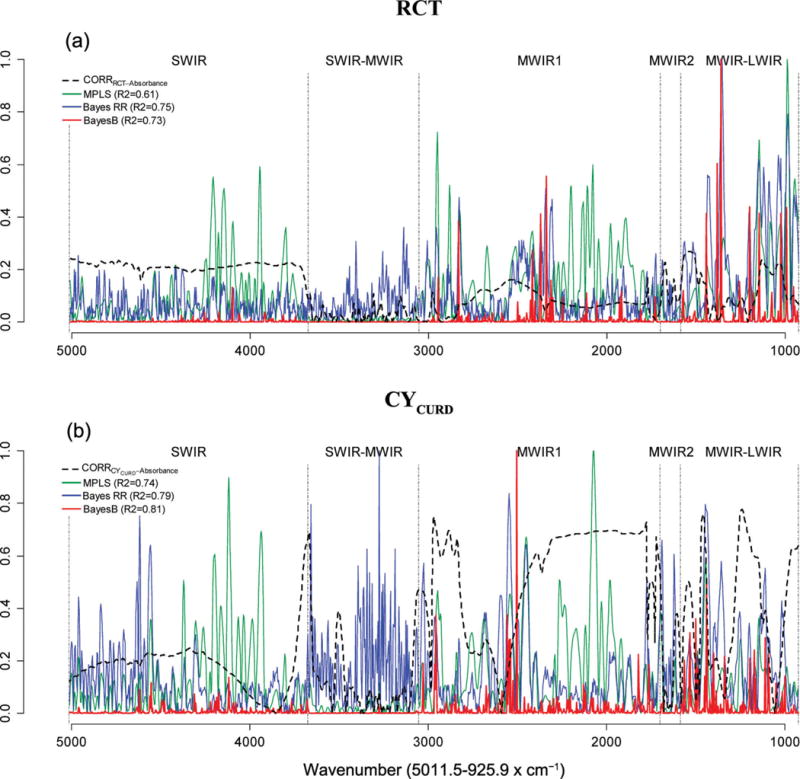
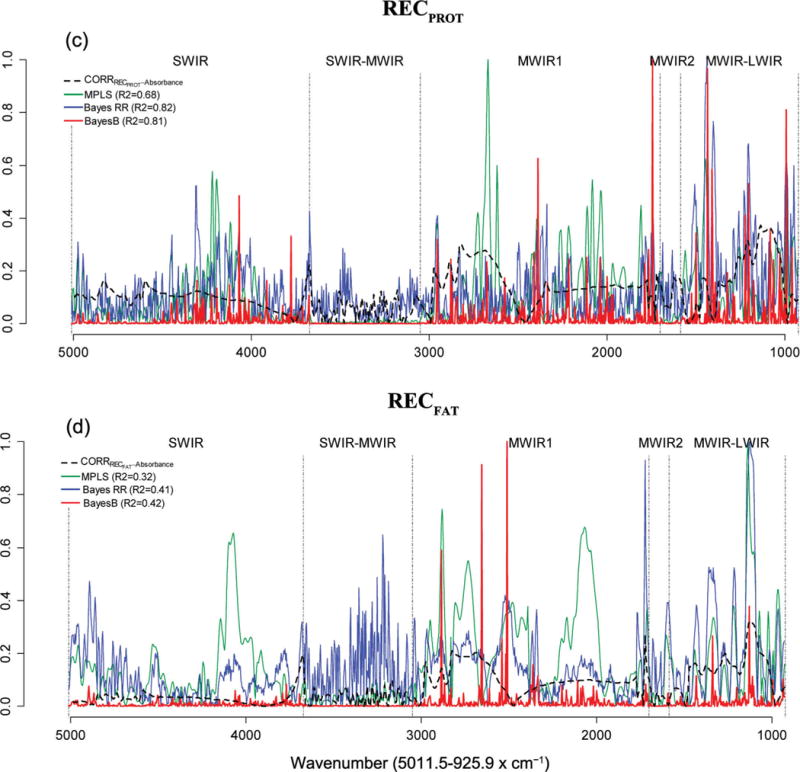
Absolute values of estimated effects (solid curves) and marginal correlations (CORR) with phenotype (dashed curve) by wavelength (horizontal axis). RCT = rennet coagulation time, min; CY_CURD = cheese yield, weight of fresh curd as a percentage of the milk processed by weight; REC_PROTEIN = recovery of protein, protein of the curd as a percentage of the protein of the milk processed; REC_FAT = recovery of fat, fat of the curd as a percentage of the fat of the milk processed; SWIR = short-wavelength infrared or near-infrared; MWIR = mid-wavelength infrared; LWIR = long-wavelength infrared; MPLS = modified partial least squares regression; Bayes RR = Bayes ridge regression. Color version available online.

Absolute values of estimated effects (solid curves) and marginal correlations (CORR) with phenotype (dashed curve) by wavelength (horizontal axis). RCT = rennet coagulation time, min; CY_CURD = cheese yield, weight of fresh curd as a percentage of the milk processed by weight; REC_PROTEIN = recovery of protein, protein of the curd as a percentage of the protein of the milk processed; REC_FAT = recovery of fat, fat of the curd as a percentage of the fat of the milk processed; SWIR = short-wavelength infrared or near-infrared; MWIR = mid-wavelength infrared; LWIR = long-wavelength infrared; MPLS = modified partial least squares regression; Bayes RR = Bayes ridge regression. Color version available online.

The same figures (FA in Figure 2 and technological traits in Figure 3) show the absolute values of estimated effects for the MPLS, Bayes RR, and Bayes B methods, characterized by very different patterns of effect size. The Bayes RR and MPLS methods generated many intermediate estimates in all regions of the spectra, typical of shrinkage estimation procedures. In contrast, with Bayes B (a variable selection method), the effects on most regions were small or null and very few waves had sizable effects.

The results of validation in an independent sample are summarized in Table 4 for milk FA proportions and Table 5 for technological traits. As expected, the R² values in the independent data sets (TST sets) were lower than those of the calibration R² reported in Tables 2 and 3. In most cases, the external validation R² was 10 to 20 percentage points smaller than the calibration R² value. The standard deviations of validation R² ranged from 5 to 10 percentage points across traits and methods (Tables 4 and 5), the greatest variability being for the 2 REC traits and the lowest for RCT.

Table 4.

Prediction R-squared (R²_VAL), square root of the mean-squared prediction error (RMSE) in testing data sets by trait and model, and pair-wise comparisons of prediction accuracies of the models for 4 milk FA¹

Trait2 and model	R2VAL				RMSE	Pair-wise comparisons
	Mean	Minimum	Maximum	SD		PLS	MPLS	Bayes RR	Bayes A	Bayes B
C10:0
PLS	0.44	0.33	0.57	0.07	0.49	—	100	100	100	100
MPLS	0.56	0.44	0.68	0.07	0.43	***	—	80	100	100
Bayes RR	0.59	0.50	0.68	0.06	0.41	***	***	—	100	96
Bayes A	0.66	0.58	0.75	0.05	0.38	***	***	***	—	64
Bayes B	0.67	0.55	0.75	0.06	0.38	***	***	***	NS	—
C14:1 cis-9
PLS	0.30	0.20	0.41	0.06	0.28	—	88	100	100	100
MPLS	0.33	0.18	0.44	0.06	0.27	***	—	48	100	100
Bayes RR	0.33	0.25	0.42	0.05	0.27	***	NS	—	96	100
Bayes A	0.38	0.28	0.48	0.06	0.26	***	***	***	—	96
Bayes B	0.48	0.37	0.65	0.06	0.24	***	***	***	***	—
C16:0
PLS	0.41	0.25	0.60	0.08	2.82	—	100	100	100	100
MPLS	0.51	0.34	0.70	0.08	2.55	***	—	84	100	96
Bayes RR	0.54	0.40	0.70	0.07	2.45	***	***	—	84	92
Bayes A	0.58	0.46	0.72	0.07	2.33	***	***	***	—	72
Bayes B	0.60	0.42	0.74	0.08	2.30	***	***	***	NS	—
C18:0
PLS	0.26	0.09	0.38	0.08	1.65	—	80	92	100	100
MPLS	0.30	0.16	0.43	0.08	1.61	***	—	64	100	100
Bayes RR	0.31	0.17	0.42	0.07	1.57	***	NS	—	96	96
Bayes A	0.45	0.24	0.59	0.08	1.40	***	***	***	—	76
Bayes B	0.49	0.30	0.65	0.11	1.35	***	***	***	***	—

¹PLS = partial least squares regression; MPLS = modified partial least squares regression, Bayes RR = Bayes ridge regression; R²_VAL = coefficient of determination calculated as the square of the correlation between observed and predicted values; Mean, Minimum, Maximum = mean, minimum, and maximum of the R² of 25 replicates; RMSE = mean of the root mean square errors of 25 replicates; the values above the diagonal indicate the percentage of replicates where the model in the column had a higher prediction R²_VAL than the model in the row; the asterisks below the diagonal indicate P-values from paired t-tests comparing the R²_VAL of the model in the column and the model in the row:

^***Significant differences at the 0.001 level; NS indicates no significant difference at the 0.05 level.

²C10:0 = decanoic (capric) acid; C14:1 cis-9 = 9-tetradecenoic (myristoleic) acid; C16:0 = hexadecanoic (palmitic) acid; C18:0 = octadecanoic (stearic) acid; each FA is expressed as a percentage of the total FA by weight.

Table 5.

Prediction R-squared (R²_VAL), square root of the mean-squared prediction error (RMSE) in testing data sets by trait and model, and pair-wise comparisons of prediction accuracies of the models for milk technological properties

Trait2 and model	R2VAL				RMSE	Pair-wise comparisons
	Mean	Minimum	Maximum	SD		PLS	MPLS	Bayes RR	Bayes A	Bayes B
RCT
PLS	0.50	0.41	0.59	0.05	4.14	—	96	100	100	96
MPLS	0.57	0.41	0.65	0.05	3.82	***	—	92	88	92
Bayes RR	0.60	0.48	0.67	0.05	3.70	***	***	—	60	80
Bayes A	0.60	0.47	0.68	0.05	3.67	***	***	NS	—	72
Bayes B	0.63	0.53	0.73	0.06	3.59	***	***	**	*	—
CYCURD
PLS	0.66	0.55	0.76	0.07	1.11	—	84	96	96	92
MPLS	0.68	0.54	0.80	0.07	1.07	***	—	48	80	84
Bayes RR	0.68	0.56	0.78	0.07	1.08	***	NS	—	80	80
Bayes A	0.70	0.59	0.81	0.07	1.04	***	***	***	—	72
Bayes B	0.71	0.57	0.82	0.06	1.03	***	***	***	NS	—
RECPROTEIN
PLS	0.47	0.30	0.63	0.09	1.75	—	100	100	100	100
MPLS	0.60	0.37	0.75	0.10	1.52	***	—	96	96	80
Bayes RR	0.65	0.47	0.79	0.09	1.42	***	***	—	48	44
Bayes A	0.65	0.46	0.80	0.09	1.42	***	***	NS	—	48
Bayes B	0.65	0.47	0.80	0.09	1.44	***	***	NS	NS	—
RECFAT
PLS	0.21	0.07	0.36	0.08	3.31	—	88	80	88	92
MPLS	0.28	0.14	0.42	0.09	3.13	***	—	4	16	52
Bayes RR	0.23	0.07	0.37	0.08	3.24	**	***	—	84	92
Bayes A	0.24	0.08	0.38	0.08	3.22	***	***	**	—	92
Bayes B	0.28	0.14	0.42	0.09	3.13	***	NS	***	***	—

¹PLS = partial least squares regression; MPLS = modified partial least squares regression, Bayes RR = Bayes ridge regression; R²_VAL = coefficient of determination calculated as the square of the correlation between observed and predicted values; Mean, Minimum, Maximum = mean, minimum, and maximum of the R² of 25 replicates; RMSE = mean of the root mean square errors of 25 replicates; the values above the diagonal indicate the percentage of replicates where the model in the column had a higher prediction R²_VAL than the model in the row; the asterisks below the diagonal indicate P-values from paired t-tests comparing the R²_VAL of the model in the column and the model in the row: ***, **, and *: significant differences at the 0.001, 0.01, and 0.05 levels, respectively; NS indicates no significant difference at the 0.05 level.

²RCT = rennet coagulation time, min; CY_CURD = cheese yield, weight of fresh curd as a percentage of the milk processed by weight; REC_PROTEIN = recovery of protein, protein of the curd as a percentage of the protein of the milk processed; REC_FAT = recovery of fat, fat of the curd as a percentage of the fat of the milk processed.

Bayes A and Bayes B had the highest prediction accuracy across traits, except for REC_FAT, where Bayes B and MPLS gave the same results. Pair-wise comparisons showed that the PLS had the lowest prediction accuracy across traits; MPLS was better than PLS but less accurate than the Bayes A and Bayes B methods, except for REC_FAT, where no significant differences were found. Bayes RR (a shrinkage method) produced somewhat mixed results: for some traits (e.g., REC_PROTEIN, RCT), it performed better than MPLS, but for other traits (e.g., REC_FAT), its performance was worse. Tables 6 and 7 show the intercept and regression coefficient estimates from regressions of the observed phenotype and predictions from the testing data set. A null intercept (0) and a unit slope (1) were interpreted as indicating no prediction bias. The estimated intercepts of the Bayesian models were closer to 0 and the estimated slopes consistently closer to 1 than those of PLS and MPLS, except for C16:0, REC_PROTEIN, and REC_FAT, where estimated intercept and slope of Bayes B and MPLS were very similar. Table 6 also shows the proportion (across TRN-TST partitions) of cases where a 95% CI for the intercept (slope) included 0 (1). These proportions were clearly higher for the Bayesian methods, suggesting that their prediction bias is smaller than that of PLS or MPLS, following the same trend described above.

Table 6.

Estimated intercept and slope of the regression between predictions and phenotypes in testing data sets, by trait and model for the 4 milk FA¹

Trait2 and model	Intercept	% Intercept = 0	Slope	% Slope = 1
C10:0, %
PLS	0.39	64	0.87	52
MPLS	0.19	68	0.94	64
Bayes RR	0.02	84	0.99	88
Bayes A	0.00	68	1.00	76
Bayes B	0.13	52	0.96	52
C14:1 cis-9, %
PLS	0.19	56	0.83	52
MPLS	0.16	60	0.85	48
Bayes RR	0.03	80	0.98	80
Bayes A	0.04	76	0.96	80
Bayes B	0.04	60	0.96	56
C16:0, %
PLS	4.12	56	0.88	56
MPLS	1.41	60	0.96	64
Bayes RR	−0.11	64	1.00	72
Bayes A	0.20	72	1.00	76
Bayes B	1.41	68	0.96	64
C18:0, %
PLS	2.19	36	0.75	32
MPLS	2.06	32	0.76	32
Bayes RR	0.49	72	0.99	76
Bayes A	0.40	68	0.95	72
Bayes B	0.74	60	0.91	64

¹PLS = partial least squares regression; MPLS = modified partial least squares regression; Bayes RR = Bayes ridge regression; Intercept = mean of the intercept estimated between observed and predicted values (of each replicate) in 25 replicates; % Intercept = 0 is the percentage of times (over 25 replicates) in which the estimated 95% CI for the intercept included zero; Slope = mean of the slope estimated between observed and predicted values (of each replicate) in 25 replicates; % Slope = 1 is the percentage of times (on 25 replicates) in which the estimated 95% CI for the slope included 1.

²C10:0 = decanoic (capric) acid; C14:1 cis-9 = 9-tetradecenoic (myristoleic) acid; C16:0 = hexadecanoic (palmitic) acid; C18:0 = octadecanoic (stearic) acid; each FA is expressed as a percentage of total FA by weight.

Table 7.

Estimated intercept and slope of the regression between predictions and phenotypes in testing data sets, by trait and model for the milk technological traits¹

Trait2 and model	Intercept	% Intercept = 0	Slope	% Slope = 1
RCT, min
PLS	1.67	72	0.93	68
MPLS	1.14	76	0.95	76
Bayes RR	0.24	92	1.00	84
Bayes A	0.36	84	0.99	80
Bayes B	1.08	68	0.96	72
CYCURD, %
PLS	1.21	64	0.92	60
MPLS	0.94	68	0.94	68
Bayes RR	0.68	76	0.96	76
Bayes A	0.67	72	0.96	68
Bayes B	0.86	48	0.94	56
RECPROTEIN, %
PLS	10.24	48	0.87	48
MPLS	6.59	48	0.92	44
Bayes RR	2.61	64	0.97	68
Bayes A	3.00	64	0.96	64
Bayes B	6.88	40	0.91	44
RECFAT, %
PLS	21.82	40	0.76	36
MPLS	11.56	56	0.87	56
Bayes RR	7.53	68	0.91	68
Bayes A	9.00	68	0.90	68
Bayes B	11.19	56	0.87	56

¹PLS = partial least squares regression; MPLS = modified partial least squares regression; Bayes RR = Bayes ridge regression; Intercept = mean of the intercept estimated between observed and predicted values (of each replicate) in 25 replicates; % Intercept = 0 is the percentage of times (over 25 replicates) in which the estimated 95% CI for the intercept included zero; Slope = mean of the slope estimated between observed and predicted values (of each replicate) in 25 replicates; % Slope = 1 is the percentage of times (on 25 replicates) in which the estimated 95% CI for the slope included 1.

²RCT = rennet coagulation time, min; CY_CURD = cheese yield, weight of fresh curd as a percentage of the milk processed by weight; REC_PROTEIN = recovery of protein, protein of the curd as a percentage of the protein of the milk processed; REC_FAT = recovery of fat, fat of the curd as a percentage of the fat of the milk processed.

DISCUSSION

Phenotypic Values for Milk FA Proportions and Technological Traits

The average fractions of total milk FA of the 4 FA considered in the present study were within the range found in Holsteins (Bobe et al., 2008; Garnsworthy et al., 2010) and various other breeds (Heck et al., 2009; Poulsen et al., 2012). The 85 herds sampled for the present study were from mountain farms rearing Brown Swiss cows fed predominantly hay and concentrates, with some silage on only a small percentage of the farms and without the use of pasture or fresh forage (Sturaro et al., 2013). The RCT average value found in the present study is longer than the average coagulation time found in 33 studies on Holstein cows reviewed by Bittante et al. (2012), despite the fact that they found the values for Brown Swiss cows to be 11% shorter than those for the Holstein breed. This is likely explained by 2 factors: the low quantity of rennet added and the inclusion of late-coagulating samples (Bittante et al., 2013b).

The fresh CY_CURD found in the present study was similar to that found by Martin et al. (2009) in Montbéliarde cow milk and greater than that found by the same authors and by Cologna et al. (2009) in Holstein cow milk, which characterized by lower fat and protein contents. In addition, the average REC_FAT and REC_PROTEIN in the present study were similar to those measured by Bynum and Olson (1982) and by Mistry et al. (2002).

FTIR Calibrations of Technological Properties

Prediction of milk fat content using FTIR calibrations is very accurate (Ferrand et al., 2011; Soyeurt et al., 2011) and the method is approved by the International Committee on Animal Recording (ICAR, 2012) as an official method for milk recording. This reflects the ability of the FTIR spectrum to capture information on the main chemical bonds characterizing the lipids: C–C, C–H, and C=O (Bittante and Cecchinato, 2013). Predictions of individual FA are usually much less accurate because of the great similarity among them in terms of chemical bonds. Soyeurt et al. (2006) computed the calibration equations from a GC analysis of 49 milk samples using PLS and obtained calibration R² values of 0.77, 0.12, 0.91, and 0.73 and cross-validation R² values of 0.64, 0.07, 0.82, and 0.69 for capric, myristoleic, palmitic, and stearic acids in milk, respectively. By applying PLS to the 4,000 to 900 cm⁻¹ FTIR spectral data of 267 randomly selected milk samples analyzed by GC, De Marchi et al. (2011) obtained cross-validation R² of 0.52, 0.44, 0.49, and 0.65, respectively, for prediction of the amounts of the same 4 FA in milk. By selecting the same number of samples according to spectral variability, adopting a mathematical pretreatment of spectral data before PLS, and selecting only a quarter of the FTIR spectrum, Soyeurt et al. (2011) improved the calibration R² values to 0.91, 0.58, 0.92, and 0.87, and the validation R² values to 0.90, 0.50, 0.86, and 0.74, respectively, for the 4 FA. By applying PLS to the first derivative of spectral data of 1,236 analyzed samples to predict the amounts of the same 4 FA in milk, Maurice-Van Eijndhoven et al. (2013) obtained R² values of 0.96, 0.80, 0.98, and 0.91 from calibration, and of 0.85 to 0.94, 0.64 to 0.80, 0.86 to 0.93, and 0.58 to 0.80 from validation, according to the breed of cow.

Predicting FA proportions in milk fat (FA profile) is more difficult than predicting FA content in milk because only the proportions and not the quantities of different chemical bonds can be taken into account, which explains the smaller R² values obtained from FA calibration and especially from validation in predicting fat composition with respect to milk composition.

Soyeurt et al. (2006) obtained R² cross-validation values of only 0.53, 0.23, 0.50, and 0.09 for capric, myristoleic, palmitic, and stearic acids, respectively. Using the larger preselected data set with mathematical pretreatment and only one quarter of the spectral range, the same authors were able to improve prediction accuracy to R² values of 0.75, 0.39, 0.55, and 0.39 for these FA (Soyeurt et al., 2011). Prediction accuracies obtained in our study were in line with previous reports. Using records from 1,179 milk samples from Brown Swiss cattle, with no mathematical pretreatment or spectral area selection, and with replicated external validations on samples from different farms and dates, with the PLS method, we obtained validation R² values of 0.44, 0.30, 0.41, and 0.26 for prediction of the fat content of capric, myristoleic, palmitic, and stearic FA, respectively (Table 4). With the best performing model (Bayes B), we achieved prediction R² values of 0.67, 0.48, 0.60, and 0.49 for prediction of the fat content of capric, myristoleic, palmitic, and stearic FA, respectively (Table 4). It is worth noting that the fat content of milk from the Brown Swiss breed is characterized by lower genetic variability estimates compared with milk from the Holstein Friesian breed (Cecchinato et al., 2011b; Samorè et al., 2012), in part because the DGAT1 gene in the Brown Swiss breed is monomorphic (Cecchinato et al., 2012b).

A previous study on predicting MCP was carried out on a similar data set of 1,200 milk samples from Brown Swiss cows in different regions but using an FTIR spectrum of 4,000 to 900 cm⁻¹ collected with a different spectrometer (Cecchinato et al., 2009). Calibration was carried out using PLS on 4 calibration subsets of 170 to 175 cows, whereas validation was performed on the remaining 858 to 863 cows from the same herds. The calibration R² values for RCT ranged from 0.61 to 0.69 according to the different subsets. Results from Cecchinato et al. (2009) are similar to those obtained in the present study with different animals, spectrometer, and spectral interval using PLS (0.53, Table 3). The validation R² values obtained in the previous study on randomly selected cows varied from 0.61 to 0.72, whereas the values obtained in the present study using PLS methods on randomly selected herds were smaller, varying from 0.41 to 0.59 (Table 5). This was expected because the out-of-herd prediction problem identified in this study was much more challenging than that identified by Cecchinato et al. (2009).

The only published results from FTIR prediction of the remaining milk technological traits (CY_CURD, REC_FAT, and REC_PROTEIN) were obtained from the same data set as that used in the present study (Ferragina et al., 2013). The MPLS method was adopted with 10, 12, and 16 principal components for the 3 traits, respectively, some mathematical pretreatments, and, in the case of REC_PROTEIN, exclusion of the spectral regions affected by water absorbance (SWIR-MWIR and MWIR-2). The calibration R² values obtained in the previous study were 0.85, 0.49, and 0.86 for CY_CURD, REC_FAT, and REC_PROTEIN, respectively. The corresponding values obtained in the present study using the MPLS method were similar (0.74, 0.32, and 0.68, Table 3). In the previous study, the cross-validation R² values were 0.83, 0.41, and 0.81, whereas in the present research, the external validation R² values for PLS (Bayes B) were 0.66 (0.71), 0.21 (0.28), and 0.47 (0.65) for CY_CURD, REC_FAT, and REC_PROTEIN, respectively. Fat retention in the curd (REC_FAT) is more dependent on physical properties, such as fat globule size, curd-firming rate, and curd cutting (Fagan et al., 2007; Cipolat-Gotet et al., 2013) than on chemical composition, which could explain the low accuracy of all the prediction models.

To our knowledge, ours is the first study to have considered using Bayesian shrinkage and variable selection methods for predicting milk composition and technological traits using FTIR. Comparison of the methods yielded conclusive results: Bayesian methods, especially Bayes B, outperformed PLS and MPLS across traits.

Coefficients of Individual FTIR Waves

Generally, FTIR data have a larger number of predictors, so that for regression, the number of parameters (p) to be estimated (the effect on the wavelengths) is potentially greater than sample size (n). Traditional statistical methods cannot accommodate this type of large-p-small-n regression, although dimension-reduction regression, shrinkage estimation, and variable selection methods can. A naïve “variable selection” method includes preselection of predictors based on regions of the spectrum (e.g., regions affected by water absorbance) or individual wave correlations (Rutten et al., 2009). Another popular calibration method uses PLS (Soyeurt et al., 2006, 2011; Ferrand et al., 2011), which is based on reducing the size of the set of predictors. Other authors have taken a different approach to preselection of the waves whose absorbances are to be analyzed using PLS. In particular, Ferrand et al. (2011) combined a genetic algorithm (GA) with PLS and obtained a substantial reduction in the number of waves to be considered (112 to 150 waves) and increased accuracy in predicting the content of several FA in milk. Subsequently, Ferrand-Calmels et al. (2014) compared several alternative methods to PLS on untreated milk FA data from cows, sheep and goats: PLS on de-noised data using first-derivative or wavelet transformation and multi-resolution analysis, PLS on GA-based preselected waves, the use of penalization methods such as the least absolute shrinkage and selection operator (LASSO), and elastic net methods. They concluded that the best results were obtained with PLS on untreated or first-derivative data or GA-based preselected waves, according to the different FA.

Bayesian methods have not previously been used in the calibration of milk traits from FTIR spectra, although they have been studied for near-infrared spectra of other materials (Thodberg, 1996; Pérez-Marìn et al., 2012). Our results (see Figures 2 and 3) indicate that the methods examined in our study (PLS, MPLS, and the 3 Bayesian methods) use milk FTIR spectrum information in very different ways. Bayes RR is a shrinkage procedure so it does not perform variable selection but instead tends to use information from all the available wavelengths. At the other extreme, Bayes B uses variable selection, and our results suggest that predictions from this method are mostly based on a relatively small number of wavelengths with large effects. The MPLS procedure represented an intermediate situation.

The Bayes RR method assigns small effects to almost all waves, even within the regions affected by water absorbance (“water” regions), which are characterized by small-effect coefficients in MPLS and Bayes B; this was particularly clear in the case of the equations for CY_CURD. As already noted, Bayes B was highly selective among the 1,060 waves considered. For instance, estimated effects were all small in the “water” regions (SWIR, SWIR-MWIR, and MWIR-2).

In this work, different calibration models were compared and the estimated coefficients, in particular those estimated by the Bayesian models, are used as predictor variables. Being aware of this, we tried to give an alternative explanation and interpretation of the estimated coefficients obtained. We compared the Bayes B selected waves with the waves characteristic of different chemical bonds (Bittante and Cecchinato, 2013; e.g., the MWIR1 region for the FA), and the profile of estimated effects suggests that this method was able to capture a subset of wavelengths that were more informative for predicting milk composition and technological traits. Bayes B could be useful in identifying informative waves, through the solution of the n ≪ p problem, and for understanding the structure and functions of molecules involved in each trait.

CONCLUSIONS

Infrared spectroscopy is a rapid, nondestructive, and inexpensive technique that allows accurate predictions to be made of the content of many chemical compounds in various food materials, mainly because the many chemical bonds of the analyzed material affect specific areas of the IR spectrum. Being a secondary method, IRS requires a calibration equation that links the IR spectrum with a primary analysis carried out on a “training” or “calibration” set of samples. When IRS is not used to predict the content of a given substance in the sample but instead used to predict features such as ratios among nutrients, physico-technological properties, or the geographical origin or production system of the analyzed sample, the nature of the prediction is mainly correlative in nature and accuracy is lower. In these cases, the choice of method for selecting and “weighing” the information hidden in the absorbances of individual waves in the IRS could be important. The results of the present study showed that the 5 methods tested use individual wave absorbance information in very different ways, and in ways very different from the simple correlations between individual wave absorbances and milk traits and the measured value of the trait to be predicted. Compared with PLS, which is currently the most widely used calibration method, MPLS and the 3 Bayesian methods tested showed significantly greater prediction accuracy. Accuracy increased when moving from calibration to external validation methods, and when moving from PLS and MPLS to Bayesian methods, particularly Bayes A and Bayes B. As Bayes B performed best in predicting “difficult-to-predict” milk traits, it appears to be a promising tool for deriving prediction equations for use in industry to control the quality milk submissions and to make genetic improvements to these milk traits. Bayes B had a remarkable ability to select a small subset of important waves from the 1,060 in the FTIR spectrum, whereas dimension-reduction methods (e.g., PLS, MPLS) and the Bayes RR shrinkage estimation procedure tended to use information from a large number of spectral waves. Further studies are needed to understand the relationship and significance between the estimated coefficients and the chemical bonds corresponding to the wavelength with the largest estimates. Bayes B showed an impressive selection ability and this capacity could make it an interesting instrument for researchers to identify the chemical bonds more closely related to the expression of the predicted trait, which may shed light on the nature and effects of the trait studied.