Implementing Clinical Research Using Factorial Designs: A Primer

Abstract

Factorial experiments have rarely been used in the development or evaluation of clinical interventions. However, factorial designs offer advantages over randomized controlled trial designs, the latter being much more frequently used in such research. Factorial designs are highly efficient (permitting evaluation of multiple intervention components with good statistical power) and present the opportunity to detect interactions amongst intervention components. Such advantages have led methodologists to advocate for the greater use of factorial designs in research on clinical interventions (Collins, Dziak, & Li, 2009). However, researchers considering the use of such designs in clinical research face a series of choices that have consequential implications for the interpretability and value of the experimental results. These choices include: whether to use a factorial design, selection of the number and type of factors to include, how to address the compatibility of the different factors included, whether and how to avoid confounds between the type and number of interventions a participant receives, and how to interpret interactions. The use of factorial designs in clinical intervention research poses choices that differ from those typically considered in randomized clinical trial designs. However, the great information yield of the former encourages clinical researchers’ increased and careful execution of such designs.

There is increasing recognition of the need for more efficient research strategies to accelerate progress in the treatment of health and behavioral health problems (e.g., Glasgow, 2013; Glasgow, Klesges, Dzewaltowski, Bull, & Estabrooks, 2004; Riley, Glasgow, Etheredge, & Abernethy, 2013). One promising approach to enhancing research progress is the use of the factorial experiment (Collins et al., 2009; Collins, Kugler, & Gwadz, 2016). While factorial experiments have a long history of use in psychology, they have been little used in research on clinical interventions. The factorial experiment is one strategy recommended in the innovative Multiphase Optimization Strategy (MOST: Collins et al., 2009), a framework for treatment development and evaluation. MOST holds that such designs be used in screening experiments to evaluate multiple intervention components (ICs) that are candidates for ultimate inclusion in an integrated behavioral or biobehavioral treatment. Factorial experiments are recommended for this screening function since they are highly efficient (using relatively small numbers of participants to screen multiple ICs) and they yield information that shows how different ICs work together (i.e., whether they yield additive or interactive effects). In addition, because they typically experimentally evaluate relatively discrete intervention components, they have the potential to yield especially informative data on the change mechanisms activated by specific treatments. Several recent research studies using factorial designs have now appeared and these attest to the value of such designs (Cook et al., 2016; Fraser et al., 2014; McClure et al., 2014; Schlam et al., 2016).

The vast majority of investigations of treatment efficacy and effectiveness over the past 30–40 years have used the randomized controlled trial (RCT) design. While factorial designs offer some advantages for certain research goals, their use can entail critical decisions regarding design, implementation, analysis, and interpretation. This paper is intended to alert the investigator to such challenges as this may inform decisions about whether to use a factorial design, and how to do so. This paper will use smoking treatment research to illustrate its points, but its content is broadly relevant to the development and evaluation of other types of clinical interventions. Also, it will focus primarily on research design and design implementation rather than on statistical analysis (for relevent discussion of statistical analysis see Box, Hunter, & Hunter, 2005; Keppel, 1991).

Basic Elements of RCT and Factorial Designs

In an RCT an “active” treatment arm or condition is statistically contrasted with a “control” treatment arm or condition (Friedman, Furberg, & Demets, 2010). The two conditions should be identical except that the control condition lacks one or more ICs or features that are provided to the active condition. The random assignment of participants to the treatment arms means that the two groups of assigned participants should differ systematically only with regard to exposure to those features that are intentionally withheld from the controls. In smoking cessation research a common RCT design is one in which participants are randomly assigned to either an active pharmacotherapy or to placebo, with both groups also receiving the same counseling intervention.

Of course, there are many different types of RCT designs. For instance, RCTs need not have a true placebo or control condition. Thus, two different active treatments might be contrasted with one another in a two-group design, such as a comparison of two different counseling approaches (e.g., skill training vs. supportive counseling), each paired with the same medication. Neither one of these conditions would be a control condition in a strict sense, since each delivers a different form of active treatment. In addition, an RCT might have a control condition, but this might be used in comparisons with many active treatment conditions. For instance, in the comparative treatment design, multiple active treatment conditions are contrasted with a single common control condition (e.g., each of four conditions might receive a different active medication, and each is then compared with a single placebo condition).

A full factorial experiment with k factors, each comprising two levels, contains 2^k unique combinations of factor levels. In this case, a factor is a type or dimension of treatment that the investigator wishes to experimentally evaluate; a “level” is a value that a factor might take on, such as whether an intervention component is of high versus low intensity, or is provided [“on”] or not provided [“off”]. In a full factorial experiment, factors are completely crossed; that is, the factors and their levels are combined so that the design comprises every possible combination of the factor levels. For example, a recent factorial experiment (Schlam et al., 2016) crossed 5 2-level factors, resulting in 32 combinations of factor levels (see Table 1). In this case, each of the 32 unique combinations of factor levels could be viewed as constituting a different treatment or treatment condition. In a factorial experiment a person is randomly assigned to a treatment (or treatment condition) from a pool of treatments that collectively comprises all possible combinations of factor levels. Thus, the typical RCT might be viewed as just a single-factor, factorial experiment with that factor comprising two levels: one, an “on” active treatment condition and the other an “off” control treatment condition.

Table 1.

Factors and their levels in Schlam et al. 2016

	Cessation Interventions		Adherence Interventions
Condition	Medication Duration (8 vs. 26 weeks)	Maintenance Phone Counseling (Intensive vs. none)	Maintenance Medication Adherence Counseling (MMAC vs. none)	Automated Phone Adherence Counseling (Auto phone vs. none)	Electronic Monitoring Adherence Feedback (feedback vs. no feedback)
1	Extended	Intensive	MMAC	Auto phone	Feedback
2	Extended	Intensive	MMAC	Auto phone	No feedback
3	Extended	Intensive	MMAC	None	Feedback
4	Extended	Intensive	MMAC	None	No feedback
5	Extended	Intensive	None	Auto phone	Feedback
6	Extended	Intensive	None	Auto phone	No feedback
7	Extended	Intensive	None	None	Feedback
8	Extended	Intensive	None	None	No feedback
9	Extended	None	MMAC	Auto phone	Feedback
10	Extended	None	MMAC	Auto phone	No feedback
11	Extended	None	MMAC	None	Feedback
12	Extended	None	MMAC	None	No feedback
13	Extended	None	None	Auto phone	Feedback
14	Extended	None	None	Auto phone	No feedback
15	Extended	None	None	None	Feedback
16	Extended	None	None	None	No feedback
17	Standard	Intensive	MMAC	Auto phone	Feedback
18	Standard	Intensive	MMAC	Auto phone	No feedback
19	Standard	Intensive	MMAC	None	Feedback
20	Standard	Intensive	MMAC	None	No feedback
21	Standard	Intensive	None	Auto phone	Feedback
22	Standard	Intensive	None	Auto phone	No feedback
23	Standard	Intensive	None	None	Feedback
24	Standard	Intensive	None	None	No feedback
25	Standard	None	MMAC	Auto phone	Feedback
26	Standard	None	MMAC	Auto phone	No feedback
27	Standard	None	MMAC	None	Feedback
28	Standard	None	MMAC	None	No feedback
29	Standard	None	None	Auto phone	Feedback
30	Standard	None	None	Auto phone	No feedback
31	Standard	None	None	None	Feedback
32	Standard	None	None	None	No feedback

Note. This table reflects the combinations of intervention components (conditions) that is generated by the crossing of two levels of five factors in a factorial design (Schlam et al. 2016). The table shows that the crossing of the five factors generates 32 unique combinations of intervention components; participants in the experiment were randomly assigned to one of these conditions so that approximately 1/32 of the N was assigned to each condition.

Note that in the Schlam et al. (2016) experiment (Table 1), all participants in the experiment received one level of each factor. Thus, some participants would receive an “on” or “Hi” level of every factor (an active intervention component); other participants would receive the “off” or “Low” levels of every factor (the “control” levels); and other participants would receive a mixture of the two levels of the various factors. The fact that half of the participants are assigned to one of the two levels of each factor allows the entire N of the experiment to be used to evaluate the effects of each factor. For instance, to evaluate the main effect of Medication Duration, the outcomes of all participants who received Extended Medication (mean of Conditions 1–16: Table 1) would be compared to the outcomes of all those who received Standard Medication (mean of Conditions 17–32). Similarly, the entire N of the experiment is used to test interaction effects. A two-way interaction reflects the extent to which the effect of one factor differs depending on the level of another factor. For instance, the interaction of Medication Duration and Maintenance Phone Counseling is computed by examining whether the effect of Medication Duration when Maintenance Phone Counseling is “off” (the mean of Conditions 9–16 compared to the mean of Conditions 25–32) is different from the effect of Medication Duration when Maintenance Phone Counseling is “on” (the mean of Conditions 1–8 compared to the mean of Conditions 17–24). In sum, factorial experiments are efficient because each of the effects in the model is tested with the same N that would alternatively have been used to contrast just the experimental and control conditions in a 2-group RCT (assuming that each factor in the factorial experiment comprises only two levels: Collins et al., 2016).

It is possible for a factor to have three or more levels (say “High,” “Medium,” and “Low” levels). However, once a single factor has more than two levels, the experiment loses some of its efficiency since it is no longer the case that every factor level is represented by half of the total N. (If a factor has 4 levels, only 25% of the total N would be exposed to a particular level of that factor.) This means that estimations of effects at a level of that factor will tend to be less reliable, and that tests involving particular factor levels (e.g., when unpacking interaction effects) will have less power if focused comparisons are made with regard to particular factor levels (if factor levels are assumed to be quantitative, as in medication dosages, then a linear term could be used to represent multiple factor levels and conserve power). However, it is important to note that even two-level factors can be used to model intervention intensities at more than two levels. For instance, in Piper et al., (2016) three 2-level factors were used to model counseling intensity as reflected across 8 different experimental conditions (formed by crossing of the three factors: Prequit “Preparation” in-person counseling: On/Off; Postquit In-Person Cessation counseling: Intense/Minimal; and Postquit Phone Cessation Counseling: Intense/Minimal). This design, which broke-up counseling contact into three clinically meaningful factors, resulted in participants getting counseling that ranged from minimal phone and minimal in-person cessation counseling at one extreme, to relatively intense versions of all three counseling components. In theory, if increased counseling intensity as modeled with these three factors significantly enhanced outcomes, then each should yield strong additive effects relative to its control condition. Thus, this design not only roughly captured counseling intensity, but also had the potential to reveal which types of counseling were especially effective relative to their control condition (e.g., phone vs. in-person, prequit vs. post quit). Thus, the use of 2-level factors may not be as restricting as it might seem.

As an example of the statistical power that is available when each factor has two levels, the sample size used in the Schlam study (N = 544) affords power at ≥ 80% to detect main effect differences in abstinence rates between levels of each of the 5 factors (Table 1): e.g., a difference in abstinence rates of 20% vs. 31% for the two factor levels with α=.05 (two-tailed test). This is the same level of power as would exist for an RCT testing only a single active treatment versus a control treatment. Given a particular N, Type I error rate, and effect size, and regardless of number of factors, a factorial design with each factor comprising two levels, affords the same statistical power for testing the main effects of each factor as does a 2-group RCT that tests a single factor.

Whether to Use an RCT or a Factorial Design

A research design should reflect the goals of the research endeavor. In general, if the major goal of a study is to contrast directly one “treatment” with another treatment (e.g., a control treatment), then an RCT is usually the best choice. Note that here “treatment” is used to connote a set of intervention components (ICs); e.g., a particular type, dose, and duration of medication, type of counseling that is delivered for a particular number of sessions of a particular duration, and so on. Thus, if an investigator were interested, for instance, in the effects of a medication given at a particular dose and duration, and when used with counseling of a particular type, intensity, and delivery system, and how this compares with usual care (which also may contain multiple components), s/he should use an RCT. The statistical analyses would reveal whether the experimental treatment “package” differs in effects from the usual care treatment. However, conducting an RCT that comprises ICs whose joint effects are unknown, poses clear risks. This is because research shows that the effectiveness of a IC can be substantially modulated by the other ICs with which it is used (Cook et al., 2016; Fraser et al., 2014; Schlam et al., 2016); i.e., they may interact. Thus, in an RCT designed to evaluate a medication, the effect of the medication might be significantly altered by features of the psychosocial intervention that accompanies it (e.g., by the type or intensity of counseling, the number of treatment delivery modalities, and so forth). In other words, if the treatment elements in an RCT have not been experimentally tested in a factorial experiment so that their joint effects are known, the effects of an active IC (e.g., an active medication) might reflect either its main effects or its interaction with another treatment element.

One might use a dismantling or additive treatment strategy as an alternative to a factorial design to try to explore how each IC affects an outcome. For instance, if an RCT shows that a multicomponent treatment is quite effective, the investigator might conduct a series of subsequent RCTs in which elements of the treatment are systematically added or removed in order to discover which IC or set of ICs is especially responsible for the treatment’s effectiveness. Thus, in an additive or “stacked” design, the investigator might start with what he or she identifies as a base intervention IC (e.g., cessation counseling), and then systematically add other ICs that were comprised by the multifactorial treatment, resulting perhaps in the following combinations of ICs to be compared in a single 4-group RCT: 1) cessation counseling alone; 2) cessation counseling + 16 weeks of cessation medication; 3) cessation counseling + cessation medication + prequit counseling, and 4) cessation counseling + cessation medication + prequit counseling + maintenance phone counseling. This strategy would be less efficient than a factorial experiment in that a comparison of just two of the above combinations of ICs would require the same sample size to achieve adequate statistical power as would a factorial comparison of all four ICs. This is because in the additive RCT, each participant would be assigned to only one level of the treatment factor (one of the four combinations). Moreover, such a design would not distinguish between additive and interactive effects of the tested ICs.

Even if one were interested in evaluating multicomponent treatments, it is still possible that factorial designs could prove useful. For instance, it is entirely possible that one factor (Factor 1) in a factorial experiment could comprise active medication plus a collection of 3 counseling components (skill building, support, and motivational intervention) as one level, while the second level would comprise a different medication and different counseling elements. This factor, containing the two different multicomponent treatments, could appear in a factorial experiment alongside additional factors: e.g., Factor 2 could be the provision of an “active” smoking cessation focused website versus no website, and Factor 3 could be a duration factor, which would indicate whether the medication and counseling treatments contrasted in the first factor last either 26 or 8 weeks. Thus, this factorial experiment could provide a direct contrast of two multicomponential treatments such as ones that might be contrasted in an RCT (active medication + counseling versus placebo medication + counseling). In addition, it would explore the effects of other factors (the website or treatment duration) that might affect the outcome (e.g., long-term abstinence) through either main or interactive effects. It is important to note, though, that this strategy does not allow the investigator to determine the separate effects of the individual ICs that make up the multicomponent treatments: the counseling and medication ICs. Nor does it reveal how any of the ICs would work if used as a sole treatment (the main effects of other factors and interaction effects would, no doubt, influence the outcomes associated with any given component.)

In sum, unless the investigator has access to clearly relevant data (preferably from factorial experiments) s/he should have strong concerns about how the elements in a treatment (the ICs) might interact. Should 3 or 6 counseling sessions be used? Should counseling comprise both support and skill training? Should counseling be by phone or in-person? Should sessions be 10 or 30 minutes in length? Such uncertainty favors the use of a factorial design. Only factorial designs permit efficient screening of multiple ICs or dimensions (e.g., length of treatment), revealing their main effects and interactions and permitting the identification of those that are compatible or most promising (Collins et al., 2016). However, factorial experiments do not permit strong inferences about how well a particular grouping of components (occurring as levels of different factors) will work as an integrated treatment as compared to a control. After all, only a small portion of a sample in a factorial experiment will get a particular set of components (e.g., in the design depicted in Table 1 only 1/32 of the N will get a particular combination of components).

Effect Coding Effects

When taking a general linear model approach to the analysis of data from RCTs and factorial experiments, analysts must decide how to code categorical independent variables. This problem is avoided if an analysis of variance package is used, because such packages typically default to effect coding. However, as noted by Kugler et al. (Kugler, Trail, Dziak, & Collins, 2012), in regression analyses investigators may use either dummy coding (also known as reference cell coding) or effect coding (also known as unweighted effects coding) (cf. Cohen, Cohen, West, & Aiken, 2003). In dummy coding, a binary variable, a reference group (e.g., a control group) is assigned a value of zero (0) and the other group (e.g., an active treatment group) is assigned a value of one (1). Effect coding of a binary variable is the same except that the zero for the reference group is replaced with −1.

When a study design has two or more factors and interactions are included in the models, dummy coding and effect coding yield the same overall model fit, but yield different estimates of component effects, which should be interpreted differently; i.e., the parameter estimates, standard errors, and statistical significance for both main and interaction effects may differ for models computed with the two types of coding (Kugler et al., 2012). In general, when dummy coding is used, the effects corresponding to main effects in a standard ANOVA are similar to simple effects, i.e., the effect of a variable when all other variables in the model are set to the level coded as zero. A major concern with dummy coding is that a “main effect” in such models is actually a weighted combination of both the factor’s main effect and its interactions with other components; in other words, it does not correspond to the common interpretation of a main effect as being the effect of manipulating a factor averaged across the other factors. For instance, in the design depicted in Table 1, the effect of Extended Medication would be reflected by the average effect of all Extended Medication conditions (1–16) versus the average effect of all Standard Medication conditions (17–32). With effect coding, when the experimental conditions have equal (or nearly equal) numbers of participants, the main effect of a factor does not reflect the effects of interaction effects that may be present in the data.

It is worthwhile noting that the presence of other factors (and ICs) in a factorial experiment can affect the level of outcome of any single factor. Thus, the abstinence rate averaged across all Extended Medication “on” conditions would reflect the effects of other components (e.g., Automated Phone Adherence Counseling: see Table 1). Investigators should remain cognizant of this and not assume that an IC will yield a similar outcome level (e.g., abstinence rate) when tested with different ICs (or none). (Significance tests of experimental effects [e.g., main effects, interaction effects] are designed to account for the other factors included in the experiment because these other factors contribute to the means of both the “on” and “off” levels of a factor [e.g., to the means of both the Extended and Standard Medication conditions]. However, even significance tests of a given factor can be affected by the other factors included in an experiment: See discussion below.)

Thus, investigators must decide if they wish to directly compare two treatment conditions (and these may be multicomponential) with one another, without the results being affected by the presence of other experimental factors being manipulated. If they wish to do so, they would choose an RCT. Or, if the effectiveness and compatibility of potentially important features of treatment have not been empirically established, and investigators wish to examine the effects of multiple ICs or dimensions simultaneously, allowing for the separate analysis of their main and interactive effects, they would choose a factorial design.

Achieving the Right Component Comparisons

We have stressed that a factorial design typically does not provide direct tests of different combinations of ICs and therefore limits inferences about such combinations. For example, let us assume that an investigator wishes to compare the nicotine patch and varenicline as smoking cessation agents, but also wants to draw conclusions about the effectiveness of the combination of those two agents (Koegelenberg et al., 2014) relative to monotherapy (either agent by itself) and to combination NRT (e.g., patch plus lozenge). The investigator designs an experiment with the following factors: Factor 1: varenicline versus no varenicline; Factor 2: nicotine patch versus no nicotine patch; Factor 3: nicotine lozenge versus no nicotine lozenge. The crossing of the three medication factors means that participants in the experiment would get one of 8 combinations of the medications: no medication, varenicline alone, nicotine patch alone, nicotine lozenge alone, varenicline + patch, varenicline + lozenge, patch + lozenge, or all three agents. Note that this design allows the investigator to study the effects of the three individual agents versus its control (“off” level), but, it does not directly contrast the various individual medication conditions with one another, and the combination medication conditions (e.g., varenicline + nicotine patch) are not directly contrasted with the other medication conditions nor with a control condition. Rather, the design would test for an interaction between these two agents; i.e., whether they produce effects that are significantly different from the sum of their main effects. One could make meaningful inferences about how well the agents would work together by examining the main effects of each treatment versus its corresponding control condition; positive effects of each in the absence of an interaction between them would allow one to conclude that they exert additive effects, and the size of these effects would convey information about the potential magnitude of their additive effects. Further information relative to their joint effects could be gained by examining the magnitude and direction of their interactive effects. But, it remains the case that the individual medications are not directly juxtaposed to one another in the above design, nor is their combination directly statistically contrasted with another medication condition.

In the above case the investigator might be better served by an RCT that contrasts three separate treatment groups that receive: varenicline, varenicline + the nicotine patch, and combination NRT, with each group receiving the same counseling intervention in addition to medication. Of course, this design would be resource-intensive and would not provide some of the information that would be yielded by a factorial design (e.g., whether NRT and varenicline interact with one another, the effect of the nicotine patch without another medication, whether all three medications produce additive effects). Also, with an RCT, it is possible that any differences observed amongst the contrasted medication conditions would actually reflect interactions between the medications and the features of the counseling intervention, and one would never know this. In a factorial design, counseling (On/Off) could be included as an additional factor.

The above dichotomy (RCT vs. completely crossed factorial design) does not exhaust the options available to investigators (e.g., factorial experiments with factors with more than two levels; which should be considered with care because they tend to be resource intensive: Collins et al., 2009). The main point is that in decisions about design choice, the investigator must identify the principal hypotheses and select an experimental design that makes the best use of available resources to test those hypotheses, recognizing that no single experimental design can efficiently address all possible research questions.

Selecting the Right Factors and Components in a Factorial Design: Design and Clinical Considerations

Selecting the Right Number of Factors

Challenges of Numerous Factors

If an investigator decides to use a factorial design, s/he has numerous choices to make, including choices about the number and types of factors to include. The number of factors is important for several reasons.

Staff burden

It is tempting to take advantage of the efficiency of the factorial experiment and use it to evaluate many components since power is unrelated to the number of factors, and therefore, a single experiment can be used to screen many components. However, the number of factors used and the types and number of levels per factor can certainly affect staff burden. A 5-factor design with 2-levels/factor yields some 32 unique combinations of components (Table 1), and requires that at least five different active or “on” ICs be delivered. Moreover, if instead of “off” or no-treatment conditions, less intensive levels of components are used, then even more ICs must be delivered (albeit some of reduced intensity). While staff can certainly deliver a very large number of components (e.g., Piper et al., 2016; Schlam et al., 2016), it can present challenges to staff as they must learn to deliver the many different combinations of components and deliver just the right combination to the right patients, at the right times. The extent of this challenge is, of course, affected by the nature of the ICs included; including a factor such as a longer medication duration may result in little additional burden for staff, but including additional counseling interventions might greatly increase the complexity of learning and delivering ICs.

In our experience staff burden tends to be greater in our factorial experiments than in our RCTs, and the burden increases with the number of factors used. In a common form of RCT with two treatment conditions, both conditions might get the same counseling intervention, but one would get active medication and the other placebo medication. In essence, from the perspective of treatment staff, both treatment groups would receive exactly the same treatment. But, as noted above, in a factorial experiment with many factors, the staff must learn to deliver numerous combinations of components, with each combination needing to be well integrated and coherently delivered. This can be challenging since the components in a factorial experiment are not necessarily selected to be especially compatible with one another; they may represent distinct, alternative approaches to intervention, making their integration challenging when they co-occur (see “Selecting Factors: Factor and Intervention Component Compatibility” below).

Patient burden

A large number of ICs can also increase burden on participants. This burden may occur in various ways; increased visits, more assessments (to measure mechanisms of change), more work (e.g., carrying out prescribed activities, homework), a greater learning demand, and simply more time spent in treatment. Of course, this burden might be apparent only in certain conditions of an experiment (those exposed to large numbers of “on” components). With multiple, moderately intense IC’s, the differences in treatment contact, and perhaps burden, amongst treatment conditions can become quite marked. In the Schlam 5-factor experiment (e.g., Schlam et al., 2016: Table 1), at the extremes, some participants were scheduled to receive 30 more intervention contacts than were others (who were assigned to few “on” levels of factors.) Clearly, this burden could increase attrition or noncompliance.

Clinical relevance and generalizability

The number of ICs may affect the clinical relevance and generalizability of the research findings. Increased numbers of ICs and assessments may create nonspecific or attentional effects that distort component effects. For instance, while a real world application of a treatment might involve the administration of only two bundled ICs (counseling + medication), a factorial experiment might involve 6 or more ICs. Such a large number of ICs (admittedly only a portion of all subjects would get 4 or more) could either enhance outcomes with regard to the main effects of some factors (e.g., due to increased contact or involvement with the treatment team) or degrade them (due to overlap/redundancy of component effects, or alternatively fatigue, frustration, or simple inattention to critical therapeutic elements; see (Fraser et al., 2014) for an example of the last). Such effects would be manifest in interactions amongst components (e.g., the effectiveness of a component might be reduced when it is paired with other components) or in increased data missingness. Either of these influences could affect main effects. Moreover, if higher order interactions are not examined in models, researchers will not know if an intervention component is intrinsically weak (or strong) or is meaningfully affected by negative (or positive) interactions with other factors. Of course, burden and interactions amongst components might certainly affect outcomes in an RCT, but the intent of the RCT is to determine whether the treatment works as a whole (not to evaluate promise of individual ICs); thus such effects would merely be factored into the net effects of the treatment.

Finally, including numerous ICs in an experiment could cause staff or counselors to spontaneously adjust their delivery of an intervention component because of their awareness of the total intensity of treatment provided to a participant. This could certainly affect the external validity of the results. Counselors could either reduce the intensity of an intervention component when it is one of many that a participant receives, or they could increase the intensity of an intervention component if the participant is receiving little other treatment. Of course, problems with intervention fidelity may occur in RCTs as well as in factorial experiments, but they may be a greater problem in the latter where differences in treatment intensity can be much more marked and salient (e.g., four “on” counseling components versus one). In short, maintaining treatment delivery fidelity may take more care, training and supervision in a factorial experiment than in an RCT.

Statistical Significance

Including additional factors in an experiment might certainly affect the significance tests of a given factor. For instance, if the added factors have very weak effects (i.e., the outcome is unchanged whether the levels are “on” or “off”), then their presence will reduce power because they reduce the degrees of freedom in the estimate of sigma (part of the denominator of the t statistic). The reduction in power will be greater if we control experiment-wise error, due to the larger number of main and interaction effects. On the other hand, if the additional components have strong effects (i.e., the outcome changes substantially between the “on” and “off” levels of each factor), then their presence should reduce the estimate of sigma (all other things being equal) and hence increase the value of the t-statistic (often overwhelming the loss of degrees of freedom). Including numerous factors might also increase the occurrence of interactions, which might affect the magnitude of a main effect (despite the lack of correlation between main and interaction effects with effect coding). For instance, if the “on” level of Factor A is highly effective at the “off” level of Factor B, but ineffective at the “on” level of Factor B, this will certainly influence the magnitude of the main effect of Factor A versus the situation where Factor B was not included in the experiment and all participants were given instead what was the “off” level of Factor B.

Finally, it is important to note that if investigators include multiple, discrete IC’s in a factorial experiment the effects of the individual ICs may be limited to the extent that the various ICs exert their effects via similar or redundant pathways (Baker et al., 2016). Thus, to the extent that two ICs affect coping execution or withdrawal severity, their co-occurrence in the experiment could reduce estimates of their main effects via negative interaction. One might think of this as interventions “competing” for a limit subset of participants who are actually capable of change or improvement; in a sense this subsample would be spread across multiple active intervention components.

In sum, in a factorial experiment, the effects, relative effects, and statistical significance of ICs will likely change depending upon the number and types of components that co-occur in the experimental design. This arises, in part, from the fact that the effects of any given factor are defined by its average over the levels of the other factors in the experiment. It is important, therefore, for researchers to interpret the effects of a factorial experiment with regard to the context of the other experimental factors, their levels and effects. This does not reflect any sort of problem inherent in factorial designs; rather, it reflects the trade-offs to consider when designing factorial experiments.

Steps to Reduce the Burden of Multiple Components

The staff burden posed by multiple interventions may be addressed somewhat by use of dynamic databases that guide intervention delivery by staff and by using automated ICs (e.g., via automated phone calls) or automated assessments (e.g., automated emails to prompt completion of an online survey).

The choice of control conditions can also affect burden and complexity for both staff and patients. In this regard, “off” conditions (connoting a no-treatment control condition as one level of a factor) have certain advantages. They are relatively easy to implement, they do not add burden to the participants, and they should maximize sensitivity to experimental effects (versus a low-treatment control). Of course, less intensive (versus no-treatment) control conditions might be used for substantive reasons or because they ensure that every participant gets at least some treatment.

In addition, the complexity of delivering multiple combinations of components can be reduced by using a fractional factorial design (Collins et al., 2009), which reduces the number of different component combinations per the number of factors used. While implementing fewer combinations of components can make an experiment easier to conduct, such designs confound some higher order interactions (with main effects and lower order interactions), and so should be used only when higher order interactions are believed to be negligible (i.e., approximately zero). While more research on IC interactions is surely needed, our research has consistently found such interactions (Cook et al., 2016; Fraser et al., 2014; Piper et al., 2016; Schlam et al., 2016). Thus, it might be difficult in many cases to assume conditions that would justify the use of a fractional factorial design.

One point that the investigator should keep in mind regarding the increased burden imposed by numerous intervention components is that if the burden is really imposed by requirements of treatment (versus, say assessment related to research needs), then the burden or treatment complexity reflects the nature of the multiple ICs as they would occur in real world circumstances. The different ICs when used in real world settings would entail different amounts of contact or different delivery routes and their net real world effects would reflect these influences. Thus, it is important to recognize that such effects do not really constitute experimental artifacts, but rather presage the costs of complex treatments as used in real world application, presumably something worth knowing.

Advantages and Adaptations to Multiple Factors

Factorial designs can pose challenges, but they offer important advantages that can offset such challenges. Of course, there is increased efficiency as investigators can screen more components at a reduced expenditure of resources. In addition, even if large numbers of ICs produce burden, the investigator can powerfully explore the relation between burden and outcome by examining how outcomes or adherence are related to measures of burden (e.g., total contacts entailed, number of active ICs assigned, or total estimated time required). While burden may affect outcomes in a multicomponent treatment that is evaluated in an RCT, the investigator in an RCT typically has much weaker strategies to investigate it since all participants are typically exposed to very similar levels of burden (counseling + active medication versus counseling + placebo medication).

In addition, the use of a large number of factors allows for built-in evaluations of the robustness of the main effects of the ICs. This is because, as noted earlier, such effects are determined by averaging over the other component effects (with effect coding). As Fisher observed (Fisher, 1971) (also see Collins et al., 2009; Finney, 1955), if a main effect emerges against a backdrop of the averaged effects of other components, it demonstrates the robustness of such effects across considerable variability, akin to the demonstration of reliability across treatment facets as per generalizability theory (Brennan, 2001). Therefore, main effects that are resilient with regard to the effects of multiple other ICs, might be resilient to variability in real world clinical settings (although experimental factors typically do not resemble the number and types of environmental influences that often reduce external validity (Couper, Hosking, Cisler, Gastfriend, & Kivlahan, 2005). In sum, despite some complexities, factorial experiments remain the most efficient means of determining the relative effectiveness of multiple components, setting their levels of intensity, and determining how well they work together (Chakraborty, Collins, Strecher, & Murphy, 2009).

Selecting Factors: Factor and Intervention Component Compatibility

There are multiple issues to consider when selecting which particular factors and ICs to use in a factorial experiment. In an RCT, one would presumably evaluate a treatment that has been shown to work as a unified whole, or that shows great promise of doing so; its constituents are selected to work well together. In a factorial experiment though, one might select components that reflect distinct alternatives to one another (i.e., that reflect alternative views of change mechanisms or incompatible intervention dimensions: 8 vs. 26 weeks of treatment). Because factorial experiments can be used to screen multiple, potentially divergent components, it is important to consider whether such components will be compatible or “mergeable” with one another. Components that reflect divergent approaches to treatment might produce a combination that makes little sense theoretically or clinically, or that is confusing to participants. For example, counseling strategies that emphasize immediate, absolute abstinence could not be effectively meshed with approaches that emphasize gradual smoking reduction. Similarly, highly directive and nondirective counseling strategies might create a confusing amalgam for participants. One might try to avoid incompatibility by making two conflicting combinations different levels of the same factor, in which case participants would get one or the other, but not both. This means, however, that neither component would be paired with a no-treatment control, which could reduce power (if each component is at least somewhat effective) and compromise inference (e.g., in the case of nonsignificance one could not determine if both or neither component was effective).

If an investigator anticipates severe problems from including a particular factor in an experiment, perhaps due to its nature or the burden entailed, s/he should certainly consider dropping it as an experimental factor. Indeed, the MOST approach to the use of factorial designs holds that such designs be used to decompose a set of compatible ICs, ones that might all fit well in an integrated treatment package (to identify those that are most promising). That is, one should include only those ICs that are thought to be compatible, not competitive.

Adjusting ICs to Achieve Compatibility: Potential Costs

Investigators may wish to adjust ICs to enhance their compatibility with other components. For instance, investigators might choose to reduce the burden of an IC by cutting sessions or contact times. This might reduce the meaning of the factor because it might make the IC unnecessarily ineffective or unrepresentative.

Alternatively, an investigator might modify an intervention when it co-occurs with a particular, second intervention component. For instance, assume that a design has three factors; two are medication factors (e.g., varenicline, on/off, in one factor and NRT product [nicotine patch vs. nicotine lozenge], in a second factor). The third factor is an adherence factor (i.e., an automated medication counter with counseling, on/off). Thus, this experiment would address which type of NRT exerts additive or interactive effects when used with varenicline, and whether the adherence intervention exerts main or interactive effects. The investigator might tailor the adherence factor so that it is appropriate for the different types of medication that the participant is to receive (use instructions, delivery systems, and adverse events are very different for the different types of medication (Fiore et al., 2008). Obviously the investigator must make the intervention relevant to each medication type, but such adjustment raises questions. Is the adherence intervention different enough in its various forms (across medications) so that it no longer constitutes a single, coherent component? If that is true, its effects cannot be interpreted in a straightforward manner. For instance, if an interaction were found between the two medication factors and the adherence component, is it because the adherence intervention was made more or less effective due to the way it was changed, or instead because of differences intrinsic to type of medication (e.g., side effects strongly constrain adherent use for one medication and not the other)? If no adherence main effect is found, is that because this component was inconsistently delivered (adjusted for each medication)? In sum, investigators should be cognizant of the possible effects of such intervention adjustment and consider options for addressing them (e.g., by making only essential adjustments to a component, nesting an adjusted factor in the design).

We have stressed the notion that adjusting ICs can compromise interpretation. However, a failure to integrate ICs can also exact costs. How meaningful would it be to test an adherence IC that did not address the specific or characteristic challenges that pertain to the particular medication being used by a patient? In sum, the manipulation of multiple ICs may require balancing conflicting goals: viz. how to keep ICs consistent and stable each time they are used; how to make them clinically meaningful and distinct, but integrated with the other components with which they might be paired; and how to set their intensity so they are clinically meaningful but not too burdensome. Such balancing is done routinely in developing a single integrated treatment for RCT evaluation; it presents additional challenges when numerous, and perhaps dissimilar, components are evaluated in a factorial experiment yielding 30 or more IC combinations. In short, the investigator must balance the desire for a uniform intervention with its compatibility with co-occurring components, recognizing that a significant change in a factor level, contingent upon its co-occurrence with other factors, challenges the inferences that might be drawn from a factorial design.

Data analysis and Interpretation

Certainly any research evaluation of intervention effectiveness can pose analytic and interpretive challenges. However, some challenges are of particular relevance to factorial designs.

Experimentwise error

Experimentwise error may be more of a problem in factorial designs than in RCTs because multiple main and interactive effects are typically examined. In a 5-factor experiment there are 31 main and interaction effects for a single outcome variable, and more if an outcome is measured at repeated time points and analyzed in a longitudinal model with additional time effects. If more than one outcome variable is used in analyses, the number of models computed and effects tested grow quickly. Various approaches have been suggested for dealing with the challenge posed by so many statistical comparisons being afforded by complex factorial designs (Couper et al., 2005; Green, Liu, & O’Sullivan, 2002). However, it is important to note that if a factorial experiment has been conducted for the purpose of screening multiple ICs to identify those that are most promising (as per the MOST approach), then statistical significance should probably be viewed as a secondary criterion. As opposed to an RCT, where the focus is on demonstrating effects that are highly unlikely to be due to chance, the screening experiment is focused on relative promise of the tested ICs.

Mediators and nonfactorial influences

Investigators using factorial designs may wish to pay particular attention to the assessment of two types of dependent measures other that the primary outcomes: 1) mediators, and 2) variables that may potentially index unintended influences on outcomes. Mediators may be particularly informative in factorial designs since mediational influences can be associated precisely to particular, relatively discrete ICs and their interactions. For instance, in an RCT one treatment condition might get active medication, two kinds of cessation counseling (skill training and intratreatment support), and extended maintenance or relapse prevention phone calls. The other arm or condition in the RCT would receive the same intervention but with placebo instead of active medication. Conducting mediation analyses using the RCT data might reveal that increased self-efficacy and decreased craving appear to mediate the beneficial effects of active medication on long-term abstinence. However, it is unclear that it is really the main effect of medication that accounts for long term abstinence. Since medication is bundled with other ICs it is impossible to determine if its effects are due to the medication per se or instead due to its interactions with other ICs (medication may allow patients to benefit more from counseling). Thus, by systematically manipulating the provision of relatively discrete, individual ICs, factorial experiments may allow investigators to achieve a better understanding of how ICs work, an understanding that may be invaluable for combining them so that they activate complementary mechanisms.

Investigators may also wish to include measures in their factorial experiments that assess potential alternative explanations for their findings. We have discussed how the manipulation of multiple treatment factors might create unintended effects due to overall burden, inducement of optimism, apparent incompatibility of components or delivery routes, differential staff delivery, and so on. Investigators should consider using measures that would be sensitive to such effects. For instance, investigators might assess measures of burden (treatment fatigue) and determine if these are especially highly related to particular ICs or to an increasing number of ICs. Indeed, even without the use of special assessments, investigators might correlate the number of ICs a person receives (regardless of type) to outcomes. Interestingly, in our factorial research thus far, the best outcomes (across multiple experiments) tend to be produced by combinations of two ICs, not more (Cook et al., 2016; Fraser et al., 2014; Piper et al., 2016; Schlam et al., 2016), suggesting the possible influence of burden, or ceiling effects (e.g., the ICs produce effects via redundant mechanisms).

Interactions: Challenges to Interpretation

Chakraborty et al., (Chakraborty et al., 2009) noted that factorial designs may not perform optimally for intervention selection in cases where there are weak main effects, but relatively strong interaction effects. Unfortunately, this situation may be a fairly common occurrence in factorial experiments of clinical interventions (e.g., Cook et al., 2016; Piper et al., 2016; Schlam et al., 2016).

Complex interactions can produce several challenges. For instance, some interactions may be due to the overall burden due to subjects receiving large numbers of components. This might result in subadditive or negative interactions in which interventions produce less benefit, or even produce net decreases in benefit, when they co-occur with another intervention(s). This can pose interpretive challenges as it may be difficult to separate the effects of a component per se from the impact of burden. In addition, a higher order interaction may not be due to a single uniquely performing combination of ICs, but rather due to multiple combinations of ICs, some of which may overperform, and others underperform, in relation to what is implied by relevant main effects and lower order interactions.

Figure 1, (from Cook et al., 2016) arises from a 4-factor experiment that illustrates some of the challenges of interpreting interactions for the purpose of identifying especially promising ICs. This figure shows the data patterns associated with a significant interaction amongst factors delivered to smokers who were not yet willing to make a quit attempt, but who were willing to try to reduce their smoking. In theory, smoking reduction should ultimately lead to quit attempts and greater quitting success (cf. Baker et al., 2011; Moore et al., 2009). The four factors were: Nicotine Gum (on/off), Nicotine Patch (on/off), Behavioral Reduction Counseling (on/off), and Motivational Interviewing (on/off). This interaction was generated by an analysis of covariance on percent reduction in smoking rate (cigarettes smoked/day) that occurred from baseline to 12 Weeks after the start of treatment. Figure 1 shows that it is difficult to definitively identify the most promising combination of ICs. In essence, three 2-component combinations look essentially indistinguishable in terms of smoking reduction: Nicotine Gum + Behavioral Reduction, Nicotine Gum + Nicotine Patch, and Behavioral Reduction + Motivational Interviewing. Because all four of the components are involved in one or more of the best performing combinations, it might be tempting to think that the optimal combination would comprise all four. Figure 1 shows that this is not the case as the combination of all four performed relatively poorly. Thus, interaction effects may not highlight a clear “winner” in terms of the most promising IC(s). (Moreover, interactions do not directly test whether a combination of components is superior to the condition where all factors are set to the “off” level.)

Figure 1. Outcomes Reflecting the 4-way Interaction from the Cook et al., (2016) Experiment.

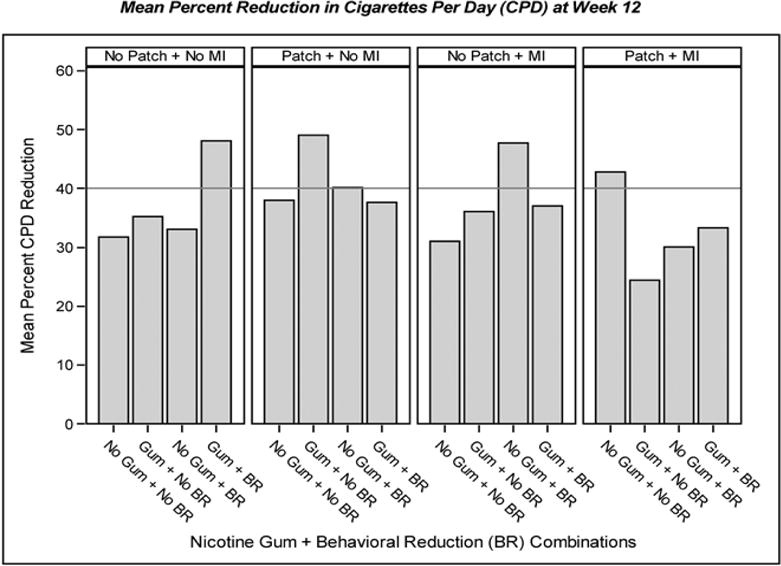
Note. This figure describes the results of a four-factor factorial experiment (Cook et al., 2016) and depicts the data patterns that reflect the significant 4-way interaction found in the experiment. Participants were smokers who were trying to reduce their smoking and the outcome is mean percent smoking reduction 12 weeks after treatment initiation. The four factors were: “Gum” = Nicotine Gum vs. “No Gum”; “Patch” = Nicotine Patch vs. “No Patch”; “BR” = Behavioral Reduction Counseling vs. “No BR”; and “MI” = Motivational Interviewing vs. “No MI”.

It is important to note that interpretation of complex higher order interactions may not be aided by simple effects testing. First, it is highly unlikely that such testing would have distinguished amongst the three leading combinations shown in Figure 1 (the differences in outcomes are too small). Second, such tests would have been grievously underpowered, and increasing the sample size to supply the needed power would have compromised the efficiency of the factorial design (Green et al., 2002). Thus, instead of using simple effects tests, researchers might interpret interaction effects via practices used in engineering; i.e., by inspecting differences in performance of one or more ICs across levels of other relevant ICs, and then relating this information to relevant main effects (cf. Box et al., 2005; Cox & Reid, 2000). This, of course, has limitations, such as not permitting strong inference regarding the source(s) of the interaction.

Higher order interactions can reflect complex patterns that defy easy interpretation. However, they also reveal information that is unique and of potentially great value. Further, this problem is reduced if factorial designs are used as screening experiments, whose purpose is not to identify the single best combination of ICs (Collins et al., 2009). Rather such experiments are used to identify the ICs that are amongst the best. Therefore, finding that several combinations of ICs yield promising effects is compatible with the goal of a screening experiment, which is to distill the number of ICS to those holding relatively great promise. In keeping with this, the data in Figure 1 suggest that we can winnow potentially promising combinations from 16, to 3. Which one of those three might be deemed most promising might be addressed via other criteria (effects on abstinence, costs, and so on) and in a follow-up RCT.

Privileging Main Effects

The challenges that may arise in interpreting interactions support strategies to select ICs based chiefly on main effects (Collins et al., 2009; Wu & Hamada, 2011), which is the approach taken in engineering and other fields that use screening experiments (Wu & Hamada, 2011). This approach has several advantages. For instance, relative to some complex interactions, main effects are more easily interpreted (Collins et al., 2014); a factor’s main effects are interpretable even when it interacts with other factors. When effect coding is used, each effect is orthogonal to every other effect in the analysis model (orthogonal when the n’s are equal in each experimental condition, and nearly orthogonal when the n’s differ by a modest amount). Thus, a significant main effect reflects an experimental effect that occurs on average across all other factors in the model even when the relevant factor is involved in significant interactions (Chakraborty et al., 2009). (Interactions should be considered in interpretations and selection; they just do not invalidate the main effect.) Collins and her colleagues have proposed relatively straightforward steps for identifying promising components, steps that arise from engineering research and that prioritize main effects versus interactions (Collins et al., 2014).

In addition, the efficiency of a factorial experiment depends in part on the extent to which higher order interactions are not found. If interactions are found, and inferential statistics must be used to unpackage such interactions, such simple effects tests would require examining the effects of ICs in only subgroups of the sample. In essence, if it is necessary to follow-up an interaction by identifying which particular subgroups differ from one another, some of the efficiency of the factorial design may be lost. However, it is important to note that interaction effects can be highly informative without simple effects tests (Baker et al., 2016; Box et al., 2005).

Conclusions

Ambitious, multifactor, factorial experiments designed to evaluate clinical ICs can and do work for the purpose of intervention component screening (Baker et al., 2016; Collins et al., 2016; Collins, Murphy, & Strecher, 2007; Fraser et al., 2014). We are confident, based upon our conduct of several factorial experiments on clinical interventions (Baker et al., 2016; Cook et al., 2016; Fraser et al., 2014; Piper et al., 2016; Schlam et al., 2016), that such experiments can be designed and used to identify ICs that are especially worthy of further investigation with an eye to assembling an optimized treatment package (Collins et al., 2016). We believe that their potential to yield unique data, and to do so efficiently, should make factorial screening experiments a core strategy in the process of developing effective treatments (Collins et al., 2016). For instance, not only do such designs permit the screening of multiple intervention components in a single experiment, but compared with RCT designs, factorial experiments permit more precise estimates of mediational effects. This paper highlights decisions and challenges related to the use of factorial designs, with the expectation that their careful consideration will improve the design, implementation, and interpretation of factorial experiments.

Highlights.

1. Factorial designs are highly efficient but offer special challenges

2. Review of issues that determine whether a factorial design is appropriate

3. Review of problems may arise when using factorial designs (e.g., interaction effects)

4. Strategies for addressing the challenges that may arise from factorial designs