Demographic stability and high historical connectivity explain the diversity of a savanna tree species in the Quaternary

Abstract

Background and Aims Cyclic glaciations were frequent throughout the Quaternary and this affected species distribution and population differentiation worldwide. The present study reconstructed the demographic history and dispersal routes of Eugenia dysenterica lineages and investigated the effects of Quaternary climate change on its spatial pattern of genetic diversity.

Methods A total of 333 individuals were sampled from 23 populations and analysed by sequencing four regions of the chloroplast DNA and the internal transcribed spacer of the nuclear DNA. The analyses were performed using a multi-model inference approach based on ecological niche modelling and statistical phylogeography.

Key Results Coalescent simulation showed that population stability through time is the most likely scenario. The palaeodistribution dynamics predicted by the ecological niche models revealed that the species was potentially distributed across a large area, extending over Central-Western Brazil through the last glaciation. The lineages of E. dysenterica dispersed from Central Brazil towards populations at the northern, western and south-eastern regions. A historical refugium through time may have favoured lineage dispersal and the maintenance of genetic diversity.

Conclusions The results suggest that the central region of the Cerrado biome is probably the centre of distribution of E. dysenterica and that the spatial pattern of its genetic diversity may be the outcome of population stability throughout the Quaternary. The lower genetic diversity in populations in the south-eastern Cerrado biome is probably due to local climatic instability during the Quaternary.

INTRODUCTION

Phylogeography has been used to understand the patterns and processes that caused geographical distributions of gene lineages (Avise, 1998). However, due to a lack of fossil records for most species in the Neotropics (Hugall et al., 2002), our understanding of dispersal routes and the historical dynamics in the geographical distribution of these species is compromised. In this context, the use of ecological niche modelling (ENM) coupled with phylogeographical statistical analyses has been proposed to test spatially explicit demographical hypotheses (see Carstens and Richards, 2007; Richards et al., 2007; Collevatti et al., 2012a, 2013a, 2015a). In addition, historical lineage dispersal may be recovered using a coalescent model framework based on a relaxed random walk (RRW) model (Lemey et al., 2009, 2010). Combined with ecological niche modelling, this approach can be an important addition to phylogeographical inferences, as it reproduces explicit dispersal routes in time and space (see Collevatti et al., 2015a, b).

Quaternary climate changes have resulted in significant shifts in the geographical distributions of plant species (Comes and Kadereit, 1998) and are considered a key cause of speciation (Rull, 2008). In Brazil during glacial periods of the Quaternary, there was no advance of glaciers as occurred in the northern hemisphere; instead, during the Last Glacial Maximum (LGM) there was a drop in temperature and humidity (Salgado-Labouriau et al., 1998). In the Cerrado biome, the pollen fossil records indicate that the LGM was characterized by a drier climate (Salgado-Labouriau et al., 1998; Behling, 2003), and thus there was a wider distribution of grasslands at the beginning of the Holocene (6000–5000 BP) compared to the end of the period (Behling and Hooghiemstra, 2001). Due to the high geomorphological diversity, soil and climate heterogeneity, and the large number of endemic species, the Cerrado biome is a good model for understanding the role of historical processes in the geographical patterns of species genetic diversity and distribution (see Collevatti et al., 2012a, b, c, 2013b, c; Novaes et al., 2013).

Phylogeographical studies have revealed that the Quaternary climate changes have differently affected the genetic diversity and phylogeographical patterns of plant species in the Cerrado biome (e.g. Collevatti et al., 2012a, b, 2015b; Novaes et al., 2013; Ribeiro et al., 2016) because the effects depend on biological characteristics of each species, as well as geographical features and climate change at each site (Hewitt, 2000). For instance, both Caryocar brasiliense (Collevatti et al., 2012a) and Tabebuia aurea (Collevatti et al., 2015b), widely distributed savanna tree species, showed smaller ranges at the LGM than at the present day and higher genetic diversity in populations at the edge of the distribution. By contrast, Tabebuia impetiginosa from seasonally dry forest showed a retraction from the LGM to the present day and high genetic diversity in most populations (Collevatti et al., 2012c). Furthermore, such studies have also revealed evidence of recent colonization for the southern region of the Cerrado biome in contrast to the northern region (Novaes et al., 2013).

Eugenia dysenterica is a widely distributed tree species in the savannas of the Cerrado biome. Pollination is mainly performed by bumble bees (Bombus sp.) (Proença and Gibbs, 1994), and seeds are dispersed by mammals such as monkeys and bats (Artibeus lituratus for example; Bredt et al., 2012). Due to its wide distribution, E. dysenterica can be an appropriate biological model to test biogeographical hypotheses for the Cerrado biome. Previous studies using both isozymes and microsatellite markers showed moderate genetic diversity and relatively high genetic differentiation among populations of E. dysenterica (Telles et al., 2003; Telles and Diniz-Filho, 2005; Barbosa et al., 2015). In addition, the patterns of genetic differentiation in this species cannot be explained solely by way of isolation by distance or stepping-stone models (Barbosa et al., 2015), suggesting that historical range shifts may have affected the patterns of genetic differentiation. Moreover, Diniz-Filho et al. (2016) showed that the low genetic diversity in populations in the south-eastern region of the species’ range might be related to historical climatic instability.

Here, we undertook an extensive sampling of E. dysenterica populations encompassing a large area of the Cerrado biome and used a multi-model inference approach, combining the RRW model, ENM and statistical phylogeography to reconstruct the demographical history and dispersal routes of E. dysenterica. The pollen fossil records (Behling and Hooghiemstra, 2001) and phylogeographical studies (e.g. Collevatti et al., 2012a; Bonatelli et al., 2014) on Neotropical savannas have (Telles and Diniz-Filho, 2005; Barbosa et al., 2015) shown a range expansion during the Quaternary (from LGM to the present day) and previous studies on E. dysenterica revealed a significant genetic structure, mainly in the south-eastern portion of the species distribution. Thus, we expected populations of E. dysenterica to show a range retraction during glacial phases with low genetic diversity in peripheral populations and in south-east Brazil, which probably was the last region of the Cerrado biome to become environmentally suitable after the LGM.

MATERIALS AND METHODS

Population sampling

We sampled 333 adult individuals of Eugenia dysenterica D.C. (Myrtaceae) from 23 localities in the Cerrado biome (Fig. 1, Supplementary Data Table S1 in Appendix S1). Samples from a single individual of Eugenia blastantha (O. Berg) D. Legrand and Eugenia uniflora L. were included as outgroups in the coalescent analyses (Table S1).

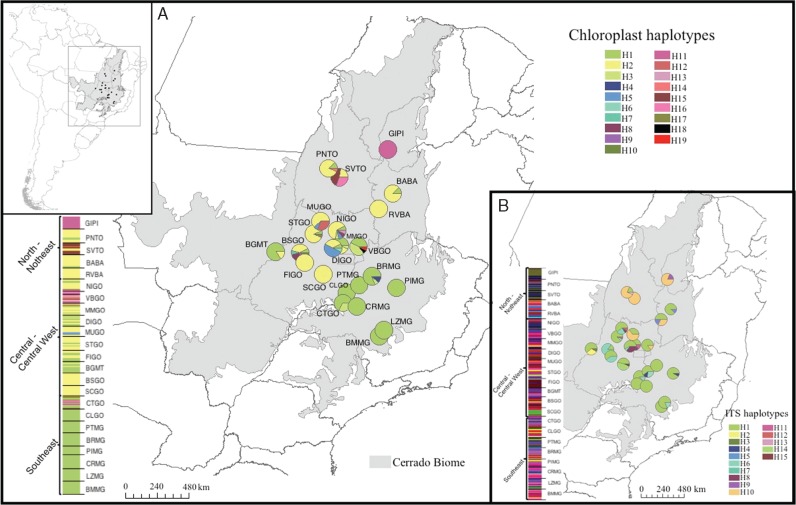
Fig. 1.

Geographical distribution of haplotypes and Bayesian clustering for cpDNA (A) and ITS (B), based on 23 populations of Eugenia dysenterica sampled in the Cerrado biome. Different colours were assigned for each haplotype according to the figure legend and the pie charts represent the haplotype frequency in each sampled population. For Bayesian clustering, each colour represents an inferred cluster (seven clusters for cpDNA and 11 for ITS) grouped by Cerrado geographical regions. For details on population codes and localities see Table S1.

Sequencing analyses

Four intergenic spacers of chloroplast DNA (cpDNA): psbA-trnH (Azuma et al., 2001), trnS-trnG, trnC-ycf6 (Demesure et al., 1995), and trnL-trnlD (Taberlet et al., 1991) and the nuclear ribosomal (nrDNA; hereafter ITS) region ITS1 + 5·8S+ITS2 (Desfeux and Lejeune, 1996) were sequenced. The fragments were amplified by polymerase chain reaction (PCR) in a 20-μL volume containing 1·13 μm of each primer, 1·15 units of Taq DNA polymerase (Phoneutra, Brazil), 250 μm of each dNTP, 1× reaction buffer (10 mm Tris-HCl, pH 8·3, 50 mm KCl, 1·5 mm MgCl₂), 375 μg of bovine serum albumin and 4·5 ng of template DNA. The amplifications were performed using a GeneAmp PCR System 9700 (Applied Biosystems, Foster City, CA, USA) using the following conditions: 94 °C for 5 min (one cycle); 94 °C for 1 min, annealing for 1 min (64 °C for psbA-trnH, 62 °C for trnL-trnlD, 60 °C for trnS-trnG, 58 °C for trnC-ycf6 and ITS), and 72 °C for 1 min (35 cycles); and 72 °C for 30 min (one cycle). The PCR products were sequenced on an ABI 3500 automated DNA sequencer (Applied Biosystems) using the BigDye Terminator cycle sequencing kit (GE Health-Care, Uppsala, Sweden) according to the manufacturer’s instructions. All fragments were sequenced in both forward and reverse directions.

Sequences were analysed and edited to obtain consensus using the software SEQSCAPE 2.6 (Applied Biosystems). Multiple sequence alignments were obtained using ClustalX (Thompson et al., 1997). For statistical analyses, the sequences of the four chloroplast regions were concatenated.

Genetic diversity and population structure

Nucleotide (π) and haplotype (h) diversities (Nei, 1987) were estimated for each population and overall populations using the software Arlequin 3.11 (Excoffier et al., 2005). The phylogenetic relationships among haplotypes were inferred using median-joining network analysis implemented by the software Network 4.6.2 (Forster et al., 2004).

To test the hypothesis of population differentiation, we performed an analysis of molecular variance (AMOVA, Excoffier et al., 1992) and estimated F_ST using Arlequin 3.11 (Excoffier et al., 2005), with 10^000 random permutations. We also analysed population structure using Bayesian clustering implemented in the software BAPS v5.3 (Corander et al., 2008). cpDNA and ITS were analysed as separate partitions with a linkage model for sequences. We performed population admixture analysis based on mixture clustering with estimated number of clusters (K) and an upper limit of K = 23.

Phylogeographical reconstruction

Population demography.

To test the hypothesis of effective population size retraction followed by an expansion, we used Fu’s (1997) neutrality test implemented in Arlequin 3.11 (Excoffier et al., 2005). We then used the coalescent model (Kingman, 1982) to estimate demographical parameters. For this analysis, cpDNA and ITS data were combined, but separate priors were given for each partition. No heterozygous individuals were found in ITS sequences; therefore, recombination was neglected in all coalescent analyses. To set the priors, evolutionary model selection for both cpDNA and ITS regions was performed using Akaike’s information criterion (AIC), as implemented in the software JMODELTEST 2 (Darriba et al., 2012). For chloroplast regions, the model F81+I was selected (−lnL = 2734·3086) and for ITS, HKY was selected (−lnL = 722·0467).

The demographic parameters θ = 2μN_e (mutation parameter, where N_e is effective population size), g [exponential growth rate, where θ_t = θ_now exp (−gt), t is time in mutational units] and M = 2N_em/θ (scale migration rate, where m is the migration rate) were estimated based on the Bayesian method using the Markov chain Monte Carlo (MCMC) approach implemented in Lamarc 2·1·9 (Kuhner, 2006). The analyses were run with 20 initial chains of 4000 steps and three final chains of 50^000 steps. We performed two runs to check for convergence and stability of the outcome using Tracer 1·6 (Rambaut and Drummond, 2007) and the combined results were then generated. Results were considered when effective sample size (ESS) was ≥ 200. Effective population size was obtained from θ (Kingman, 1982) using a generation time of 15 years (based on expert opinion).

Finally, we performed a coalescent extended Bayesian skyline plot (EBSP) analysis (Heled and Drummond, 2008) implemented in BEAST 1·8·3 (Drummond et al., 2012) to understand changes in effective population size throughout time. We used the substitution models reported above and the relaxed molecular clock model (uncorrelated lognormal) for both chloroplast and ITS. For chloroplast regions, we used the substitution rate previously estimated for chloroplast non-coding regions, 1·52 × 10⁻⁹ per nucleotide year⁻¹ (Yamane et al., 2006). For ITS, Kay et al. (2006) estimated the mutation rates for different Angiospermae families. We used the average mutation rate for the family Fabaceae (the phylogenetically closest family to Myrtaceae in the work). The mutation rates for Fabaceae species ranged from 2·00 × 10⁻⁹ to 3·30 × 10⁻⁹ per nucleotide year⁻¹, with an average of 2·92 ± 0·69 × 10⁻⁹ per nucleotide year⁻¹. Three independent analyses were run for 30 million generations and convergence and stationarity were checked using Tracer 1·6. Results were considered when ESS was ≥200 and the independent runs were combined.

Coalescent tree and time to most recent common ancestor.

The time to most recent common ancestor (TMRCA) was estimated using coalescent analysis implemented in the software BEAST 2 (Bouckaert et al., 2014), assuming a relaxed molecular clock (uncorrelated lognormal). The ucld.stdev parameter (standard deviation of the uncorrelated lognormal relaxed clock) and the coefficient of variation were inspected for among-branch rate heterogeneity within the data. We also assumed a constant population size based on the results of the coalescent analysis performed with Lamarc and the EBSP (see results below) and the same evolutionary models and mutation rates used in the EBSP. For this analysis, we included the outgroup sequences from E. blastantha and E. uniflora. MCMC conditions and number of runs also remained unchanged. The independent runs were analysed using Tracer1·6, and results were considered when ESS ≥ 200. We also ran an empty alignment (sampling only from priors) to verify the sensitivity of the results to the given priors. The analysis showed that our data are informative because posterior values differed from those obtained from empty alignment.

Lineage dispersal

We inferred phylogeographical diffusion processes using the RRW model and simultaneously reconstructed the demographic history through time using the framework proposed by Lemey et al. (2009, 2010). We performed three analyses, one using both cpDNA and ITS partitions with unlinked priors but sharing the same location matrix, and the others using each region (cpDNA and ITS) separately to detect different contributions of seed and pollen dispersal. We used Bayesian stochastic search variable selection (BSSVS), which considers a limited number of rates (at least k−1) to explain the phylogenetic diffusion process, and sampling locality was added as discrete characters (k = 23 localities). Priors for sequence evolution were the same as for TMRCA analysis. For the diffusion process, we used the symmetric substitution model that uses a standard continuous-time Markov chain (CTMC) in which the transition rates between locations are reversible. For tree prior, we used the coalescent GMRF Bayesian Skyride model (Minin et al., 2008) and for location state rate, the prior CTMC rate reference (Ferreira and Suchard, 2008). Four runs were performed with 30 million generations, and stability was analysed using Tracer 1·6 (ESS ≥ 200). The annotate tree (maximum clade credibility tree) was generated with 10 % of burnin. Spatio-temporal reconstruction was performed using SPREAD 1·0·6 (Bielejec et al., 2011). We also analysed the well-supported transition rates using the Bayes factors (BF) test and transition rates between localities were considered only for BF > 3·0.

Demographical history simulation

Palaeodistribution modelling and demographical hypotheses.

We obtained 163 occurrence records of E. dysenterica across the Neotropics (Supplementary Data Table S2 in Appendix S1; Fig. S1 in Appendix S2) from online databases, such as ‘Lista de Espécies da Flora do Brasil’ (http://floradobrasil.jbrj.gov.br) and Species Link (http://splink.cria.org.br). All records were examined for probable errors and duplicates, and the nomenclature was examined for synonymies. The occurrence records were mapped in a grid of cells of 0·5° × 0·5° (longitude × latitude), encompassing the Neotropics to generate the matrix of presences used to calibrate the ENMs.

Environmental space was characterized by climatic simulations for pre-industrial (representing current climate conditions), mid-Holocene (6 ka) and LGM (21 ka) conditions derived from four atmosphere−ocean general circulation models (AOGCMs): CCSM4, CNRM-CM5, MIROC-ESM and MRI-CGCM3 (see Supplementary Data Table S3). These AOGCMs provide spatially explicit climatic simulations for the three periods at the resolution of 0·5° of latitude and longitude, and were obtained from the ecoClimate database (www.ecoclimate.org; Lima-Ribeiro et al., 2015).

From each AOGCM, we built environmental layers composed of five bioclimatic variables: annual mean temperature, annual temperature range, precipitation during driest and wettest months, and precipitation during the warmest quarter. These variables were selected using factorial analysis with Varimax rotation from the 19 bioclimatic variables available from the ecoClimate. We also included the subsoil pH (30–100 cm; Harmonized World Soil Database 1.1; FAO et al., 2009) as a ‘constraint variable’ to improve ENMs.

The distribution of E. dysenterica was first modelled for current (pre-industrial) climate, and then projected onto mid-Holocene and LGM palaeoclimatic conditions to infer its spatial distribution at that time. For this, we used 13 different algorithms (see Supplementary Data Table S4).

The procedures for modelling were performed using the ensemble approach (for details see Diniz-Filho et al., 2009; Collevatti et al., 2013b). The combination of all ENMs and AOGCMs resulted in 52 independent predictive maps (13 ENMs × 4 AOGCMs) for each time period (pre-industrial, 6 ka, 21 ka). Furthermore, a hierarchical ANOVA was used to quantify and map the uncertainties due to modelling components (13 ENMs × 4 AOGCMs × 3 time periods; for details see Terribile et al., 2012).

The 52 predictive maps were combined to obtain the consensus map for each time period. The consensus maps from all time periods were combined to generate a map of the historical refugia (stable environments through time). To generate this map, we considered all grid cells with suitability values ≥0·5 in the three time periods as refugia.

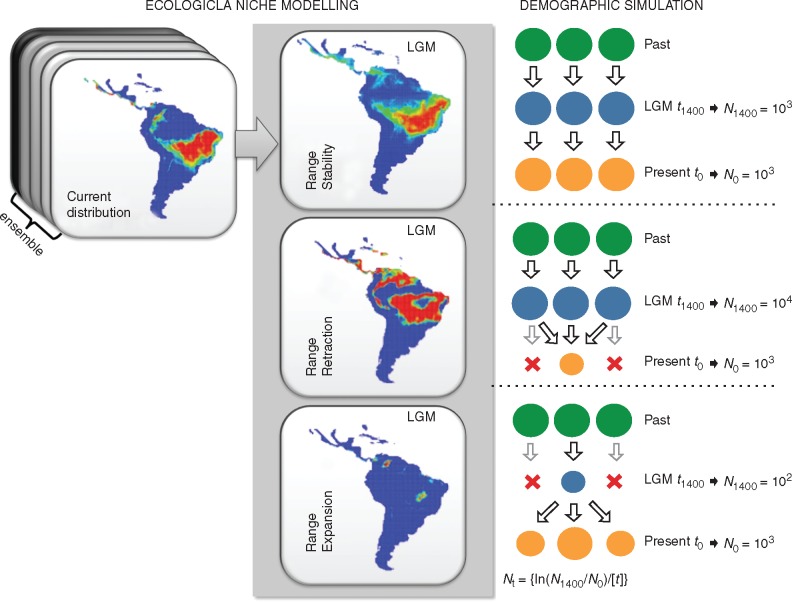
To set the demographical hypotheses, we first classified the 52 predictive maps using the range difference between predictive maps for current and LGM distributions. The maps were classified according to three general demographical scenarios: (1) ‘Range Stability’: no difference in range size; (2) ‘Range Retraction’: range size larger in the LGM than at the present day; and (3) ‘Range Expansion’: range size smaller in the LGM than at the present day.

Demographic history simulation.

The demographic scenarios were simulated based on coalescent analysis (Kingman, 1982), using the software BayeSSC (Excoffier et al., 2000) according to the framework described by Collevatti et al. (2012c, 2013b). We used the demographic parameters generated with Lamarc software and the same priors used in TMRCA analysis. The number of generations until the LGM (21 ka) was calculated using a generation time of 15 years.

To model the demographic scenarios, we considered population dynamics backwards from t₀ (present) to t₁₄₀₀ (generations ago at 21 ka), with sizes N_t = [ln(N₁/N₀)/(t)]. At t₀, all demes had the same population size N₀ and the N₁ shift among scenarios according to our theoretical expectation (see Fig. 2 for details). Due the variation in E. dysenterica effective population sizes (Table 1), we performed simulations with N₀ = 100, 1000 and 10^000 for all scenarios. The scenario ‘Range Expansion’ was simulated with an exponentially negative population growth from present to 21 ka, reaching N₁₄₀₀ = 10 if N₀ = 100, or N₁₄₀₀ = 100 if N₀ = 1000, and N₁₄₀₀ = 1000 if N₀ = 10^000. By contrast, the ‘Range Retraction’ scenario was simulated with an exponentially positive population growth, attaining N₁₄₀₀ = 100 if N₀ = 10^000, or N₁₄₀₀ = 10^000 if N₀ = 1000, and N₁₄₀₀ = 1000 if N₀ = 100. To simulate migration, we considered that all current demes are descendants from lineages originally in deme 1 at t generations ago; that is, while the coalescent tree builds back through time, there is a 0·01 per generation chance that each lineage in deme x will migrate to deme 1. For the ‘Range Retraction’ hypothesis, we considered that each lineage in deme x will migrate to deme 1 and then shrink until extinction.

Fig. 2.

Schematic representation the demographic history scenarios simulated for the 23 populations of Eugenia dysenterica sampled in the Cerrado biome, and their geographical representation as predicted by ecological niche models (ENMs). Circles represent hypothetical demes and indicate population stability or shrinkage through time. LGM, Last Glacial Maximum; Pres, present-day; N₀, effective population size at time t₀ (present); N₁, effective population size at time t₁₄₀₀ (1400 generations ago); N_t, logarithmic function for effective population size variation in coalescent simulation. The migration rate was 0·01 per generation.

Table 1.

Genetic diversity and demographic parameters for the 23 populations of Eugenia dysenterica for combined cpDNA data and for ITS.

Population	N	cpDNA				ITS				Combined cpDNA and ITS nrDNA
		k	h	π	π (SD)	k	h	π	π (SD)	θ	θ (95 % interval)	Ne	Ne (95 % interval)	g	g (95 % interval)
North-North-east
GIPI	16	1	0·0000	0·0000	−	2	0·3250	0·0007	0·0009	0·0000362	0·000019–0·000506	14·047	7·373–196·352	863·5559	−411·8888 to 948·7377
PNTO	16	3	0·3417	0·0002	0·0002	3	0·4250	0·0012	0·0012	0·0002920	0·000124–0·001434	113·310	48·118–556·461	639·9023	−419·4743 to 954·7830
SVTO	13	3	0·6923	0·0027	0·0016	1	0·0000	0·0000	−	0·0001980	0·000029–0·000543	76·834	11·253–210·710	623·0991	−422·3260 to 946·8101
BABA	16	2	0·2333	0·0001	0·0002	2	0·2333	0·0010	0·0011	0·0003080	0·000032–0·001010	119·519	12·418–391·929	242·4670	−423·4413 to 935·2922
RVBA	12	1	0·0000	0·0000	−	3	0·6667	0·0024	0·0019	0·0002590	0·000148–0·000311	100·504	57·431–120·683	883·5572	−415·9880 to 965·4857
Central-Central West
NIGO	14	6	0·6044	0·0006	0·0005	2	0·4945	0·0011	0·0011	0·0005410	0·000278–0·001770	209·934	107·877–686·845	705·3689	−416·4996 to 953·7907
VBGO	14	4	0·6703	0·0009	0·0006	2	0·2637	0·0006	0·0008	0·0006370	0·000187–0·001271	247·187	72·565–493·209	387·6548	−416·3308 to 943·4803
MMGO	14	3	0·6044	0·0004	0·0004	4	0·5824	0·0021	0·0017	0·0012940	0·000382–0·002367	502·134	148·234–918·510	877·6107	−408·9587 to 966·3562
DIGO	14	4	0·6593	0·0006	0·0005	3	0·5824	0·0025	0·0020	0·0003550	0·000170–0·001037	137·757	65·968–402·406	581·2074	−418·0161 to 956·9668
MUGO	13	3	0·5641	0·0020	0·0012	4	0·6026	0·0019	0·0016	0·0005210	0·000129–0·001375	202·173	50·058–533·566	276·9472	−435·1879 to 941·9162
STGO	16	3	0·2417	0·0002	0·0002	3	0·2417	0·0006	0·0007	0·0003140	0·000092–0·000662	121·847	35·700–256·888	836·3442	−415·9074 to 943·8014
FIGO	13	6	0·8205	0·0011	0·0007	2	0·2821	0·0006	0·0008	0·0008090	0·000215–0·001703	313·931	83·430–660·846	732·0306	−432·1317 to 954·6408
BGMT	13	2	0·2821	0·0001	0·0002	3	0·5641	0·0034	0·0025	0·0002160	0·000050–0·001008	83·818	19·402–391·153	291·2787	−420·1152 to 939·9433
BSGO	15	1	0·0000	0·0000	−	2	0·5143	0·0012	0·0012	0·0001700	0·000074–0·000382	65·968	28·716–148·234	553·7289	−418·6677 to 947·1393
SCGO	13	1	0·0000	0·0000	−	3	0·6154	0·0036	0·0026	0·0003490	0·000167–0·000449	135·429	64·804–174·234	869·0465	−421·7687 to 957·5895
South-east
CTGO	15	2	0·4762	0·0005	0·0004	1	0·0000	0·0000	−	0·0000897	0·000017–0·000248	34·808	6·597–96·236	813·2421	−427·2343 to 943·2240
CLGO	16	1	0·0000	0·0000	−	2	0·2333	0·0005	0·0007	0·0001710	0·000030–0·000277	66·356	11·641–107·489	697·5346	−415·8263 to 952·0951
PTMG	15	1	0·0000	0·0000	−	3	0·5905	0·0017	0·0015	0·0001230	0·000113–0·000232	47·730	43·849–90·027	392·2598	−432·0983 to 944·6149
BRMG	16	2	0·3417	0·0003	0·0003	1	0·0000	0·0000	−	0·0000916	0·000028–0·000535	35·545	10·865–207·606	786·5530	−430·9998 to 952·9603
PIMG	12	1	0·0000	0·0000	−	2	0·1667	0·0007	0·0009	0·0001750	0·000041–0·000642	67·908	15·910–249·127	785·3443	−428·1085 to 956·2967
CRMG	16	1	0·0000	0·0000	−	1	0·0000	0·0000	−	0·0000258	0·000013–0·000174	10·012	5·045–67·520	279·6221	−433·1575 to 945·4802
LZMG	16	1	0·0000	0·0000	−	2	0·3250	0·0007	0·0009	0·0000400	0·000014–0·000404	15·522	5·433–156·771	519·4392	−435·1287 to 947·2409
BMMG	15	1	0·0000	0·0000	−	2	0·1333	0·0006	0·0008	0·0001900	0·000123–0·000642	73·729	47·730–249·127	859·3399	−409·8901 to 959·7484
Mean	14·40	2·30	0·2749	0·0003	0·0005	2·35	0·3546	0·0013	0·0013	0·000334		129·5906		618·5289
SD		1·63	0·2929			0·88	0·2287			0·000306		118·8403		232·3967
Overall	333	19	0·6795	0·0010	0·0006	15	0·5640	0·0019	0·0015	0·003349	0·002418–0·005113	2250·019402	75·1919–167·9388	507·9428	−118·4123 to 949·5776

N, number of individuals sampled; k, number of haplotypes; h, haplotype diversity; π, nucleotide diversity; SD, standard deviation; θ, coalescent parameter; N_e, effective population size; g, exponential growth parameter.

The simulated values of haplotype and nucleotide diversities for the three alternative demographic scenarios (2000 simulations) were compared with the empirical values of haplotype and nucleotide diversities (mean for the 23 populations). One-tailed probability (P) and AIC were estimated for each scenario. The log-likelihood was estimated as the product of the height of the empirical frequency distribution at the observed value of diversity by the maximum height of the distribution (BayeSSC; www.stanford.edu/group/hadlylab/ssc/index.html). AIC was transformed into AIC weight evidence (AICw; [−0·5 (AIC − AIC_min)]) (Burnhan and Anderson, 2002) and we also obtained ΔAIC (the difference of AICw between each model and the best model). Models with ΔAIC < 2 were considered as equally plausible to explain the observed pattern (Zuur et al., 2009).

Spatial pattern in genetic diversity

To determine whether the differentiation is an effect of isolation by distance, population pairwise genetic differentiation (linearized pairwise F_ST) was correlated with the geographical distance matrix (using a logarithmic scale) using the Mantel test implemented in the software SAM 4.0 (Rangel et al., 2010). The statistical significance was verified with 10 000 random permutations.

To verify whether changes in the potential geographical distribution of the species generated a spatial pattern in haplotype diversity and effective population size (N_e), we obtained the distances between each population and the centroid of the current and 21-ka distributions, and the centroid of the historical refugium. To test whether the populations at the edge of the distribution have lower haplotype diversity and N_e, we related them to distance from the historical refugium edge. We also analysed the effect of habitat stability on haplotype diversity and the effective population size N_e of each population. The measure of stability was defined as the difference between the current and the LGM values of climatic suitability. Analyses were performed using quantile regression (Cade and Noon, 2003).

Results

Genetic diversity and population structure

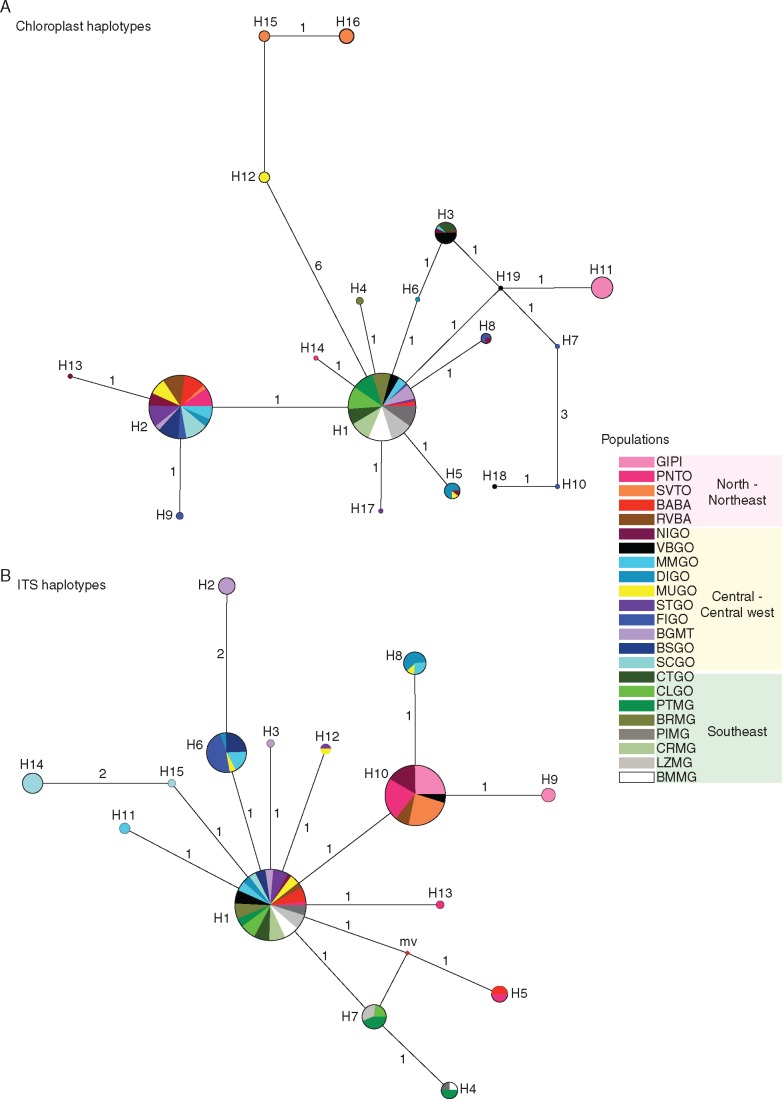
The combined data of chloroplast intergenic spacers generated fragments of 1915 bp and ITS generated fragments of 448 pb. We found 19 and 15 different haplotypes for cpDNA and ITS, respectively (Fig. 1). Haplotype and nucleotide diversities varied among populations (Table 1). Chloroplast haplotypes H1 and H2 were very widespread, as well as H1 and H10 for ITS (Fig. 1) and the phylogenetic relationships did not match the geographical distribution of the lineages (Fig. 3). AMOVA showed significant genetic differentiation among populations for both cpDNA (F_ST = 0·590; P < 0·001) and nuclear ITS (F_ST = 0·425; P < 0·001; for details about pairwise F_ST, see Supplementary Data Table S5 and S6).

Fig. 3.

Phylogenetic relationships among haplotypes using median-joining network of 23 populations of Eugenia dysenterica sampled in the Cerrado biome. Circumference size is proportional to haplotype frequency. The number of mutations is shown along lines in the network; ‘mv’ is the median vector. Different colours were assigned for each population according to the figure legend, grouped by Cerrado geographical region.

Bayesian clustering for cpDNA indicated an optimal partition of seven groups and showed congruence with population geographical distribution (Fig. 1A). Populations from South-east Brazil were grouped in the same cluster (Fig. 1A, green cluster). Almost all populations from Central Brazil were grouped in one cluster (yellow cluster), although some populations showed high admixture (Fig. 1A). For ITS, the Bayesian clustering indicated an optimal partition of 11 groups and there was no congruence with population geographical distribution (Fig. 1B).

Phylogeographical reconstruction

Population demography.

Fu’s neutrality test was significant for both cpDNA (Fs = −5·8638; P = 0·042) and ITS (Fs = −8·6688; P < 0·010). Coalescent analyses showed low values of mutation parameter θ for all populations and overall populations (θ = 0·033, Table 1). The values of g showed evidence of constant population size through time (Table 1). This result was corroborated by EBSP analysis that showed no population expansion through time (see Supplementary Data Fig. S2). For all population pairs we observed a negligible gene flow with fewer than 1·0 migrants per generation (see Supplementary Data Table S7).

Coalescent tree and TMRCA.

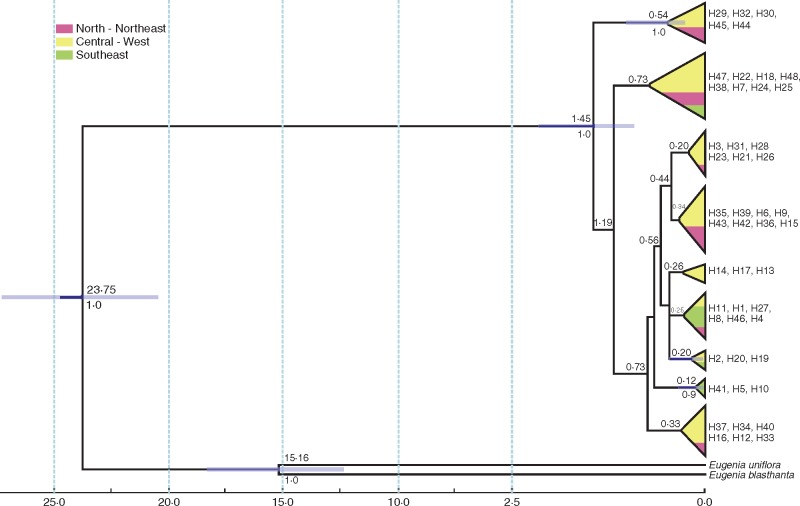
The TMRCA for E. dysenterica lineages dated to the Pleistocene, ∼ 1·45 ± 0·6 Ma, with the coalescence of haplotypes from the MUGO (H29, H32, H30) and SVTO (H45, H44) populations with the remaining haplotypes (Fig. 4). The coalescent tree shows evidence of incomplete lineage sorting.

Fig. 4.

Relationships and time to most recent common ancestor (TMRCA) of haplotypes of 23 populations of Eugenia dysenterica lineages with cpDNA and ITS data combined. The blue bar corresponds to the 95 % highest posterior probability of the TMRCA; numbers below the branches are node supports (showing only nodes with posterior probability ≥ 0·9); numbers above the branches are the node dating (TMRCA). The time scale is in millions of years (Ma) before present. The colours represent Cerrado geographical regions.

Lineage dispersal.

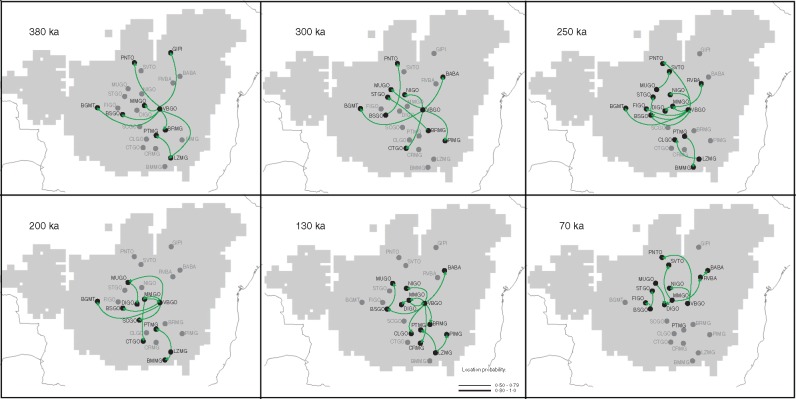
The analysis of lineage diffusion reveals that most dispersal events of E. dysenterica lineages occurred during the Middle Pleistocene, and no dispersal event was observed during the LGM (Fig. 5; Supplementary Data Fig. S3).

Fig. 5.

Spatio-temporal dynamics of lineage diffusion among the 23 populations of Eugenia dysenteria sampled in the Cerrado biome, for 410, 380, 300, 250, 200, 130 and 70 ka. Arrows between locations represent branches in the tree along which the relevant location transition occurs. The map was adapted from the .kml file provided by SPREAD software generated using Google Earth (http://earth.google.com). For details on population codes and localities see Table S1.

The dispersal route, for the analysis using both partitions, started from the VBGO population in Central Brazil towards populations at the edge of the distribution range (LZMG, BGMT and GIPI; see Fig. 5 and Fig. S3). From ∼300 ka, dispersal occurred in multiple directions and the last dispersal events were observed during the Late Pleistocene (∼70 ka; Fig. 5; Fig. S3). For ITS (see Fig. S4), the dispersal route departed from Central-West Brazil (population BSGO), suggesting that pollen dispersal followed a different route compared to seed dispersal. The Bayes factor showed that most links among localities are well supported (BF > 8·0). The diffusion analyses based only on chloroplast DNA did not converge, and the diffusion tree showed no support (results not shown).

Demographical history simulation

Palaeodistribution modelling and demographic hypotheses.

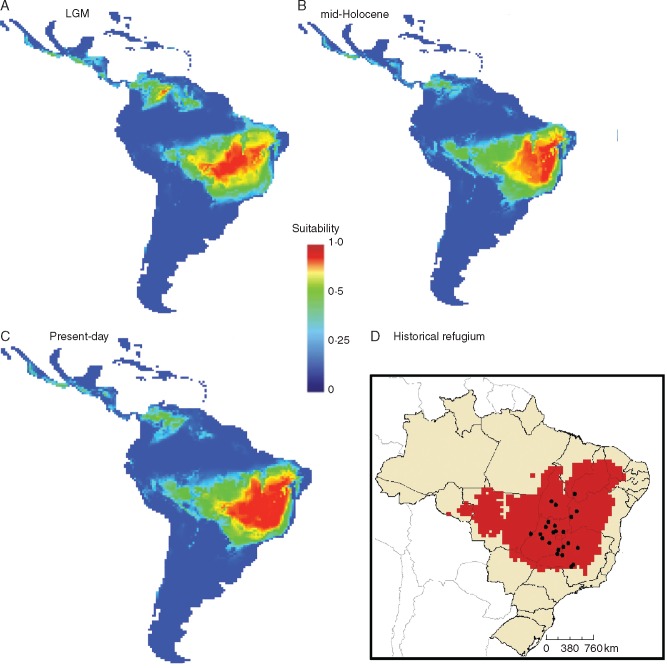
The ensemble of models from ENMs predicted that E. dysenterica was potentially distributed across a large area, extending over Central-Western Brazil through the last glaciation (Fig. 6A). The highest levels of suitability were restricted to Central Brazil; however, during the mid-Holocene (Fig. 6B) a loss of climatic suitability occurred in the western region and increased suitability in the east and north that was maintained to the present day (Fig. 6C). In addition, a wide region across the Cerrado biome probably acted as an historical refugium, maintaining populations of E. dysenterica during the climate changes throughout the last glaciation (Fig. 6D). In general, range size increased only slightly through time (see Supplementary Data Fig. S5). When we consider the occurrence area of the species, the hierarchical ANOVA revealed a higher proportional variance from the time component than variance from the modelling method (see Supplementary Data Table S8), indicating that ENMs were able to detect the effects of climate variation on the distribution dynamics of E. dysenterica, despite AOGCM variation (see Fig. S6).

Fig. 6.

Potential distribution of Eugenia dysenterica in the Neotropics, based on the consensus of the 13 ecological niche models and four atmosphere-ocean global circulation models used for modelling the palaeodistribution during the (A) LGM (21 ka), (B) mid-Holocene (6 ka) and (C) present-day. The historical refugium (D) shows areas climatically suitable throughout the period investigated.

The scenario of ‘Range Expansion’ was the most frequent hypothesis from ENM predictions (38·5 % of the 52 maps; Supplementary Data Tables S9 and S10), followed by ‘Range Retraction’ (36·5 %) and ‘Range Stability’ (25·0 %).

Demographical history simulation.

Simulations using N₀ = 100, 1000 and 10^000 retrieved the same final results, and thus we only show the results for N₀ = 1000. The scenario of ‘Range Stability’ was the most likely hypothesis to predict the observed genetic parameters of E. dysenterica, using AICw criteria (Supplementary Data Tables S9 and S11).

Spatial patterns in genetic diversity

Differentiation was slightly correlated with geographical distance for both chloroplast DNA (Mantel test, r² = 0·181, P = 0·04) and ITS (r² = 0·149, P = 0·04).

The quantile regression revealed that populations closer to the centroid of the current and 21-ka range and the historical refugium have higher haplotype diversity and effective population size (N_e) for chloroplast DNA (see Supplementary Data Figs S7-S10). The analysis also showed that haplotype diversity and N_e are related to habitat stability (see Fig. S11). Populations in areas with stable habitat suitability tend to maintain their population size and genetic diversity.

Discussion

The results show that the lineages of E. dysenterica dispersed from Central Brazil toward Western, Northern and South-eastern Brazil, matching the geographical dynamics recovered by the palaeodistribution modelling through the last glacial cycle. The wide stable area in Central Brazil predicted by ENMs, comprising all studied populations, probably favoured the past connection among populations. Indeed, coalescent simulation showed population stability through time as the most likely scenario among alternative demographic hypotheses, which corroborates our theoretical prediction and Extended Bayesian Skyline Plot result. Despite ENMs predicting the ‘Range Expansion’ scenario as being the most frequent, the difference between the scenarios was low. In fact, palaeodistribution modelling showed more changes in suitability through time than gaining new areas, especially in South-east Brazil.

The predicted historical refugium for E. dysenterica is wide and continuous, similar to other savanna species from the Cerrado biome (e.g. Caryocar brasilisiense, Collevatti et al., 2012a; Dipteryx alata, Collevatti et al., 2013c). This result is consistent with the hypothesis proposed by Ab’Sáber (2000), which suggests a large savanna refugium in Central Brazil during the Pleistocene, and is probably the main factor allowing uninterrupted lineage dispersal among populations of E. dysenterica, as predicted by spatial diffusion analysis.

The spatial dynamics of climatically suitable areas through time also affected the spatial distribution of genetic diversity in E. dysenterica. Populations at the edge of the potential distribution and of the historical refugium showed lower genetic diversity and effective population size. The central region of the potential distribution has high levels of genetic diversity and may be the centre of genetic diversity of E. dysenterica and probably the most basal region of its geographical distribution, which is consistent with the estimated TMRCA. In addition, the extant lineages started to disperse from VBGO, a population at the centre of the potential distribution of E. dysenterica. Lineage diversification started during the early Pleistocene, with divergence of lineages from the populations nearest to the centroid of the distribution (MUGO and SVTO). In fact, most E. dysenterica lineages diverged in the Middle Pleistocene, after ∼ 500 ka. The coalescence dates are relatively recent compared to other tree species from savannas in the Cerrado biome (e.g. Caryocar brasilisiense ∼ 3·3 Ma, Collevatti et al., 2012a; Tabebuia aurea, ∼4·4 Ma, Collevatti et al., 2015b). The times of coalescence events are directly related to effective population size (Kingman, 1982). Populations with higher N_e values tend to present older coalescence times, which corroborate the results observed for E. dysenterica populations. The older coalescence events were observed in populations at the centre of the geographical range, where the highest effective population sizes were observed.

Our findings are also consistent with the central-peripheral model, which predicts that central populations have higher effective size and number of migrants than peripheral populations (Soule, 1973; Eckert et al., 2008). Due to lower effective population sizes, populations in peripheral localities may lose genetic diversity due to genetic drift, and consequently may have a reduction in adaptive capacity leading to local extinction (Eckert et al., 2008). In addition, as expected, most populations with low genetic diversity are from the south-eastern E. dysenterica distribution, matching the findings of Barbosa et al. (2015), based on microsatellite markers. Moreover, evidence of inbreeding depression in emergence traits and initial development was observed for the species in nursery conditions from south-eastern populations (Chaves et al., 2011). The fossil records show that grasslands replaced savannas in South-eastern Brazil during the late Quaternary (Salgado-Labouriau et al., 1998; Behling and Hooghiemstra, 2001; Behling, 2003), where current environmental conditions have been established only at the end of the Holocene (Behling, 2002). The recent colonization of this region from more stable northernmost areas may have caused differentiation of lineages in south-eastern populations. The cycles of range expansion and retraction due to glaciation and interglacial periods may have led to the loss of genetic diversity in this peripheral area or to low genetic diversity due to the founder effect (see Excoffier et al., 2009). Nevertheless, this pattern was not observed for Tabebuia aurea (Collevatti et al., 2015b), whose populations with lower genetic diversity are in the north-east region of the Cerrado biome, a region potentially occupied by this species only during the mid-Holocene.

Finally, the relationships between genetic diversity and effective population size with suitability and stability of the potential distribution of E. dysenterica reveal that populations in regions with higher suitability and lower climate instability have greater effective population size and therefore are less susceptible to effects of genetic drift and inbreeding (Palstra and Ruzzante, 2008), since genetic diversity is dependent on N_e (Wright, 1931). Populations in the climatically unstable south-eastern region also showed lower genetic diversity for microsatellite loci (Diniz-Filho et al., 2016).

In conclusion, our findings suggest that the central region of the Cerrado biome is the centre of E. dysenterica lineage diversification. The pattern of genetic diversity in E. dysenterica may be the outcome of population stability through periods of the Quaternary, and the wide historical refugium may be responsible for maintaining genetic diversity, and the differences found in the south-eastern populations are probably due to the local environmental conditions during the late Quaternary. This study supports the idea that ENM coupled with statistical phylogeography is very conducive for understanding a species’ demographic history. Furthermore, these results provide important information for understanding the evolutionary processes underlying population spatial distribution.

Supplementary Data

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the following. Appendix S1: supplementary tables (Tables S1–S11) with sampling locations and details on ENM, genetic structure and demographic scenarios. Appendix S2: supplementary figures (Figs S1–S11) with details on ENM, demographic history and spatial genetic diversity.