Functional materials discovery using energy–structure–function maps

Abstract

Molecular crystals cannot be designed like macroscopic objects because they do not assemble according to simple, intuitive rules. Their structure results from the balance of many weak interactions, unlike the strong and predictable bonding patterns found in metal–organic frameworks and covalent organic frameworks. Hence, design strategies that assume a topology or other structural blueprint will often fail. Here, we combine computational crystal structure prediction and property prediction to build energy–structure–function maps describing the possible structures and properties available to a candidate molecule. Using these maps, we identify a highly porous solid with the lowest density reported for a molecular crystal. Both crystal structure and physical properties, such as the methane storage capacity and guest selectivity, are predicted using the molecular diagram as the only input. More generally, energy–structure–function maps could be used to guide the experimental discovery of materials with any target function that can be calculated from predicted crystal structures, such as electronic structure or mechanical properties.

Predictive calculations of material structure and properties have been used successfully for zeolites¹, new allotropes of common elements², cathode materials for batteries³, redox-active frameworks⁴, organic photovoltaics⁵, metal oxides⁶ and porous solids⁷. It is a major challenge for computational materials research, however, to identify new materials that are more than hypothetical. This requires us to compute both the property of interest and the material’s stability with respect to alternative atomic configurations. Computational prediction of both stability and function has great potential to discover materials with arresting properties^6,8,9 but it is difficult in practice because of the computational expense of exploring vast structural landscapes, coupled with the need for accurate lattice energies and reliable property predictions. Inexpensive calculations have been used to enumerate large libraries of metal–organic frameworks (MOFs) and to predict their gas adsorption properties^7,10. However, these methods are based on assumed framework topologies and they do not tell us about the relative energies of the hypothetical structures and which structures, if any, can be synthesized. To predict, select, and then synthesize new functional materials, we need a simple, digestible description of the probable structure–function space, rather than the potential space, which will always be astronomically large¹¹.

This design challenge is particularly acute for molecular crystals, whose complex structural landscapes are defined by competing, weak structure-determining interactions. Hence, small changes to molecular structure can cause profound changes in crystal packing. It is therefore difficult to apply structure–function relationships learned from one system to a new molecule, which might pack in a totally different way. Likewise, polymorphism is commonplace in molecular crystals¹². Hence, there are few molecular analogues of isoreticular MOFs¹³ or covalent organic frameworks¹⁴, whose lattice energies are dominated by a specific bonding pattern across a broad range of building blocks. The a priori design of functional molecular crystals, therefore, demands a predictive strategy that does not rely on intuitive bonding rules or assumed topologies. Crystal structure prediction (CSP) methods^15,16 have been developed to determine the stable crystalline arrangements that are available to a molecule. Each predicted structure encodes a set of physical properties: this ensemble of structures and their properties defines an energy–structure–function (ESF) map, representing the possible material properties associated with the molecule. Each structure’s likelihood of being stable and accessible to experiment relates to its predicted lattice energy. We illustrate this function mapping approach for porous organic molecular crystals¹⁷, which are rare because molecules tend to pack densely¹⁸. Previously, we predicted the crystal structures of organic cages^19,20, where most of the possible crystal packings are porous because of the intrinsically porous molecular structure. Without such built-in porosity, the lowest energy crystal structures for molecules are, with few exceptions²¹, close-packed and non-porous. Here, we use ESF maps to guide us to molecular materials with remarkable porosity levels and high predicted gas selectivities, avoiding any assumptions or intuitive guesses about the crystal packing. We show that ESF maps can reveal a rich landscape of undiscovered structures and properties for known molecules²², as well as predicting the properties of hypothetical molecules for specific target applications, before realizing these in the laboratory.

Energy landscapes predict porous phases

Directional intermolecular interactions^22,23,24 and geometries that hinder close packing²⁵ are both known to promote porosity. We therefore studied a series of awkwardly-shaped molecules with different hydrogen bonding functionalities (Fig. 1) with the aim of locating stable, porous crystals.

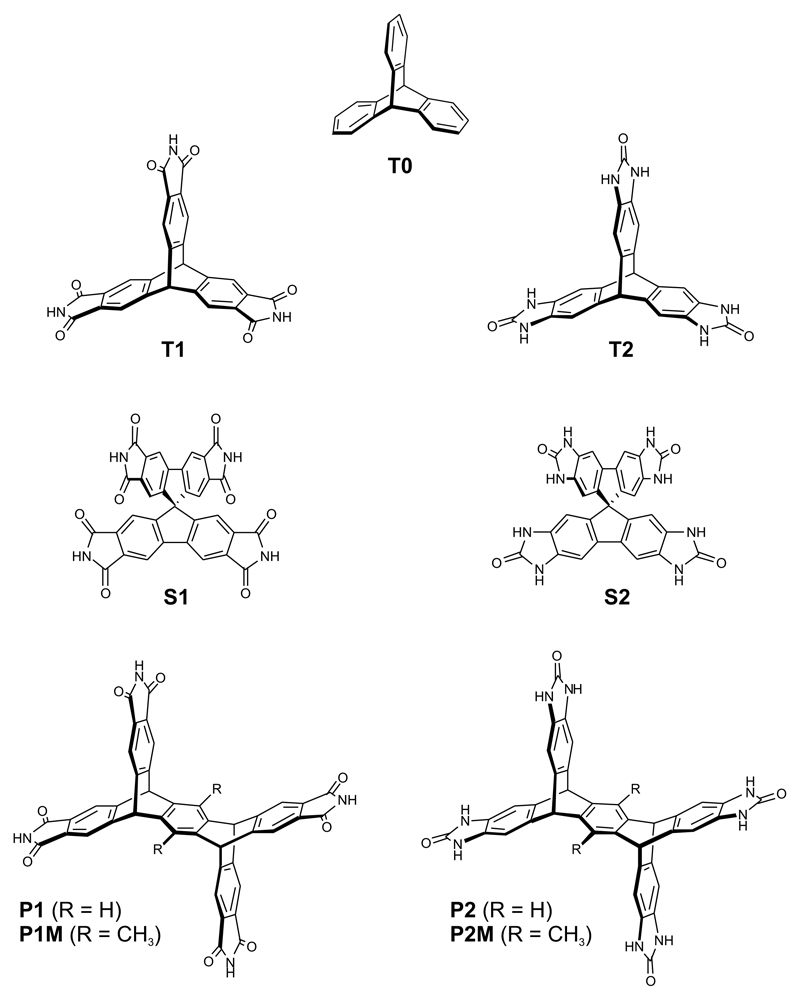
Figure 1. Candidate building blocks for porous solids.

The molecules are based on triptycene (T0, T1, T2), spiro-biphenyl (S1, S2) or pentiptycene (P1, P2, P1M, P2M) cores. 1 = imide series, 2 = benzimidazalone series.

Benzimidazalone T2 was synthesized previously by Mastalerz²², who reported a crystal structure with a low density (0.755 g cm^-3) and an experimental Brunauer–Emmett–Teller surface area (SA_BET) of 2796 m² g^-1. T1 is an imide analogue of T2 whose only known crystal structure is a solvate that exhibits strong hydrogen bonding to the solvent²⁶. We include triptycene, T0, for comparison, as a non-hydrogen bonding analogue. The spiro-linked tetrahedral analogues, S1 and S2, and the expanded, tie-shaped pentiptycene analogues, P1 and P2, are all unknown. It is not obvious which of these molecules should give rise to stable porous phases: except for T0, they all have potential to form intermolecular hydrogen bonds and, in principle, P1 and P2 (or their methylated analogues P1M and P2M, Fig. 1) might form more open frameworks than T2 because of their longer organic struts, by analogy with isoreticular framework design strategies^13,14.

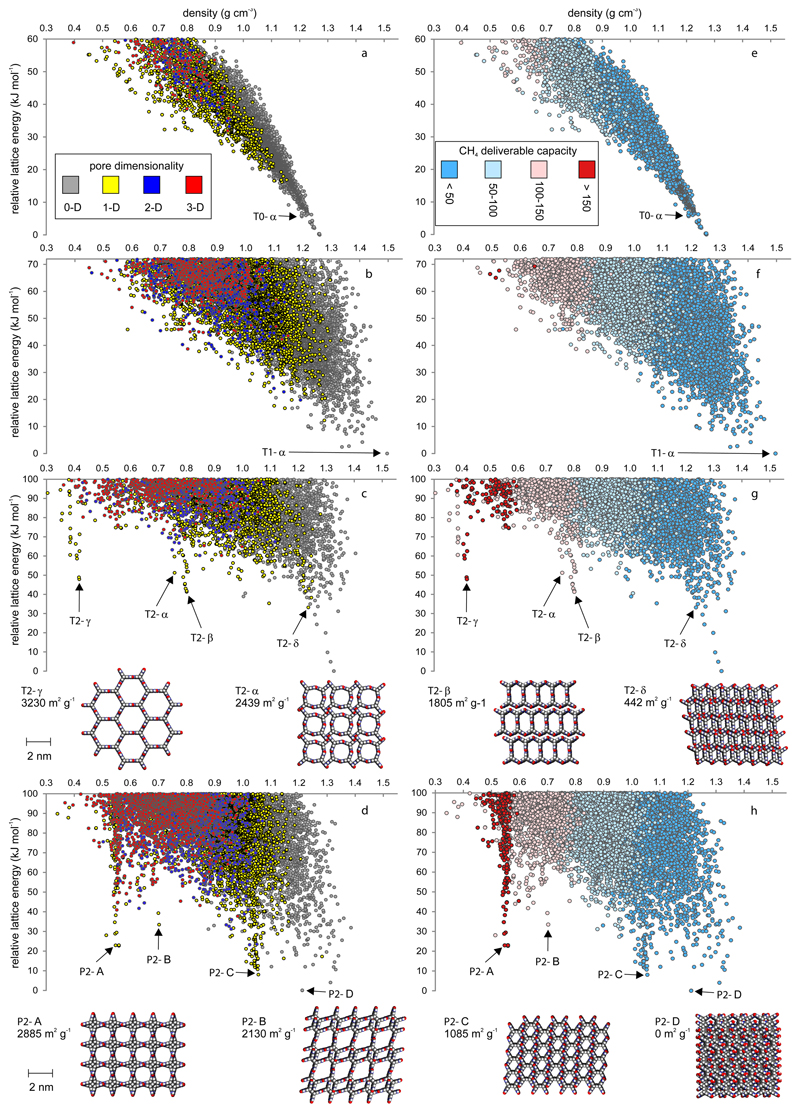
Unbiased searches of the lattice energy surface²⁷ were used to predict the possible crystal structures of these molecules (Fig. 2a–d for T0, T1, T2 and P2, Fig. S1-2 for S1, S2, P1, P1M and P2M). An analysis of the lower edge of the energy vs density representation of the crystal structure landscape is important in the search for stable porous structures. This ‘leading edge’ comprises the lowest energy possible structures at any given density, and stable porous molecular frameworks have been identified before in this region²⁸.

Figure 2. From structure prediction to energy–structure–function maps.

a–d, CSP energy-density plots for a, T0; b, T1; c, T2, and; d, P2, where each point corresponds to a computed crystal structure. T2, c, and P2, d, structures selected from the leading edge of the energy also shown. The symbols are color coded by pore channel dimensionality, assessed using a CH₄ probe radius, 1.7 Å. e–h, Energy–structure–function (ESF) maps showing the calculated methane deliverable capacities for e, T0; f, T1; g, T2, and; h, P2, projected onto the energy-density plot. Symbols color coded by deliverable capacity (v STP/v, 65–5.8 bar, 298 K).

The landscapes for T0 and T1 (Fig. 2a,b) are typical for organic molecules: the lowest energy structures are densely packed and the leading edge of the energy vs density distribution decreases nearly monotonically due to the energetic cost of void space in a solid. The known, non-porous crystal structure of triptycene is accurately reproduced by one of the lowest-energy calculated structures (T0-α, Figs. 2a, S3). Intermolecular hydrogen-bonding in imide T1 broadens the density distribution of the predicted structures (Fig. 2b), but again the lattice energy decreases monotonically and most structures are non-porous.

The energy vs density distribution of structures for T2 (Fig. 2c) is strikingly different. Multiple low density structures are predicted with energies significantly below the bulk of the landscape, indicating unusual stability for their respective densities. In particular, two low-energy ‘spikes’ are apparent at densities of ~0.8 and ~0.4 g cm^-3, both containing structures with 1-D pores. Their energetic separation from the bulk of the landscape suggests a sizeable energy barrier to transformation to denser structures. Structures within these spikes feature hydrogen-bonded networks (Fig. S4) with 2-D rings propagating along a third direction to form 1-D pore channels. Decomposition of the lattice energy into its physical contributions shows that the structures on the leading edge of the landscape are those with the most stabilizing electrostatic interactions (Fig. S5-7). The low energy spikes on the T2 landscape result from optimization of the strongly directional electrostatic interactions via oriented, polar hydrogen bonds. These spikes are an immediate indication that T2 might be a better choice for porosity generation than its imide analogue, T1, even without analysis of the various predicted structures. As discussed later, all structures highlighted for T2 in Fig. 2c (T2-α–T2-δ) are stabilized by solvent inclusion in their voids, such that they are more stable than the predicted global minimum.

The previously reported²² crystal structure for T2 is found in the 0.8 g cm^-3 spike (T2-α, Fig. 2c) and its calculated lattice energy is 51 kJmol^-1 above the predicted global energy minimum. Since T2-α is a known structure—a ‘landmark’ on the energy map—then other structures with comparable energies might also be experimentally accessible. Indeed, the predicted energy minimum in the 0.8 g cm^-3 spike is a new porous structure, T2-β, which contains hydrogen bonded chains along the pore channels as well as extensive π–π stacking (Fig. 2) that is not found in T2-α. Remarkably, we also predict structures in the 0.4 g cm^-3 spike with lattice energies that are comparable with T2-α and T2-β, despite having exceptionally low packing fractions of approximately 0.2 (c.f., 0.37 and 0.39 for T2-α and T2-β). The minimum energy structure in this spike, T2-γ, is again dominated by hydrogen-bonded chains, but here the hydrogen bonds are linear, optimizing the directional intermolecular electrostatic interactions (Fig. S6) and resulting in hexagonal pore channels (pore diameter = 1.99 nm, Fig. 2). T2-γ has a high calculated surface area of 3230 m² g^-1 and an exceptionally low predicted density of 0.417 g cm^-3. The densest 1-D porous structure on the energy landscape, T2-δ, is also highlighted in Fig. 2c. T2-δ is predicted to be the most stable of the possible porous structures for T2, with a calculated lattice energy that is lower than T2-α, T2-β or T2-γ. The previously reported structure²² for T2, T2-α, has the highest calculated lattice energy of the four porous forms highlighted here, suggesting that T2-α might not be the only porous polymorph of this molecule.

The spikes in the energy surface for T2 stem from its shape and symmetry, which allows a strong hydrogen bonding network to form along the channels, frustrating interpenetration. By contrast, the spiro-linked benzimidazalone, S2, which is pseudo-tetrahedral, shows no unusually stable low density regions (Fig. S1). P2 also shows pronounced spikes extending below the bulk of its energy landscape (Fig. 2d), and we highlight three porous structures from its leading edge, P2-A, P2-B and P2-C (Fig. 2d), each of which exhibits extensive intermolecular hydrogen bonding and a high predicted surface area. As for T2, the most stable predicted porous structures for P2 have 1-D pore channels. By contrast, the dimethyl analogue of P2, P2M, shows less pronounced spikes in its energy surface (Fig. S1), and some of the most stable predicted porous structures have 2-D or 3-D pore topologies. This sensitivity to small chemical changes highlights the non-intuitive relationship between molecular structure and the crystal energy-structure landscape.

There were no pronounced spikes in the lattice energy surfaces for the pentiptycene imides P1 and P1M, nor the spiro-linked imide S1 (Fig. S1), suggesting that imides will be less effective than benzimidazalones at generating porosity, both for triptycene and pentiptycene frameworks.

Energy–structure–function maps

Pore topologies and computed surface areas (Fig. 2a–d) are inexpensive descriptors for porosity, but for practical applications we are rarely interested in those parameters per se. However, we can project any computable property onto these energy landscapes to guide the selection of materials for specific purposes. For example, methane storage^29,30 is an important goal for natural gas-powered vehicles, and we therefore calculated the methane deliverable capacity⁷ (298 K, 65–5.8 bar) for each structure in the predicted ensembles to create ESF maps (Figs. 2e–h, S2). Unsurprisingly, the T0 map shows no structures with high methane capacities (Fig. 2e). There are also very few structures predicted for T1 with reasonable deliverable capacities (>150 v STP/v), and their relative lattice energies are high (Fig. 2f). By contrast, the T2 map shows multiple structures with capacities that exceed 150 v STP/v (Fig. 2g). More importantly, the minimum-energy structure in the 0.4 g cm^-3 spike, T2-γ, has one of the highest predicted methane capacities in the T2 structure ensemble (159 v STP/v). The deliverable capacity for T2-α is calculated to be 109 v STP/v; that is, 32% lower than for T2-γ, and closer to T2-β (115 v STP/v). We can therefore predict, a priori, that T2 has stronger potential for methane storage than is suggested by its known structure, T2-α.

P2 also has low-energy predicted structures with calculated methane capacities above 150 v STP/v (Fig. 2h). Hence, ESF maps suggest, at a glance, that T2 and P2 are the most promising candidates here for methane storage. These maps also suggest that the more synthetically elaborate, hypothetical P2 offers little advantage over T2 for methane storage since both T2-γ and P2-A have similar predicted capacities of 159 and 153 v STP/v, respectively.

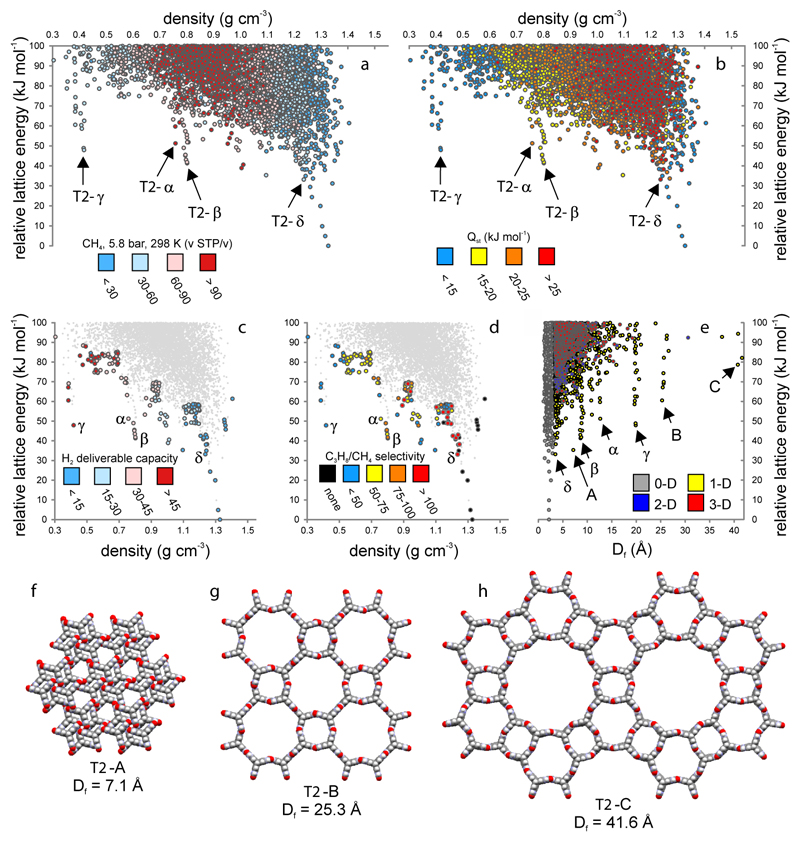
The ESF map for methane adsorption in T2 at 5.8 bar (the depletion pressure) shows a different pattern (Fig. 3a); smaller-pore structures such as T2-α and T2-β adsorb more methane than T2-γ, as reflected in the isosteric heats of adsorption (Fig. 3b). This reduced adsorption in T2-γ at the depletion pressure is the main reason for its superior predicted methane deliverable capacity (Fig. S8). T2-γ is also predicted to have the highest hydrogen deliverable capacity (47.1 kg m^-3 or 11.3 wt.%) assuming gas storage at 100 bar/77 K and gas delivery at 5 bar/160 K (Fig. 3c)³¹.

Figure 3. Energy–structure–function maps for T2.

a, Volumetric methane capacity at 5.8 bar/298 K (the depletion pressure). b, Isosteric heat of adsorption for methane. c, Calculated H₂ deliverable capacity (kg m^-3, 100 bar/77 K, 5 bar/160 K) for structures selected from the leading edge of the ESF; T2-γ is favoured. d, Simulated propane/methane selectivity (1 bar/298 K); T2-β and T2-δ are favoured. e, Relative lattice energy vs D_f, the largest free sphere, which relates to pore size; symbols colored by pore dimensionality. (f–h) Selected hypothetical structures from the leading edge: T2-A, T2-B and T2-C correspond to labels A, B and C in e.

Small pores and relatively strong adsorption are often beneficial for applications such as hydrocarbon separation. Calculations for propane and methane adsorption in structures on the leading edge of the T2 energy landscape (Fig. S9-10) suggest that the hypothetical small-pore polymorph, T2-β, might have a good balance of adsorption capacity and selectivity (C₃H₈/CH₄ = 78.1) for separating these two industrially important gases at 298 K and 1 bar (Fig. 3d). There are also denser porous structures on the leading edge of this map, such as T2-δ, that are predicted to have even higher propane/methane selectivity (C₃H₈/CH₄ = 119.7). T2-α and T2-γ, by contrast, have good predicted adsorption capacities for hydrocarbon gases but poorer selectivities. We therefore predict that T2-β and T2-δ (or other leading-edge structures with similar densities to T2-δ; see red points in Fig. 3d) have good potential for propane/methane separation. Likewise, T2-δ is predicted to have high selectivity for ortho-xylene over the meta- and para-xylene isomers (Fig. S11). T2-α, T2-β and T2-γ are predicted to be weakly ortho-xylene selective, but much less so than T2-δ.

‘Spikes’ also emerge when the lattice energy for T2 is plotted against calculated pore size (D_f), rather than density (Fig. 3e). This is because there are related structures with common packing motifs, such as hydrogen-bonded channels with specific pore diameters (Fig. 3f–h and Fig. S12–13). These channels recall inorganic zeolites, and it is conceivable that some of the higher energy forms, such as T2-B or T2-C, might be accessed by using structure-directing agents.¹ Again, ESF maps are revealing, even without analysis of the individual structures: comparison with other candidate molecules (Fig. S14) shows that T2 and P2 are the only molecules here that might form a mesoporous solid with 2 nm or larger pores. Thinking beyond porous solids, ESF maps could be prepared where lattice energy is plotted against any other calculable parameter; for example, to identify molecules that have low-energy structures with a suitable electronic band gap for solar energy harvesting.

Crystallization verifies ESF map predictions

Computation suggests that T2 has a rich, unrevealed chemistry: crystallization screens were therefore performed for T2 and its imide analogue, T1, as a comparison.

Despite extensive studies across multiple solvents and desolvation protocols, we were unable to isolate a stable, unsolvated porous crystalline phase of T1 (Fig. S15–16). However, T1 crystals grown by sublimation revealed a previously unreported dense structure that was predicted accurately by the global energy minimum structure on the T1 energy landscape (T1-α, Fig. S16). Efforts to grow equivalent solvent-free crystals of T2 failed due to decomposition before sublimation. However, slow diffusion of acetone into a saturated dimethylacetamide (DMAc) solution of T2 led to crystallization of a solvated form of the predicted hexagonal T2-γ, isolated initially as T2∙(DMAc)_7.79. The T2-γ polymorph was also found to crystallize from other solvent combinations, such as DMSO/acetone and N-methyl-2-pyrrolidone/acetone.

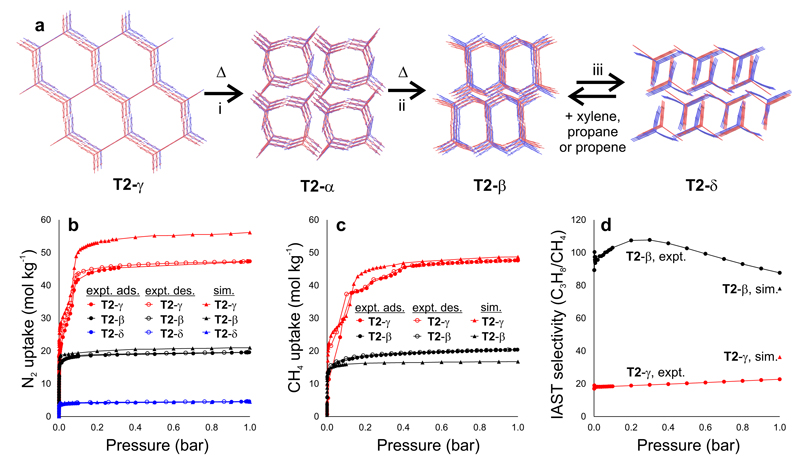
The T2∙(DMAc)_7.79 material was desolvated by first exchanging DMAc for acetone then pentane, followed by overnight evacuation. At 240 K, no residual solvent was found in the 1-D pores and a density of 0.412 g cm^-3 was determined by crystallography. Single crystal data were recorded up to 500 K, demonstrating good thermal stability for desolvated T2-γ. There is excellent agreement between the predicted structure and the experimental desolvated structure for T2-γ (Fig. 4a). The structure of the previously reported polymorph²², T2-α, is also accurately reproduced by one of the predicted structures (Fig. 4a).

Figure 4. Predicted and experimental structures and gas adsorption isotherms for polymorphs of T2.

a, Overlays of predicted (red) and experimental (blue) structures for T2-γ, T2-α; T2-β; and T2-δ, ordered by increasing predicted density; the transformation conditions for interconverting these polymorphs were as follows: i: loss of solvent at RT, heating at 340 K or mechanical grinding at RT; ii: 358–383 K; iii: direct removal of DMSO and then acetone from DMSO/acetone solvate. All four phases can be isolated as stable solvent-free frameworks in the laboratory. b,c, Predicted and experimental gas adsorption isotherms for T2-γ (red), T2-β (black) and T2-δ (blue). b, nitrogen (77 K) and c, methane (115 K); adsorption = filled symbols; desorption = unfilled symbols. All simulations were performed using the CSP structures. d, Pressure-dependent IAST selectivity of propane over methane determined for equimolar mixtures, using experimental isotherms at 298 K (Fig. S19). The ESF selectivity predictions (Fig. 4d) are marked as upper triangles and colored accordingly for T2-β (black) and T2-γ (red).

A type-IV nitrogen (N₂) adsorption isotherm was obtained for fully desolvated T2-γ with a sharp step at P/P_o = 0.06, in agreement with grand canonical Monte Carlo (GCMC) adsorption simulations (Fig. 4b), attributable to nitrogen condensation in the uniform hexagonal pores³² (Fig. S17). The experimental surface area, SA_BET, was estimated to be 3425 ± 82 m² g^-1, in good agreement with our a priori prediction (3230 m² g^-1). T2-γ has the lowest density of any molecular solid reported in the Cambridge Structural Database to date^21,33. It is also the largest pore size observed for an extrinsically porous molecule (1.99 nm), rather than a cage³³. The promise of T2-γ for methane adsorption, suggested by ESF maps (Figs. 2g, S18), was also confirmed by experiment. The saturation methane capacity at 115 K for T2-γ was found to be 47.4 mol kg^-1 (437.4 v STP/v), both by experiment and by simulations (Fig. 4c).

T2-γ is stabilized by solvent exchange with pentane, but the DMAc/acetone solvate of T2-γ taken directly from the crystallization mother liquor transforms to a solvate of T2-α under light grinding or when left to stand at room temperature. Likewise, heating the T2-γ solvate isolated from a DMSO/acetone mixture for 60 min at 340 K transformed it to a T2-α solvate. Further heating of this T2-α solvate (30 min, 358 K) caused another transformation to a third phase, which was identified by comparison of CSP-derived and experimental powder X-ray diffraction (PXRD) patterns as the predicted T2-β polymorph. T2-β could also be isolated in desolvated form by heating T2-α in DMSO/acetone to 110 °C for 3 hours before exchanging the solvent in the pores with acetone and then n-pentane prior to evacuation. If the acetone solvent exchanged material was evacuated directly, without first exchanging for n-pentane, then the predicted unsolvated T2-δ phase could also be isolated. A single crystal structure of the T2-δ acetone solvate revealed a close size match between the 1-D pores and the ordered acetone guests, which interact with the T2 molecules. The absence of such strong solvent–framework interactions rationalizes why the n-pentane solvate of T2-β does not transform to T2-δ during evacuation of the pores. Hence, by using different crystallization solvents and desolvation protocols, we can access in the laboratory at least four of the predicted structures on the leading edge of the energy landscape for T2; the known T2-α form, plus three new polymorphs: T2-β, T2-γ and T2-δ.

There is good agreement between experimental nitrogen adsorption isotherms and adsorption isotherms predicted from the CSP-derived structures for all three of the new polymorphs, T2-β, T2-γ and T2-δ (Fig. 4b). Likewise, the methane adsorption isotherms for T2-β and T2-γ can be predicted a priori (Fig. 4c). Our prediction that T2-β would have better propane/methane selectivity than T2-γ (Fig. 3d) was also realized by experiments that showed enhanced ideal propane/methane selectivity for T2-β, as calculated using ideal adsorbed solution theory (IAST) (Figs. 4d, S19). However, studies on the denser T2-δ polymorph revealed some limitations of these a priori predictions. T2-δ was predicted to have superior hydrocarbon selectivity compared to T2-β (Fig. 3d,e), but experiments show that T2-δ transforms back to T2-β upon exposure to either ortho-xylene or propane (Figs. 4a, S20‒22). By contrast, neither nitrogen nor methane adsorption causes the expansion of T2-δ to the T2-β phase.

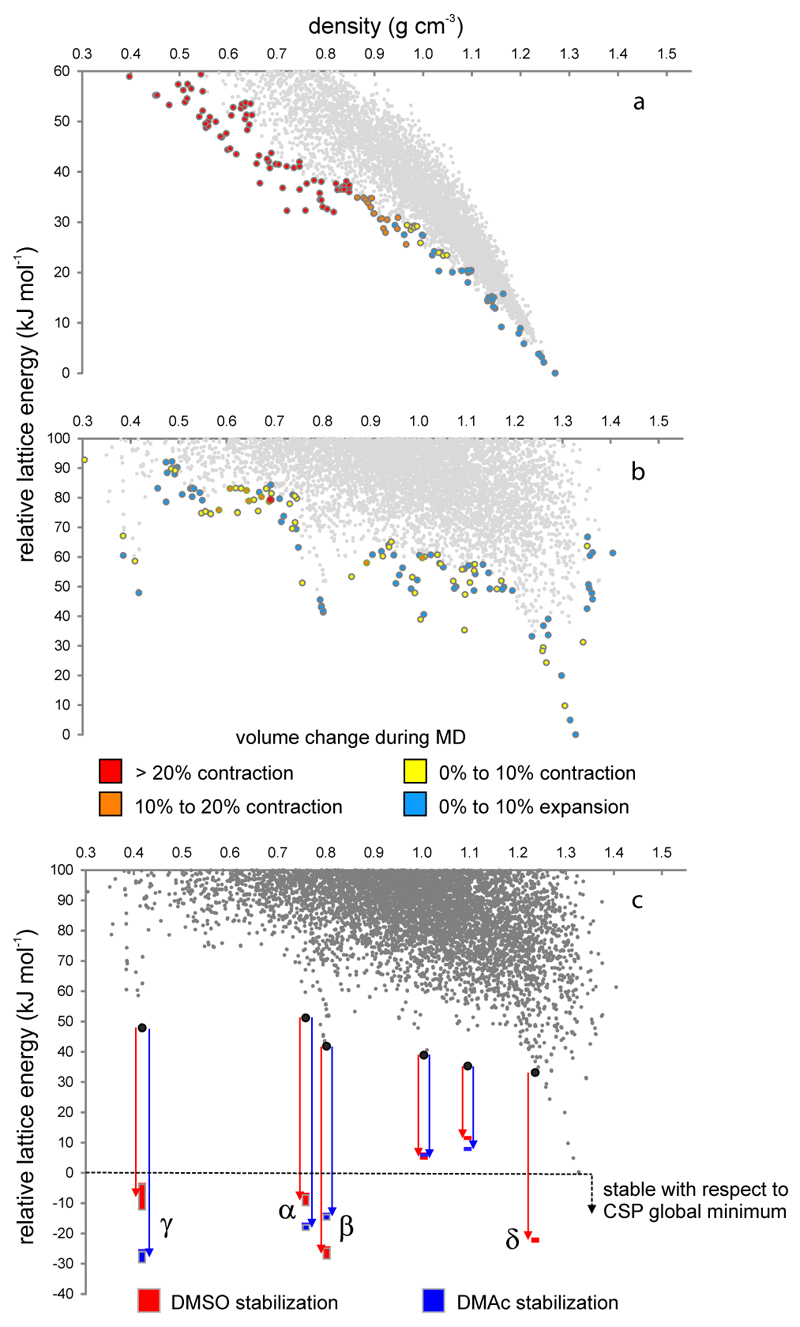
To better understand the phase changes between the various T2 polymorphs, and to explore the thermal stability of the predicted, solvent-free structures of T0, T1 and T2, we used molecular dynamics (MD) simulations to probe the dynamical stability to thermal motion at 300 K (Figs. 5a,b, S23−S24). Most of the leading edge structures for T2 were found to be stable; in particular, T2-δ, T2-β and T2-γ showed only small structural fluctuations about the CSP structure during 500 ps simulations (Figs. 5a, S24). By contrast, MD simulations for T2-α show a partial transformation to the T2-β structure, in line with experimental observations (Fig. 4a). The phase transformations observed for solvates in our crystallization experiments suggest that the presence of polar solvent in the pores of T2-γ and T2-α lowers the barrier to interconversion to denser forms. In the case of T2-δ, solvation by propane or by ortho-xylene (but not N₂ or CH₄) can cause expansion to the less dense form, T2-β. In contrast to T2, almost all low density predicted structures (ρ < 1 g cm^-3) for T0 were unstable during the MD simulations, rapidly collapsing to denser structures at room temperature (Fig. 5b). T1, which did not yield stable porous structures by experiment, showed intermediate behavior, with many low density structures collapsing during MD, but some remaining stable at 300 K (Fig. S23). These results show that MD simulations for leading edge structures can provide a qualitative indication of the likely experimental stability of interesting, low density forms.

Figure 5. Crystal structure stability and solvent stabilization.

a, b, Volume change during molecular dynamics calculations at T = 300 K for leading edge structures of a, T0 and b, T2. Large (> 10%) contraction corresponds to collapse of porosity present in the temperature-free predicted structures. c, Calculated stability of DMSO and DMAc solvated structures of T2-α, β, γ, δ and two predicted porous structures of intermediate density. The solid bars give energy ranges for each fully solvated structure. T2-δ is unable to accommodate DMAc in the simulations. All energies are shown relative to the global minimum energy predicted structure.

We also probed the influence of solvent on the T2 energy landscape to understand why porous polymorphs are formed instead of the dense and non-porous predicted global minimum structure. Solvent stabilization calculations were performed on the four observed polymorphs, T2-α, T2-β, T2-γ and T2-δ, plus two other ‘leading edge’ structures, using Monte Carlo and lattice energy minimization methods (Fig. 5c, S25-26). Simulations with both DMSO and DMAc show that the four observed polymorphs are energetically favored over the global minimum predicted structure when the channels are fully solvated, explaining why porous networks crystallize from solution in preference to a dense, nonporous phase.

ESF maps predict an ultra-low density solid

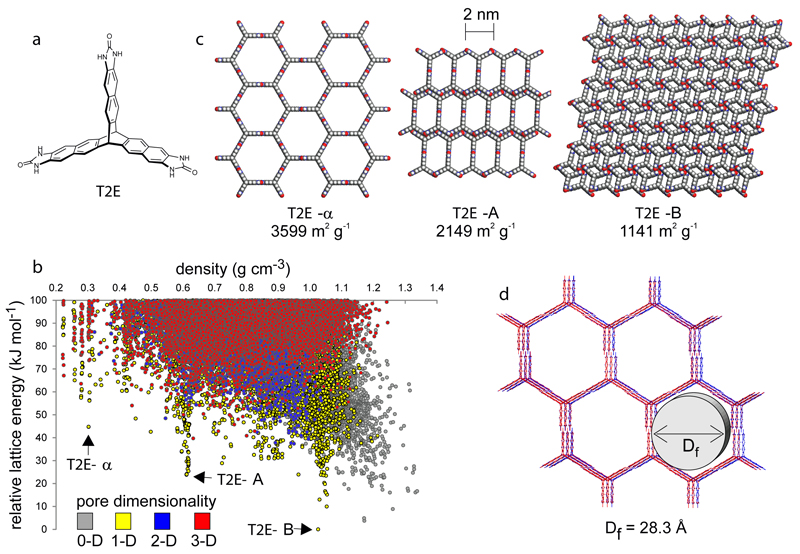
The existence of T2-γ and the electrostatic stabilization that we calculated for this material (Fig. S5-6) suggested the possibility of designing molecular crystals with even higher porosity levels. The energy landscape for the extended pentiptycene molecule, P2, did not predict the existence of any competitive structures with densities lower than T2-γ. For example, P2-A (Fig. 2d) has a higher predicted density (0.559 g cm^-3) than T2-γ. We therefore calculated the crystal energy landscape for a hypothetical extended form of T2, T2E (Fig. 6a). This landscape again contains distinct low-energy spikes, as for T2 and P2, and a leading-edge structure was identified (T2E-α, Fig. 6b) that has a predicted density of just 0.303 g cm^-3 and hexagonal pore channels with diameter of 2.83 nm. T2E-α is isostructural to T2-γ (Fig. 6c) and it is located 44.7 kJ mol^-1 above the predicted global minimum structure (T2E-B). Comparison with T2-γ, which lies 47.8 kJ mol^-1 above its predicted global minimum, suggested that T2E-α might also be stabilized by solvent inclusion. We therefore devised a synthetic route to T2E (Supporting Information, Fig. S27) and grew crystals of this material from DMF/acetone and DMSO/CHCl₃, yielding the predicted T2E-α phase as a solvate (Fig. 6d). Preliminary studies suggest that T2E-α can be prepared as a bulk, phase pure solvate (Fig. S27) with 2.8 nm hexagonal pore channels. This is the largest pore size observed for any molecular organic crystal to date, including intrinsically mesoporous organic cages³³. We predict that T2E-α will have remarkable properties, if scaled up and successfully desolvated in the bulk: for example, it should have high volumetric and gravimetric deliverable capacities for hydrogen (43.8 kg m^-3 and 14.5 wt.%, respectively) assuming gas storage at 100 bar/77 K and gas delivery at 5 bar/160 K. Unlike all other molecules studied here, T2E has a global minimum predicted structure, T2E-B (Fig. 6b,c), that is predicted to be highly porous (1141 m² g^-1). We therefore anticipate that T2E might be resistant to loss of porosity, so long as it remains crystalline, which is not obvious from the molecular structure in isolation.

Figure 6. Predicted and experimental structures and properties for T2E.

a, Extended benzimidazolone analogue of T2, T2E. b, CSP energy-density plot. c, Selected structures for T2E drawn from the leading edge of the energy vs. density landscape; T2E-α, T2E-A, and the global minimum structure, T2E-B. d, Overlay of predicted and experimental structures for T2-α. ESF maps for T2E are shown in Fig. S28.

Outlook

In summary, we have demonstrated the power of energy–structure–function maps for the computationally-led discovery of new materials, in this case guiding us to three new porous polymorphs of a known molecule, T2, each of which has quite different physical properties, plus an ultra-low density form of a new molecule, T2E-α. Thinking longer term, it is challenging for computers to generate abstract chemical design hypotheses or rules of thumb: for example, while it might be intuitive to chemists that an equal number of hydrogen bond donors and acceptors makes imidazalones better than imides for open framework generation, a computer would not reach that conclusion unaided. ESF maps, therefore, open the door for more autonomous computer aided materials design schemes in the future – for example, where a computational algorithm evolves a set of candidate molecules, perhaps chosen initially using human knowledge, and selects for energetically favourable candidates with superior function that emerge from the resulting dynamic molecular library. This mapping approach is not limited to porous materials but will find wider use in the discovery of functional solids, particularly as we expand our ability to calculate other physical properties from structure.

Methods

Crystal structure prediction (CSP)

Crystal structure prediction (CSP) was performed using a quasi-random sampling procedure, as implemented in the Global Lattice Energy Explorer software²⁷. Molecules were first sketched in ChemDraw, followed by an initial molecular geometry optimization with the COMPASS force field, as implemented in the Materials Studio software package³⁴ . Force field optimized molecular geometries were further refined by re-optimization using density functional theory (DFT) with the M06-2X exchange-correlation functional and 6-311G** basis set. Molecular DFT calculations were performed with the Gaussian09 software³⁵. These molecular geometries were held rigid throughout crystal structure generation and lattice energy minimization.

Trial crystal structures were generated with one molecule in the asymmetric unit in each of the 89 space groups in which non-polymeric Z`=1 organic molecular crystal structures are reported in the Cambridge Structure Database: P2₁/c; P2₁2₁2₁; P1; P2₁; Pbca; C2/c; Pna2₁; Cc; Pca2₁; C2; P1; Pbcn; Pc; P2₁2₁2; P4₃2₁2; P4₁; P3₂; Fdd2; Pccn; P2/c; P6₁; I4₁/a; R3; C222₁; P4₂/n; P3₂21; Aba2; P32₁c; Iba2; R3; I4; Pnma; R3c; I4₁cd; P2₁/m; I4; Pnna; P4₂bc; P3; I4₁; P4₂; Pmc2₁; Pbam; P6₃; Pnn2; Pnc2; C2/m; P4/n; Ibca; P6₅22; Fddd; Pcca; P2; P6₂; P31c; P3; Ccc2; Pba2; P4₂2₁2; P4₁22; P4; I222; I42d; P4nc; Ccca; Pm; Pmna; Cmc2₁; Pcc2; P6₃22; P6₄; P31c; P222; P4/ncc; P4n2; I4₁22; Pbcm; Pmn2₁; F222; C222; P2₁3; I23; P222₁; R3c; P3₂12; P3₁12; P4b2; P42c and P2/m.

The generation of crystal structures involves a low-discrepancy sampling of all structural variables within each space group: unit cell lengths and angles; molecular positions and orientations within the asymmetric unit. Space group symmetry was then applied and a geometric test was performed for overlap between molecules. Molecular clashes were removed by lattice expansion (the SAT-expand method in ref 27). All accepted trial structures were lattice energy minimized and the search was run until a total of 5,000 lattice energy minimizations had been performed in each space group (445,000 energy minimizations per molecule). Lattice energy calculations were performed with an anisotropic atom–atom potential using DMACRYS³⁶. Electrostatic interactions were modelled using an atomic multipole description of the molecular charge distribution (up to hexadecapole on all atoms) from the B3LYP/6-31G** calculated charge density using a distributed multipole analysis. Atom–atom repulsion and dispersion interactions were modelled using a revised Williams intermolecular potential³⁷. Charge–charge, charge–dipole and dipole–dipole interactions were calculated using Ewald summation, while all other intermolecular interactions were summed to a 30 Å cut-off between molecular centres-of-mass. For a given molecule, the relative lattice energy of a given predicted crystal structure was evaluated as the difference between its calculated lattice energy and the lattice energy of the global minimum on the energy vs density landscape of that given molecule. Duplicate structures were removed from the set using COMPACK³⁸, based on matching interatomic distances within 30-molecule clusters. Unless stated otherwise, best geometric overlays between predicted and experimentally determined single crystal structures are given by the lowest root mean square deviation of atomic positions in a 15 molecular cluster, RMSD₁₅.

The packing coefficient, PC, of a given predicted crystal structures was evaluated as the ratio between the gas phase molecular volume, V_g, and the crystal volume per molecule, V_c:

$$PC=\frac{V_g}{V_c}$$ (1)

Connolly molecular volumes at DFT equilibrium geometries were used as the gas phase molecular volume, V_g, and calculated using Materials Studio³⁴. Crystal volume per molecule, V_c, was evaluated as the unit cell volume divided by the number of molecules per unit cell. Calculated T0, T1, T2, T2E, S1, S2, P1, P2, P1M and P2M gas phase molecular volumes, V_g, are 244.47, 369.09, 344.46, 479.91, 474.40, 442.78, 568.05, 544.45, 607.28 and 586.52 ų, respectively.

Throughout, Greek letters α, β, γ, etc, are used to refer to predicted crystal structures corresponding to experimentally observed polymorphs, whereas as-yet unobserved predicted structures are labelled A, B, C, etc.

Energy–structure–function maps

Each structure in each CSP dataset was assigned a unique identification code. To generate the energy-structure-function maps, these structures then underwent a series of property calculations and the results were tabulated. For properties such as methane capacity, calculations were performed for all CSP derived structures for a given molecule. For computationally more expensive property calculations, a ‘leading edge’ of low-energy structures across the computed density range was first selected.

Supercell generation

For each of the CSP structures used to generate the ESF maps, a supercell representation of the crystal structure was adopted in the geometric property calculations and adsorption/separation simulations. A supercell was obtained by replicating the unit cell in three dimensions so that the minimum of the projections of its crystallographic a, b, and c cell vectors onto the Cartesian X, Y, and Z axes was greater than 24.0 Å.

Geometric analysis

Full topological analysis was performed on the CSP structures using the void analysis tool Zeo++³⁹. This calculates the geometrical parameters of the pore space, if any, within each structure based on the Voronoi decomposition. The outputs from this analysis include the pore dimensionality (0-D, 1-D, 2-D or 3-D), the largest inclusion sphere (D_i), and the largest free sphere (D_f). A probe radius of 1.70 Å was used in all calculations to represent methane. Monte Carlo sampling was also performed to calculate accessible surfaces (e.g., Fig. 2) and pore volumes.

Methane and hydrogen capacity calculations

Methane adsorption was predicted for each structure at a temperature of 298 K and pressures of 5.8, 65, and 100 bar. Hydrogen uptakes were predicted for each structure at 100 bar/77 K and 5 bar/160 K. All the adsorption predictions were performed using grand-canonical Monte Carlo (GCMC) simulations involving a 50,000-cycle equilibration period and a 50,000-cycle production run. In hydrogen adsorption simulations, quantum diffraction effects of hydrogen at low temperatures were accounted for using the so-called Feynman–Hibbs quantum effective potentials.⁴⁰

Heats of adsorption

The isosteric heat of adsorption (Q_st) for methane at zero coverage (infinite dilution) in each adsorbent at 298 K was obtained from energy differences computed in the canonical (NVT) ensemble, via the Widom test particle method, given as:

$$Q_{\text{st}}=RT-\left\{{\langle U_1\rangle }_1-{\langle U_0\rangle }_0-\langle U_{\text{g}}\rangle \right\}$$ (2)

where R is the gas constant, U_N is the total energy of the host with N guest molecules present, 〈⋯〉_X is the ensemble average at constant V, T, and X guest molecules, and 〈U_g〉 is the average energy of an isolated guest molecule in vacuo at the same temperature.

Leading edge collation

As molecular dynamics and separation simulations are computationally more expensive, it was important to limit the amount of structures used. This was achieved by creating the leading edge for each CSP dataset. A script was written to separate all the structures into bins of width 0.05 g cm^-3, and any structures up to 10 kJ mol^-1 above the lowest energy structure in that bin were extracted and tabulated to create the leading edge. Hydrogen-bond analysis, hydrocarbon separation simulations and thermal stability simulations were carried out for a subset of T2 leading edge structures determined to be distinct based on their simulated powder diffraction profiles.

Hydrocarbon separation simulations

Configurational-bias Monte Carlo (CBMC) simulations were performed for leading edge structures for T2 to predict the separation performance of structures in the predicted ensemble for three hydrocarbon separations: propane/methane, xylene isomers, and propane/propene. Simulations were conducted for equimolar mixtures at a total pressure of 1 bar (298 K). The CBMC simulations performed included a 300,000-cycle equilibration period and a 300,000-cycle production run.

Hydrogen-bonding analysis

Hydrogen bonds were identified using PLATON⁴¹. The frequency of hydrogen bond patterns were determined using the “Motif search” functionality in Mercury⁴².

Approximate computational costs

Approximately three weeks (in real time) and 400,000 CPU hours, with over 200 CPUs devoted uniquely to these calculations, were needed to perform CSP for T2E—the largest molecule investigated here—resulting in the final set of structures and associated lattice energies. We note that this timescale is significantly shorter than the time required to develop a synthesis for T2E and to isolate diffractable single crystals (around 3 months). The computational cost of CSP for these molecules scales approximately as the square of the number of atoms in the molecule, so was correspondingly smaller for the other molecules studied.

Estimates, in real time, for various property calculations, using 256 CPUs:

• Geometry-based analysis: 1 day; 6,000 crystal structure

• Zero-coverage isosteric heats of adsorption: 1 week; 10,000 crystal structures

• Methane capacity: 6 weeks; 10,000 crystal structures

• Hydrogen capacity: 2 weeks; 150 crystal structures

• Propane/methane or propane/propene separation: 3 weeks; 150 crystal structures

• Xylene separation: 4 weeks; 150 crystal structures

Isotherm simulations

Adsorption isotherms were simulated using the GCMC method with the RASPA code.⁴³ All systems were modelled using force fields, and the corresponding CSP structures for the experimental T2 phases were used.

Thermal stability simulations

Molecular dynamics (MD) simulations were performed in DL_POLY4.07⁴⁴ for structures selected from the low-energy ‘leading edge’ of the CSP energy landscapes for T0, T1, T2 and on select structures for P2M and T2E. A force field was generated based on G09 (M06-2X/6-31G**) equilibrium bond lengths and angles with OPLS2005 atom types from DL_FIELD⁴⁵, bond, angle and torsional terms with bond constraints applied to all bonds to conserve the equilibrium value. MULFIT^46,47 was used to fit atomic charges to the molecular electrostatic potential generated by the B3LYP/6-31G** distributed multipole analysis atomic multipoles. Van der Waals interactions were modelled using the revised Williams intermolecular potential³⁷ with a long-range interaction cutoff of 15 Å and an Ewald precision of 1×10^-6. Each structure was expanded to a supercell such that the minimum cell dimension was greater than 65 Å, relaxed using a 10,000 step zero-temperature minimization in the NVT ensemble using the Berendsen thermostat (with a relaxation time of 0.1 ps) and a 0.001 ps timestep using the Velocity Verlet integrator. The relaxed cell was used as the input for an extended 500 ps simulation in the NPT ensemble using the Berendsen thermostat and barostat (with relaxation times of 0.1 and 10.0 ps respectively) at a temperature of 300 K and a pressure of 1 atms, with a timestep of 0.0025 ps. Additional high temperature MD simulations on T2-α, T2-β, T2-γ and T2-δ were performed at 500 K. For P2M, CHELPG derived point-charges from a G09 B3LYP/6-31G** calculation were used in place of MULFIT generated charges.

Solvent stabilization calculations

Monte Carlo simulations were performed to insert acetone, DMSO and DMAc into selected porous structures using towhee-7.1.0⁴⁸ in the NVT ensemble, using a temperature of 5000 K to enhance sampling of solvent positions. The resulting structures were lattice energy minimized. A force field was generated based on DFT equilibrium bond lengths and angles with UFF derived force-constants, dihedral terms and improper torsions with CHELPG derived point-charges. Atom–atom repulsion and dispersion interactions were modelled using the W99 intermolecular potential with the addition of isotropic S parameters. Simulations of solvent insertion into selected predicted structures were performed in fixed molecule:N ratios (where N is the number of solvent per molecule, with values in the range 1 to 14) with the solvent positions initiated from a template structure placed on a cubic grid. Each simulation was run for 20,000 Monte-Carlo cycles with sampling performed every 10 cycles. An interaction cutoff of half the minimum cell dimension was used. A selection of Monte Carlo moves were allowed (intra-box deletion/insertion, partial configuration bias regrowth, single-atom translations, centre-of-mass rotations and translations) using configurational-biased Monte Carlo (CBMC). The resulting configurations were processed and the gas-phase optimized molecular geometry overlaid back onto the simulation structures. Rigid molecule lattice energy minimization was attempted on all valid structures using DMACRYS³⁶ with electrostatic and atom-atom repulsion and dispersion interactions modelled as described in the CSP methodology section. Each trial structure was subject to a 3 step optimization procedure. In the first stage electrostatic interactions were modelled using point-charges derived from a B3LYP/6-311G** calculation. In the subsequent steps, electrostatics were modelling using an atomic multipole description up to the hexadecapole on all atoms. Structures in which the host framework became distorted were removed; this was monitored by comparison of the host frameworks to the starting solvent-free crystal structure using the COMPACK algorithm³⁸ with an overlay based on 200- molecule clusters; only structures with an RMSD₂₀₀ < 0.8 Å were retained.

Comparison of the energies of solvated crystal structures with the low energy, non-solvated predicted structures requires a correction for the energetic cost of removing solvent molecules from their pure phase. For this, Monte Carlo simulations were performed on solvent boxes containing 50 molecules, in the NVT ensemble at 300 K. The simulation cell lengths were taken such that the density matched the experimental density of each solvent. Simulations consisted of 100,000 Monte Carlo cycles, with Monte Carlo centre-of-mass translations and rotations using a 5.5 Å cutoff. Configurations from the end 50,000 steps were sampled every 50 Monte Carlo cycles and subject to constant volume lattice energy minimizations using DMACRYS with parameters as previously described and a 15 Å interaction cut-off.

The stability of the solvated porous crystal structures, relative to the dense, global minimum CSP structure and pure solvent, was calculated as:

$$E_{Rel,Solvated}=E_{Latt(Host+Solvent)}+N\left(-E_{Solvent}+\frac{3}{2}RT\right)$$ (3)

where E_{Latt(Host+Solvant)} is the calculated lattice energy of the solvated CSP structure containing N solvent molecules per host molecule, and E_Solvant is the calculated energy of the pure solvent. The $\frac{3}{2}RT$ (calculated at 300 K) is an equipartition estimate of the loss in internal energy of solvent molecules, assuming free rotation in the liquid phase and loss of solvent molecule rotational freedom in the crystal.

For all solvents (acetone, DMAc and DMSO) there exist porous structures (T2-α, T2-β, T2-γ) which fall below the lowest energy unsolvated T2 crystal structure. The presence of solvent sufficiently stabilizes these structures such that they are energetically more favorable then the dense packed phase, T2-D, when fully solvated. In all cases, the porous structures (T2-α, T2-β and T2-γ) are the most favored forms. The more densely packed porous polymorphs (T2-δ, T2-A and T2-E) show negligible solvent stabilization with the exception of T2-δ with DMSO which displays a similar extent of stabilization to the more porous structures. The voids of T2-δ are too small to accommodate DMAc. For T2-γ the maximum in the solvent stabilization energy is seen at a ratio of 8 DMAc per T2 molecule, in good agreement with the experimentally determined ratio of 7.79 per T2.

Full details of all computational methods are given in the Supporting Information.

Synthesis and Measurements

Full details of synthesis, crystallization and sublimation methods, solvent exchange protocols, X-ray structure determination, and gas sorption analysis are given in the Supporting Information. T1²⁶ and T2²² were synthesized as described previously. T2E was synthesized by a new route that is described in the Supporting Information.

Data Availability

The computational data that support the findings of this study, including all predicted crystal structures and properties, are available in ePrints Soton with the identifier doi: 10.5258/SOTON/404749. Experimentally determined crystal structures, including structure factors, have been deposited as CIFs with The Cambridge Crystallographic Data Centre as entries 1478355-1478365, these files are available free of charge via www.ccdc.cam.ac.uk/data_request/cif.

Supplementary Material

Supplementary Information is available in the online version of the paper.