Abstract
To effectively predict the thermal conductivity and viscosity of alumina (Al2O3)-water nanofluids, an artificial neural network (ANN) approach was investigated in the present study. Firstly, using a two-step method, four Al2O3-water nanofluids were prepared respectively by dispersing different volume fractions (1.31%, 2.72%, 4.25%, and 5.92%) of nanoparticles with the average diameter of 30 nm. On this basis, the thermal conductivity and viscosity of the above nanofluids were analyzed experimentally under various temperatures ranging from 296 to 313 K. Then a radial basis function (RBF) neural network was constructed to predict the thermal conductivity and viscosity of Al2O3-water nanofluids as a function of nanoparticle volume fraction and temperature. The experimental results showed that both nanoparticle volume fraction and temperature could enhance the thermal conductivity of Al2O3-water nanofluids. However, the viscosity only depended strongly on Al2O3 nanoparticle volume fraction and was increased slightly by changing temperature. In addition, the comparative analysis revealed that the RBF neural network had an excellent ability to predict the thermal conductivity and viscosity of Al2O3-water nanofluids with the mean absolute percent errors of 0.5177% and 0.5618%, respectively. This demonstrated that the ANN provided an effective way to predict the thermophysical properties of nanofluids with limited experimental data.
Keywords: nanofluids, thermal conductivity, viscosity, artificial neural network, experimental data
1. Introduction
Considering the higher thermal conductivity of many solid materials, including Cu, CuO, TiO2, ZnO, Fe3O4, MgO, Al2O3 and graphite, dispersing solid particles in the conventional coolants (such as water, oil, ethylene glycol, refrigerant, etc.) is one of the most efficient ways to enhance the heat transfer process [1]. However, a large number of experimental results indicated that the lower suspension stability of large particles seriously limited the practical application of the traditional liquid-solid mixture. In the 1990s, the idea of nanofluids consisting of nanoparticles and base fluid was firstly introduced by Choi [2]. Due to the potential advantages in flow and heat transfer performance, nanofluids become a focus in the field of thermal science [3].
Thermal conductivity and viscosity are the most important physical parameters and play crucial roles for studying nanofluids. Over the last two decades, various experimental investigations have been published to evaluate the effects of nanoparticles on thermal conductivity and the viscosity characteristics of base fluids. References [4,5,6,7,8,9,10,11,12,13] respectively reviewed the experimental and theoretical developments of various nanofluids’ thermophysical parameters. According to their analysis, it could be found that the addition of nanoparticles did enhance the thermal conductivity and viscosity of base fluids in varying degrees. However, it was unfortunate that there were still many differences in the measurements of thermal conductivity and viscosity due to the effects of nanofluids manufacturing and measuring technologies [14]. In addition, considering the complex mechanisms, including nanoparticle heat transport [15,16], nano-shells at the interface between liquid and particle [17,18,19,20], Brownian motion [21,22], and clustering of nanoparticles [23,24], the thermal conductivity and viscosity of nanofluids are very difficult to predict accurately using the traditional model-based approach. For these cases, it is very valuable to further study the experimental characteristics and predictive modeling of nanofluids’ thermal conductivity and viscosity.
In recent years, with the development of artificial intelligence technology, various data-driven modeling approaches have been put forward to solve the thermal science problem [25,26]. Inspired by the biological brain, an artificial neural network (ANN) can effectively establish the relationship between the input and output variables without considering the detailed physical process, which attracts increasing attention in terms of predicting the thermophysical properties of nanofluids. Hojjat et al. [27] firstly analyzed the application of a three-layer feed forward neural network on the thermal conductivities prediction of various non-Newtonian nanofluids. They found that the ANN predicted values were in agreement with the experimental data. The average and maximum errors were only 1.6% and 5.8%, respectively. On this basis, Longo et al. [28], Mehrabi et al. [29,30], Ariana et al. [31], Esfe et al. [32,33,34,35,36,37,38], and Vakili et al. [39] successively designed different ANN models (such as a feed forward neural network, adaptive neuro-fuzzy inference system, diffusional neural networks, etc.) to further verify the effectiveness of ANN in the modeling and prediction of nanofluid thermal conductivity. All of their results demonstrated that ANN was an effective tool in comparison with the traditional model-based approach for describing the enhancement behavior of nanofluid thermal conductivity. In addition, attracted by the better nonlinear mapping and recognition abilities of ANN, Yousefi et al. [40], Mehrabi et al. [41], Zhao et al. [42,43], and Heidari et al. [44] also extended the ANN based modeling approach to the prediction of nanofluid viscosity. As reported in their analysis, ANN could be used for predicting the viscosity of nanofluids with satisfactory accuracy.
Up to now, much valuable literature has demonstrated the effectiveness of different ANN models for modeling and predicting the thermalphysical properties of nanofluids. However, considering the data characteristics of nanofluids’ properties and the modeling process of an ANN, there are still many difficulties or obstacles to be resolved. For example, most of the developed ANN had only one output (thermal conductivity, viscosity, or density) and were usually trained by using a large number of samples, which were obtained from different experiments. Fewer publications discussed the multiple parameter modeling and prediction performance of ANNs, especially with limited experimental data. This may means that the application of ANNs in nanofluids is still in its infancy.
Based on the above background, this study presents a further investigation into the prediction of Al2O3-water nanofluid thermal conductivity and viscosity by using ANN and the limited experimental data. With the influences of nanoparticle volume fraction (1.31%, 2.72%, 4.25%, and 5.92%) and temperature (from 296 to 313 K), four different Al2O3-water nanofluids were prepared and measured. On this basis, a RBF neural network with multiple outputs was constructed and verified through the experimental data.
2. Experimental Methods
2.1. Materials and Method of Preparing Nanofluids
In this study, a two-step method is used to manufacture the Al2O3-water nanofluids with different nanoparticle volume fraction. The spherical Al2O3 particles (Xuan Cheng Jing Rui New Material Co., Ltd, Xuancheng, China) with an average diameter of 30 nm, a purity of 99.9%, a density of 3.6 g/cm3, and the specific surface area of 15 m2/g are selected. During the manufacturing, the measurement of the masses of the nanoparticles is carried out by using an electronic balance with an accuracy of 1 mg. The volume fractions of the nanoparticles (1.31%, 2.72%, 4.25%, and 5.92%) are calculated according to the following function:
| (1) |
where is the volume fraction of the nanoparticle, is the weight fraction of the nanoparticle, and and are the densities of the nanoparticle and base fluid, respectively.
To keep the stability of the nanofluids, the sodium dodecylbenzene sulfonate (SDBS) from Guangzhou Chemical Reagent Factory (Guangzhou, China) is added as the dispersing agent. The mass of the SDBS is quantitatively determined with the electronic balance and equal to that of nanoparticle, based on the existing experiment investigations [45,46]. Moreover, periodical magnetic stirring and ultrasonic oscillating are applied to prepare the nanofluids, considering that the fact that the stability process technologies of nanofluids in different studies are not very unified. The times of periodical magnetic stirring and ultrasonic oscillating are usually determined according to the actual conditions. In the present study, the corresponding times of the above stability process technologies are 12 h and 5 h, respectively.
Figure 1 shows the manufactured Al2O3-water nanofluids after different standing times (0 h, 36 h, and 72 h). It can be seen that there is no obvious sedimentation for the above four different nanofluids, which means that they were manufactured successfully. In addition, Figure 2 presents the Scanning Electron Microscope (SEM) image of the Al2O3 nanoparticle with a volume fraction of 5.92% in water. It is clearly observed that most of the nanoparticles can be spherical and have good dispersion.
Figure 1.
The manufactured Al2O3-water nanofluids with different nanoparticle volume fractions after different standing times; (a) 0 h; (b) 36 h; (c) 72 h.
Figure 2.
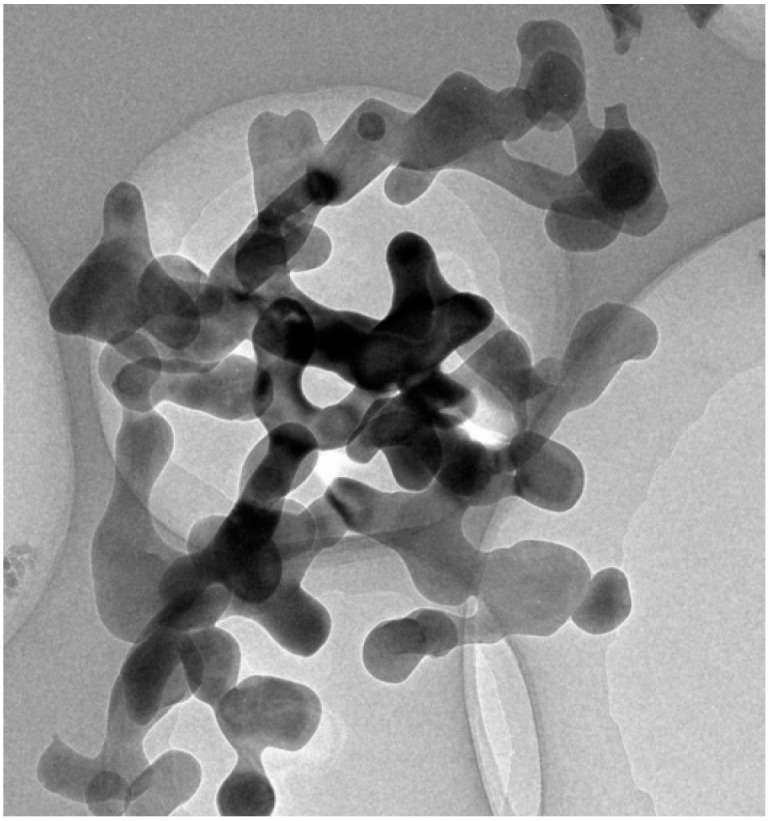
Scanning Electron Microscope (SEM) image of the Al2O3 nanoparticle with a volume fraction of 5.92% in water.
2.2. Method of Investigating the Thermal Conductivity and Viscosity
To effectively measure the thermal conductivity of Al2O3-water nanofluids, a transient hot-wire apparatus designed by Xi’an Xiatech Electronic Technology Co., Ltd (Xi’an, China) is applied. The measuring accuracy of this apparatus is ±2%–3% in the thermal conductivity range of 0.001–20 W/m·K and temperature range of 113–423 K. Considering the constant temperature requirement, an external temperature-controlled bath is used, as shown in Figure 3. For the viscosity measurement of Al2O3-water nanofluids, the apparatus (Figure 4) including a Kinexus pro + Super Rotation Rheometer (Malvern Instruments Ltd, Malvern, UK) and a Silent Air Compressor (Shanghai Dynamic Industry Co., Ltd, Shanghai, China), is applied in the present experiment. Since the viscosities of Al2O3-water nanofluids are usually not very high, the Peltier Cylinder Cartridge is selected. The size of the cup is C14 (DIN standard). The diameter of the bob is 14 mm. Both the cup and bob are sandblasted to reduce slippage. The angular velocity of the rheometer is ranged from 10 nrad/s to 500 rad/s. The temperature resolution of this viscosity measuring equipment is 0.01 K in the temperature range of 233–473 K. More detailed devices information and the experimental procedure for viscosity measurement are referenced in [47,48,49].
Figure 3.
Measuring equipment of thermal conductivity for Al2O3-water nanofluids.
Figure 4.
Measuring equipment of viscosity for Al2O3-water nanofluids.
3. Modeling Method Based on ANN
As an effective data-driven modeling approach, an ANN is put forward based on the inspiration from the human brain’s structure and activity mechanism. Nowadays, there are many different ANNs for various applications. In the fields of curve-fitting and nonlinear predictive modeling, the RBF neural network exhibits better ability in comparison with others [43].
3.1. RBF Neural Network Theory
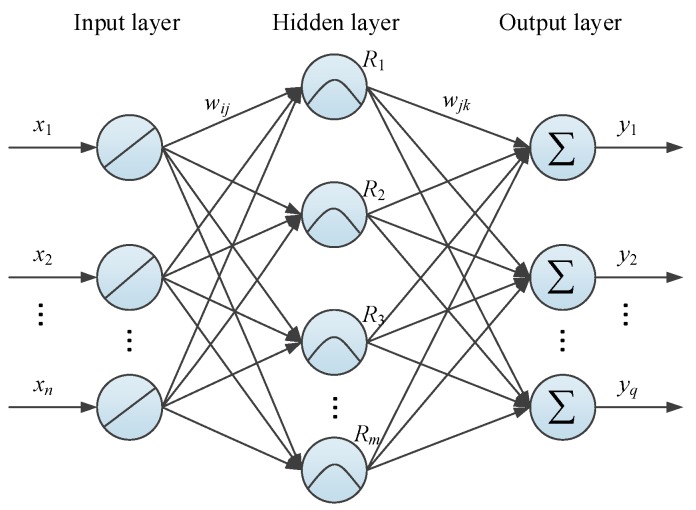
In general, an RBF neural network (as shown in Figure 5) is constituted by an input layer, hidden layer, and output layer. The input and output layer correspond to the dendrite and synapse of biological neurons, respectively. Similarly to the function of cyton, the hidden layer plays a role of intermediation to process the input-output information and deliver it to the output layer. The connections between different layers are established through a series of artificial neurons and weights. Theoretically, the modeling process of an RBF neural network is to solve the mapping from to (). Assuming the input vector of an RBF neural network is , the response of th neuron in the output layer () can be obtained using the following linear weighting function [50]:
| (2) |
where is the connection weight between the th hidden layer neuron and the th output layer neuron and and are the numbers of neurons in the corresponding layer, respectively.
Figure 5.
Typical architecture of an radial basis function (RBF) neural network.
Different from those of many other ANN, the responses of RBF neural networks’ th hidden layer neuron are usually determined by the RBF. When it selects the Gauss function, the corresponding can be defined as:
| (3) |
where is the Euclidean distance between input vector and the th neuron center and is width of the th neuron.
Analyzing Equations (2) and (3), it can be easily found that the key to RBF neural network training is how to determine , , and . In the past decades, different unsupervised and supervised algorithms have been developed to solve the above problem [51]. In this study, the network parameters are updated by using a orthogonal least square (OLS) approach, for which the minimizing function is shown in Equation (4). More detailed information about OLSs can be found in [52].
| (4) |
where and are the network output and desired output of the th output layer node, respectively.
3.2. Implementing Procedure
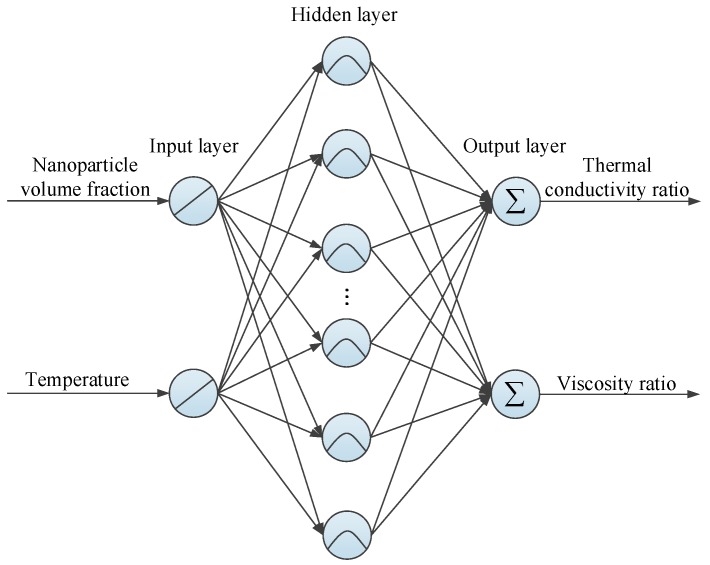
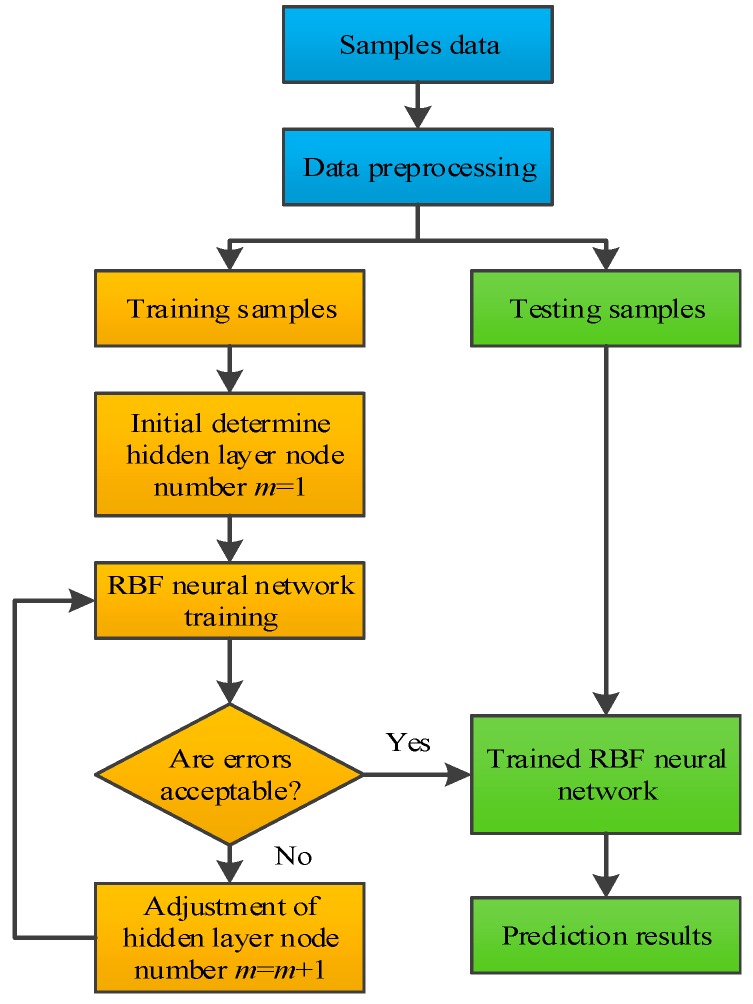
In the present investigation, a typical three layer RBF neural network is developed. For the Al2O3-water nanofluids with the determined nanoparticle size, nanoparticle volume fraction and temperature are the most important factors for influencing the thermal conductivity and viscosity. Therefore, both the input and output layers of the RBF neural network consist of two neurons, as illustrated in Figure 6. The neurons in the hidden layer and others are determined in the training process. Figure 7 presents the detailed procedure for implementing the modelling and prediction of nanofluids based on the RBF neural network. To improve the training accuracy, all the input and output variables are normalized.
| (5) |
where is the original value, is the normalized value, and and are the corresponding maximum and minimum of .
Figure 6.
The RBF neural network developed in this study.
Figure 7.
Implementing process of the RBF neural network for modeling and prediction.
To effectively evaluate the predictive accuracy of the RBF neural network, four important parameters, namely root mean squared error (RMSE), mean absolute percentage error (MAPE), sum of squared error (SSE), and statistical coefficient of multiple determination (R2), are used.
| (6) |
| (7) |
| (8) |
| (9) |
where P is the desired value, Q is the network output value, and t is the number of samples.
4. Results and Discussion
4.1. Enhancement of Thermal Conductivity
To verify the effectiveness of the above thermal conductivity measuring apparatus, water is measured first. Considering the temperature balance of the testing sample and the fluid in bath, the testing temperature can be determined when it remains constant for 20 min. Every experimental data is the average value of five measurements with a frequency interval of 5 min. Table 1 presents the experimental thermal conductivity of water in the temperature range of 288–318 K. According to the comparison, it is concluded that the thermal conductivity apparatus has good precision for the present study. Based on the experimental data, the measurement uncertainty of thermal conductivity is less than 5% for water.
Table 1.
Thermal conductivity measurement and analysis for water.
| Temperature (K) | Reference Values (W/(m·K)) | Measure Values (W/(m·K)) | Deviation (%) |
|---|---|---|---|
| 288 | 0.5916 | 0.595 | 0.5747 |
| 293 | 0.6003 | 0.6019 | 0.2665 |
| 298 | 0.6088 | 0.6111 | 0.3778 |
| 303 | 0.6173 | 0.6185 | 0.1944 |
| 308 | 0.6245 | 0.6252 | 0.1121 |
| 313 | 0.6318 | 0.6292 | −0.4115 |
| 318 | 0.6379 | 0.6374 | −0.0784 |
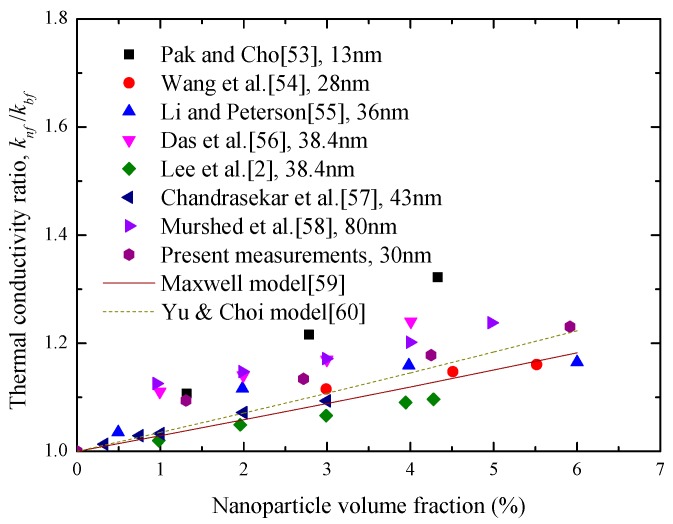
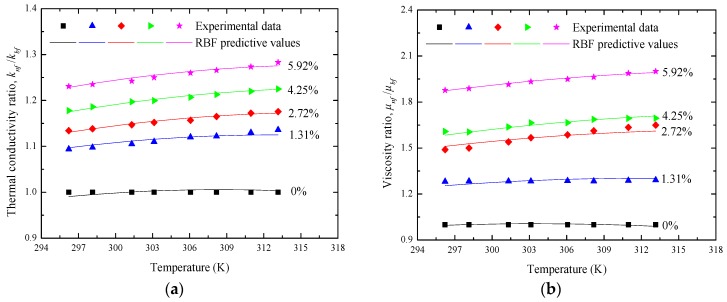
Figure 8 presents the change of the thermal conductivity ratio () between Al2O3-water nanofluids and water with different nanoparticle volume fractions at room temperature. From Figure 8, it is found that the thermal conductivity of water can be enhanced obviously with the increase of the Al2O3 nanoparticle. For example, at a nanoparticle volume fraction of 1.31%, the enhancement of water thermal conductivity is 9.4%. When the volume fraction of the Al2O3 nanoparticle increases to 5.92%, the can change to 1.231. In addition, Figure 8 compares the present measurements with many experimental data obtained from the existing publications. The results show that they are in good agreement with both the qualitative and quantitative aspects. This may mean that both the sample preparation and thermal conductivity measurements are successful. In addition, it is also clearly observed from Figure 8 that the enhancement of the Al2O3 nanoparticle on water thermal conductivity cannot be described accurately by using the well-known Maxwell model and the Yu and Choi model due to the complex influence mechanisms such as the interfacial layer, nanoparticle Brownian motion, and clustering.
Figure 8.
Variations of Al2O3-water nanofluids with nanoparticle volume fraction at room temperature [2,53,54,55,56,57,58,59,60].
Maxwell model [59]
| (10) |
where , , and are the thermal conductivity of nanofluids, the nanoparticle, and base fluid, respectively.
Yu & Choi model [60]
| (11) |
| (12) |
where , is the thermal conductivity of interfacial layer, , is thickness of interfacial layer, and is the radius of nanoparticle.
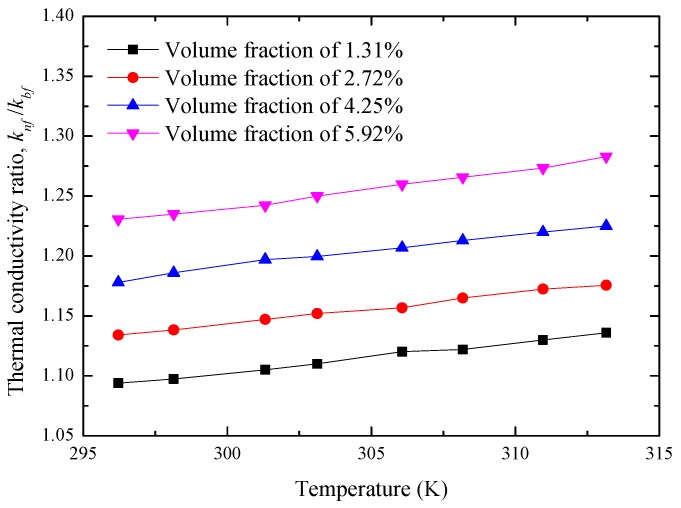
Considering the effects of temperature ranging from 296 to 313 K, Figure 9 presents the variation of with various volume fractions. It can be found that, for any volume fraction of the Al2O3 nanoparticle, the corresponding can linearly improve with the increase of temperature, which is usually explained by the enhancement of nanoparticle Brownian motion. In the present study, taking the nanofluids with an Al2O3 volume fraction of 2.72% as an example, the maximum of 1.283 is obtained at the nanoparticle volume fraction of 5.92% and a temperature of 313 K.
Figure 9.
Variations of with temperature for different nanoparticle volume fractions of Al2O3-water nanofluids.
4.2. Viscosity Investigation
Before experimentally analyzing the viscosity of Al2O3-water nanofluids, it is also necessary to evaluate the apparatus’s effectiveness by selecting water as a sample. Both the measuring frequency and data analysis method are same as those for thermal conductivity. From the contrastive analysis shown in Table 2, it can be inferred that the measurements of viscosity are effective, with a maximum deviation of 0.988% in the temperature ranges of 288–318 K. In addition, the experimental analysis indicates that the measurement uncertainty of water viscosity is less than 5% using the above mentioned approach when the shear rate changes.
Table 2.
Viscosity measurement and analysis for water.
| Temperature (K) | Reference Values (mPa·s) | Measure Values (mPa·s) | Deviation (%) |
|---|---|---|---|
| 288 | 1.1426 | 1.1517 | −0.7955 |
| 293 | 1.0094 | 0.9998 | 0.9517 |
| 298 | 0.8938 | 0.8943 | −0.0658 |
| 303 | 0.8029 | 0.7958 | 0.8791 |
| 308 | 0.7226 | 0.7182 | 0.6106 |
| 313 | 0.6634 | 0.6693 | −0.8866 |
| 318 | 0.6008 | 0.6043 | −0.5876 |
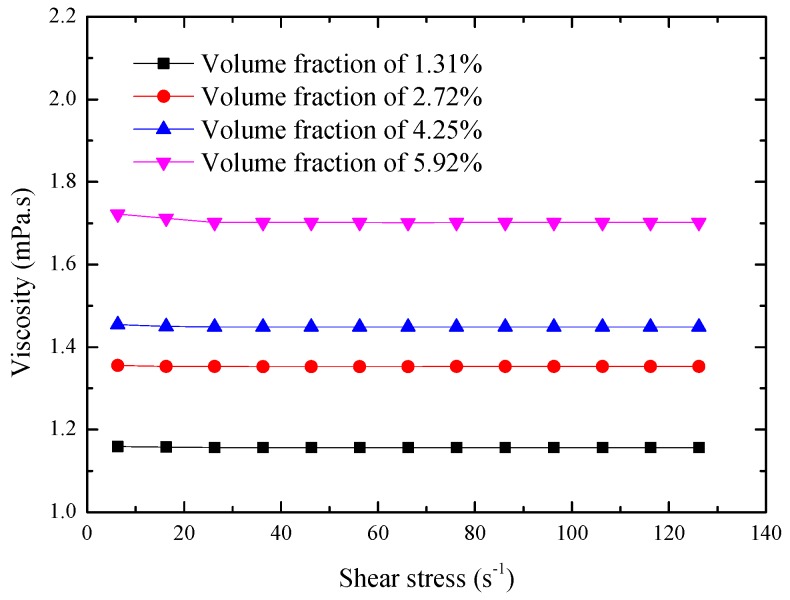
To investigate the influence of Al2O3-water nanofluids, Figure 10 presents the relationship between the shear rate and nanofluid viscosity at the temperature of 298 K. The results show that, with the increase of the shear rate from 6.326 s−1 to 126.2 s−1, the viscosities of Al2O3-water nanofluids with different Al2O3 volume fractions do not change significantly. This may mean that the viscosities of the Al2O3-water nanofluids obtained in the present study display Newtonian behavior.
Figure 10.
Rheological behaviors of Al2O3-water nanofluids at room temperature.
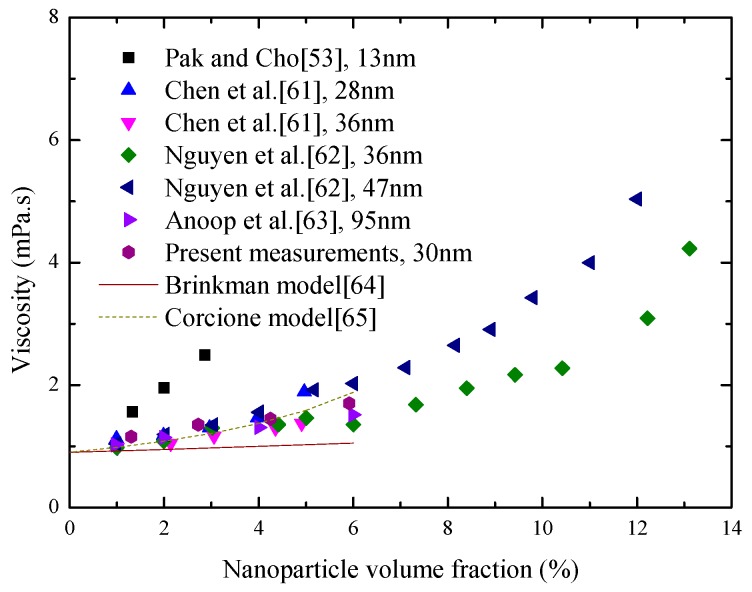
Considering the influence of the Al2O3 volume fraction at the temperature of 298 K, the experimental viscosities of the Al2O3-water nanofluids are given and compared with much published data in Figure 11. All the results show that the suspension of Al2O3 nanoparticles can increase the viscosity of water, and there is a slight non-linear relationship between the viscosity of nanofluids and nanoparticle volume fraction. Moreover, a careful inspection of Figure 11 reveals that the theoretical viscosities obtained by the classical Brinkman model are significantly lower than the corresponding measurements. Compared to the Brinkman model, the Corcione model can effectively describe the effect of nanoparticle volume fraction on viscosity, but its prediction precision is not very ideal. This is because the viscosity of nanofluids depends strongly on many known and unknown factors.
Figure 11.
Variations of Al2O3-water nanofluids’ viscosity with nanoparticle volume fraction at room temperature [53,61,62,63,64,65].
The Brinkman model [64] is as follows:
| (13) |
where and are the viscosity of nanofluids and base fluid, respectively.
The Corcione model [65] is as follows:
| (14) |
| (15) |
where is the molar mass of base fluid molecule, is avogadro’s number, is the density of base fluids at temperature of 293 K, and is the diameter of nanoparticle.
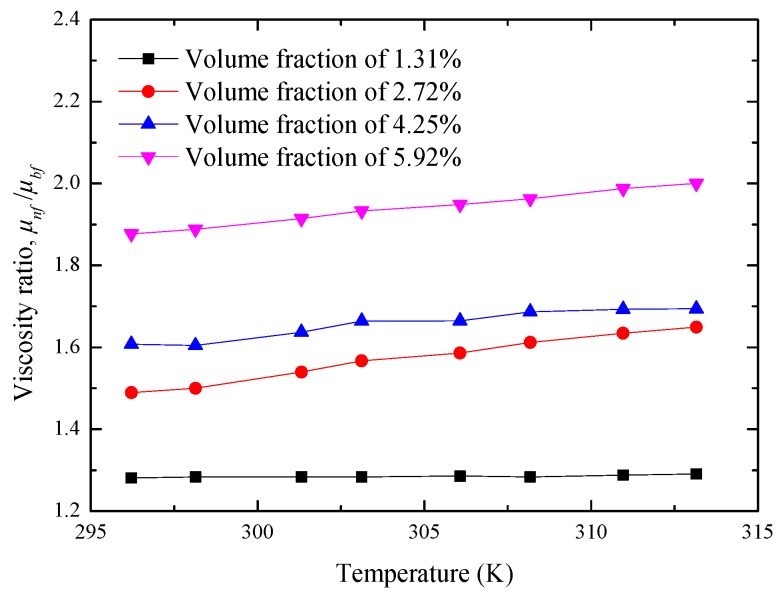
Figure 12 presents the variation of the viscosity ratio, , between nanofluids and water as the functions of temperature and nanoparticle volume fraction. From Figure 12, it is observed that, for the manufactured Al2O3-water nanofluids in this study, temperature has an enhanced effect on viscosity in the temperature ranges of 296–313 K. At the nanoparticle volume fraction of 4.25%, the fractions are respectively 1.605, 1.664, 1.687, and 1.694 when the temperatures are 298 K, 303 K, 308 K, and 313 K.
Figure 12.
Variations of with temperature for different nanoparticle volume fractions of Al2O3-water nanofluids.
4.3. Predictive Analysis of RBF Neural Networks
Based on the above experiment, the limited experimental data (40) are used to discuss the modeling and prediction processes of the RBF neural network for the thermal conductivity and viscosity of Al2O3-water nanofluids. Among them, the ratio of training and testing samples is 3:1.
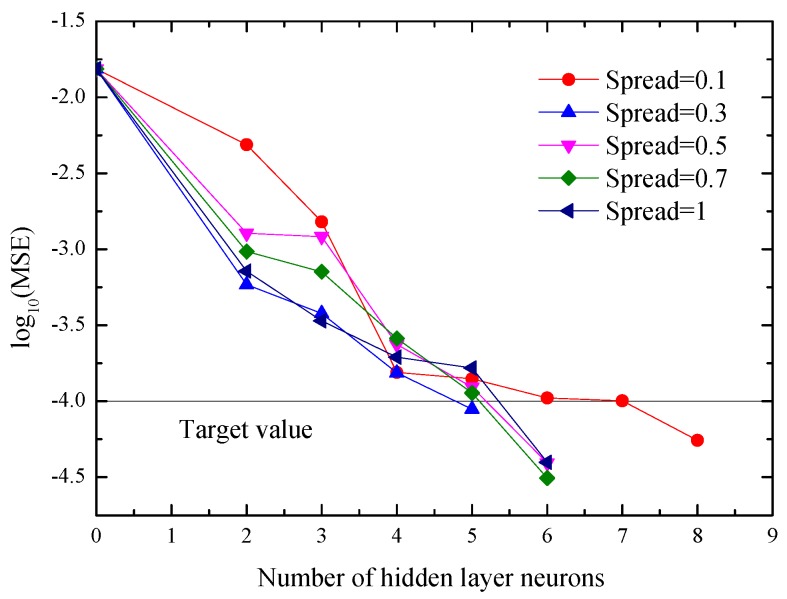
For the RBF neural network, Spread is usually a very important factor for influencing the training process. Figure 13 shows the relationships of mean square error (MSE) and the number of hidden layer neurons with different values of Spread. Table 3 lists the effect of Spread on network modeling accuracy. Comprehensively analyzing the results reported in Figure 13 and Table 3, it is found that both the network structure and modeling performance cannot be changed significantly with different values of Spread in this study. Therefore, the network structure of 2-8-2 neurons with the Spread of 0.1 is used. The related weights and biases of a 2-8-2 RBF neural network can be found in Table 4.
Figure 13.
Relationships of mean square error (MSE) and the number of hidden layer neurons with different values of Spread.
Table 3.
Performance evaluation of the RBF neural network for the total samples with different values of Spread.
| Parameters | Evaluation Criteria | Spread | ||||
|---|---|---|---|---|---|---|
| 0.1 | 0.3 | 0.5 | 0.7 | 1 | ||
| knf/kbf | RMSE | 8.572 × 10−3 | 6.797 × 10−3 | 4.140 × 10−3 | 4.346 × 10−3 | 4.043 × 10−3 |
| MAPE(%) | 0.5177 | 0.4803 | 0.2872 | 0.3197 | 0.2866 | |
| SSE | 2.939 × 10−3 | 1.848 × 10−3 | 6.857 × 10−4 | 7.556 × 10−4 | 6.538 × 10−4 | |
| R2 | 0.999944 | 0.999965 | 0.999987 | 0.999986 | 0.999988 | |
| μnf/μbf | RMSE | 1.423 × 10−2 | 2.311 × 10−2 | 1.624 × 10−2 | 1.381 × 10−2 | 1.658 ×10−2 |
| MAPE(%) | 0.5618 | 1.3862 | 0.8233 | 0.7169 | 0.8280 | |
| SSE | 8.094 × 10−3 | 2.137 × 10−2 | 1.055 × 10−2 | 7.634 × 10−3 | 1.100 × 10−2 | |
| R2 | 0.999913 | 0.999770 | 0.999887 | 0.999918 | 0.999882 | |
Table 4.
Weight and bias coefficients of the developed RBF neural network.
| Neuron | Hidden Layer | Output Layer | ||||
|---|---|---|---|---|---|---|
| Weights wij and Biases | Weights wjk and Biases | |||||
| Nanoparticle Volume Fraction | Temperature | Biases | Thermal Conductivity | Viscosity | Biases | |
| 1 | 0.7184 | 1 | 1.1894 | −61.8011 | −143.4012 | −4.7283 |
| 2 | 0 | 1 | 1.1894 | −4.4132 | −18.1112 | −6.1187 |
| 3 | 1 | 1 | 1.1894 | 24.4808 | 49.7229 | |
| 4 | 0.4595 | 1 | 1.1894 | 92.2675 | 218.6915 | |
| 5 | 0.2208 | 0.9930 | 1.1894 | −76.4725 | −178.5244 | |
| 6 | 0 | 0.9841 | 1.1894 | 36.6988 | 86.1722 | |
| 7 | 0.7184 | 1 | 1.1894 | −61.8011 | −143.4012 | |
| 8 | 0 | 1 | 1.1894 | −4.4132 | −18.1112 | |
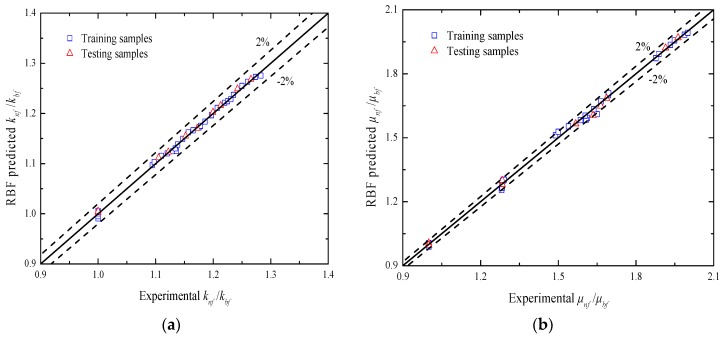
Figure 14 and Figure 15 compare the RBF predicted thermophysical properties of Al2O3-water nanofluids with the corresponding experimental data. Table 5 lists the predictive evaluation criteria of the RBF neural network for the training and testing samples. As shown in Figure 14 and Table 5, the RBF neural network has a high accuracy for modeling the thermal conductivity and viscosity of Al2O3-water nanofluids with limited experimental data. All the prediction errors of thermal conductivity and nearly 92.5% of those of viscosity are within the ±2% error band. It is worth noting that there is a higher accuracy for the testing dataset but not the training ones. This is because the samples of the testing dataset are very few in this study. In addition, the results analysis of Figure 15 reveals that the effects of nanoparticle volume fraction and temperature on the above two thermophysical properties can be effectively extracted in the data-driven prediction of the RBF neural network. All of the above investigations demonstrate that a RBF neural network provides a successful alternative to the traditional model-based prediction approach for the thermal conductivity and viscosity of Al2O3-water nanofluids.
Figure 14.
Scatter plots of (a) and (b) for the RBF predicted results and experimental data.
Figure 15.
Comparisons of the experimental and RBF predicted results for (a) and (b) .
Table 5.
Performance evaluation of the RBF neural network for the training and testing samples.
| Parameters | Evaluation Criteria | Training Samples | Testing Samples |
|---|---|---|---|
| knf/kbf | RMSE | 4.464 × 10−3 | 3.974 × 10−3 |
| MAPE (%) | 0.3230 | 0.3098 | |
| SSE | 5.977 × 10−4 | 1.579 × 10−4 | |
| R2 | 0.999985 | 0.999988 | |
| μnf/μbf | RMSE | 1.419 × 10−2 | 1.263 × 10−2 |
| MAPE (%) | 0.7472 | 0.6261 | |
| SSE | 6.040 × 10−3 | 1.594 × 10−3 | |
| R2 | 0.999913 | 0.999932 |
5. Conclusions
In this paper, the experiments on Al2O3-water nanofluid preparation and thermophysical properties measurement are performed to obtain the effects of nanoparticle volume fraction and temperature on thermal conductivity and viscosity. All the experimental results showed that both thermal conductivity and viscosity could be enhanced with the increase of the Al2O3 nanoparticle volume fraction and temperature. On this basis, considering the advantage of a RBF neural network in modeling, a case study was investigated to discuss the application of a RBF neural network on the prediction of nanofluids’ thermal conductivity and viscosity with 40 sets of experimental data. By comparing the RBF predictive values and the experimental data, it was demonstrated that RBF neural network not only exhibited good modeling accuracy (thermal conductivity: = 8.572 × 10−3, = 0.5177%, = 2.939 × 10−3, = 0.999944; viscosity: = 1.423 × 10−2, = 0.5618%, = 8.094 × 10−3, = 0.999913), but also could effectively extract the influences of nanoparticle volume fraction and temperature on Al2O3-water nanofluids’ thermal conductivity and viscosity.
Acknowledgments
The authors acknowledge the financial support from the Fundamental Research Funds for the Central Universities (No. HEUCFJ170304) and are thankful for Fengchen Li and Tongzhou Wei for their experimental support.
Author Contributions
Ningbo Zhao prepared the Al2O3-water nanofluids, and performed the measurements of thermophysical properties of nanofluids. Zhiming Li provided the program codes of RBF neural network and wrote the basic theory of the RBF neural network.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Zhao N.B., Li S.Y., Yang J.L. A review on nanofluids: Data-driven modeling of thermalphysical properties and the application in automotive radiator. Renew. Sustain. Energy Rev. 2016;66:596–616. doi: 10.1016/j.rser.2016.08.029. [DOI] [Google Scholar]
- 2.Lee S., Choi S.U.S., Li S., Eastman J.A. Measuring thermal conductivity of fluids containing oxide nanoparticles. J. Heat Transf. 1999;121:280–289. doi: 10.1115/1.2825978. [DOI] [Google Scholar]
- 3.Zhao N.B., Yang J.L., Li S.Y., Wang Q. Numerical investigation of laminar thermal-hydraulic performance of Al2O3–water nanofluids in offset strip fins channel. Int. Commun. Heat Mass Transf. 2016;75:42–51. doi: 10.1016/j.icheatmasstransfer.2016.03.024. [DOI] [Google Scholar]
- 4.Murshed S.M.S., Leong K.C., Yang C. Thermophysical and electrokinetic properties of nanofluids-a critical review. Appl. Therm. Eng. 2008;28:2109–2125. doi: 10.1016/j.applthermaleng.2008.01.005. [DOI] [Google Scholar]
- 5.Li Y., Zhou J., Tung S., Schneider E., Xi S. A review on development of nanofluid preparation and characterization. Powder Technol. 2009;196:89–101. doi: 10.1016/j.powtec.2009.07.025. [DOI] [Google Scholar]
- 6.Zhao N.B., Yang J.L., Li H., Zhang Z.Y., Li S.Y. Numerical investigations of laminar heat transfer and flow performance of Al2O3-water nanofluids in a flat tube. Int. J. Heat Mass Transf. 2016;92:268–282. doi: 10.1016/j.ijheatmasstransfer.2015.08.098. [DOI] [Google Scholar]
- 7.Mahbubul I.M., Saidur R., Amalina A.M. Latest developments on the viscosity of nanofluids. Int. J. Heat Mass Transf. 2012;55:874–885. doi: 10.1016/j.ijheatmasstransfer.2011.10.021. [DOI] [Google Scholar]
- 8.Sarkar J., Ghosh P., Adil A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015;43:164–177. doi: 10.1016/j.rser.2014.11.023. [DOI] [Google Scholar]
- 9.Hossain M.S., Saidur R., Sabri M.F.M., Said Z., Hassani S. Spotlight on available optical properties and models of nanofluids: A review. Renew. Sustain. Energy Rev. 2015;43:750–762. doi: 10.1016/j.rser.2014.11.010. [DOI] [Google Scholar]
- 10.Angayarkanni S.A., Philip J. Review on thermal properties of nanofluids: Recent developments. Adv. Colloid Interface Sci. 2015;225:146–176. doi: 10.1016/j.cis.2015.08.014. [DOI] [PubMed] [Google Scholar]
- 11.Solangi K.H., Kazi S.N., Luhur M.R., Badarudin A., Amiri A., Sadri R., Zubir M.N.M., Gharehkhani S., Teng K.H. A comprehensive review of thermo-physical properties and convective heat transfer to nanofluids. Energy. 2015;89:1065–1086. doi: 10.1016/j.energy.2015.06.105. [DOI] [Google Scholar]
- 12.Devendiran D.K., Amirtham V.A. A review on preparation, characterization, properties and applications of nanofluids. Renew. Sustain. Energy Rev. 2016;60:21–40. doi: 10.1016/j.rser.2016.01.055. [DOI] [Google Scholar]
- 13.Murshed S.M.S., Estellé P. A state of the art review on viscosity of nanofluids. Renew. Sustain. Energy Rev. 2017;76:1134–1152. doi: 10.1016/j.rser.2017.03.113. [DOI] [Google Scholar]
- 14.Sidik N.A.C., Mohammed H.A., Alawi O.A., Samion S. A review on preparation methods and challenges of nanofluids. Int. Commun. Heat Mass Transf. 2014;54:115–125. doi: 10.1016/j.icheatmasstransfer.2014.03.002. [DOI] [Google Scholar]
- 15.Hamilton R.L., Crosser O.K. Thermal conductivity of heterogeneous two component systems. Ind. Eng. Chem. Fundamen. 1962;1:187–191. doi: 10.1021/i160003a005. [DOI] [Google Scholar]
- 16.Azmi W.H., Sharma K.V., Mamat R., Najafi G., Mohamad M.S. The enhancement of effective thermal conductivity and effective dynamic viscosity of nanofluids—A review. Renew. Sustain. Energy Rev. 2016;53:1046–1058. doi: 10.1016/j.rser.2015.09.081. [DOI] [Google Scholar]
- 17.Liu M., Ding C., Wang J. Modeling of thermal conductivity of nanofluids considering aggregation and interfacial thermal resistance. RSC Adv. 2016;6:3571–3577. doi: 10.1039/C5RA16327G. [DOI] [Google Scholar]
- 18.Xue Q., Xu W.M. A model of thermal conductivity of nanofluids with interfacial shells. Mater. Chem. Phys. 2005;90:298–301. doi: 10.1016/j.matchemphys.2004.05.029. [DOI] [Google Scholar]
- 19.Jiang H., Li H., Xu Q., Shi L. Effective thermal conductivity of nanofluids considering interfacial nano-shells. Mater. Chem. Phys. 2014;148:195–200. doi: 10.1016/j.matchemphys.2014.07.031. [DOI] [Google Scholar]
- 20.Cheng N.S., Law A.W.K. Exponential formula for computing effective viscosity. Powder Technol. 2003;129:156–160. doi: 10.1016/S0032-5910(02)00274-7. [DOI] [Google Scholar]
- 21.Xuan Y., Li Q., Hu W. Aggregation structure and thermal conductivity of nanofluids. AIChE J. 2003;49:1038–1043. doi: 10.1002/aic.690490420. [DOI] [Google Scholar]
- 22.Masoumi N., Sohrabi N., Behzadmehr A. A new model for calculating the effective viscosity of nanofluids. J. Phys. Appl. Phys. 2009;42:055501. doi: 10.1088/0022-3727/42/5/055501. [DOI] [Google Scholar]
- 23.Prasher R., Phelan P.E., Bhattacharya P. Effect of aggregation kinetics on the thermal conductivity of nanoscale colloidal solutions (nanofluid) Nano Lett. 2006;6:1529–1534. doi: 10.1021/nl060992s. [DOI] [PubMed] [Google Scholar]
- 24.Xu J., Yu B., Zou M., Xu P. A new model for heat conduction of nanofluids based on fractal distributions of nanoparticles. J. Phys. Appl. Phys. 2006;39:4486. doi: 10.1088/0022-3727/39/20/028. [DOI] [Google Scholar]
- 25.Yang K.T. Artificial neural networks (ANNs): A new paradigm for thermal science and engineering. J. Heat Transf. 2008;130:093001. doi: 10.1115/1.2944238. [DOI] [Google Scholar]
- 26.Ghaedi A. Simultaneous prediction of the thermodynamic properties of aqueous solution of ethylene glycol monoethyl ether using artificial neural network. J. Mol. Liq. 2015;207:327–333. doi: 10.1016/j.molliq.2015.04.015. [DOI] [Google Scholar]
- 27.Hojjat M., Etemad S.G., Bagheri R., Thibault J. Thermal conductivity of non-newtonian nanofluids: Experimental data and modeling using neural network. Int. J. Heat Mass Transf. 2011;54:1017–1023. doi: 10.1016/j.ijheatmasstransfer.2010.11.039. [DOI] [Google Scholar]
- 28.Longo G.A., Zilio C., Ceseracciu E., Reggiani M. Application of artificial neural network (ANN) for the prediction of thermal conductivity of oxide-water nanofluids. Nano Energy. 2012;1:290–296. doi: 10.1016/j.nanoen.2011.11.007. [DOI] [Google Scholar]
- 29.Mehrabi M., Sharifpur M., Meyer J.P. Adaptive neuro-fuzzy modeling of the thermal conductivity of alumina-water nanofluids; Proceedings of the ASME 2012 Third International Conference on Micro/Nanoscale Heat and Mass Transfer; Atlanta, GA, USA. 3–6 March 2012; pp. 155–161. [Google Scholar]
- 30.Mehrabi M., Sharifpur M., Meyer J.P. Application of the FCM-based Neuro-fuzzy inference system and genetic algorithm-polynomial neural network approaches to modelling the thermal conductivity of alumina-water nanofluids. Int. Commun. Heat Mass Transf. 2012;39:971–977. doi: 10.1016/j.icheatmasstransfer.2012.05.017. [DOI] [Google Scholar]
- 31.Ariana M.A., Vaferi B., Karimi G. Prediction of thermal conductivity of alumina water-based nanofluids by artificial neural networks. Powder Technol. 2015;278:1–10. doi: 10.1016/j.powtec.2015.03.005. [DOI] [Google Scholar]
- 32.Esfe M.H., Saedodin S., Bahiraei M., Toghraie D., Mahian O., Wongwises S. Thermal conductivity modeling of MgO/EG nanofluids using experimental data and artificial neural network. J. Therm. Anal. Calorim. 2014;118:287–294. doi: 10.1007/s10973-014-4002-1. [DOI] [Google Scholar]
- 33.Esfe M.H., Saedodin S., Naderi A., Alirezaie A., Karimipour A., Wongwises S., Goodarzi M., Dahari M. Modeling of thermal conductivity of ZnO-EG using experimental data and ANN methods. Int. Commun. Heat Mass Transf. 2015;63:35–40. doi: 10.1016/j.icheatmasstransfer.2015.01.001. [DOI] [Google Scholar]
- 34.Esfe M.H., Wongwises S., Naderi A., Asadi A., Safaei M.R., Rostamian H., Dahari M., Karimipour A. Thermal conductivity of Cu/TiO2-water/EG hybrid nanofluid: Experimental data and modeling using artificial neural network and correlation. Int. Commun. Heat Mass Transf. 2015;66:100–104. doi: 10.1016/j.icheatmasstransfer.2015.05.014. [DOI] [Google Scholar]
- 35.Esfe M.H., Afrand M., Wongwises S., Naderi A., Asadi A., Rostami S., Akbari M. Applications of feed forward multilayer perceptron artificial neural networks and empirical correlation for prediction of thermal conductivity of Mg(OH)2-EG using experimental data. Int. Commun. Heat Mass Transf. 2015;67:46–50. doi: 10.1016/j.icheatmasstransfer.2015.06.015. [DOI] [Google Scholar]
- 36.Esfe M.H., Rostamian H., Afrand M., Karimipour A., Hassani M. Modeling and estimation of thermal conductivity of MgO-water/EG (60:40) by artificial Neural network and correlation. Int. Commun. Heat Mass Transf. 2015;68:98–103. doi: 10.1016/j.icheatmasstransfer.2015.08.015. [DOI] [Google Scholar]
- 37.Esfe M.H., Naderi A., Akbari M., Afrand M., Karimipour A. Evaluation of thermal conductivity of COOH-functionalized MWCNTs/water via temperature and solid volume fraction by using experimental data and ANN methods. J. Therm. Anal. Calorim. 2015;121:1273–1278. doi: 10.1007/s10973-015-4565-5. [DOI] [Google Scholar]
- 38.Esfe M.H., Saedodin S., Sina N., Afrand M., Rostami S. Designing an artificial neural network to predict thermal conductivity and dynamic viscosity of ferromagnetic nanofluid. Int. Commun. Heat Mass Transf. 2015;68:50–57. doi: 10.1016/j.icheatmasstransfer.2015.06.013. [DOI] [Google Scholar]
- 39.Vakili M., Yahyaei M., Kalhor K. Thermal conductivity modeling of graphene nanoplatelets/deionized water nanofluid by MLP neural network and theoretical modeling using experimental results. Int. Commun. Heat Mass Transf. 2016;74:11–17. doi: 10.1016/j.icheatmasstransfer.2016.03.010. [DOI] [Google Scholar]
- 40.Yousefi F., Karimi H., Papari M.M. Modeling viscosity of nanofluids using diffusional neural networks. J. Mol. Liq. 2012;175:85–90. doi: 10.1016/j.molliq.2012.08.015. [DOI] [Google Scholar]
- 41.Mehrabi M., Sharifpur M., Meyer J.P. Viscosity of nanofluids based on an artificial intelligence model. Int. Commun. Heat Mass Transf. 2013;43:16–21. doi: 10.1016/j.icheatmasstransfer.2013.02.008. [DOI] [Google Scholar]
- 42.Zhao N.B., Li S.Y., Wang Z.T., Cao Y.P. Prediction of viscosity of nanofluids using artificial neural networks; Proceedings of the ASME 2014 International Mechanical Engineering Congress & Exposition; Montreal, QC, Canada. 14–20 November 2014; [DOI] [Google Scholar]
- 43.Zhao N.B., Wen X.Y., Yang J.L., Li S.Y., Wang Z.T. Modeling and prediction of viscosity of water-based nanofluids by radial basis function neural networks. Powder Technol. 2015;281:173–183. doi: 10.1016/j.powtec.2015.04.058. [DOI] [Google Scholar]
- 44.Heidari E., Sobati M.A., Movahedirad S. Accurate prediction of nanofluid viscosity using a multilayer perceptron artificial neural network (MLP-ANN) Chemom. Intell. Lab. Syst. 2016;155:73–85. doi: 10.1016/j.chemolab.2016.03.031. [DOI] [Google Scholar]
- 45.Yang L., Du K., Niu X., Li Y., Zhang Y. An experimental and theoretical study of the influence of surfactant on the preparation and stability of ammonia-water nanofluids. Int. J. Refrig. 2011;34:1741–1748. doi: 10.1016/j.ijrefrig.2011.06.007. [DOI] [Google Scholar]
- 46.Xia G., Jiang H., Liu R., Zhai Y. Effects of surfactant on the stability and thermal conductivity of Al2O3/de-ionized water nanofluids. Int. J. Therm. Sci. 2014;84:118–124. doi: 10.1016/j.ijthermalsci.2014.05.004. [DOI] [Google Scholar]
- 47.Malvern. [(accessed on 15 April 2017)]; Available online: http://www.malvern.com/en/products/product-range/kinexus-range/kinexus-pro-plus/
- 48.Aladag B., Halelfadl S., Doner N., Maré T., Duret S., Estellé P. Experimental investigations of the viscosity of nanofluids at low temperatures. Appl. Energy. 2012;97:876–880. doi: 10.1016/j.apenergy.2011.12.101. [DOI] [Google Scholar]
- 49.Li H., Wang L., He Y., Hu Y., Zhu J., Jiang B. Experimental investigation of thermal conductivity and viscosity of ethylene glycol based ZnO nanofluids. Appl. Therm. Eng. 2015;88:363–368. doi: 10.1016/j.applthermaleng.2014.10.071. [DOI] [Google Scholar]
- 50.Turnbull D., Elkan C. Fast recognition of musical genres using RBF networks. IEEE Trans. Knowl. Data Eng. 2005;17:580–584. doi: 10.1109/TKDE.2005.62. [DOI] [Google Scholar]
- 51.Iliyas S.A., Elshafei M., Habib M.A., Adeniran A.A. RBF neural network inferential sensor for process emission monitoring. Control Eng. Pract. 2013;21:962–970. doi: 10.1016/j.conengprac.2013.01.007. [DOI] [Google Scholar]
- 52.Chen S., Cowan C.F.N., Grant P.M. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans. Neural Netw. 1991;2:302–309. doi: 10.1109/72.80341. [DOI] [PubMed] [Google Scholar]
- 53.Pak B.C., Cho Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. 1998;11:151–170. doi: 10.1080/08916159808946559. [DOI] [Google Scholar]
- 54.Wang X., Xu X., Choi S.U.S. Thermal conductivity of nanoparticle-fluid mixture. J. Thermophys. Heat Transf. 1999;13:474–480. doi: 10.2514/2.6486. [DOI] [Google Scholar]
- 55.Li C.H., Peterson G.P. The effect of particle size on the effective thermal conductivity of Al2O3-water nanofluids. J. Appl. Phys. 2007;101:44312. doi: 10.1063/1.2436472. [DOI] [Google Scholar]
- 56.Das S.K., Putra N., Thiesen P., Roetzel W. Temperature dependence of thermal conductivity enhancement for nanofluids. J. Heat Transf. 2003;125:567–574. doi: 10.1115/1.1571080. [DOI] [Google Scholar]
- 57.Chandrasekar M., Suresh S., Chandra B.A. Experimental investigations and theoretical determination of thermal conductivity and viscosity of Al2O3/water nanofluid. Exp. Therm. Fluid Sci. 2010;34:210–216. doi: 10.1016/j.expthermflusci.2009.10.022. [DOI] [Google Scholar]
- 58.Murshed S.M.S., Leong K.C., Yang C. Enhanced thermal conductivity of TiO2-water based nanofluids. Int. J. Therm. Sci. 2005;44:367–373. doi: 10.1016/j.ijthermalsci.2004.12.005. [DOI] [Google Scholar]
- 59.Maxwell J.C. A Treatise on Electricity and Magnetism. Clarendon Press; Oxford, UK: 1981. [Google Scholar]
- 60.Yu W., Choi S.U.S. The role of interfacial layer in the enhanced thermal conductivity of nanofluids: A renovated Maxwell model. J. Nanopart. Res. 2003;5:167–171. doi: 10.1023/A:1024438603801. [DOI] [Google Scholar]
- 61.Chen H., Ding Y., He Y., Tan C. Rheological behaviour of ethylene glycol based titania nanofluids. Chem. Phys. Lett. 2007;444:333–337. doi: 10.1016/j.cplett.2007.07.046. [DOI] [Google Scholar]
- 62.Nguyen C.T., Desgranges F., Roy G., Galanis N., Maré T., Boucher S., Angue M.H. Temperature and particle-size dependent viscosity data for water-based nanofluids-hysteresis phenomenon. Int. J. Heat Fluid Flow. 2007;28:1492–1506. doi: 10.1016/j.ijheatfluidflow.2007.02.004. [DOI] [Google Scholar]
- 63.Anoop K.B., Kabelac S., Sundararajan T., Das S.K. Rheological and flow characteristics of nanofluids: Influence of electroviscous effects and particle agglomeration. J. Appl. Phys. 2009;106:034909. doi: 10.1063/1.3182807. [DOI] [Google Scholar]
- 64.Brinkman H.C. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952;20:571. doi: 10.1063/1.1700493. [DOI] [Google Scholar]
- 65.Corcione M. Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers. Manag. 2011;52:789–793. doi: 10.1016/j.enconman.2010.06.072. [DOI] [Google Scholar]