The Case for Biocalculus: Design, Retention, and Student Performance

Models for developing and implementing biology-oriented Calculus I courses at two institutions are presented. These courses are aligned with Vision and Change curriculum recommendations and maintain core calculus concept rigor, but DWF rates meaningfully and significantly decreased.

Abstract

Calculus is one of the primary avenues for initial quantitative training of students in all science, technology, engineering, and mathematics fields, but life science students have been found to underperform in the traditional calculus setting. As a result, and because of perceived lack of its contribution to the understanding of biology, calculus is being actively cut from biology program requirements at many institutions. Here, we present an alternative: a model for learning mathematics that sees the partner disciplines as crucial to student success. We equip faculty with information to engage in dialogue within and between disciplinary departments involved in quantitative education. This includes presenting a process for interdisciplinary development and implementation of biology-oriented Calculus I courses at two institutions with different constituents, goals, and curricular constraints. When life science students enrolled in these redesigned calculus courses are compared with life science students enrolled in traditional calculus courses, students in the redesigned calculus courses learn calculus concepts and skills as well as their traditional course peers; however, the students in the redesigned courses experience more authentic life science applications and are more likely to stay and succeed in the course than their peers who are enrolled in traditional courses. Therefore, these redesigned calculus courses hold promise in helping life science undergraduate students attain Vision and Change recommended competencies.

INTRODUCTION

In this paper, we aim to equip faculty and administration, particularly of undergraduate life science departments, to have productive discussions about the quantitative skills and training of their students. We discuss how mathematics courses such as calculus are related to competencies outlined in curricular reform documents such as Vision and Change (American Association for the Advancement of Science [AAAS], 2011). We point out where traditional content versions of these courses fall short of these needs, particularly with respect to modeling skills and student attrition. Here, we present two alternative models for how Calculus I might be modified with stakeholder input to better meet the needs of life sciences programs. These redesigned courses meet certification or graduate school and pre-med requirements but seek to engage students with more relevant content and empower them with metacognitive activities. We also offer promising results on learning and attrition among life science students enrolled in traditional Calculus I versus the redesigned experiences.

CALLS FOR IMPROVING QUANTITATIVE LITERACY—CAN CALCULUS HELP?

The case for integrating mathematics and computational science into biology curricula is well established. Concerns range from students’ innumeracy (Brent, 2004) to potential for misuse of mathematical models in making policy decisions (White, 2001; May, 2004). Forward-thinking organizations and professional societies recognize scientists will need to interact with information in new ways. They will need to be able to handle big data and think about and model complex systems, which requires more experience with statistics and modeling of dynamical systems (National Research Council [NRC], 2003; Karsai and Kampis, 2010; AAAS, 2011). The arguments made by these organizations and societies not only are calls within the higher educational system in the United States but are part of a worldwide movement (Matthews et al., 2010).

Vision and Change (AAAS, 2011) is one of the most influential documents in calling for change among life science majors to meet the needs of 21st-century life scientists. Two of its six core competencies explicitly mention quantitative skills: the ability to use quantitative reasoning and the ability to use modeling and simulation. Two additional competencies refer to interdisciplinary collaboration and connections. “The ability to use quantitative reasoning” is a broad competency and might be ascribed to any foundational science, or mathematics or statistics course. However, one course in mathematics or statistics, especially a traditionally designed course, would not be nearly enough to empower students to use modeling and simulation, since these are skills typically honed not in introductory mathematics courses but in subsequent mathematics courses (NRC, 2013). Research on best practices in teaching quantitative literacy suggests students should have both a strong foundation in mathematics connected with data and writing and multiple opportunities to practice these skills throughout the curriculum. (Dilts and Salem, 2004; Gross, 2004; Steen, 2005). Therefore, to achieve the desired quantitative fluency, programs must consider redesigning foundational mathematics courses to encompass such goals such as modeling and simulation and must require additional mathematics courses and/or infuse quantitative skills into biology courses (for some suggestions on topics and case studies, see NRC, 2003).

Statistics and calculus are typical foundational courses required by biology programs and have been used to provide these important foundations (Gross, 2004; Jungck, 2005; Ledder et al., 2013). Unfortunately, some life science degree programs (such as those in both our schools) have dropped mathematics requirements such as calculus, despite Vision and Change calling for what is considered advanced applied mathematics skills. At Unity, where calculus was removed from the list of requirements, life science faculty expressed a worry that prospective life sciences students would choose programs without calculus requirements over programs with calculus requirements. They also expressed concern that calculus contributes to attrition (which is supported by evidence; e.g., see Ellis et al., 2016) and believed calculus was not relevant enough for student careers to justify the requirement.

The dropping of calculus as a requirement is also a national conversation. In the early 1990s, calculus was removed from the list of requirements for wildlife biologist certification, though it remains an optional course (Wildlife Society, 2014). In 2001, Gary White delivered a speech to the Wildlife Society, making a passionate call for its re-inclusion: “It’s the ability to conceptualize problems into an exacting formulation and then proceed to a solution that is gained through classes such as calculus” (White, 2001, p. 384). At the same time, statistics is gaining recognition as an important requirement, particularly due to the recent changes in the Medical College Admission Test (MCAT), and so calculus is losing ground to statistics as a program requirement. In this paper, we do not debate the value of statistics but examine alternative models for calculus design that may better meet program needs than traditional calculus courses and is an appropriate course vehicle for improving students’ understanding of modeling and interdisciplinary connections.

A CALL FOR MATHEMATICIANS TO JOIN IN THIS EFFORT

The national call is not just a call to action for life science departments; there is an equal need and call for mathematics departments to meet the demand of life sciences. The NRC provides an in-depth exploration of the future of the mathematics discipline in its publication The Mathematical Sciences in 2025. In this document, the NRC urges mathematics educators to introduce more applications into the mathematics curriculum to meet the growing need for mathematics in a variety of disciplines, including the biological sciences (NRC, 2013). A report from the President’s Council of Advisors on Science and Technology (2012) made a more drastic suggestion that mathematics would be more meaningful if taught by the science discipline faculty instead of by mathematicians. Some life science departments have hired mathematicians devoted to teaching dedicated biocalculus or mathematical modeling as courses administered by the biology department (e.g., the College of William and Mary, University of Chicago). While we encourage this sort of integration, it is not the only solution if departments can collaborate fully. Whatever the solution, the desire is for true interdisciplinarity, encouraging integration as a way to help promote student success and to help students make connections across disciplines (NRC, 2003; Bialek and Botstein, 2004; Dilts and Salem, 2004; AAAS, 2011).

What biologists also have in common with mathematics faculty, department chairs, and deans is that all are vested in student success. The report recommendations advocating for interdisciplinary collaboration in course design are backed by education research into student success. For example, expectancy-value theory (e.g., Eccles, 1983; Wigfield and Eccles, 2000; Plante et al., 2013) is a learning theory that links student expectancy (the belief in one’s ability) and value (drivers of student engagement that include how useful the task is) to achievement. In particular, the Plante et al. (2013) paper, which focuses on the expectancy-value framework applied to mathematics and language arts, suggests that educational design for high student achievement address both expectancy and task values. When looking at biology students, it has been noted that these students also are typically more “math-averse” than students in other science fields (Hoy, 2004; Matthews et al., 2010; Steen, 2005). Because students typically learn more effectively and have been shown to achieve more when they enjoy what they are learning (Bandura, 1986; Ma and Kishor, 1997), it is no surprise that their motivation and achievement have also been shown to be influenced by the value they attach to the mathematics they are learning (Fennema and Sherman, 1978; Grootenboer and Hemmings, 2007; Harackiewicz et al., 2014). To illustrate this point, using biology to motivate mathematics has been shown to increase student appreciation of mathematics and motivate new questions in biology (Karsai and Kampis, 2010; Servedio et al., 2014). We also know that genuine real-world context can lead to positive gains in appreciation for math (Chiel et al., 2010; Matthews et al., 2010). In an upper-level dynamics of biological systems course, cross-listed with biology and biomedical engineering, biology students were more interested in and willing to do mathematical modeling and engineering students appreciated biology more (Chiel et al., 2010). Thus, this is a mutually beneficial effort.

In the case of foundational courses such as calculus, there are many examples of calculus courses being successfully designed to meet quantitative needs of life science majors (e.g., Ledder et al., 2013). Unfortunately, students and the outside community can perceive a “biocalculus” or “applied calculus” course as less rigorous, which affects recruitment into such courses, despite indications to the contrary (Comar, 2013). For example, in a biocalculus sequence at Benedictine, Biocalculus I and Calculus I students perform similarly and, as a result, can switch to or from the biocalculus track at any time (Comar, 2008, 2013). In a Biocalculus I course at the University of Illinois, students were twice as likely to take another mathematics course and are as well prepared as traditional calculus students to take Calculus II as judged by final letter grade (Uhl and Holdener, 2013). Finally, in an interesting high school study, Lukens and Feinstein (2000) offered a two-period learning community between AP Calculus and AP Biology in which the mean AP score in the learning community was nearly 25% higher than the control group. This indicates that calculus and life science can mutually benefit from interdisciplinary collaboration.

Motivated by our desire to meet the needs of our biology majors and guided from the evidence in the literature, in this paper we examine both student performance and retention in our two distinct and independently developed biocalculus courses: one at Unity College (Unity) and another at the University of Portland (UP). These courses are designed to build on what we know about how students learn and have the conceptual rigor of their traditional counterparts. While both courses have a similar goal, due to our different institutional structures and needs, there are necessarily distinctions in both course structure and in the forms of assessing student performance. However, we offer readers a comparative glimpse into approaching the redesign of calculus courses to address competencies in Vision and Change (AAAS, 2011), such as quantitative reasoning, modeling, simulation, and interdisciplinary collaboration, and show that both courses result in similar positive effects on student performance, course retention, and value in the eyes of life science programs.

CONTEXT, CULTURE, AND MOTIVATION BEHIND BIOCALCULUS IMPLEMENTATION

One important consideration highlighted by the Vision and Change report (AAAS, 2011) and the Mathematical Association of America Notes volume Undergraduate Mathematics for the Life Sciences: Models, Processes, and Directions (Ledder et al., 2013) is that transformative curricular change should match the culture of your institution. In this paper, we focus on Calculus I as a foundational course at two colleges: Unity and UP. Calculus I is already a recognized feature at these institutions as well as in many curricula throughout the nation. It also has recognition in the outside community, for example, among certification societies, medical schools, and graduate schools. However, as supported by the discussion above, we acknowledge the importance of preexisting skills and skills separate from the traditional umbrella of calculus (e.g., NRC, 2003; Hoy, 2004; Robeva and Laubenbacher, 2009). We outline how we have each incorporated modified versions of calculus for the life sciences and present both the challenges and the encouraging outcomes of these implementations.

Unity

Unity is a small, environmental, liberal arts college in rural Maine with fewer than 1000 students. It has a history of innovation in interdisciplinary teaching (e.g., see Arnett and Van Horn, 2009). Although traditional universities can be stifled by departmental culture (AAAS, 2011), Unity is less affected, because of its arrangement into interdisciplinary departments called centers, made possible in part by its small size. There is no math department; mathematics faculty have appointments in different centers, which affords the opportunity to influence mathematics curricula for other programs.¹

Unity underwent an intensive academic master-planning process starting in 2009 in preparation for its accreditation visit. Although it is an environmental and sustainability science–focused college, the major requirements were redesigned with fewer requirements and more flexibility in the spirit of a liberal arts education. At this time, Calculus I was required by the ecology, marine biology, wildlife biology, environmental biology, aquaculture and fisheries, and environmental science majors. It was not a prerequisite to any other class in the catalogue except for Calculus II, which was offered only “by arrangement,” meaning if enough students requested it. Because statistics was required in most majors already, thereby meeting the one-course general education mathematics requirement, faculty were considering dropping the calculus requirement from many of these programs. Redesigning the calculus course sequence to meet the needs of students and programs became essential to attract students and to keep it relevant enough to continue to be a requirement for the majors.

Although the situation above could be described as a threat, it was also an opportunity. Students already agreed that the most interesting material in Calculus I occurred in the applications. Historically, the “applications of derivatives” section was a discussion of derivatives and, for this three-credit course, was presented in the last weeks of the course. Because many courses and programs were being redesigned, collaborative work with multiple programs was possible, and strategic hiring of new faculty in these programs encouraged those hired to be especially aware of and keen to integrate quantitative training. Under the new programs, Calculus I was now a requirement for wildlife biology, earth and environmental science, and the Graduate School Core for Biological Sciences, and served as an option for biology (formerly environmental biology and ecology), marine biology, and sustainable energy and management. Of this group, the largest proportion of students would be in wildlife biology, many of whom would be pursuing certification by Wildlife Society standards (Wildlife Society, 2014). With these stakeholders in mind, the course was given its unifying theme: the study of change.

UP

UP is a private Catholic university of approximately 3800 undergraduates, with professional schools in engineering, business, education, and nursing, in addition to the College of Arts and Sciences. Due to the professional schools, there is no shortage of demand for calculus. UP, although more traditionally structured than Unity, also places importance on collaboration between departments, with many cotaught and cross-listed courses. Owing to its small size and focus on community, faculty regularly collaborate on teaching and research projects, with an emphasis on providing interdisciplinary undergraduate research opportunities. The mathematics department, in particular, regularly interacts with many other departments within the College of Arts and Science and with the four professional schools.

Although UP and Unity differ in size and structure, UP is similar to Unity and many other colleges and universities across the nation in that the biology department decided in 2010 that the traditional calculus course was not meeting the needs of their majors (the second largest major on campus). In an attempt to relax the mathematical requirements for a biology degree, they decided to no longer require calculus for the biology major. For programs like those at UP, with pre-med students as the primary stakeholders, there is pressure on some biology and math programs (NRC, 2003) to include calculus as a requirement, even though the MCAT does not require calculus. Therefore, despite the removal of a calculus requirement, there was still a demand for this course from the life science majors who were on the pre-med track. Further, due to the emphasis on interdisciplinary learning on campus, there was encouragement from the biology and mathematics departments to create a course that could better meet the needs of these students.

At UP, biology students were demonstrating generally lower performance in the standard calculus course than their science, technology, engineering, and mathematics (STEM) counterparts and poor quantitative reasoning skills in subsequent courses. Creating a Calculus I course motivated by problems in biology (value) seemed a natural consequence of adopting the value-expectancy framework in the endeavor to increase biology student performance in Calculus I.

CURRICULUM DESIGN METHODS

In this section, we discuss curriculum design methods in detail for a number of reasons. The first is that we suggest curriculum design is an important step in interdisciplinary collaboration and that successful interdisciplinary collaboration is vital to improved curriculum design (Redish and Cooke, 2013). Therefore, we offer our approach with the invitation for other mathematics faculty to adopt similar strategies for collaboration with biology faculty. The second reason is that it is important for methodological reasons to understand how we approached the need to increase student value of calculus, leveraging the expectancy-value theory framework noted earlier (Eccles, 1983; Plante et.al, 2013). The third reason is to emphasize that, while the emergent curriculum designs have some features in common, they also have differences due to the cultural constraints and needs of our institutions and students; yet these differences can lead to similar positive outcomes in student learning and retention. The resulting curricular materials can be accessed by contacting the authors and at the Calculus page on QUBES Hub at https://qubeshub.org/groups/calculus.

Unity

At Unity, an inventory of calculus skills for biology student learners was given to faculty for rating, and a representative subset of faculty was selected for follow-up interviews. Based on the results, mathematical content was chosen, and then ordered in the course, and, if applicable, in the mathematics curriculum. After mathematics content scaffolding was addressed, activities for both metacognition and writing were added. As a direct result of this close faculty collaboration, which has been shown to be a critical aspect of successful creation of interdisciplinary courses (Redish and Cooke, 2013), the marine biology major changed Calculus I from optional back to required, and a program review of the biology major conducted in 2016 resulted in a similar recommendation to the faculty.

At first, all Unity faculty were surveyed on a list of possible topics for a set of calculus and modeling courses. Each of the survey questions was discussed for clarity with faculty within the Center for Biodiversity before the questions were delivered to all faculty at the college. As a result of this conversation, each mathematics topic was redescribed using biological and environmental language and potential applications. As soon as the survey was redesigned (available in the Supplemental Material), it was delivered to all faculty at a campus-wide professional development day, with the survey provided via email as a follow-up. It is interesting to note that the same faculty surveyed reported different opinions of importance on the exact same concept after the biological explanations were added, often ranking them higher. For example, the mathematical term “derivative” seemed more important once it was explained as “instantaneous rate of change.” Also, “first-order differential equations” seemed more important to faculty when explained as “exponential growth and logistic growth models.” The top topic survey results are shown in Table 1, with the average ranking in column 1, the mathematical term in column 2, and the explanations/topic translations added to the survey after the focus group in column 3. Exponential functions, particularly with respect to feedback loops, were considered the most important, followed by data fitting and computer skills, and then concepts of rate of change and limits with applications to more complicated population growth models and long-term behavioral predictions.

TABLE 1.

Unity survey results of all topics with an average rating of 1–2 in order of importance

Average rankinga	Topic	Biological and environmental interpretation	Pre–curriculum changesb	Post–master curriculum changesb
1.3	Exponential function	Feedback loops	Some in Alg/Trig	Alg/Trig, Calc I
1.4	Fitting data to a model		Stats	All MA classes
1.5	Computer skills	Excel, some logical thinking for programming	TI calculator in ALL classes, Excel in Stats	TI calculator and Excel in all MA classes, MATLAB/R programming in Calc II
1.5	Derivative	Concept, not computation	Calc I	Calc I
1.5	Population growth models	Logistic growth, Excel	n/a	Calc I, Calc II
1.8	Equilibrium analysis	Equilibria, stability, climate change, and population management	n/a	Calc I, Calc II
1.8	Limits	Carrying capacity	Calc I	Alg/Trig, Calc I

^aA rating of 1 is the most important and deemed a need and 4 is deemed by faculty as unimportant to include in the calculus curriculum.

^bAlg, algebra; Trig, trigonometry; Calc, calculus. MA refers to the rubric used for all college-level mathematics and statistics courses. TI refers to a Texas Instruments graphing calculator.

To demonstrate why the survey results are important, a traditionally taught Calculus I class taught out of any of the best-selling calculus books would emphasize analytic techniques to compute the derivative of a function (e.g., Stewart, 2015). So in this class what might be emphasized are techniques to compute instantaneous rate of change (the derivative) algebraically, and students would practice rules to compute derivatives. For example, students would compute the derivative of 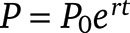as 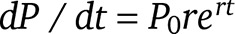via a rule known as the chain rule. However, students would not see the version presented in ecological terms, which is the differential equation, , until Calculus II if using the popular Stewart (2015) book (see Chapter 9 in that volume). Even when students do see this alternate form in Calculus II, little attention is paid to the assumptions behind the model and the analytical techniques for model exploration. The verbal interpretation of this latter equation is that the instantaneous rate of population growth is proportional to the current population size. This is also known as the simplest case of a feedback loop, as the larger the size of the population (right-hand side of the equation), the larger change there will be (left-hand side of the equation). Moving between verbal explanations and their algebraic formulations is part of the modeling skill set (C. D. Eaton et al., unpublished results). While both uses of derivatives require the understanding of a derivative, modeling with derivatives is an application that may appear at the end of a traditional Calculus I course, or later, and will usually focus primarily on the practice of solving a differential equation via certain algebraic techniques. At that point in a traditional Calculus I course, the emphasis is on the technique and not usually on the interpretation of the model, its relationship to biological questions, or other related concepts such as equilibrium. In a traditional mathematics sequence, these concepts often do not appear until after Calculus II in a dedicated course on differential equations or modeling. However, these topics are accessible to students early in calculus, and a carefully crafted biocalculus course can reorder these topics to appear earlier.

After results of this survey from faculty were reviewed, a representative from each of the program stakeholders (wildlife biology, biology and marine biology, and sustainable energy management) was invited for a follow-up discussion. Despite the differences in disciplines, three common themes that motivated their interest in requiring calculus quickly emerged from the interviews:

1. Graduate schools require at least one semester of calculus.

2. Calculus deepens the understanding of foundational principles in modeling interactions.

3. Calculus is correlated to certain desirable dispositional outcomes.

These interviews, as well as the best practices advocated for such interdisciplinary courses, informed the next steps in both the Calculus I and II redesign. Because it was perceived as a requirement of a professional certification or graduate school, calculus was not relabeled as biocalculus. For a better understanding of how calculus could deepen the understanding of foundational principles in modeling interactions, more emphasis was placed on introductory modeling (e.g., of one population) in Calculus I, and more advanced modeling was introduced in Calculus II (e.g., predator–prey interactions). In other words, the entire set of math offerings was designed to de-emphasize proofing techniques and calculation and instead to emphasize concepts that prepare students for grappling with systems-thinking issues in biology (e.g., see Brent, 2004). However, despite a de-emphasis on proof and calculation rigor, it was important that a redesigned calculus course would maintain rigor in other ways related to conceptual and professional needs. As a result, calculus was designed so that students would be challenged in other ways more complementary to our goal to increase student value of calculus; for example, students were assigned reading and expositing journal articles in their fields that use calculus-based modeling techniques to answer important theoretical or practical questions.

Finally, communication outcomes were also scaffolded throughout the entire mathematics curriculum to address both program-level writing outcomes and dispositional and metacognitive outcomes. In Calculus I, students read and responded to Talent Is Overrated (Colvin, 2008) or Practicing Mind (Sterner, 2005), which complemented the expectancy design component (Schippers, 2012). Students also responded to weekly writing prompts, some of which were related to personal learning goals (expectancy) and some of which were related to application and utility of the mathematical concept (value) taught. Professional communication in Calculus I was integrated mostly through group work and writing of one population-management plan, one investigative lab report, and one PowerPoint presentation. At the end of the course, each student was required to read a journal article in his or her area of interest (value) that used some mathematical tools or concepts related to the course and to then present an exposition of the article to the class. The Calculus II course built on this work with an eye to developing individual writing competencies in preparation for graduate school, particularly because this course is taken primarily by applied statistics and mathematics minors, as it is not required by any major. For more information on the writing aspects of the Calculus II course, see Eaton and Wade (2014).

The resulting curriculum designed after all stakeholder feedback is available in the Supplemental Material. It is common for science programs to have trouble finding room for additional four-credit or lab courses, particularly in the first 2 years (Kubatko et al., 2013). Therefore, this curriculum is for a three-credit course series without a lab or recitation. A supplemental instructor program was used in the first semester to support students, and a more informal work-study version (an undergraduate who ran additional office hours and study session hours) was offered in subsequent semesters (for more information on supplemental instruction, see Blanc et al., 1983). This curriculum used a text called Mathematics for the Life Sciences by Bodine et al. (2014) that was developed for the University of Tennessee’s well-known first-year biomath program.

UP

At UP, the motivations for the development of a biocalculus course were slightly different from those of Unity. Although many of our students and faculty were aware of the aforementioned merits of life science students taking calculus, the biology department had decided in 2010 to remove calculus from the list of required courses. Therefore, the goal was to design a course that life science students would actually want to take (value), even though it was no longer required of them. Calculus was to be made interesting and rewarding (value).

Biology faculty were asked for feedback regarding course content and format, but most of the course development was driven by a requirement that students learn the same mathematical content as those students taking traditional calculus, since students interested in taking future mathematics courses, such as Calculus II, would need to have the same mathematical background to succeed in subsequent non-biology–focused courses. Because all pre-med students at UP are still advised to take calculus to better prepare them for medical school, UP also decided to keep the course name Calculus I and just label the biocalculus section number appropriately. To help readers in making this distinction, here the UP biocalculus course is referred to as Calculus I (Bio). The structure of Calculus I (Bio) is very similar to that of the traditional calculus courses, with the majority of the course consisting of a combination of lecture and group activities. However, the Calculus I (Bio) version incorporates journal assignments, many of which address student metacognition (expectancy), and the content focuses more on biological applications and modeling (value). Although most assessments directly relate to modeling problems in biology, Calculus I (Bio) students are required to take three common quizzes with students in the traditional calculus sections. The design of these common quizzes is more in line with assessments in traditional calculus. The purpose in administering the quizzes to the biocalculus students is to gauge how well they understand the core calculus concepts taught in traditional calculus in comparison with their traditional calculus counterparts, since these are the primary measures for competency in Calculus I within the mathematics department.

As there is not yet the demand for a Calculus II (Bio), consistency with the core concepts in the standard Calculus I classes was maintained for the students who would go on to take a second semester of calculus. Fred Adler’s Modeling the Dynamics of Life: Calculus and Probability for Life Scientists (2012) text helped make this task less daunting, as the text covers most of the mathematics of a standard calculus course. Although there are many other calculus for life sciences texts that also cover the core calculus concepts (e.g., Neuhauser, 2010; Greenwell et al., 2014), we elected to use the Adler text at UP specifically because it places an emphasis first and foremost on modeling biological systems and second on the mathematical tools that can help study such systems (value). Adler’s text also begins with a chapter dedicated to discrete-time dynamical systems, so that the biocalculus course in many ways is more demanding for students than the standard calculus course: this course covers all of the traditional content in addition to an introduction to dynamical systems. The resulting curriculum is presented in the Supplemental Material, alongside the curriculum of the non-biology–oriented sections. The intended focus of this course is to model biological systems, and the calculus tools introduced in the course are meant to enlighten students regarding the complex behaviors of these systems.

As a consequence of the student performance in this course, similar to what has happened at Unity, UP biology faculty have begun a discussion to add calculus back to their major requirements. The faculty appreciate the emphasis on modeling and report that students are transferring the modeling and analytical skills they learned in biocalculus to their subsequent biology courses (though this claim has yet to be rigorously assessed). Enrollment in the biocalculus course has also continued to increase as a result of more faculty recommending the course to their advisees and more students recommending the course to their peers.

STUDENT RETENTION

Recall that a major goal with the redesign of calculus is to increase student persistence and performance. Therefore, Unity and UP both collected data on course retention, as calculus courses are often considered “weeder courses” with high failure and withdrawal rates. One way colleges and universities measure these data are with “DWF” rates, the percentage of students who earn a “D,” “W,” or “F” letter grade (as opposed to a “C” or higher). Traditional calculus DWF rates are in the 30–40% range (Brakke and Helpern, 2014). Our courses aimed to decrease the DWF rates, increasing the retention of life science students. What is presented below are promising preliminary results that should help spark conversations with administrators about the benefits of devoted biocalculus courses.

Unity

Figure 1A summarizes the results on DWF rates (referring to the percentage of students that either earn a “D” or “F” or withdraw) at Unity. During the 2010–2011 academic year, the traditional, non-biology–specific, Calculus I had a DWF rate of 30%. More specifically, 12% of students withdrew from the course. During initial reforms from Fall 2011 to Fall 2012, while using an early version of the Bodine et al. (2014) book, starting inventory and interview work with faculty, and solidifying program changes, the DWF rate dropped significantly and meaningfully to 25%. This average includes the Spring 2011 and Fall 2012 semesters, in which the “W” rate was unusually high due to changing program requirements, a time during which students in a phased-out wildlife program opted for newly redesigned majors (biology and wildlife fisheries and management) that did not require calculus. Over the next 3 years, Spring 2013 through Spring 2014, the DWF rate averaged 7%, and “W” rates were dramatically reduced to 0%.

FIGURE 1.

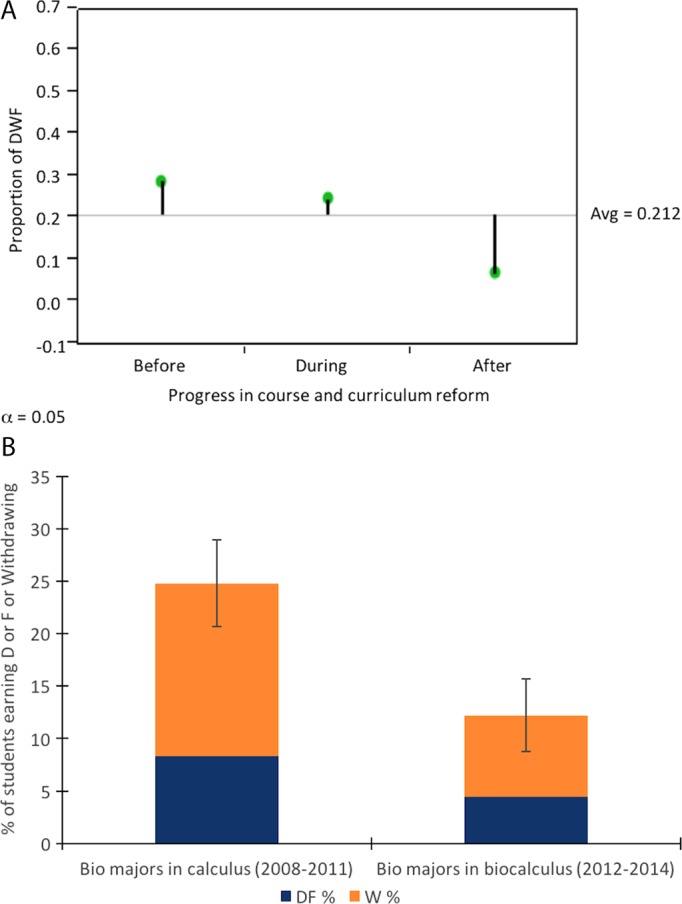
(A) DWF proportions from Fall 2010 to Spring 2014 for biocalculus at Unity before, during, and after the curricular and program changes as represented by a trend analysis using JMP statistical software. (B) DWF (in blue) and “W” (in orange) percentages at UP for biology students in traditional calculus from 2008 to 2011 compared with biology students in biocalculus from 2012 to 2014.

UP

From Fall 2008 to Spring 2011, the DWF and “W” rates were 24.8 and 16.5%, respectively, for biology majors in the traditional calculus course. From Fall 2012 through Spring 2014, the DWF and “W” rates dropped to 12.2 and 7.78%, respectively, for biology majors enrolled in the new course specifically designed for the biology majors. These data are shown in Figure 1B.

Owing to the strong positive response at UP from biology students and faculty, and because the primary difference between our biocalculus course and standard calculus course is the focus on modeling and biological applications, we have reason to believe that this modeling focus in biology for the biocalculus course is playing a large role in our observed increase in retention. This observation is a topic of further investigation.

Note that, at both institutions, the DWF rate for biology majors after biocalculus was implemented significantly (at Unity, one-sided z-test p value = 0.013) and meaningfully decreased. In fact, it was approximately halved. At Unity, grades for writing integration in the form of lab reports for investigations and blogging for metacognition may allow for alternative summative assessment other than high-stakes testing, which may influence grades. However, at UP, journal assignments (which included questions to promote metacognition) were the only graded writing assignment, making up only 0.5% of the total grade, and therefore had little direct effect on the overall course grade outcome.

STUDENT PERFORMANCE

One of our primary goals for creating a biocalculus version of Calculus I was to provide students with a solid foundation in the ways mathematics can be used in their disciplines. While changing the focus to applications rather than mathematical methods would provide a decent start to accomplishing this goal, we wanted to ensure that our students were still learning the basic mathematical concepts taught in traditional calculus courses. Assuring conceptual rigor is important in order to foster positive discussions with mathematics faculty when collaborating on these courses. It is also important for stakeholders (e.g., programs, graduate schools, employers) that may insist that a biocalculus class is not as “rigorous” as a traditional calculus course. To gain access to any of the student performance assessment tools used in this study, please email the authors.

Unity

Unity tracked student performance through the Calculus Concept Inventory (CCI), which is modeled after the Force Concept Inventory of Physics (Hestenes et al., 1992; Epstein, 2007, 2013). The CCI has been validated by Epstein (2007), resulting in a calculator-free, 22-question, multiple-choice instrument. It assesses students’ conceptual understanding of calculus and does not test computational ability, which is consistent with the aims of the course. Scores on the CCI are correlated with the level of interactive engagement activities in the course and students’ previous exposure to calculus.

Because every calculus course at Unity has been modified, we were looking for an assessment tool that we could use to compare learning gains in our modified course with those of students in traditional calculus courses. The CCI is the only such calculus concept tool used widely (e.g., Hamilton et al., 2010; Park, 2013; Chai et al. 2015). In the future, we will also assess concept transference to applied problems in biology, since these tools are actively under development. The University of Tennessee and NIMBioS now have a National Science Foundation (NSF) award (DUE #1544375) to create a quantitative skills assessment for biology majors that would directly address the impacts on biology questions that need quantitative techniques (for more information, contact pambishop@nimbios.org). We therefore plan to conduct future investigations using these assessments that may better capture the full impact of our biocalculus courses.

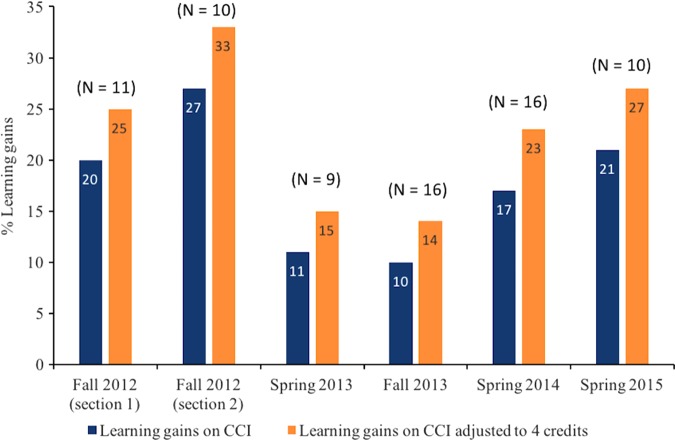
The CCI pretest was given on the first day of class, and the posttest was given during the final exam period for five semesters from Fall 2012 to Spring 2015. Every student completed the exam within the time allotted. The CCI pretest held no value, but students were given instructions to try as best as possible, as this test would be used to gauge current student understanding. The CCI posttest was combined with a take-home problem-based final for a total final exam grade that would equal up to 10% of the final grade. We know from extensive testing on the CCI (Epstein, 2013), that the range of CCI results is 21–44% for a four-credit interactive engagement calculus I course at the University of Michigan and the largest predictor of learning gain is prior exposure to calculus. This is in contrast to traditional four-credit calculus classrooms that experience CCI gains at a maximum of 21% to a low of negative gains. To compare Unity calculus concept gains in a three-credit course with those of students in University of Michigan four-credit courses, we compare per-credit CCI gains by adjusting Unity scores by factor of 1.33. We were unable to adjust for prior exposure to calculus; however, we know the incoming Scholastic Aptitude Test scores of students at the University of Michigan (mid 50% range is 690–790 in the 2015 freshman profile) are much higher than those at Unity (mid 50% range of voluntarily reported scores is 490–560), so this likely has a significant effect on CCI learning gains.

Figure 2 summarizes the results from the CCI gains at Unity, and the data for each semester separately are included in the Supplemental Material. In all but two semesters (referred to as gateway exam semesters), students at Unity were learning just as much per credit as the University of Michigan students. As mentioned in the results when discussing the adjustment of CCI gains, the comparison is not perfect in terms of credit hour and the amount of CCI content alignment in the course. With these considerations of prior calculus exposure influencing CCI gains in mind, adjusted learning gains within the University of Michigan comparison range during Fall 2012, Spring 2014, and Spring 2015 should be considered a success.

FIGURE 2.

Learning gains on the CCI at Unity from Fall 2012 to Spring 2015. Class size is shown in parentheses for each section.

However, the dramatic drop in learning gains during Spring and Fall 2013 seen in Figure 2 caused additional concern and investigation. The biggest difference in these semesters was the adoption of a “gateway exam,” a best practice used by the comparison group at University of Michigan (Epstein, 2013). This strategy was removed by Spring 2014 due to decreases in learning gains and student feedback about a higher stress level. To add further evidence that the bounce back of CCI learning gains was negatively affected by gateway exams at Unity, we analyzed an additional semester of CCI data without gateway exams in Spring 2015. There may be other explanations for variations in CCI score; for example, the “W” rate due to program changes could result in some self-selection, inflating CCI results. Also, variation in the level of involvement in those semesters and the use of a work-study student instead of a dedicated supplemental instructor may be a factor, since supplemental instructor programs contribute to learning gains (e.g., see Blanc et al., 1983). However, we think that these have a minor effect due to the bounce back after the gateway exams were removed.

This prompted us to consider how the best practices of mathematical preparation of life science students may differ in ways other than the content of the mathematics. Further investigation is needed to distinguish whether only Unity students respond negatively to the gateway exam because of cultural differences between institutions (small environmental liberal arts vs. large public school with prestigious engineering program) or whether life science students (more broadly) respond differently.

UP

Instead of using the CCI that Unity used, UP chose to implement “common quizzes” taken by all calculus students in both standard calculus and biocalculus, so that we could observe how well the biocalculus students were doing in comparison with those students whose course work focused more heavily on methods than on applications and modeling. Because the main focus of these common quizzes was to determine how well biocalculus students were learning the basic concepts and also to gauge how well they were prepared for more traditional mathematics courses in the future, the format of the common quizzes was the same as that of quizzes typically administered in traditional calculus courses. All other quizzes and exams in biocalculus, however, had much more of a modeling and application focus than these common quizzes.

The first quiz, the “precalculus quiz,” was given on the third day of class for all students. This quiz was designed to test the students’ knowledge coming into the course and was thus used as a form of preassessment of the quantitative skills of students entering the calculus course. It contained multiple-choice and true–false questions on topics from precalculus, algebra, and trigonometry. The second quiz, the “differentiation rules quiz,” was administered during the seventh week of classes. This quiz consisted of short-answer questions designed to test students’ understanding of the concept of a derivative and their knowledge of differentiation rules. Students in the traditional and biocalculus courses received instruction on the content in quiz 2 at different times in the semester: students in traditional calculus took this test about 1 week after they received instruction on the entirety of the quiz 2 material, while students in biocalculus took this test only 1 day after receiving instruction on all the material.

The third and “final quiz” was given during the last week of classes and served as a postcalculus quantitative skills assessment. It consisted of a variety of short-answer problems on limits, derivatives, and integrals. It was designed to test students’ overall understanding of the core calculus concepts and methods covered throughout the semester. A two-sample t-test for comparing the difference of means in independent samples was used to determine significant differences in the averages on each common quiz, with a 0.05 level of significance. Effect sizes were calculated using Cohen’s d.

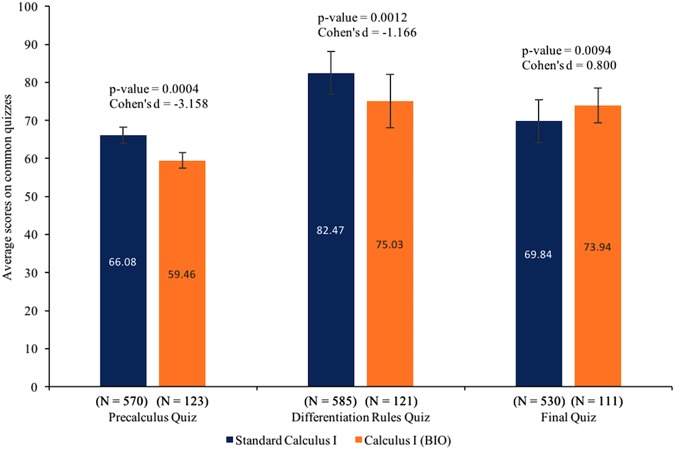
Figure 3 displays the results from each of the three common quizzes over the course of six semesters. The structure of the common quizzes remained consistent throughout these semesters, with only minor changes in the questions asked. Course design and delivery for both the regular calculus courses and the biocalculus course remained consistent throughout all semesters, and class sizes ranged from 15 to 26 students. The same instructor taught every section of Calculus I (Bio).

FIGURE 3.

Common quiz percentages at UP for students in standard calculus vs. students in biocalculus from Fall 2012 through Spring 2014.

Figure 3 reveals a significant difference, with large effect size, between the common quiz averages for standard Calculus I and Calculus I (BIO) for all three common quizzes. For the first quiz, this was not an unexpected result. This quiz is designed to test students’ existing knowledge of precalculus, trigonometry, and algebra. Therefore, it was no surprise that the biology students’ scores were significantly lower (by 6.62 percentage points) than those of the standard calculus students, since, as mentioned earlier, these students have been shown to exhibit lower performance in mathematics. Therefore, students enrolled in Calculus I (Bio) are starting behind those (almost exclusively non-biology majors) enrolled in traditional calculus.

By the second common quiz, students remain behind their traditional counterparts, with the biocalculus students scoring an average of 7.44% below the standard calculus students but closing the achievement gap noticed in the first quiz.

The results for the final quiz were the most surprising and the most encouraging, with biocalculus students scoring significantly higher (on average 4.09 percentage points) than the standard calculus students. Although the effect size was smaller than for the previous two quizzes, it is a large effect size (0.800). Our interpretation of these combined results is that, while the biology students may come in with less mathematical background, and while it may take them slightly longer to get up to speed (either due to their weaker background, or due to the course timeline, or possibly both), in the end, the results suggest that they are coming out of the course with at least the same, if not a better, understanding of the core mathematical concepts. This is a critical result to ensure the mathematical rigor in the biocalculus course.

CONCLUDING REMARKS

From two different motivations, for two different institutions with different structural constraints, emerged two different but similar biology-oriented calculus solutions. Both solutions integrated metacognition, some changes in math content, and a focus on applications and in-depth modeling projects in biology. Although the course topics are very different from a standard calculus course and, in some cases, more highly credit constrained, preliminary results suggest that students are completing the courses at higher rates and are gaining near-equivalent or better conceptual knowledge than their “traditional” counterparts. Adding a biology-oriented calculus option to the standard mathematics offerings may therefore allow biology students to achieve the same level of content knowledge expected of math-intensive math, physics, and engineering students.

Note that, in both course redesigns, two design features were incorporated to create a calculus experience tailored for the needs of life science students: metacognitive activities in the form of written reflections/journals (expectancy) and the use of life science examples and modeling to frame mathematical discussions (value). The act of engaging students in metacognitive practice is related to expectancy, because it helps students with low mathematical confidence, encouraging more active participation in their own learning, and increases performance confidence (e.g., Legg and Locker, 2009). In particular, reflection is associated with increased self-efficacy and confidence (Schippers, 2012). We suggest that meaningful applications and the interdisciplinary collaborations promote the task-value component for students and that the methodology may foster the value-expectancy for students, especially when the mathematics classroom is regularly referenced by our stakeholder partners and other students. But this benefit is not independent of the value-expectancy framework under which we add the life science context. Both metacognition and value-expectancy affect the decision-making process (Fleming and De Martino, 2014). Finally, biology students are likely to have a distinct framework for learning acquisition built for biology compared with their STEM counterparts, and a biology application–rich classroom better leverages this uniqueness when scaffolding further mathematical knowledge (for a discussion on the analogous case of physics as applied to biology learners, see Redish and Kuo, 2015).

We urge life science departments to take a close look at the quantitative education of their students. Instead of concluding that traditional calculus is not serving the students in their program and subsequently eliminating it from program requirements, as was done at Unity and UP, we suggest life science departments instead consider opening a dialogue across disciplines to investigate possibilities of modified calculus courses that are better tailored to meet the needs and interests of this unique student population. We encourage interaction of mathematics faculty with the entire life science faculty, since the quantitative needs within life science are diverse, although there is often convergence around the most urgent needs. We also encourage mathematics departments to listen to these needs, because mathematics courses like calculus can be embraced if their relevance is made apparent.

We recognize that implementation of interdisciplinary material is difficult for mathematicians with limited knowledge of biological applications and for biologists with limited exposure to mathematical techniques; however, departments can benefit by finding ways to encourage faculty to participate in interdisciplinary curricular development and assessment. We know of at least one new NSF IUSE (Mathematics) award, SUMMIT-P, which focuses on the importance of interdisciplinary conversations with a variety of partner disciplines to inform foundational mathematics courses, a promising national experiment. Further, rewarding these efforts is essential (NRC, 2003, 2013). Professional societies can also reward their members’ participation by highlighting educational activities, assisting in publication, and disseminating educational materials (NRC, 2003). Efforts such as QUBES (Quantitative Undergraduate Biology Education and Synthesis, qubeshub.org; Donovan et al., 2015) can be of assistance in yielding results in these arenas.

We hope that we have provided three major tools to advance quantitative biology education. The first is in the transparent sharing of collaborative curricular design so that one can fully engage all life science faculty stakeholders. The second is by presenting some preliminary evidence that student quantitative skill and concept learning is not sacrificed (as we have witnessed among our previously underperforming life science students) as a way to engage mathematics faculty or other stakeholders who worry about preserving rigor. The third and final is in providing evidence at two institutions that attrition rates can dramatically decrease, DWF rates being a key performance indicator used in discussions with program and institution administrators.