Analysis of Machine Learning Techniques for Heart Failure Readmissions

Abstract

Background

The current ability to predict readmissions in patients with heart failure is modest at best. It is unclear whether machine learning (ML) techniques that address higher dimensional, non-linear relationships among variables would enhance prediction. We sought to compare the effectiveness of several ML algorithms for predicting readmissions.

Methods and Results

Using data from the Telemonitoring to Improve Heart Failure Outcomes trial, we compared the effectiveness of Random Forests (RF), Boosting, RF combined hierarchically with Support Vector Machines (SVM) or Logistic Regression (LR) and Poisson Regression against traditional LR to predict 30-day and 180-day all-cause and heart fauilre-only readmissions. We randomly selected 50% of patients for a derivation set and the remaining patients comprised a validation set, repeated 100 times. We compared c-statistics for discrimination and distributions of observed outcomes in risk deciles for predictive range. In 30-day all-cause readmission prediction, the best performing ML model, RF, provided a 17.8% improvement over LR (mean c-statistics 0.628 and 0.533, respectively). For readmissions due to heart failure, Boosting improved the c-statistic by 24.9% over LR (mean c-statistic 0.678 and 0.543, respectively). For 30-day all cause readmission, the observed readmission rates in the lowest and highest deciles of predicted risk with RF (7.8% and 26.2%, respectively) showed a much wider separation than LR (14.2% and 16.4%, respectively).

Conclusions

ML methods improved the prediction of readmission after hospitalization for heart failure compared with LR and provided the greatest predictive range in observed readmission rates.

High rates of readmission after hospitalization for heart failure impose tremendous burden on patients and the healthcare system ^1-3. In this context, predictive models facilitate identification of patients at high risk for hospital readmissions and potentially enable direct specific interventions toward those who might benefit most by identifying key risk factors. However, current predictive models using administrative and clinical data discriminate poorly on readmissions ^4-8. The inclusion of a richer set of predictor variables encompassing patients' clinical, social, and demographic domains, while improving discrimination in some internally validated studies ⁹ does not necessarily markedly improve discrimination ¹⁰, particularly in the dataset to be considered in this work. This richer set of predictors might not contain the predictive domain of variables required, but does represent a large set of data not routinely collected in other studies.

Another possibility for improving models, rather than simply adding a richer set of predictors, is that prediction might improve with methods that better address the higher order interactions between the factors of risk. Many patients may have risk that can only be predicted by modeling complex relationships between independent variables. For example, no available variable may be adequately explanatory; however, interactions between variables may provide the most useful information for prediction.

Modern machine learning (ML) approaches can account for non-linear and higher dimensional relationships between a multitude of variables that could potentially lead to an improved explanatory model ^{11, 12}. A number of methods have emerged from the ML community that can construct predictive models using many variables and their rich non-linear interactions ^13-15. Three widely used ML approaches may provide utility for readmission prediction: Random Forest (RF), Boosting, and Support Vector Machines (SVM). A primary advantage of ML methods is that they handle non-linear interactions between the available data with similar computational load. RF involves the creation of multiple decision trees ¹⁶ that sort and identify important variables for prediction ^{14, 17}. Boosting algorithms harness the power of weaker predictors by creating combined and weighted predictive variables ^{18, 19}. This technique has been applied to preliminary learning work with electronic health records ²⁰. SVM is a methodology that creates clearer separation of classes of variables using non-linear decision boundaries, or hyperplanes, from complex multi-dimensional data in possibly infinite dimensional spaces ^21-26.

In this study, we tested whether these ML approaches could predict readmissions for heart failure more effectively than traditional approaches using logistic regression (LR) ^{7, 9, 27, 28}. We tested these strategies using data that included detailed clinical and socio-demographic information collected during the Telemonitoring to Improve Heart Failure Outcomes (Tele-HF) trial ²⁹, a National Institutes of Health-sponsored randomized clinical trial to examine the effect of automated telemonitoring on readmission following hospitalization for heart failure ^{10, 29, 30}. We further tested whether the ML techniques could be improved when used hierarchically where outputs of RF were used as training inputs to SVM or LR. We evaluated these approaches by their effect on model discrimination and predictive range in order to understand ML techniques and evaluate their effectiveness when applied to readmissions for heart failure.

Methods

Data Source

Data for this study were drawn from Tele-HF, which enrolled 1653 patients within 30 days of their discharge after an index hospitalization for heart failure ³⁰. In addition to the clinical data from the index admission, Tele-HF used validated instruments to collect data on patients' socioeconomic, psychosocial, and health status. This study collected a wide array of instrumented data, from comprehensive, qualitative surveys to detailed hospital examinations, including many pieces of data not routinely collected in practice, providing a larger exploratory set of variables that might provide information gain.

The primary outcome was all-cause readmission or mortality within 180 days of enrollment ²⁹. A committee of physicians adjudicated each potential readmission to ensure that the event qualified as a readmission rather than another clinical encounter (e.g., emergency department visit) and to determine the primary cause of the readmission. The comprehensive nature in which outcomes were tracked and determined across the various sites makes this a well-curated dataset that can potentially leverage this information where other trials may not, as readmissions often occur at other institutions external to the study network ³¹. Results of the Tele-HF study revealed that outcomes were not significantly different between the telemonitoring and control arms in the primary analysis ²⁹.

Analytic Sample Selection

For this study, we included all patients whose baseline interviews were completed within 30 days of hospital discharge to ensure that the information was reflective of the time of admission. Of the 1653 enrolled patients, we first excluded 36 who were readmitted or died before the interview, 574 whose interviews were completed after 30 days from discharge, and 39 who were missing data on >15 of the 236 baseline features to create a study sample of 1004 patients for the 30-day readmission analysis set. To create the 180-day readmission analysis set, we further excluded 27 patients who died before the end of the study and had no readmission events, leaving 977 patients in the sample.

Feature Selection

We used 472 variables (called “features” in the ML community) for input. We first gathered the full 236 baseline patient characteristics available in Tele-HF ^{10, 30}. This set included data extracted from medical record abstractions, hospital laboratory results, physical examination information as well as quality of life, socioeconomic, and demographic information from initial patient surveys. The polarity of qualitative and categorical questions was altered if necessary to ensure that the lowest values reflect a strongly negative answer or missing data, and the highest values correspond to strongly positive answers (see Supplemental Materials). In addition, we created dummy variables for each of the 236 features to indicate whether the value was missing or not (0 and 1 values).

Definition of Outcomes

We developed methods to predict 4 separate outcomes: (1) 30-day all-cause readmission; (2) 180-day all-cause readmission; (3) 30-day readmission due to heart failure; and (4) 180-day readmission due to heart failure. We trained predictive models for each of these outcomes and compared them to each other.

Predictive Techniques

We built models using both traditional statistical methods and ML methods to predict readmission, and compared model discrimination and predictive range of the various techniques. For traditional statistical methods, we used an LR model ¹⁰, and a Poisson Regression (PR). Three machine learning methods - RF, Boosting, and SVM - were used for readmission prediction.

Logistic Regression

A recent study from Tele-HF had used random survival forest methods to select from a comprehensive set of variables for Cox regression analysis ¹⁰. The paper had a comprehensive evaluation of the most predictive variables in the Tele-HF dataset, using various techniques and various validation strategies. Using the variables selected in the paper would provide the most accurate representation of an LR model on the Tele-HF dataset for comparison purposes. Therefore, we used the same selected variables for our current study to compare model performance, as the current analysis is concerned with finding improved analytic algorithms for predicting 30-day readmissions rather than primarily with variable selection.

In order to verify that this LR model, which leverages the comprehensive variable selection technique in prior work ¹⁰, was the best model for comparison, we compared its performance against other LR models built using varied feature selection techniques. The first model selected variables for LR by lasso regularization, the next a forward, stepwise feature selection technique based upon each variable's likelihood ratio. All models were validated over 100 bootstrapped iterations; the former could not find a set of predictive variables, the latter varied in features chosen but selected, on average, only 5 variables. The model built using features selected from the work of Krumholz et al outperformed the other techniques, when comparing mean c-statistics. For a further detailed discussion of the other LR models built, we refer readers to the Supplementary Material.

Comparison Techniques

Given the flexibility of non-linear methods, the complexity of the desired models might overwhelm the available data, resulting in overfitting. While all the available variables can be used in ML techniques such as RF and Boosting, which are robust to this overfitting, we may require some form of feature selection to help prevent overfitting in less robust techniques like SVM ²². Further explanation of the predictive techniques, as well as the evaluation method, is provided in the Supplemental Materials and additionally in referenced by Hastie et al.¹⁶.

Hierarchical Methods

To overcome the potential for overfitting in LR and SVM, we developed hierarchical methods with RF. Previous hierarchical methods used RF as a feature selection method, since it is well-suited to a dataset of high dimensionality with varied data types, to identify a subset of features to feed into methods such as LR and SVM ²². RF is well known to use out-of-bag estimates and an internal bootstrap to help reduce and select only predictive variables and avoid over-fitting, similarly to AdaBoost³². RF is well-known to be able to take varied data-types as well as high-dimensional data and reduce to a usable subset, which we also verify through our bootstrapped cross-validation (through use of a derivation and validation set) ³³. However, rather than use the list of variables supplied by RF as the inputs to SVM or LR, the Tele-HF dataset allowed us to use the probability predicted by RF as the inputs to SVM and to LR to create two new hierarchical methods.

The Tele-HF dataset has comprehensive outcomes information for all patients. We leveraged this by designing two prediction models using all of the aforementioned methods in a hierarchical manner. We used the RF algorithm as a base for this technique. The RF model, trained on all of the available features, then produced a probability for a number of readmission events (e.g. 0-12 events in this dataset). These probabilities were then given to LR and SVM as inputs to build models from. A detailed discussion of the method by which RF and SVM as well as RF and LR are combined together is in the Supplementary Material.

Analytic Approach

For each of the predictive techniques above, we iterated the analyses illustrated in Figure 1 100 times. To construct the derivation and validation data sets, we split the cohort into 2 equally-sized groups, ensuring equal percentages of readmitted patients in each group. To account for a significant difference in numbers of patients who were readmitted and not readmitted in each group, we weighted the ML algorithms. The weight selected for the readmitted patients was the ratio of not-readmitted patients to readmitted patients in the derivation set. The testing and selecting of appropriate weights are further detailed in the Supplemental Materials.

Figure 1. Statistical analysis flow.

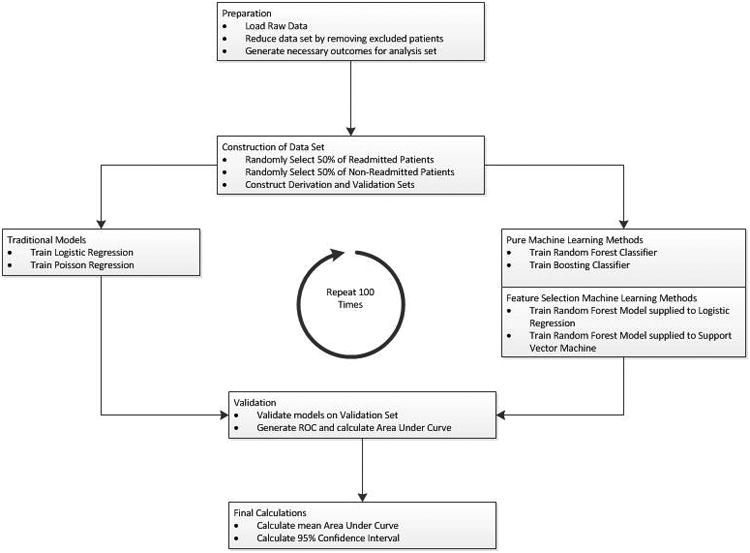
The data are split into derivation and validation sets. These sets are passed to each algorithm for comparison.

Once the derivation and validation sets were created, a traditional LR model was trained. We used SAS and the 5 most important variables as identified previously ¹⁰: blood urea nitrogen, glomerular filtration rate, sex, waist-to-hip ratio, and history of ischemic cardiomyopathy. The remaining techniques were created using the full raw data of 472 inputs for each patient, and were trained on the different readmission outcome labels.

We trained models to predict either the 30-day readmission or 180-readmission outcome. While we supplied the same input data to each method, we varied the outcome information provided. Since the 180-day readmission set contains more outcomes information, including the total number of readmission events during the trial, it is possible that it might be easier to predict 180-day readmission, given the propensity of some patients to be readmitted multiple times. To provide a range of modeling for the final binary prediction (readmitted/not readmitted), we ran 5 distinct training methods based upon the labels provided to the algorithm, known as supervised learning. For 30-day readmission prediction, we first generated 3 different training models with the same baseline data, but 3 different outcomes: 30-day binary outcomes, 180-day binary outcomes, and 180-day counts of readmissions. We then used the predictive models created by these 3 training methods to predict 30-day readmission outcomes in the validation cohort. Similarly, to test 180-day readmission, we generated 2 different training methods with same baseline data but different outcomes namely 180-day binary outcomes and 180-day counts of readmissions. A detailed description of how these methods vary from each other is available in the Supplemental Materials.

We ran the models generated on the validation set and calculated the area under the receiver operating characteristics (ROC) curve (c-statistic), which provided a measure of model discrimination. The analysis was run 100 times in order to provide robustness over a potentially poor random split of patients and to generate a mean c-statistic with a 95% confidence interval (CI). We also evaluated the risk stratification abilities of each method. The probabilities of readmission generated over the 100 iterations were then sorted into deciles. Finally, we calculated the observed readmission rate of each decile to determine the predictive range of the algorithms.

These models should be used prospectively, to provide clinicians with decision making points. For each iteration, we calculated the positive predictive value (PPV), sensitivity, specificity, and f-score, a common measurement in machine learning²⁵, which is calculated as:

$$F-\mathit{\text{score}}=2\ast \frac{\mathit{\text{PPV}}\ast \mathit{\text{Sensitivity}}}{\mathit{\text{PPV}}+\mathit{\text{Sensitivity}}}$$

The f-score provides a balance between PPV and sensitivity, similarly to a c-statistic, but at designated thresholds on the ROC curve. The data-driven decision threshold for prospective modeling measurements was that which maximized the f-score.

Further, to test whether a narrowed focus of prediction could improve discrimination, we conducted the same analyses using heart-failure-only readmission instead of all-cause readmission.

All ML analyses were developed in R. The list of R packages used in this study are included in the Supplemental Materials. The Human Investigation Committee at the Yale School of Medicine approved the study protocol.

Results

Baseline characteristics of patients in 30-day and 180-day analytic samples are detailed in Table 1. In both analytic samples, the proportion of females and African-Americans was approximately 40%. Ninety percent of patients had New York Heart Association Class II or III heart failure, with almost 70% having left ventricular ejection fraction <40%. A history of hypertension (77%) and diabetes (45%) was common. The 30-day all-cause readmission rate was 17.1% while the 180-day all-cause readmission rate was 48.9%. No sex-specific or race-specific differences were found.

Table 1. Patient Characteristics.

	30-Day		180-Day
Characteristic	All N (%)	Readmission N (%)	All N (%)	Readmission N (%)
N	1004 (100.0)	149 (14.8)	977 (100.0)	478 (48.9)
Median age (SD)	62 (15.7)	62 (15.9)	62 (15.7)	62 (15.4)
Females	415 (41.3)	58 (38.9)	403 (41.2)	193 (40.4)
Race
White	507 (50.5)	84 (56.4)	491 (50.3)	253 (52.9)
African American	393 (39.1)	55 (36.9)	385 (39.4)	188 (39.3)
Other	104 (10.4)	10 (6.7)	101 (10.3)	37 (7.8)
New York Heart Association
Class I	56 (5.6)	7 (4.7)	54 (5.5)	31 (6.5)
Class II	515 (51.3)	85 (57.0)	500 (51.2)	256 (53.6)
Class III	355 (35.4)	52 (35.0)	347 (35.5)	160 (33.4)
Class IV	58 (5.8)	2 (1.3)	57 (5.8)	20 (4.2)
Missing	20 (1.9)	3 (2.0)	19 (2.0)	11 (2.3)
Medical History
LVEF† % <40	687 (68.4)	99 (66.4)	668 (68.4)	317 (66.3)
Hypertension	771 (76.8)	116 (77.9)	752 (77.0)	376 (78.7)
Diabetes	450 (44.8)	57 (38.3)	439 (44.9)	200 (41.8)
Myocardial Infarction	257 (25.6)	47 (31.5)	250 (25.6)	131 (27.4)
Stroke	96 (9.6)	15 (10.1)	92 (9.4)	44 (9.2)
Ischemic Cardiomyopathy	235 (23.4)	44 (29.5)	228 (23.3)	127 (0.27)
Clinical Values (Mean/SD)
Albumin	3.32 (0.53)	3.25 (0.61)	3.31 (0.53)	3.33 (0.55)
Blood Urea Nitrogen	25.2 (17.8)	28.7 (20.3)	26.3 (16.8)	29.1 (17.5)
Creatinine	1.40 (0.77)	1.53 (0.80)	1.45 (0.72)	1.55 (0.80)
Hemoglobin	12.3 (1.94)	12.0 (1.80)	12.4 (1.94)	12.1 (1.87)
Glomerular Filtration Rate	58.5 (27.4)	52.8 (24.6)	58.8 (27.4)	54.4 (27.2)
Potassium	4.08 (0.57)	4.19 (0.58)	4.08 (0.57)	4.09 (0.56)

^*All values are mean (standard deviation) unless noted.

^†LVEF, Left Ventricular Ejection Fraction

30-Day All-Cause Model Discrimination

The discrimination of the different predictive models for 30-day all-cause readmission represented by c-statistic values is illustrated in Figure 2a. LR had a low c-statistic of 0.533 (95% CI: 0.527-0.538). Boosting on the input data had the highest c-statistic (0.601, 95% CI: 0.594-0.607) in 30-day binary outcome with 30-day training case. Boosting also had the highest c-statistic for the 30-day binary outcome with 180-day binary training (0.613, 95% CI: 0.607-0.618). For the 30-day outcomes with 180-day counts training, the RF technique had the highest c-statistic (0.628, 95% CI: 0.624-0.633).

Figure 2. Forest plots for c-statistics and 95% confidence intervals for each method with respect to prediction of 30-day and 180-day all-cause readmission (2a and 2b).

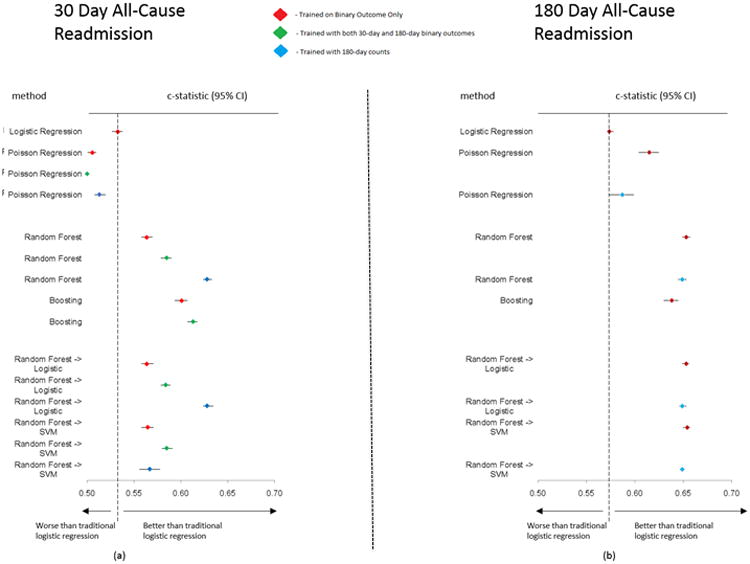
Diamond represents c-statistic and the line represents the 95% confidence interval. SVM, Support Vector Machine. Color coding for model training: Red - trained in 30-day binary case only; Green - trained with 30-day and 180-day binary outcome; Blue - trained with 180-day counts case.

180-day All-Cause Model Discrimination

The c-statistic values for different models in predicting the 180-day readmission are graphically illustrated in Figure 2b. LR again showed a low c-statistic (0.574, 95% CI: 0.571-0.578) for the 180-day binary case. The RF into SVM hierarchical method had the highest achieved c-statistic across all methods (0.654; 95% CI: 0.650-0.657) in 180-day binary outcome, and 180-day count case (0.649; 95% CI: 0.648-0.651).

30-Day All-Cause Model Predictive Range

Deciles of the probabilities/responses generated by the algorithms were plotted against the observed rate of readmission in each decile in Figure 3. For each training version of the method, we plotted the values from the method and training version with the highest c-statistic (i.e., best RF from the three 30-day training scenarios). In Figure 2a, the RF has the same mean c-statistic and similar CI as the RF into LR hierarchical model. In Figure 3, for RF, the readmission rates were markedly higher at the tenth decile of probabilities (26.2%) than the first decile of probabilities (7.8%) showing a higher predictive range than LR (14.2% and 16.4%, respectively), whereas for the RF into LR hierarchical model, the actual readmission rates varied only from 10.6% to 19.0% from first to tenth decile, despite the same mean c-statistic for RF and RF into LR.

Figure 3. Deciles of algorithm risk versus readmission rates (%) for the best 30-day all-cause models for each method.

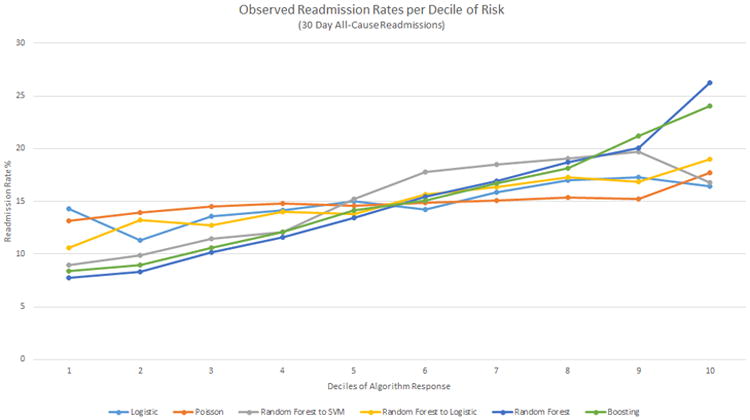
The y-axis presents the observed readmission rates in each decile, the x-axis the ordered deciles of risk predicted. SVM, Support Vector Machine.

180-Day All-Cause Model Predictive Range

When the predicted probabilities of each algorithm were separated into deciles and plotted against the real readmission rate per decile, RF into SVM had the largest difference in readmission rate from first decile (31.0%) to tenth decile (69.4%), whereas LR had a readmission rate of 40.5% in the first decile and 60.1% in the tenth decile (Figure 4).

Figure 4. Deciles of algorithm risk versus readmission rates (%) for the best 180-day all-cause models for each method.

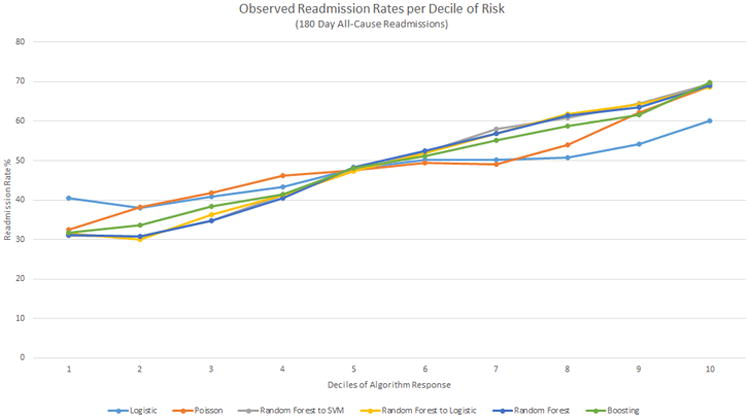
The y-axis presents the observed readmission rates in each decile, the x-axis the ordered deciles of risk predicted. SVM, Support Vector Machine.

Readmission Due to Heart Failure Discrimination

As illustrated in Figures 5a and 5b, for heart failure-only readmissions, the LR model again had a low c-statistic for the 30-day binary case (0.543; 95% CI: 0.536-0.550) and the 180-day binary case (0.566; 95% CI: 0.562-0.570). Boosting had the best c-statistic for the 30-day binary-only case (0.615; 95% CI: 0.607-0.622) and for the 30-day with 180-day binary case training (0.678; 95% CI: 0.670-0.687). The highest c-statistic for other prediction cases were RF for the 30-day with 180-day counts case training (0.669; 95% CI: 0.661-0.676); RF into SVM for the 180-day binary-only case (0.657; 95% CI: 0.652-0.661); and RF into SVM for the 180-day counts case (0.651; 95% CI: 0.646-0.656).

Figure 5. Forest plots for c-statistics and 95% confidence intervals for each method with respect to prediction of 30-day and 180-day heart failure readmission (5a and 5b).

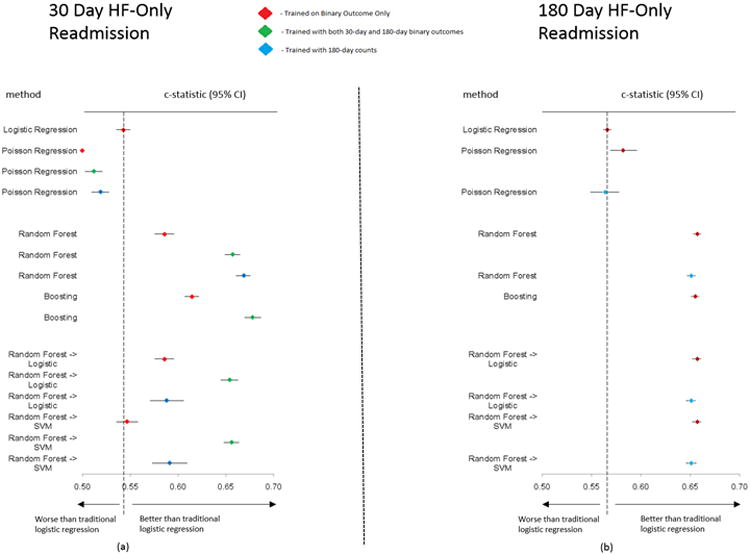
Diamond represents c-statistic and the line represents the 95% confidence interval. SVM, Support Vector Machine. Color coding for model training: Red - trained in 30-day binary case only; Green - trained with 30-day and 180-day binary outcome; Blue - trained with 180-day counts case.

Readmission Due to Heart Failure Predictive Range

When the deciles of risk prediction were plotted against the observed readmission rate, RF and Boosting each had the biggest differences between first and tenth deciles of risk (1.8%-11.9% and 1.4%-12.2%, respectively). Although the hierarchical methods of RF into LR and RF into SVM had similar c-statistics (0.654; 95% CI: 0.645-0.663 and 0.656; 95% CI: 0.648-0.664 respectively) in Figure 6, only RF into LR clearly identifies low- and high-risk groups. The risk stratification for the 180-day heart failure-only case follows closely with c-statistics, similar to the 180-day all-cause case (Figure 7).

Figure 6. Deciles of algorithm risk versus readmission rates (%) for the best 30-day heart failure-only models for each method.

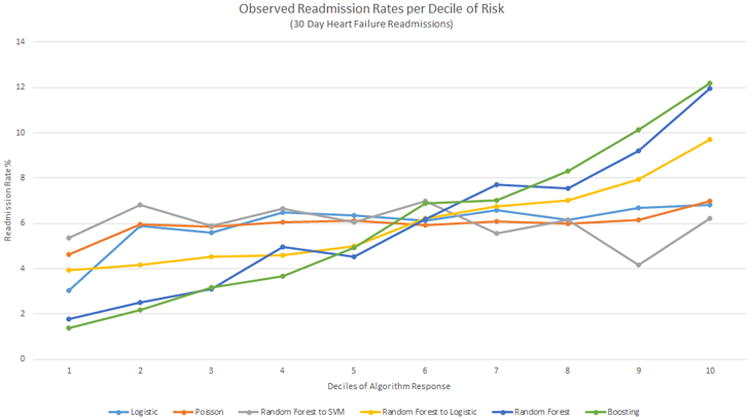
The y-axis presents the observed readmission rates in each decile, the x-axis the ordered deciles of risk predicted. SVM, Support Vector Machine.

Figure 7. Deciles of algorithm risk versus readmission rates (%) for the best 180-day heart failure-only models for each method.

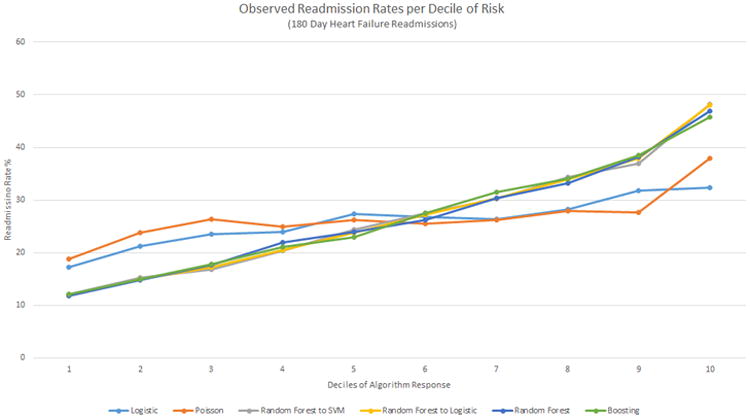
The y-axis presents the observed readmission rates in each decile, the x-axis the ordered deciles of risk predicted. SVM, Support Vector Machine.

Improvements over Logistic Regression

Table 2 shows the percentage improvement in prediction of the best-trained model for each ML technique over LR for each outcome predicted. RF achieved a 17.8% improvement in discrimination over LR, the best 30-day all-cause readmission improvement. Similarly, the hierarchical method of RF into SVM achieved a 13.9% improvement for 180-day all-cause readmission; Boosting achieved a 24.9% improvement for 30-day readmission due to heart failure; and the hierarchical method of RF into SVM achieved a 16.1% improvement over LR for 180-day readmission due to heart failure.

Table 2. Percent Improvement of Machine Learning Methods over Baseline, Traditional Logistic Regression.

	Poisson Regression	Random Forest	Boosting	Random Forest To Logistic Regression	Random Forest To Support Vector Machine
30-Day All-Cause Readmission Prediction	-3.75%	17.8%	15.0%	17.8%	9.76%
180-Day All-Cause Readmission Prediction	7.14%	13.8%	11.0%	13.8%	13.9%
30-Day Heart Failure-Only Readmission Prediction	-5.71%	23.2%	24.9%	20.4%	20.8%
180-Day Heart Failure Only Readmission Prediction	2.83%	16.1%	15.7%	16.1%	16.1%

Prediction Results

Table 3 shows the prospective prediction results of the best model for 30-day all-cause readmission, 180-day all-cause readmission, 30-day heart failure-only readmission, and 180-day heart failure-only readmission. 30-day all-cause readmission had a positive predictive value of 0.22 (95% CI: 0.21-0.23), sensitivity of 0.61 (0.59-0.64), and a specificity of 0.61 (0.58-0.63) at a maximal f-score of 0.32 (0.31-0.32); 180-day all-cause readmission had a positive predictive value of 0.51 (0.51-0.52), a sensitivity of 0.92 (0.91-0.93), and a specificity of 0.18 (0.20-0.21) at a maximal f-score of 0.66 (0.65-0.66); 30-day heart failure-only readmission had a positive predictive value of 0.15 (0.13-0.16), a sensitivity of 0.45 (0.41-0.48), and a specificity of 0.79 (0.76-0.82) at a maximal f-score of 0.20 (0.19-0.21); 180-day heart failure-only readmission had a positive predictive value of 0.51 (0.50-0.51), a sensitivity of 0.94 (0.93-0.95), and a specificity of 0.15 (0.13-0.17) at a maximal f-score of 0.66 (0.65-0.66). The 30-day predictions, in general, were better at identifying negative cases while the 180-day predictions were better able to correctly identify positive cases.

Table 3. Prospective Prediction Results (Mean and 95% Confidence Intervals).

	Positive Predictive Value	Sensitivity	Specificity	F-Score
30-Day All-Cause Readmission	0.22 (0.21-0.23)	0.61 (0.59-0.64)	0.61 (0.58-0.63)	0.32 (0.31-0.32)
180-Day All-Cause Readmission	0.51 (0.51-0.52)	0.92 (0.91-0.93)	0.18 (0.20-0.21)	0.66 (0.65-0.66)
30-Day Heart Failure-Only Readmission	0.15 (0.13-0.16)	0.45 (0.41-0.48)	0.79 (0.76-0.82)	0.20 (0.19-0.21)
180-Day Heart Failure Only Readmission	0.51 (0.50-0.51)	0.94 (0.93-0.95)	0.15 (0.13-0.17)	0.66 (0.65-0.66)

Discussion

In our study to model risk of readmissions in a sample of patients hospitalized with heart failure, the ML analytic techniques we applied improved discrimination modestly compared with the traditional method of LR. These ML models also provided better identification of groups at low and high risk for readmission by increasing predictive range compared with LR. These results are consistent with our hypothesis that ML methods can leverage complex higher-level interactions among a multitude of variables to improve discrimination and predictive range with respect to heart failure outcomes compared with traditional linear models. We used readmissions among patients with heart failure as a test case to examine the advantage of ML algorithms over traditional statistical analysis to see if such an approach could be applied to other outcomes prediction and predictive range problems.

Models developed from ML algorithms to improve discrimination and predictive range can be evaluated using several measures or methods. The modest improvement in discrimination represented by c-statistics across the various ML methods, while promising, is ultimately insufficient. Further, the models selected, at a data-driven threshold that optimizes the f-score, optimized the correct classification of negative cases but had a large number of false positives, as seen in the low positive predictive value and f-score. This threshold decision would be varied if further cost information was inputted to the model or the selected threshold optimized on another factor, such as reducing false alarms, etc. We found that while discriminatory power was similar across certain methods, the range in observed events among deciles of predicted risk varied greatly. Analyzing multiple aspects of models provides a stronger understanding of those models. With regard to 30-day all-cause readmission case, RF better differentiates low- and high-risk groups compared with all other methods including the hierarchical RF into LR model. Despite similar discrimination (mean c-statistic) between the 2 methods, RF actually has a better predictive range. In other words, RF better discriminates patients in low- and high-risk strata, whereas hierarchical RF into LR better discriminates patients in the middle deciles of risk. This suggests that a combination of various approaches, with possible deployment of different methods at different strata of risk, can improve discrimination of the overall model and may improve the predictive range.

There have been some suggestions in the literature about how to improve predictive range of risk strata and overall discrimination. Wiens et al. ²⁶ showed that use of time-based information can improve their predictive range and overall discrimination when predicting the risk of Clostrium Difficile infection in hospitalized patients. In an earlier study examining heart failure mortality prediction using cytokine measurements, use of the baseline cytokine measurements alone did not significantly improve discrimination ³⁴. However, the addition of serial cytokine measurements over follow-up time to the predictive model improved discrimination for 1-year mortality³⁴. Thus, perhaps leveraging serially collected telemonitoring data on daily health and symptoms of patients could improve discrimination and predictive range of our predictions.

The general experience with LR is that readmissions after index hospitalizations for heart failure are more difficult to predict than mortality outcomes. In a meta-analysis, Ouwerkerk et al. analyzed 117 heart failure outcome prediction models with 249 variables; the average c-statistic to predict mortality was 0.71 and hospitalization was 0.63 ¹². Tele-HF study data were collected to identify and track heart failure-related symptoms, and we find that narrowing our prediction to heart failure-only readmissions improves the discrimination and predictive range of each method.

Ultimately, despite the increase in a wide array of data, from quality of life questionnaires to hospital examinations, as well as the increase in complex methods to perform predictions, questions do arise from the modest c-statistics. The incremental gains over the LR models do indicate the power of the machine learning methods. However, a deeper analysis of why, even with data from a multitude of domains, the models remain at a consistent level with prior work does raise the question of what other data might be collected that would provide predictive value, and whether it is currently being collected or not. It seems that a deeper study into other possible important predictors of readmission might need to be carried out in order to better understand why current administrative claims and clinical studies models have had varied, but moderate, success.

Limitations

The discrimination and range of prediction is likely affected by several limitations of the Tele-HF dataset. First, the number of patients is small in comparison to the number of variables measured per patient. As a result, while rich in terms of patient features, the small number of patients makes the dataset vulnerable to overfitting. Further, many variables included in models with stronger c-statistics from prior studies are not present in Tele-HF ^{9, 27}, which could affect performance. Time-to-event analysis conducted on the Tele-HF dataset produced a c-statistic of 0.65 ¹⁰. This finding suggests there are measurable domains of variables not analyzed in this study that might be more predictive in all heart failure patients. However, with the moderate-at-best c-statistics, it is possible that the best set of features in predicting risk in heart failure patients has not yet been collected.

The interpretation of the results can be varied depending upon the particular dataset and purpose of modeling. For example, the prediction threshold selected by optimal f-score may not be desirable for a particular intervention that designed when considering a model, such as when used a prospective fashion. Further, the numeric ranges of the probabilities generated by the algorithms do not necessarily match, and thus the thresholds considered across each method vary. While the output of the algorithm provides a predicted probability of readmission, the value in this is not the number provided but where this lies in the predictive range of the method and, thus, whether it can be classified as low or high risk, where the observed rates are considered. This is a result of each method basing its distance (and thus probability) of observations in the model on different metrics, resulting in a different calculation of a final probability. If, these probabilities would be desirable for direct use, the values could be scaled to match comparable intervals across methods.

The trial arm of Tele-HF may provide further insights into the value of time-to-event analysis by permitting inclusion of the daily telemonitoring responses by patients in the intervention arm as a time-series signal to be processed for time-dependent risk models. In order to determine the accuracy of additional methods, a direct comparison in the predictions of each individual patient (both risk and outcome) needs to be made between methods rather than net reclassification index work, which has not been shown to be effective in many cases at understanding and improving model discrimination performance ^{35, 36}. Finally, in order to address the viability of the model and the clinical predictors it is built upon, an external validation cohort should be used. However, as the clinical predictors collected in studies are often varied, it becomes important to distinguish unique predictors in internal validation, as well as understand the impact each predictor has on the models for better interpretation. As this is a post-hoc analysis of a randomized controlled trial, the generalizability of such models is a limitation. Nevertheless, the goal of this study was to compare methods, not to introduce a new model. Therefore, there is little reason to think that a population-based sample would yield a different result. While the data from such a trial spans a diverse set of hospitals and patients, and is well curated, once the understanding of such strengths and weakness of ML methods is understood, they should be extended to data derived from other sources as well, including electronic health records, which will likely affect results due to a consideration of varied data availability as well as a more heterogeneous patient population

Conclusions

The results of our study support the hypothesis that ML methods, with the ability to leverage all available data and their complex relationships, can improve both discrimination and range of prediction over traditional statistical techniques. The performance of the ML methods varies in complex ways, including in discrimination and predictive range. Future work needs to focus on further improvement of predictive ability through advanced methods and more discerning data, so as to facilitate better targeting of interventions to subgroups of patients at highest risk for adverse outcomes.

What is Known.

• - Prediction models for readmissions in heart failure are often modest, at best, at discriminating between readmitted and non-readmitted patients.

• - Prediction models for readmissions in heart failure often preselect a small number of variables with which a logistic regression model is developed

What the Study Adds.

• - This study introduces comparisons of multiple popular machine learning methods for comparison against traditional techniques.

• - This study introduces selecting models that can select variables for us from a larger, comprehensive dataset.

• - This study shows the improvements in using both machine learning methods and a comprehensively-collected dataset, to help readers understand factors that contribute to readmission and limitations to current results in readmission prediction.