Short-Term and Long-Term Educational Mobility of Families: A Two-Sex Approach

Abstract

We use a multigenerational perspective to investigate how families reproduce and pass their educational advantages to succeeding generations. Unlike traditional mobility studies that have typically focused on one-sex influences from fathers to sons, we rely on a two-sex approach that accounts for interactions between males and females—the process in which males and females mate and have children with those of similar educational statuses and jointly determine the educational status attainment of their offspring. Using data from the Panel Study of Income Dynamics, we approach this issue from both a short-term and a long-term perspective. For the short term, grandparents’ educational attainments have a direct association with grandchildren’s education as well as an indirect association that is mediated by parents’ education and demographic behaviors. For the long term, initial educational advantages of families may benefit as many as three subsequent generations, but such advantages are later offset by the lower fertility of highly educated persons. Yet, all families eventually achieve the same educational distribution of descendants because of intermarriages between families of high- and low-education origin.

Introduction

Educational attainment is the main pathway through which families¹ transmit their social status across generations in contemporary societies. Education not only is the first source of stratification that one experiences as an adult but also has the potential to change the social circumstances of one’s offspring, grandchildren, and subsequent generations. The multigenerational process of educational reproduction is complex: it combines the inheritance of educational status and the biological reproductive success of families across generations (Mare 1997; Mare and Maralani 2006). Such a view, however, is incomplete, overlooking interactions of families with one another through the formation of marriages. Mating rules, such as assortative mating by education, may play an important role in shaping educational inequality across generations because marriages determine the social makeup of families and create the family backgrounds of members of the next generation (Mare and Schwartz 2006). We use the term “two-sex approach” in this article to refer to a perspective that takes into account assortative mating as well as both paternal and maternal characteristics in the educational mobility of families.

Building on this two-sex approach, we examine both the short-term mobility of families based on empirical mobility data from three generations of American families and the long-term mobility of families that combines the short-term patterns with population simulation results. Our short-term mobility analysis examines whether the influence of grandparents’ education on grandchildren’s education is fully mediated by the parent generation—that is, whether social mobility follows a Markovian process (Mare 2011). This assumption implies that grandparents neither directly transmit their educational status to their grandchildren independently of parents nor influence their grandchildren’s educational outcomes through demographic behaviors of any generation—such as whether, when, and whom to marry and whether to have children. This study examines this assumption by quantifying grandparents’ influence on grandchildren, which is either direct or in combination with their own and their offspring’s demographic behaviors, beyond what a pure Markovian mobility regime implies.

Based on three-generation education mobility results from the short-term analysis, we then conduct a long-term mobility analysis that simulates trends in the educational composition of offspring and descendants from college-educated and high school–educated family origins. The long-term analysis addresses fundamental albeit hypothetical questions: Can an increase in education in one generation permanently change the educational prospects of future generations? If not, how long can one generation’s influence persist? To investigate these questions, we combine estimates of educational assortative mating, fertility differences by education, and intergenerational transmission of educational status to show the formation, growth, and status reproduction of families in each generation. By simulating these processes to a long-run equilibrium, we examine whether the educational composition of progeny from college- and high school–educated families remains distinct or converges to the same distribution. The long-term analysis reveals population-level implications for mobility that are often left unexamined in studies based on inter-generational status associations alone.

We extend two-sex social mobility models that ignore demographic processes (e.g., Beller 2009) and two-sex population models that do not include social mobility (Caswell 2001; Pollak 1986, 1987, 1990; but see Preston and Campbell 1993). Three features of our two-sex model distinguish it from one-sex models. First, the model takes into account the interdependence of demographic behaviors of both sexes, through educational assortative mating and constraints imposed by the availability of potential mates in the marriage market. Second, it considers gender differences in demographic rates, such as levels of fertility and mortality, and educational differences in these rates. And third, it examines multigenerational effects from both paternal and maternal sides of families, recognizing differences in the effects of some kin relative to others and different mobility outcomes for sons and daughters.

This article provides a multigenerational example of how social inequality persists as a result of the interactions of demography and social mobility (Bloome 2014; Duncan 1966; Lam 1986; Maralani 2013; Mare 1997; Mare and Maralani 2006; Matras 1961, 1967; Musick and Mare 2004; Preston 1974; Preston and Campbell 1993; Schnore 1961). Following Mare and Song (2014), we show that social stratification in multiple generations works through both the transmission of social status from one generation to subsequent generations and demographic mechanisms that govern the growth and decline of families. The mobility and reproduction of families combine in a complex way. The present study advances this idea by showing the separate and joint effects of males and females in the process of educational reproduction of families, through mating with those of similar educational characteristics and transmitting statuses to offspring and progeny of both sexes.

Short-Term and Long-Term Multigenerational Social Mobility

Traditional social mobility studies, which have mostly focused on the intergenerational association of status between parents and offspring (e.g., Blau and Duncan 1967; Erikson and Goldthorpe 1992; Featherman and Hauser 1978; Hout 1983, 1988) and have occasionally included grandparents as well (Hodge 1966; Warren and Hauser 1997), provide a short-term perspective on families’ social status reproduction across generations. These studies have addressed the extent to which individuals’ socioeconomic attainments are determined by their parents’ socioeconomic and demographic characteristics. Recently, a growing number of studies have extended the parent-offspring paradigm to three generations because of not only the increasing availability of three-generation data but also substantive concerns (Bol and Kalmijn 2015; Chan and Boliver 2013; Erola and Moisio 2007; Hertel and Groh-Samberg 2014; Jæger 2012; Møllegaard and Jæger 2015; Pfeffer 2014; Wightman and Danziger 2014; Zeng and Xie 2014). Given the considerable increase in life expectancy, many persons now share a substantial portion of their lifetime with their grandchildren compared with several generations ago (Uhlenberg 1996). The concurrent trends in falling fertility and the rise in single-parent households may also have increased interactions between grandparents and grandchildren, especially in multigenerational households (Bengtson 2001; Ruggles 2007). These demographic trends may have changed grandparents’ roles in the social status attainment of their grandchildren, leading to a stronger association between grandparents’ and grandchildren’s social statuses even after parents’ status is accounted for.

Whether grandparents directly influence grandchildren’s socioeconomic status has important implications for our understanding of the persistence of socioeconomic inequality along family lines. In the absence of grandparent influence on grandchildren net of the influences of parents’ statuses, the two-generation paradigm suffices to explain mobility in three or more generations (Mare 2011). The transmission of social status, however, represents only one form of grandparent influence on grandchildren. Another type of influence is through demographic behaviors that tie generations together. Grandparents’ socioeconomic characteristics may influence parents’ marriage and fertility preferences, intentions, and decisions, all of which make up the family background of the grandchildren in terms of parents’ marital status, socioeconomic characteristics, and level and timing of childbearing. Even if grandparents’ socioeconomic status is independent of parents’ demographic behaviors, differential demographic behaviors among socioeconomic groups may jointly produce grandparent influences on grandchildren (Maralani 2013; Mare and Maralani 2006). For example, without resource constraints, grandparents with more offspring and grandchildren have a greater capacity to influence subsequent generations than those with fewer grandchildren, whereas those without grandchildren cannot pass on advantages or disadvantages beyond the offspring generation.

The short-term patterns of social reproduction across three generations may also generate long-run inequalities among families (e.g., Clark 2014; Piketty 2014). Absent differences in net fertility and marriage patterns among persons with varying educational attainment, educational inequalities persist between generations only as a result of differential social mobility chances. If mobility rates are fixed over time, individuals’ mobility outcomes will eventually become independent of the initial social advantage or disadvantage of their ancestral families, leading to the same equilibrium distribution of socioeconomic statuses of descendants from all families (Bartholomew 1982; Mare and Song 2014). Under these conditions, intergenerational and multigenerational influences in the social reproduction of families are transient, indicating that the short-term unequal social statuses among families do not generate long-term inequality among individuals descended from different ancestral origins.

The interplay between social mobility and demographic behaviors may further complicate the long-term social reproduction of families if education groups vary in fertility and marriage patterns. When families’ socioeconomic statuses are positively associated with their reproductive success, the effects of social mobility and fertility are mutually reinforcing: individuals from high-status families are more likely to have high-status offspring and to have more offspring who survive to reproductive ages (e.g., Lee and Campbell 1997). As a result, their descendants account for a disproportionately large share of the high-status population in later generations (Mare and Song 2014). Conversely, when the association between socioeconomic status and fertility is negative, offspring from high-education families are more likely to attain high status, but that advantage to high-education families is offset by their lower fertility. To link short-term mobility to long-term mobility, we first examine parent and grandparent effects in marriage and fertility behaviors of couples and the transmission of educational status from couples to their children and grandchildren. We then simulate the process of social stratification many generations hence by fixing the mobility and demographic behaviors in each generation and estimating the equilibrium differences among families with unequal origins in educational status.

One-Sex and Two-Sex Approaches to Intergenerational Mobility

Social mobility studies typically rely on a one-sex approach, in which male and female populations are considered independently. Such studies focus on the socioeconomic attainments of either males or females and their connections to the attainments of their parents, sometimes taking account of the separate influences of mothers and fathers in the intergenerational transmission of status (e.g., Beller 2009). These studies often ignore the interdependence of males and females through the marriage market, even in mobility research that takes demographic processes into account (e.g., Maralani 2013; Mare and Maralani 2006). A two-sex approach to social mobility focuses on male and female populations together, including their interactions in the marriage market, their differential survival, and their (two-sex) patterns of fertility. From a two-sex perspective, the process of family reproduction starts with the mating of males and females according to age/sex-specific mating rules and ends when the couples complete their lifetime fertility. The mating rule that takes into account the availability of males and females and the interaction frequency between the two sexes is a key mechanism that governs population dynamics (Bessa-Gomes et al. 2010; Caswell and Weeks 1986; Goodman 1953; Keyfitz 1968; Pollak 1990; Schoen 1981). Furthermore, these population dynamics models can be adapted to take account of assortative mating and differential fertility by social attributes, such as education, income, occupation, and race (Fernández and Rogerson 2001; Kalmijn 1991a, 1991b; Mare 1991; Qian 1997, 1998; Schwartz 2010, 2013; Schwartz and Mare 2005). The extent of intermarriages based on these social attributes reflects the rigidity of boundaries between groups with varying social statuses (Blau 1977) and the distribution of social and economic resources that couples pass on to the next generation (Mare 2000). Parental resources are more unequally distributed among families when parents show a closer resemblance in social status than when the formation of marital unions is completely random. The rise in educational homogamy since the 1970s has contributed to increases in family inequalities that persist across generations (Schwartz and Mare 2005).

The two-sex approach can be enriched even further when we take account of the influences of maternal and paternal grandparents on educational outcomes for grandchildren. Grandparents may raise grandchildren during episodes of need, set up trust funds for grandchildren’s education, and regularly provide practical or monetary support to grandchildren (Cherlin and Furstenberg 1986; Coall and Hertwig 2010; DeLeire and Kalil 2002; Silverstein and Marenco 2001). Additionally, they may influence the marriage and fertility patterns of their children, thereby affecting the varying numbers of grandchildren born in different socioeconomic groups. Compared with the one-sex approach to social mobility, a two-sex approach that includes mothers’ and grandparents’ effects can show differences between the roles of paternal and maternal family lines in social mobility.

We use a two-sex model that takes account of how both sexes contribute to differential demographic reproduction and multigenerational transmission of educational attainment. The model extends the one-sex patrilineal multigenerational demographic and social mobility model proposed in Mare and Song (2014). The two-sex approach provides a more complete view of how patterns of intermarriage among socioeconomic groups, as well as differential fertility and mortality, shape social inequality among families.

Social and Demographic Mobility Models

One-Sex Approach

We first modify Mare and Maralani’s (2006) one-sex model to examine the influences of parents’ educational attainments on educational outcomes of offspring:²

$$S_{j\mid i}=F_i·m_i·r_i·p_{j\mid i}$$ (1)

where S_j|i denotes the number of men (women) in the offspring’s generation who are in education group j and have fathers (mothers) in education group i; F_i denotes the number of men (women) in the paternal (maternal) generation who are in education group i; m_i denotes the probability that a man (woman) in education group i gets married; r_i denotes the expected number of sons (daughters) who are born to a man (woman) in education group i and survive to adulthood; and p_j|i denotes the probability that a son (daughter) born to a man (woman) in education group i enters education group j.

In a three-generation model, the marriage component m, the fertility component f, and the mobility component p all depend on both fathers’ (mothers’) and grandfathers’ (grandmothers’) educational attainments:

$$S_{j\mid ik}=F_{ik}·m_{ik}·r_{ik}·p_{j\mid ik}$$ (2)

where S_j|ik denotes the number of men (women) in the offspring’s generation (G3) who are in education group j and have fathers (mothers in G2) in education group i and grandfathers (grandmothers in G1) in education group k; F_ik denotes the number of men (women) in the paternal (maternal) generation (G2) who are in education group i and have fathers (mothers in G1) in education group k; m_ik denotes the probability that a man (woman) in education group i with a father (mother) in education group k gets married; r_ik denotes the expected number of sons (daughters) who are born to a father (mother) in education group i and a grandfather (grandmother) in education group k and survive to adulthood; and p_j|ik denotes the probability that a son (daughter) born to a father (mother) in education group i and a grandfather (grandmother) in education group k will enter education group j. This model accounts for differences in marriage behavior by men’s (women’s) level of education but only under very restrictive assumptions—for example, that the availability of partners of the opposite sex is completely unconstrained or that the matching of men’s and women’s educational attainments follows complete male dominance or complete female dominance. In other words, the model does not account for the interaction of male and female populations.

Based on the social mobility and demographic model in Eq. (2), we define the social reproduction effect (SRE) as the relative advantage of a college father (mother) compared with a high school father (mother) to produce college sons (daughters) given the grandfather’s (grandmother’s) education fixed at high school—that is,

$$\mathit{Net}{\mathit{SRE}}_{k\mid j}^P=\frac{S_{k\mid kj}}{F_{kj}}/\frac{S_{k\mid jj}}{F_{jj}}=\frac{m_{kj}{r}_{kj}{p}_{k\mid kj}}{m_{jj}{r}_{jj}{p}_{k\mid jj}},$$ (3)

where education groups k and j refer to college and high school, respectively.

We define the net social reproduction effect of grandfathers (grandmothers) as the relative advantage of a high school father (mother) with a college grandfather (grandmother) relative to a high school father (mother) with a high school grandfather (grandmother) to produce college sons (daughters)—that is,

$$\mathit{Net}{\mathit{SRE}}_{k\mid j}^{GP}=\frac{S_{k\mid jk}}{F_{jk}}/\frac{S_{k\mid jj}}{F_{jj}}=\frac{m_{jk}{r}_{jk}{p}_{k\mid jk}}{m_{jj}{r}_{jj}{p}_{k\mid jj}},$$ (4)

where p_k|jk is the conditional probability that a man (a woman) completes college education if he (she) has a high school father (mother) and a college grandfather (grandmother). The social reproduction effect shows the compound effect of demography and mobility rather than the pure mobility effect, which can be defined as p_k|jk/p_k|jj.

The total social reproduction effect is the relative advantage of a college grandfather (grandmother) compared with a high school grandfather (grandmother) to produce college grandsons (granddaughters) unconditional on the parent’s education—that is,

$$\text{Total}{\mathit{SRE}}_{k\mid j}^{GP}=\sum _i{m}_k^{G1}{r}_k^{G1}{p}_{i\mid k}^{G2}{m}_{ik}^{G2}{r}_{ik}^{G2}{p}_{k\mid ik}^{G3}/\sum _i{m}_j^{G1}{r}_j^{G1}{p}_{i\mid j}^{G2}{m}_{ij}^{G2}{r}_{ij}^{G2}{p}_{k\mid ij}^{G3}.$$ (5)

Two-Sex Approach

The two-sex model incorporates marriages between pairs of adult males and females with varying levels of educational attainment, the mean number of surviving children born for each paternal-maternal educational combination, and educational mobility between parents and offspring.³ Relying on the framework of two-sex population renewal models (Caswell 2001; Goodman 1953; Keyfitz 1968; Pollak 1986, 1987, 1990), we specify the two-sex demographic model of social mobility for males and females as

$$D_{k\mid ij}={\mathrm{\mu }}^{ij}(F,M)·r_{ij}^d·p_{k\mid ij}^d$$ (6)

$$S_{k\mid ij}={\mathrm{\mu }}^{ij}(F,M)·r_{ij}^s·p_{k\mid ij}^s,$$ (7)

where D_k|ij (S_k|ij) denotes the number of daughters (sons) who are in education group k and have mothers in education group i and fathers in education group j; μ^ij(F, M) denotes the number of marriages between females in education group i and males in education group j; $r_{ij}^d\left(r_{ij}^s\right)$ denotes the mean number of surviving daughters (or sons) born to each union of women of education i and men of education j who have completed their childbearing; and $p_{k\mid ij}^d$ and $p_{k\mid ij}^s$ denote the probability of obtaining education group k for daughters and sons born to females of education i and males of education j, respectively. Differences between the $r_{ij}^d$ and $r_{ij}^s$ result from male to female sex ratio at birth and differential survival rates of daughters and sons to adulthood.

We adopt Schoen’s harmonic mean mating rule (Schoen 1981, 1988), which assumes a particular functional form for how the number of marriages between two social groups depends on the relative number of single women and men in these groups and the mutual attraction of members in these groups. The harmonic mean mating rule specifies that

$${\mathrm{\mu }}^{ij}(F,M)=\frac{{\mathrm{\alpha }}_{ij}{F}_i{M}_j}{F_i+M_j},{\mathrm{\alpha }}_{ij}>0,\sum _j{\mathrm{\alpha }}_{ij}\le 1\forall i,\sum _i{\mathrm{\alpha }}_{ij}\le 1\forall j,$$ (8)

where α_ij is the “force of attraction” between women in education group i and men in education group j as a result of mating opportunity constraints as well as mate preferences among all groups (Schoen 1988); F_i is the total number of eligible women in education group i; and M_j is eligible men in education group j. The parameter α_ij is estimated from the observed numbers of unions between men and women and single persons with those attributes (Qian and Preston 1993). The advantage of this function is that it incorporates constraints from the marriage market through the parameters of F_i and M_j and individual preferences through α_ij. A limitation of this function, however, is that it assumes no competition among education groups (the so-called zero spillover mating rule) (Pollak 1990).

Using the two-sex model, we can estimate the net social reproduction effects of parents analogous to those defined for the one-sex models. The net reproduction effect of parents is the advantage of college parents (assuming both parents are college graduates) relative to high school parents (assuming both parents are high school graduates) to produce college offspring given grandparents’ education fixed at high school—that is,

$$\mathit{Net}{\mathit{SRE}}_{k\mid j}^P=\frac{\frac{{\mathrm{\mu }}^{\mathit{kjj},\mathit{kjj}}(F,M)\left(r_{\mathit{kjj},\mathit{kjj}}^s{p}_{k\mid \mathit{kjj},\mathit{kjj}}^s+r_{\mathit{kjj},\mathit{kjj}}^s{p}_{k\mid \mathit{kjj},\mathit{kjj}}^d\right)}{M_{\mathit{kjj}}+F_{\mathit{kjj}}}}{\frac{{\mathrm{\mu }}^{\mathit{jjj},\mathit{jjj}}(F,M)\left(r_{\mathit{jjj},\mathit{jjj}}^s{p}_{k\mid \mathit{jjj},\mathit{jjj}}^s+p_{\mathit{jjj},\mathit{jjj}}^s{p}_{j\mid \mathit{jjj},\mathit{jjj}}^s\right)}{M_{\mathit{jjj}}+F_{\mathit{jjj}}}},$$ (9)

where μ_kjj, ^kjj(F, M) refers to the number of marriages between college-educated females and males whose parents are high school graduates; $r_{\mathit{kjj},\mathit{kjj}}^s(r_{\mathit{kjj},\mathit{kjj}}^d)$ refers to their number of sons (daughters); and $p_{k\mid \mathit{kjj},\mathit{kjj}}^s(p_{k\mid \mathit{kjj},\mathit{kjj}}^d)$ refers to the probability that their sons (daughters) complete college. Effects for educational heterogamous parents can be defined similarly by fixing the educational attainment of one parent and varying the attainment of the other.

We derive the net social reproduction effects of grandparents by incorporating grandparents’ educational characteristics into μ, r, and p. For example, if all grandparents and parents are educationally homogamous, the net effect is the relative advantage of a high school father and a high school mother with all four college grandparents relative to a high school father and a high school mother with all four high school grandparents to produce college offspring—that is,

$$\mathit{Net}{\mathit{SRE}}_{k\mid j}^{GP}=\frac{\frac{{\mathrm{\mu }}^{\mathit{jkk},\mathit{jkk}}(F,M)\left(r_{\mathit{jkk},\mathit{jkk}}^s{p}_{k\mid \mathit{jkk},\mathit{jkk}}^s+r_{\mathit{jkk},\mathit{jkk}}^d{p}_{k\mid \mathit{jkk},\mathit{jkk}}^d\right)}{M_{\mathit{jkk}}+F_{\mathit{jkk}}}}{\frac{{\mathrm{\mu }}^{\mathit{jjj},\mathit{jjj}}(F,M)\left(r_{\mathit{jjj},\mathit{jjj}}^s{p}_{k\mid \mathit{jjj},\mathit{jjj}}^s+r_{\mathit{jjj},\mathit{jjj}}^d{p}_{k\mid \mathit{jjj},\mathit{jjj}}^d\right)}{M_{\mathit{jjj}}+F_{\mathit{jjj}}}}.$$ (10)

Effects for educationally heterogamous grandparents may be defined by fixing the educational attainments of three grandparents and varying the attainment of one grandparent.

The total social reproduction effect of grandparents is the relative advantage of college grandparents (indexed by k) compared with high school grandparents (indexed by j) to produce college-educated grandchildren. We sum over the number of college grandchildren from parents with varying levels of education (indexed by a and b) conditional on grandparents’ education—that is,

$$\text{Total}{\mathit{SRE}}_{k\mid j}^{GP}=\frac{\frac{{\sum }_a{\sum }_b{\mathrm{\mu }}^{\mathit{akk},\mathit{bkk}}\left(F^{\prime },M^{\prime }\right)\left(r_{\mathit{akk},\mathit{bkk}}^s{p}_{k\mid \mathit{akk},\mathit{bkk}}^s+r_{\mathit{akk},\mathit{bkk}}^d{p}_{k\mid \mathit{akk},\mathit{bkk}}^d\right)}{{\sum }_a{F}_{\mathit{akk}}^{\prime }+{\sum }_b{M}_{\mathit{bkk}}^{\prime }}}{\frac{{\sum }_a{\sum }_b{\mathrm{\mu }}^{\mathit{ajj},\mathit{bjj}}\left(F^{″},M^{″}\right)\left(r_{\mathit{ajj},\mathit{bjj}}^s{p}_{k\mid \mathit{ajj},\mathit{bjj}}^s+r_{\mathit{ajj},\mathit{bjj}}^d{p}_{k\mid \mathit{ajj},\mathit{bjj}}^d\right)}{{\sum }_a{F}_{\mathit{ajj}}^{″}+{\sum }_b{M}_{\mathit{bjj}}^{″}},}$$ (11)

where $F^{\prime }={\mathrm{\mu }}^{kk}(F,M)r_{kk}^d{p}_{a\mid kk}^d,M^{\prime }={\mathrm{\mu }}^{kk}(F,M)r_{kk}^s{p}_{b\mid kk}^s,F^{″}={\mathrm{\mu }}^{jj}(F,M)r_{jj}^d{p}_{a\mid jj}^d$, and $M^{″}={\mathrm{\mu }}^{jj}(F,M)r_{jj}^s{p}_{b\mid jj}^s$ are estimated from marriage, net fertility, and mobility terms from previous generations.

Important special cases of this general unrestricted model include random mating, in which the expected number of marriages results only from the number of men and women at risk to various combinations of educational attainments (α_ij = α for all i, j), and endogamous mating, in which men and women marry only within their own education groups (α_ij = 0 if i ≠ j). A multigenerational version of the formula incorporates both parents and grandparents’ educational characteristics into the mating, fertility, and mobility rules.

Data and Measures

Because of its prospective design and long duration, the Panel Study of Income Dynamics (PSID) is uniquely well suited for our two-sex multigenerational analysis. Begun in 1968, the PSID was conducted annually until 1997 and biennially thereafter. All household members recruited into the PSID in 1968 are considered to carry the PSID “gene” and are targeted for the collection of detailed socioeconomic information and subsequent follow-up. Members of new households created by the offspring of original targeted household members retain the PSID gene themselves and become permanent PSID respondents.

To create our multigenerational sample, we first obtain a Family Identification Mapping System (FIMS)⁴ sample that links PSID respondents (G3) to their parents (G2) who are also PSID respondents. Based on the retrospective information from the family interview for household heads and their wives (G2), we obtain parental information for the grandparent generation (G1), who may not be PSID respondents. Therefore, we have information from all of the four biological grandparents of PSID respondents in G3.⁵

We create two analytical samples: a mobility sample and a marriage/fertility sample. The mobility sample includes education information of PSID sample members and their biological fathers, mothers, and all four grandparents. Individuals who grew up in single-parent families and have incomplete education information for one or several parents and grandparents are excluded from the analyses.⁶ We convert years of school completed into four categories (0–11, 12, 13–15, and 16+).

The marriage/fertility sample is generated from the PSID Marriage History File, which contains details about persons in PSID families at the time of the interview in any wave between 1985 and 2013 (PSID User Manual 2013). We merge the Marriage History File with the 1968–2013 Individual File to obtain educational attainments for individuals and their spouses. Some spouses, however, do not have follow-up records on the Individual File if they leave PSID households because they do not carry the PSID “gene.” In these cases, we rely on household head and wife information from the 1975–2013 Family File to find missing information on spouses. To give each individual in the marriage/fertility sample the same weight, we restrict our analyses to the first marriage of each individual.⁷ We measure individuals’ fertility by the number of live births, as recorded in the Individual File, which counts all children of an individual up to 2013. Because many individuals may have not finished their reproduction by 2013, we control for age group (25–35, 36–45, 46–55, and 56–65) in our fertility estimates to account for individuals’ varying years of exposure to fertility. The measure of an individual’s number of offspring may come from several spouses rather than solely from the spouse whom we include in the marriage data file.

We restrict our analytical samples to PSID grandchildren who were aged 25 to 65 in 2013, assuming that all such persons have finished their education by age 25 and childbearing by age 65.⁸ Our final mobility sample consists of 3,352 sons and 3,385 daughters as well as 6,737 families with nonmissing values on educational attainment for both parents and all four grandparents. Our marriage sample, which includes respondents who have nonmissing data on the educational attainment of both husband and wife, consists of 10,419 and 10,281 eligible males and females, respectively. We restrict the fertility sample to respondents who have complete educational information on spouse, both parents, and spouse’s parents, which yields a sample of 14,171 married couples.⁹

Short-Term Multigenerational Influences

We begin with one-sex analyses that examine mating, fertility, and mobility patterns for sons, fathers, and grandfathers (Table 1), and daughters, mothers, and grandmothers (Table 2), respectively. For all multigenerational models, we assume that the effects of parents’ and grandparents’ educational attainments on grandchildren are additive. We present results only from basic models that include grandparents’ and parents’ education and grandchildren’s age groups. These estimates are also used in our reported simulations. In analyses not reported here, we estimate models that include race, family size, and geographic location as well as interactions between these variables and grandparents’ and parents’ educational attainments. The results of these extra analyses yielded grandparent effects that are largely consistent with those from the basic models presented in this article.

Table 1.

One-sex multigenerational marriage, fertility, and mobility models: Men

Variable	Marriage		Marital Fertility		Mobility
	Ever Married (logit)		Children Ever Born (negative binomial)		Son’s Education (ordered logit)
	2-Generation	3-Generation	2-Generation	3-Generation	2-Generation	3-Generation
Men’s Education (ref. = 0–11)
12	0.397*** (0.071)	0.385*** (0.072)	−0.163*** (0.024)	−0.160*** (0.025)	--	--
13–15	0.579*** (0.080)	0.563*** (0.082)	−0.263*** (0.027)	−0.258*** (0.028)	--	--
16+	0.789*** (0.085)	0.770*** (0.090)	−0.343*** (0.028)	−0.337*** (0.030)	--	--
Father’s Education (ref. = 0–11)
12	--	0.068 (0.063)	--	−0.016 (0.020)	0.707*** (0.086)	0.619*** (0.087)
13–15	--	0.024 (0.083)	--	0.010 (0.028)	1.284*** (0.106)	1.111*** (0.109)
16+	--	0.059 (0.080)	--	−0.020 (0.027)	2.157*** (0.102)	1.991*** (0.105)
Paternal Grandfather (ref. = 0–11)
12	--	--	--	--	--	0.419*** (0.078)
13–15	--	--	--	--	--	0.389*** (0.117)
16+	--	--	--	--	--	0.691*** (0.110)
Age Group (ref. = 25–35)
36–45	1.297*** (0.071)	1.298*** (0.071)	0.196*** (0.033)	0.196*** (0.033)	--	--
46–55	1.470*** (0.064)	1.478*** (0.064)	0.173*** (0.031)	0.172*** (0.031)	--	--
56–65	2.277*** (0.077)	2.291*** (0.078)	0.327*** (0.030)	0.325*** (0.030)	--	--
Intercept	−0.457*** (0.075)	−0.488*** (0.081)	0.670*** (0.034)	0.675*** (0.034)	--
Cut Point 1	--	--	--	--	−1.222*** (0.075)	−1.129*** (0.077)
Cut Point 2	--	--	--	--	0.975*** (0.073)	1.088*** (0.075)
Cut Point 3	--	--	--	--	2.276*** (0.082)	2.405*** (0.084)
N	10,419	10,419	7,233	7,233	3,352	3,352
Log-Likelihood	−5,025.9	−5,025.3	−12,135.1	−12,134.3	−4,136.0	−4,107.6
Brant Test	--	--	--	--	7.43	11.83

Notes: A significant result from the Brant test indicates that the proportional odds assumption in the ordered logistic model is violated. Numbers in parentheses are robust standard errors.

Source: Panel Study of Income Dynamics, 1968–2013.

^***p < .001 (two-tailed tests)

Table 2.

One-sex multigenerational marriage, fertility, and mobility models: Women

Variable	Marriage		Marital Fertility		Mobility
	Ever Married (logit)		Children Ever Born (negative binomial)		Daughter’s Education (ordered logit)
	2-Generation	3-Generation	2-Generation	3-Generation	2-Generation	3-Generation
Women’s Education (ref. = 0–11)
12	0.477*** (0.079)	0.414*** (0.080)	−0.255*** (0.020)	−0.250*** (0.020)	--	--
13–15	0.691*** (0.087)	0.616*** (0.090)	−0.355*** (0.023)	−0.352*** (0.024)	--	--
16+	0.844*** (0.092)	0.781*** (0.099)	−0.522*** (0.025)	−0.518*** (0.027)	--	--
Mother’s Education (ref. = 0–11)
12	--	0.285*** (0.069)	--	−0.022 (0.018)	1.013*** (0.087)	0.864*** (0.089)
13–15	--	0.285*** (0.085)	--	0.008 (0.023)	1.683*** (0.102)	1.464*** (0.105)
16+	--	0.086 (0.093)	--	−0.011 (0.027)	2.722*** (0.122)	2.456*** (0.127)
Maternal Grandmother (ref. = 0–11)	--	--	--	--	--	--
12	--	--	--	--	--	0.496*** (0.076)
13–15	--	--	--	--	--	0.697*** (0.113)
16+	--	--	--	--	--	0.671*** (0.122)
Age Group (ref. = 25–35)
36–45	1.207*** (0.075)	1.207** (0.075)	0.112*** (0.028)	0.112*** (0.028)	--	--
46–55	1.596*** (0.069)	1.634*** (0.070)	0.105*** (0.025)	0.104*** (0.025)	--	--
56–65	2.178*** (0.083)	2.240*** (0.084)	0.141*** (0.025)	0.139*** (0.026)	--	--
Intercept	−0.296*** (0.083)	−0.433*** (0.089)	0.927*** (0.028)	0.933*** (0.029)	--	--
Cut Point 1	--	--	--	--	−1. (0.080) 415***	−1.303*** (0.081)
Cut Point 2	--	--	--	--	0.971*** (0.075)	1.111*** (0.077)
Cut Point 3	--	--	--	--	2.259*** (0.083)	2.420*** (0.085)
N	10,281	10,281	7,276	7,276	3,385	3,385
Log-Likelihood	−4,529.7	−4,518.7	−11,919.7	−11,918.7	−4,039.3	−4,002.9
Brant Test	--	--	--	--	15.3*	20.5

Notes: A significant result from the Brant test indicates that the proportional odds assumption in the ordered logistic model is violated. Numbers in parentheses are robust standard errors.

Source: Panel Study of Income Dynamics, 1968–2013.

^*p < .05;

^**p < .01;

^***p < .001 (two-tailed tests)

The marriage and fertility results in Tables 1 and 2 suggest that a person’s number of children and likelihood of getting married mostly depend on his or her own educational attainment. On average, individuals with higher education are more likely to marry than their low-education counterparts but tend to have lower fertility. The mobility results are consistent with Hertel and Groh-Samberg’s (2014) findings that grandfathers’ social class is directly associated with their grandsons’ socioeconomic attainment.¹⁰ Overall, the marriage, fertility, and mobility models suggest that the association between grandparents’ and grandchildren’s education results from both the direct influence of grandparents on grandchildren’s education and also the influence of grandparents on parents’ demographic behaviors. For example, mothers’ fertility may contribute to the relationship between grandmothers’ and grandchildren’s education.

We present two-sex assortative mating and fertility estimates in Tables 3 and 4. As discussed earlier, we account for differential marital rates and mating preferences for males and females by using the harmonic mean mating function. The parameter for the “force of attraction” (α_ij) represents the likelihood that men and women from two education groups will form unions. This value is a function of preferences between two education groups and constraints imposed by the sizes of the two groups. In Table 3, we present the estimates of α_ij for a two-generation model that takes into account only husband’s and wife’s individual characteristics. The results suggest that the strongest attraction exists between males and females with 16 or more years of schooling (α = .089) and between those with 12 years of schooling (α = .086). Among all the education pairs, the attraction force is the smallest between individuals with 16 or more years of schooling and those with less than 12 years of schooling (α = .004).¹¹

Table 3.

Two-sex assortative mating and force of attraction

Schooling, Men	Schooling, Women	Observed Assortative Mating
		No. of Eligible Males (age 25–65)	No. of Eligible Females (age 25–65)	No. of Eligible Male Person-Years (age 25–65)	No. of Eligible Female Person-Years (age 25–65)	No. of Marriages	Force of Attraction (αij)
0–11	0–11	1,651	1,485	19,528	13,760	473	0.059
	12	1,651	3,968	19,528	32,094	517	0.043
	13–15	1651	2,613	19,528	22,104	136	0.013
	16+	1,651	2,157	19,528	21,425	43	0.004
12	0–11	4,147	1,485	43,540	13,760	402	0.038
	12	4,147	3,968	43,540	32,094	1,591	0.086
	13–15	4,147	2,613	43,540	22,104	744	0.051
	16+	4,147	2,157	43,540	21,425	307	0.021
13–15	0–11	2,508	1,485	26,601	13,760	114	0.013
	12	2,508	3,968	26,601	32,094	627	0.043
	13–15	2,508	2,613	26,601	22,104	744	0.062
	16+	2,508	2,157	26,601	21,425	432	0.036
16+	0–11	1,990	1,485	21,874	13,760	38	0.004
	12	1,990	3,968	21,874	32,094	255	0.020
	13–15	1,990	2,613	21,874	22,104	402	0.037
	16+	1,990	2,157	21,874	21,425	960	0.089
Total	Total	10,296	10,223	111,543	89,383	7,782	––

Notes: The expected number of eligible person years = average age at marriage (for the married) × the number of married + (60–18) × the number of unmarried.

Source: Panel Study of Income Dynamics, 1968–2013.

Table 4.

Two-sex multigenerational marriage and fertility models for men and women

Variable	Marriage		Marriage		Marital Fertility
	Men Ever Married (logit)		Women Ever Married (logit)		Couples (negative binomial)
	2-Generation	3-Generation	2-Generation	3-Generation	2-Generation	3-Generation
Men’s Education (ref. = 0–11)
12	0.397*** (0.071)	0.383*** (0.073)	--	--	−0.106*** (0.017)	−0.102*** (0.018)
13–15	0.579*** (0.080)	0.565*** (0.082)	--	--	−0.154*** (0.020)	−0.150*** (0.021)
16+	0.789*** (0.085)	0.770*** (0.091)	--	--	−0.176*** (0.023)	−0.171*** (0.024)
Women’s Education (ref. = 0–11)
12	--	--	0.477*** (0.079)	0.403*** (0.081)	−0.177*** (0.018)	−0.175*** (0.018)
13–15	--	--	0.691*** (0.087)	0.600*** (0.090)	−0.219*** (0.021)	−0.220*** (0.021)
16+	--	--	0.844*** (0.092)	0.760*** (0.100)	−0.338*** (0.024)	−0.339*** (0.025)
Men’s Father (ref. = 0–11)
12	--	0.059 (0.068)	--	--	--	0.013 (0.016)
13–15	--	0.047 (0.088)	--	--	--	0.022 (0.022)
16+	--	0.069 (0.090)	--	--	--	0.022 (0.022)
Men’s Mother (ref = 0–11)
12	--	0.044 (0.070)	--	--	--	−0.026 (0.016)
13–15	--	−0.106 (0.084)	--	--	--	−0.046* (0.021)
16+	--	0.008 (0.097)	--	--	--	−0.024 (0.024)
Women’s Father (ref. = 0–11)
12	--	--	--	0.105 (0.074)	--	−0.027 (0.016)
13–15	--	--	--	0.147 (0.093)	--	−0.035 (0.021)
16+	--	--	--	0.121 (0.098)	--	−0.049* (0.022)
Women’s Mother (ref. = 0–11)
12	--	--	--	0.239** (0.076)	--	0.014 (0.016)
13–15	--	--	--	0.228* (0.092)	--	0.065** (0.021)
16+	--	--	--	0.023 (0.106)	--	0.036 (0.024)
Age Group (ref. = 25–35)
36–45	1.297*** (0.071)	1.296*** (0.071)	1.207*** (0.075)	1.209*** (0.075)	0.149*** (0.022)	0.149*** (0.022)
46–55	1.470*** (0.064)	1.473*** (0.065)	1.596*** (0.069)	1.648*** (0.071)	0.123*** (0.021)	0.122*** (0.021)
56–65	2.277*** (0.077)	2.285*** (0.079)	2.178*** (0.083)	2.260*** (0.085)	0.210*** (0.020)	0.209*** (0.021)
Intercept	−0.457*** (0.075)	−0.487*** (0.085)	−0.296*** (0.083)	−0.470*** (0.091)	0.881*** (0.025)	0.888*** (0.026)
N	10,419	10,419	10,281	10,281	14,171	14,171
Log-Likelihood	−5,025.9	−5,023.2	−4,529.7	−4,517.0	−23,479.7	−23,470.3

Notes: A significant result from the Brant test indicates that the proportional odds assumption in the ordered logistic model is violated. Numbers in parentheses are robust standard errors.

Source: Panel Study of Income Dynamics, 1968–2013.

^*p < .05;

^**p < .01;

^***p < .001 (two-tailed tests)

Table 4 shows marriage estimates from binary logistic models for men and women. The results are largely consistent with one-sex results presented in Tables 1 and 2, suggesting that men’s likelihood of getting married depends only on their own educational characteristics, whereas women’s likelihood is associated with both their own and their mothers’ educational attainments. The two-sex fertility model in Table 4 includes both a couple’s and all four of their parents’ educational characteristics as determinants of the couple’s fertility. The expected number of children for the 56–65 age group is approximately 3.0 (= e^{(0.210 + 0.881)}) for couples who both have education below high school and is only 1.8 (= e^{(−0.176 − 0.338 + 0.210 + 0.881)}) for husbands and wives who are in the highest education group. The coefficients suggest that wives’ education plays a slightly stronger role than husbands’ education in determining the couple’s total number of children. The three-generation results further show moderate association between the couple’s parents’ education and their total number of children after controlling for the couple’s education.

Finally, we show the two-sex educational mobility results from ordinal logistic regressions in Table 5. Unlike the one-sex mobility models presented in Tables 1 and 2, the two-sex models include both parents’ and all four grandparents’ educational characteristics. Our tests of differences between the two-generation and three-generation models (not shown here but available from the authors on request) indicate that grandparents’ education is still associated with their grandsons’ and granddaughters’ education, even after parents’ education is taken into account. The three-generation models with no constraints in Table 5 show net associations with each of the four grandparents. We test whether these associations differ among the four grandparents by fitting a variety of nested models. Our preferred models¹² show equal net associations of paternal and maternal grandparents’ educational attainments with grandchildren’s schooling but unequal associations for grandfathers and grandmothers. A possible explanation for this result is that grandfathers and grandmothers interact with their grandchildren in different ways: grandfathers may specialize in “task-oriented, instrumental family roles,” whereas grandmothers’ roles are more expressive, nurturing, and related to “kin-keeping” (Cherlin and Furstenberg 1986:123–127).

Table 5.

Two-sex multigenerational mobility models for men and women aged 25–65

Variable	Men			Women
	2-Generation	3-Generation	3-Generation (constraints)	2-Generation	3-Generation	3-Generation (constraints)
Father’s Education (ref. = 0–11)
12	0.454*** (0.091)	0.362*** (0.093)	0.362*** (0.093)	0.476*** (0.086)	0.366*** (0.089)	0.369*** (0.089)
13–15	0.869*** (0.113)	0.699*** (0.117)	0.701*** (0.116)	0.707*** (0.108)	0.527*** (0.110)	0.531*** (0.110)
16+	1.517*** (0.114)	1.330*** (0.118)	1.327*** (0.131)	1.416*** (0.115)	1.223*** (0.119)	1.219*** (0.118)
Mother’s Education (ref. = 0–11)
12	0.644*** (0.097)	0.556*** (0.099)	0.553*** (0.099)	0.750*** (0.092)	0.609*** (0.095)	0.611*** (0.095)
13–15	0.956*** (0.117)	0.819*** (0.119)	0.820*** (0.119)	1.193*** (0.112)	0.980*** (0.115)	0.981*** (0.115)
16+	1.590*** (0.129)	1.412*** (0.131)	1.410*** (0.130)	2.008*** (0.134)	1.753*** (0.140)	1.755*** (0.139)
Paternal Grandfather (ref. = 0–11)
12	--	0.206* (0.090)	0.143* (0.061)	--	0.101 (0.092)	0.049 (0.062)
13–15	--	0.138 (0.126)	0.198* (0.088)	--	0.130 (0.127)	0.087 (0.093)
16+	--	0.399** (0.128)	0.392*** (0.086)	--	0.396** (0.127)	0.307*** (0.088)
Paternal Grandmother (ref. = 0–11)
12	--	0.124 (0.086)	0.154** (0.059)	--	0.263** (0.088)	0.277*** (0.059)
13–15	--	0.106 (0.118)	0.091 (0.079)	--	0.371** (0.123)	0.447*** (0.084)
16+	--	0.187 (0.142)	0.206* (0.095)	--	0.138 (0.134)	0.200* (0.097)
Maternal grandfather (ref: 0–11)
12	--	0.082 (0.091)	0.143* (0.061)	--	0.002 (0.090)	0.049 (0.062)
13–15	--	0.257* (0.125)	0.198* (0.088)	--	0.039 (0.131)	0.087 (0.093)
16+	--	0.392** (0.124)	0.392*** (0.086)	--	0.210 (0.136)	0.307*** (0.088)
Maternal Grandmother (ref. = 0–11)
12	--	0.182* (0.089)	0.154** (0.059)	--	0.294*** (0.088)	0.277*** (0.059)
13–15	--	0.069 (0.115)	0.091 (0.079)	--	0.519*** (0.122)	0.447*** (0.084)
16+	--	0.216 (0.137)	0.206* (0.095)	--	0.269 (0.149)	0.200* (0.097)
Cut Point 1	−0.856*** (0.089)	−0.735*** (0.091)	−0.733*** (0.090)	−1.228*** (0.086)	−1.109*** (0.087)	−1.106*** (0.087)
Cut Point 2	1.414*** (0.092)	1.563*** (0.094)	1.563*** (0.094)	1.208*** (0.083)	1.360*** (0.085)	1.363*** (0.085)
Cut Point 3	2.765*** (0.100)	2.935*** (0.104)	2.935*** (0.103)	2.547*** (0.092)	2.725*** (0.094)	2.727*** (0.094)
N	3,352	3,352	3,352	3,385	3,385	3,385
Log-Likelihood	−4,047.9	−4,012.4	−4,013.5	−3,958.6	−3,913.5	−3,914.2
Brant Test	13.9	37.2	37.2	20.9	41.7	41.7

Notes: A significant result from the Brant test indicates that the proportional odds assumption in the ordered logistic model is violated. Numbers in parentheses are robust standard errors.

Source: Panel Study of Income Dynamics, 1968–2013.

^*p < .05;

^**p < .01;

^***p < .001 (two-tailed tests)

Based on the coefficients of parents’ and grandparents’ education from the marriage, fertility, and intergenerational educational mobility models, we estimate the net and total social reproduction effects of parents and grandparents in Table 6 by comparing the college and the high school subgroups. The mobility probability ratios in the last column show that individuals are more likely to obtain a college degree if both of their parents are college graduates. The ratio of the probability of finishing college by having college-educated parents rather than high school–educated parents is 2.94. In addition, having all four grandparents as college graduates makes individuals 1.4 times more likely than those without any college grandparents to graduate from college, and only 1.2 and 1.1 times more likely if a person has only either a paternal grandfather or maternal grandmother respectively with a college education.

Table 6.

Short-term net and total social reproduction effects

	Social Reproduction Effect		Mobility Probability Ratios
	Net Effect	Total Effect
Parents
One-sex (father)	2.132	2.132	2.448
One-sex (mother)	1.917	1.917	2.468
Two-sex	1.063	1.063	2.943
Grandparents
One-sex (grandfather)	1.123	1.307	1.234
One-sex (grandmother)	1.129	1.088	1.135
Two-sex	0.438	0.674	1.410

Notes: For the net social reproduction effect, we compare parents (or grandparents) who are college graduates with those who are high school graduates in producing college offspring (or grandchildren). For the total effect of grandparents, we compare grandparents who are college graduates with those who are high school graduates in producing college grandchildren. For the mobility probability ratios, we calculate the ratio between the probability of finishing college by having college parents rather than high school parents (or college grandparents and high school parents versus high school grandparents and parents). These figures are calculated based on Eqs. (3), (4), (5), (9), (10), and (11).

Source: Panel Study of Income Dynamics, 1968–2013.

The net social reproduction effects of parents are smaller than the mobility probability ratios because education is negatively associated with the probability of marriage and the level of fertility, especially when both fathers’ and mothers’ educational levels are taken into account. The one-sex model suggests that a college father produces 2.1 times as many college-educated sons as a high school father, whereas the two-sex model further suggests that a couple who both have college degrees produces 1.1 times as many college offspring as a couple with only high school diplomas.

In addition, the net and total social reproduction effects of grandparents are smaller than those of parents. The grandfather net effect from one-sex models suggests that a college-educated grandfather and a high school–educated father produce 10 % more college sons than a high school–educated grandfather and a high school–educated father. A college-educated grandfather produces 30 % more college-educated grandsons than a high school–educated grandfather in total. The effect becomes 0.44 in two-sex models, suggesting that a high school–educated couple with all four parents as college graduates produces fewer college-educated offspring than a high school–educated couple with all four parents as high school graduates. The main reason for this result is that the probability of union formation between a high school–educated man with college-educated parents and a high school–educated woman with college-educated parents is smaller than that between a high school–educated man with high school–educated parents and a high school–educated woman with high school–educated parents.¹³ For the same reason, two college couples produce only 0.67 times as many college-educated grandchildren as two high school–educated couples.

Long-Term Multigenerational Influences

The short-term mechanisms in the transmission of educational advantages in three generations also have implications for the long-term educational reproduction of families. We use the eventual advantages of high-education families in producing high-education progeny compared with those of low-education families as an example to show such a long-term trend. If a family has at least one parent holding a college degree, compared with another family in which neither parent holds a college degree, what are the differences in the number of progeny in subsequent generations who themselves have college degrees? Our long-term analysis relies on the marriage, fertility, and mobility rules described in the Methods section and the parameters estimated from the short-term analyses presented in Tables 1, 2, 3, 4, and 5. We simulate the educational distribution of families by generations and explore the evolution of educational reproduction of college- and non-college-origin families before the simulation system achieves its equilibrium.

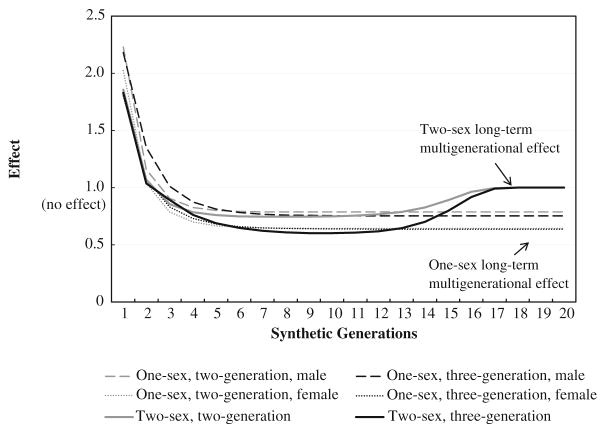
Figure 1 presents simulation results based on one-sex and two-sex approaches for both two-generation and three-generation models of short-term effects. We first allow for patterns of differential marriage and net fertility in the one-sex simulations before incorporating assortative mating in the two-sex simulations. The gray dashed and dotted lines represent the one-sex, two-generation multigenerational effects for males and females, respectively. All solid lines represent results from two-sex models. All the black lines represent results that incorporate grandparent effects in the mating, fertility, and mobility rules. We focus on the relative educational reproductive success of college-origin over non-college-origin families as defined by the ratio of college progeny per college family to college progeny per non-college-origin family. A value more than 1 means that college-origin families produce more college descendants than non-college-origin families. As discussed earlier, because of the negative relationship between education and fertility, educational advantages for the progeny of college families may be offset by their lower fertility.

Fig. 1.

Multigenerational reproduction of college education. We define the effect as the ratio of college progeny per college family over college progeny per non-college family. The ratio = 1 means no multigen-erational effect

Figure 1 reveals four principal findings. First, within the first three generations, families that start with college education produce more college descendants than families that start with non-college education: the values of the ratio for all the lines stay above 1. This result implies that for first-generation college families, the achievement of going to college not only changes the educational outcomes of the present generation but also may benefit as many as three generations ahead. Second, the ratio from the one-sex models falls below 1.0 and converges to a value between 0.6 and 1.0 over the next 5 to 10 generations, depending on the model, meaning that fertility disadvantages of college-origin families offset their initial educational mobility advantages, and eventually college-origin families produce fewer college-educated descendants than noncollege families. Thus, the effect of being in the higher education group is negative over the longer term because the lower fertility of this group more than offsets the mobility advantages that this group can provide for its offspring in the short term. Third, a comparison of the gray lines with the black lines shows that the long-run educational reproduction of families depends on whether the mating, fertility, and mobility processes are Markovian (only parents matter) or non-Markovian (both parents and grandparents matter). Under a three-generation model (black lines), the ratio converges to the equilibrium more slowly and reaches a lower value than under a two-generation model. For example, for the one-sex male models, the ratio declines from 0.8 in a two-generation model to 0.75 in a three-generation model. This result suggests that when both parents and grandparents are involved in the educational reproduction of families, educational inequality between college and non-college families is greater than when only parents are involved. Moreover, this inequality is even greater when all four grandparents (the black solid line), rather than only one grandparent (the black dashed and dotted lines), are considered. Finally, the two-sex results gradually converge to an equilibrium ratio equal to 1, a value that indicates no long-term relative educational reproduction advantages among families after roughly 17 generations. Therefore, the multigenerational influences caused by a family’s initial educational status and fertility persist for a finite albeit large number of generations rather than stabilizing at a level that reflects net fertility differences among education groups.

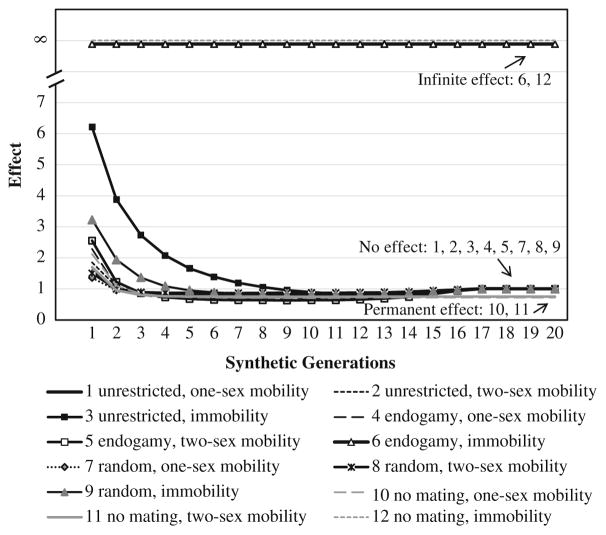
The equilibrium results point to very different conclusions about long-term effects of socioeconomic differences among families, depending on whether one adopts a one-sex or two-sex model. To investigate the differences between the two approaches, we simulate a combination of one-sex and two-sex mating and mobility models (Table 7). For the one-sex mating model, we assume no marriage market effects—that is, that the number of marriages is strictly determined by the number and preferences of either males or females but not the interaction of the male and female populations. For the two-sex mating models, we assume three alternative mating rules as described earlier: unrestricted, endogamous, and random mating. For educational mobility, we distinguish between models assuming immobility (in which individuals inherit their same-sex parent’s educational status) and models assuming mobility (in which individuals’ education may differ from their parents’ education). We further divide the latter into one-sex and two-sex mobility models. The one-sex mobility model assumes that parents influence only offspring of the same sex, whereas the two-sex model assumes that parents influence offspring of both sexes. These combinations of assumptions make up Scenarios 1–12, as summarized at the bottom of Fig. 2. The one-sex and two-sex models shown in Fig. 1 refer to Scenarios 10 and 2, respectively, which assume that both mating and mobility follow either one-sex or two-sex rules.

Table 7.

Hypothetical long-term mating and mobility rules (with differential fertility)

	Mating Rule	Mobility
		Yes		No
		One-Sex Same-Sex Parent	Two-Sex	One-Sex Same-Sex Parent
Two-Sex	Unrestricted	1	2	3
	Endogamous	4	5	6
One-Sex	Random	7	8	9
	No mating	10	11	12

Notes: We also experimented with mobility patterns in which both sons and daughters were influenced by their fathers. The results were the same as those from the one-sex mobility, in which sons and daughters are only influenced by the same-sex parent.

Fig. 2.

Multigenerational reproduction of college education based on various scenarios of mating and mobility rules. We define the effect as the ratio of college progeny per college family over college progeny per non-college family

Figure 2 shows that except for Scenarios 6 and 12, all models that take into account two-sex mating rules indicate a decay of long-term educational disparity among families, whereas all one-sex models without any mating rules indicate a permanent disparity between families. In all two-sex scenarios except Scenario 6, high- and low-education–origin families are connected because the mating rules allow marriages formed between progeny from families of different educational origins. In Scenarios 4 and 5, when only endogamy is allowed, intermarriages between high-education and low-education families can still occur through mobility—for example, progeny born into low-education families achieve upward mobility and marry those from high-education families. In Scenario 6, marriages between high- and low-education–origin families never occur given that their progeny always marry within their own education groups, and intergenerational immobility precludes any intermarriage that occurs as a result of mobility. Therefore, in the presence of intermarriage, whether explicitly permitted by the marriage rule (Scenarios 1, 2, 3, 7, 8, and 9) or in subsequent generations as a result of intergenerational mobility (Scenarios 4 and 5), more and more progeny in later generations carry both high-education and low-education ancestry in their background. Over generations, an increasing proportion of high-education families have low-education descendants who are also descendants of low-education families, and vice versa. Such a pattern illustrates Bernheim and Bagwell’s (1988) argument that intermarriage makes independent, persistent family dynasties demographically impossible. The educational distributions of progeny of high- and low-education families become increasingly alike over generations, implying that the educational disparities among families eventually disappear.

Although the two-sex approach allows for a more complete set of demographic mechanisms than the one-sex approach, the two-sex approach is not always superior to the one-sex approach. The one-sex approach is still useful when the transmission of education and other social characteristics are sex linked. For example, social positions in the patriarchal societies during China’s historical dynasties (Lee and Campbell 1997; Lee and Wang 1999; Mare and Song 2014) and the priest status in the ancient Jewish population (Goldstein 2008) were inherited only through male lines. This is analogous to the inheritance of the human Y chromosome, which can be passed down only from paternal grandfathers to fathers and then to sons. Although marriages connect family lineages—in effect, creating progeny as social descendants of both their paternal and maternal families—their sex-linked characteristics are still uniquely linked to their paternal families. When comparing descendants who carry the sex-linked characteristics from families with and without such characteristics, we need to count only male descendants in the male line, not all social descendants in both lines. The one-sex model is enough to explain the evolution of inequality in the distribution of sex-linked characteristics between the two groups of families. In other words, the two-sex approach is not simply an extension of the one-sex approach. The two models imply different institutional frameworks and underlying social processes with regard to the inheritance of social status and the family connections formed by marriage.

Conclusion

Our analyses of families’ educational reproduction in the United States yield two main findings. First, in our analysis of short-term multigenerational effects, a two-sex approach provides a more nuanced summary of the influences of grandparents’ educational attainments on their grandchildren’s education. Mothers, grandmothers, and maternal grandparents may influence grandchildren’s educational outcomes, even when paternal and paternal grandparent characteristics are controlled. Furthermore, models that incorporate demographic behaviors of parents suggest that grandparents also influence grandchildren’s education by influencing whether and whom the parents marry and how many children they have. Although these estimates of the grandparent effects may be subject to measurement errors and omitted variable biases (Behrman and Taubman 1985), they are still indicative of associations in socioeconomic statuses within families across generations.

Our analysis of long-term effects shows the circumstances in which social inequality in a given generation may have a much more sustained impact than usually recognized in mobility research. One-sex and two-sex approaches show similar trends within the first several generations,¹⁴ suggesting that the initial educational advantages of families may benefit as many as three generations ahead, but such advantages are later offset by a negative fertility gradient with educational attainment. In this way, differential fertility and social mobility may jointly shape future educational distributions of progeny. In the long run, the one-sex approach implies that differential fertility creates permanent differences between high-education and low-education families, whereas the two-sex approach implies that all families eventually achieve the same educational distribution of descendants. The two-sex model shows that the mixing of socioeconomic backgrounds created by intermarriage between high- and low-education persons tends to offset any short-term patterns of socioeconomic status persistence across generations.

Along with several other studies (Lam 1986; Maralani 2013; Mare 1997; Mare and Maralani 2006; Matras 1961, 1967; Preston 1974), we illustrate that demography plays an important role in creating and changing intergenerational inequality. The transmission of intergenerational inequality involves not only the inequality among those who have offspring but also the inequality between those who have offspring and those who do not. Such a conclusion does not depend on whether grandparents have a direct effect on their grandchildren’s social attainment. Even if social mobility is Markovian, the effect of demography becomes cumulative over generations. The joint role of demography and mobility determines the socioeconomic reproduction of families and the social metabolism of a society.

Our analyses also link short-term mobility and demographic behaviors with the long-term educational reproductive success of families. Whereas the short-term results suggest considerable inequality in mobility opportunities in each generation, the long-term results show an equalizing trend in educational outcomes across families. The demographic behaviors we consider in this study include only assortative mating and differential marriage and fertility, but future research may consider more complex demographic strategies of families, including the duration of marriage; ages of parents at childbearing; generation gaps between grandparents, parents, and grandchildren; childhood family structure of each generation; and the periods of observations.

The analyses shown in this article apply to a single country in a single historical epoch. They focus on only a single dimension of socioeconomic achievement—educational attainment—measured dichotomously. They use multivariate models that include a modest list of individual- and family-level variables, short of the state of the art in studies that focus purely on two-generation relationships with no attention to demographic processes or in studies that focus on a single demographic outcome rather than its interdependence with social mobility. They do not address problems of causal inference, which attempt to isolate true multigenerational effects (rather than descriptive associations that may be spurious in a rigorous causal analysis). Although the grandparent effects shown in our analysis may not be causal, they provide important descriptive information of three-generation social mobility pattern and suggest a long-term mobility trend that does not depend on having a rigorous model but whether to take a one- or two-sex approach. Because of data limitations, we also primarily focus on children in traditional two-parent families, overlooking potentially unequal grandparent influences between single- and two-parent families. And it is beyond the scope of this article to specify the circumstances under which analysts should focus exclusively on what we term “short-term” effects, when they should go several generations beyond the observation span of their data, when they should examine the implied equilibrium distributions from a short-term model, and when they should consider specific historical effects that may disrupt the intergenerational trajectories implied by ahistorical models alone.

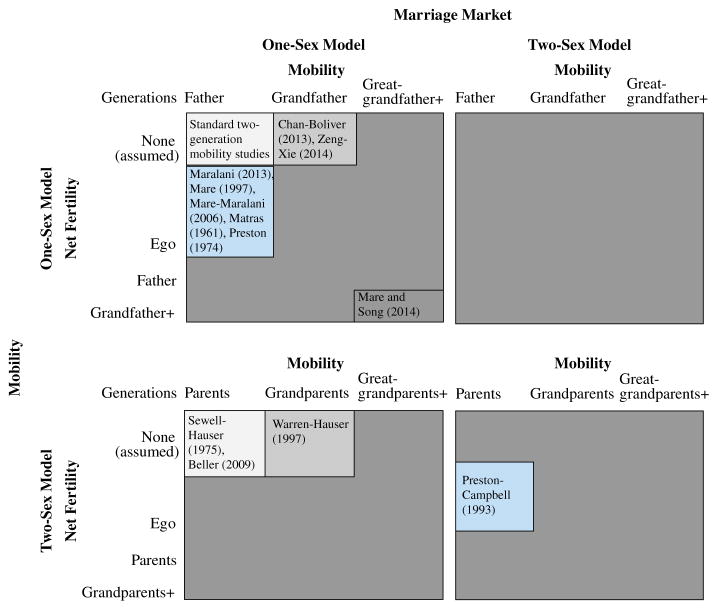
Despite these limitations, our work provides valuable descriptive associations in educational status in multiple generations. Our analyses illustrate a wide variety of possible processes through which educational inequalities among persons in one generation may persist or change in subsequent generations. The full set of possible types of social mobility analyses is shown in Fig. 3. The intergenerational transmission of socioeconomic advantage may be exclusively through a direct connection between parents and offspring or, additionally, through other more remote kin, such as grandparents, who may exert their effects across more than one generation. Intergenerational mobility may be essentially a one-sex process through which family advantages are embodied in the standing of just one parent or, alternatively, both parents may have independent effects on their children (and possibly grandchildren as well). Intergenerational social mobility may be considered in isolation from demographic processes, especially fertility and mortality, or in combination with these processes. Finally, we may regard the male and female populations as reproducing independently via their respective one-sex marriage markets, or as interacting populations that constrain each other and, through assortative marriage, modify the distributions of family socioeconomic positions in successive generations. The exemplary studies cited in the taxonomy in Fig. 3 show that most research has focused on relatively simple processes and much remains to be learned about multigenerational and demographic processes governing social mobility.

Fig. 3.

Taxonomy of multigenerational effects