Theory of Partitioning of Disease Prevalence and Mortality in Observational Data

Abstract

In this study, we present a new theory of partitioning of disease prevalence and incidence-based mortality and demonstrate how this theory practically works for analyses of Medicare data. In the theory, the prevalence of a disease and incidence-based mortality are modeled in terms of disease incidence and survival after diagnosis supplemented by information on disease prevalence at the initial age and year available in a dataset. Partitioning of the trends of prevalence and mortality is calculated with minimal assumptions. The resulting expressions for the components of the trends are given by continuous functions of data. The estimator is consistent and stable. The developed methodology is applied for data on type 2 diabetes using individual records from a nationally representative 5% sample of Medicare beneficiaries age 65+. Numerical estimates show excellent concordance between empirical estimates and theoretical predictions. Evaluated partitioning model showed that both prevalence and mortality increase with time. The primary driving factors of the observed prevalence increase are improved survival and increased prevalence at age 65. The increase in diabetes-related mortality is driven by increased prevalence and unobserved trends in time-periods and age-groups outside of the range of the data used in the study. Finally, the properties of the new estimator, possible statistical and systematical uncertainties, and future practical applications of this methodology in epidemiology, demography, public health and health forecasting are discussed.

1. Introduction

Prevalence is an epidemiologic characteristic which is easily measured using survey data or medical records. Analyses of prevalence trends play an influential role in health policy planning and are widely used to assess the extent to which a given health problem affects the population. However, conclusions about the relative success or failure of a health policy change cannot be made directly from trends of disease prevalence because temporal changes in age-adjusted prevalence rates are the result of two simultaneously occurring competing processes: i) changes in incidence and ii) changes in survival. Health interventions and disease treatment guidelines are usually aimed at decreasing the incidence and increasing the survival rate for a disease. If successful, these measures will push the observed prevalence in different directions. A related quantity of interest is the mortality rate by cause or more generally, the mortality for individuals after the onset of a specific disease. This is also known as the incidence-based mortality rate(Chu et al. 1994). The time trend of incidence-based mortality (Mozaffarian et al. 2016; Smith et al. 2013; Thun et al. 2013) is defined by the same factors that define the time trends in the disease prevalence rate, as well as trends in mortality in the general population. In contrast to disease prevalence, improvements in incidence and survival push the observed incidence-based mortality for a specific disease in the same direction, because improved incidence reduces the total number of people with the disease and improved survival further reduces the number of deaths associated with the disease.

In this paper, we develop a new methodological approach for the decomposition of trends in disease prevalence and incidence-based mortality into their constituent components (such as trends in incidence, survival, and prevalence prior to observation) and for the evaluation of the strength and the direction of the contribution of each respective component. The methodology described in this study offers a number of distinct strengths: i) computation of disease prevalence and incidence-based mortality as well as their partitioning through a set of exact formulas without making simplifying assumptions, ii) evaluation of the individual contributions of each component to the total time trend by direct calculation using exact formulas applied to real data, iii) a set of natural generalizations including applications to medical costs, complications of a specific disease, the incorporation of disease risk factors and the use of the historical trends of each of the model components beyond the region directly measured in data.

The only previously existing methodological approach of this type was developed by Tunstall-Pedoe for the partitioning of mortality trends through the use of an approximate formula for the simple decomposition of the annual percent change (APC) for mortality as a sum of APC’s of cardiovascular disease incidence and case fatality (percentage of 28-day fatalities)(Tunstall-Pedoe et al. 1999). This approximation is valid only for events (disease onset and death) occurring within a short time of each other and requires that the APC be small and the disease of interest be the primary cause of death. Other methods of decomposition used in demography and epidemiology (see refs.(Canudas-Romo 2003; Horiuchi, Wilmoth and Pletcher 2008; Vaupel and Romo 2003) for a comprehensive review) are not related to the decomposition of prevalence into its constituent components.

Although the primary focus of this paper is to introduce the methodology and describe the mathematics involved in its execution, an example involving type 2 diabetes mellitus is also considered. The application of the methodology to disease prevalence and mortality is intended to address an aspect of a current Public Health problem—with some notable exceptions such as cardiovascular disease (Will, Yuan and Ford 2014), the prevalence rate of many chronic diseases including diabetes has been increasing with time (Akinbami et al. 2012; Bauer et al. 2014; Coresh et al. 2007; Egan, Zhao and Axon 2010). Understanding the contribution each individual component makes to the overall effect on disease prevalence and mortality and how these contributions have changed over time in response to changes in health policy, population age-structure and epidemiologic characteristics could be of great use in identifying likely targets for pro-active policy interventions.

2. Theory

2.1 Mathematical formalism

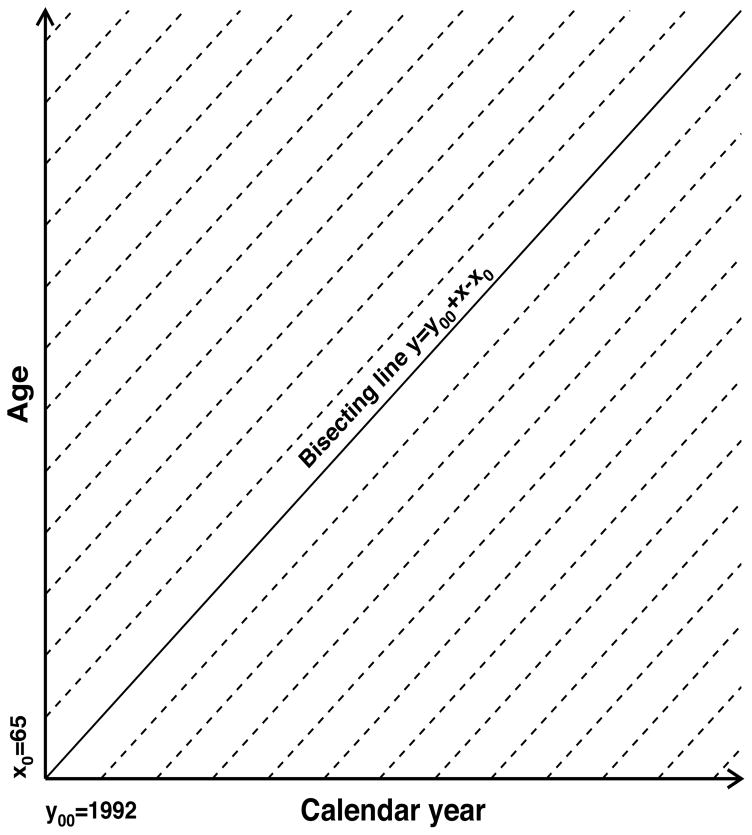
Data collected in an observational study represent information on eligible individuals over given periods of age and time. In this study, we use a nationally representative 5% sample of the U.S. Medicare population provided for research as restricted access public use files by the Centers for Medicare and Medicaid Services. This database provides individual heath related information on U.S. Medicare beneficiaries after age 65 from 1991 to 2013. The long time period and level of detail provided by such data allow us to calculate disease prevalence and mortality at any point after a certain look-back period (12 months is used in this study) necessary to collect individual information for evaluation of disease presence. Figure 1 presents the Lexis diagram in the plane over age (in years; denoted by x) and calendar time (in years; denoted by y). Each of the dashed lines in the Lexis diagram uniquely corresponds to a birth cohort with the birth time y_b =y−x for any point (x,y) belonging to the cohort-specific dashed line. Therefore, epidemiologic characteristics at a given point of time are defined by the history of the cohort represented by a leftward move along the respective line in the Lexis diagram down to bounds of the available region. The bound is defined by an initial year (y₀₀) or minimal age (x₀) observed in the data. These two subareas are separated by the bisecting line defined as y=y₀₀+x− x₀. Above the bisecting line, the starting point is defined by the initial conditions y=y₀₀ with various ages while below the line the initial point is defined by boundary condition x=x₀ with various years. The cohort-specific bounding point is defined as x̄₀ = max(x₀, y₀₀ − y_b) and ȳ₀= y_b+ x̄₀. Definitions of ages and times as well as functions of survival analyses used in the paper are collected in Table 1.

Fig. 1.

The two dimensional diagram (Lexis diagram) to show the age-time area in which data are available and represent events (such as disease onset or deaths) that occur to individuals belonging to different cohorts. Calendar time is represented on the horizontal axis, while age is represented on the vertical axis. Dashed lines show time/age points for specific cohorts. Information about a cohort is available starting from bounding lines, i.e., either y₀₀ = 1992 or x₀ = 65. Calculation of age-adjusted rates for a specific time requires integration over all ages starting from x₀, so regions both below and above bisecting line contribute to the integral for any y > y₀₀.

Table 1.

Summary of Mathematical Functions

Ages and calendar times used as arguments in the survival functions
x	Current age in years	y	Current (calendar) time in years
x0	Minimal age observed in data (see Figure 1)	y00	Initial time in data (see Figure 1)
x̄0 = max(x0, y00 − yb)	The cohort-specific bounding (minimal) age	ȳ0 = yb + x̄0	The cohort-specific bounding (minimal) time
τ, x̄0 < τ ≤ x	Age at diagnosis	yd = y − x + τ	Time of diagnosis
x00 = y00 − y + x	The cohort specific age at y00	y0 = y − x + x0	The cohort-specific time of reaching age x0
		yb = y − x	Time of birth for a cohort
Survival analysis functions for age-specific prevalence and mortality
Pc(x, yb)		Probability of being prevalent at age x in cohort with birth time yb
Ic(τ, yb)		Incidence density function for birth cohort yb. The normalization rule for the density is ${\int }_{{\overline{x}}_0}^{\infty }{I}_c(\tau ,y_b)d\tau =1$
Mc(x, yb)		Mortality density function for birth cohort yb. The normalization rule for the density is ${\int }_{{\overline{x}}_0}^{\infty }{M}_c(x,y_b)dx=1$
$\begin{array}{c}\overline{S}(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)\\ {\overline{f}}_c(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)=-{\overline{S}}_x^{\prime }(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)\end{array}$		Survival function and respective density function of a patient group formed at age x̄0 and time ȳ0, diagnosed before x̄0, and survived to x (i.e., living x − x̄0 years after cohort forming)
$\begin{array}{c}S(x-\tau ,\tau ,y_d)\\ f_c(x-\tau ,\tau ,y_d)=-S_x^{\prime }(x-\tau ,\tau ,y_d)\end{array}$		Survival function and respective density function of a patient group diagnosed at age τ and time yd, and survived to x (i.e., living x − τ years after cohort forming)
St(x − τ, τ, yd) and μ(x, y)		Survival function and respective mortality hazard function in the general population for the cohort formed at age τ and yd, i.e., St(0, τ, yd) = 1.
Survival analysis functions for age-adjusted prevalence and mortality
P(x, y)		Prevalence at age x and time y
I(x, y)		Incidence hazard function at age x and time y
M(x, y)		Incidence based mortality hazard function at age x and time y
P(y)		Age-adjusted prevalence at time y
M(y)		Age-adjusted Incidence-based mortality hazard function at time y
$\begin{array}{c}{S}^r(x-\tau ,\tau ,y_d)\\ f^r(x-\tau ,\tau ,y_d)=-S_x^{r^{\prime }}(x-\tau ,\tau ,y_d)\end{array}$		Relative survival and respective density function of a patient group diagnosed at age τ and year yd, and reached age x (i.e., living x − τ years after diagnosis and cohort forming)
$\begin{array}{c}{\overline{S}}^r(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)\\ {\overline{f}}^r(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)=-{\overline{S}}_x^{r^{\prime }}(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)\end{array}$		Relative survival and respective density function of a patient group function of a patient group formed at age x̄0 and time ȳ0, diagnosed before x̄0, and survived to age x (i.e., living x − x̄0 years after cohort forming)
p(x)		the density of age distribution in a standard year
T(y) and T̂(y)		Specific contributions to the time trends of age-adjusted disease prevalence and incidence-based mortality (discussed in detail in Interpretation of partitioning components)

The idea for the representation of the formulas for prevalence is based on that the probability of being prevalent P_c(x, y_b) at age x in cohort c with birth time y_b requires either

1. being prevalent (represented by initial prevalence P_c(x̄₀, y_b)) in the initial age x̄₀ (and year ȳ₀) for the cohort and surviving to age x (represented by the survival probability S̄(x − x̄₀, x̄₀, ȳ₀) of a patient diagnosed no later than x̄₀), or

2. being incident at an earlier age τ, x̄₀ < τ ≤ x (represented by incidence density function I_c(τ, y_b)) and having survival longer than x − τ (represented by survival probability S(x−τ, τ, y_d) of a patient diagnosed at age τ and year y_d).

Therefore

$$P_c(x,y_b)=P_c({\overline{x}}_0,y_b)\overline{S}(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)+{\int }_{{\overline{x}}_0}^x{I}_c(\tau ,Y_b)S(x-\tau ,\tau ,y_d)d\tau$$ (1)

where we integrate over all possible ages at diagnosis. Similarly, for mortality (we consider incidence-based mortality, i.e., mortality after disease onset) the probability of dying in the age interval (x,x +dx) requires having death in the interval (x,x + dx) and either being prevalent at the boundary point (x̄₀,ȳ₀) for this cohort or being incident at an earlier age x − τ. Death is represented by a respective density function M_c(x, y_b) such that

$$M_c(x,y_b)=P_c({\overline{x}}_0,y_b){\overline{f}}_c(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)+{\int }_{{\overline{x}}_0}^x{I}_c(\tau ,y_b)f_c(x-\tau ,\tau ,y_d)d\tau$$ (2)

The densities f̄_c (x−x̄₀, x̄₀, ȳ₀) and f_c (x−τ, τ, y_d) in (2) are related to respective survival functions in (1): ${\overline{f}}_c()=-{\overline{S}}_c^{\prime }()$ and $f_c()=-S_c^{\prime }()$, where derivatives are taken in respect to the first argument. Details of derivation of eqs. (1) and (2) and some properties of the contributed functions are given in Appendix A.

The exact definition of P_c(x, y_b) is the fraction of individuals born in year y_b and living with the disease at age x of the total number of individuals born in year y_b. Similarly, I_c(τ, y_b) and M_c(x, y_b) are the cohort incidence and mortality densities defined through the number of new incident and death cases per cohort size (i.e., the number of individuals born in year y_b). However, the cohort size for the studied population is not usually known with sufficient accuracy. What is known (or can be estimated) is the current population at risk i.e., the population currently living in the same age and calendar year (denoted as y = y_b + x) or calendar year of diagnosis (denoted as y_d = y_b + τ). Therefore, we avoid dealing with cohort prevalence and incidence/mortality densities and use their standard definitions involving the population at risk rather than birth cohort size. Within these definitions, the cohort prevalence and incidence/mortality densities are expressed through accepted definitions of prevalence and hazard functions of incidence and mortality: P_c(x, y_b) = P(x, y)S_t(x, 0, y_b), M_c(x, y_b) = M(x, y_d) S_t (x,0, y_b), and I_c(τ, y_b) = I(τ, y_d) S_t (τ,0, y_b), where S_t (x,0, y_b) is the survival function of the cohort born during year y_b. Using these expressions in eq. (1) results in occurrence of three survival functions in the right hand side which can be combined in the relative survival functions (i.e., the ratios of survival probabilities for individuals with the disease and general population):

$$\begin{array}{l}{\overline{S}}^r(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)=\frac{\overline{S}(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)}{S_t(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)}=\frac{S_t({\overline{x}}_0,0,y_b)}{S_t(x,0,y_b)}\overline{S}(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0),\\ S^r(x-\tau ,\tau ,y_d)=\frac{S(x-\tau ,\tau ,y_d)}{S_t(x-\tau ,\tau ,y_d)}=\frac{S_t(\tau ,0,y_b)}{S_t(x,0,y_b)}S(x-\tau ,\tau ,y_d).\end{array}$$ (3)

The resulting expression for age-specific prevalence is:

$$P(x,y)=P({\overline{x}}_0,{\overline{y}}_0){\overline{S}}^r(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)+{\int }_{{\overline{x}}_0}^{x}I(\tau ,y_d)S^r(x-\tau ,\tau ,y_d)d\tau .$$ (4)

where ȳ₀ = y_b + x̄₀ = y−x+x̄₀ and y_d = y−x+τ.

Combining survival probabilities for mortality results in the ratio of density f_c (or f̄_c) to the survival probability in the general population, that can be further transformed as

$$\begin{array}{l}\frac{f(x-\tau ,\tau ,y_d)}{S_t(x-\tau ,\tau ,y_d)}=-\frac{S^{\prime }(x-\tau ,\tau ,y_d)}{S_t(x-\tau ,\tau ,y_d)}=-\frac{{\left(S_t(x-\tau ,\tau ,y_d)S^r(x-\tau ,\tau ,y_d)\right)}^{\prime }}{S_t(x-\tau ,\tau ,y_d)}\\ =f^r(x-\tau ,\tau ,y_d)+S^r(x-\tau ,\tau ,y_d)\mu (x,y)\end{array}$$ (5)

The function μ(x,y) is the mortality hazard function in the general population. Note because $S_t(x-\tau ,\tau ,y_d)=exp\left(-{\int }_{\tau }^x\mu (v,y_d+v-\tau )dv\right)$, we have $S_t^{\prime }(x-\tau ,\tau ,y_d)=\mu (x,y_d+x-\tau )S_t(x-\tau ,\tau ,y_d)$. We see that all terms at μ(x,y) give the prevalence and finally we obtain the incidence-based mortality in terms of μ(x,y) and functions previously derived.

$$M(x,y)=P(x,y)\mu (x,y)+P({\overline{x}}_0,{\overline{y}}_0){\overline{f}}^r(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)+{\int }_{{\overline{x}}_0}^{x}I(\tau ,y_d)f^r(x-\tau ,\tau ,y_d)d\tau$$ (6)

Explicit representation (i.e., avoiding a function maximum used in the definition of x̄₀) of prevalence and mortality as functions of x and y that allows for expressing prevalence and mortality in terms of x, y, and constants, requires considering two regions below and above the bisecting line, i.e., the regions defined by inequalities y ≥ y₀₀ + x − x₀ and y < y₀₀ + x − x₀. Thus

$$\begin{array}{l}P(x,y)=P(x_{00},y_{00}){\overline{S}}^r(y-y_{00},x_{00},y_{00})+{\int }_{x_{00}}^{x}I(\tau ,y_d)S^r(x-\tau ,\tau ,y_d)d\tau ,\\ M(x,y)=P(x,y)\mu (x,y)+P(x_{00},y_{00}){\overline{f}}^r(y-y_{00},x_{00},y_{00})+{\int }_{x_{00}}^{x}I(\tau ,y_d)f^r(x-\tau ,\tau ,y_d)d\tau \end{array}$$ (7)

for y< y₀₀ + x − x₀ and

$$\begin{array}{l}P(x,y)=P(x_0,y_0){\overline{S}}^r(x-x_0,x_0,y_0)+{\int }_{x_0}^{x}I(\tau ,y_d)S^r(x-\tau ,\tau ,y_d)d\tau ,\\ M(x,y)=P(x,y)\mu (x,y)+P(x_0,y_0){\overline{f}}^r(x-x_0,x_0,y_0)+{\int }_{x_0}^{x}I(\tau ,y_d)f^r(x-\tau ,\tau ,y_d)d\tau \end{array}$$ (8)

for y≥y₀₀ + x− x₀. The formulas (7) and (8) coincide for y=y₀₀ + x − x₀. In these formulas we denote the age at y₀₀ as x₀₀ = y₀₀ − y+x and year at x₀ as y₀ = y−x+x₀.

The quantity of interest is the time trend of age adjusted prevalence (over the age region (x₀,x_max)) and mortality as well as their partitioning. Age-adjusted prevalence and incidence-based mortality based on (7) and (8) are:

$$\begin{array}{l}P(y)={\int }_{x_0}^{\infty }(P(x_0,y_0){\overline{S}}^r(x-x_0,x_0,y_0)I(x\le y-y_{00}+x_0)+\\ +P(x_{00},y_{00}){\overline{S}}^r(y-y_{00},x_{00},y_{00})I(x>y-y_{00}+x_0)\\ +{\int }_{max(x_0,x_{00})}^{x}I(\tau ,y_d)S_d^r(x-\tau ,\tau ,y_d)d\tau )p(x)dx\end{array}$$ (9)

and

$$\begin{array}{l}M(y)={\int }_{x_0}^{\infty }(P(x,y)\mu (x,y)+P(x_0,y_0){\overline{f}}^r(x-x_0,x_0,y_0)I(x\le y-y_{00}+x_0)\\ +P(x_{00},y_{00}){\overline{f}}^r(y-y_{00},x_{00},y_{00})I(x>y-y_{00}+x_0)\\ +{\int }_{max(x_0,x_{00})}^{x}I(\tau ,y_d)S^r(x-\tau ,\tau ,y_d)d\tau )p(x)dx\end{array}$$ (10)

where I() is the indicator function and p(x) is the density of age distribution in a standard year. Recall, x₀₀ = y₀₀ − y+x, y_d = y− x+τ, and y₀ = y−x+x₀ are functions of y and the integration variables x and τ. Age-adjusted prevalence and mortality are functions of three and four contributing factors, respectively:

$$\begin{array}{l}P(y)=P_0(y)+P_{00}(y)+P_{is}(y),\\ M(y)=M_{P\mu }(y)+M_0(y)+M_{00}(y)+M_{is}(y)\end{array}$$ (11)

The derivative of P(y) with respect to y represents the time trend of age-adjusted prevalence and are determined by trends in the respective components including initial prevalence (i.e., prevalence at x₀ or y₀₀), incidence rates, relative survival after disease onset and in patients with the disease at initial point of observation. Explicit differentiation results in seven terms (note that max(x₀, x₀₀) depends on y because of x₀₀). Thus,

$$P_y^{\prime }(y)=T_{p0}(y)+T_{p00}(y)+T_{\overline{S}}(y)+T_{{\overline{S}}_{00}}(y)+T_{X00}(y)+T_{\mathit{inc}}(y)+T_S(y)$$ (12)

with explicit expressions for terms

$$\begin{array}{l}{T}_{p0}(y)={\int }_{x_0}^{x_0+y-y_{00}}{P}_y^{\prime }(x_0,y_0){\overline{S}}^r(x-x_0,x_0,y_0)p(x)dx,\\ T_{p00}(y)={\int }_{x_0+y-y_{00}}^{\infty }{P}_y^{\prime }(y_{00}-y+x,y_{00}){\overline{S}}^r(y-y_{00},y_{00}-y+x,y_{00})p(x)dx,\\ T_{\overline{S}}(y)={\int }_{x_0}^{x_0+y-y_{00}}P(x_0,y_0){\overline{S}}_y^{r^{\prime }}(x-x_0,x_0,y_0)p(x)dx,\\ T_{\overline{S}00}(y)={\int }_{x_0+y-y_{00}}^{\infty }P(x_{00},y_{00}){\overline{S}}_y^{r^{\prime }}(y-y_{00},y_{00}-y+x,y_{00})p(x)dx,\\ T_{X00}(y)={\int }_{x_0+y-y_{00}}^{\infty }I(x_{00},y_{00})S^r(y-y_{00},x_{00},y_{00})p(x)dx,\\ T_{\mathit{inc}}(y)={\int }_{x_0}^{\infty }{\int }_{max(x_0,x_{00})}^x{I}_y^{\prime }(\tau ,y_d)S^r(x-\tau ,\tau ,y_d)p(x)d\tau dx,\\ T_S(y)={\int }_{x_0}^{\infty }{\int }_{max(x_0,x_{00})}^{x}I(\tau ,y_d)S_y^{r^{\prime }}(x-\tau ,\tau ,y_d)p(x)d\tau dx.\end{array}$$ (13)

Derivative of mortality includes nine terms

$$M_y^{\prime }(y)={\widehat{T}}_{\mu }(y)+{\widehat{T}}_P(y)+{\widehat{T}}_{p0}(y)+{\widehat{T}}_{p00}(y)+{\widehat{T}}_{\overline{S}}(y)+{\widehat{T}}_{{\overline{S}}_{00}}(y)+{\widehat{T}}_{X00}(y)+{\widehat{T}}_{\mathit{inc}}(y)+{\widehat{T}}_S(y)$$ (14)

with

$$\begin{array}{l}{\widehat{T}}_{\mu }(y)={\int }_{x_0}^{\infty }{\mu }_y^{\prime }(x,y)P(x,y)p(x)dx,\\ {\widehat{T}}_P(y)={\int }_{x_0}^{\infty }\mu (x,y)P_y^{\prime }(x,y)p(x)dx,\\ {\widehat{T}}_{p0}(y)={\int }_{x_0}^{x_0+y-y_{00}}{P}_y^{\prime }(x_0,y_0){\overline{f}}^r(x-x_0,x_0,y_0)p(x)dx,\\ {\widehat{T}}_{p00}(y)={\int }_{x_0+y-y_{00}}^{\infty }{P}_y^{\prime }(y_{00}-y+x,y_{00}){\overline{f}}^r(y-y_{00},x_{00},y_{00})p(x)dx,\\ {\widehat{T}}_{\overline{S}}(y)={\int }_{x_0}^{x_0+y-y_{00}}P(x_0,y_0){\overline{f}}_y^{r^{\prime }}(x-x_0,x_0,y_0)p(x)dx,\\ {\widehat{T}}_{\overline{S}00}(y)={\int }_{x_0+y-y_{00}}^{\infty }P(x_{00},y_{00}){\overline{f}}_y^{r^{\prime }}(y-y_{00},x_{00},y_{00})p(x)dx,\\ {\widehat{T}}_{X00}(y)={\int }_{x_0+y-y_{00}}^{\infty }I(x_{00},y_{00})f^r(y-y_{00},x_{00},y_{00})p(x)dx,\\ {\widehat{T}}_{\mathit{inc}}(y)={\int }_{x_0}^{\infty }{\int }_{max(x_0,x_{00})}^x{I}^{\prime }(\tau ,y_d)f^r(x-\tau ,\tau ,y_d)p(x)d\tau dx,\\ {\widehat{T}}_S(y)={\int }_{x_0}^{\infty }{\int }_{max(x_0,x_{00})}^{x}I(\tau ,y_d)f_y^{r^{\prime }}(x-\tau ,\tau ,y_d)p(x)d\tau dx.\end{array}$$ (15)

Non-trivial technical aspects of derivation of the derivatives (13) and (15) are discussed in Appendix B.

2.2. Interpretation of partitioning components

The three terms contributing to disease prevalence in eq. (11) correspond to the contributions of individuals with disease onset i) before x₀ = 65 (the age of eligibility for Medicare coverage for the majority of the general population) for the cohorts with y≥y₀₀ +x− x₀ (i.e., cohorts below the bisecting line the Lexis diagram in Figure 1), ii) before y₀₀ = 1992 for the cohorts y<y₀₀ +x− x₀ (i.e., cohorts above the bisecting line in Figure 1), and iii) after x₀ = 65 and after y₀₀ = 1992 (i.e., in the shaded area in the Lexis diagram in Figure 1). Mortality in eq. (11) has four terms, M_Pμ(y) and three others: M₀(y), M₀₀(y), and M_is(y) which have the same meaning as the three equivalent terms in prevalence. These three terms represent the mortality rates of individuals with disease onset before x₀, before y₀₀, and after both x₀ and y₀₀ respectively. These terms are expressed in terms of relative survival and therefore represent the mortality of individuals with the disease relative to the mortality in the general population. The additional term in eqs. (11), M_Pμ(y), represents mortality for the prevalent population with the mortality rate as in the general population. In sum, eq. (11) models two components of mortality: i) the effect of prevailing trends in the general population and ii) the effect of relative mortality in individuals with the disease.

The time trend of disease prevalence, represented by the first derivative of the age-adjusted prevalence, has seven terms. The main contributions are T_inc(y) and T_S(y) that reflect effects of trends in disease incidence and survival after the disease onset. Occurrence of five other terms reflects the fact that we observe individual follow-up not from their birth date. They can be combined in two terms reflecting the effects on two bounds x=x₀ and y=y₀₀: T₀ (y) = T_p0(y) + T_S̄(y) and T₀₀(y) = T_p00 (y) + T_S̄00(y) + T_X00(y), respectively. The terms T_p0(y)and T_S̄(y) reflect the effects of time trends in initial prevalence (i.e., prevalence at x₀ = 65) and trends in survival of these individuals. The contributions of these terms can be considered separately if the respective hypotheses are of interest. The three terms contributing to T₀₀ (y) (i.e., T_p00(y), T_S̄00(y), and T_X00(y)) are the only terms contributing to disease prevalence that survive in the limit y→y₀₀. They are responsible for the reconstruction of the correct derivative in the region of y~y₀₀. Specifically, the first and second terms characterize the time trend in initial prevalence and survival for y=y₀₀, respectively. The last term equals age-adjusted incidence rate in the limit y→y₀₀. Its occurrence reflects the lack of information about incidence before y₀₀. With time the fraction of unknown information about incidence goes down and the contribution from this term to the total time trends decreases.

Similarly, seven of the nine terms in the decomposition of mortality can be combined into four terms: T̂_inc (y) and T̂_S(y)represent the effects of incidence and survival for individuals diagnosed after x₀ and y₀₀, while T̂₀ (y) = T̂_p0(y) + T̂_S̄(y) and T̂₀₀(y) = T̂_p00(y) + T̂_S̄00(y) + T̂_X00(y) reflect the effects on two bounds x = x₀ and y=y₀₀. Two additional terms occurring in the formula for mortality are T̂_μ(y) and T̂_P (y). They reflect the effects of trends in mortality in the general population and in prevalence of the given disease.

3. Statistical Estimation of Model parameters from observational data

The quantities of interest (i.e., T(y) and T̂(y)) are expressed in terms of derivatives of survival analysis functions in respect of time. In our approach, we use explicit analytic parameterization for all functions for which derivatives are needed. An alternative approach based on numerical differentiation would require us to deal with numerical instabilities typical for numerical evaluation of derivatives. Since integration is performed numerically, the integrand must be calculated with maximal accuracy—this condition is satisfied by our approach involving analytic differentiation of the parametric models of these functions. Specifically we need to develop and estimate three disease-specific models for a specific disease which are involved in the expressions for prevalence and mortality as well as their derivatives: i) models for prevalence at x₀ (i.e., prevalence at the starting age of observation) and all years y≥y₀₀, and prevalence at y₀₀ (i.e., at the beginning year of observation) and all ages x≥x₀, ii) the model for the incidence rate for all x≥x₀ and y≥y₀₀; and iii) models for relative survival of individuals prevalent at x₀, prevalent at y₀₀, and incident at x>x₀ and y>y₀₀. Furthermore, for the modeling of incidence-based mortality, models for mortality in the general population need to be developed.

We use individual medical records from a nationally representative 5% sample of Medicare beneficiaries age 65+ to estimate the model parameters for the models enumerated above. Medicare data provide individual records for individuals above age 65 (i.e., x₀ = 65) and starting in 1992 (i.e., y₀₀ = 1992). Collection of all records with the disease-specific ICD-9-codes for an individual allows us to reconstruct individual disease-specific trajectories and then create the following datasets for further analyses using the methods from Akushevich et al. (Akushevich et al. 2012):

• D1Prevalence rates for boundaries of the region (Figure 1), i.e., one-year-specific prevalence rates i) for x₀ and all years y≥y₀₀ and ii) for y₀₀ and all ages x≥x₀.
• D2Incidence rates in one-year groups over age and year.
• D3Individual survival times. The dataset contains individual records including age and year at the first record interpreted as incident or prevalent cases and time to death/censoring. For prevalent cases x=x₀ or y=y₀₀.
• D4Prevalence and mortality in one-year groups over age and year. This dataset will be only used for comparison to the results of modeling of these measures.

Estimation strategy of model parameters involves B-splines in order to evaluate y - and x₀₀ -dependences occurring in the expressions for prevalence, mortality, and their derivatives. An important feature of B-splines necessary for our study is that they allow for the calculation of derivatives explicitly and without additional simplifying assumptions. Other dependencies such as age-dependencies of incidence, survival, and mortality in the general population as well as survival time dependence are modeled by appropriate (known or empirically based) models adopted for them, such as the linear model of disease incidence, the Gompertz model for age patterns for mortality in the general population, and the Weibull model for survival time distribution.

3.1. Model for prevalence at boundaries

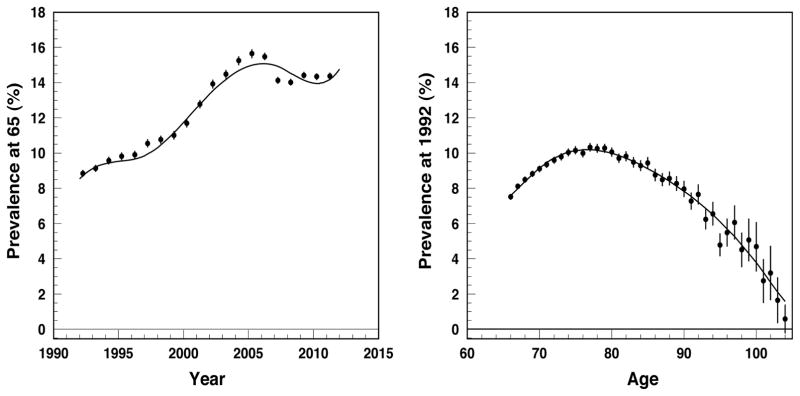
First, the y₀-dependence of initial prevalence (dataset D1) are modeled using B-splines as P(x₀, y₀) = Σ_iα_iB_i,n(y₀), where n is the degree of B-splines (n = 3 in our analysis) and i runs over all B-splines the number of which is defined by the number of used knots. The functions B_i,n(y₀) are polynomial functions completely known when the sets of knots are fixed and parameters α_i are subject for estimation. The first derivative of P(x₀,y₀) is then explicitly calculated because $B_{i,n}^{\prime }(\overline{y})$ is represented in terms of B-splines of a lower degree for that we also have explicit representation. Note also that the approach gives the derivative of P(x₀, y₀) with respect to y₀, however since y₀ = y−x+x₀ it is equal to the derivative with respect to y: dP(x₀,y₀)/dy₀ = dP(x₀,y₀)/dy. Similarly, B-splines provide the fit for x₀₀ (where x₀₀ = y₀₀ − y+x) dependence of P(x₀₀,y₀₀) together with the first derivative in respect of x₀₀ thus providing the derivative in respect of y : dP(x₀₀,y₀₀)/dx₀₀ = −dP(x₀₀,y₀₀)/dy. Empirical estimates and the B-spline models for both y₀ - dependence of P(x₀,y₀) and x₀₀-dependence of P(x₀₀,y₀₀) are shown in Figure 2.

Figure 2.

Prevalence at 65, P(x₀, y₀) vs. y₀, (left panel) and at 1992, P(x₀₀, y₀₀) vs. x₀₀, (right panel) of diabetes: empiric estimates (dots) and B-spline model (solid line).

3.2. Model for incidence

Assume that for each y_d the age-dependence of incidence rates I(τ, y_d) from dataset D2 is explicitly parameterized through the sets of model parameters ${\beta }_{\mathit{inc}}=\{{\beta }_i^{\mathit{inc}}(y_d)\}$ dependent on y_d (e.g., linearly $I(\tau ,y_d)=\tau {\beta }_1^{\mathit{inc}}(y_d)+{\beta }_2^{\mathit{inc}}(y_d))$, and y_d -dependence of each parameter ${\beta }_i^{\mathit{inc}}(y_d)$ is fitted by B-splines providing the first derivative $d{\beta }_i^{\mathit{inc}}(y_d)/d{y}_d=d{\beta }_i^{\mathit{inc}}(y_d)/dy$. Thus

$$\frac{dI(\tau ,y_d)}{dy}={\sum }_i\frac{\partial I(\tau ,y_d)}{\partial {\beta }_i^{\mathit{inc}}}\frac{d{\beta }_i^{\mathit{inc}}(y_d)}{d{y}_d}$$

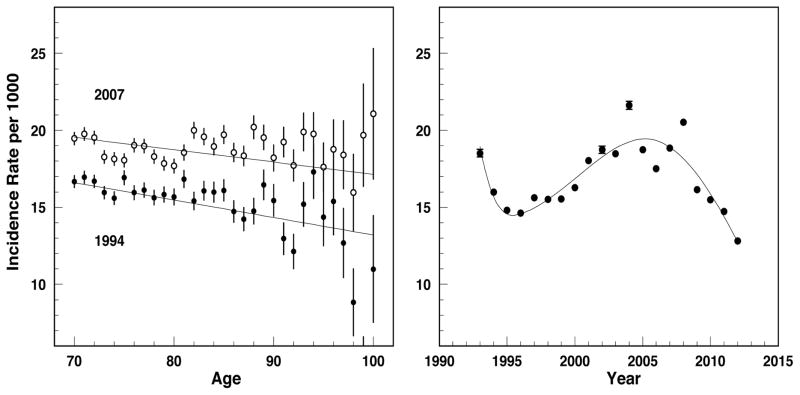
Figure 3 presents the age- dependence of age-specific rates for two selected years (left panel) and y_d - dependence of age-adjusted incidence rates (right panel) together with the B-spline models fitting y_d - dependences of age-specific rates with subsequent age-adjustment for the second case. The results presented in Figure 3 justify the choice of the linear model for the age-specific rates of diabetes (another model can be chosen for another disease). Note that the age adjusted rates can be represented by a linear model only approximately and the spline approximation that provides partial smoothing of this effect could be an alternative.

Figure 3.

Incidence rate of type 2 diabetes I(τ, y_d): age pattern for selected years of diagnosis (left plot) and year-at-diagnosis patterns for age-adjusted rate (right panel). Dots show empiric estimates and curves show the models: linear model for age-patterns (left plot) and B-spline model for age-adjusted rates (right plot).

3.3. Models for survival

The models describing age- and survival-time-dependences for the three specific relative survival functions S̄^r(x−x₀, x₀,y₀), S̄^r(y−y₀₀,x₀₀,y₀₀), and $S_d^r(x-\tau ,\tau ,y_d)$ have to be specified, parameterized, and estimated. We use the approach based on maximizing the likelihood for individual survival data (Dickman et al. 2004), which can be outlined in general terms as follows and specified for the three relative survival functions below. An individual i in dataset D3 is characterized by i) the age of diabetes diagnosis or initial age of follow-up (x_0i), ii) final age of follow-up (x_i), and iii) the death/censoring indicator d_i at age x_i. Denoting survival function for an individual i as S(x_i,x_0i)and using the standard likelihood for total survival L = ∏_i (h(x_i))^d_iS(x_i, x_0i) and the definitions of relative survival, S(x_i, x_0i) = S_t(x_i, x_0i) S^r = (x_i, x_0i; β), and respective hazard functions h(x) = h_t(x) + h^r(x,β), we construct the log likelihood as

$$I(\beta )=-{\sum }_i{\int }_{x_{0i}}^{x_i}{h}_t(u)du-{\sum }_i{\int }_{x_{0i}}^{x_i}{h}^r(u,\beta )du+{\sum }_i{d}_{i}log(h_t(x_i)+h^r(x_i,\beta ))$$ (16)

Here β is the set of parameters for the relative survival and respective hazard. The first term does not depend on β and therefore can be omitted. The only item that we need to know about the general population is the population hazards at the age of death for all individuals in the datasets. This information is obtained from the Human Mortality Database.

Specific parameterization is required to describe the age- and survival time dependences of relative survival functions. We assume that the Weibull model is flexible enough (Carroll 2003; Zhu et al. 2011) and can be applied for the three relative survival functions involved in (7) and (8).

For S̄^r(x−x₀,x₀,y₀) we use S̄^r (x−x₀,x₀, y₀) = exp(−exp(σ⁻¹ (log(x−x₀) − μ))) in which parameters μ = μ(y₀)and σ = σ(y₀) are estimated for each y₀ using maximizing the likelihood (16), and then y₀ - dependences of μ and σ are fitted by B-splines providing derivatives dμ/dy₀ = dμ/dy and dσ/dy₀ = dσ/dy. Thus,

$$\frac{d{\overline{S}}^r(x-x_0,x_0,y_0)}{dy}=\frac{\partial {\overline{S}}^r(x-x_0,x_0,y_0)}{\partial \mu }\frac{d\mu }{d{y}_0}+\frac{\partial {\overline{S}}^r(x-x_0,x_0,y_0)}{\partial \sigma }\frac{d\sigma }{d{y}_0}$$

The partial derivatives are calculated explicitly and derivatives of μ and σ in respect to y₀ are provided by B-splines.

Similarly, we use S̄^r(y−y₀₀, x₀₀, y₀₀) = exp(−exp(σ⁻¹ (log(y−y₀₀) − μ))), and parameters μ = μ(x₀₀) and σ = σ(x₀₀) depend on x₀₀ and are estimated using (16). The dependences are given by B-splines and dμ/dx₀₀ = dμ/dy and dμ/dx₀₀ = −dμ/dy. Now the relative survival function depends on y explicitly, therefore

$$\frac{d{\overline{S}}^r(y-y_{00},x_{00},y_{00})}{dy}=\frac{\partial {\overline{S}}^r(y-y_{00},x_{00},y_{00})}{\partial y}-\frac{\partial {\overline{S}}^r(y-y_{00},x_{00},y_{00})}{\partial \mu }\frac{d\mu }{d{x}_{00}}-\frac{\partial {\overline{S}}^r(y-y_{00},x_{00},y_{00})}{\partial \sigma }\frac{d\sigma }{d{x}_{00}}$$

Finally, we use S^r(x − τ, τ, y_d) = exp(−exp(σ⁻¹(log(x − τ) − μ))) where the dependence of μ and σ on τ are explicitly represented through the quadratic function of τ with the sets of parameters ${\beta }_{\mu }=\{{\beta }_{\mu }^i\}$ and ${\beta }_{\sigma }=\{{\beta }_{\sigma }^i\}$ and each parameter ${\beta }_{\mu ,\sigma }^i$ is y_d-specific (i.e., estimated for each year y_d). Then y_d dependence of each parameter ${\beta }_{\mu ,\sigma }^i$ is fitted by B-splines providing respective derivatives $d{\beta }_{\mu ,\sigma }^i/d{y}_d=d{\beta }_{\mu ,\sigma }^i/dy$. Therefore,

$$\frac{d{S}_d^r(x-\tau ,\tau ,y_d)}{dy}={\sum }_i\frac{\partial S_d^r(x-\tau ,\tau ,y_d)}{\partial {\beta }_{\mu }^i}\frac{d{\beta }_{\mu }^i}{d{y}_d}+{\sum }_i\frac{\partial I{S}_d^r(x-\tau ,\tau ,y_d)}{\partial {\beta }_{\sigma }^i}\frac{d{\beta }_{\sigma }^i}{d{y}_d}$$

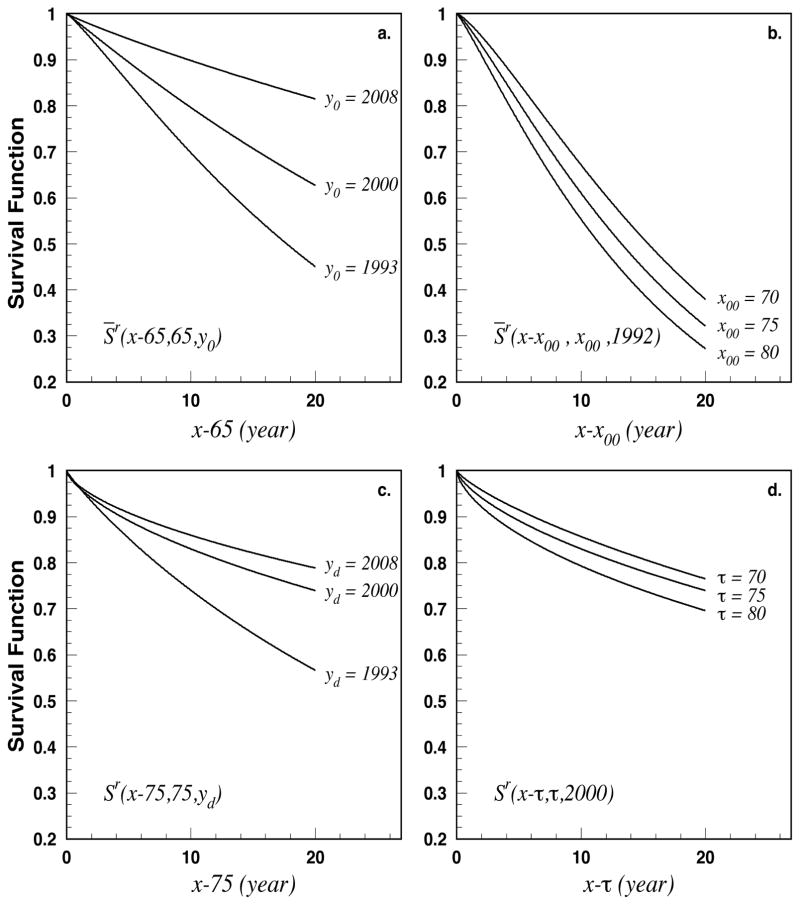
Figure 4 presents the results for the relative survival functions. Projections of time survival for selected ages and years are shown for all three survival functions involving in (7) and (8). Note that empirical estimates of relative survival are not necessary for our modeling so they are not presented in Figure 4.

Figure 4.

Relative survival functions for selected ages and years at diagnoses. Specifically, a) relative survival vs. time after 65 for individuals prevalent at 65 for three y₀ (years at x₀ = 65), b) relative survival vs. time after x₀₀ for individuals prevalent at 65 for three x₀₀ (age at y₀₀ = 1992), c) relative survival vs. time after diagnosis for individuals diagnosed at age 75 in three years of diagnosis y_d, and d) relative survival vs. time after diagnosis for individuals diagnosed in 2000 in three ages of diagnosis τ.

4. Partitioning for Diabetes Prevalence and Mortality and Their Time Trends

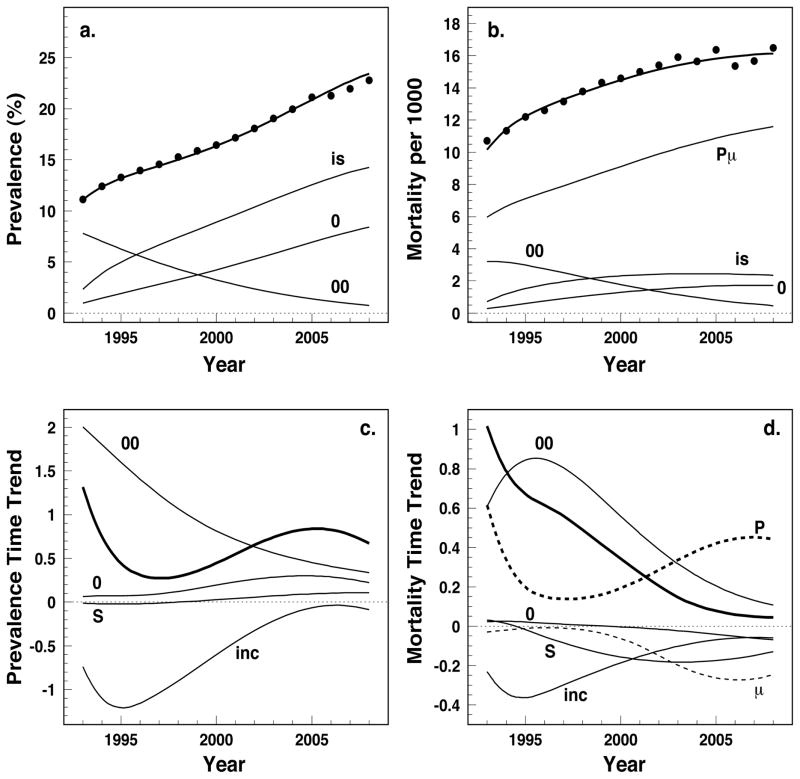
Application of estimated models to 5%-Medicare data resulted in predicted age-adjusted prevalence, P(y), and incidence-based mortality, M(y), according eqs. (9) and (10). Their patterns are presented by thick lines in the upper panels of Figure 5; the actual empirical patterns (dots) are provided for comparison. The three terms (P₀(y), P₀₀(y), and P_is(y)) contributing to prevalence and four terms (M_Pμ(y), M₀(y), M₀₀(y), and M_is(y)) contributing to the mortality rate according to eq. (11) are also shown. The curves in these plots are marked by labels corresponding to subscripts of the respective contributions from eq. (11). Excellent agreement between the theoretical predictions and the empirical estimates are detected for both prevalence and the incidence-based mortality of diabetes.

Figure 5.

Prevalence and incidence-based mortality, their time trends as well as partitioning of these measures: a) type 2 diabetes prevalence, b) incidence-based mortality, c) time trend of prevalence and d) time trend of the incidence-based mortality. Dots in upper plots show empiric estimates for prevalence and mortality. Thick curves show theoretical predictions given by eqs. (9), (10), (12)–(13), and (14)–(15), respectively. Thin curves represent components of the theoretical predictions (eqs. (11)–(15)). Label for each thin curve exactly corresponds to the subscript of respective term in eqs. (11) for upper plots and (13),(15) for lower plots.

The term with the double integral in eq. (9), P_is(y), that contains the product of incidence and relative survival gives the most essential contribution to diabetes prevalence. The contribution of prevalence at 1992, P₀₀(y), decreases with time because of two reasons: i) mortality of individuals prevalent at 1992 is larger than mortality in the general population and ii) the relative contribution of the region above the bisecting line to the integral with respect to x (see Figure 1) decreases with time. In contrast the contribution of prevalence at age 65, P₀(y), goes up because of increased prevalence at 65 with time (Figure 2) and the increased contribution of the region below the bisecting line to the integral with respect to x in (9). The major contribution to the incidence-based mortality is the term containing the product of prevalence and mortality in the general population (i.e., M_Pμ(y). This term would be the only contribution if the mortality rates of individuals with diabetes and of the general population are the same. The gap between this term and mortality, given by the thick line (i.e., M(x, y)), is due to three remaining contribution terms showing the effects of the individuals prevalent at the boundaries (M₀(y) and M₀₀(y) represented by the curves ‘0’ and ‘00’) and the individuals diagnosed during follow-up (M_is(y) and the curve ‘is’). The patterns of these curves reproduce those observed for prevalence and are explained by the same reasoning.

Both prevalence and mortality increase with time so their derivative over calendar time is positive. Explicit calculations allowed us to evaluate time patterns of the components responsible for these trends of prevalence (12),(13) and mortality (14),(15). The total derivative of prevalence ( $P_y^{\prime }(y)$ and thick curve) largely reproduces the shape of the curve marked by ‘inc’, that is the total prevalence trend is defined primarily by the dynamics of diabetes incidence. The term containing the derivative of incidence, T_inc(y), is negative, i.e., incidence is decreasing over time driving the prevalence downwards. The effect of survival (T_S(y) and the curve marked by “S”) pushes the prevalence upwards reflecting increased life-span of patients with diabetes. The curve marked by “0” contains two contributions, T₀(y) = T_p0(y) + T_S̄(y), the first representing prevalence at 65 is dominant and increasing driving the total prevalence up. Another contribution T_S̄(y) reflecting survival of patients prevalent at 65 is positive (similarly to T_S(y)) and small. The remaining contribution marked by “00” comprises all effects related to the boundary at y₀₀, i.e., T₀₀(y) = T_p00(y) + T_S̄00(y) + T_X00(y). This contribution is largely technical because it reflects the fraction of the effects coming from incidence and survival trends before 1992. As expected this fraction decrease with time. In sum, the total prevalence increases over time as the three contributions pulling the prevalence up overpower the downward effect of incidence.

The presentation of the partitioning of mortality trends (Figure 5d) largely reflects the picture obtained for prevalence in Figure 5c. The most important contribution to the mortality trend is the term containing the derivative of prevalence T̂_P(y) (marked by “P”, thick dashed curve). Its shape reproduces the shape of total prevalence change (thick line in Figure 5c) and deviates only because of the factor containing the mortality rate in the general population which is time dependent. Other curves on Figure 5d reflect the effects of relative survival and respective mortality. Although the size of the effects is not large (as follows from Figure 5b), they can have significant contributions to the mortality time trend (Figure 5d). Their signs, sizes, and time trends reflect what we observed for prevalence with the exception of the terms reflecting survival that change sign. For example, incidence and survival results in decreasing mortality. However, mortality still increases. This is a consequence of negative tendencies in past (i.e., before 1992) that are represented by the term “00”, i.e., T̂₀₀(y) = T̂_p00(y) + T̂_S̄00(y) + T̂_X00(y).. An additional term, T̂_μ(y), is marked by μ (dashed curve), this reflects the effect of the general change in mortality in the general population, that is the mortality of patients with diabetes not related to diabetes itself (i.e., death due to other causes) is going down just as in the general population.

5. Discussion and Conclusion

In this study, we developed an approach for the modeling of disease prevalence and incidence-based mortality (i.e., mortality for individuals who had a diagnosis earlier in life). The model provides analytical expressions for these epidemiologic characteristics which allows for the analysis of the relative contributions of incidence and survival as important components of total prevalence and incidence-based mortality.

The approach provides expressions for the partitioning of the time trends of these quantities. All of the components that are responsible for trends in disease prevalence and mortality are evaluated through explicit expressions. These components include disease incidence and survival as well as effects at the boundaries of the region available for analysis (in the case of 5%-Medicare we observe the effects after 1992 for individuals aged 65+). For mortality, additional information about the mortality rate in the general population is required.

The results of the partitioning analyses are presented in Figure 5 and described in detail in “Partitioning for Diabetes Prevalence and Mortality and Their Time Trends” earlier in this text. Based on this analysis we can conclude that i) the theory describes empirical estimates for prevalence and mortality with good accuracy, ii) among the possible contributions T(y) and T̂(y) in eq. equation (12) and (14), the contributions of incidence and survival after age 65 have the greatest effect on diabetes prevalence and diabetes-related mortality, and iii) the dynamics of diabetes prevalence and mortality are generated by causes consistent with improvements in population health: decreased incidence and improved survival.

Use of our methodology offers new opportunities in public health. Researchers obtain the opportunity to clearly identify the sources of observed processes at the level of disease prevalence and mortality. The methodology presented in this paper provides a formal method for the decomposition of an observed trend in prevalence and incidence-based mortality into their constituent parts. Practically, this can be used as a public health planning tool, to identify areas of concern which, either due to the size of the effect, the direction of the trend, or the observed rate of change, require targeted attention from health agencies. Furthermore, over time improvements in diagnostic technology and the body of knowledge on the pathological characteristics of a disease lead to improved ascertainment (i.e. the ability to identify the presence of a disease) and more tightly defined guidelines for making a valid diagnosis. Improved ascertainment is likely to lead to an increase in the incidence of a disease as individuals who were previously left undiagnosed are identified. The effect of changes in diagnostic guidelines is more ambiguous as depending on whether elements were added or removed from the definition of a valid diagnosis incidence and by extent prevalence could be pushed in either direction. A standardized method for the partitioning of an existing prevalence trend into the time-trends of its components and, more importantly, the relative strength of the contribution of each component over time, will aid in both correctly assessing the relative success of a health intervention and identifying time-periods of special interest for more in depth analysis (e.g. a sharp spike in the relative strength of the contribution associated with incidence could indicate either an area of public health interest, or an improvement in ascertainment).

Our approach lends itself to multiple natural generalizations allowing for the estimation and partitioning of quantities such as i) the effects of disease-specific medical costs (respective costs are added into integrand) (Akushevich et al. 2011; Akushevich et al. 2016), ii) the effects of recovery and/or long-term remission (respective survival functions have to be used as additional factors) (Akushevich et al. 2013b), and iii) the effects of complications for patients with a specific disease (specific patient selections and respective changes in mathematical formalism have to be included) (Akushevich et al. 2013a; Yashkin, Picone and Sloan 2015). The expressions for prevalence and mortality can also be used in improving the accuracy of future projections in health forecasting.

The components contributing to time trends are obtained not using a fitting procedure and/or maximum likelihood, but direct calculation using expressions representing each component as continuous functions of available data. Statistical estimates of parameters characterizing the time patterns of prevalence at the bounds, incidence and survival are obtained using B-splines. Since B-splines provide consistent estimates of model parameters (Strawderman and Tsiatis 1996) and the trend components are continuous functions of the B-spline parameters, the estimates of the trend components are consistent. The estimates are largely model independent; therefore, the risk of model misspecification is minimal. The only model we use is the Weibul model for survival time. The model is quite flexible and its choice is not critical for the estimation procedure: two-dimensional splines for survival can be used instead.

The level of detail our approach provides is highly dependent on the length and scope present in the data. When Medicare data or a dataset of a similar size is used, statistical uncertainties are not expected to be large. In the general case the statistical uncertainty has to be estimated using a bootstrapping approach or through analytic estimates of error propagation. However, systematic uncertainties (biases) could be noticeable. Possible sources for the systematical uncertainties include i) the possibility of non-precise separation of incident and prevalent cases, ii) the effect of time trends in the fraction of individuals covered by Medicare Advantage (a private alternative to traditional Medicare which does not contribute data to Medicare datasets), and/or iii) changes in the structure of the population of Medicare beneficiaries due to specific events such as initiation of Medicare coverage of Part D in 2006. Separate research to evaluate the contributions of these factors to the total systematical error is required. In sum, the estimation of the time trend components is consistent and stable, however further investigation of systematic uncertainties would improve overall accuracy of the estimates.

In summary, notable strengths of our approach include: i) modeling of all components used in our models using explicit expressions; ii) lack of simplifying assumptions; iii) stability and consistency of the resulting estimates; and iv) wide availability of large administrative health data like that used in the study. The application of this approach to the case of diabetes found that both its prevalence and incidence-based mortality increases with time. The primary driving factor of the observed prevalence increase is improved survival and increased prevalence at age 65. The increase in diabetes-related mortality is driven by increased prevalence and unobserved trends beyond the region observed in the data.

Appendix A. Derivation of expressions for prevalence (1) and mortality (2)

The formulae (1) and (2) can be understood in terms of the numbers of individuals. Let N₀ be the size of a birth cohort and N_I (τ)Δτ be the number of individuals with disease onset within the age period Δτ. The total number of sick (and alive) individuals at age x(N_d(x)) is the sum of all individuals who survived to age x after diagnoses at τ over all age periods, i.e.,

$$N_d(x)={\sum }_n{N}_I({\tau }_n){(\mathrm{\Delta }\tau )}_{n}S(x-{\tau }_n,{\tau }_n)$$

where S(x − τ_n, τ_n) is the survival function of individuals diagnosed at age period [τ_n, τ_n + (Δτ)_n] who survived to age x. Considering infinitely small age periods (i.e., Δτ → 0) and defining P_c(x, y_b) = N_d(x)/N₀ and I_c(τ, y_b) = N_I(τ)/N₀, we obtain the formula $P_c(x,y_b)={\int }_0^x{I}_c(\tau ,y_b)S(x-\tau ,\tau ,y_d)d\tau$. Then the formula (1) is obtained when we split the integration region in two parts (from 0 to x̄₀ and from x̄₀ to x) and use respective notation for the first part: ${\int }_0^{{\overline{x}}_0}{I}_c(\tau ,y_b)S(x-\tau ,\tau ,y_d)d\tau =P_c({\overline{x}}_0,y_b)\overline{S}(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)$. Exactly the definition of S̄(x − x̄₀, x̄₀, ȳ₀) is:

$$\overline{S}(x-{\overline{x}}_0,{\overline{x}}_0,{\overline{y}}_0)=\frac{{\int }_0^{{\overline{x}}_0}{I}_c(\tau ,y_b)S(x-\tau ,\tau ,y_d)d\tau }{{\int }_0^{{\overline{x}}_0}{I}_c(\tau ,y_b)S({\overline{x}}_0-\tau ,\tau ,y_d)d\tau }.$$

The survival function in the numerator can split as S(x − τ, τ, y_d) = S(x − x̄₀, x̄₀, ȳ₀|τ)S(x̄₀ − τ, τ, y_d). The function S(x − x̄₀, x̄₀, ȳ₀|τ) is the survival function for a cohort of patients formed at age x̄₀ and time ȳ₀ and diagnosed at age τ, τ < x̄₀. If the dependence on τ is weak for a disease, we can put S(x − x̄₀, x̄₀, ȳ₀|τ) ≈ S(x − x̄₀, x̄₀, ȳ₀), and therefore obtain S̄(x − x̄₀, x̄₀, ȳ₀) ≈ S(x − x̄₀, x̄₀, ȳ₀). Thus, the difference between empiric estimates or estimated models for the two survival functions reflects the force of dependence of S(x − x̄₀, x̄₀, ȳ₀|τ) on τ.

Let the number of individuals diagnosed at the age interval [τ, τ + Δτ] and then died during age interval [x, x + Δx] is N_IM(τ, x). The total number of individuals died in the age interval [x, x + Δx] is defined through the density of the incidence-based mortality M(x, y_b) and equals:

$$M(x,y_b)\mathrm{\Delta }x={\sum }_n{N}_{IM}({\tau }_n,x){(\mathrm{\Delta }\tau )}_n\mathrm{\Delta }x={\sum }_n{N}_I({\tau }_n)\frac{N_{IM}({\tau }_n,x)}{N_I({\tau }_n)}{(\mathrm{\Delta }\tau )}_n\mathrm{\Delta }x$$

Considering infinitely small age periods (i.e., Δτ→0 and Δx→0) and defining $f_c(x-{\tau }_n,{\tau }_n,y_d)=\frac{N_{IM}({\tau }_n,x)}{N_I({\tau }_n)}$ we obtain the formula $M_c(x,y_b)={\int }_0^x{I}_c(\tau ,y_b)f_c(x-\tau ,\tau ,y_d)d\tau$. Splitting the integration region and using definitions of f̄_c(x − x̄₀, x̄₀, ȳ₀) similarly as in the case of disease prevalence considered above we obtain eq. (2)

Appendix B. Derivation of the derivatives of prevalence and mortality

In this Appendix technical aspects of derivation of the derivatives (13) and (15) are discussed. Rewrite eq. (9) by rewriting integration limits explicitly:

$$\begin{array}{l}P(y)={\int }_{x_0}^{y-y_{00}+x_0}P(x_0,y_0){\overline{S}}^r(x-x_0,x_0,y_0)p(x)dx+{\int }_{y-y_{00}+x_0}^{\infty }P(x_{00},y_{00}){\overline{S}}^r(y-y_{00},x_{00},y_{00})p(x)dx\\ +{\int }_{x_0}^{y-y_{00}+x_0}\left({\int }_{x_0}^{x}I(\tau ,y_d)S_d^r(x-\tau ,\tau ,y_d)d\tau \right)p(x)dx+{\int }_{y-y_{00}+x_0}^{\infty }\left({\int }_{y_{00}-y+x}^{x}I(\tau ,y_d)S_d^r(x-\tau ,\tau ,y_d)d\tau \right)p(x)dx\end{array}$$ (17)

Derivation of the right hand side is based on the Barrow’s Fundamental Theorem of Calculus which can be adopted for our case as: ${\left({\int }_a^{x}f(x,y)dy\right)}_x^{\prime }=f(x,x)+{\int }_a^x{f}_x^{\prime }(x,y)dy$, i.e., when we need to differentiate a function over an argument that is both in the integration limits and in integrand we have the two terms with and without integration. Differentiation of the first term in P(y) results:

$$P(x_0,y_{00}){\overline{S}}^r(y-y_{00},x_0,y_{00})p(y-y_{00}+x_0)+T_{p0}(y)+T_{\overline{S}}(y)$$

The second term of P(y) gives

$$-P(x_0,y_{00}){\overline{S}}^r(y-y_{00},x_0,y_{00})p(y-y_{00}+x_0)+T_{p00}(y)+T_{\overline{S}00}(y)$$

As we see first terms of these two contributions cancel in the sum resulting in T_p0(y) + T_S̄(y) + T_p00(y) + T_S̄00(y).

Differentiation of the third term in eq. (17) results:

$$\begin{array}{l}p(y-y_{00}+x_0){\int }_{x_0}^{y-y_{00}+x_0}I(\tau ,y_{00}-x_0+\tau )S_d^r(y-y_{00}+x_0-\tau ,\tau ,y_{00}-x_0+\tau )d\tau \\ +{\int }_{x_0}^{y-y_{00}+x_0}\left({\int }_{x_0}^x{I}_y^{\prime }(\tau ,y_d)S^r(x-\tau ,\tau ,y_d)d\tau \right)p(x)dx\\ +{\int }_{x_0}^{y-y_{00}+x_0}\left({\int }_{x_0}^{x}I(\tau ,y_d)S_y^{r^{\prime }}(x-\tau ,\tau ,y_d)d\tau \right)p(x)dx\end{array}$$ (18)

The last term in the expression for P(y) contains y in integration limits for both first and second integral, therefore the Barrow’s theorem has to be applied twice resulting:

$$\begin{array}{l}-p(y-y_{00}+x_0){\int }_{x_0}^{y-y_{00}+x_0}I(\tau ,y_{00}-x_0+\tau )S_d^r(y-y_{00}+x_0-\tau ,\tau ,y_{00}-x_0+\tau )d\tau \\ +{\int }_{y-y_{00}+x_0}^{\infty }{\left({\int }_{y_{00}-y+x}^{x}I(\tau ,y_d)S_d^r(x-\tau ,\tau ,y_d)d\tau \right)}_y^{\prime }p(x)dx\\ =-p(y-y_{00}+x_0){\int }_{x_0}^{y-y_{00}+x_0}I(\tau ,y_{00}-x_0+\tau )S_d^r(y-y_{00}+x_0-\tau ,\tau ,y_{00}-x_0+\tau )d\tau \\ +{\int }_{y-y_{00}+x_0}^{\infty }I(y_{00}-y+x,y_{00})S_d^r(y-y_{00},y_{00}-y+x,y_{00})p(x)dx\\ +{\int }_{y-y_{00}+x_0}^{\infty }\left({\int }_{y_{00}-y+x}^x{I}_y^{\prime }(\tau ,y_d)S^r(x-\tau ,\tau ,y_d)d\tau \right)p(x)dx\\ +{\int }_{y=y_{00}+x_0}^{\infty }\left({\int }_{y_{00}-y+x}^{x}I(\tau ,y_d)S_y^{r^{\prime }}(x-\tau ,\tau ,y_d)d\tau \right)p(x)dx\end{array}$$ (19)

First terms of (18) and (19) cancel, second terms of (19) is T_X00(y), and sum of remaining terms (last two terms of (18) and (19)) gives T_inc(y)+ T_S(y). The sum of surviving terms gives finally the right hand side of eq. (12).

The calculation for derivative of mortality is similar.