Abstract
The induced dipole and the classical Drude oscillator represent two major approaches for the explicit inclusion of electronic polarizability into force field-based molecular modeling and simulations. In this work, we explore the equivalency of these two models by comparing condensed phase properties computed using the Drude force field and a multipole and induced dipole (MPID) model. Presented is an approach to map the electrostatic model optimized in the context of the Drude force field onto the MPID model. Condensed phase simulations on water and 15 small model compounds show that without any reparametrization, the MPID model yields properties similar to the Drude force field with both models yielding satisfactory reproduction of a range of experimental values and quantum mechanical data. Our results illustrate that the Drude oscillator model and the point induced dipole model are different representations of essentially the same physical model. However, results indicate the presence of small differences between the use of atomic multipoles and off-center charge sites. Additionally, results on the use of dispersion particle mesh Ewald further support its utility for treating long-range Lennard Jones dispersion contributions in the context of polarizable force fields. The main motivation in demonstrating the transferability of parameters between the Drude and MPID models is that the more than 15 years of development of the Drude polarizable force field can now be used with MPID formalism without the need for dual-thermostat integrators nor self-consistent iterations. This opens up a wide range of new methodological opportunities for polarizable models.
I. INTRODUCTION
More sophisticated modeling of electrostatic interactions represents an important step towards more accurate empirical force fields (FFs).1–3 For the widely used additive force fields, electrostatics are computed as the summation of pairwise Columbic interactions between fixed partial atomic charges. The magnitudes of these partial charges were empirically increased during force field parametrization to account for the electronic polarization effects from an aqueous environment in a mean-field, average manner. In contrast, electronic induction is explicitly modeled in polarizable force fields. It has been shown that the improved modeling of electron distribution response to external electric fields associated with polarizable FFs leads to improved modeling of peptide folding cooperativity,4 base flipping and ion condensation of DNA,5,6 and more reliable crystal structure predictions.7
A variety of polarizable FFs have been developed using different formalisms to model polarizability.8–19 Two of the most widely used polarizable FFs are the AMOEBA FF18,20–23 and the Drude FF.19,24–33 Both have undergone more than a decade of continuous development and have parameters covering a wide range of biomolecules such as proteins,23,28 nucleic acids,31 lipids,29,34 and carbohydrates.30 The AMOEBA FF adopts the point induced dipole model in which each atom carries an induced dipole moment determined by the electric field and its atomic polarizability. Permanent dipole and quadrupoles are also assigned to each atomic site for a more accurate description of electrostatic interactions. The Drude FF adopts the classical Drude oscillator model where auxiliary charges (Drude oscillators or particles) are attached to non-hydrogen atoms with harmonic springs, and the displacement of the Drude particle relative to its parent atom represents the response to the external electric field. Virtual particles representative of lone pairs are included in the Drude FF to improve the treatment of electrostatic interactions typically involving hydrogen bond acceptors.
The charge distribution between a Drude particle and its parent atom is a finite difference representation of a dipole moment. Similarly, lone pairs can be considered as real space representations of permanent multipoles. Such analogy between the classical Drude oscillator model and the multipole and induced dipole (MPID) model suggests that in theory one can interconvert polarizable FFs between the two models. However, in practice whether such FF mapping is feasible depends critically on how good these finite difference approximations are and the quality of the original FF parametrization.
In this work, we convert the Drude polarizable force field from its original classical Drude oscillator formalism onto a permanent multipole and induced dipole formalism, which we refer to as MPID. We show that a direct mapping without any reparametrization can transfer the Drude FF into the MPID FF, yielding a similar level of agreement as the Drude FF in reproducing condensed phase properties of organic liquids, crystals, and interfaces. This study is partly inspired by our recent algorithm developments involving spherical harmonic treatment of multipoles and analytic treatment of induced dipole moments based on perturbation theory (PT) that significantly improves the computational speed and numerical stability for evaluating electrostatics in the context of multipole and induced dipole formalisms, respectively.35–37 We also incorporate the dispersion particle mesh Ewald (PME) method38 in the MPID simulations for more accurate modeling of long range van der Waals (vdW) interactions. Our results thus also serve as an additional validation of these novel simulation algorithms.
Using the perturbation theory approach for induced dipole with the MPID model allows fully reversible, symplectic, and highly energy conserving integration for molecular dynamics (MD) simulations, in contrast with any iterative self consistent field (SCF) methods. While the Drude model is usually used together with a carefully designed dual Langevin thermostat integrator25 for computational efficiency, where the Drude particles are coupled to a low temperature thermostat and the real atoms are thermostated at the simulation temperature, the MPID model can be directly used with ordinary integrators and allows for a larger time step. In addition, it avoids the need to set a Drude particle mass, Drude bond force constant, and Drude thermostat temperature and friction constant, though these issues are typically not a concern to users as they were determined during development of the Drude force field.25 The fact that the MPID model can be used as a drop-in replacement for the potential energy term for almost any existing integrator will facilitate the use of polarizable models in emerging simulation techniques, such as the reversible reference system propagation algorithm (r-RESPA)39 or the orthogonal space random walk (OSRW) method.40
The original polarizable hybrid quantum mechanics and molecular mechanics (QM/MM) method of Warshel and Levitt8 used induced dipoles to describe the MM response to the presence of a QM region, and the same approach has been used in more recently developed QM/MM methods such as the effective fragment potential,41,42 the TINKTEP QM/MM implementation of the AMOEBA force field,43 and the LICHEM QM/MM interface code.44 Examples of Drude oscillators being used as the polarizable MM part include a Gaussian/TINKER implementation by Lu and Zhang,45 a TURBOMOLE/CHARMM implementation by Riahi and Rowley,46 and the ChemShell QM/MM interface code.47,48 Given that the Drude force field has undergone extensive development efforts, and the currently available QM/MM tools with induced dipoles provide different treatments of QM/MM coupling and support different QM programs compared with the QM/MM implementations using the Drude model, the ability to map Drude parameters onto induced dipole functional forms will allow the community to access a wider range of the tools available for QM/MM simulations. In summary, the MPID model presented in this work improves the portability and expands the applicability of force fields developed for the classical Drude oscillator model.
II. METHODS
A. Mapping the Drude FF parameters into the MPID model
Mapping the FF parameters for induced dipoles is straightforward, as the atomic polarizability α is equivalent in both models. In the Drude FF, Drude particles are only attached to non-hydrogen atoms, so a mixture of polarizable and non-polarizable atoms is also present in the MPID FF as only non-hydrogen atoms carry induced dipole moments. Another important feature of the Drude FF is the anisotropic atomic polarizability implemented by assigning heterogeneous spring constants based on a pre-defined local reference frame for the virtual spring between a polarizable atom and its Drude particle.49 Converting this anisotropy into the MPID FF involves treating α as a diagonal tensor with its element α11, α22, and α33 explicitly given as FF parameters using the same reference frame.
In the Drude FF, the interaction between two induced dipole on atoms separated by one or two covalent bonds (the 1-2 or 1-3 interactions) is screened by a Thole damping function,50
where u = rij(αiαj)−1/6 is the dimensionless distance between atoms i and j based on their distance rij and atomic polarizabilities αi and αj and a is a Thole screening factor given by a = ai + aj as the sum of the two atomic Thole factors. This screening function is equivalent to the following smeared charge density implemented in MPID:
More specifically, the Thole damping function is implemented within the quasi internal (QI) coordinates for spherical harmonic multipoles,35,36 with damped interactions for up to hexadecapole derived and listed in Table I (see Eqs. (17)–(19) in Ref. 36 for more details). We note that Thole damping is universally applied to all induced dipole interactions in the MPID FF, in contrast with the Drude FF where only 1-2 and 1-3 induced dipole interactions were damped. A universal Thole damping scheme simplifies the induction calculation in MPID and by nature prevents polarization catastrophe, without the need to apply Drude hardwall constraints51 as in Drude simulations. For atoms that have no damping factor in the Drude FF, for example, the water oxygen atoms, a very large atomic Thole factor a = 8 is used.
TABLE I.
The spherical harmonic Thole damping factors for the energies (λ0 and λ1c/1s) and forces (λ0′ and λ1c/1s′) calculation in the QI frames.
| l = 0 | λ0 | |
| Charge | λ0′ | |
| l = 1 | λ0 | |
| Dipole | λ1c/1s | |
| λ0′ | ||
| λ1c/1s′ | ||
| l = 2 | λ0 | |
| Quadrupole | λ1c/1s | |
| λ0′ | ||
| λ1c/1s′ | ||
| l = 3 | λ0 | |
| Octopole | λ1c/1s | |
| λ0′ | ||
| λ1c/1s′ | ||
| l = 4 | λ0 | |
| Hexadecapole | λ1c/1s | |
| λ0′ | ||
| λ1c/1s′ |
Thole screening in the MPID FF differs from that in the AMOEBA FF in several aspects. The functional form is different, as AMOEBA assumes a smeared charge density given by . For the Thole screening factor a, MPID adopts an atom based factor a = ai + aj, while in the AMOEBA FF, a = min(ai, aj) is used and for most atoms, ai takes a constant value of 0.39. In addition, a single exclusion rule is used in the MPID FF in which for the 1-2 and 1-3 interactions only induced dipole–induced dipole interactions are computed, and the permanent multipole–permanent multipole and the permanent multipole—induced dipole interactions are excluded. In contrast, a more complicated set of two exclusion rules is used in the AMOEBA FF, resulting in two separate sets of dipoles (which are labeled with p and d subscripts), whose average appears in the energy expression.20,22
Lone pairs in the Drude FF are virtual particles carrying fixed point charges, with positions determined by the coordinates of their parent real atoms. To convert lone pairs into permanent multipoles, one can approximate the charge distribution composed of a real atom and its lone pairs using point multipole expansion at the real atom site. For the Drude to MPID mapping, the multipole expansion is truncated at the octupole order. For atoms without lone pairs in the Drude FF, the partial atomic charges were kept the same. Thus a mixture of atoms carrying point charges and atoms carrying permanent multipoles from point charges to octupole moments is present in the MPID FF. The remaining parts of the potential energy function, including the functional forms and FF parameters for all bonded terms and the nonbonded vdW interaction term, are identical between the Drude and MPID FFs.
Apart from the FF mapping of electrostatic interactions, two additional modifications were introduced in the MPID FF concerning the usage of novel algorithms for computing nonbonded interactions. The induced dipole moments are evaluated using the third order perturbation theory with optimized empirical coefficients (OPT3).37 The crux of OPT3 is to replace the self-consistent field iterations with a power series expansion motivated by perturbation theory.36 Truncating the expansion at third order and empirically optimizing the coefficients of each term against diverse molecular data yields OPT3, which is an efficient and accurate approximation to the full SCF solution.37 While an incompletely converged SCF solution is susceptible to severe artifacts resulting from inconsistencies in the polarization forces and energies, the PT based approaches are fully analytic, making them immune to such effects. The analytic nature of PT methods allows them to be used exactly as existing fixed-point-charge models are currently, thus permitting the use of the many integration techniques that have been developed over the last half century.37 The long range vdW interactions are evaluated using the dispersion PME (DPME) method.38,52 In particular, the direct-space correction algorithm developed by Wennberg et al. is used to handle the Lorentz–Berthelot combination rule for vdW parameters in the MPID FF.38
B. Molecular dynamics simulations and calculations of experimental observables
All methods described above have been implemented in the mpole module in the CHARMM simulation package,53 and all molecular mechanics (MM) calculations and molecular dynamics simulations were carried out with CHARMM. The MD integration time step, Δt equals 1 fs for simulations using the Drude FF and 2 fs for those with the MPID FF. Temperature and pressure control is performed with Nose-Hoover thermostats54,55 and Andersen barostats56 using the tpcontrol module in CHARMM. The Drude dual thermostat method25 is applied to Drude simulations, where non-Drude particles were coupled to a thermostat at the desired simulation temperature with characteristic response time τ = 0.1 ps and all the Drude particles were coupled to a thermostat at 1 K with τ = 0.005 ps. For MPID simulations, a single thermostat with τ = 0.1 ps was used. Pressure was kept at 1 atm using an Andersen barostat with response time of 0.2 ps for both Drude and MPID simulations.
Condensed phase simulations were carried out with periodic boundary conditions (PBCs). For the Drude FF, electrostatic interactions were calculated using PME57 with a real space cutoff of 12 Å on an approximately 1 Å grid with the sixth-order spline, and vdW interactions were truncated at 12 Å with a switch smoothing function from 10 to 12 Å. The nonbonded interaction lists were generated with a distance cutoff of 16 Å and updated heuristically. The PME κ value equals 0.34, and long-range corrections (LRCs) were applied to take account of vdW interactions beyond the truncation with an isotropic approximation.
For the MPID FF, both electrostatics and vdW interactions were evaluated using PME methods. For electrostatics, the PME splitting parameter κ = 0.45 and a real space cutoff of 8.9 Å were used for charges and dipoles, while a slightly smaller real space cutoff of 8.7 Å was used for interactions involving higher order multipoles (quadrupoles and octupoles) as they attenuate faster than charges and dipoles. For vdW interactions, a real space cutoff of 12 Å and a κ value of 0.34 were used for the DPME term. Covalent bonds to hydrogen atoms were constrained by SHAKE58 in all simulations.
Simulations of neat liquids were carried out using cubic boxes composed of 256 molecules for most organic molecules studied. For N-methylacetamide (NMA) and hexadecane, 128 and 64 molecules were simulated, respectively. Starting structures were prepared using Packmol59 and were equilibrated with 10 ps NVT simulations, followed by 10 ps NPT simulations using a 0.5Δt time step (0.5 fs for the Drude and 1 fs for the MPID simulations). 10 ns production runs were then carried out with Δt time step (1 fs for Drude and 2 fs for MPID) in the NPT ensemble. Coordinates were saved every 1 ps. From the 10 ns MD simulations, molecular volume is computed as
where V is the volume of the simulation box and N is the number of molecules. Heat of vaporization is computed as
where is the average potential energy per molecule from bulk phase simulations, k is the Boltzmann constant, T is the simulation temperature, and is the average potential energy of a single molecule from 10 ns gas phase simulations. Static dielectric constant is evaluated with
where M is the total dipole moment of the whole simulation system and is the optical dielectric constant estimated from the Clausius-Mossotti equation from molecular polarizability.1 Isothermal compressibility is computed from the fluctuation of volume,
Additional simulations were carried out in the canonical NVT ensemble to compute viscosity, with system volume set to be the ensemble averaged volumes from the NPT simulations and the starting coordinates and velocities to be those from the last frames of the 10 ns NPT simulations. 11 ns NVT simulations were run, and the last 10 ns were used in the analysis for which pressure tensors were recorded every integration step. The shear viscosity η is obtained from the autocorrelation function of off-diagonal pressure tensor components (Pxy, Pyz, and Pxz) following the Green-Kubo formalism:
The coordinates and velocities for the last frame of the NVT simulations were used to initialize NVE simulations for the calculation of self-diffusion coefficient D0. The system size correction proposed by Yeh and Hummer is used,
where L is the length of the simulation box, η is the viscosity, and DPBC is the uncorrected diffusion coefficient calculated from the mean squared displacement of the center-of-mass coordinate ri for each molecule with the Stokes-Einstein relation,
Crystal structure simulations were run for the orthorhombic crystals of benzene, α-D-galactose, and β-D-glucose. For each crystal structure, the unit cell was transformed using the P212121 symmetry operators to generate a 2 × 2 × 2 crystal lattice containing 32 molecules. Starting unit cell structures were taken from the Cambridge Structural Database (CSD) with CSD id BENZEN02, ADGALA01, and GLUCSE01, respectively. 11 ns NPT simulations were carried out, with the last 10 ns used for the analysis.
MD simulations of water/vapor, alkane/vapor, and alkane/water interfaces were carried out to evaluate surface tensions. Simulation systems of vapor interfaces were prepared by taking the last frames of liquid NVT simulations and changing the periodic boundary condition from L × L × L cubic boxes to L × L × 3L tetragonal ones to create slabs with two vapor interfaces. 11 ns NVT simulations were carried out, with the last 10 ns used for the analysis. The length of the production run was doubled to 20 ns for alkane/vapor systems due to the difficulty in converging surface tensions. For alkane/water interfaces, water molecules were filled in the L × L × 3L alkane/vapor systems, and simulations were carried out in the NPAT ensemble,60,61 which allows Lz variation to maintain a constant normal pressure (P) of 1 atm and a constant surface area (A) of L2. The octane/water system contains 216 octane and 3852 water molecules, while the hexadecane/water system contains 64 hexadecane and 2030 water molecules. 11 ns NPAT simulations were carried out, with the last 10 ns used for the analysis. The surface or interfacial tension γ is computed as
where Lz is the length of the simulation box normal to the interface, Pzz is the normal component of the internal pressure tensor, and Pxx and Pyy are the tangent components. The prefactor of 0.5 takes into account that there are two interfaces in the simulations.
III. RESULTS
A. Intramolecular properties
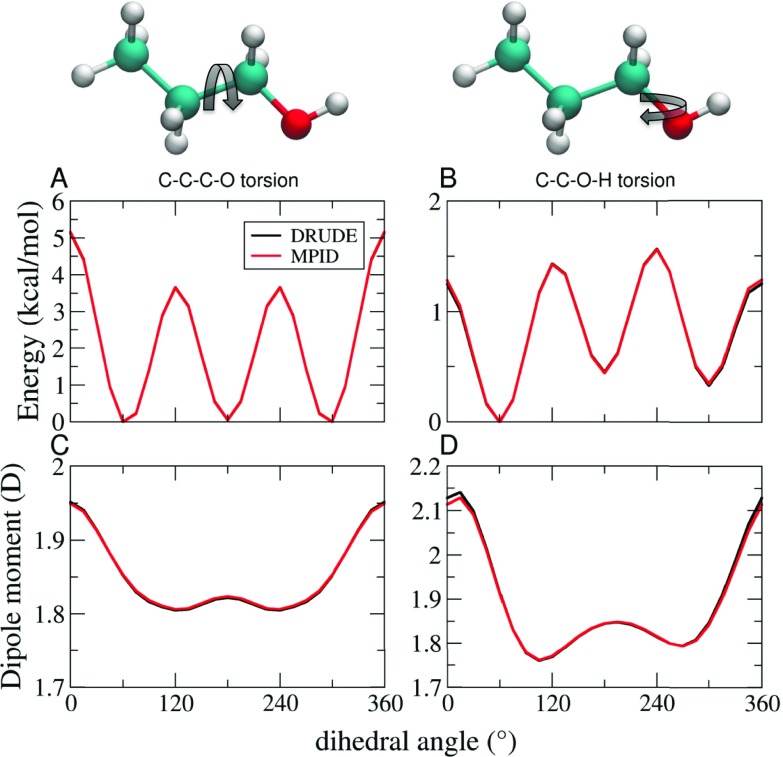
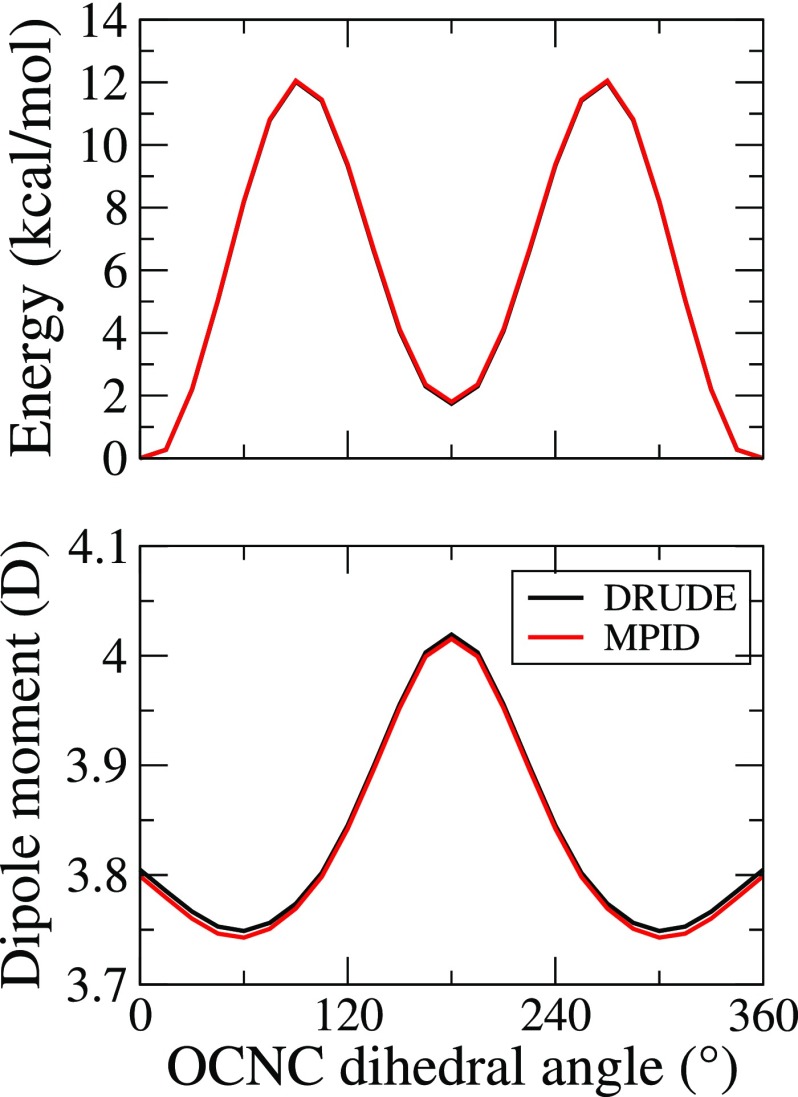
We initially investigate the ability of MPID to reproduce intramolecular properties that were originally parametrized using the Drude formalism. Potential energy scans around dihedrals of 1-propanol were performed as an example of intramolecular interactions, since dihedrals are the softest degrees of freedom of the internal bonded terms. As shown in Fig. 1, the one-dimensional energy scans around both the CCCO and CCOH torsions agree well between the Drude and MPID FFs. The largest deviation was observed when the CCOH dihedral equals 0°, with MPID overestimating the total potential energy by 0.04 kcal/mol. A similar level of agreement was obtained for the dipole moments as a function of conformation for both the CCCO and CCOH surfaces. Similar analysis was performed for rotation about the peptide bond in N-methylacetamide (Fig. 2). Again, potential energies and the dipole moments are nearly identical as a function of conformation. These, and similar results for diethylether and butane (Figs. S1 and S2 in the supplementary material), show that the mapping procedure yields nearly ideal agreement between the two FFs.
FIG. 1.
Potential energy surfaces for rotation around dihedral angles in 1-propanol from the Drude and MPID calculations are performed for the (a) C–C–C–O and (b) C–C–O–H torsions. The dependence of total dipole moment of the molecule on those torsions is shown in (c) and (d), respectively.
FIG. 2.
Potential energy surfaces for rotation around the peptide bond for N-methylacetamide from the Drude and MPID calculations.
B. Intermolecular interactions
The parametrization of water models is usually the first step in force field development. For the Drude FF, three water models were developed, including SWM4-DP,24 SWM4-NDP,26 and SWM6.27 The SWM4-DP model assigns positive charges to the Drude particles and was not used in subsequent development and applications as negatively charged Drude particles are a physically more meaningful representation of the electronic degrees of freedom. We convert the SWM4-NDP and the SWM6 water models from the classical Drude oscillator formalism to the MPID formalism, and compared the equilibrium geometries and energetics of gas phase water clusters. As shown in Table II, the optimized geometries of the water dimer were very similar between the Drude and the MPID formalism for both water models. The differences associated with FF mapping are between 0.004 and 0.006 Å for the oxygen-oxygen distances, and about 0.02 kcal/mol for the interaction energies. These differences are much smaller than the deviation of computational results from experimental measurements.62,63 Calculation results of larger water clusters (H2O)n for n = 3-10 are listed in Table S1 of the supplementary material. The optimized geometries computed with polarizable FFs were compared with those from ab initio calculations at the MP2 level with complete basis set (CBS) limit.64 The Drude and the MPID SWM6 models had very similar structural deviations as measured by unweighted average root mean square deviations (RMSDs) (Table II), while the MPID SWM4 model is worse than the associated Drude model. Concerning the energetic deviations for these geometries, they are larger with MPID for both water models. These results indicate that the interactions of water clusters are very sensitive to the off-center charge distributions as represented by lone pairs in the Drude FF, and converting them into point multipoles at the atomic sites cannot reproduce all electrostatic characteristics of the off-center lone pairs. Consistent with this are quantum mechanical/molecular mechanical (QM/MM) calculations of water clusters suggesting that the water molecules have large quadrupole moments that require six partial charge sites to be adequately represented.65 Additional studies are required to determine if this can be overcome by reparametrizing the multipoles or the presence of off-center charges is necessary to accurately treat subtle aspects of hydrogen bond interactions.
TABLE II.
Properties of the SWM4-NDP and the SWM6 water models with the Drude and the MPID FFs. For water dimer, the interaction energy, the distance between oxygen atoms (dOO), the acceptor angle (θA), the donor angle (θD), and the total dipole moment are listed. For water clusters, unweighted average energy difference and structural RMSDs for 23 conformations with n = 3-10 are listed. The properties of liquid water, including heat of vaporization ΔH, molecular volume 〈v〉, isothermal compressibility κT, shear viscosity η, self-diffusion constant D0, and dielectric constant ε, were obtained at 298.15 K and 1 atm.
| Drude | MPID | ||||
|---|---|---|---|---|---|
| SWM4-NDP | SWM6 | SWM4-NDP | SWM6 | Expt. | |
| Water dimer | |||||
| Energy (kcal/mol) | -5.15 | -5.27 | -5.13 | -5.25 | -5.44 |
| dOO (Å) | 2.828 | 2.787 | 2.834 | 2.791 | 2.98 |
| θA (deg) | 70.8 | 56.5 | 69.2 | 56.4 | 58 |
| θD (deg) | 56.8 | 55.6 | 56.7 | 55.6 | 51 |
| Dipole (D) | 2.062 | 2.480 | 2.096 | 2.473 | 2.643 |
| Water cluster (H2O)n = 3-10 | |||||
| 〈RMSD〉 (Å) | 0.218 | 0.213 | 0.248 | 0.211 | |
| 〈EMM-EMP2〉 (kcal/mol) | 3.32 | 2.45 | 4.48 | 2.88 | |
| Liquid water | |||||
| ΔH (kcal/mol) | 10.499 (0.002) | 10.52 (0.00) | 10.35 (0.00) | 10.40 (0.00) | 10.51 |
| 〈v〉 (Å3) | 29.898 (0.006) | 29.87 (0.01) | 30.26 (0.00) | 30.25 (0.00) | 30.00 |
| κT (10−10 m2N−1) | 3.86 (0.03) | 4.15 (0.05) | 4.07 (0.04) | 4.21 (0.04) | 4.52 |
| η (cP) | 0.66 (0.02) | 0.89 (0.01) | 0.66 (0.01) | 0.91 (0.02) | 0.89 |
| D0 (10−5 cm2/s) | 2.92 (0.17) | 2.13 (0.02) | 3.03 (0.37) | 2.11 (0.06) | 2.3 |
| ε | 78.0 (0.4) | 75.3 (1.7) | 73.8 (1.1) | 71.5 (1.0) | 78.4 |
While there is a small degradation in the ability to treat the water clusters with the MPID-based water models, as evident in Table II, the SWM6 water model represents a substantial improvement over the SWM4-NDP model for water clusters, while yielding similar or improved agreement for a number of condensed phase properties.27 For the Drude model, SWM6 incurs more computational cost due to the two additional lone pairs for each water molecule. With the MPID formalism, both SWM6 and SWM4-NDP water models lead to the same simulation speed as both models place charges on hydrogen atoms and multipoles on oxygen atoms. Thus, the SWM6 model is the default water model for the MPID FF, and it was used throughout the remainder of this study.
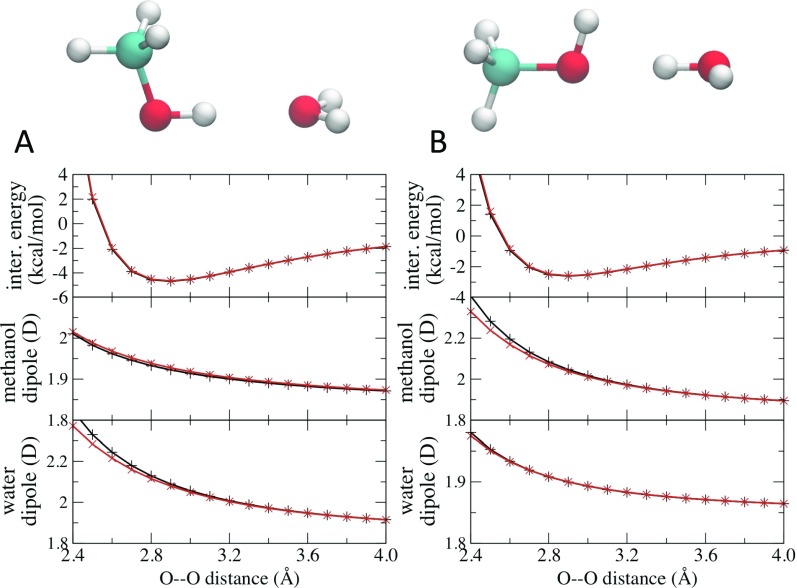
Additional analysis of intermolecular interactions involved those between a methanol molecule and a water molecule with methanol being either the hydrogen bond donor [Fig. 3(a)] or the acceptor [Fig. 3(b)]. In both cases, the interaction energies between methanol and water computed using the MPID formalism agreed with those from the Drude calculations for the donor-acceptor distances from 2.4 Å to 4.0 Å. The derivatives of potential energies, i.e., forces, also agreed well (see Fig. S1 of the supplementary material). The magnitudes of dipole moments for water and methanol increased when the two molecules approached each other, as one would expect from fully polarizable FFs, and their dependence on the donor-acceptor distances compared favorably between the two formalisms. As shown in Fig. 3, MPID led to slightly weaker intermolecular interactions compared to Drude when the distances between water oxygen and methanol oxygen became small. The deviation was due to the underestimation of the dipole moments of hydrogen bond acceptor molecules. With donor-acceptor distance less than 2.5 Å, the intermolecular interaction was dominated by the strongly unfavorable repulsion terms such that the difference in electrostatics has little impact on the conformational sampling of molecular dynamics simulations. The small difference in the dipole moments of the acceptor oxygen atoms at short distances further suggests small deviations between the models associated with the use of lone pairs on the Drude vs. multipoles in MPID. Similar results were observed for the interaction between NMA and water with NMA being either a hydrogen bond donor or acceptor (Fig. S4 of the supplementary material). The interaction energies between two benzene molecules computed with both Drude and MPID also agree very well, with the benzene dimer either in the sandwich or the T-shaped conformations (Fig. S5 of the supplementary material).
FIG. 3.
Interaction energies between methanol and water, and their dipole moments along the distance between the methanol oxygen and the water oxygen atom calculated using the Drude (black) and the MPID (red) FFs. Both molecules were constrained at their equilibrium geometries, and the scanning was carried out with the donor-acceptor distance from 2.4 Å to 4.0 Å.
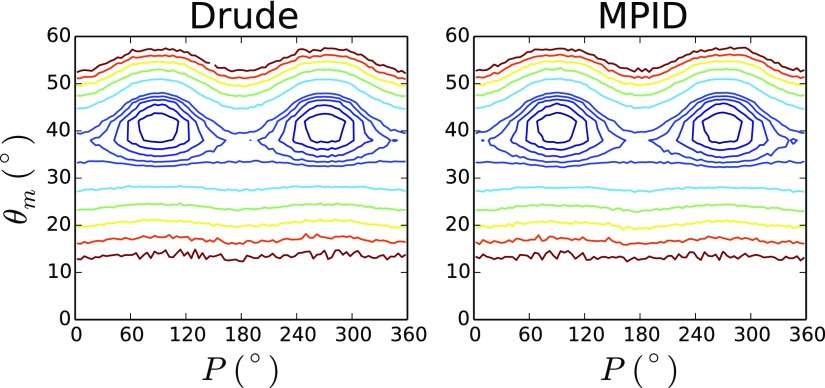
A final test involved ring puckering in tetrahydrofuran (THF) analyzed using the 2D potential of mean force (PMF) surfaces on the puckering phase angle and amplitude66 computed from MD trajectories used to evaluate the condensed phase properties (see below). As shown in Fig. 4, the Drude and the MPID FFs lead to identical PMFs for THF ring puckering. This further suggests that the small alteration in nonbonded interactions associated with the electrostatic mapping from Drude to MPID has minimal impact on the bonded, internal degrees of freedom.
FIG. 4.
2D PMF surfaces of ring puckering phase angle P and amplitude θm for THF. Contours were plotted at the interval of 0.1 kcal/mol from 0.1 to 0.5 kcal/mol, and at the interval of 0.5 kcal/mol from 0.5 to 3 kcal/mol.
C. Condensed phase properties of liquids
Condensed phase properties of water and of a series of small molecules were calculated from 10 ns NPT simulations. Before comparing the MPID results with those from the Drude model and the experimental values, we first explore the effects of the two algorithmic approximations introduced in the simulation protocols of the MPID model for evaluating nonbonded interactions. The OPT3 method37 was used for the calculation of induced dipole at each integration step as a computationally efficient replacement of the commonly used iterative SCF solvers. The DPME method38 was used to explicitly evaluate the r−6 dispersion interactions beyond the 12 Å cutoff as an alternative to applying standard isotropic LRC. While the isotropic LRC is adequate for neat liquids it is inappropriate for heterogeneous systems, such as lipid bilayers, where the DPME method will be of utility based on the specific treatment of the long-range interactions in the context of the Ewald formalism. However, for neat liquids, both methods should yield similar results, offering a test of the recently implemented DPME method. For all 13 liquids considered in this work, MD simulations were carried out using the same MPID FF parameters, with induced dipoles computed using either the SCF or the OPT3 solver, and long range vdW interactions evaluated using either LRC or DPME (Table S2 of the supplementary material). Condensed phase properties obtained from simulations with the SCF dipole solver and the OPT3 algorithm were found to agree within simulation uncertainties. This is encouraging because the linear coefficients in the OPT3 method were optimized using the AMEOBA FF,37 and our results suggest that this set of coefficients is transferable to other polarizable force fields employing the induced point dipole model. The more expansive OPT4 algorithm also leads to good agreement with the SCF dipole solver, but the improvement over the OPT3 method is not significant for the MPID model to justify its additional computational cost (Table S2). Similarly, replacing LRC with the more versatile DPME method leads to small, typically negligible change compared to the deviations associated with FF mapping. In short, our liquid simulations validate the OPT3 and the DPME methods, and they will be used in the context of the MPID FF.
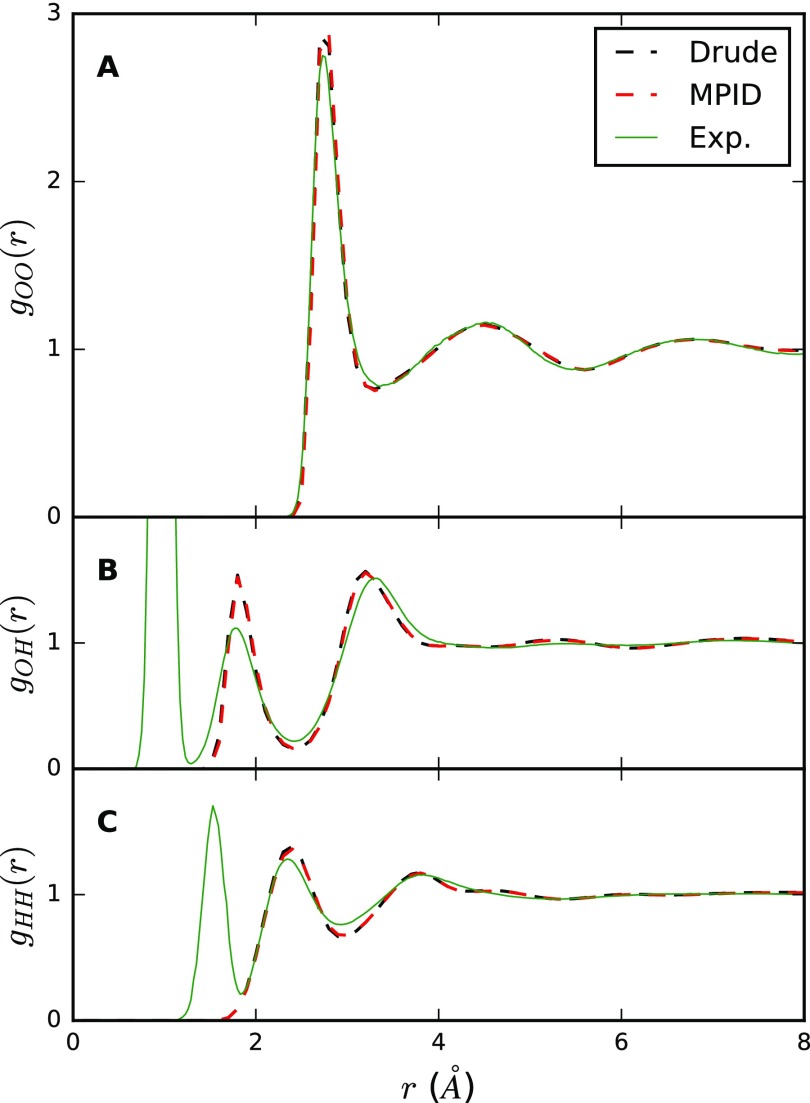
Liquid water properties at ambient conditions are shown in Table II. Mapping the Drude SWM6 model onto MPID leads to a slightly smaller heat of vaporization (ΔH) and a slightly larger molecular volume (〈v〉). As the SWM6 model was explicitly optimized to match these experimental observables with the Drude formalism, the MPID FF has larger deviation from experimental values (1% relative error for ΔH and 〈v〉) than the Drude FF. For properties that were not the directly targeted during the SWM6 parametrization such as the isothermal compressibility (κT), Drude and MPID calculations led to very similar results compared to the experimental data. We also compared the self-diffusion constant of water, a transport property very sensitive to the short-range liquid structures. Diffusion constants calculated from MD trajectories without system size correction agreed within uncertainties (1.76 ± 0.02 × 10−5 cm2/s with the Drude model and 1.75 ± 0.06 × 10−5 cm2/s with MPID), and as the calculated shear viscosities were very similar, the corrected diffusion constant D0 also agreed well (2.13 × 10−5 cm2/s with the Drude model and 2.11 × 10−5 cm2/s with MPID). As shown in Fig. 5, the atom-atom radial distribution functions (RDFs) obtained from the Drude and MPID simulations are very similar, and both reproduce well the experimental neutron diffraction data.67 The temperature dependence of water density obtained from both models also closely resembles each other, and the temperature of maximum density is found to be around 250 K for the MPID model (Fig. S6 of the supplementary material).
FIG. 5.
Radial distribution functions of the oxygen-oxygen (a), oxygen-hydrogen (b), and hydrogen-hydrogen (c) atom pairs of water at ambient condition computed from MD simulations with Drude (black) and MPID (red).
While water molecules in additive FFs assume a fixed dipole moment, with polarizable FFs their dipole moments vary according to the instant electric environment. MPID led to an average dipole moment of 2.40 D for liquid water at ambient conditions, which was slightly smaller than the original Drude value of 2.43 D, and the difference was due to the population of strongly polarized water being slightly smaller (Fig. S7 of the supplementary material). The dielectric constant (ε) of water from the MPID model is 72 ± 1, which is smaller than the Drude value of 75 ± 2 and the experimental value of 78.4. The deviation between MPID and experimental dielectric constants is larger than most current state-of-the-art water models, indicating the approximations introduced in the electrostatics mapping have non-negligible effects on the long-range structure of water. We anticipate that a reparametrization of the SWM6 water model within the MPID formalism can fully reproduce experimental dielectric constant as well as the density and the heat of vaporization, and this will be pursued in a further study.
Thirteen neat organic liquids were simulated using both the Drude and the MPID model, and their condensed phase properties were compared with data from the experimental measurements in Table III. Heat of vaporization and molecular volumes were computed for all organic molecules considered, including methanol, ethanol, tetrahydrofuran, diethyl ether, dimethyl ether, methanethiol, N-methylacetamide, benzene, and five alkanes (ethane, butane, octane, hexadecane, and cyclohexane). Two higher order fluctuation properties, dielectric constants and isothermal compressibility were also used to benchmark the MPID model. In particular, dielectric constants were computed for polar molecules, and isothermal compressibility was computed for those simulated at 298.15 K. As shown in Table III, the MPID FF was able to accurately reproduce these experimental observables. For example, the ΔH and 〈v〉 of methanol equal 8.98 kcal/mol and 66.97 Å3 with the MPID model, which is very close to the experimental values of 8.95 kcal/mol and 67.23 Å3, respectively. The dielectric constant is 29.6, close to the experimental ε of 32.6. Predicted isothermal compressibilities were very consistent between the Drude and MPID formalism, although both deviated substantially from experiments. As the MPID FFs were generated by direct mapping from the Drude FFs without any reparametrization, no improvement in the correlation with experimental measurements should be expected for MPID compared to the original Drude models.
TABLE III.
Condensed phase properties of neat organic liquids from simulations and experiments.
| Drude | MPID | Expt. | ||
|---|---|---|---|---|
| Methanol | ΔH (kcal/mol) | 9.13 (0.02) | 8.98 (0.00) | 8.95 |
| (298.15 K) | 〈v〉 (Å3) | 66.59 (0.02) | 66.97 (0.03) | 67.23 |
| ε | 29.4 (0.8) | 29.6 (0.9) | 32.61 | |
| κT (10−10 m2N−1) | 7.31 (0.08) | 7.31 (0.04) | 12.48 | |
| Ethanol | ΔH (kcal/mol) | 9.87 (0.02) | 9.69 (0.01) | 10.11 |
| (298.15 K) | 〈v〉 (Å3) | 97.92 (0.03) | 98.43 (0.02) | 96.92 |
| ε | 20.5 (1.3) | 18.3 (0.2) | 24.85 | |
| κT (10−10 m2N−1) | 10.7 (0.3) | 10.9 (0.2) | 11.53 | |
| Tetrahydrofuran | ΔH (kcal/mol) | 7.75 (0.03) | 7.83 (0.01) | 7.65 |
| (298.15 K) | 〈v〉 (Å3) | 134.57 (0.04) | 134.93 (0.04) | 135.6 |
| ε | 7.35 (0.05) | 7.52 (0.06) | 7.43 | |
| κT (10−10 m2N−1) | 9.1 (0.3) | 9.2 (0.1) | 8.04 | |
| Diethyl ether | ΔH (kcal/mol) | 6.57 (0.02) | 6.61 (0.04) | 6.48 |
| (298.15 K) | 〈v〉 (Å3) | 176.1 (0.1) | 176.0 (0.1) | 173.9 |
| ε | 4.75 (0.03) | 4.59 (0.05) | 4.24 | |
| κT (10−10 m2N−1) | 20.4 (0.5) | 19.7 (0.3) | 19.75 | |
| Dimethyl ether | ΔH (kcal/mol) | 5.20 (0.01) | 5.25 (0.01) | 5.14 |
| (248.34 K) | 〈v〉 (Å3) | 104.00 (0.03) | 104.42 (0.03) | 104.9 |
| ε | 7.48 (0.06) | 7.47 (0.05) | 6.53 | |
| Methanethiol | ΔH (kcal/mol) | 5.86 (0.01) | 5.87 (0.01) | 5.87 |
| (278.9 K) | 〈v〉 (Å3) | 90.28 (0.07) | 90.72 (0.04) | 90.17 |
| ε | 8.90 (0.08) | 8.80 (0.06) | n.a. | |
| N-methylacetamide | ΔH (kcal/mol) | 14.00 (0.02) | 14.29 (0.02) | 13.7 |
| (373 K) | 〈v〉 (Å3) | 135.71 (0.06) | 138.16 (0.02) | 135.9 |
| ε | 70 (4) | 60 (4) | 100 | |
| Benzene | ΔH (kcal/mol) | 8.19 (0.02) | 8.21 (0.02) | 8.08 |
| (298.15 K) | 〈v〉 (Å3) | 146.9 (0.3) | 146.5 (0.1) | 148.00 |
| κT (10−10 m2N−1) | 7.9 (0.5) | 9.6 (1.4) | 9.66 | |
| Ethane | ΔH (kcal/mol) | 3.36 (0.01) | 3.63 (0.01) | 3.53 |
| (184.55 K) | 〈v〉 (Å3) | 90.4 (0.1) | 90.8 (0.1) | 91.8 |
| Butane | ΔH (kcal/mol) | 5.20 (0.02) | 5.49 (0.03) | 5.37 |
| (272.65 K) | 〈v〉 (Å3) | 160.8 (0.1) | 160.35 (0.04) | 160.5 |
| Octane | ΔH (kcal/mol) | 9.92 (0.05) | 10.01 (0.02) | 9.92 |
| (298.15 K) | 〈v〉 (Å3) | 272.68 (0.07) | 272.40 (0.09) | 269.8 |
| κT (10−10 m2N−1) | 13.1 (0.3) | 12.4 (0.1) | 12.82 | |
| Hexadecane | ΔH (kcal/mol) | 19.60 (0.06) | 19.86 (0.10) | 19.44 |
| (298.15 K) | 〈v〉 (Å3) | 488.6 (0.3) | 489.0 (0.2) | 488.3 |
| κT (10−10 m2N−1) | 8.5 (0.1) | 8.7 (0.3) | 8.57 | |
| Cyclohexane | ΔH (kcal/mol) | 7.08 (0.03) | 7.18 (0.02) | 7.89 |
| (298.15 K) | 〈v〉 (Å3) | 189.34 (0.07) | 189.75 (0.06) | 180.6 |
| κT (10−10 m2N−1) | 16.6 (1.0) | 13.7 (0.3) | 11.30 |
Comparison of the molecular volumes obtained from Drude and MPID simulations showed that 〈v〉 typically increased with MPID for polar molecules. The largest changes were observed for water (1.3% increase), ether (1.0% increase), and NMA (1.8% increase), suggesting that the intermolecular interactions were slightly underestimated by MPID. This is consistent with the gas phase observations that MPID leads to slightly smaller interaction energies for the water dimer (Table II) and the methanol-water dimer (Fig. 3), and might be recovered by, for example, a systematic increase of atomic polarizability in the MPID FF. However, the increase of 〈v〉 associated with MPID sometimes moved the computational results towards experimental values such as for methanol and methanethiol, and in general, the relative deviations between MPID calculations and experiments are comparable to those between Drude and experiments (Table IV). This suggests that the deviations between MPID and Drude represent off-diagonal errors compared to the target of force field parametrization-experimental properties, and the direct mapping approach presented here can generate a polarizable force field based on the MPID formalism that is ready to be used in MD simulations.
TABLE IV.
The mean signed deviations (MSDs), root mean square deviations (RMSDs), average relative deviations (ARD), and average absolute relative deviations (AARDs) of condensed phase properties for all 13 liquids considered in this work.
| Drude vs. Expt. | MPID vs. Expt. | MPID vs. Drude | ||
|---|---|---|---|---|
| Heats of vaporization | MSD | -0.028 | 0.047 | 0.067 |
| (kcal/mol) | RMSD | 0.261 | 0.308 | 0.171 |
| ARD | -0.7% | 0.5% | 1.3% | |
| AARD | 2.2% | 2.5% | 1.9% | |
| Molecular volumes | MSD | 0.72 | 1.08 | 0.35 |
| (Å3) | RMSD | 2.62 | 2.77 | 0.76 |
| ARD | 0.2% | 0.6% | 0.4% | |
| AARD | 1.0% | 1.1% | 0.5% | |
| Dielectric constants | MSD | −6 | −8 | −2 |
| RMSD | 12 | 16 | 4 | |
| ARD | -5.1% | -8.6% | -4.4% | |
| AARD | 13% | 15% | 5% | |
| Isothermal compressibilities | MSD | -0.1 | -0.3 | -0.2 |
| (10−10 m2 N−1) | RMSD | 2.6 | 2.0 | 1.2 |
| ARD | -1.1% | -2.3% | 0.2% | |
| AARD | 16% | 11% | 6% |
D. Crystal properties
Crystal structure simulations of small molecules provide a sensitive method of testing nonbonded parameters in force field optimization and validation,68,69 and they were routinely used in the development of nucleic acid and carbohydrate force fields.30,70–73 NPT simulations of benzene (CSD id: BENZEN02), α-D-galactose (ADGALA01), and β-D-glucose (GLUCSE01) crystals were carried out with the MPID and the Drude models, and the ensemble averaged lattice parameters computed from the last 10 ns production runs were compared with the crystallographic data. As shown in Table V, the crystal shapes and volumes agreed well between Drude simulations, MPID simulations, and experiments. The largest relative deviation of the MPID lattice constants was 1.1% compared with Drude results and 2.7% compared with experimental values, occurring with the lattice constants a and c of the D-glucose crystal. These two lattice constants changed in the opposite directions such that the unit cell volumes were the same between Drude and MPID, which was very close to the experimental volume.
TABLE V.
Crystal lattice parameters and volumes from crystal simulations with the Drude FF and the MPID FF.
| Simulation system | Lattice constant | Drude | MPID | Expt. | |
|---|---|---|---|---|---|
| BENZEN02 | Benzene 270 K | a (Å) | 7.407 (0.005) | 7.387 (0.004) | 7.460 |
| b (Å) | 9.677 (0.003) | 9.664 (0.001) | 9.666 | ||
| c (Å) | 7.118 (0.004) | 7.121 (0.002) | 7.034 | ||
| Volume (Å3) | 510.2 (0.5) | 508.3 (0.3) | 507.21 | ||
| ADGALA01 | α-D-galactose 298.15 K | a (Å) | 6.000 (0.002) | 6.008 (0.001) | 5.939 |
| b (Å) | 8.043 (0.003) | 8.018 (0.001) | 7.871 | ||
| c (Å) | 15.875 (0.007) | 15.896 (0.002) | 15.800 | ||
| Volume (Å3) | 766.1 (0.5) | 765.8 (0.2) | 738.58 | ||
| GLUCSE01 | β-D-glucose 298.15 K | a (Å) | 8.878 (0.000) | 8.958 (0.001) | 9.205 |
| b (Å) | 12.757 (0.001) | 12.789 (0.001) | 12.640 | ||
| c (Å) | 6.901 (0.000) | 6.821 (0.000) | 6.654 | ||
| Volume (Å3) | 781.59 (0.07) | 781.51 (0.07) | 774.20 |
E. Interface properties
The last set of simulations involved more heterogeneous systems including water/air, alkane/air, and alkane/water interfaces. Surface tensions of water, octane, and hexadecane were calculated using the pressure profiles obtained from NVT simulations with both the Drude and the MPID FFs. As listed in Table VI, MPID led to slightly larger surface tensions compared to Drude and shifted the simulation results closer to experimental measurements. We emphasize that the standard isotropic LRC applied in the Drude simulations is much less accurate compared to the dispersion PME used in the MPID simulations for describing long range vdW interactions in such highly anisotropic systems. This is consistent with the isotropic treatment of the system making it formally only suitable for homogenous systems. For the interfacial tension at the octane/water and hexadecane/water interfaces, MPID and Drude agreed within the statistical uncertainties. The simulation results were also close to the experimental values, albeit being slightly smaller. The alkane/water interfacial tension can be considered as a direct estimation of the strength of hydrophobic interactions, and the ability to reproduce experimental values with both the Drude and the MPID FFs served as good validation for both polarizable models.
TABLE VI.
Surface tension of water, octane, and hexadecane, and interfacial tension of octane/water interface and hexadecane/water interface computed from simulations using the Drude FF and the MPID FF. The Drude simulations were carried out with LRC for long range vdW interactions, while MPID simulations were run with DPME.
| Tension (dyn/cm) | Drude | MPID | Expt. |
|---|---|---|---|
| Water/vapor | 59.4 (0.5) | 60.3 (0.4) | 72.0 |
| Octane/vapor | 17.1 (0.1) | 21.6 (2.6) | 21.1 |
| Hexadecane/vapor | 21.7 (0.7) | 24.3 (1.6) | 27.0 |
| Octane/water | 48.4 (0.8) | 47.5 (0.7) | 50.8 |
| Hexadecane/water | 50.2 (1.1) | 49.9 (1.2) | 53.3 |
IV. DISCUSSIONS AND CONCLUSION
In this work, we map the CHARMM Drude FF from its original classical Drude oscillator formalism on to the multipole and induced dipole formalism, and validate the resulting MPID polarizable FF using a range of molecular systems including 14 liquids, 3 crystals, and 5 interfaces. The difference between the MPID model and the Drude model in predicting experimental observables was found to be small, typically much smaller than the inherent deviations between computation and experiments. Our results suggest that the MPID model, which directly utilizes the empirically optimized parameters from the Drude FF, offers similar quality in reproducing condensed phase properties compared with the original Drude model.
The similarity between the classical Drude oscillator model and the induced point dipole model has often been speculated.74–77 Here we quantify their similarity using an extensive set of molecules with realistic polarizable force field parameters. The fact that the Drude FF can be directly converted into MPID without any reparametrization illustrates that the Drude oscillator model and the induced dipole model are different representations of the same physical model for including electronic polarization.
As part of this study, we convert the atomic monopole and lone pair associated charges to point multipoles. While the resulting intermolecular interactions from this mapping are highly similar, some alterations in hydrogen bonding, including degradation in the agreement with the energies of water clusters, upon going from the Drude to MPID models are observed. While additional investigations are required, this indicates that the use of off-center lone pairs may impart advantages over the use of multipoles alone with respect to the treatment of intermolecular interactions. In addition, the use of Lennard-Jones parameters on Drude particles has been shown to improve the accuracy of modeling of Mg2+-water interactions78 and in the treatment of halogens (Lin and MacKerell, work in progress), which represents an additional possible advantage of the Drude model not directly accessible to the MPID formalism as presented.
Doing the conversion undertaken in this study in the opposite direction would also be feasible. For example, Devereux et al. present a study on expressing multipoles with distributed lone pairs for computationally efficient MD simulations.79 Chialvo et al. investigated the effect of replacing the Gaussian induced dipole polarization in the Gaussian polarizable charge water model with a Gaussian Drude oscillator model.75 Concerning the integration methods, Albaugh et al. developed extended Lagrangian approaches for AMOEBA where auxiliary induced dipoles are propagated.80,81
While MPID adopted the same multipole and induced dipole formalism as the AMOEBA FF, there exist a number of differences. To model bonded interactions, MPID uses simple harmonic functions as in the CHARMM or AMBER additive force fields, while AMOEBA includes higher order anharmonic as well as coupling terms. The vdW interactions are modeled with the 12-6 Lennard-Jones potentials in MPID and with a buffered 14-7 potential as proposed by Halgren82 in AMOEBA. Most importantly, the treatment of electrostatic interactions also differs. MPID only assigns induced dipole to non-hydrogen atoms, thus largely reducing the number of inducible dipole moments to evaluate at each time step. Similarly, permanent multipoles are only assigned to a subset of atoms in MPID. The molecular systems modeled by MPID contain atomic sites represented at different levels of detail, either carrying a point charge only, or a point charge and an induce dipole, or multipole expansion to octupole plus induce dipole. This leads to significant improvement in computational efficiency.
Further speed-up of MPID comes from novel simulation algorithms, including evaluating multipole interactions in the QI spherical harmonic coordinates35 and computing induced dipoles with perturbation theory.36,37 Our results serve as a further validation of the implementations of these algorithms in CHARMM and show that the recently developed OPT3 method offers very high level of accuracy in reproducing chemical properties. Furthermore, it is shown that the dispersion PME method may be used in conjunction with the MPID model allowing for more accurate treatment of long-range dispersion interactions. We note that DPME is also compatible with the Drude model. In summary, MPID provides a computationally efficient polarizable force field based on the multipole and induced dipole model for general usage.
The primary practical benefit of the work presented here is that force fields developed for one model can now be used with the other. What this means is that the more than 15 years of Drude FF development efforts can be readily used with the more than 30 years of developments in integrators used to treat a wide variety of ensembles, for example, the constant surface tension NPγT ensemble,60,61 or the enhanced sampling self-guided Langevin dynamics method.83–85 We note that the MPID FF does not require dual-temperature extended-Lagrangian integrators, or any self-consistent iterative method. For any application employing a CHARMM-like all-atom fixed-charge FF, the MPID FF could be used as a simple drop-in replacement. Future efforts will extend the present work to biological macromolecules.
SUPPLEMENTARY MATERIAL
See supplementary material for two additional tables and seven additional figures comparing the Drude and MPID results.
ACKNOWLEDGMENTS
Financial support from the NIH to ADM (Grant Nos. GM051501 and GM072558) and B.R.B. (Intramural Research Program of the National Heart, Lung, and Blood Institute Z01 HL001051) are acknowledged. Computational resources were provided by the University of Maryland Computer-Aided Drug Design Center and the LoBoS computer cluster at NIH. J.H. thanks Dr. Yihan Shao for helpful discussions.
REFERENCES
- 1.Huang J. et al. , J. Phys. Chem. Lett. 5, 3144 (2014). 10.1021/jz501315h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cisneros G. A. et al. , Chem. Rev. 114, 779 (2014). 10.1021/cr300461d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Albaugh A. et al. , J. Phys. Chem. B 120, 9811 (2016). 10.1021/acs.jpcb.6b06414 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Huang J. and A. D. MacKerell, Jr., Biophys. J. 107, 991 (2014). 10.1016/j.bpj.2014.06.038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lemkul J. A., Savelyev A., and MacKerell A. D., J. Phys. Chem. Lett. 5, 2077 (2014). 10.1021/jz5009517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Savelyev A. and MacKerell A. D., J. Phys. Chem. Lett. 6, 212 (2015). 10.1021/jz5024543 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Schnieders M. J. et al. , J. Chem. Theory Comput. 8, 1721 (2012). 10.1021/ct300035u [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Warshel A. and Levitt M., J. Mol. Biol. 103, 227 (1976). 10.1016/0022-2836(76)90311-9 [DOI] [PubMed] [Google Scholar]
- 9.Rick S. W., Stuart S. J., and Berne B. J., J. Chem. Phys. 101, 6141 (1994). 10.1063/1.468398 [DOI] [Google Scholar]
- 10.Rick S. W. and Berne B. J., J. Am. Chem. Soc. 118, 672 (1996). 10.1021/ja952535b [DOI] [Google Scholar]
- 11.Liu Y.-P. et al. , J. Chem. Phys. 108, 4739 (1998). 10.1063/1.475886 [DOI] [Google Scholar]
- 12.Stern H. A. et al. , J. Chem. Phys. 115, 2237 (2001). 10.1063/1.1376165 [DOI] [Google Scholar]
- 13.Kaminski G. A. et al. , J. Comput. Chem. 23, 1515 (2002). 10.1002/jcc.10125 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Patel S. and Brooks C. L., J. Comput. Chem. 25, 1 (2004). 10.1002/jcc.10355 [DOI] [PubMed] [Google Scholar]
- 15.Patel S., Mackerell A. D., and Brooks C. L., J. Comput. Chem. 25, 1504 (2004). 10.1002/jcc.20077 [DOI] [PubMed] [Google Scholar]
- 16.Xie W. and Gao J., J. Chem. Theory Comput. 3, 1890 (2007). 10.1021/ct700167b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xie W. et al. , J. Chem. Theory Comput. 3, 1878 (2007). 10.1021/ct700146x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ponder J. W. et al. , J. Phys. Chem. B 114, 2549 (2010). 10.1021/jp910674d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lemkul J. A. et al. , Chem. Rev. 116, 4983 (2016). 10.1021/acs.chemrev.5b00505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ren P. and Ponder J. W., J. Comput. Chem. 23, 1497 (2002). 10.1002/jcc.10127 [DOI] [PubMed] [Google Scholar]
- 21.Ren P. and Ponder J. W., J. Phys. Chem. B 107, 5933 (2003). 10.1021/jp027815+ [DOI] [Google Scholar]
- 22.Ren P., Wu C., and Ponder J. W., J. Chem. Theory Comput. 7, 3143 (2011). 10.1021/ct200304d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shi Y. et al. , J. Chem. Theory Comput. 9, 4046 (2013). 10.1021/ct4003702 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lamoureux G., A. D. MacKerell, Jr., and Roux B., J. Chem. Phys. 119, 5185 (2003). 10.1063/1.1598191 [DOI] [Google Scholar]
- 25.Lamoureux G. and Roux B., J. Chem. Phys. 119, 3025 (2003). 10.1063/1.1589749 [DOI] [Google Scholar]
- 26.Lamoureux G. et al. , Chem. Phys. Lett. 418, 245 (2006). 10.1016/j.cplett.2005.10.135 [DOI] [Google Scholar]
- 27.Yu W. et al. , J. Chem. Phys. 138, 034508 (2013). 10.1063/1.4774577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lopes P. E. M. et al. , J. Chem. Theory Comput. 9, 5430 (2013). 10.1021/ct400781b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chowdhary J. et al. , J. Phys. Chem. B 117, 9142 (2013). 10.1021/jp402860e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.He X., Lopes P. E., and A. D. Mackerell, Jr., Biopolymers 99, 724 (2013). 10.1002/bip.22286 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Savelyev A. and MacKerell A. D., J. Comput. Chem. 35, 1219 (2014). 10.1002/jcc.23611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Savelyev A. and MacKerell A. D., J. Phys. Chem. B 118, 6742 (2014). 10.1021/jp503469s [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Li H. et al. , J. Phys. Chem. B 119, 9401 (2015). 10.1021/jp510560k [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Peng X. et al. , J. Chem. Theory Comput. 12, 2973 (2016). 10.1021/acs.jctc.6b00128 [DOI] [PubMed] [Google Scholar]
- 35.Simmonett A. C. et al. , J. Phys. Chem. 140, 184101 (2014). 10.1063/1.4873920 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Simmonett A. C. et al. , J. Phys. Chem. 143, 074115 (2015). 10.1063/1.4928530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Simmonett A. C. et al. , J. Phys. Chem. 145, 164101 (2016). 10.1063/1.4964866 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wennberg C. L. et al. , J. Chem. Theory Comput. 11, 5737 (2015). 10.1021/acs.jctc.5b00726 [DOI] [PubMed] [Google Scholar]
- 39.Tuckerman M., Berne B. J., and Martyna G. J., J. Phys. Chem. 97, 1990 (1992). 10.1063/1.463137 [DOI] [Google Scholar]
- 40.Zheng L., Chen M., and Yang W., Proc. Natl. Acad. Sci. U. S. A. 105, 20227 (2008). 10.1073/pnas.0810631106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gordon M. S. et al. , Chem. Rev. 112, 632 (2012). 10.1021/cr200093j [DOI] [PubMed] [Google Scholar]
- 42.Gaenko A. et al. , J. Chem. Theory Comput. 9, 222 (2013). 10.1021/ct300614z [DOI] [PubMed] [Google Scholar]
- 43.Dziedzic J. et al. , J. Phys. Chem. 145, 124106 (2016). 10.1063/1.4962909 [DOI] [PubMed] [Google Scholar]
- 44.Kratz E. G. et al. , J. Comput. Chem. 37, 1019 (2016). 10.1002/jcc.24295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lu Z. and Zhang Y., J. Chem. Theory Comput. 4, 1237 (2008). 10.1021/ct800116e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Riahi S. and Rowley C. N., J. Comput. Chem. 35, 2076 (2014). 10.1002/jcc.23716 [DOI] [PubMed] [Google Scholar]
- 47.Geerke D. P. et al. , J. Chem. Theory Comput. 3, 1499 (2007). 10.1021/ct7000123 [DOI] [PubMed] [Google Scholar]
- 48.Boulanger E. and Thiel W., J. Chem. Theory Comput. 10, 1795 (2014). 10.1021/ct401095k [DOI] [PubMed] [Google Scholar]
- 49.Harder E. et al. , J. Phys. Chem. B 112, 3509 (2008). 10.1021/jp709729d [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Thole B. T., Chem. Phys. 59, 341 (1981). 10.1016/0301-0104(81)85176-2 [DOI] [Google Scholar]
- 51.Yu H. et al. , J. Chem. Theory Comput. 6, 774 (2010). 10.1021/ct900576a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wennberg C. L. et al. , J. Chem. Theory Comput. 9, 3527 (2013). 10.1021/ct400140n [DOI] [PubMed] [Google Scholar]
- 53.Brooks B. R. et al. , J. Comput. Chem. 30, 1545 (2009). 10.1002/jcc.21287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Nosé S., J. Phys. Chem. 81, 511 (1984). 10.1063/1.447334 [DOI] [Google Scholar]
- 55.Hoover W. G., Phys. Rev. A 31, 1695 (1985). 10.1103/physreva.31.1695 [DOI] [PubMed] [Google Scholar]
- 56.Andersen H. C., J. Phys. Chem. 72, 2384 (2008). 10.1063/1.439486 [DOI] [Google Scholar]
- 57.Darden T., York D., and Pedersen L., J. Chem. Phys. 98, 10089 (1993). 10.1063/1.464397 [DOI] [Google Scholar]
- 58.Ryckaert J.-P., Ciccotti G., and Berendsen H. J. C., J. Comput. Phys. 23, 327 (1977). 10.1016/0021-9991(77)90098-5 [DOI] [Google Scholar]
- 59.Martínez L. et al. , J. Comput. Chem. 30, 2157 (2009). 10.1002/jcc.21224 [DOI] [PubMed] [Google Scholar]
- 60.Zhang Y. et al. , J. Phys. Chem. 103, 10252 (1995). 10.1063/1.469927 [DOI] [Google Scholar]
- 61.Feller S. E., Zhang Y., and Pastor R. W., J. Phys. Chem. 103, 10267 (1995). 10.1063/1.469928 [DOI] [Google Scholar]
- 62.Dyke T. R., Mack K. M., and Muenter J. S., J. Phys. Chem. 66, 498 (1977). 10.1063/1.433969 [DOI] [Google Scholar]
- 63.Curtiss L. A., Frurip D. J., and Blander M., J. Phys. Chem. 71, 2703 (1979). 10.1063/1.438628 [DOI] [Google Scholar]
- 64.Shields R. M. et al. , J. Phys. Chem. A 114, 11725 (2010). 10.1021/jp104865w [DOI] [PubMed] [Google Scholar]
- 65.Niu S., Tan M.-L., and Ichiye T., J. Phys. Chem. 134, 134501 (2011). 10.1063/1.3569563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Altona C. and Sundaralingam M., J. Am. Chem. Soc. 94, 8205 (1972). 10.1021/ja00778a043 [DOI] [PubMed] [Google Scholar]
- 67.Soper A. K., Chem. Phys. 258, 121 (2000). 10.1016/s0301-0104(00)00179-8 [DOI] [Google Scholar]
- 68.MacKerell A. D. et al. , J. Phys. Chem. B 102, 3586 (1998). 10.1021/jp973084f [DOI] [PubMed] [Google Scholar]
- 69.Mackerell A. D., Feig M., and Brooks C. L., J. Comput. Chem. 25, 1400 (2004). 10.1002/jcc.20065 [DOI] [PubMed] [Google Scholar]
- 70.Guvench O. et al. , J. Comput. Chem. 29, 2543 (2008). 10.1002/jcc.21004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Hatcher E. R., Guvench O., and MacKerell A. D., J. Chem. Theory Comput. 5, 1315 (2009). 10.1021/ct9000608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Guvench O. et al. , J. Chem. Theory Comput. 7, 3162 (2011). 10.1021/ct200328p [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Baker C. M., Anisimov V. M., and MacKerell A. D., J. Phys. Chem. B 115, 580 (2011). 10.1021/jp1092338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Schmollngruber M. et al. , Phys. Chem. Chem. Phys. 17, 14297 (2015). 10.1039/c4cp04512b [DOI] [PubMed] [Google Scholar]
- 75.Chialvo A. A. et al. , J. Phys. Chem. B 119, 5010 (2015). 10.1021/acs.jpcb.5b00595 [DOI] [PubMed] [Google Scholar]
- 76.Li A. et al. , J. Phys. Chem. B 120, 8668 (2016). 10.1021/acs.jpcb.6b03392 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Wang H. and Yang W., J. Phys. Chem. 144, 224107 (2016). 10.1063/1.4953558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Lemkul J. A. and MacKerell A. D., J. Phys. Chem. B 120, 11436 (2016). 10.1021/acs.jpcb.6b09262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Devereux M. et al. , J. Chem. Theory Comput. 10, 4229 (2014). 10.1021/ct500511t [DOI] [PubMed] [Google Scholar]
- 80.Albaugh A., Demerdash O., and Head-Gordon T., J. Phys. Chem. 143, 174104 (2015). 10.1063/1.4933375 [DOI] [PubMed] [Google Scholar]
- 81.Albaugh A., Niklasson A. M. N., and Head-Gordon T., J. Phys. Chem. Lett. 8, 1714 (2017). 10.1021/acs.jpclett.7b00450 [DOI] [PubMed] [Google Scholar]
- 82.Halgren T. A., J. Am. Chem. Soc. 114, 7827 (1992). 10.1021/ja00046a032 [DOI] [Google Scholar]
- 83.Wu X. and Brooks B. R., Chem. Phys. Lett. 381, 512 (2003). 10.1016/j.cplett.2003.10.013 [DOI] [Google Scholar]
- 84.Wu X. and Brooks B. R., J. Phys. Chem. 134, 134108 (2011). 10.1063/1.3574397 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Wu X. and Brooks B. R., J. Phys. Chem. 135, 204101 (2011). 10.1063/1.3662489 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for two additional tables and seven additional figures comparing the Drude and MPID results.