Abstract
Background:
A glycolipopeptide biosurfactant produced by Pseudomonas aeruginosa strain IKW1 reduced the surface tension of fermentation broth from 71.31 to 24.62 dynes/cm at a critical micelle concentration of 20.80 mg/L. The compound proved suitable for applications in emulsion stabilization in food, as well as in cosmetic and pharmaceutical formulations.
Methods:
In the present study, Plackett-Burman design (PBD) and response surface method (RSM) were employed to screen and optimize concentrations of trace nutrients in the fermentation medium, to increase surfactant yield.
Results:
The PBD selected 5 significant trace nutrients out of the 12 screened. The RSM, on the other hand, resulted in the production of 84.44 g glycolipopeptide/L in the optimized medium containing 1.25 mg/L nickel, 0.125 mg/L zinc, 0.075 mg/L iron, 0.0104 mg/L boron, and 0.025 mg/L copper.
Conclusion:
Significant second-order quadratic models for biomass (P<0.05; adjusted R2=94.29%) and biosurfactant (R2=99.44%) responses suggest excellent goodness-of-fit of the models. However, their respective non-significant lack-of-fit (Biomass: F=1.28; P=0.418; Biosurfactant: F=1.20; P=0.446) test results indicate their adequacy to explain data variations in the experimental region. The glycolipopeptide is recommended for the formulation of inexpensive pharmaceutical products that require surface-active compounds.
Keywords: Pseudomonas aeruginosa, Surface-active agents, Fermentation, Nickel, Copper
INTRODUCTION
Biosurfactants are amphiphilic compounds that reduce the free surface enthalpy per unit area of surfaces and interfaces[1]. They are derived from biological sources including plants, animals, and microorganisms; however, world commercial interest has focused, principally, on microbial derivatives from bacteria, yeasts, and molds[2].
Microbial surfactants are of diverse chemical nature, including glycolipids[3], flavolipids[4], lipopeptides[5], and glycolipopeptides[6-8]. Each biosurfactant performs specialized function(s) in their respective producing organisms. Such functions include solubilization, emulsification, pathogenesis, antibiosis, swarming motility, as well as wetting of and attachment to surfaces[9].
Commercial interest in biosurfactant production has heightened over the years owing to their increasingly widening applications. Surface-active compounds are applied for different purposes in pharmaceutical, detergent, food, cosmetic, petroleum, and agricultural sectors, as well as the environment[10,11]. A threatening bottleneck in microbial production of biosurfactants is the economics of production[1]. Several strategies exist to increase biosurfactant yield, that include the use of low-cost substrates, medium optimization, strain improvement, and development of fermentation conditions[12,13].
Optimization of fermentation media involving major and trace nutrients, as well as environmental and fermentation conditions has been documented[14-16]. A good number of biosurfactant fermentation media compositions incorporating both major and minor nutrients have been reported without information on source of trace element composition. A remarkable study on trace mineral composition of a biosurfactant medium has been reported by Joshi et al.[17].
Trace elements are required in small amounts and play essential roles in cellular metabolism, mostly as enzyme co-factors and/or side groups in some microbial metabolites[18]. Selection of significant trace elements for incorporation into fermentation media is an uphill task from the viewpoint of variable size. A classical method for screening large variables is the use of Plackett-Burman design (PBD). It is a small-sized two-level factorial experimental design programmed to identify critical physicochemical parameters from N number of variables in N+1experiments without recourse to the interaction effects between and among the variables. Since the sample size is traditionally small, the interaction effects are completely shrouded in the main effects. PBD therefore simply screens the design space to detect large main effects[19]. The selected parameters are further optimized by the means of an appropriate design technique of a response surface method (RSM). This method is a collection of statistical techniques that uses design of experiments to build models, evaluate the effect of factors and predict optimum conditions for the factors[20]. The objective of the present study was to optimize the conditions of trace nutrients in a fermentation medium using PBD and RSM to improve biosurfactant yield.
MATERIALS AND METHODS
Producing organism
The bacterium, Pseudomonas aeruginosa strain IKW1, was earlier isolated[6,21]. The stock culture of the bacterium was retrieved and subcultured in Tryptic Soy Agar by the quadrant-streak plate technique at 30°C for 36 h. The bacterium was passed a second time through the reactivation step in the same medium for 24 h, after which a loop-full of culture was used to inoculate freshly prepared Luria broth in 50-mL Erlenmeyer flask containing 10 mL of medium. Flasks were incubated on a rotary shaker at 150 rpm at room temperature (28±2°C) for 18 h.
Optimization experiments
Screening trace elements
The PBD incorporated into MINITAB 17 statistical software (trial version) was used to screen 12 trace nutrients in 20 randomized experimental runs. The nutrients were purchased from Sigma Aldrich, USA and included NaCl, KCl, CaCl2, MgSO4.7H2O, CuSO4.5H2O, NiCl2.6H2O, FeCl3, ZnCl2.7H2O, K3BO3, MoNa2O4.2H2O, CoCl2, and MnSO4.4H2O. Each was tested only at two levels, low and high. Biosurfactant concentration (g/L) served as the only response variable. Fermentation medium was formulated according to the experimental design and based on 50 mL of each formulation dispensed into 250-mL Erlenmeyer flask. Phosphorus (1.0 g/L (NH4)2HPO4/NH4H2PO4) and carbon (5% v/v waste frying sunflower oil with composition of [% w/w] stearic acid [2.21], palmitic acid [6.11], volatile fractions (16.23), oleic acid [22.34], and linoleic acid [50.76]; saponification value 76 and density [30°C] 283.3 kg/m3) sources were added to the media, and flasks were corked and sterilized by autoclaving at 121°C for 15 min. Upon cooling, filter-sterilized urea (1.19 g/L) and inoculum (10% v/v-108 cells/mL) were added to the medium, and flasks were incubated on a rotary shaker agitating at 150 rpm at room temperature for 72 h. All arrangements were made in triplicates.
Biosurfactant quantification was performed as described elsewhere[6]. Data were analyzed using the same statistical software that generated the design. Significant trace elements were selected for RSM and optimization.
Response surface design and fermentation studies
The experimental design employed to fit the multiple regression models of the fermentation study was a 25-1 half-fractional factorial central composite rotatable design. The test variables were Ni2+, Zn2+, Fe3+, B3+, and Cu2+; each at five levels. The selection of factor levels for RSM followed, on one hand, the method of the path of steepest ascent, a procedure that moves nutrient levels sequentially in the direction of maximum increase in the response investigated, and on the other, a consideration for the introduction of biomass concentration as a second response variable to facilitate the determination of biosurfactant production yield, Yp/x. Results of preliminary screening for the effects of increasing concentrations of metals on the growth of the bacterium were also considered in the selection of factor levels of significant trace nutrients from PBD for biomass and biosurfactant formation. Actual levels of each factor were calculated using the equation of Myers and Montgomery[20].
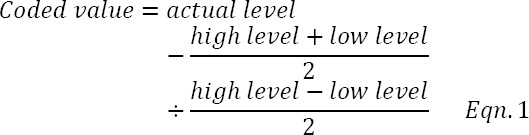
The coded levels were determined as follows: X1=(Ni2+-0.75)/0.25, X2=(Zn2+–0.075)/0.025, X3= (Fe3+–0.075)/0.025, X4=(B3+–0.03)/0.01, and X5=(Cu2+-0.075)/0.025. The response variables were biomass Y1 (g/L) and biosurfactant Y2 (g/L) concentrations. The experimental design required 32 experimental runs, which were set up in 250-mL Erlenmeyer flasks, each containing 50 mL of fermentation medium composed (g/L) of Na2HPO4/KH2PO4 (2:1; 4.5), MgSO4.7H2O (0.2), NaCl (0.5), CaCl2 (0.5), KCl (0.5), MoNa2O4.2H2O (0.05 mg/L), CoCl2.6H2O (0.05 mg/L), and MnSO4.4H2O (0.05 mg/L). Different concentrations of the five significant trace elements obtained from PBD screening were then added to the flasks according to the actual values of the factor levels specified by the coded values in Table 1. Medium pH was adjusted to 7.0 with KOH pellets[4]. Waste frying oil was subsequently added to each flask at 5% (v/v) concentration and flasks, without nitrogen source, were sterilized by autoclaving at 121°C for 15 min. Upon cooling, filter-sterilized urea (1.19 g/L) and inoculum (10% v/v–108 cells/mL) were introduced into flasks prepared in triplicates, and then the flasks were incubated on rotary shakers agitating at 150 rpm at room temperature for 72 h.
Table 1.
Placket-Burman design matrix (randomized) for trace element contribution to biosurfactant formation in coded units
| Run | A | B | C | D | E | F | G | H | J | K | L | M | BSC (g/L) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | -1 | -1 | -1 | 1 | -1 | 1 | -1 | 1 | 1 | 1 | 1 | -1 | 23.58 |
| 2 | 1 | 1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | 25.96 |
| 3 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | 24.21 |
| 4 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | -1 | -1 | -1 | 21.43 |
| 5 | -1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | -1 | 1 | -1 | 1 | 24.19 |
| 6 | 1 | 1 | -1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | -1 | 1 | 28.96 |
| 7 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | 31.73 |
| 8 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | -1 | 1 | -1 | 1 | 1 | 32.75 |
| 9 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | 17.45 |
| 10 | 1 | -1 | 1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | 1 | 1 | 36.02 |
| 11 | 1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 24.72 |
| 12 | -1 | 1 | -1 | 1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | 1 | 23.48 |
| 13 | 1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | -1 | 22.31 |
| 14 | 1 | -1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | -1 | 1 | -1 | 27.08 |
| 15 | -1 | -1 | -1 | -1 | 1 | -1 | 1 | -1 | 1 | 1 | 1 | 1 | 33.27 |
| 16 | -1 | 1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 25.31 |
| 17 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | -1 | -1 | -1 | 1 | -1 | 28.78 |
| 18 | 1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | 1 | -1 | -1 | -1 | 21.08 |
| 19 | 1 | -1 | -1 | -1 | -1 | 1 | -1 | 1 | -1 | 1 | 1 | 1 | 33.10 |
| 20 | -1 | -1 | 1 | -1 | 1 | -1 | 1 | 1 | 1 | 1 | -1 | -1 | 23.29 |
A, boron; B, calcium, C, cobalt; D, copper; E, iron; F, potassium; G, magnesium; H, manganese; J, molybdenum; K, sodium; L, nickel; M, zinc; ‘1’, high value; ‘-1‘, low value; BSC, biosurfactant concentration
Determination of biomass (Y1) and biosurfactant (Y2) concentrations
Small portions of 72-h fermentation broth from each experimental setting (10 mL) were centrifuged at 8,000 ×g for 10 min. Cell-free supernatants were collected, and the cell pellets were washed twice in de-mineralized water. The supernatants were subjected to 0.45-µM and 0.2-µM Millipore membrane filtrations and subsequently to acid precipitation with 6N HCl, pH 2.0. Biomass and biosurfactant concentrations were determined from cell pellets and acid precipitates of supernatants, respectively as described previously[6].
Statistical analysis
All data generated from the factorial experiment were subjected to multiple regression analysis using least squares to build the regression models. A second-order (quadratic) function was used to fit the data generated. Experimental design, data analysis, interaction plotting, and optimization of factor conditions were done with MINITAB 17 statistical software, while Excel 2007 was used for confirmation of model fits where predicted responses were plotted against experimentally-derived data. All hypotheses were tested at 95% confidence level.
For the five factors considered in the optimization experiment, the quadratic model took the form below:
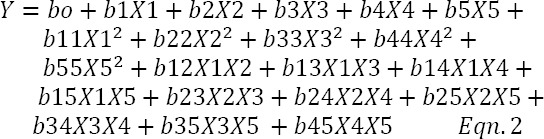
where b0 is the value of the fixed response at the central point (0, 0, 0, 0, 0); b1, b2, b3, b4, and b5 the coefficients of the linear terms; b11, b22, b33, b44, and b55 the coefficients of the quadratic terms; b12, b13, b14, b15, b23, b24, b25, b34, b35, and b45 are the coefficients of the cross products (interactive terms).
Verification experiments
Studies to confirm the validity of the results of the optimization experiment were done by setting up glycolipopeptide production in the optimized medium. The medium had the same composition as that described in Materials and Methods with concentrations of nickel, zinc, iron, boron, and copper incorporated in accordance with the results of the various optimized conditions. Fermentation was conducted in 250-mL Erlenmeyer flasks containing 50 mL of fermentation medium supplemented with 5% (v/v) waste frying sunflower oil as carbon source. Cooled sterilized media were supplemented with filter-sterilized urea (1.19 g/L) and then inoculated with 10% (v/v–108 cells/mL) inoculum of Pseudomonas aeruginosa strain IKW1. Flasks were incubated as earlier described and biomass and biosurfactant concentrations determined as described in Ekpenyong et al.[6]. Means of triplicate determinations of concentrations of biomass and biosurfactant from corroborating experiments were compared with those predicted by the regression models.
RESULTS AND DISCUSSION
Plackett-Burman design
The design matrix of the PBD for the effects of 12 trace nutrients on biosurfactant production and their responses are shown in Table 1. Results showed the highest biosurfactant concentration of 36.02 g/L in run 10. However, the results of the trace element modeling experiment by PBD revealed that only 5 out of 12 nutrient elements significantly influenced the glycolipopeptide production. The non-selection of the remaining seven elements suggests their non-significant (P>0.05) contributions to the response under investigation at the confidence level selected for the study.
Results of the trace element screen test by PBD indicated the same results as trace element modeling experiment. Figure 1 is the normal plot of the standardized effect of the significant nutrients, showing the magnitude and direction of their significant effects. The Figure reveals that nickel has the highest significant positive effect on biosurfactant production by the bacterium since its effect is positioned the furthest to the right of the response line. Other nutrients with significant enhancement effect on biosurfactant production were zinc, iron, and boron, which is in agreement with the Joshi et al.’s study[17]. However, the Figure reveals a significant reductive effect of copper on glycolipopeptide production by the bacterium since its effect is positioned to the left of the biosurfactant response line. Figure 2 shows the main effects plots of significant trace nutrients on the response variable and confirms the results displayed in Figure 1. Nickel has been shown to make the highest contribution to biosurfactant production, whereas copper exerts a negative effect on biosurfactant production.
Fig. 1.
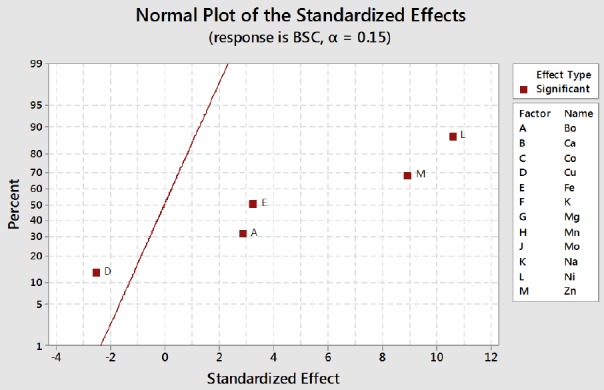
Normal plot of standardized effects of significant trace nutrients of a Plackett-Burman design for glycolipoeptide-biosurfactant production. Bo is used loosely to indicate boron and not as a chemical symbol.
Fig. 2.
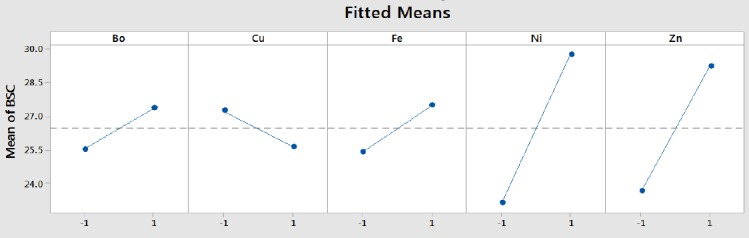
Main effects plots of contributions of significant trace elements to glycolipopeptide-biosurfactant production by Pseudomonas aeruginosa strain IKW1. BSC, biosurfactant concentration
The analysis of variance (ANOVA) result for significant trace elements is demonstrated in Table 2 and confirms nickel as having the most significant (P<0.05) enhancement effect on biosurfactant production given by its very large F value. The linear regression coefficient of determination, adjusted R2 of 91.81%, indicates that the model equation (below), given in un-coded units, was significant and could explain 91.81% of the variability in the response data. The equation reveals that nickel has the largest coefficient that is preceded by a positive sign, confirming once again its strong enhancement effect on biosurfactant formation.
Table 2.
Analysis of variance (ANOVA) of the regression model from the Plackett-Burman design for trace element contribution to biosurfactant formation in un-coded units
| Source | DF | Adj. SS | Adj. MS | F value | P value |
|---|---|---|---|---|---|
| Model | 5 | 428.38 | 85.677 | 43.61 | 0.000 |
| Linear | 5 | 428.38 | 85.677 | 43.61 | 0.000 |
| Bo | 1 | 16.42 | 16.417 | 8.36 | 0.012 |
| Cu | 1 | 12.45 | 12.450 | 6.34 | 0.025 |
| Fe | 1 | 20.97 | 20.972 | 10.67 | 0.006 |
| Ni | 1 | 220.85 | 220.847 | 112.41 | 0.000 |
| Zn | 1 | 157.70 | 157.697 | 80.27 | 0.000 |
| Error | 14 | 27.51 | 1.965 | ||
| Total | 19 | 455.89 |
Model Summary: S, 1.40166; R2, 93.97%; adjusted R2, 91.81%; predicted R2, 87.69%; P<0.05, 5% significance level. Bo is used loosely to indicate boron and not as a chemical symbol. DF, degrees of freedom; SS, sum of squares; MS, mean sum of squares.
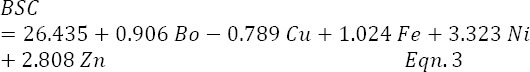
Response surface optimization
Experimental data of the response surface method
Table 3 shows the actual factor levels corresponding to coded factor levels for a 25-1 half-fractional factorial, a central composite rotatable design of RSM. The experimental responses from the 32 experimental runs of the surface methodology are presented in Table 4. Maximum biomass concentration of 21.07 g/L was obtained at conditions set at (X1, X2, X3, X4, X5)=(-1, -1, 1, -1, -1) corresponding to 0.5 mg/L nickel, 0.05 mg/L zinc, 0.1 mg/L iron, 0.02 mg/L boron, and 0.05 mg/L copper. In these conditions, biosurfactant concentration obtained was 29.56 g/L. However, the highest biosurfactant concentration of 57.21 g/L was acquired at conditions set at (X1, X2, X3, X4, X5)=(1, 1, 1, -1, -1) corresponding to 1 mg/L nickel, 0.1 mg/L zinc, 0.1 mg/L iron, 0.02 mg/L boron, and 0.05 mg/L copper and a corresponding biomass concentration of 19.53 g/L. Glycolipopeptide production yield, Yp/x, under these conditions would be 2.93. The attainment of peak biomass and biosurfactant concentrations at different experimental runs suggest the requirement of different trace nutrient conditions for cellular growth and metabolite synthesis, especially metabolites obtained during or near idiophasic metabolism of organisms.
Table 3.
Actual factor levels corresponding to coded factor levels for 25-1 half-fractional factorial central composite rotatable design of response surface method
| Variable (mg/L) | Actual values | |||||
|---|---|---|---|---|---|---|
| Code | -2 | -1 | 0 | 1 | 2 | |
| NiCl2.6H2O | X1 | 0.250 | 0.50 | 0.750 | 1.00 | 1.250 |
| ZnSO4.7H2O | X2 | 0.025 | 0.05 | 0.075 | 0.10 | 0.125 |
| FeCl3 | X3 | 0.025 | 0.05 | 0.075 | 0.10 | 0.125 |
| K3BO3 | X4 | 0.010 | 0.02 | 0.030 | 0.04 | 0.050 |
| CuSO4.5H2O | X5 | 0.025 | 0.05 | 0.075 | 0.10 | 0.125 |
Table 4.
Actual factor levels corresponding to coded factor levels for the CCRD of the response surface optimization showing biomass and biosurfactant concentrations
| Run order | X1 | X2 | X3 | X4 | X5 | NiCl2 (mg/L) | ZnSO4 (mg/L) | FeCl3 (mg/L) | K3BO3 (mg/L) | CuSO4 (mg/L) | BMC (g/L) | BSC (g/L) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 | 0.750 | 0.075 | 0.075 | 0.030 | 0.075 | 16.86 | 41.03 |
| 2 | -2 | 0 | 0 | 0 | 0 | 0.250 | 0.075 | 0.075 | 0.030 | 0.075 | 14.36 | 29.55 |
| 3 | -1 | -1 | -1 | 1 | -1 | 0.500 | 0.050 | 0.050 | 0.040 | 0.050 | 8.96 | 36.04 |
| 4 | 1 | -1 | 1 | 1 | -1 | 1.000 | 0.050 | 0.100 | 0.040 | 0.050 | 12.98 | 38.32 |
| 5 | 0 | 0 | 0 | 2 | 0 | 0.750 | 0.075 | 0.075 | 0.050 | 0.075 | 13.52 | 28.39 |
| 6 | 0 | 0 | 0 | -2 | 0 | 0.750 | 0.075 | 0.075 | 0.010 | 0.075 | 18.52 | 36.57 |
| 7 | 0 | 0 | 0 | 0 | -2 | 0.750 | 0.075 | 0.075 | 0.030 | 0.025 | 15.39 | 46.47 |
| 8 | -1 | 1 | -1 | -1 | -1 | 0.500 | 0.100 | 0.050 | 0.020 | 0.050 | 11.35 | 38.32 |
| 9 | -1 | 1 | 1 | 1 | -1 | 0.500 | 0.100 | 0.100 | 0.040 | 0.050 | 18.26 | 35.31 |
| 10 | 1 | -1 | -1 | -1 | -1 | 1.000 | 0.050 | 0.050 | 0.020 | 0.050 | 10.62 | 32.19 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0.750 | 0.075 | 0.075 | 0.030 | 0.075 | 18.76 | 41.22 |
| 12 | 0 | -2 | 0 | 0 | 0 | 0.750 | 0.025 | 0.075 | 0.030 | 0.075 | 9.67 | 36.82 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0.750 | 0.075 | 0.075 | 0.030 | 0.075 | 18.87 | 41.46 |
| 14 | -1 | 1 | -1 | 1 | 1 | 0.500 | 0.100 | 0.050 | 0.040 | 0.100 | 13.28 | 27.54 |
| 15 | -1 | -1 | 1 | 1 | 1 | 0.500 | 0.050 | 0.100 | 0.040 | 0.100 | 13.41 | 26.79 |
| 16 | 0 | 0 | 2 | 0 | 0 | 0.750 | 0.075 | 0.125 | 0.030 | 0.075 | 16.59 | 40.45 |
| 17 | 1 | 1 | -1 | 1 | -1 | 1.000 | 0.100 | 0.050 | 0.040 | 0.050 | 12.38 | 31.07 |
| 18 | 1 | 1 | -1 | -1 | 1 | 1.000 | 0.100 | 0.050 | 0.020 | 0.100 | 16.58 | 30.01 |
| 19 | 0 | 0 | -2 | 0 | 0 | 0.750 | 0.075 | 0.025 | 0.030 | 0.075 | 8.95 | 28.12 |
| 20 | 0 | 2 | 0 | 0 | 0 | 0.750 | 0.125 | 0.075 | 0.030 | 0.075 | 15.38 | 46.05 |
| 21 | 1 | 1 | 1 | 1 | 1 | 1.000 | 0.100 | 0.100 | 0.040 | 0.100 | 8.47 | 39.67 |
| 22 | 0 | 0 | 0 | 0 | 2 | 0.750 | 0.075 | 0.075 | 0.030 | 0.125 | 11.04 | 37.58 |
| 23 | 1 | -1 | 1 | -1 | 1 | 1.000 | 0.050 | 0.100 | 0.020 | 0.100 | 11.94 | 41.40 |
| 24 | -1 | -1 | 1 | -1 | -1 | 0.500 | 0.050 | 0.100 | 0.020 | 0.050 | 21.07 | 29.56 |
| 25 | 1 | 1 | 1 | -1 | -1 | 1.000 | 0.100 | 0.100 | 0.020 | 0.050 | 19.53 | 57.21 |
| 26 | 0 | 0 | 0 | 0 | 0 | 0.750 | 0.075 | 0.075 | 0.030 | 0.075 | 18.94 | 42.08 |
| 27 | -1 | 1 | 1 | -1 | 1 | 0.500 | 0.100 | 0.100 | 0.020 | 0.100 | 17.39 | 37.99 |
| 28 | 0 | 0 | 0 | 0 | 0 | 0.750 | 0.075 | 0.075 | 0.030 | 0.075 | 19.04 | 41.68 |
| 29 | -1 | -1 | -1 | -1 | 1 | 0.500 | 0.050 | 0.050 | 0.020 | 0.100 | 9.47 | 31.07 |
| 30 | 0 | 0 | 0 | 0 | 0 | 0.750 | 0.075 | 0.075 | 0.030 | 0.075 | 18.83 | 40.78 |
| 31 | 1 | -1 | -1 | 1 | 1 | 1.000 | 0.050 | 0.050 | 0.040 | 0.100 | 9.57 | 30.24 |
| 32 | 2 | 0 | 0 | 0 | 0 | 1.250 | 0.075 | 0.075 | 0.030 | 0.075 | 12.35 | 39.00 |
X1, nickel; X2, zinc; X3, iron; X4, boron; X5, copper; BMC, biomass concentration; BSC, biosurfactant concentration
Regression model for biomass concentration, Y1
The data presented in Table 4 was subjected to multiple regression analyses using least squares regression to fit a second-order (quadratic) regression model for biomass concentration, Y1. The model stipulated 20 predictors; however, the result of ANOVA of the model in Table 5 reveals that 5 interactive terms were removed by stepwise selection, since their contributions were not significant at P=0.05. The T values of the predictor coefficients (data not shown) suggest that all model predictors, except the linear terms of zinc and iron, made significant negative contributions to the model, implying their reductive effects on biomass formation. The model equation is presented in un-coded units as equation 4 below:
Table 5.
Analysis of variance of the 25-1 half-fractional factorial central composite rotatable design of an response surface method for biomass regression model in un-coded units
| Source | DF | Adjusted SS | Adjusted MS | F value | P value |
|---|---|---|---|---|---|
| Model | 15 | 435.332 | 29.0222 | 35.12 | 0.000 |
| Linear | 5 | 199.895 | 39.9790 | 48.38 | 0.000 |
| Ni | 1 | 9.551 | 9.5508 | 11.56 | 0.004 |
| Zn | 1 | 39.117 | 39.1171 | 47.34 | 0.000 |
| Fe | 1 | 88.627 | 88.6273 | 107.26 | 0.000 |
| Bo | 1 | 39.117 | 39.1171 | 47.34 | 0.000 |
| Cu | 1 | 23.483 | 23.4828 | 28.42 | 0.000 |
| Square | 5 | 134.701 | 26.9401 | 32.60 | 0.000 |
| Ni*Ni | 1 | 35.179 | 35.1787 | 42.57 | 0.000 |
| Zn*Zn | 1 | 49.773 | 49.7729 | 60.23 | 0.000 |
| Fe*Fe | 1 | 45.202 | 45.2022 | 54.70 | 0.000 |
| Bo*Bo | 1 | 5.395 | 5.3951 | 6.53 | 0.021 |
| Cu*Cu | 1 | 37.463 | 37.4633 | 45.34 | 0.000 |
| Two-way interaction | 5 | 100.737 | 20.1473 | 24.38 | 0.000 |
| Ni*Fe | 1 | 33.931 | 33.9306 | 41.06 | 0.000 |
| Ni*Bo | 1 | 6.126 | 6.1256 | 7.41 | 0.015 |
| Zn*Fe | 1 | 7.182 | 7.1824 | 8.69 | 0.009 |
| Fe*Bo | 1 | 10.530 | 10.5300 | 12.74 | 0.003 |
| Fe*Cu | 1 | 42.968 | 42.9680 | 52.00 | 0.000 |
| Error | 16 | 13.221 | 0.8263 | ||
| Lack-of-fit | 11 | 9.748 | 0.8862 | 1.28 | 0.418 |
| Pure error | 5 | 3.473 | 0.6946 | ||
| Total | 31 | 448.554 |
Model Summary: S, 0.909022; R2, 97.05%; adjusted R2, 94.29%; Predicted R2, 86.75%; P<0.05, 5% significance level.Bo is used loosely to indicate boron and not as a chemical symbol. DF, degrees of freedom; SS, sum of squares; MS, mean sum of squares
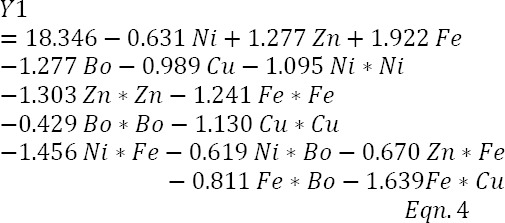
The metal, iron, is described as the only macro-bio-element of the heavy metals and the most biologically relevant trace nutrient[18]. The effect of its linear term on biomass formation was understandably pronounced, and the significant reductive effect of its quadratic term suggests possible toxicity at high concentrations and therefore its trace requirement. Abalos et al.[14] have reported a similar result trend during production of rhamnolipid from a strain of Pseudomonas aeruginosa.
The requirement of zinc for biomass formation derives from its role in DNA-binding proteins and a variety of enzymes. Zinc is also known to act as a Lewis base needed to activate water for involvement in aqueous reactions[6].
The significance of a model is given by its goodness-of-fit test, often expressed as the coefficient of determination R2, which is the percentage of the variations in the response that can be explained by independent factors and their interactions. In this study, the biomass regression model (Table 5) was highly significant (F=35.12; P=0.000) with an adjusted R2 of 94.29%, indicating that only 5.71% of the variability in the response is not explainable by the model.
A well-fitted model estimated by adjusted R2 might not adequately explain data variations in the region of experimentation. The lack-of-fit test is therefore frequently used as a support test for adequacy of the fitted model. The ANOVA table for the biomass regression model in this study shows a non-significant lack-of-fit (F=1.28; P=0.418) for the model, which suggests its adequacy for the explanation of data variations in the region of experimentation.
The regression plot of experimental against predicted biomass responses is presented as Figure 3 and reveals a coefficient of determination, R2 of 0.9705, which is in agreement with the R2 for the model in the ANOVA table.
Fig. 3.
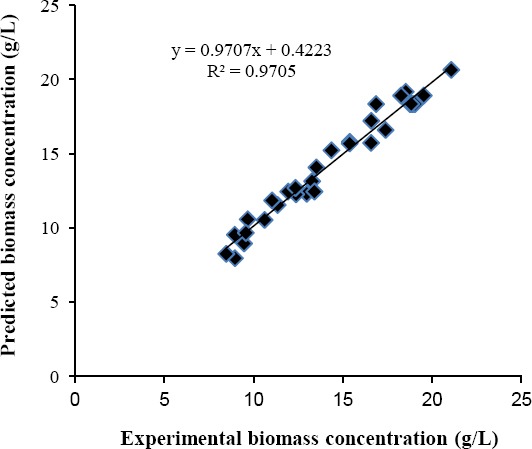
Experimental biomass concentration plotted against biomass concentration predicted by the fitted model.
Regression model for biosurfactant concentration, Y2
The ANOVA for the biosurfactant regression model presented in Table 6 indicated that the model was highly significant (F=371.07; P=0.000). All the linear predictor terms and only the square terms of nickel, iron, and boron were significant. Six of the interactive predictor terms were also significant; however, Fe*Cu interaction, although included in the model, was not significant (P=0.051). The magnitude and direction of significant effect of model predictors are given by the T values of the coefficient estimates of the predictors (data not shown) and reveal that the linear, but not the quadratic terms of nickel, zinc, and iron, significantly enhanced biosurfactant formation. It is probably because of the enhancing effect of Fe*Cu that the term was included in the model, to increase biosurfactant concentration as long as the adjusted R2 of the model was not negatively affected. The model equation, in un-coded units, is therefore presented as equation 5 below.
Table 6.
Analysis of variance of the 25-1 half fractional factorial central composite rotatable design (CCRD) of an response surface method for biosurfactant regression model in un-coded units
| Source | DF | Adjusted SS | Adjusted MS | F value | P value |
|---|---|---|---|---|---|
| Model | 15 | 1388.26 | 92.551 | 371.07 | 0.000 |
| Linear | 5 | 676.69 | 135.338 | 542.62 | 0.000 |
| Ni | 1 | 132.49 | 132.493 | 531.21 | 0.000 |
| Zn | 1 | 104.04 | 104.042 | 417.14 | 0.000 |
| Fe | 1 | 230.83 | 230.826 | 925.46 | 0.000 |
| Bo | 1 | 100.57 | 100.573 | 403.23 | 0.000 |
| Cu | 1 | 108.76 | 108.758 | 436.05 | 0.000 |
| Square | 3 | 326.18 | 108.726 | 435.92 | 0.000 |
| Ni*Ni | 1 | 105.31 | 105.312 | 422.24 | 0.000 |
| Fe*Fe | 1 | 105.03 | 103.033 | 421.11 | 0.000 |
| Bo*Bo | 1 | 161.50 | 161.502 | 647.52 | 0.000 |
| 2-Way Interaction | 7 | 385.39 | 55.056 | 220.74 | 0.000 |
| Ni*Fe | 1 | 198.88 | 198.881 | 797.38 | 0.000 |
| Ni*Bo | 1 | 6.57 | 6.566 | 26.33 | 0.000 |
| Zn*Fe | 1 | 84.23 | 84.227 | 337.69 | 0.000 |
| Zn*Bo | 1 | 45.93 | 45.935 | 184.17 | 0.000 |
| Zn*Cu | 1 | 25.23 | 25.226 | 101.14 | 0.000 |
| Fe*Bo | 1 | 23.45 | 23.450 | 94.02 | 0.000 |
| Fe*Cu | 1 | 1.11 | 1.108 | 4.44 | 0.051 |
| Error | 16 | 3.99 | 0.249 | ||
| Lack-of-Fit | 11 | 2.90 | 0.263 | 1.20 | 0.446 |
| Pure Error | 5 | 1.09 | 0.219 | ||
| Total | 31 | 1392.25 |
Model Summary: S, 0.499416; R2, 99.71%; adjusted R2, 99.44%; predicted R2, 98.77%; P<0.05, 5% significance level. Bo is used loosely to indicate boron and not as a chemical symbol. DF, degrees of freedom; SS, sum of squares; MS, mean sum of squares.
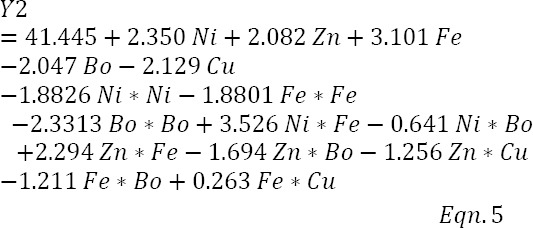
The model was shown to have an adjusted R2 value of 99.44%, suggesting that only 0.56% of the variability in biosurfactant responses could not be explained by it, and that the observed variations were due to the factor effects and not due to noise. To confirm the adequacy of the biosurfactant model in explaining the variations about the data, an examination of the lack-of-fit test result in the ANOVA table was made and demonstrated a non-significant (F=1.20; P=0.446) lack-of-fit, indicating the adequacy of the model to explain data in the experimental region.
A plot of experimental biosurfactant concentrations against predicted concentrations obtained by solving equation 5 is presented in Figure 4 as the final ratification of the fit of the biosurfactant regression model and confirms a goodness-of-fit, R2 (unadjusted) value of 99.97%.
Fig. 4.
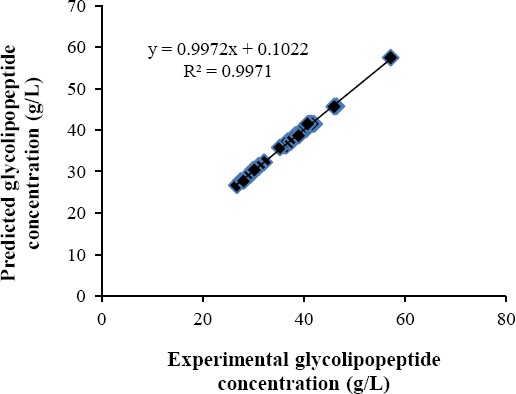
Experimental biosurfactant concentrations versus theoretical values predicted by the regression model.
Contour and surface plots for biomass (Y1) and biosurfactant (Y2) concentrations
Biomass response plots were made with the vertical axis representing biomass concentration (Y1) and two horizontal axes representing the most significant two- way interaction (X3, X5)=(Fe, Cu). The plots led to maximal biomass formation with the remaining three factors (X1, X2, X4)=(Ni, Zn, Bo) held at their optimum levels. Biomass concentration under this condition was in excess of 20 g/L. The contour and surface plots displayed in Figure 5 reveal that maximal biomass would be accumulated under the high levels of iron and low levels of copper.
Fig. 5.
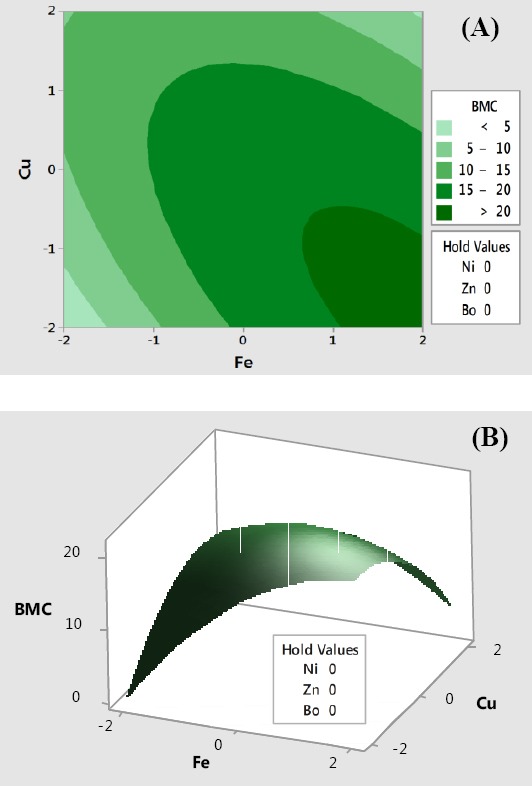
Contour (A) and surface (B) plots of two-way interactions of independent variables for maximal biomass production. Bo is used loosely to indicate boron and not as a chemical symbol. BMC, biomass concentration
The biosurfactant response plots (Fig. 6) were made with the vertical axis representing biosurfactant concentration (Y2) and two horizontal axes representing the two most significant variables (X4, X5)=(Bo, Cu) that led to maximal biosurfactant formation with the remaining three factors (X1, X2, X3)=(Ni, Zn, Fe) held at their optimum levels. Maximal biosurfactant concentration under this condition was in excess of 80 g/L. The contour and surface plots reveal that the highest biosurfactant concentration would be obtained when fermentation medium contains low levels of both copper and boron, with the concentrations of nickel, zinc, and iron supplied at high levels.
Fig. 6.
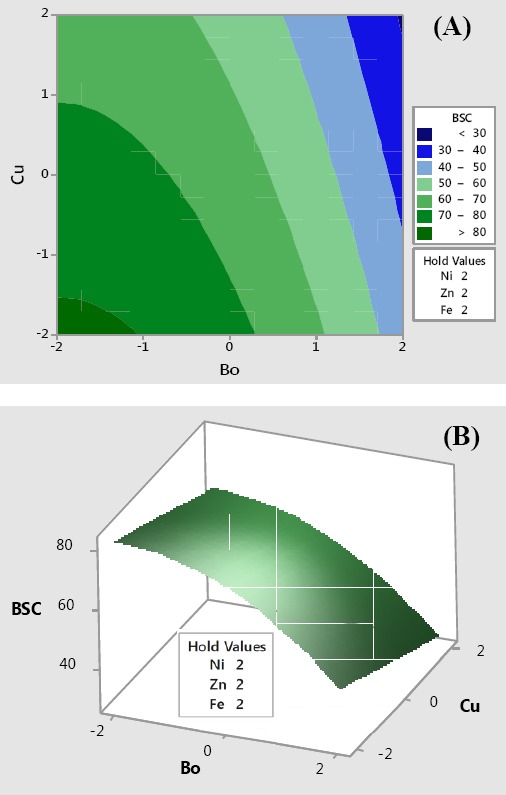
Contour (A) and surface (B) plots of two-way interactions of independent variables for maximal glycolipopeptide production. Bo is used loosely to indicate boron and not as a chemical symbol. BSC, biosurfactant concentration
Boron, a micro-nutrient with intermediary properties of metals and non-metals, is known as a regulator of certain pathways that require serine proteases or oxidoreductases involving co-enzymes like nicotinamide adenine dinucleotide and nicotinamide adenine dinucleotide phosphate for activity[22]. These activities of boron in bacteria could very well be the reason for its very little requirement both for cellular growth and secondary metabolism.
Copper, on the other hand, is mostly important in cytochrome C oxidases; oxygen-dependent terminal oxidases in the electron transport chain of aerobic organisms[23]. The interaction therefore between boron and copper has to be very important in biosurfactant synthesis since the whole process is energy driven; copper to generate energy and boron to inhibit the process.
Nickel is a transition metal useful only in a few selected reactions. It associates with iron in NiFe hydrogenases; an enzyme system that splits molecular hydrogen into protons and electrons. The metal is also intrinsically bound to urease; an enzyme that catalyses the splitting of urea into carbon dioxide and ammonia thus supplying nitrogen in its available form for cellular metabolism[18,24]. The preference of urea as a nitrogen source for glycolipopeptide biosurfactant production by Pseudomonas aeruginosa strain IKW1 (unpublished data) demystifies the significant enhancement effect of nickel on biosurfactant production and suggests a correlation between urease activity and biosurfactant production in the bacterium.
Selection of optimum conditions for response variables
For situations where biomass accumulation is desired instead of the surface-active compound, which was not the case in this study, the highest predictable biomass concentration of 26.55 g/L was obtained at trace mineral conditions set at (X1, X2, X3, X4, X5)=(-1.0707, -0.0202, 2.0, -2.0, -1.8788) corresponding to 0.482 mg/L nickel, 0.074 mg/L zinc, 0.125 mg/L iron, 0.010 mg/L boron, and 0.028 mg/L copper.
For tertiary oil recovery and spilled oil remediation where maximum concentrations of both responses are desired, trace mineral conditions set at (X1, X2, X3, X4, X5)=(0.2626, 0.9495, 2.0, -2.0, -2.0) corresponding to 0.816 mg/L nickel, 0.099 mg/L zinc, 0.125 mg/L iron, 0.01 mg/L boron, and 0.025 mg/L copper, which would lead to 23.4 g/L biomass and 57.55 g/L biosurfactant.
Finally, for detergent, food, cosmetic, and pharmaceutical applications where maximum surface-active compound and zero microbial cells are desired, the response optimizer set conditions for maximum biosurfactant concentration of 81.92 g/L at (X1, X2, X3, X4, X5)=(2.0, 2.0, 2.0, -1.9596, -2) corresponding to 1.25 mg/L nickel, 0.125 mg/L zinc, 0.125 mg/L iron, 0.0104 mg/L boron, and 0.025 mg/L copper.
Verification experiments
Table 7 shows that maximum biosurfactant concentration obtained in the validation experiments under conditions (X1, X2, X3, X4, X5) =(2, 2, 2, -1.9596, -2) corresponding to 1.25 mg/L nickel, 0.125 mg/L zinc, 0.125 mg/L iron, 0.0104 mg/L boron, and 0.025 mg/L copper was 84.44 g/L with a corresponding biomass concentration of 19.14 g/L, giving a production yield (Yp/x) of 4.41. When fermentation conditions were set to maximize both responses, biosurfactant yield of 2.26 was achieved. Compared to the 81.92 g/L biosurfactant concentration predicted by the optimizer, the concentration obtained in the confirmation experiment was only 0.03% higher, thus validating the prediction of the response optimizer. A glycolipopeptide biosurfactant concentration of 84.44 g/L, when compared to 23.86 g/L obtained from a previous (control) experiment (unpublished data), reveals a ~3.54fold increase in biosurfactant concentration, thereby making separate optimization experiments for trace nutrients appropriate for developing the fermentation media for the production of microbial metabolites.
Table 7.
Design codes, actual values, experimental and predicted responses of validation experiments of an RSM for glycolipopeptide production
| Parameters | BMC maximized | BSC maximized | BMC and BSC maximized |
|---|---|---|---|
| X1 | -1.0707 | 2 | 0.2626 |
| X2 | -0.0202 | 2 | 0.9495 |
| X3 | 2 | 2 | 2 |
| X4 | -2 | -1.9596 | -2 |
| X5 | -1.8788 | -2 | -2 |
| Ni (mg/L) | 0.482 | 1.25 | 0.816 |
| Zn (mg/L) | 0.074 | 0.125 | 0.099 |
| Fe (mg/L) | 0.125 | 0.125 | 0.125 |
| Bo (mg/L) | 0.010 | 0.010 | 0.010 |
| Cu (mg/L) | 0.028 | 0.025 | 0.025 |
| eBMC (g/L | 25.74 | 19.14 | 25.14 |
| pBMC (g/L) | 26.55 | NP | 23.40 |
| eBSC (g/L) | 25.96 | 84.44 | 56.83 |
| pBSC (g/L) | NP | 81.92 | 57.55 |
X1, nickel (Ni); X2, zinc (Zn); X3, iron (Fe); X4, boron (Bo); X5, copper (Cu); eBMC, experimental biomass concentration; pBMC, predicted biomass concentration; eBSC, experimental biosurfactant concentration; pBSC, predicted biosurfactant concentration; NP, not predicted. Bo is used loosely to indicate boron and not as a chemical symbol.
PBD selected nickel, zinc, iron, boron, and copper as the most significant (P<0.05; adjusted R2=91.82%) trace minerals for glycolipopeptide biosurfactant production. Optimization of the nutrients by RSM resulted in 84.44 g/L of the biosurfactant under conditions set at (X1, X2, X3, X4, X5)=(2, 2, 2, -1.9596, -2). These conditions corresponded to 1.2500 mg/L nickel, 0.125 mg/L zinc, 0.125 mg/L iron, 0.0104 mg/L boron, and 0.025 mg/L copper, giving a production yield, Yp/x of 4.41. In conclusion, PBD and RSM are dependable tools for selecting and optimizing conditions of nutrients for biosurfactant production.
ACKNOWLEDGEMENTS
The authors are grateful to the government of Cross River State, Nigeria for the research grant (CRS/SB/P/149/30) awarded for this work through their Ministry of Education, Scholarship and Grant unit. Sincere gratitude also goes to Mr. Obi Oyeka-Director of Bez Pharmacy and Stores, Calabar, Nigeria and Dr. Samuel Ekpata for their financial assistance towards this research.
Footnotes
CONFLICT OF INTEREST. None declared.
REFERENCES
- 1.Desai JD, Banat IM. Microbial production of surfactants and their commercial potential. Microbiology and molecular biology reviews. 1997;61(1):47–64. doi: 10.1128/mmbr.61.1.47-64.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Abouseoud M, Maachi R, Amrane A, Boudergua S, Nabi A. Evaluation of different carbon and nitrogen sources in production of biosurfactant by Pseudomonas fluorescens. Desalination. 2008;223(1-3):143–151. [Google Scholar]
- 3.Banat IM, Franzetti A, Gandolfi I, Bestetti G, Martinotti M G, Fracchia L, Smyth TJ, Marchant R. Microbial biosurfactants production, applications and future potential. Applied microbiology and biotechnology. 2010;87(2):427–444. doi: 10.1007/s00253-010-2589-0. [DOI] [PubMed] [Google Scholar]
- 4.Bodour AA, Drecs KP, Maier RM. Distribution of biosurfactant-producing bacteria in undisturbed and contaminated arid southwestern soils. Applied and environmental microbiology. 2003;69(6):3280–3287. doi: 10.1128/AEM.69.6.3280-3287.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Morikawa M, Daido H, Takao T, Murata S, Shimonishi Y, Imanaka T. A new lipopeptide biosurfactant produced by Arthrobacter sp. strain MIS38. Journal of bacteriology. 1993;175(20):6459–6466. doi: 10.1128/jb.175.20.6459-6466.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ekpenyong M, Antai SP, Asitok A. A Pseudomonas aeruginosa strain IKW1 produces an unusual polymeric surface-active compound in waste frying oil-minimal medium. International journal of sciences. 2016;5(6):108–123. [Google Scholar]
- 7.Ilori MO, Amund DI. Production of a peptidoglycolipid bioemulsifier from Pseudomonas aeruginosa grown on hydrocarbon. Zeitschrift für naturforschung c. 2001;56(7-8):547–552. doi: 10.1515/znc-2001-7-812. [DOI] [PubMed] [Google Scholar]
- 8.Thavasi R, Jayalakshmi S, Balasubramaian T, Banat IM. Biosurfactants production by Corynebacterium kutscheri from waste motor lubricant oil and peanut oil cake. Letters in applied microbiology. 2007;45(6):686–691. doi: 10.1111/j.1472-765X.2007.02256.x. [DOI] [PubMed] [Google Scholar]
- 9.Ron EZ, Rosenberg E. Natural roles of biosurfactants. Environmental microbiology. 2001;3(4):229–236. doi: 10.1046/j.1462-2920.2001.00190.x. [DOI] [PubMed] [Google Scholar]
- 10.Pacwa-Plociniczak M, Plaza GA, Piotrowska-Seget Z, Cameotra SS. Environmental applications of biosurfactants:recent advances. International journal of molecular sciences. 2011;12(1):633–654. doi: 10.3390/ijms12010633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Sachdev DP, Cameotra SS. Biosurfactants in agriculture. Applied microbiology and biotechnology. 2013;97(3):1005–1016. doi: 10.1007/s00253-012-4641-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sekhon KK, Khanna S, Cameotra SS. Enhanced biosurfactant production through cloning of three genes and role of esterase in biosurfactant release. Microbial cell factories. 2011;10:49. doi: 10.1186/1475-2859-10-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thavasi R, Subramanyam Nambaru VRM, Jayalakshmi S, Balasubramanian T, Banat IM. Biosurfactant production by Pseudomonas aeruginosa from renewable resources. Indian journal of microbiology. 2011;51(1):30–36. doi: 10.1007/s12088-011-0076-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Abalos A, Maximo F, Manresa MA, Bastida J. Utilization of response surface methodology to optimize the culture media for the production of rhamnolipids by Pseudomonas aeruginosa AT10. Journal of chemical technology and biotechnology. 2002;77(7):777–784. [Google Scholar]
- 15.Deepika KV, Kalam S, Sridhar PR, Podile AR, Bramhachari PV. Optimization of rhamnolipid biosurfactant production by mangrove sediment bacterium Pseudomonas aeruginosa KVR-HR42 using response surface methodology. Biocatalysis and agricultural biotechnology. 2016;5:38–47. [Google Scholar]
- 16.Rodrigues L, Teixeira J, Oliveira R, van der Mei HC. Response surface optimization of the medium components for the production of biosurfactants by probiotic bacteria. Process biochemistry. 2006;41(1):1–10. [Google Scholar]
- 17.Joshi S, Yadav S, Nerurkar A, Desai AJ. Statistical optimization of medium components for the production of biosurfactant by Bacillus licheniformis K51. Journal of microbiology and biotechnology. 2007;17(2):313–319. [PubMed] [Google Scholar]
- 18.Nies DH. Microbial heavy-metal resistance. Applied microbiology and biotechnology. 1999;51(6):730–750. doi: 10.1007/s002530051457. [DOI] [PubMed] [Google Scholar]
- 19.Cavazzuti M. Optimization Methods:from Theory to Design, London:Springer. 2013 [Google Scholar]
- 20.Myers R H, Montgomery D C. Response Surface Methodology: Product and Process Optimization Using Designed Experiments. Second ed. New York: John Wiley & Sons; 2002. [Google Scholar]
- 21.Raorane CJ, Gavimath CC, Kukreja GP, Kalsekar DP, Kulkarni SM, Ravishankar BE, Hooli RS. Isolation, identification and phylogenetic analysis of phthalic acid-degrading bacteria. International journal of advanced biotechnology and research. 2012;3(4):804–809. [Google Scholar]
- 22.Hunt CD. Dietary boron:progress in establishing essential roles in human physiology. Journal of trace elements in medicine and biology. 2012;26(2-3):157–160. doi: 10.1016/j.jtemb.2012.03.014. [DOI] [PubMed] [Google Scholar]
- 23.Michel H, Behr J, Harrenga A, Kannt A. Cytochrome C oxidase:structure and spectroscopy. Annual review of biophysics and biomolecular structure. 1998;27:329–356. doi: 10.1146/annurev.biophys.27.1.329. [DOI] [PubMed] [Google Scholar]
- 24.Maier T, Jacobi A, Sauter M, Bock A. The product of the hypB gene, which is required for nickel incorporation into hydrogenases, is a novel guanine nucleotide-binding protein. Journal of bacteriology. 1993;175(3):630–635. doi: 10.1128/jb.175.3.630-635.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]


