Decisions in motion: passive body acceleration modulates hand choice

Decisions of hand choice are a fundamental aspect of human behavior. Whereas these decisions are typically studied in stationary subjects, this study examines hand choice while subjects are in motion. We show that accelerations of the body, which differentially modulate the biomechanical costs of left and right hand movements, are also taken into account when deciding which hand to use for a reach, possibly based on bottom-up processing of the otolith signal.

Abstract

In everyday life, we frequently have to decide which hand to use for a certain action. It has been suggested that for this decision the brain calculates expected costs based on action values, such as expected biomechanical costs, expected success rate, handedness, and skillfulness. Although these conclusions were based on experiments in stationary subjects, we often act while the body is in motion. We investigated how hand choice is affected by passive body motion, which directly affects the biomechanical costs of the arm movement due to its inertia. With the use of a linear motion platform, 12 right-handed subjects were sinusoidally translated (0.625 and 0.5 Hz). At 8 possible motion phases, they had to reach, using either their left or right hand, to a target presented at 1 of 11 possible locations. We predicted hand choice by calculating the expected biomechanical costs under different assumptions about the future acceleration involved in these computations, being the forthcoming acceleration during the reach, the instantaneous acceleration at target onset, or zero acceleration as if the body were stationary. Although hand choice was generally biased to use of the dominant hand, it also modulated sinusoidally with the motion, with the amplitude of the bias depending on the motion’s peak acceleration. The phase of hand choice modulation was consistent with the cost model that took the instantaneous acceleration signal at target onset. This suggests that the brain relies on the bottom-up acceleration signals, and not on predictions about future accelerations, when deciding on hand choice during passive whole body motion.

NEW & NOTEWORTHY Decisions of hand choice are a fundamental aspect of human behavior. Whereas these decisions are typically studied in stationary subjects, this study examines hand choice while subjects are in motion. We show that accelerations of the body, which differentially modulate the biomechanical costs of left and right hand movements, are also taken into account when deciding which hand to use for a reach, possibly based on bottom-up processing of the otolith signal.

to reach for an object, the brain needs to decide on a movement plan (Shadmehr et al. 2016), part of which may involve which hand to use (Beurze et al. 2007; Schweighofer et al. 2015). Hand choice is known to be affected by a number of factors, including the relative position of each hand to the object (Coelho et al. 2013; Oliveira et al. 2010; Przybyla et al. 2013), biomechanical costs (Schweighofer et al. 2015), recent choice success (Stoloff et al. 2011), handedness (Bryden et al. 2000; Gabbard et al. 2003; Scharoun et al. 2016), and skill demands of a task (Mamolo et al. 2006).

In the deliberations preceding hand choice, the brain may assign a value (the “action value”), or cost, to each of the above factors and compare their summed value between the two hands. Recently, Schweighofer et al. (2015) quantified the relative contribution of a number of these factors, including expected biomechanical costs, expected task success, and overall handedness, on the hand choices for reaches to different targets. Their model attributes the behavioral observation that subjects choose their hand ipsilateral to a target to the associated biomechanical costs. Their model also accounts for the observation that subjects bias their choice to the hand that is more successful, typically the dominant hand.

Can this model, based on effector-specific costs, also explain hand selection in more complex real-life conditions, when the body is in motion? Whereas some effector-specific action values remain unchanged during body motion, such as handedness, the biomechanical costs depend on the inertial forces imposed by body motion and will change when the body is undergoing acceleration.

Several studies have shown that the brain anticipates Coriolis torques on the limb that are generated during active torso rotation (Pigeon et al. 2013; Sainburg et al. 1999) and adapts reaches while on a rotating or translating platform (Lackner and Dizio 1994; Sarwary et al. 2013). However, it is unclear if, and how, the brain anticipates biomechanical costs in deciding which hand to use when one is reaching for a target during passive whole body translations. Heuristically, we can derive various hypotheses of how acceleration signals, as detected by the vestibular system, could affect the decision of hand choice.

Ideally, the brain has an internal representation of the forthcoming accelerations based on current vestibular inputs and prior exposure to the stimulus, in addition to an internal model of the body dynamics (Prsa et al. 2015). On the basis of this internal model of task dynamics, the brain then calculates the future biomechanical costs of the individual hands’ movements before deciding between them. We will refer to this as the “forthcoming acceleration hypothesis.”

A second possibility is that the brain processes vestibular inputs in a bottom-up manner, using the instantaneous acceleration signal at the moment of target onset, and assumes the acceleration to remain constant. On the basis of this constant acceleration, the brain computes the biomechanical cost that underlies the deliberation of hand choice. We will refer to this possibility as the “constant acceleration hypothesis.” Motivation for this hypothesis comes from our recent work showing that the instantaneous acceleration caused by passive body motion affects target selection for saccadic eye movements (Rincon-Gonzalez et al. 2016). More specifically, we showed that the selection bias relates to the magnitude of the acceleration signal at the onset of the potential target, and not the acceleration signal at the onset of the saccade.

These results on target selection for saccades also prompt the formulation of a third hypothesis for hand selection. It may be that the cost computations based on presumed, future accelerations are too complicated to be carried out on the short timescale required in self- motion, and therefore the acceleration is completely ignored and thus will not affect hand choice for a given target. We refer to this suggestion as the “zero acceleration hypothesis.”

In the present study, we quantified the effect of passive whole body sinusoidal translation on the decision of hand choice in a unimanual reaching task. Subjects had to select either their left or right hand to reach to a single target, presented at different locations relative to the body and at different phases of the body motion. In addition, we modeled the hand choice predictions for the three outlined hypotheses and compared their predictions with the behavioral observations. The model that involves a constant acceleration, i.e., the acceleration at target onset, into the biomechanical cost calculation best reflected the behavioral results.

METHODS

Participants

Twelve subjects (6 women, ages 22–32 yr), with normal or corrected-to-normal vision and no known motor deficits participated in the experiment. The Edinburg Handedness Inventory (Oldfield 1971) showed that all subjects were right-handed (mean laterality quotient: 85, SD: 16). Subjects gave their written informed consent before the experiment. The study was approved by the ethics committee of the faculty of social sciences of Radboud University Nijmegen, The Netherlands.

Setup

Subjects were translated with the use of a linear sled. The sled, powered by a linear motor (TB15N; Technotion, Almelo, The Netherlands), was controlled by a Kollmorgen S700 drive (Danaher, Washington, DC). Subjects were seated with their interaural axis aligned with the direction of the sled motion. They were restrained by a five-point seat belt, and their head was fixed with an ear-fixed mold. The subject could immediately stop the sled by using emergency buttons on either side of the chair. During the experiment, the sled moved sinusoidally either with an amplitude of 0.15 m and a period of 1.6 s, resulting in a peak velocity of 0.59 m/s and peak acceleration of 2.3 m/s², or with an amplitude of 0.25 m and a period of 2.0 s, yielding a peak velocity of 0.79 m/s and peak acceleration of 2.5 m/s². We refer to these profiles as “low-acceleration” (2.3 m/s²) and “high-acceleration” (2.5 m/s²) motion profiles. Note that although the difference in peak acceleration is small, the average “power” of these motion profiles differed by a factor of ~3 due to the additional difference in amplitude.

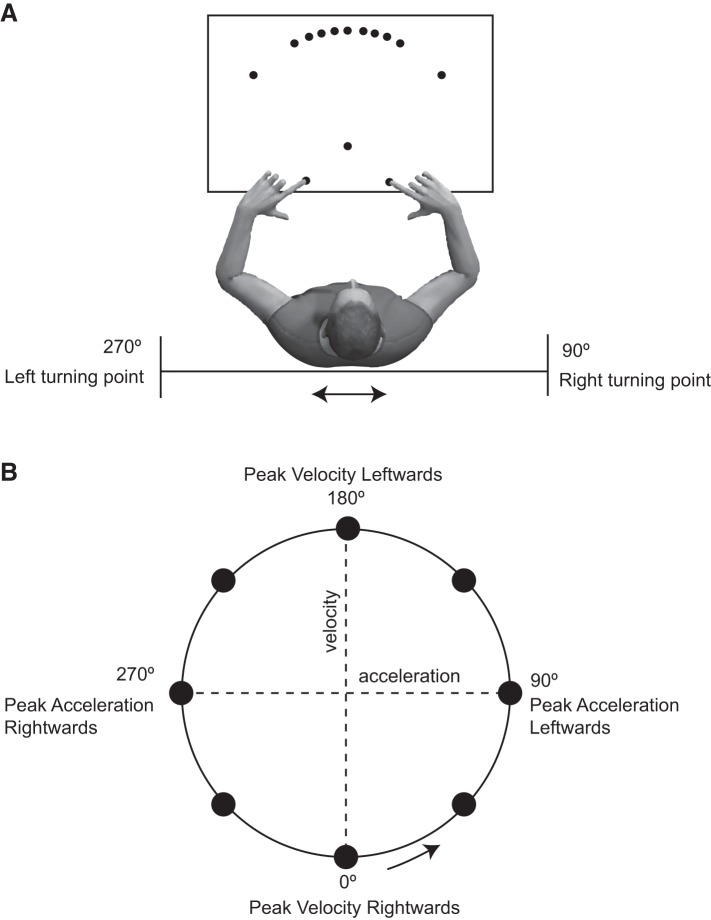
Stimuli were presented on a 27-in. touch screen monitor (ProLite; Iiyama, Tokyo, Japan) that was mounted on the sled, i.e., body-fixed, in front of the subjects at the level of their thoracic diaphragm. The experiment was performed in a dimly lit room, induced by the backlight of the touch screen. The touch screen had full HD 1080p resolution (1,920 × 1,080). Two start positions and 11 target positions were presented as disks of 3.5 cm in diameter. Start positions were at a distance of 30 cm from the subject’s sternum and 9 cm on either side of the body midline (Fig. 1A). Targets were defined at a 30-cm distance from the point midway between two start locations, at 11 different directions: −40°, −20°, −15°, −10°, −5° 0°, 5°, 10°, 15°, 20°, and 40°. A fixation dot with a diameter of 2.5 cm was also presented in front of the body midline, 12 cm in front of the two starting positions.

Fig. 1.

Experimental setup and paradigm. A: schematic overview of the setup (not to scale). Subjects were seated on a linear sled and made unimanual reaches toward targets presented on a sled-mounted touch screen. B: targets were prompted at 8 different phases of the sinusoidal sled motion, indicated by the black circles in the acceleration-velocity phase plot.

The position of the sled and the positions of the tips of the left and right index finger were recorded at 500 Hz using an Optotrak Certus system (Northern Digital, Waterloo, ON, Canada). The exact phase of the sled motion at the time of target presentation was determined with the use of a photo diode in combination with the Optotrak data. The experiment and sled were controlled using custom-written software in Python.

Experimental Paradigm

Subjects performed a hand-selection reaching task while their whole body was in sinusoidal motion, with either the low- or high-acceleration profile. Before the start of a trial, subjects had to place the tips of the index fingers of their left and right hand at the start positions. Once the touch screen detected the fingers on the start positions, the color of the start positions changed from green to yellow. A trial started with presentation of 1 of the 11 possible targets at 1 of 8 different phases of the motion (from 0° to 360° in steps of 45°; see Fig. 1B). Subjects had to reach as fast and accurately as possible with either their left or right hand to this target, which disappeared when it was touched, and then return to the start position. If subjects missed the target, they had to make a corrective movement to reach the target to continue to the next trial. In 9% of the trials, two targets were presented, which required reaches of both hands. These catch trials were introduced to prevent subjects from selecting a hand before target onset.

Subjects performed four sessions on separate days: the high acceleration on 2 days, and the low acceleration on the other 2 days. Each session consisted of 4 identical blocks interspersed by small breaks every 176 trials (excluding ~16 catch trials), during which the sled stood still. A session lasted ~45 min with a total of 704 trials (excluding ~63 catch trials) per session. In each session, there were 16 repetitions of each target (11 targets) and phase (4 phases) combination. On one day of each acceleration profile, targets were presented at the motion reversals (phases 90° and 270°), when the sled was at maximum acceleration and had zero velocity, and at the center of the motion sinusoid (phases 0° and 180°), when the sled was at maximum velocity and had zero acceleration. On the other day of each motion profile, these phase angles were shifted by 45° so that targets were prompted at phases 45°, 135°, 225°, and 315°. Note, however, that because of the screen latency, targets appeared ~100 ms (derived from the photodiode data) after the sled moved through the desired phase angle, yielding an additional phase shift of 22.5° and 18° for the low- and high-acceleration motion, respectively. Subsequent trials were tested 1¼ motion cycle apart, i.e., probing the phase that was shifted 90° forward compared with the previous trial. The order of the sessions, i.e., the phases of target onset, and the order of the motion profiles (low acceleration and high acceleration) were counterbalanced across subjects.

Model of Hand Choice

We simulated the three hypotheses outlined in the Introduction to set up predictions that guide the interpretation of hand choice at the various phases of passive sinusoidal body translation in our experiment. We followed the approach of Schweighofer et al. (2015), who modeled hand choice in body-stationary conditions based on a combination of expected biomechanical costs, expected task success, handedness, and the history of hand choice. In our modeling approach, we included only expected biomechanical costs, because that is the only factor that is directly affected by the passive acceleration. To compute the expected biomechanical costs, the brain not only needs to have an accurate internal model of limb biomechanics but also needs to make assumptions about the upcoming whole body accelerations. According to the forthcoming-acceleration hypothesis, the brain will accurately anticipate forthcoming sinusoidal acceleration signals and calculates the future biomechanical costs of both hand movements before deciding which hand to use. According to the constant-acceleration hypothesis, the brain will use the acceleration signal at target onset in the cost computation underlying the decision of hand choice and assumes acceleration will remain constant during the response. According to the zero-acceleration hypothesis, the brain will not incorporate the body acceleration signals at all in the computation of biomechanical cost and the decision of hand choice, but decides as if the body is stationary. This hypothesis predicts that hand choice does not depend on the phase of the motion.

Biomechanical cost estimation.

We computed the biomechanical costs for the forthcoming-, constant-, and zero-acceleration hypotheses on the basis of a planar two-link arm model (for details see Bakker et al. 2015). We imposed the assumed acceleration profiles on the shoulders of the arm model to compute the required shoulder and elbow torques to follow a minimum-jerk trajectory (Flash and Hogan 1985) from the start to the target position in body-centered coordinates. The inverse dynamics calculations were performed using the method developed by Casius et al. (2004). For the forthcoming-acceleration hypothesis, the shoulder acceleration profile follows the actual acceleration of the sled motion, taking the reaction time and movement time of the reaching movement into account, whereas for the constant-acceleration hypothesis, the torques were computed on the basis of acceleration of the shoulder at the moment of target onset. Finally, for the zero-acceleration hypothesis, the torques were computed for a world-stationary shoulder position. Following Schweighofer et al. (2015), we then applied the linear muscle model used by van Beers et al. (2004) to compute the motor commands necessary to generate these torques. We did this for each hand, for movements to each of the 11 targets for all 8 phase angles at which targets were presented. For the above computations, we assumed, based on the data, a reaction time (the time between target onset and movement onset) of 300 ms and a movement time of 400 ms. For our final biomechanical cost estimate, we squared the motor commands and summed them over time and over the two joints. The parameters for the two-link arm model are given in Table 1.

Table 1.

Parameters of two-link model

Parameter	Value
Length of upper link	0.35 m
Length lower link	0.45 m
Mass of upper link	1.764 kg
Mass of lower link	1.818 kg
Center of mass from joint, upper link	0.168 m
Center of mass from joint, lower link	0.193 m
Moment of inertia, upper link	0.0394 kg·m2
Moment of inertia, lower link	0.0749 kg·m2
Damping coefficient, upper link	0.8 kg·m2/s
Damping coefficient, lower link	0.8 kg·m2/s
Muscle time constant of excitation	0.04 s
Muscle time constant of activation	0.03 s

Damping coefficients were obtained from Nakano et al. (1999), muscle parameters were taken from van der Helm and Rozendaal (2000). All other parameters were taken from Kawato (1995). If necessary, they were rescaled according to the arm length used.

Note that we computed biomechanical cost in exactly the same way as Schweighofer et al. (2015) but applied it to self-motion conditions, under which the torques and motor commands are different than during the stationary situation considered by Schweighofer et al. (2015). Because the imposed sinusoidal acceleration varies over time, its effects on the torques and motor commands vary over time, as well. As a result, the expected biomechanical cost will depend on the moment of movement initiation, and thus on the phase of the sinusoidal motion at which the target appeared for both the forthcoming- and constant-acceleration hypotheses.

Choice model.

The action value in our hand-choice model depends only on the expected biomechanical costs. The action value for the right hand, for target k and phase φ at which the target appeared, is defined as

$$V_{k,\phi ,right}=-Cos{t}_{k,\phi ,right}$$

and a similar definition applies for the left hand. The minus sign reflects the fact that higher biomechanical costs should result in lower action values. We hypothesized that the arm with the highest action value will be preferred to reach for the target. We therefore determined the action value for each hand, for a given target k and phase φ, and transformed the difference between these two into a probability p_k,φ,right of choosing the right hand by using a softmax function (Schweighofer et al. 2015):

$$p_{k,\phi ,right}=\frac{1}{1+e^{-\beta \left(V_{k,\phi ,right}\right)-V_{k,\phi },left}}$$

where β is a parameter that determines how sharp the transition between favoring the left or the right hand is around the point when their action values are equal. We set β to 0.1, but the model predictions hardly change if other positive values are used. The probability of using the left hand is, by definition:

$$p_{k,\phi ,left}=1-p_{k,\phi ,right}$$

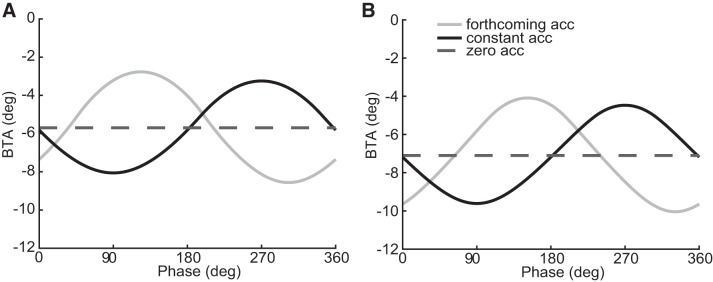
Figure 2 shows the predicted hand choice patterns based on these three hypotheses, separately for the two motion profiles (left vs. right). The balanced target angle (BTA), i.e., the target direction for which both hands are chosen equally often, is plotted as a function of the phase at which the target appeared. The gray curves show the predicted choice pattern when the choice is based on the upcoming acceleration, taking reaction time and movement duration into account (forthcoming-acceleration hypothesis). The black curves show the predictions when the body acceleration, as sensed at target onset, is assumed to remain constant in the cost calculations underlying hand choice (constant-acceleration hypothesis). Both models predict a sinusoidal modulation of hand choice with sled phase, but they are shifted relative to one another in phase by almost 180°. The differences between the two motion profiles are relatively small. Finally, the dashed lines show the model predictions of hand choice for the zero-acceleration hypothesis, demonstrating a constant BTA across the different phases of the sled motion. Note that all curves were given a vertical offset of about −6° and −7° to reflect that our subjects had such offsets (that is, they had a general preference to choose the right hand).

Fig. 2.

Choice model predictions. Balanced target angle (BTA) as a function of the phase of the sled motion at target onset for forthcoming-acceleration (gray), constant-acceleration (black), and zero-acceleration (dashed) hypotheses. A: low-acceleration motion. B: high-acceleration motion. All curves were given a vertical offset to reflect the observed offset of the subjects; acc, acceleration.

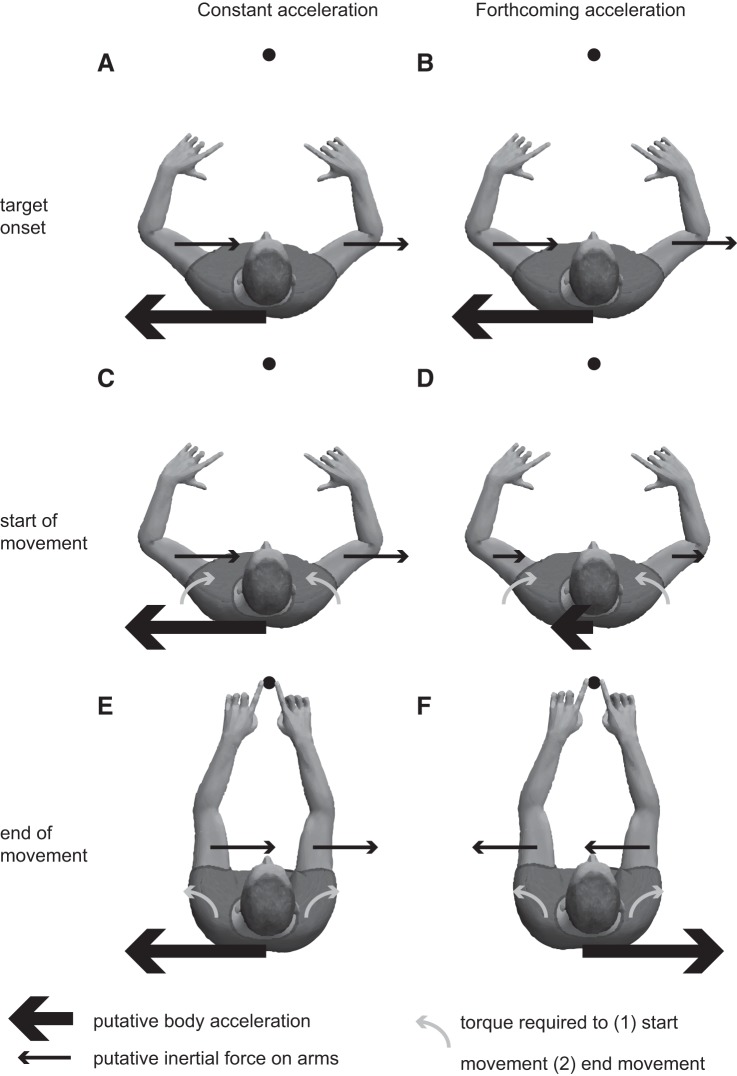
To understand why the predictions of the forthcoming- and constant-acceleration hypotheses differ so much, consider the situation where the central target appears when the sled is in its rightmost position (phase of 90°) of the acceleration motion (Fig. 3, A and B). At this moment, the sled acceleration is leftward and has its peak value. As a result of this acceleration, the arms experience an inertial force to the right. According to the constant-acceleration hypothesis, the sled acceleration is assumed constant in the biomechanical cost predictions so that the arms experience an inertial force to the right throughout the entire reaching movement (Fig. 3C). This force supports the initial part of a left-hand reach (because that hand should be moved forward and to the right), whereas it opposes the initial part of a right-hand reach. However, toward the end of the reaches, the hands must decelerate to come to a rest on the target. As a result, the shoulder torques for the left hand should be directed counterclockwise and those for the right hand, clockwise (Fig. 3E). In other words, for the last part of the reaching movements, the assumed sled acceleration supports the right-hand response, whereas it opposes that of the left hand. Since the hands also move away from the subject, the moment arms of the torques are longer at the final than at the initial part of the movement. As a result, the net effect of the sled acceleration on the reaching movements is dominated by the effect during the deceleration phase of the reaches. The assumed inertial force opposes the deceleration torque around the shoulder for the left-hand response, whereas it supports the deceleration phase of the right-hand response. Therefore, in this situation, the right hand has the lowest cost and is preferred, as shown in Fig. 2 (note that a negative BTA indicates that the direction at which both hands are chosen equally often is shifted toward leftward targets, which corresponds to an increased preference for right-hand choices).

Fig. 3.

Overview of the putative inertial forces on the arms, the body acceleration, and the torques during the experiment. A: at target onset, constant acceleration. B: at target onset, forthcoming acceleration. C: at reach onset, constant acceleration. D: at reach onset, forthcoming acceleration. E: end of reach movement, constant acceleration. F: end of reach movement, forthcoming acceleration. Thick black arrows indicate assumed direction of body acceleration, thin black arrows indicate assumed inertial forces on the arms, and gray arrows indicate net torques required to start the reach movement and end the reach movement. In some cases the inertial forces will reduce the required active torques, and in other cases they will increase the required active torque.

Now consider the forthcoming-acceleration hypothesis, again for the central target appearing at a phase of 90° of the acceleration motion (Fig. 3B). This model takes the actual sled acceleration into account, so we must take the reaction time (300 ms) and movement time (400 ms) into account. The initial part of the reaching movement then takes place when the sled is near its central position and its acceleration is small (Fig. 3D). As a result, there is little effect of the sled motion on the initial part of the reaching movements. The final phase of the reaches, however, occurs when the sled approaches its leftmost position and acceleration is directed to the right (Fig. 3F). As a result, the arms will experience an inertial force to the left (Fig. 3F). This supports the deceleration torque around the shoulder for the left-hand response, whereas it opposes the deceleration phase for the right-hand response. Overall, the left-hand response is supported by the inertial forces caused by the sled acceleration in this situation, leading to a BTA close to zero in Fig. 2. A similar reasoning can be made for other phases of target onset. This leads to a phase difference of ~180° between the sinusoidal modulation predicted by these two hypotheses, because the sled has moved almost half a period between target onset (considered by the constant-acceleration hypothesis) and the final phase of the response movement (considered by the forthcoming-acceleration hypothesis).

Data Analysis

Offline data analyses were performed in MATLAB 2015b (The MathWorks). Choice data were based on the touch screen measurements. We determined hand choice as the hand that was the first hand that departed from the touch screen, i.e., that left the start position to reach for the target. Hand choice preferences were quantified as the proportion of right-hand choices for each target direction. We summarized the psychometric data by fitting a cumulative Gaussian distribution using a maximum likelihood approach (Wichmann and Hill 2001):

$$P\left(x\right)=\lambda +\left(1-2\lambda \right)\frac{1}{\sigma \sqrt{2\pi }}\underset{-\infty }{\overset{x}{{\displaystyle \int }}}{e}^{-{(y-\mu )}^2/2{\sigma }^2}dy$$

in which x represents the target direction. The mean of the curve, µ, represents the BTA, where a negative BTA indicates a shift toward more right-hand than left-hand choices. Parameter σ is the standard deviation of the Gaussian, and λ represents the lapse rate, accounting for errors caused by subject lapses or mistakes, and was restricted to small values (λ < 0.1). We first determined the psychometric functions for each phase of the motion and each motion profile, with each psychometric curve characterized by its own µ, σ, and λ values, amounting to 24 parameters to describe the whole data set for one subject.

The forthcoming- and constant-acceleration hypotheses predict that the BTA varies approximately sinusoidally, but with different phase relationships relative to the whole body motion (Fig. 2). To examine whether there is a sinusoidal modulation of the BTA, and if so, to also determine the phase relationship, we fitted per subject a single psychometric model to all psychometric data (all 8 phases together) of a single motion profile, and assumed for µ:

$$BTA\left(phase\right)=A\cdot \sin \left(phase-phase0\right)+B$$

We further assumed a fixed σ (reflecting variability in choice behavior) and λ (lapse rate) for the eight phases. In this model, B represents the offset, i.e., handedness, and A is the amplitude of the sinusoidal BTA modulation. Phase0 indicates the phase of the BTA modulation with respect to the phase of the sled motion (see Fig. 1B), i.e., the phase shift, for which the two hypotheses make different predictions. Hence, this model had five free parameters to characterize the psychometric data for one motion profile.

The zero-acceleration hypothesis predicts a constant, i.e., phase-independent, choice bias. We operationalized this hypothesis by fitting a psychometric model that assumed for µ:

$$BTA\left(phase\right)=constant$$

and fixed σ and λ for the eight phases. This model contains only three parameters to describe the choice data.

We compared these models using the Akaike information criterion (AIC; Burnham and Anderson 2002),

$$AIC=-2\log L+2k$$

where L represents the total likelihood of the data given the model, and k is the number of free parameters. The likelihood was taken as the sum of the likelihood values for the eight psychometric curves whose µ values were derived from the sinusoidal or the constant model. AIC provided us an estimate of model quality based on both its goodness of fit and complexity. In addition to the model comparisons, we performed paired-sample t-tests to determine if the estimated parameters of the sinusoidal fits differed between the two motion profiles.

To test whether hand choice is the outcome of a competition between hands, we examined the reaction times based on the kinematics of the index fingers recorded using Optotrak. Missing Optotrak data were first reconstructed via spline interpolation using the function interp1 in MATLAB. Only data with a maximum of up to 10% missing frames in the first 500 ms of a trial were included for further analyses. In total, 5.4% (SD 5.7%) of the trials were excluded for further analyses because of this restriction. Of the remaining trials, the position data were low-pass filtered using a fifth-order, bidirectional Butterworth filter with a cutoff frequency of 10 Hz. Data were converted into a body-centered reference frame by subtracting the position of the sled, provided by another Optotrak marker. Reaction times were then calculated on the basis of velocity signals taken from the filtered position data, defined as the first point after target onset at which the hand speed exceeded 7.5 cm/s. Reaction times <200 ms and >500 ms were excluded from further analyses [4.4% (SD 4.3%) of the trials].

We examined how reaction time depended on target direction, comparing reaches to targets around the BTA, for which competition of hand choice is supposed to be strongest, and reaches to peripheral targets. The targets around the BTA were taken as the two targets closest to the subject’s mean BTA value, whereas the reaction times for the single leftmost and rightmost peripheral targets were taken as a proxy for the least competitive situation. To test for reaction time differences, we performed a three-factor ANOVA, with the factors hand (left or right), direction (BTA or periphery), and condition (low acceleration or high acceleration). Furthermore, we examined whether reaction times depended on the phase where the target was presented. To this end, we performed another three-factor ANOVA, with the factors hand (left or right), phase (8 different phases), and condition (low acceleration or high acceleration).

RESULTS

We examined the effect of passively induced sinusoidal body translations on hand choice in a unimanual reaching task. At different phases of the body motion, participants had to select either their left or right hand to reach to a target, presented from a set of 11 possible directions. The BTA was defined as the target angle for which the subject selected both hands equally often. We measured how the BTA varied as a function of the phase of two sinusoidal motion profiles that differed in their frequency and amplitude (low- vs. high-acceleration motion).

Choice Bias Modulates with Body Motion

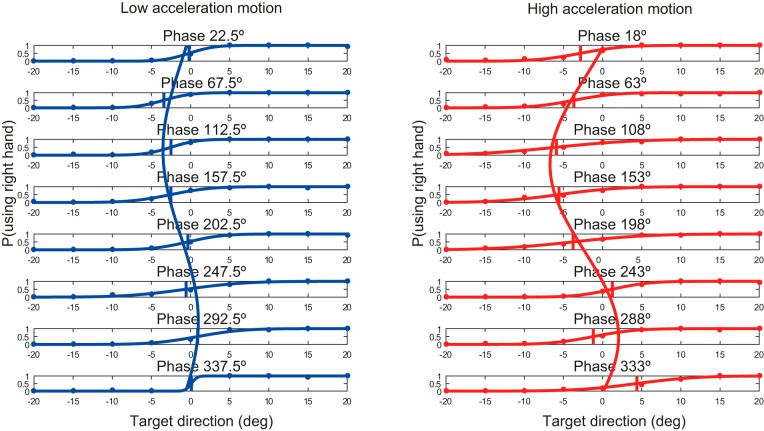
Figure 4 shows the hand choice data from a representative subject, separately for the eight different phases, for low (left)- and high-acceleration motion (right). Each panel shows the proportion of right-hand choices (circles) and the separately fitted psychometric curve as a function of target angle. For the peripheral targets, the choice was consistently to the ipsilateral hand (i.e., to the right hand if the target was at 20°, to the left hand if the target was at −20°). This was also true for the −40° and the 40° target, but for clarity these were omitted from the psychometric plots.

Fig. 4.

Psychometric curves representing hand choice of a representative subject during 8 possible phases of the motion. Left, low-acceleration motion. Right, high-acceleration motion. BTA is indicated as a vertical line for each phase. The curves overlaying the panels show the best-fit curves for this subject.

The psychometric fits provide an estimate of the BTA, the target angle for which the subject chose the left and right hand equally often, which is indicated by the thin vertical line in each panel. If the BTA is shifted to the left, subjects selected the right hand more often; if the BTA is shifted to the right, subjects chose the left hand more often. For the subject represented in Fig. 4, the BTA was generally negative for the various phases, suggesting that this subject chose the right hand more often than the left hand. In addition to this negative bias, the BTA changed consistently with phase, for both the low- and high-acceleration motion. For phase angles around 112.5°, when the body accelerated to the left, the highly negative BTA suggests a strong bias for right-hand choices, whereas for phases around 292.5°, when the body accelerated to the right, the positive BTA suggests that choice was biased to the left hand. The modulation of the hand choice bias is more prominent for the high- than low-acceleration motion.

We examined if the σ values of the psychometric curves differed over the eight phases for all subjects. A repeated-measures ANOVA showed that σ did not differ between phases, both in the low-acceleration condition [F(3.2, 35.6) = 0.64, P = 0.60] and in the high-acceleration condition [F(3.8, 14.4) = 1.4, P = 0.24], suggesting that the variability of choice behavior did not depend on the phase of the motion.

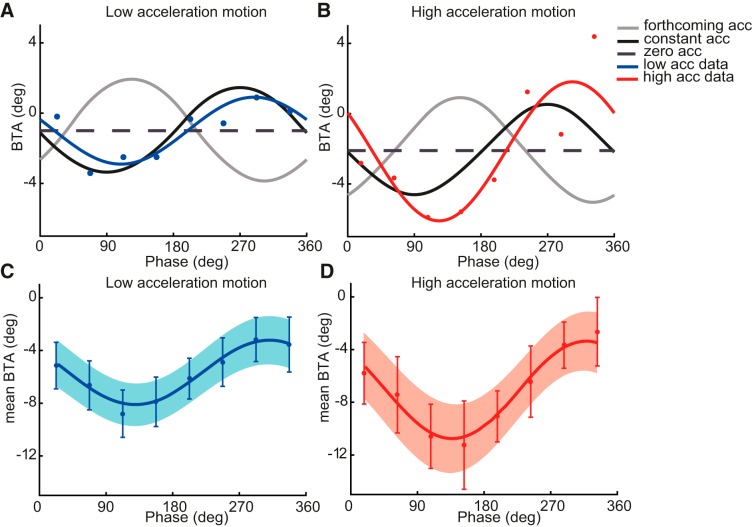
Figure 5, A and B, replots the BTA values for the same subject as in Fig. 4, but now with phase on the abscissa. Figure 5, C and D, shows the mean BTA values (±SE) across all subjects, in the same format. Overall, subjects showed a negative bias, which means that the right hand was generally chosen more often than the left hand. We also tested the consistency of this effect over the course of the experiment, because subjects had to learn how to deal with the inertial forces. To this end, we split the hand choices into the first and second half of the trials and fitted psychometric functions to these sets separately. We did not find significant differences between the fit parameters based on the first and second half of the trials (all P > 0.13), which indicates that there was no observable learning effect in our task.

Fig. 5.

BTA as a function of phase. A and B: best-fit curves for the representative subject from Fig. 4 for low-acceleration (A; blue) and high-acceleration motion (B; red). Model predictions are shown for the forthcoming-acceleration (gray), constant-acceleration (black), and zero-acceleration hypotheses (dashed line). All curves were given a vertical offset to reflect the offset of this subject. C and D: mean sinusoidal fits of BTA. Data points indicate the mean BTA values of the individual psychometric fits, accompanied by mean SE bars, for the low-acceleration (C; blue) and high-acceleration phases (D; red). Shaded area indicates the SE of the mean sinusoidal fits.

As Fig. 5 shows, the choice bias seems to vary consistently with phase, following a sinusoidal modulation. We tested whether the µ values, as determined by independent psychometric fits, are indeed more parsimoniously described by a sinusoidal relationship with phase [µ = A·sin(phase − phase0) + B] than by a phase-independent relationship (µ = constant). Given the earlier reported lack of systematic modulation of σ with phase, we also assumed σ constant across the phases for the sinusoidal fits. To account for the difference in degrees of freedom of the two descriptions, we used the AIC in the model comparison. We found lower AIC values (indicating a better model) for the psychometric model that enforced a sinusoidal relation between µ and phase (mean AIC = 1,322.2) than for the model that assumed a constant µ across phase (mean AIC = 1,454.7). This sinusoidal modulation of the BTA suggests that of our three hypotheses, i.e., the forthcoming-, constant-, and zero-acceleration hypotheses, the latter can be rejected because it predicts a constant BTA across the different phases of the body motion. The best-fit curves (red and blue solid lines) of the sinusoidal account overlay the panels in Fig. 4. These best-fit curves are also plotted in Fig. 5, A and B. Across subjects, the mean best-fit curve (the average of the individual subjects’ fits) are superimposed on the mean subjects’ data in Fig. 5, C and D, showing that they nicely capture the observed sinusoidal modulation of the BTA with phase. Table 2 summarizes the best-fit parameter values of this sinusoidal account (A, B, phase0, σ, and λ) separately for the two motion profiles.

Table 2.

Sinusoidal fit parameters

	Low Acceleration					High Acceleration
Subject	A	B	Phase0	σ	λ	A	B	Phase0	σ	λ
1	1.1	−1.1	206.4	3.4	0.003	1.9	−1.5	185.0	3.3	0.003
2	4.2	3.8	210.7	7.1	0.028	6.2	2.7	216.5	7.8	0.025
3	2.7	−10.2	210.0	6.3	0.006	4.5	−24.0	190.5	10.3	0.000
4	1.7	−4.3	211.0	4.7	0.014	2.0	−2.9	241.4	6.4	0.000
5	1.2	−16.8	185.3	16.6	0.014	3.1	−10.5	198.7	10.3	0.050
6	2.2	−4.8	225.2	7.8	0.010	0.6	−3.0	299.8	7.7	0.011
7	1.9	−1.0	176.7	3.5	0.019	4.0	−2.1	195.4	6.3	0.020
8	1.8	−12.6	198.2	7.5	0.027	3.7	−16.3	212.2	11.9	0.000
9	2.0	−7.3	171.3	6.1	0.000	4.2	−7.8	210.6	5.5	0.000
10	5.5	−8.9	187.3	7.7	0.011	9.3	−16.0	195.1	10.9	0.000
11	1.6	−4.4	173.7	6.1	0.000	1.7	−4.0	228.3	5.8	0.010
12	4.9	−0.5	199.1	8.3	0.049	6.1	0.6	239.8	9.2	0.025
Mean	2.5	−5.7	196	7.1	0.015	3.9	−7.1	217.8	7.9	0.012
SD	1.5	5.8	17.3	3.4	0.014	2.4	8.1	31.9	2.6	0.016
Forthcoming acceleration	2.9	−5.7	36.0			3.0	−7.1	64.0
Constant acceleration	2.4	−5.7	183.0			2.6	−7.1	183.0

The amplitude of the sinusoidal modulation is characterized by fit parameter A, which is significantly greater for the high- than the low-acceleration motion [t(11) = 3.5, P < 0.01]. This suggests that with larger accelerations of the body, which are accompanied by a higher power of the sinusoid, there are larger shifts in the choice bias across phase. As further illustrated by Fig. 5, the data show a negative offset (meaning more right-hand choices for left targets). The sinusoidal fits capture this by parameter B, which did not differ between the two acceleration profiles [t(11) = 0.96, P = 0.36]. This corroborates the notion that handedness does not change between the two motion profiles.

Parameter σ captures the variability in the choice responses, which was ~7.5°, i.e., slightly more than the distance between two targets. This value did not differ significantly between the two motion profiles [t(11) = 1.05, P = 0.32], suggesting that choice variability did not significantly differ between the two motion profiles. Parameter λ, which accounts for subjects’ lapses, had only a small value in both motion profiles (mean: 0.012 vs. 0.015).

Finally, given that the data are best described by a sinusoidal relationship with phase, the phase offset can be used to distinguish between the two remaining hypotheses (forthcoming vs. constant acceleration). The fitted phase offsets were 196° (SD 17°) and 218° (SD 32°) for the low- and high-acceleration motion, respectively. This difference was statistically significant [t(11) = 2.6, P < 0.05].

The phase offset following from the predictions of the forthcoming-acceleration hypothesis (36° for low acceleration and 64° for high acceleration) deviated substantially from these values. In contrast, the phase offsets according to the constant-acceleration predictions are much closer to the experimentally observed ones, being 183° for both motion profiles. This is graphically shown in Fig. 5, A and B, demonstrating that simulations based on the constant acceleration hypothesis (black line) were most in line with the observed results, even though this did not completely account for the differences in the BTA amplitude observed between the low- and high-acceleration profiles.

Figure 6 depicts the observed choice bias vs. the predicted choice bias based on the constant-acceleration (black symbols) and forthcoming-acceleration (gray symbols) hypotheses. Each symbol represents one phase in one of the motion profiles. The constant-acceleration hypothesis shows a positive correlation with the choice bias (r = 0.63, P < 0.01). The forthcoming-acceleration hypothesis shows a negative correlation with the subjects’ data (r = −0.79, P < 0.0005). This correlation shows again that the constant-acceleration model provides a better description of the behavioral data than the forthcoming-acceleration model.

Fig. 6.

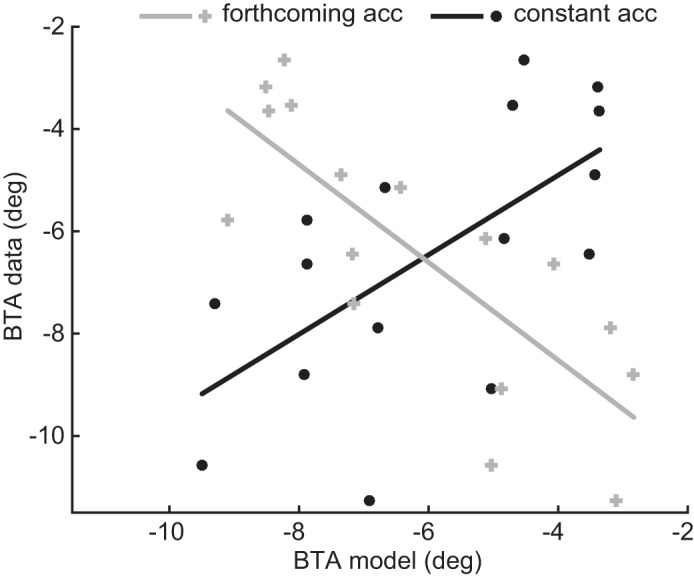
Correlation between BTA behavioral data and BTA model predictions for forthcoming acceleration (gray) and constant acceleration (black). Lines indicate regression.

Reaction Times Reflect Competition Between Hands

Finally, to provide further evidence that the paradigm evokes a competition process in which both hands compete for movement execution, we performed a reaction time analysis. In this analysis, we compared reaction times of movements to the two targets closest to subjects’ individual BTAs, with those to the two targets furthest in the periphery. We reasoned that a stronger competition between the two hands arises near the BTA, where subjects selected both hands equally often, and thus a longer reaction time than for the decision of hand choice with peripheral targets, where there is a consistent hand choice.

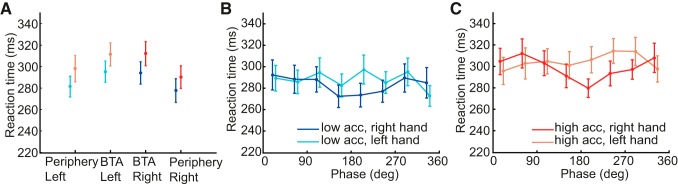
Figure 7A supports this notion: reaction times were longer for targets around the BTA than in the periphery. A repeated-measures ANOVA on the reaction times pooled across the phases, with independent variables of hand choice (left, right), target direction (BTA, periphery), and acceleration condition (low, high), revealed a main effect of target direction [F(1,11) = 35.4, P < 0.001], confirming a competition process, and a main effect of acceleration condition [F(1,11) = 20.9, P < 0.005], indicating that reaction times are longer in the high-acceleration condition. There was no main effect of hand choice and no interaction effect.

Fig. 7.

Mean reaction times accompanied by SE bars. A: mean reaction times for targets at the BTA and targets in periphery. Data for the low-acceleration motion are shown in blue and data for the high-acceleration motion in red. Light colors indicate the left hand, and dark colors the right hand. B and C: mean reaction times of the right and left hand for the 8 probed phases for low-acceleration motion (B) and high-acceleration motion (C). Light colors indicate the left hand, and dark colors the right hand.

Furthermore, we examined the effect of phase on reaction time by performing a repeated-measures ANOVA, with independent variables of hand choice (left, right), phase (8 phases), and acceleration condition (high, low), but now with the reaction times pooled over all targets. This also showed a main effect of condition [F(1,11) = 18.9, P < 0.005], with the low-acceleration condition having shorter reaction times. Moreover, the analysis revealed an interaction effect between hand and phase [F(1.8, 19.3) = 10.3, P < 0.005]. This is illustrated for the two conditions in Fig. 7, B and C. The right hand is shown in dark colors, and the left hand in light colors. At the phase where the reaction time for the right hand is at about its lowest value, the reaction time for the left hand is at about its highest value for both conditions. This suggests that the change in choice bias with phase is also mimicked by a change in reaction time between the two hands.

DISCUSSION

We examined the effect of passive whole body sinusoidal translation on hand preference in a reaching task in which right-handed participants were free to use either their right or left hand. At eight possible phases of the whole body motion, we established a psychometric curve describing hand choice as a function of target direction. From these curves, we determined the target angle for which the subject selected both hands equally often, i.e., the balanced target angle (BTA). Subjects preferred to reach with the hand ipsilateral to the target, with an overall preference for reaches with their dominant, right hand. Relative to this general handedness preference, the choice bias modulated sinusoidally with the phase of the body motion, and the amplitude of this modulation was larger for the higher acceleration motion.

To interpret our behavioral findings, we tested three models that account for the decision process preceding hand choice by making different assumptions about the inclusion of whole body acceleration in the computation of biomechanical costs. These models determined hand choice based on the lowest biomechanical costs but differed in their assumptions about future body acceleration when the cost computations were performed. These models, accounting for hand choice based on biomechanical cost functions, cannot be taken to suggest that no other cost functions play a role in this form of decision making, such as, for example, cognitive costs (Schütz and Schack 2013).

We found that the constant-acceleration hypothesis provides the best account of our data. This model assumes that the brain takes the instantaneous acceleration signal at the moment of target onset and assumes it will remain constant over the reach duration to compute expected motor costs. This model not only predicted a sinusoidal modulation of hand choice but also had the closest phase relationship with the data.

The model simulating the forthcoming-acceleration hypothesis assumed a full and correct prediction of acceleration from the start to the end of the upcoming reach, including reaction time. This model showed a sinusoidal modulation of hand choice, like the behavioral data, but could not match the phase of the experimentally observed modulation, being ~180° out of phase. Thus this model was not able to explain the behavioral data. We also tested variations of this model, but none accounted for the behavioral choice data (not shown). For example, simulations with different values of reaction time and movement time did not provide an adequate account of the forthcoming-acceleration hypothesis. Adding the return movement from the reach end point to the start location, and the costs of keeping the nonmoving hand stable, all based on the forthcoming-acceleration hypothesis, did not make the model more explanatory. We also calculated the biomechanical costs in terms of absolute (Shadmehr et al. 2016) or squared torque instead of summed motor command (see methods), which did not make the forthcoming-acceleration hypothesis more valid. Also, adding an effect of history of hand choice, as proposed in the original model of Schweighofer et al. (2015), or taking the slight curvature of the finger trajectories into account could not account for the behaviorally observed phase-dependent hand preferences. Finally, we tested whether using minimum end-point variance (Harris and Wolpert 1998) as a cost measure, instead of motor commands, could explain the data, again to no avail. Thus the forthcoming-acceleration hypothesis, and all variations based on this hypothesis, is unable to account for the observed hand choices during body accelerations.

The third model simulated the zero-acceleration hypothesis, suggesting no influence of body acceleration and velocity on hand choice. This model could not account for the data because it predicts no dependence of choice behavior on the phase of the motion, whereas we observed a clear sinusoidal modulation.

Thus the constant-acceleration hypothesis provides the most parsimonious account of the data. The idea behind this model is that the brain uses the acceleration signal at the onset of target presentation, as if it takes a vestibular snapshot, derived from the otolith signal, and assumes it to remain constant in the cost computations for hand choice. This notion is in line with our previous study (Rincon-Gonzalez et al. 2016), in which we found that target choice for saccadic eye movements was affected by the magnitude of the acceleration signal at the onset of a potential target, rather than at the onset of the saccade. Taking into consideration that the eyes are biomechanically hardly affected by accelerations, because of their negligible mass, the effect of acceleration may not relate to a motor cost calculation, but rather to a reflexive interaction between visual and vestibular signals for saccade control. Because motor costs of arm movements are affected by body acceleration due to the arm’s inertia, one would expect the brain to make predictions about the full acceleration instead of assuming it to be constant. Do our results imply that the brain is not able to make predictions about future biomechanical costs for arm choice decisions during passive translation?

It has been reported in previous literature that the brain is able to take into account biomechanical costs for reach decisions in stationary environments (Cos et al. 2011, 2014; Habagishi et al. 2014; Schweighofer et al. 2015). In addition, we have shown that subjects are able to learn to compensate for the perturbing forces when reaching while under passive whole body translation (Sarwary et al. 2013). If subjects are able to learn the perturbing forces associated with passive translation, why do they not make a correct inference about the future motor costs associated with choosing the left or right arm to reach for a target, i.e., why do they not follow the forthcoming-acceleration hypothesis? It is possible that the brain either is not able to make correct predictions about upcoming accelerations from a repetitive, cyclical motion or is not able to integrate this information into its biomechanical cost calculations. The main difference in prediction mechanisms between our study and that of Sarwary et al. (2013) is that in the latter, subjects initiated the start of the passive motion themselves, whereas in the current experiment the body motion was completely passive. Moreover, Sarwary et al. (2013) investigated motor adaptation of one movement trajectory for two acceleration profiles that only differed in sign. In the current study, we examined hand selection for 11 different movement paths, each with 8 different acceleration profiles due to the 8 possible phases of the passive body motion at target onset. Subjects had no control over which target was presented and at what acceleration it was presented when an action was required. As a result, it may be that subjects never built a full internal representation, i.e., a prior, of the task dynamics and consequently behaved biomechanically suboptimally (Acerbi et al. 2014; Beck et al. 2012). However, this interpretation does not explain why subjects instead assumed a constant acceleration to perform a cost calculation that resulted in a hand choice.

If the brain has no correct internal model of the task dynamics available, it has to rely more on feedback mechanisms than feedforward commands to generate successful actions. In the current experiment, the targets were rather large and time constraints were absent. As a consequence, subjects could act appropriately without the need for building an accurate internal model of the task dynamics. However, these feedback mechanisms do benefit from approximate feedforward control, and as an approximation, the brain may have decided to base its initial action on the instantaneous acceleration and leave the fine-tuning to the feedback mechanisms. An alternative could be that the brain decides on a default strategy when uncertain about future accelerations, i.e., it assumes acceleration constant just like the pull of gravity.

Another option is that the brain cannot incorporate passive whole body motion in building an internal model of the correct task dynamics. From this perspective, it would be interesting to perform the same experiment in the presence of self-generated body motion. For example, in the building of an internal model of self-motion, it has been shown that neurons in the vestibular nuclei already distinguish between self-generated and passive head motion (Cullen et al. 2011). How this information is further distinguished in components of head and body motion is still an open question. It can be speculated that in the absence of body motion reafference, there is more uncertainty about the predicted body motion, making the brain rely more on bottom-up mechanisms in decisions about hand choice.

Finally, our results demonstrate longer reaction times for reaches toward targets around the BTA compared with targets in the periphery, suggesting that we have probed a competitive process for hand selection (Churchland et al. 2008; Cisek 2007). This difference in reaction time also has been found in other hand choice studies (Oliveira et al. 2010; Stoloff et al. 2011). Importantly, Oliveira et al. (2010) showed that by restricting reaches to only one hand, this reaction time difference disappeared, suggesting that hand choice is a critical factor for the reaction time differences between the target directions. The interaction effect in our data between the changes in left- and right-hand reaction time and phase supports the notion of a competitive process, suggesting that the difference in reach reaction time between the left and right hand depends on the BTA, i.e., the target direction that induces balanced hand choices. We lack an explanation for why reaction times were generally longer in the higher acceleration motion compared with the lower acceleration condition. It can be speculated that subjects felt less pressed to respond quickly with a longer period time and amplitude (2.0 s and 0.25 m vs 1.6 s and 0.15 m).

In conclusion, our study unequivocally shows an influence of passive whole body motion on the decision of hand choice. Our modeling effort suggests the involvement of a biomechanical cost calculation underlying these choices, based on the acceleration signal at the moment of target presentation, presumably transmitted by the vestibular system.

GRANTS

This work was supported by European Research Council Grant EU-ERC-283567 (to W.P.M.) and Netherlands Organization for Scientific Research Grants NWO-VICI: 453-11-001 (to W.P.M.) and NWO-VENI: 451-10-017 (to L.P.S.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

R.S.B., R.H.W., L.P.S., and W.P.M. conceived and designed research; R.S.B. and R.H.W. performed experiments; R.S.B., R.H.W., R.J.v.B., L.P.S., and W.P.M. analyzed data; R.S.B., R.J.v.B., L.P.S., and W.P.M. interpreted results of experiments; R.S.B. and R.J.v.B. prepared figures; R.S.B. drafted manuscript; R.S.B., R.J.v.B., L.P.S., and W.P.M. edited and revised manuscript; R.S.B., R.H.W., R.J.v.B., L.P.S., and W.P.M. approved final version of manuscript.