Principal Components Adjusted Variable Screening

Abstract

Marginal screening has been established as a fast and effective method for high dimensional variable selection method. There are some drawbacks associated with marginal screening, since the marginal model can be viewed as a model misspecification from the joint true model. A principal components adjusted variable screening method is proposed, which uses top principal components as surrogate covariates to account for the variability of the omitted predictors in generalized linear models. The proposed method is demonstrated with superior numerical performance compared with the competing methods. The efficiency of the method is also illustrated with the analysis of the Affymetrix genechip rat genome 230 2.0 array data and the European American SNPs data.

1. Introduction

We consider the problem of ultrahigh dimensional regression, i.e. the dimension of predictors used for predicting a response of interest, p, is much larger than sample size, n. It is often asssumed that only a relatively small subset of the predictors contribute to the response. As a result, an efficient method of variable selection, which can identify the most important predictors, plays a key role in the ultra-high dimensional regression.

One group of variable selection methods are based on penalized methods which can select variables and estimates parameters simultaneously through solving an ultrahigh dimensional regression with some pre-specified penalties leading to sparsity. These methods include bridge regression (Frank and Friedman, 1993), LASSO (Tibshirani, 1996), SCAD (Fan and Li, 2001), Dantzig selection (Candes and Tao, 2007), and other folded concave regularization methods (Fan and Lv, 2011; Zhang and Zhang, 2012). When the dimension is very high, however, these methods may have heavy implementation costs and face challenges in computational feasibility.

Recently, variable screening methods have been re-discovered and advocated in the ultra-high dimensional setting, including sure independence screening (SIS) method (Fan and Lv, 2008), marginal bridge regression based method (Huang et al., 2008) and some others. Specifically, SIS method in (Fan and Lv, 2008) selects important variables in ultrahigh dimensional linear models based on the marginal correlations of each predictor with the response. They showed that the correlation ranking of the predictors possesses a sure independence screening property, that is, the important variables can be selected with probability close to one. Later, the marginal screening method was extended to generalized linear models (Fan and Song, 2010). Various screening methods have been developed, to name a few, tilting methods (Hall et al., 2009), generalized correlation screening (Hall and Miller, 2009), nonparametric screening (Fan et al., 2011), robust rank correlation based screening (Li et al., 2012), and quantile-adaptive model-free feature screening (He et al., 2013).

These marginal screening methods face a number of challenges. For example, if the marginal working model is too far away from the true model, it is hard to ensure the sufficient conditions for sure screening to hold. Consequently marginally unimportant but jointly important variables may not be preserved in marginal screening. Meanwhile, the marginal screening methods may include noise variables that are weakly correlated with the important predictors. It can potentially increase false positive rate.

To address these issues, in this paper, we propose a principal component-adjusted screening (PCAS) method for generalized linear models. The key idea is to use principal components as surrogate covariates to account for omitted covariates in marginal screening. Specifically, we fit p marginal regressions by maximizing the marginal likelihood including not only the screened predictor but also some selected principal components. Then we consider an independence learning by ranking the maximum marginal likelihood estimators or maximum marginal likelihood.

PCAS method has several advantages. First, PCAS retains top principal components as surrogate covariates, thus retains the information in those predictors that are not included in the marginal screening. Second, it possesses good properties of the conditional screening to reduce the correlation among predictors and thus reduce the noise in the process of variable selection. Finally, unlike the conditional sure independence screening method (Barut et al., 2012) where certain variables are known to be responsible for the outcomes, PCAS does not need these prior information of the predictors. Extensive numerical results show that the proposed PCAS method has superior performance to the original SIS method. As an important remark, computing the principal components in the implementation only requires eigenvalue-decomposition of an n by n matrix regardless of the dimensionality p.

The setup of generalized linear models is introduced in section 2. Section 3 discussed the computation of principal components. In section 4, we introduced the PCAS procedure with maximum marginal likelihood estimators (MMLE) and marginal likelihood ratio (MLR). Simulation results are presented in section 5 and two real data analysis results are illustrated in section 6. Section 7 gives concluding remarks.

2. Generalized linear models

Consider the generalized linear model where the probability density function of a response variable Y takes the form f_Y(y; θ) = exp{yθ−b(θ)+c(y)}, with known functions b(·), c(·), and the natural parameter θ. Suppose that the observed data {(X_i, Y_i), i = 1, ···, n} are identically independent distributed copies of (X, Y), where X_i = (1, X_i1, ···, X_ip)^T and X_i1, ···, X_ip are p-dimensional covariates for subject i. β = (β₀, β₁, ···, β_p)^T is a (p+1)-vector of parameter. We are interested in identifying the sparsity structure of β from the equation

$$E(Y\mid \mathbf{X}=\mathbf{x})=b^{\prime }(\theta (\mathbf{x}))=g^{-1}(\sum _{j=0}^p{\beta }_j{x}_j),$$ (1)

where x = {x₀, x₁, ···, x_p}^T is a (p+1)-vector with x₀ = 1 when considering the intercept, b′(θ) is the first order derivative of b(θ) with respect to θ and g is the link function. For demonstration purposes, in the paper we only take canonical link function, that is g = (b′)⁻¹, into consideration. In this case, $\theta (x)={\displaystyle \sum _{j=0}^p}{\beta }_j{x}_j$. The ordinary linear model Y = X^Tβ + ε, where ε is the random error, is a special case of model (1) by using the identity link, i.e. g(μ) = μ. Considering binary response data, the logistic regression is another special case of model (1) by using the logit link g(μ) = log(μ/(1 − μ)).

3. Principal component analysis

Principal component analysis is a widely used tool for high dimensional data analysis in many fields, such as signal processing and dimension reduction. Based on projecting a dataset to another coordinate system by determining the eigenvectors and eigenvalues of the matrix, principal component analysis involves calculations of a covariance matrix of a dataset to minimize the redundancy as well as maximize the variance (Shlens, 2014). A common method to find the eigenvectors and eigenvalues is singular value decomposition (SVD), which decomposes a matrix into a set of rotation and scale matrices. Suppose X̄ is a matrix with n rows and p columns (p > n) and columns are normalized to be norm one. A singular value decomposition of X̄ is given by ${\overline{\mathbf{X}}}_{n\times p}={\overline{\mathbf{U}}}_{n\times n}(\text{diag}({\lambda }_1,\dots ,{\lambda }_n),0_{n\times (p-n)}){\overline{\mathbf{V}}}_{p\times p}^T$, where Ū and V̄ are orthonormal matrices with dimensions n and p respectively and diag(λ₁, …, λ_n) is a diagonal matrix with diagonal elements λ₁, …, λ_n. Additionally, λ₁ ≥ λ₂ ≥ … ≥ λ_n ≥ 0. Since

$${\overline{\mathbf{X}}}^T\overline{\mathbf{X}}=\overline{\mathbf{V}}\text{diag}({\lambda }_1^2,\dots ,{\lambda }_n^2,0,\dots ,0){\overline{\mathbf{V}}}^T,$$

it is clear that the columns of V̄ are the principal directions of X̄. Thus, the principal components, that is, the projection of X’s rows on these directions, should be X̄V̄ = Ū_n×ndiag(λ₁, …, λ_n). In other words, each column of Ū represents each principal component up to some scale.

To calculate Ū, we note $\overline{\mathbf{X}}{\overline{\mathbf{X}}}^T=\overline{\mathbf{U}}\text{diag}({\lambda }_1^2,\dots ,{\lambda }_n^2){\overline{\mathbf{U}}}^T$. Therefore, if we perform an eigenvalue decomposition on X̄X̄^T, which is a matrix with much smaller dimensions when p is much larger than n, then the columns of Ū consist of all eigenvectors.

4. PCAS procedure

Let ${\mathcal{M}}_{★}=\{1\le j\le p:{\beta }_j^{★}\ne 0\}$ be the true sparse model with non-sparsity size s = |ℳ_★|, where ${\mathit{\beta }}^{★}={({\beta }_0^{★},{\beta }_1^{★},\dots ,{\beta }_p^{★})}^T$ denotes the true value. In this paper, we refer to principal components adjusted models as fitting models with componentwise covariates and the first K_n principal components as offset covariates.

4.1. PCAS with maximum marginal likelihood estimators

PCAS maximum marginal likelihood estimators (PCAS-MMLE) ${\widehat{\beta }}_j^M$, for j = 1, …, p, is defined as the minimizer of the negative marginal log-likelihood

$${({\widehat{\beta }}_{j,0}^M,{\widehat{\beta }}_j^M,{\widehat{\gamma }}_{j,1}^M,\dots ,{\widehat{\gamma }}_{j,K_n}^M)}^T=\underset{{\beta }_0,{\beta }_j,{\gamma }_{j,1},\cdots ,{\gamma }_{j,K_n}}{\text{argmin}}\sum _{i=1}^{n}l({\beta }_0+{\beta }_j{X}_{ij}+\sum _{k=1}^{K_n}{\gamma }_{j,k}^M{U}_{ik},Y_i),\text{for}j=1,\dots ,p,$$

where l(Y; θ) = −(θY − b(θ) + c(Y)), and {U_k} is the kth eigenvector consisting of ${\{U_{ik}\}}_{i=1}^n$. ${\widehat{\beta }}_j^M$ measures the strength of the conditional contribution of X_j given the first K_n principal components. These principal components represent the information of predictors except for X_j in the marginal model. The process can be rapidly computed.

Specifically, in ordinary linear models with normality assumption of random errors, the maximum likelihood estimator is identical to the ordinary least squares estimator written as

$${({\widehat{\beta }}_{j,0}^M,{\widehat{\beta }}_j^M,{\widehat{\gamma }}_{j,1}^M,\dots ,{\widehat{\gamma }}_{j,K_n}^M)}^T=\underset{{\beta }_0,{\beta }_j,{\gamma }_{j,1},\cdots ,{\gamma }_{j,K_n}}{\text{argmin}}\sum _{i=1}^n{(Y_i-{\beta }_0-{\beta }_j{X}_{ij}-\sum _{k=1}^{K_n}{\gamma }_{j,k}^M{U}_{ik})}^2,\text{for}j=1,\dots ,p.$$

We select a set of variables

$${\widehat{\mathcal{M}}}_{{\gamma }_n}=\{1\le j\le p:\mid {\widehat{\beta }}_j^M\mid \ge {\gamma }_n\},$$ (2)

where γ_n is a given threshold value. By ranking the importance of features according to their magnitude of marginal regression coefficients adjusted for a proportion of principal components, we retain variables with large conditional contribution given these principal components. Such an independence learning helps to decrease the dimension of the parameter space from p (possibly hundreds of thousands) to a much smaller number by choosing a large γ_n, leading to a more feasible computation. Although interpretations and implications of principal components adjusted models are still biased from the joint model, the non-sparse information about the joint model can be passed along to the marginal model under a mild condition. Hence it is suitable for the purpose of variable screening.

Since the rationale to use the principal components as surrogate covariates is to account for the effect of the omitted covariates in the marginal model, we should compute the principal components based on the p − 1 omitted covariates for each marginal regression. For simplicity of computation, we compute the principal components based on all p covariates and use these principal components as surrogate covariates. Based on our observations, the numerical performance of two methods are very close while the latter one has significantly smaller computational costs.

4.2. PCAS with marginal likelihood ratio

As an alternative method, we can also rank variables based on the likelihood reduction of the variable X_j given the first K_n principal components, which we call PCAS with maximum likelihood ratio (PCAS-MLR):

$$L_{j,n}={\mathbb{P}}_n\{l({\widehat{\beta }}_j^M{X}_j+\sum _{k=1}^{K_n}{\widehat{\gamma }}_{j,k}^M{U}_k,Y)\}-{\mathbb{P}}_n\{l({\widehat{\beta }}_0^M,Y)\},\text{for}j=1,\dots ,p,$$

where ${\mathbb{P}}_{n}f(X,Y)=n^{-1}{\sum }_{i=1}^{n}f(X_i,Y_i)$ is the empirical measure, and ${\widehat{\beta }}_0^M=\underset{{\beta }_0}{\text{argmin}}{\mathbb{P}}_{n}l({\beta }_0,Y)$. Denote L_n = (L_1,n, L_2,n, ···, L_p,n)^T. Specifically, in ordinary linear models,

$$L_{j,n}=\sum _{i=1}^n{(Y_i-{\widehat{\beta }}_j^M{X}_{ij}-{\sum }_{k=1}^{K_n}{\widehat{\gamma }}_{j,k}^M{U}_{ik})}^2-\sum _{i=1}^n{(Y_i-{\widehat{\beta }}_0^M)}^2,\text{for}j=1,\dots ,p,$$

where ${\widehat{\beta }}_0^M=\underset{{\beta }_0}{\text{argmin}}{\displaystyle \sum _{i=1}^n}{(Y_i-{\beta }_0)}^2$.

The smaller the L_j,n is, the more the variable X_j contributes. We sort the vector L_n in an ascending order and choose variables according to

$${\widehat{\mathcal{N}}}_{{\nu }_n}=\{1\le j\le p:L_{j,n}\le {\nu }_n\},$$ (3)

where ν_n is a predefined thresholding parameter. PCAS-MLR ranks the importance of features according to their marginal contributions to the magnitudes of the log-likelihood function given a proportion of principal components. Unlike PCAS-MMLE method which only uses the information of magnitudes of estimators, PCAS-MLR method makes use of more information, including the magnitudes of the estimators as well as their associated variation.

4.3. Determining the number of selected variables

It remains open on how to choose the number of selected variables d in variable screening literature. In applications, it is common for practitioners to select a fixed number of top-ranked variables, as the fixed number may reflect prior knowledge of the number of susceptible predictors or budget limitations. Another commonly used procedure is to set the size of the selected set to a number less than the sample size, for example d = [2n/log(n)] (Fan and Lv, 2008), so that the follow-up analysis can be performed in a p < n scenario. Data-driven procedures for determining the size of the important set are appealing but relatively limited. They include information criteria, such as AIC and BIC, and the false discovery rate (FDR) based methods (Barut et al., 2012; Zhao and Li, 2012). These methods, however, have large computational cost, especially in the ultra-high dimensional framework. Following (Fan and Lv, 2008), we used d = [2n/log(n)] in this paper.

4.4. Determining the number of principal components

The choice of numbers of principal components K_n is critical for PCAS. We propose to use the following two data adaptive methods. The first method is the scree plot, a classical method in factor analysis to determine the number of principal components. As a related numerical method, we can also use the maximum eigenvalue ratio criterion (Luo et al., 2009), defined as λ_j/λ_j+1 with 1 ≤ j ≤ n − 1 and λ₁ ≥ λ₂ ≥ … ≥ λ_n > 0. We choose the number of principal components that can maximize the eigenvalue ratio, that is,

$$\widehat{k}={\text{argmax}}_{1\le j\le k_{max}}({\lambda }_j/{\lambda }_{j+1}),$$ (4)

where k_max ≤ n is a prespecified maximum factor dimension. When the predictors’ correlation structure follows a factor model, it was shown in Wang (2012) that k̂ is consistent to the dimension of the linear subspace spanned by the column vectors of factors’ matrix.

5. Simulations

In this section, we present several simulated linear model examples and logistic regression model examples to evaluate the performance of the proposed procedure and to demonstrate some factors influencing the false selection rate. We implement four different scenarios to generate data. We vary the size of the nonsparse set of coefficients as well as the number of principal components from 1 to 100 for different scenarios, to gauge difficulties of simulation models on the basis of 200 simulations with sample size 500.

For each simulation setting, we apply two marginal sure independence screening (SIS) procedures based on marginal maximum likelihood estimator (MMLE) and marginal likelihood ratio (MLR), and two PCAS procedures including PCAS-MLR and PCAS-MMLE, to screen variables. The minimum model size required for each method to have a sure screening, i.e. to contain the true model ℳ_★, is used as a measure of the effectiveness of a screening method. This avoids the issues of choosing the thresholding parameter. For each simulation model, we evaluate each method by summarizing the median minimum model size (MMMS) as well as its robust estimate of the standard deviation (RSD), which is the associated interquartile range (IQR) divided by 1.34.

5.1. Simulation Model I

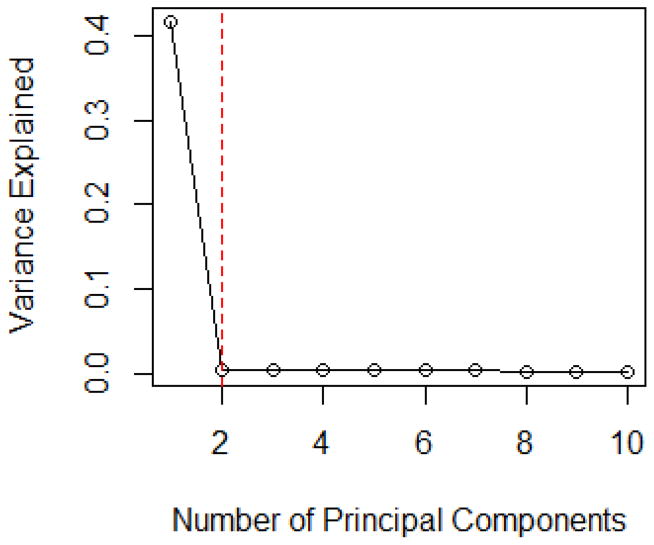
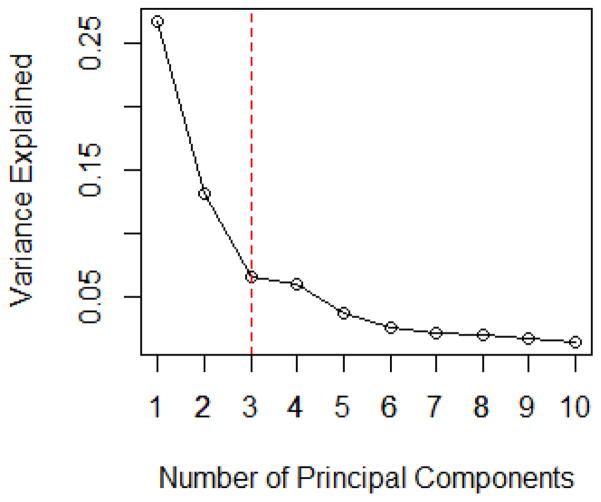
The covariates X = (X₁, ···, X_p)^T are generated from a multivariate normal distribution with mean vector 0 and compound symmetric covariance matrix Σ, where ρ = Σ_ij = 0.4, when i ≠ j. The size of the non-sparse set size s is taken as 6, 8 and 12 with the true regression coefficients recorded in Table 1. The MMMS of selected models with its associated RSD for linear models and logistic regression models with p = 1000 and p = 10000 are shown in Table 1. We record the results of PCAS with number of PCs taking as 1, 3, 5, 10, 30, 50 and 100 respectively. The case of zero PCs is SIS method (Fan and Song, 2010). The scree plot is provided as Figure 1.

Table 1.

The MMMS and RSD (in parenthesis) of the simulated examples for linear and logistic regression from simulation model I with n = 500 when p = 1000 and p = 10000. PC=0 refers to the marginal screening in Fan and Lv (2008).

PCs	Variance	SIS-PCA-MLR	SIS-PCA-MMLE	SIS-PCA-MLR	SIS-PCA-MMLE
Setting 1, linear model with p = 1000
		s = 6, β★ = (0.3,−0.3, 0.3, …)T		s = 12, β★ = (3, 4, 3, …)T
0	0	13(35)	13(35)	101(96)	101(96)
1	41.5%	7(3)	7(4)	12(0)	12(0)
3	42.2%	7(3)	7(4)	12(0)	12(0)
5	42.8%	7(3)	7(3)	12(0)	12(0)
10	44.4%	7(4)	7(4)	12(0)	12(0)
30	50.2%	8(5)	8(5)	12(0)	12(0)
50	55.4%	11(8)	10(8)	12(0)	12(0)
100	66.4%	19.5(32)	19(31)	12(1)	12(1)
Setting 2, logistic regression with p = 1000
		s = 6, β★ = (0.7,−0.7, 0.7, …)T		s = 8, β★ = (3, 4, 3, …)T
0	0	14(26)	14(26)	70.5(80)	64(82)
1	41.7%	7(3)	7(3)	21(31)	23(28)
3	42.4%	7(3)	7(3)	22.5(31)	24(30)
5	43.0%	7(4)	7(3)	25(29)	26(32)
10	44.6%	7(4)	8(4)	24(38)	27(38)
30	50.4%	8(7)	8(7)	38(49)	37(46)
50	55.5%	10(10)	10.5(10)	58(72)	60(80)
100	66.5%	22(34)	24.5(34)	532(460)	414(347)
Setting 3, linear model with p = 10000
		s = 6, β★ = (0.3,−0.3, 0.3, …)T		s = 12, β★ = (3, 4, 3, 4, …)T
0	0	90.5(501)	90.5(501)	830.5(924)	830.5(924)
1	40.3%	14.5(37)	14(35)	12(1)	12(1)
3	40.6%	15(35)	14(34)	12(1)	12(1)
5	41.0%	15(30)	14(29)	12(1)	12(1)
10	41.9%	16.5(36)	15(35)	12(1)	12(1)
30	45.2%	27(49)	25.5(45)	12(1)	12(1)
50	48.5%	36.5(100)	36.5(95)	12(2)	12(2)
100	56.1%	70.5(171)	67.5(170)	14(8)	14(7)
Setting 4, logistic regression with p = 10000
		s = 6, β★ = (0.7,−0.7, 0.7, …)T		s = 8, β★ = (3, 4, 3, …)T
0	0	112(365)	112(366)	641(742)	609.5(731)
1	41.5%	15(30)	16(29)	142(339)	146(354)
3	41.8%	16(32)	17(32)	149.5(372)	160(351)
5	42.2%	15(37)	17(36)	157(392)	168.5(394)
10	43.0%	16.5(35)	17(37)	154(351)	160(367)
30	46.3%	28(51)	26(50)	259(663)	259(646)
50	49.5%	36(68)	34.5(71)	410.5(834)	455(879)
100	57.0%	78.5(206)	80.5(238)	6837(6317)	2570(3513)

Figure 1.

The Scree Plot for Linear Models in Simulation Model I with p = 1000 and n = 500.

Since the first principal component can explain over 40% of the total variability in the observed covariate matrix, much larger than that of the rest PCs, the scree plot in Figure 1 suggests that the number of PCs taken should be one. In addition, the maximum eigenvalue ratio estimator gives the same choice, i.e. k̂ = 1. This is consistent with our observation in Table 1, where PCAS performs the best when only one PC is adjusted. The performance of PCAS method is not improved with the increase in the number of principal components. It is reasonable since the proportion of the variation that can be explained by the rest of PCs is so small that including more PCs will not be helpful to account for the additional contribution from the rest of the covariates, instead, it leads to larger estimation variation hence deteriorates the performance of PCAS. We also compute the cases for ρ = 0.2, 0.6 and 0.8. Since the results demonstrate a similar trend, we omit the details.

5.2. Simulation Model II

In this model, we evenly divide all variables into five groups, and each group of variables follows a multivariate normal distribution with mean 0 and compound symmetric covariance matrix Σ_ρ, where ρ = 0.4, 0.5, 0.6, 0.8 and 0.9 respectively. The MMMS of the selected models with its associated RSD for linear models and logistic regression models with p = 1000 and p = 10000 are shown in Table 2.

Table 2.

The MMMS and RSD (in parenthesis) of the simulated examples for linear and logistic regression model II using different number of PCs with n = 500 when p = 1000 and p = 10000.

PCs	Variance	SIS-PCA-MLR	SIS-PCA-MMLE	SIS-PCA-MLR	SIS-PCA-MMLE
Setting 1, linear model with p = 1000
		s = 6, β★ = (0.3,−0.3, 0.3, …)T		s = 12, β★ = (3, 4, 3, 4, …)T
0	0	12(35)	12(35)	30(21)	30(21)
1	18.4%	14(37)	84(66)	30.5(21)	31.5(23)
3	45.3%	19.5(32)	177.5(88)	30(19)	34.5(28)
5	63.6%	7(2)	53(26)	12(0)	39(16)
10	64.8%	7(3)	54(28)	12(1)	38(18)
30	68.9%	9(10)	63.5(40)	12(1)	35(15)
50	72.5%	14(15)	72(51)	12(1)	30.5(15)
100	79.8%	52.5(75)	119(109)	13(2)	28(15)
Setting 2, logistic regression with p = 1000
		s = 6, β★ = (0.7,−0.7, 0.7, …)T		s = 12, β★ = (−3, 4,−3, 4, …)T
0	0	13(37)	13(37)	856.5(241)	856.5(241)
1	18.7%	14.5(39)	81(73)	862(216)	879(193)
3	46.8%	19(37)	171(90)	878.5(165)	922.5(111)
5	64.7%	7(3)	50(26)	14(5)	73(35)
10	65.8%	7(3)	51(30)	15(7)	76(40)
30	69.9%	9(8)	59(39)	19(16)	84(49)
50	73.4%	12(15)	66(49)	25.5(33)	97(63)
100	80.6%	58(96)	132.5(127)	67(79)	139(98)
Setting 3, linear model with p = 10000
		s = 6, β★ = (0.3,−0.3, 0.3, …)T		s = 12, β★ = (3, 4, 3, 4, …)T
0	0	126.5(381)	126.5(381)	165.5(190)	165.5(190)
1	18.4%	154(357)	831(705)	168(186)	190(226)
3	46.8%	190.5(316)	1832.5(734)	154.5(186)	255(330)
5	64.6%	16(22)	489(242)	12(1)	179(113)
10	65.2%	16(29)	490(289)	12(1)	201(109)
30	67.3%	21.5(48)	549(325)	12(1)	206(118)
50	69.3%	34.5(74)	646(392)	12(2)	238(122)
100	74.0%	105(184)	860(590)	14(6)	284.5(162)
Setting 4, logistic regression with p = 10000
		s = 6, β★ = (0.7,−0.7, 0.7, …)T		s = 12, β★ = (−3, 4,−3, 4, …)T
0	0	163.5(302)	163.5(302)	7978.52840	7978.52840
1	2.0%	160(307)	240.5(327)	8122(2625)	8147.5(2583)
3	5.3%	167.5(300)	312(336)	8039.5(2382)	8092(2325)
5	7.4%	15(26)	51(29)	39(63)	77(40)
10	8.8%	15.5(27)	52(31)	41.5(57)	78.5(39)
30	14.1%	21(45)	56.5(36)	50(91)	85.5(46)
50	19.3%	30(65)	65.5(42)	71(118)	95(61)
100	31.3%	57(125)	87(65)	139(244)	128.5(127)

PCAS-MLR seems to outperform PCAS-MMLE in terms of smaller MMMS and RSD in many cases. Unlike PCAS-MMLE which uses only the information of magnitudes of estimators, PCAS-MLR makes use of more information, including the magnitudes of the estimators as well as their associated variation.

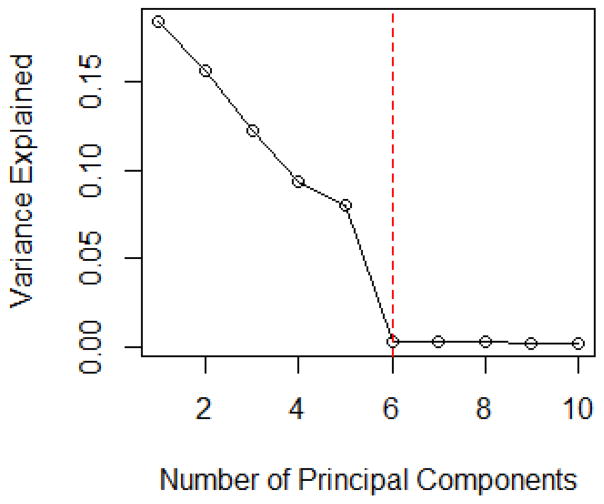
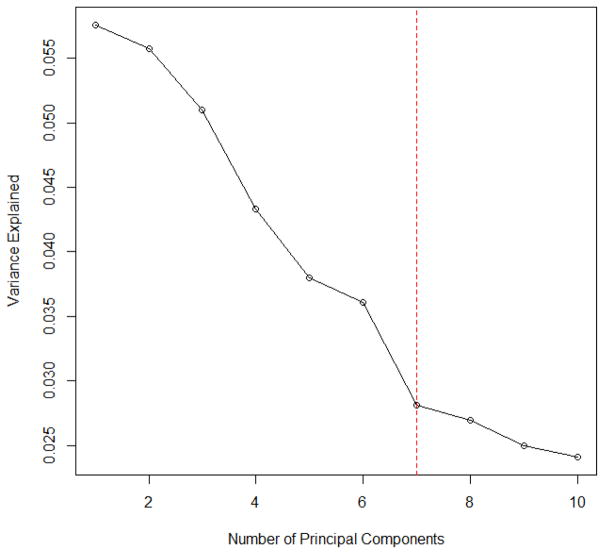
The scree plot in Figure 2 suggests to choose five principal components based on the variance explained. In addition, the maximum eigenvalue ratio estimator gives the same answer, i.e. k̂ = 5. It is obvious that PCAS method with five principal components adjusted outperforms SIS, and the performance of PCAS method is highly related to the number of PCs used.

Figure 2.

The Scree Plot for Linear Models in Simulation Model II with p = 1000 and n = 500.

5.3. Simulation Model III

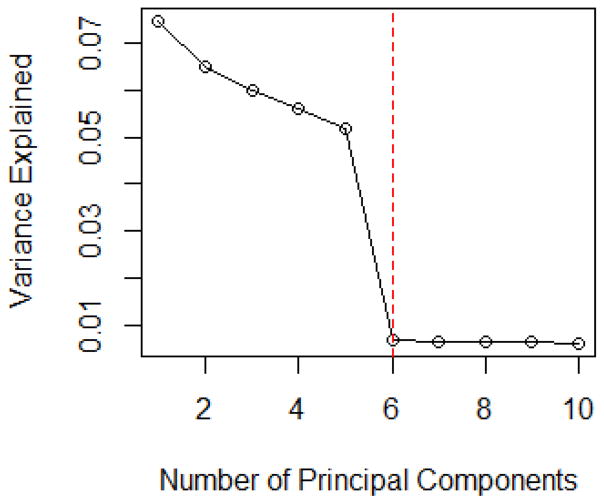
This simulation model is adopted from (Shen and Huang, 2008), where variables are generated after creating the covariance matrix. First, we generate vectors v_i, i = 1, ···, p, according to a standard normal distribution and let V = (v₁, …, v_p)′. Let C be a diagonal matrix, where among the diagonal entries, the top five values are set as 50 and the rest are randomly drawn from a standard uniform distribution. In this way we can generate covariates from a multivariate normal distribution with mean 0 and covariance matrix Σ = VCV^T. The MMMS of the selected models with its associated RSD for linear models and logistic regression models with p = 1000 and p = 10000 are shown in Table 3. The scree plot in Figure 3 suggests to choose five principal components based on the variance explained. In addition, the maximum eigenvalue ratio estimator k̂ = 5. These observations are consistent with the results in Table 3.

Table 3.

The MMMS and RSD (in parenthesis) of the simulated examples for linear and logistic regression model III using different number of PCs with n = 500 when p = 1000 and p = 10000.

PCs	Variance	SIS-PCA-MLR	SIS-PCA-MMLE	SIS-PCA-MLR	SIS-PCA-MMLE
Setting 1, linear model with p = 1000
		s = 6, β★ = (3,−3, 3,−3, …)T		s = 12, β★ = (3, 4, 3, 4, …)T
0	0	29(20)	29(20)	802.5(121)	802.5(121)
1	7.5%	157.5(173)	135.5(153)	808(229)	813.5(222)
2	14.0%	90.5(150)	50.5(120)	669.5(291)	685(284)
3	20.0%	56.5(161)	26(95)	369(372)	378.5(367)
5	30.8%	6(0)	6(0)	16(6)	15(7)
10	34.0%	6(0)	6(0)	15(6)	14.5(4)
30	44.7%	6(0)	6(0)	14.5(6)	14(6)
50	53.3%	6(0)	6(0)	14(4)	14(6)
100	69.3%	6(0)	6(0)	14(4)	15(5)
Setting 2, logistic regression with p = 1000
		s = 6, β★ = (3,−3, 3,−3, …)T		s = 8, β★ = (1.3, 1, 1.3, 1, …)T
0	0	43.5(34)	44(35)	333.5(124)	333.5(124)
1	6.9%	24(35)	24(32)	378.5(190)	613(336)
2	13.6%	18.5(19)	18(18)	364(164)	387(151)
3	19.7%	11.5(13)	9.5(10)	291(247)	272.5(237)
5	30.8%	6(0)	6(0)	8(0)	8(0)
10	34.0%	6(0)	6(0)	8(0)	8(1)
30	44.7%	6(0)	6(0)	8(0)	8(0)
50	53.3%	6(0)	6(0)	8(0)	8(0)
100	69.2%	7(4)	8(4)	8(0)	8(1)
Setting 3, linear model with p = 10000
		s = 6, β★ = (0.2,−0.2, 0.2, …)T		s = 12, β★ = (3, 4, 3, 4, …)T
0	0	98(117)	98(117)	142.5(291)	142.5(291)
1	2.1%	111(126)	106(135)	62(134)	65(142)
2	4.2%	87.5(149)	92(161)	19(72)	21(58)
3	6.2%	60(120)	54.5(123)	15(9)	15.5(11)
5	9.8%	58(127)	52(141)	12(2)	12(3)
10	11.4%	54(106)	53.5(110)	12.5(2)	13(3)
30	17.5%	73.5(152)	96.5(180)	12(3)	13(5)
50	23.3%	90(235)	101(204)	13(2)	13(3)
100	36.3%	261(383)	282.5(395)	14(13)	15(17)
Setting 4, logistic regression with p = 10000
		s = 6, β★ = (0.5,−0.5, 0.5,−0.5, …)T		s = 8, β★ = (1.3, 1, 1.3, 1, …)T
0	0	48(118)	48(118)	13(26)	13(26)
1	1.3%	42.5(110)	43(106)	13(22)	13(26)
3	3.6%	40.5(95)	44(88)	12.5(13)	13(14)
5	5.6%	38.5(73)	40(78)	11(11)	11(12)
10	7.3%	44(74)	46(84)	11(9)	12(11)
30	13.7%	61(120)	60(131)	12(17)	13(21)
50	19.7%	94.5(181)	95.5(178)	15.5(25)	16(28)
100	33.3%	186.5(351)	202(334)	34.5(66)	35(73)

Figure 3.

The Scree Plot for Linear Models in Simulation Model III with p = 1000 and n = 500.

5.4. Simulation Model IV

This simulation study imitates a genome-wide analysis where the covariates represent genotype status at each SNP across the whole genome. Furthermore, the correlation among all SNPs carries subject’s ancestry information reflection latent population substructures which should be controlled when assessing each SNP effect. The covariates X = (X₁, ···, X_p)^T is generated according to the Balding-Nichols model (Balding and Nichols, 1995) as follows. First, we generate a latent variable Y* that follows a Bernoulli distribution with parameter 0.5. Second, we generate covariates X from a multinomial distribution with parameters depending on the value of the latent variable Y*. If Y* = 0, X follows a multinomial distribution with parameters (n, (1 − p_l)², 2p_l(1 − p_l), $p_l^2$). If Y* = 1, X follows a multinomial distribution with (n, $\frac{{(1-p_l)}^2}{{(1-p_l)}^2+2R{p}_l(1-p_l)+R^2{p}_l^2},\frac{2R{p}_l(1-p_l)}{{(1-p_l)}^2+2R{p}_l(1-p_l)+R^2{p}_l^2},\frac{R^2{p}_l^2}{{(1-p_l)}^2+2R{p}_l(1-p_l)+R^2{p}_l^2}$) as the parameters, where p_l follows a Beta distribution with shape parameters $\frac{p(1-F_{ST})}{F_{ST}}$ and $\frac{(1-p)(1-F_{ST})}{F_{ST}}$. In addition, F_ST = 0.04 represents the genetic distance between two populations, p = 0.5, and the relative risk R = 0.5. We consider s = 3, 6 and 12 for different levels of sparsity. When s = 3, β* = (1, 1.3, 1)^T. When s = 6, β* = (3, −3, 3, −3, 3, −3)^T. When s = 12, β^★ = (1, 1.3, 1, 1.3, 1, 1.3, …)^T. The MMMS of the selected models with its associated RSD for linear models when s = 12 are shown in Table 4.

Table 4.

The MMMS and RSD (in parenthesis) of the simulated examples for linear model IV using different number of PCs with s = 12, β^★ = (1, 1.3, 1, 1.3, 1, 1.3, …)^T when p = 40000 and n = 500.

PCs	Variance	SIS-PCA-MLR	SIS-PCA-MMLE
		(SIS-MLR)	(SIS-MMLE)
0	0	39(70)	39(70)
1	5.9%	13(4)	13(3)
3	6.3%	13(4)	13(4)
5	6.8%	13(4)	13(4)
10	8.0%	13(4)	13(4)
30	12.2%	14(6)	14(7)
50	17.0%	15(12)	15.5(11)
100	27.8%	23(35)	22(37)

PCAS and SIS can both perfectly identify important predictors when s=3 or 6, therefore the results are not shown in the table format. This may be because the independence structure among predictors leads to the equivalence between the joint population signal and the marginal population signal. We now discuss the case when s = 6. Based on the above simulation model, we generate iid random variables X₁, ···, X_p, E(X_iX_j) = E(X_i)E(X_j) = 0 for i ≠ j and $E(X_j^2)=1$. When j ≤ s = 6, $E{X}_{j}Y=E{X}_j({\displaystyle \sum _{k=1}^s}{\beta }_k{X}_k+\epsilon )=3$ or −3. When j > s = 6, because of the independence structure, EX_jY = 0. It is similar for s = 3 case. Although still being a model misspecification, the sparsity structure of the joint model is the same as that of the marginal model. Moreover, there is a clear gap between the marginal signal and the marginal noise. As a result, we can pick up the exact number of important variables with both PCAS and SIS.

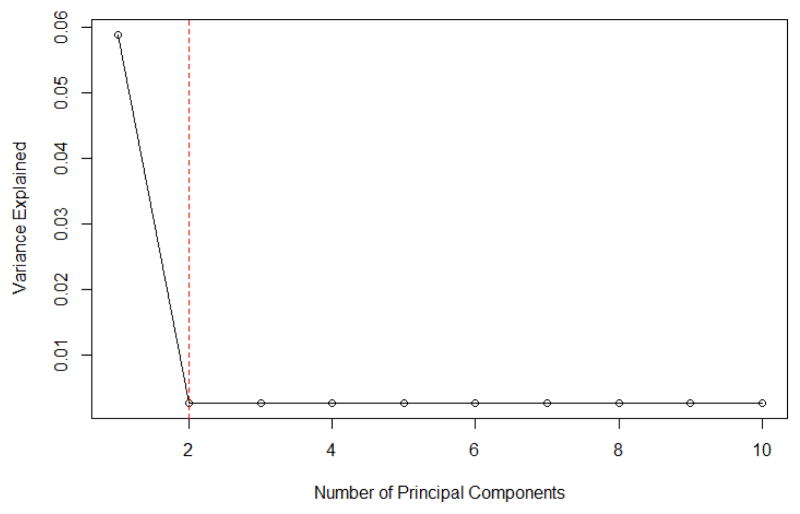
When s = 12, the scree plot in Figure 4 recommends to take one principal component. The corresponding PCAS outperforms SIS method as principal components play a critical role in capturing the correlation structure among predictors. In addition, the performance of PCAS method is not improved by the increase in the number of principal components, indicating that a certain number of principal components can capture the information among all the predictors reasonably well.

Figure 4.

Scree Plot for Linear Models in Simulation Model IV with p = 40000 and n = 500.

6. Real data analysis

6.1. Affymetric GeneChip Rat Genome 230 2.0 Array Example

To illustrate the proposed method, we analyze the dataset reported in (Scheetz et al., 2006), where 120 12-week-old male rats were selected for harvesting of tissue from the eyes and subsequent microarray analysis. The microarrays used to analyze the RNA from the eyes of these animals contain more than 31,042 different probe sets (Affymetric GeneChip Rat Genome 230 2.0 Array). The intensity values were normalized using the robust multichip averaging method (Irizarry et al., 2003) to obtain summary expression values for each probe set. Gene expression levels were analyzed on a logarithmic scale. We are interested in finding the genes that are related to the TRIM32 gene, which was found to cause Bardet-Biedl syndrome (Chiang et al., 2006) and is a genetically heterogeneous disease of multiple organ systems, including the retina. Although more than 30,000 probe sets are represented on the Rat Genome 230 2.0 Array, many of these are not expressed in the eye tissue. We focus only on the 18,975 probes that are expressed in the eye tissue.

We apply SIS and the proposed PCAS to this dataset, where n = 120 and p = 18, 975. Because the performance of PCAS-MLR is no worse than that of PCAS-MMLE, we only present the results from PCAS-MLR. With PCAS-MLR, we choose the first 2 principal components based on its scree plot shown in Figure 5 as well as the maximum eigenvalue ratio estimator k̂ = 2.

Figure 5.

Scree Plot for Rat Genome Data with p = 18975 and n = 120.

To evaluate the accuracy of two methods, we use cross validation and compare the prediction error (PE):

$$\text{PE}=\frac{1}{n}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2,$$

where y_i is the observed value and ŷ_i is the predicted value. By 6-fold cross validation, we randomly partition the data into a training data set of 100 observations and a testing set of 20 observations. On the training data set, we conduct each variable screening method to select d = 50 variables, following the suggestion in (Fan and Lv, 2008). Based on these selected variables, we obtain the ordinary least squares (OLS) estimates of the coefficients in the linear regression model, and make a prediction on the testing data set. Then we compare the predicted response with the true response, and obtain the prediction error as well as its standard deviation. As shown in Table 5, PCAS-MLR gives the prediction error 0.2278, which is about 50% smaller than 0.4636 produced by SIS. Furthermore, the much smaller standard deviation of PCAS-MLR indicates that PCAS-MLR is more robust than SIS method in this data analysis.

Table 5.

Comparison between SIS and PCA-SIS over the rats testing data.

Method	Prediction Error	Standard Deviation
SIS	0.4636	0.2563
PCA-SIS	0.2278	0.08762

6.2. European American SNP Example

Our second example is the European American SNP study in (Price et al., 2006). As part of an ongoing disease study, it consists 488 European Americans genotyped on an Affymetrix platform containing 116,204 SNPs. Similarly as in (Price et al., 2006), we use 360 observations after removing outlier individuals. We are interested in finding the SNPs that are related to the height phenotype (0/1 binary data) in European Americans, which leads to 277 variables (Price et al., 2006). We implement the proposed method and the marginal screening method on the data set, where n = 360 and p = 277. Both the scree plot in Figure 6 and the maximum eigenvalue ratio estimator k̂ = 6 suggest to use 6 principal components.

Figure 6.

Scree Plot for SNP Data with p = 277 and n = 360.

Similar as before, we implement 6-fold cross validation to partition the data into a training data set of 300 observations and a testing set of 60 observations. On the training data set, we select d = [2n/log(n)] variables using each variable screening method, and fit the logistic regression based on these selected variables. We then make a prediction on the testing data set, and evaluate the prediction effect by the area under ROC curve (AUC). The result shows that PCAS-MLR obtains a 9.42% larger AUC value than that of SIS and a relatively smaller standard deviation, indicating that PCAS-MLR is preferred in terms of accuracy and robustness.

7. Concluding remarks

In this paper, we propose a PCAS method for generalized linear models, where principal components are used as surrogate covariates to account for the variability of the omitted covariates. Compared with the marginal screening method, PCAS can represent more information of other predictors that are not included in the marginal model, and thus decrease the degree of model misspecification to a large extent. With principal components included in the marginal model, it improves the accuracy as well as the robustness of estimation when dimensionality is ultrahigh. Our proposed method shows improvement from both simulation and real data analysis results.

It is important yet challenging to decide how many principal components should be used when performing this method. In the paper, we use maximum eigenvalue ratio estimator along with the scree plot. There are a few challenges in theoretical development. First, to achieve model selection consistency, it is critical to establish that the marginal signals can preserve the sparsity structure of the joint signals. Given that the first K_n principal components are adjusted, it is challenging to derive the population marginal signals and their sparsity structure. Second, ideally we should use the principal components based on the p − 1 omitted covariates for each marginal variable X_j, but it will be computationally intensive hence we recommend to compute the principal components based on all p covariates and use them as surrogate covariates for all the marginal variables. Although this approach greatly reduces the computation costs and has almost the same numerical performance, it brings additional challenges in theoretical development since the contribution of each marginal variable is somehow overly counted in the calculation of the principal components. These are interesting topics for future research.

Software

Software in the form of R code, together with input data sets and complete documentation is available on request from the corresponding author (rsong@ncsu.edu).