Modeling Stomatal Conductance^,

Abstract

Recent advances have improved our ability to model stomatal conductance using process- or optimality-based models, and continuing research should focus on how stomata sense leaf turgor and on how to quantify the direct carbon costs of low leaf water potential.

Robust models of stomatal conductance are greatly needed to predict plant-atmosphere interactions in a changing climate and to integrate new knowledge in physiology and ecological theory. Recent years have brought major advances in the experimental and theoretical understanding underpinning both process-based and optimality-based approaches to modeling stomatal function. I review these advances, highlight areas in need of more research, and argue that these modeling approaches are poised to supersede the long-dominant empirical approach.

A reliable and general model for leaf stomatal conductance (g_s) has long been one of the holy grails of plant physiology. By controlling the exchange of water and carbon dioxide between plants and the atmosphere, stomata play a central role in the regulation of leaf and plant water status and transport, photosynthesis, drought sensitivity and tolerance, competition for soil resources, and even landscape and global hydrology (Hetherington and Woodward, 2003). An integrative formal theory—a mathematical model—that links stomatal function to plant traits and environmental variables would thus have incalculable value, both for making forward predictions and for drawing inferences about the physiology and ecology of observed stomatal behavior. My aim in this article is to summarize recent progress toward such models of stomatal conductance.

Stomatal conductance has historically been predicted almost exclusively using empirical or phenomenological models, such as the widely used Jarvis and Ball-Berry families of models (Jarvis, 1976; Ball et al., 1987). Such models are perfectly adequate for forward prediction in situations where their parameters can be estimated with confidence, and indeed, these models continue to inform gas exchange projections across the modeling community (e.g. Oleson et al., 2008). However, the phenomenology of stomatal behavior in seed plants is by now very well established, so little further progress is likely in the area of empirical modeling, nor is it likely worth pursuing given that empirical models cannot provide insight about the underlying controls on gas exchange, but can only summarize and project what we already know about stomata. (Some aspects of the phenomenology of stomatal behavior in nonseed plants remain unresolved, such as the responses to CO₂ and abscisic acid [e.g. Brodribb and McAdam, 2011; Chater et al., 2011; Ruszala et al., 2011; Brodribb and McAdam, 2017]; empirical models have yet to be thoroughly validated for these taxa, so progress remains possible on that front.) This article will therefore focus on process-based (“mechanistic”) and goal-directed (“optimality”) approaches to predicting and interpreting stomatal function.

In what follows, I will very briefly review the background to each of these approaches, describe important advances over the last decade or so, and then suggest directions for continuing work. I prefer to avoid reproducing equations and instead refer readers to articles cited herein for mathematical details.

PROCESS-BASED MODELING

Most models of stomata based on physiological mechanisms simulate two key variables: guard cell volume, or turgor pressure, and guard cell osmotic content, or osmotic pressure. The rationale for this approach is that stomatal aperture increases when guard cells expand in volume (Franks et al., 1995, 1998, 2001) and that shifts in guard cell volume often result from osmotic water movements driven by active regulation of guard cell ion transport and carbon metabolism (note that guard cell water movements can also occur passively as a result of changes in local water potential). Guard cell volume, or turgor, is typically predicted from mass balance; that is, by assuming that water potential is dictated by a steady-state balance between water supply from elsewhere in the leaf or plant and evaporative water loss to the atmosphere. Water balance can also predict the effects of turgor in adjacent epidermal or subsidiary cells, whose “backpressure” opposes stomatal opening (Meidner and Edwards, 1975; Franks et al., 1995, 1998; Vialet-Chabrand et al., 2017).

Several improvements have emerged in recent years in this basic conceptual framework for process-based modeling of g_s. These advances primarily involve three areas: improved understanding of stomatal hydromechanical diversity and its role in responses to water stress; growing awareness of the multiplicity of mechanisms underlying stomatal responses to both light and CO₂, including the role of mesophyll photosynthesis; and advances in kinetics-based modeling of guard cell osmotic pressure and volume. I discuss advances in these areas below.

Responses to Soil Moisture and Air Humidity

Some interesting features of stomatal behavior arise from the hydraulic and mechanical context in which guard cells function in the intact leaf. For example, in seed plants, the immediate passive effect of a decline in water potential in the vicinity of guard cells is to open stomatal pores (Darwin, 1898; Iwanoff, 1928; Powles et al., 2006; Buckley et al., 2011). This may seem counterintuitive, given that reduced water potential should cause guard cells to lose water and thus decrease in volume. However, the surrounding epidermal cells also lose water, which reduces their backpressure on the guard cells and produces a net opening movement known as the initial “wrong-way” response (WWR; Shackel and Brinckmann, 1985; Franks et al., 1998; Mott and Franks, 2001). This occurs whether leaf water status is perturbed by changing water supply (soil water potential, ψ_soil, or plant hydraulic conductance, K_plant) or evaporative demand (leaf to air water vapor mole fraction difference, Δw). However, the WWR is eventually followed by a “right-way” response (RWR) in which apertures decline below their initial values (Rufelt, 1963; Raschke, 1970; Comstock and Mencuccini, 1998; Buckley et al., 2011). The RWR is apparently caused by an actively mediated adjustment of guard cell osmotic pressure that is slower than, and subsequent to, the initial and more rapid change in epidermal and guard cell volumes (Darwin, 1898; Grantz and Zeiger, 1986; Grantz, 1990; Buckley, 2005). Several models capture these basic phenomena (e.g. Cowan, 1972; Delwiche and Cooke, 1977; Haefner et al., 1997; Buckley et al., 2003; Franks, 2004).

In the last decade, several important refinements to this picture of stomatal hydromechanics have emerged—refinements that influence stomatal function and have implications for how to model stomata on a mechanistic basis. Painstaking work using cell pressure probes to construct pressure-aperture relationships for guard cells and subsidiary cells (Meidner and Edwards, 1975; Zimmermann and Steudle, 1975; Franks et al., 1995, 1998) has shown that angiosperm stomata often cannot achieve their maximum apertures unless the adjacent subsidiary cells experience a marked drop in turgor pressure at the same time that the guard cells increase their turgor pressures (Franks and Farquhar, 2007). This is because the effect of epidermal backpressure on stomatal aperture is unusually strong in angiosperms, and particularly in grasses. An important consequence is that stomatal aperture can change very quickly in grasses, which Franks and Farquhar (2007) noted may enable them to respond more quickly to environmental cues, thus possibly helping to explain the ecological success and rapid diversification of grasses.

The mechanical diversity of stomata spans in both directions: whereas the epidermal effect is especially strong in grasses, Franks and Farquhar (2007) found it to be very weak or even negligible in ferns. This may have significance for understanding the evolution of stomatal responses to water status. Brodribb and McAdam (2011) found that stomata in ferns and other seedless vascular plants (SVPs) lack a WWR to humidity, which is consistent with a weak epidermal effect, but more importantly means that these species may not require an actively mediated response to overcome the epidermal effect and produce a RWR—the passive effect of water potential on guard cell turgor may be sufficient. The same authors also found that SVPs are largely insensitive to exogenous abscisic acid (ABA), giving rise to the hypothesis that seed plants evolved guard cell ABA sensitivity as a mechanism to drive the osmotic shifts needed to overcome the greater opposing force of their epidermal cells. However, other evidence shows that the genes required for ABA-mediated stomatal closure are present in all major lineages of extant land plants (Lind et al., 2015) and that some mosses (Chater et al., 2011) and lycophytes (Ruszala et al., 2011) do in fact respond to exogenous ABA. A possible resolution of these viewpoints is that it was not the existence but rather the magnitude and importance of active responses that increased over evolutionary time.

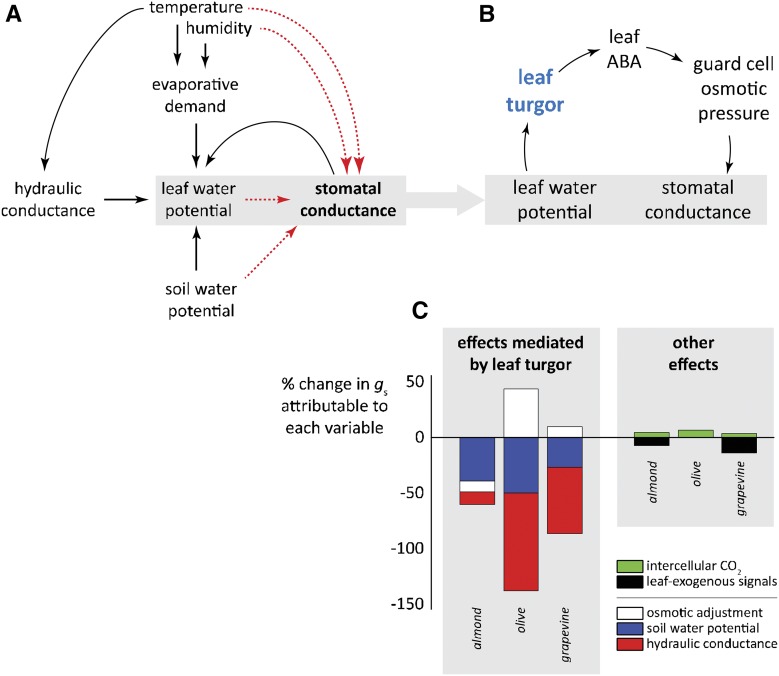
A long-standing hypothesis for stomatal closure in drying soil is the notion that ABA is generated in droughted roots and transported through the transpiration stream to stomata, where it induces stomatal closure (Davies and Zhang, 1991; Tardieu and Simonneau, 1998). This hypothesis was challenged by data showing normal drought responses in wild-type shoots grafted onto ABA-deficient rootstock (Holbrook et al., 2002; Christmann et al., 2005). Although the debate over the root-ABA hypothesis is not resolved, recent years have brought some new insights. For example, Rodriguez-Dominguez et al. (2016) found that a stomatal response to water status originating entirely within the leaf, initiated by changes in leaf turgor, could explain most or all of the observed soil drought response in three woody species (Fig. 1C), with at most a minor role for leaf-exogenous signals. A great deal of evidence suggests that leaf-endogenous ABA production may help to explain stomatal responses to both atmospheric and soil drought (Wright and Hiron, 1969; Loveys and Kriedemann, 1973; Xie et al., 2006; Bauer et al., 2013). More recently, McAdam et al. (2016) demonstrated that stomatal closure in dry air in angiosperms, but not in SVPs, is accompanied by a spike in ABA production within leaves, caused by increased expression of genes that control key steps in the ABA biosynthesis pathway (Fig. 1). These active responses exhibited lag times consistent with the delay typically observed prior to the RWR in angiosperms. Other recent evidence suggests leaf ABA may also affect leaf hydraulic conductance, which could amplify changes in leaf turgor sensed by stomata (Pantin et al., 2013).

Figure 1.

Stomatal responses to leaf turgor integrate effects of several other factors. A, Many stomatal responses arise from the effect of leaf water potential, which integrates the influences of many environmental and plant variables. Recent work has advanced the prospect of modeling these responses on a mechanistic basis by showing that the effect of leaf water potential on stomatal conductance is mediated by de novo leaf-endogeneous biosynthesis of ABA in response to reduced leaf turgor (B; McAdam et al., 2016), and stomatal responses to moderate soil drought can be explained almost entirely by effects mediated by leaf turgor (C; Rodriguez‐Dominguez et al., 2016).

These findings can be easily incorporated into the hydromechanical process-modeling framework described above. For example, differences in the influence of epidermal turgor on stomatal aperture would appear in the “net epidermal mechanical advantage” in the BMF model of Buckley et al. (2003), which is a closed-form model with a linearized pressure-aperture response, or more explicitly in modified pressure-aperture curves in the model given by Franks (2004), which requires iterative solution. Differences in the strength of an actively mediated response of guard cell osmotic pressure (π_g) to leaf water status would appear in models as variations in the magnitude of the sensitivity of π_g to leaf turgor (in the BMF model) or evaporative demand (in the Franks model). Tardieu et al. (2015) have shown how the dynamics of leaf xylem ABA resulting from production in roots and distribution in a capacitive water transport system can be modeled, and this approach could be augmented to account for leaf-endogenous ABA synthesis and coupled with approaches described earlier that account for stomatal hydromechanics. More data are needed about the dynamics of the leaf-endogenous ABA response before a general model can be built (see Outstanding Questions).

Responses to Light, CO₂, and Temperature

Few attempts have been made to predict stomatal responses to light and CO₂ on a mechanistic basis in intact leaves, partly because the mechanisms remain unresolved. Farquhar and Wong (1984) showed that the effects of irradiance and CO₂ on stomatal conductance were qualitatively very similar to their effects on mesophyll cell ATP content predicted by a biochemical photosynthesis model (Farquhar et al., 1980), and they suggested this ATP model as an empirical predictor of g_s. Dewar (2002) advanced a similar idea as a more explicit mechanistic hypothesis, noting that the light and CO₂ responses are actively mediated and, therefore, may rely on the availability of energy carriers (ATP and NADPH) from photosynthesis. He proposed the ratio of gross photosynthesis to intercellular CO₂ concentration as a convenient measure of this energy pool for modeling purposes. Similarly, Buckley et al. (2003) used Farquhar and Wong's (1984) ATP model to predict guard cell osmotic content in their model of stomatal conductance.

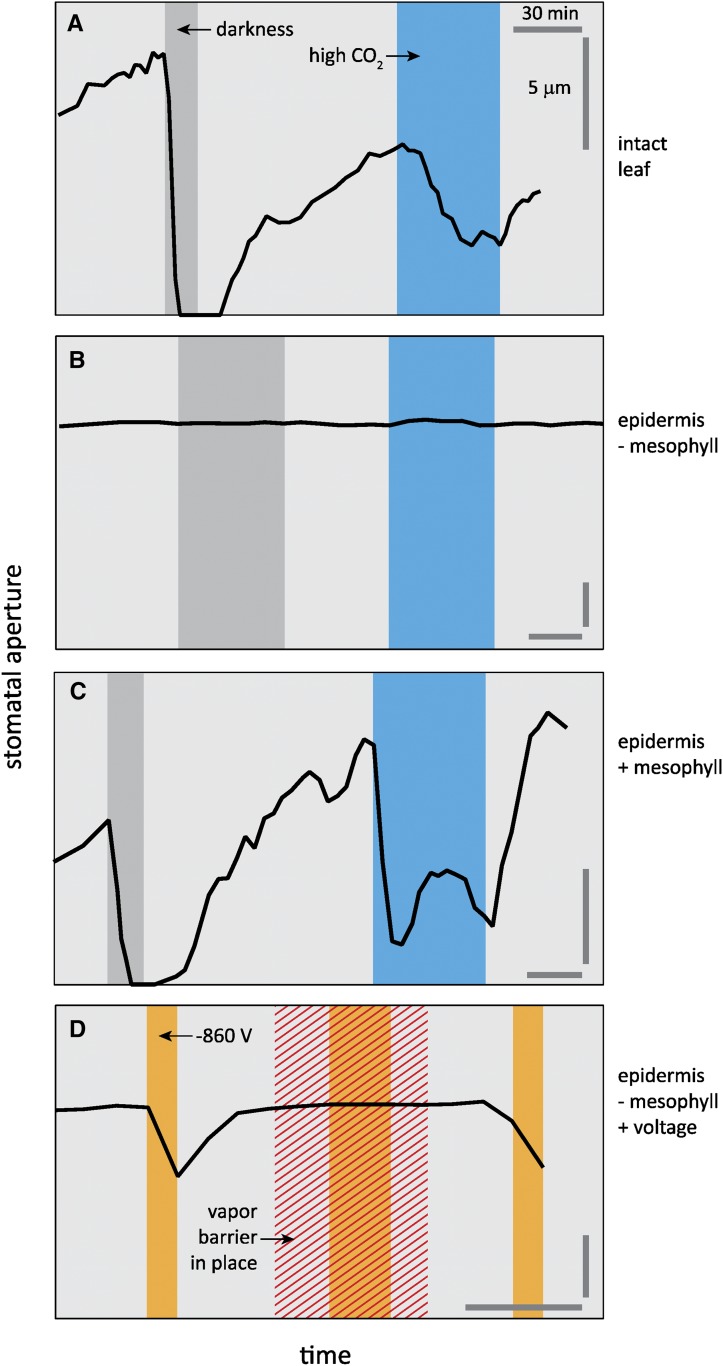
The predictions from these models are consistent with experimental evidence that mesophyll photosynthesis is involved in in the stomatal responses to light and CO₂. For example, both responses are weakened or eliminated by photosynthetic inhibitors (Schwartz and Zeiger, 1984; Lee and Bowling, 1995; Olsen et al., 2002; Messinger et al., 2006). More recent work has shown that these responses are weak or absent in epidermal peels but are recovered when those peels are placed on actively photosynthesizing mesophyll (Mott et al., 2008; McAdam and Brodribb, 2012) and that the mesophyll-epidermis interaction may be mediated by a vapor phase ion that affects the pH of the guard cell apoplast (Mott et al., 2014; Fig. 2). Busch (2014) hypothesized that the ultimate photosynthetic “sensor” driving these responses is coupled to the redox state of components of the photosynthetic electron transport chain, which would reconcile these results with other data showing that the responses are independent of the absolute rate of, or capacity for, CO₂ assimilation or electron transport (Price, 1998; von Caemmerer et al., 2004; Baroli et al., 2008).

Figure 2.

The presence of mesophyll is essential for normal stomatal responses to light and CO₂ in Tradescantia pallida, and the signal from the mesophyll may be a vapor‐phase ion. A to C, Responses of stomatal aperture to changes in photosynthetic photon flux density and ambient CO₂ concentration observed in intact leaves (A), epidermal peels (B), and epidermal peels placed onto mesophyll tissue (C). D, Responses of stomatal aperture in epidermal peels to activation of a large negative voltage (−860 V) in an electrode placed near the epidermis, with and without a barrier placed between the electrode and epidermal peel to prevent transport of matter without altering the electrical field. Modified from Mott et al. (2008) and Mott et al. (2014).

Other evidence shows that stomata can also respond to light and CO₂ independently of mesophyll photosynthesis—for example, CO₂ responses persist in darkness (Heath and Russell, 1954; Messinger et al., 2006), and the existence of a distinct low-fluence and photosynthesis-independent response to blue light was established many years ago (Shimazaki et al., 1986; Kinoshita et al., 2001; Inoue and Kinoshita, 2017). Horrer et al. (2016) recently found that the blue light response is at least partly driven by activation of starch degradation, generating simple sugars that contribute osmotically to stomatal opening. This is consistent with earlier work on isolated guard cells (MacRobbie and Lettau, 1980) and epidermal peels (Talbott and Zeiger, 1993, 1998), suggesting that inorganic ion fluxes cannot fully explain stomatal behavior and that carbohydrate metabolism is also involved (Blatt, 2016; Santelia and Lunn, 2017). Moreover, recent work suggests at least one additional mechanism that could produce a response of g_s to light: leaf hydraulic conductance increases in response to illumination (e.g. Sack et al., 2002; Nardini et al., 2005; Cochard et al., 2007; Scoffoni et al., 2008), which may enhance water delivery to the vicinity of guard cells, favoring stomatal opening. The mechanism of this response is unknown, but it may involve activation of aquaporins in bundle sheath or other leaf cells (Nardini et al., 2005) and/or the enhancement of vapor transport toward the transpiring epidermis from upper mesophyll tissue warmed by light absorption (Pieruschka et al., 2010; Rockwell et al., 2014). Peak and Mott (2011) suggested further that the stomatal response to humidity could also be explained by vapor transport coupled to temperature gradients within the leaf, provided the epidermis is warmer than the sites of evaporation deeper within the leaf; however, modeling suggests the epidermis is typically cooler than the interior of the leaf despite evaporative cooling (Pieruschka et al., 2010; Rockwell et al., 2014).

Together, these results strongly indicate the existence of multiple independent mechanisms underlying the stomatal responses to light and CO₂. No published models of g_s in intact leaves have attempted to capture these multiple responses on a mechanistic basis. However, the process framework described earlier (e.g. the BMF and Franks models) can easily accommodate such mechanisms as they come to be better understood—for example, responses mediated by guard cell ion transport or water transport conductance would be captured by the terms describing active regulation of guard cell osmotic pressure or plant hydraulic conductance, respectively.

Dynamic, Kinetics-Based Modeling of Guard Cell Osmotic Pressure

As a result of the sheer mechanistic complexity of guard cell ion transport, models of stomatal conductance typically predict guard cell osmotic pressure from hypotheses about mechanisms at a higher level of organization, as discussed earlier. However, guard cell ion transport kinetics are now understood well enough to allow prediction of dynamics of osmotic pressure from “bottom-up,” experimentally derived descriptions of the kinetics of ion transport processes (Eisenach and de Angeli, 2017; Jezek and Blatt, 2017). Hills et al. (2012) presented a computational model, OnGuard, of guard cell ion, water and pH homeostasis driven by knowledge of the kinetic properties of plasma membrane and tonoplast transporters and other subcellular processes, and Chen et al. (2012) showed that this model successfully predicts many observed emergent properties of guard cell homeostasis. Despite its recent introduction, this modeling framework has already generated powerful new insights involving emergent properties of guard cell transport. For example, Wang et al. (2012) used the model to explain how suppression of the SLAC1 anion channel (which mediates ionic efflux during stomatal closure) leads, counterintuitively, to suppression of K⁺ uptake channels (which mediate ion influx during stomatal opening) via pH-mediated effects of anion content on intracellular [Ca²⁺]. Similarly, Minguet-Parramona et al. (2016) showed that Ca²⁺ oscillations—which had been thought to play a causal role in certain stomatal movements—in fact emerge from feedbacks among the mechanisms that govern those movements; i.e. the oscillations were an effect rather than a cause of the underlying mechanisms. This modeling framework can also be used to predict how genetic manipulation of the expression of transport proteins and associated regulatory proteins might impact stomatal function (Wang et al., 2014), which is invaluable for guiding both fundamental and applied research.

Future Directions

Continuing progress toward a useful process model of stomatal conductance requires advances in several areas, including (1) careful mapping of the response of g_s to leaf turgor mediated by leaf-endogenous ABA synthesis, including the kinetics of both ABA synthesis and catabolism; (2) better clarity on the mechanism and role of changes in leaf hydraulic conductance that influence g_s; (3) determination of the location of the pressure sensor within the leaf, which in turn defines exactly which value of hydraulic conductance should be used to predict the turgor response—for example, if the sensor were located in the epidermis, then the relevant hydraulic conductance would be substantially smaller than if the sensor were located in the vasculature, because water potential declines greatly between these locations (Shackel, 1987; Buckley et al., 2015); (4) testing the mechanistic hypotheses posed by Mott et al. (2014) and Busch (2014) regarding the mesophyll-dependent light and CO₂ responses; (5) generating and testing rigorous hypotheses about how vapor transport within leaves might mediate effects of light and temperature on stomata; and (6) combining OnGuard (Hills et al., 2012) with process-based models of stomatal conductance, water transport, and photosynthesis to understand the impacts of guard cell transport in the complex milieu of the intact leaf.

Process models are often overlooked by the modeling community because they sometimes include biophysical parameters that can be very difficult to measure even in a single species. Therefore, another key challenge is to streamline process-based models into forms with fewer and more-easily estimated parameters while retaining clear and transparent links to more detailed process descriptions. We have recently shown how this might be achieved in principle by simplifying the BMF model for broader application (Buckley et al., 2012; Diaz-Espejo et al., 2012; Rodriguez-Dominguez et al., 2016). An important goal is to continue improving these and other process-based models to accommodate new experimental knowledge and to test and apply them more broadly across species and environments.

OPTIMALITY-BASED MODELING

An alternative approach to modeling stomata is based on the hypothesis that evolution has likely selected for mechanisms of stomatal regulation that tend to optimize the trade-off between carbon gain and water loss. The dominant paradigm in this area has been the work of Farquhar (1973) and Cowan and Farquhar (1977) (hereafter “CF”), who showed that total carbon gain is greatest for a given total amount of water loss over some arbitrary time interval (e.g. one day) if g_s varies so that the marginal carbon revenue of water (∂A/∂E, where A and E are net CO₂ assimilation rate and transpiration rate, respectively) remains constant over time and equal to an unspecified Lagrange multiplier (μ_w, the inverse of CF's parameter λ). This idea successfully predicts most stomatal responses to environmental and photosynthetic parameters, at least qualitatively. Together with seminal work validating CF's prediction of a conservative ratio of intercellular to ambient CO₂ concentrations (Wong et al., 1978, 1979) and the widespread adoption of empirical models for g_s based on that observation (Ball et al., 1987; Leuning, 1995), the impact of this theory on understanding of the economy and physiology of gas exchange cannot be overstated. As with process-based models, the CF theory has proven difficult to apply broadly for two reasons. First, it does not explain how to measure or interpret the Lagrange multiplier μ_w in relation to observable environmental or biophysical parameters, and second, iterative solution is required to generate accurate predictions from the theory unless one assumes negligible mesophyll and boundary layer resistances (Buckley et al., 2016). Another barrier to the theory’s adoption is that it predicts a positive response of stomata to increased atmospheric CO₂ concentration (c_a) when photosynthesis is limited by the rate of RuBP carboxylation (i.e. light-saturated or CO₂-limited conditions), which contradicts most data (e.g. Mott, 1988; Morison, 1998).

The past decade has seen a remarkable resurgence of interest and progress in relation to this theory, much of it aimed at resolving the CO₂ response issue and either linking the Lagrange multiplier μ_w to measurable variables or obviating it entirely by posing the question in a different manner. In this section, I will summarize recent and ongoing work in this field and suggest avenues for continuing progress.

The CO₂ Response Problem

Stomata generally close when atmospheric CO₂ concentration (c_a) increases (Mott 1988). The CF theory generally predicts this response under RuBP regeneration-limited conditions (high CO₂ or low light), but the theory incorrectly predicts an opening response under carboxylation-limited conditions (high light and low CO₂). This issue has been tackled by two recent lines of research. Katul et al. (2009, 2010) noted that μ_w is larger in plants grown in a CO₂-enriched environment and showed that an analytical simplification of the CF theory predicts the correct CO₂ response if one assumes a priori that μ_w varies in proportion to c_a during the day. However, Buckley and Schymanski (2014) and Buckley et al. (2016) argued that the reported shifts in μ_w under CO₂ enrichment emerge from structural acclimation of the whole plant at longer time scales, which would also cause shifts in many other parameters that are treated as constants at the diurnal time scale, such as maximum hydraulic conductance and temperature-corrected photosynthetic capacity. Medlyn et al. (2011) suggested a different resolution to the CO₂ response dilemma. They noted that the Ball-Berry family of empirical models (Ball et al., 1987; Leuning, 1995) mirrors CF for most stomatal responses, but correctly predicts a negative response to c_a. They then showed that a simplified analytical solution of CF under RuBP-regeneration-limited conditions is structurally homologous to the Ball-Berry model and that the proportionality factor between g_s and A in Ball-Berry (commonly denoted “m”) is thus related to the Lagrange multiplier μ_w. The resulting “unified stomatal optimization” model is a close analog of CF when photosynthesis is limited by light, and shifts to an empirically accurate but nonoptimal theory under light-saturated conditions.

It has not been demonstrated that the failure of CF to predict the correct c_a response in saturating light is quantitatively important for modeling photosynthesis in natural systems; c_a is likely to exhibit substantial diurnal shifts only in very dense canopies where photosynthesis can draw down atmospheric CO₂ relative to the mixed air above the canopy. Light-saturated leaves are more likely to be at the outer margins of such canopies, so the combination of depressed c_a and saturating light may only be common for deep-canopy leaves in sunflecks.

How Should the Setpoint for ∂A/∂E, and Thus the Diurnal Range of g_s, Shift over Longer Time Periods Than a Single Day's Diurnal Cycle?

The CF theory assumes a fixed total supply of water available for transpiration over some time period, and the size of that water supply, together with other parameters, implicitly defines the value of the Lagrange multiplier μ_w. However, canopy water supply varies as soil moisture declines between rain events and as plant structure changes, so the value of μ_w must likewise adjust. A naïve optimum would set μ_w so that soil water runs out just before each successive rain event; this would maximize the ratio of total carbon gain to total water loss, but is biologically unrealistic given the unpredictable timing of rainfall. Cowan (1982, 1986) showed how μ_w should gradually increase (and g_s should decrease) during a single drought to maximize carbon gain while preventing fatal desiccation in dry soil and also preventing competitors from using water, and Mäkelä et al. (1996) showed that λ (1/μ_w) should decline exponentially over time if plants are evolutionary “aware” of the mean rainfall interval.

Recent work has extended these ideas in new directions, providing new insights into the biophysical and ecological meaning of the Lagrange multiplier μ_w, which may point the way toward more widespread practical use of optimization theory for predicting stomatal behavior. For example, Lu et al. (2016) explored how μ_w should vary during multiple successive random droughts and predicted a roughly exponential decline in λ over time during drought and a sigmoidal relationship between stomatal conductance and soil moisture, with closure accelerating at low soil water contents. Wolf et al. (2016) took a different approach that avoided CF's arbitrary time interval and thereby obviated the Lagrange multiplier. They suggested that plants maximize “net” carbon gain—net CO₂ assimilation rate minus the carbon costs, Θ, caused by low leaf xylem water potential—with respect to stomatal conductance; in other words, ∂(A – Θ)/∂g_s = 0. Wolf et al. (2016) did not explicitly identify the costs in Θ but suggested they would include embolism repair and suppression of photosynthetic capacity by low water potential. They showed that maximizing A – Θ was an evolutionary stable strategy under competition for water, provided the soil water potential experienced by an individual plant is insensitive to changes in that plant's transpiration rate. They also derived a closed-form solution for optimal g_s that was structurally identical to an analytical simplification of CF published by Lloyd et al. (1995), although both solutions incorrectly predict stomatal opening in response to increased c_a. Wolf et al. (2016) compared their model (maximizing A – Θ) with an alternative theory (maximizing A – Θ – μ_wE) which they described as equivalent to the CF theory. However, the latter theory is actually equivalent to replacing A with A – Θ in the CF problem, which obviates CF’s constrained-optimization approach by generating a global optimum with respect to g_s.

Sperry et al. (2017) published a model very similar to that of Wolf et al. (2016), in which both the cost and gain functions were normalized and thus nondimensional: the cost function, Θ, was calculated as the proportional loss of hydraulic conductivity due to embolism, and the gain function was the ratio of A to its value, A_crit, at a high intercellular CO₂ concentration (corresponding to the stomatal conductance that would cause ψ_leaf to equal the threshold for runaway xylem cavitation). This is equivalent to maximizing A - A_crit⋅f_cav with respect to g_s (where f_cav is the fraction of the functional range of K_max lost to cavitation), so it implies that the instantaneous carbon costs of xylem embolism scale directly with photosynthetic capacity: for example, when K has declined by half of its functional range, the embolism repair costs are half of A_crit. However, Θ may be better interpreted as representing the hydraulic risk of lost future photosynthetic potential rather than a realized instantaneous cost (John Sperry, personal communication).

The instantaneous view posed by Wolf et al. (2016) and Sperry et al. (2017) has some blind spots. For example, evidence suggests that the cost Θ is often zero across much of the operational range of g_s: embolism in many species does not begin until leaves are close to their turgor loss point (e.g. Bartlett et al., 2016; Scoffoni et al., 2017), and although direct effects of water stress on photosynthetic capacity at moderate ψ_leaf do occur (Lawlor and Tezara, 2009), unambiguous evidence for such effects is actually somewhat rare in the literature, suggesting such effects are not universal. In conditions where Θ = 0, both theories predict that stomata should simply open as wide as possible. However, this contrasts with evidence that stomata often dynamically regulate water loss even in the absence of substantial cavitation (e.g. Cochard et al., 2002; Simonin et al., 2015). Furthermore, although such a profligate strategy might make sense when competition is fierce or soil moisture is only transiently available due to surface evaporation or rapid draining, it is otherwise unambiguously suboptimal when viewed at longer time scales because it leads to inefficiently rapid use of water that could otherwise be used more gradually and therefore more efficiently (because A/E and ∂A/∂E monotonically decrease with E in general).

A Broader Basis for Optimal Stomatal Conductance

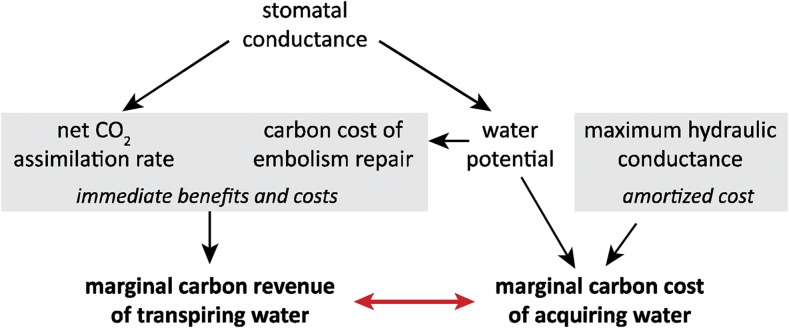
All of the theories discussed above ignore important costs, benefits, and tradeoffs that are only defined at longer time scales. For example, high E generates many costs beyond those directly resulting from low ψ_leaf—for example, the opportunity cost of foregoing use of that water more gradually and thus more efficiently, as alluded to above, and the cost of enabling high E in the first place by investing carbon in hydraulic transport infrastructure. A more general solution for predicting variations in the setpoint for μ_w and thus g_s would maximize a far broader “bottom line” that included all of these costs, as well as their benefits for photosynthesis, growth, survival, and of course, reproduction (Cowan, 2002). This necessarily requires extending the perspective to include all photosynthetic inputs, including water, N and light, and all associated C costs, whether short- or long-term. Givnish (1986) and Bloom et al. (1985) began to develop such a broader perspective, and more recent work by Prentice et al. (2014), Manzoni et al. (2013) and my own group (Buckley and Roberts, 2006a, 2006b; Buckley, 2008; Buckley et al., 2016) has expanded those efforts. A central result is that optimal long-term shifts in the marginal carbon revenue of water (μ_w) are coupled to the marginal carbon cost of acquiring that water, as well as economic parameters involving other photosynthetic inputs (Eq. 22 in Buckley et al., 2016), which in turn suggests that the immediate, leaf-level costs and benefits of water loss captured by instantaneous theories cannot fully predict optimal long-term shifts in μ_w (Fig. 3). Adding these costs to Θ in the Wolf and Sperry theories would place meaningful bounds on Θ and thus g_s even when the instantaneous carbon costs of transpiration are small.

Figure 3.

Relationships that influence the optimal value of μ_w (∂A/∂E, the marginal carbon revenue of transpiring water—the increase in leaf carbon gain that would result from an infinitesimal increase in water loss). Changes in stomatal conductance and therefore water loss lead to immediate carbon gains (in photosynthesis) and costs (of repairing xylem embolisms resulting from reduced water potential), which directly affect ∂A/∂E. However, optimal carbon partitioning requires coordination between ∂A/∂E and the marginal carbon cost of acquiring water. Optimality‐based prediction of ∂A/∂E and thus, stomatal conductance, should consider these long‐term, amortized costs as well as the direct, immediate costs and benefits of variations in stomatal conductance.

Future Directions

It is clearer today than it was a decade ago that optimization theory has great potential for predicting stomatal conductance in real systems. More work is needed to translate the results from recent creative efforts like those of Lu et al. (2016), Wolf et al. (2016) and Sperry et al. (2016) into analytical forms that contain no arbitrary abstractions, and whose parameters are experimentally quantifiable. The difficulty in relating CF’s Lagrange multiplier to measurable biophysical and environmental parameters was, after all, a critical barrier to adoption of the CF theory, and nearly 30 years passed between Givnish's (1986) initial effort to place μ_w on a biophysical basis and the more recent surge of interest in this challenge (Manzoni et al., 2013; Zhou et al., 2013; Buckley et al., 2016). The direct carbon costs of low water potential in the Wolf model is a good example of where additional work is needed. To test and apply this theory more broadly, we need to verify those costs experimentally and then develop means of quantifying them across diverse taxa. To my knowledge, although the direct costs of embolism repair have been estimated theoretically and shown to be consistent with energy stores in xylem parenchyma (Zwieniecki and Holbrook, 2009), they have not been experimentally quantified. Another issue is that these costs are represented in the Wolf theory using vulnerability curves (which relate conductivity loss to water potential), but these curves capture only the steady state balance between two absolute rates—namely, of embolism production and repair—whereas the latter absolute rate is what determines the repair cost, as commensurable with the photosynthetic gain function in these theories. Additional experimental and theoretical work is therefore needed to quantify these rates and the associated metabolic costs.

To apply the optimality principle to stomatal function over longer time scales that include major growth and structural acclimation, the theory must distinguish the stomatal responses to environmental parameters like c_a predicted by leaf-scale optimization from long-term shifts in g_s that are driven by changes in whole plant structure, and it must be able to predict shifts in the photosynthetic inputs—water, nitrogen, and light—that result from structural change (Buckley 2008, Manzoni et al., 2013; Buckley et al., 2016). It would be most parsimonious and logical to use the optimality principle to predict the latter variations as well, but as with the short-term theory, this will require clever work to streamline the underlying mathematics for practical application while retaining clear links to measurable quantities.

CONCLUSION

We now possess compact, efficient, and tractable models with a sound basis in physiology and/or economic theory, and whose parameters represent biophysically meaningful and measurable properties that can be continually clarified by experiment (see Outstanding Questions). Wider adoption of these models will improve not only the robustness of forward predictions, but also the clarity and usefulness of the mathematical “toolbox” that ecophysiologists use to understand relationships among traits and environmental conditions across taxa. It would also provide a more direct bridge between plant- and ecosystem-level properties and the rapidly expanding knowledge at finer scales provided by molecular biologists, and a foundation for better tools to inform breeding and management and to direct continuing research. None of these outcomes is possible in a paradigm dominated by empirical models.