Temporal Dynamics of Stomatal Behavior: Modeling and Implications for Photosynthesis and Water Use^,

Abstract

An analysis of stomatal behavior reveals the importance of modeling slow stomatal responses and the impacts on photosynthesis under dynamic light environments.

Stomata control gaseous exchange between the leaf and bulk atmosphere, limiting CO₂ uptake for photosynthesis and water loss by transpiration, and therefore determine plant productivity and water use efficiency. In order to function efficiently, stomata must respond to internal and external signals to balance these two diffusional processes. However, stomatal responses are an order of magnitude slower than photosynthetic responses, which lead to a disconnection between stomatal conductance and net CO₂ assimilation. Here, we discuss the influence of anatomical features on the rapidity of stomatal movement and explore the temporal relationship between net CO₂ assimilation and stomatal conductance responses. We describe how these mechanisms have been included into recent modeling efforts, increasing the accuracy and predictive power under dynamic environmental conditions, such as those experienced in the field.

Stomatal anatomical characteristics and behavior control gaseous fluxes between the internal leaf environment and the external atmosphere, with major implications for photosynthesis, plant water status, evaporative cooling, and nutrient uptake. The capacity of stomata to allow CO₂ into the leaf or lose water is known as stomatal conductance (g_s), measured as mole of flux per unit of area (mol m⁻² s⁻¹). Stomatal conductance is the reciprocal of stomatal resistance and is determined primarily by stomatal density, distribution, and pore area. Global water usage is predicted to double before 2030 (UNESCO, 2009) due to the rising global population, increasing the need for greater crop yields but with reductions in the amount of water available for their growth. This, along with more erratic precipitation episodes, is putting increasing pressure on breeders and scientists to find new crop varieties or breeding targets that would result in sustained or increased crop yields with less inputs of water. Most crop species are not indigenous to where they are currently cultivated and often are not fully adapted to the environmental conditions, potentially increasing the level of stress that the plant experiences. For decades, breeders focused mainly on selecting varieties for increased yield, decreasing the diversity of other traits of interest (e.g. stomatal behavior) and potential targets for selection. As stomata are key to plant photosynthesis and water use, this makes them attractive targets for manipulation to improve carbon uptake, optimize water use, and reduce drought stress. Earlier work used stable carbon isotopic discrimination as a proxy for time-integrated water use efficiency (WUE) and revealed that higher g_s in wheat (Triticum aestivum) resulted in a lower level of limitation of net CO₂ assimilation (A) and higher yield (Fischer et al., 1998). For this reason, previous research explored improving gas exchange via specific manipulation of steady-state g_s (e.g. by manipulating stomatal density), while we have taken a less obvious approach and are exploring the rapidity of stomatal responses that synchronize g_s with mesophyll demands for CO₂ (Lawson et al., 2010; Lawson and Blatt, 2014; Raven, 2014) to improve A, WUE, and leaf temperature.

Stomata balance CO₂ uptake and water loss by adjusting the pore aperture to changing environmental and internal cues. In general, stomata of C₃ and C₄ plants open with increasing or high light, low [CO₂], and low vapor pressure deficit (VPD), while closure is driven by the reverse, low light, high [CO₂], and high VPD (Raschke, 1975; Outlaw, 2003). However, it should be kept in mind that these environmental stimuli are rarely experienced by the plant in isolation; therefore, stomata must respond to multiple signals in a hierarchical manner (Lawson and Morison, 2004; Lawson et al., 2010; Aasamaa and Sõber, 2011). Although g_s is closely linked with mesophyll demands for CO₂ (Wong et al., 1979; Farquhar and Sharkey, 1982; Mansfield et al., 1990; Buckley and Mott, 2013), stomatal responses to changing conditions can be an order of magnitude and more slower than photosynthetic responses. Reports of correlations between A and g_s often refer to steady-state measurements or long-term observations that do not reflect the reality of field conditions, as short-term fluctuations in environmental conditions can lead to a temporal disconnection between A and g_s (Kirschbaum and Pearcy, 1988; Tinoco-Ojanguren and Pearcy, 1993; Lawson and Weyers, 1999; Lawson et al., 2010; McAusland et al., 2016). The lack of temporal synchronicity between A and g_s under natural fluctuating light conditions has important implications for photosynthetic carbon gain and for the ratio of CO₂ gained through photosynthesis to water lost by transpiration, known as WUE, as well as resulting in heterogeneity in gas exchange over individual leaves (Lawson and Weyers, 1999; McAusland et al., 2013) and within canopies (Weyers and Lawson, 1997). In this review, we will explore the temporal relationship between A and g_s responses, the impact on WUE, and the influence of anatomical characteristics on stomatal responses. Although we recognize the impact of environmental variables such as [CO₂], relative humidity, and soil water content on the temporal response of g_s, here we will only focus on changes in light intensity. As part of describing temporal responses in g_s, we will explore the use of models to better describe and allow a comparison of responses between different species. Many current and early models calculate g_s in steady state, and although they are useful as a predictive tool to assess the role of g_s on gaseous fluxes at the local and regional scale, they fail to incorporate the temporal (and spatial) heterogeneity in g_s observed in the natural environment due to ever-changing environmental conditions.

IMPACT OF THE TEMPORAL RESPONSE OF g_s ON PHOTOSYNTHESIS

Temporal Response of g_s

Due to technical considerations, most studies regarding stomatal behavior on intact leaves have used g_s as a proxy to investigate stomatal movements instead of directly measuring pore area. Despite this being a useful tool for understanding stomatal dynamics, it should be kept in mind that the relationship between g_s and pore area is not linear, as the influence of pore area on g_s decreases rapidly with the magnitude of stomatal opening (Kaiser and Kappen, 2001). Nevertheless, Kaiser and Kappen (1997, 2000, 2001) showed that g_s and pore area measurements, although on different scales, generally lead to the same conclusion regarding limitations of photosynthesis (A) and water loss. It is well known that a low g_s or slow stomatal opening can restrict the uptake of CO₂ and, therefore, A (Farquhar and Sharkey, 1982; Barradas et al., 1994; Barradas and Jones, 1996; McAusland et al., 2016), while high g_s facilitates higher rates of A but inevitably at the cost of greater water loss through transpiration (Barradas et al., 1994; Naumburg and Ellsworth, 2000; Lebaudy et al., 2008; Lawson et al., 2010; McAusland et al., 2013, 2016; Lawson and Blatt, 2014). In response to fluctuations in environmental parameters, it is commonly assumed that plants try to synchronize stomatal opening with the mesophyll demand for CO₂ and stomatal closure with the need to minimize water loss through transpiration (Cowan and Farquhar, 1977; Farquhar et al., 1980; Mott, 2009; Lawson et al., 2012; Drake et al., 2013; Jones, 2013). However, slow g_s kinetics (McAusland et al., 2016) means that the stomatal aperture lags behind the steady-state target (Kaiser and Kappen, 2000).

Light is the greatest environmental driver of photosynthesis, and stomatal response to light is one of the most well-researched stomatal behaviors (Shimazaki et al., 2007). Numerous studies have investigated steady-state stomatal responses to light; however, as these responses are measured under constant conditions, they represent situations that are rarely found in nature (Jones, 2013). Measurements of g_s collected under field conditions are highly variable and, therefore, correlate poorly with those measured under steady-state conditions in the laboratory (Poorter et al., 2016), usually due to slow g_s kinetics (McAusland et al., 2016), meaning that, when measured, stomata have not yet reached the new steady-state target (Whitehead and Teskey, 1995; Kaiser and Kappen, 2000; Lawson et al., 2010).

Stomatal Response to Dynamic Light

Several studies have investigated the dynamics of stomatal response and photosynthesis to fluctuations in environmental variables, especially light (Knapp and Smith, 1987; Kirschbaum et al., 1988; Tinoco-Ojanguren and Pearcy, 1993; Barradas et al., 1994; Lawson et al., 2010; Wong et al., 2012; McAusland et al., 2016). However, the majority of these have concentrated on the influence of sun and shade flecks on carbon gain in understory forest dwelling species (Chazdon, 1988; Chazdon and Pearcy, 1991; Tinoco-Ojanguren and Pearcy, 1993; Pearcy, 1994; Leakey et al., 2005) and for plants that have developmentally acclimated to shaded or exposed conditions (Knapp and Smith 1987, 1988), often ignoring dynamic stomatal response and the potential limitation on carbon gain or water loss. Over the diurnal period, these fluctuations in light (sun/shade flecks) drive the temporal and spatial dynamics of carbon gain and water loss (Lawson and Blatt, 2014). It is often the speed of the stomatal response to environmental fluctuations that is critical when assessing carbon uptake and WUE (Raschke, 1975; Kirschbaum and Pearcy, 1988; Lawson and Morison, 2004; Lawson et al., 2010). In the field, the response of A and g_s is largely dominated by fluctuations in photosynthetic photon flux density (PPFD; Pearcy, 1990; Way and Pearcy, 2012), which can vary on a scale of seconds, minutes, days, and even seasons (Assmann and Wang, 2001), and is driven by sun angle, cloud cover, and shading from overlapping leaves (Pearcy, 1990; Chazdon and Pearcy, 1991; Way and Pearcy, 2012); as a consequence, leaves are subjected to varying spectral qualities and light intensities. It is noteworthy that such rapid changes in PPFD will result in rapid intense modifications to leaf temperature, with greater g_s providing enhanced evaporative cooling and possible protection against heat damage (Schymanski et al., 2013).

In the 1980s to early 1990s, Pearcy and colleagues investigated the impacts of sun flecks, primarily on carbon gain and later on stomatal dynamics. They dissected the temporal photosynthetic and g_s response into different phases to explain the periods of response associated with limitations in A and overshoots of g_s leading to excess water loss. The initial phase was termed the induction and represents periods of up to 10 min during which biochemical processes rather than CO₂ supply limit carbon assimilation (Barradas and Jones, 1996). The second phase, dominated by stomatal limitation, describes slow g_s responses that constrain CO₂ diffusion and A (Lawson et al., 2010, 2012; Vialet-Chabrand et al., 2013; McAusland et al., 2016). The third phase explains the period in which g_s remains high, exceeding the amount of g_s required for maximum rates of carbon assimilation (Kirschbaum et al., 1988; Tinoco-Ojanguren and Pearcy, 1993; Lawson et al., 2010), leading to excess water loss (relative to carbon gained) and effectively a drop in WUE (McAusland et al., 2016). Studies mainly on forest understory species have reported that sun flecks may contribute 10% to 60% of the total daily carbon gain (Way and Pearcy, 2012), depending on forest type and plant age. Stomatal limitations on A have been estimated at up to 30%, with significant implications for carbon sequestration and crop yields (Fischer et al., 1998; Lawson and Blatt, 2014). Indeed, Kirschbaum et al. (1988) found that, if initial g_s values were high, A could be 6 times higher 1 min after an increase in PPFD than if initial g_s was low, an 82% g_s limitation on A, illustrating the importance of g_s in natural dynamic conditions such as those found in the field. Continued increases in g_s after A has reached light saturation also have been reported, which led to a decrease in intrinsic water use efficiency (W_i) with higher water loss for no CO₂ gain (Kirschbaum et al., 1988; Tinoco-Ojanguren and Pearcy, 1993; Lawson et al., 2010).

Differences in the speed of stomatal opening and closing and the magnitude of change in g_s in response to sun and shade flecks are known to exist between species and within individual plants (Assmann and Grantz, 1990; Ooba and Takahashi, 2003; Franks and Farquhar, 2007; Vico et al., 2011; Drake et al., 2013; Vialet‐Chabrand et al., 2013). Response times also are dependent upon the plant water status (Lawson and Blatt, 2014), leaf age (Urban et al., 2008), the history of stress (Pearcy and Way, 2012; Porcar-Castell and Palmroth, 2012; Wong et al., 2012; Zhang et al., 2012), and the duration and magnitude of changes in PPFD (Weyers and Lawson, 1997; Lawson et al., 1998, 2012; Lawson and Blatt, 2014). There is also evidence to suggest that changes in growth environment during stomatal development influence the speed of response in mature leaves (Arve et al., 2017). The speeds of opening and closing in response to changing PPFD in many species are not correlated (Ooba and Takahashi, 2003); however, Vico et al. (2011) compared 60 published gas-exchange data sets on stomatal response to PPFD to determine the impact of stomatal delays on photosynthesis and found a general parallel relationship in the rates of stomatal response, concluding that rates of stomatal opening were essentially correlated with the rate of closure. If we assumed that there is no delay in stomatal opening or closing, optimal leaf gas exchange would be achievable (Cowan and Farquhar, 1977; Lawson and Blatt, 2014), but it is important to consider the fact that specific delays in stomatal movement may be indicators of the current needs of the plant (Ooba and Takahashi, 2003; Manzoni et al., 2011; Vico et al., 2011; Drake et al., 2013). The response of g_s is thought to reflect this priority: under well-watered conditions in the canopy, stomata will remain open (particularly lower down in the canopy where VPD will be lower) in order to utilize light energy from sunflecks to maximize CO₂ diffusion into the leaf (Lawson et al., 2012; Way and Pearcy 2012), even at the cost of further water loss (Allen and Pearcy, 2000), while under drought or water-limited conditions, stomata will often close to conserve water at the expense of carbon gain (Knapp and Smith, 1988).

Influence of Anatomy on Stomatal Response

Stomatal anatomical features such as stomatal density and size are known to determine steady-state g_s (Franks and Farquhar, 2001) and are key components for determining the maximum theoretical g_s of the plant (Dow et al., 2014). Stomatal size and density vary greatly between plant species and are influenced by the growth environment (Willmer and Fricker, 1996; Hetherington and Woodward, 2003; Franks and Beerling, 2009). Stomatal density often has been negatively correlated with stomatal size (Hetherington and Woodward, 2003; Franks and Beerling, 2009). Recently, a great deal of consideration has been given to the impact of stomatal anatomical features on stomatal function and gas exchange, particularly to the morphological and mechanical diversity of stomata with reference to performance and plasticity (Franks and Farquhar, 2007). Recent studies and reviews have implied that stomatal response times to environmental perturbations are affected by physical attributes such as size and density (Drake et al., 2013; Raven, 2014), the presence or absence of subsidiary cells (Franks and Farquhar, 2001), as well as the shape of the guard cells (McAusland et al., 2016) and their clustering (Papanatsiou et al., 2016) and that manipulation of these features could have positive effects for carbon gain and WUE (Doheny-Adams et al., 2012; Lawson et al., 2012; Tanaka et al., 2013; Franks et al., 2015).

Hetherington and Woodward (2003) first suggested that dumbbell-shaped stomata could open and close faster than kidney-shaped stomata in response to environmental perturbations, as even small changes in volume in the smaller dumbbell-shaped guard cells would lead to greater stomatal opening compared with the larger kidney-shaped guard cells. Franks and Farquhar (2007) took this further by advocating other factors that may influence the speed of response, such as guard cell geometry, mechanical advantage, osmotic or turgor pressure, and the energetic cost of guard cell movements (as mentioned previously). A mechanical advantage of dumbbell-shaped stomata was suggested to be associated with the reciprocal coupling of guard and subsidiary cell osmotic and turgor pressures, leading to more rapid stomatal movements (Franks and Farquhar, 2007; Raven, 2014). These findings underlie the potential of dumbbell-shaped stomata to track changes in environmental conditions and maximize the efficiency of photosynthesis and water use through increased stomatal response times (Hetherington and Woodward, 2003; McAusland et al., 2016), a point also highlighted by Chen et al. (2017) in their analysis of stomatal evolution. Drake et al. (2013) investigated the correlation between stomatal anatomy, specifically density and size, and stomatal opening speeds and found that the maximum rate of stomatal opening was driven by size and density. Although the work of Drake et al. (2013) and the review from Raven (2014) made significant progress in linking stomatal size to function, including the speed of response to light and associated implications, the size of stomata is not the only and main determinant of the speed of response. For example, Papanatsiou et al. (2016) note that stomatal clustering can affect g_s kinetics independent of stomatal dimensions and the available pool of osmotic solutes available to drive aperture changes. The results of Drake et al. (2013) also could have been skewed by the experimental condition, as step changes in light from a state of darkness not only incur biochemical limitations on stomatal movement and assimilation but represent a state that is rarely seen in the natural environment except prior to dawn.

Recent work from Kaiser et al. (2016) using similar experimental conditions could have overestimated the biochemical limitation and underestimated the diffusional limitation on A due to the slow response of g_s from dark. Producing a step change from low to high light is more representative of the conditions experienced in the field during a diurnal period from passing clouds and overlapping leaves (McAusland et al., 2016; Vialet-Chabrand et al., 2017); therefore, more relevant information can be gained regarding the speed of stomatal response and the implications this may have for carbon assimilation and WUE. In a recent study, McAusland et al. (2016) compared the speed of stomatal responses to a step change in light, in both dumbbell- and ellipse-shaped guard cells in a range of species, including model species and crops. These authors found that guard cell shape (dumbbell or elliptical) and potentially photosynthetic type (C₃/C₄) played a key role in determining the speed of stomatal response, with dumbbell-shaped guard cells exhibiting faster responses than those with elliptical guard cells. Slow stomatal opening in response to increasing light was demonstrated to limit carbon assimilation by approximately 10%, which would equate to substantial losses in carbon gain over the course of the day, potentially negatively impacting productivity and yield, whereas slow stomatal closure when PPFD decreased resulted in a significant decrease in WUE, as overshoots in g_s by up to 80% were observed with only a negligible 5% gain in A. Closer coupling of A and g_s, therefore, has the potential to enhance carbon gain and W_i and, in turn, improve performance, productivity, and yield (Lawson et al., 2010; Lawson and Blatt, 2014; Li et al., 2016; McAusland et al., 2016; Qu et al., 2016).

MODELING THE TEMPORAL RESPONSE OF STOMATA

As mentioned above dynamic stomatal behavior plays a key role in regulating the flux of carbon and water through the soil-plant-atmosphere continuum and is an important determinant for scaling leaf-level measurements of WUE and photosynthesis to the canopy level (Weyers et al., 1997). Modeling is generally considered the most effective tool for simulating stomatal responses to environmental conditions (Damour et al., 2010), and the importance of integrating stomatal behavior into scaling models is recognized (Weyers et al., 1997; Bernacchi et al., 2007; Lawson et al., 2010; Barman et al., 2014; Bonan et al., 2014; De Kauwe et al., 2015). Many current models calculate steady-state g_s and have become successful tools for predicting the impact of g_s on water and carbon fluxes at ecosystem and regional scales. However, heterogeneity in the spatial and temporal responses of stomata often is overlooked (Weyers et al., 1997; Lawson and Weyers, 1999), limiting the confidence with which these current models can predict larger scale responses or the impact of predicted climate change (Buckley et al., 2003; Dewar et al., 2009; Baldocchi, 2014). The addition of stomatal dynamics to existing models has the potential to reveal the extent to which g_s has been inaccurately predicted by steady-state models. As stomata respond continuously to fluxes in environmental conditions and, therefore, g_s is rarely in steady state, this reinforces the need for improved mechanistic models of g_s (Damour et al., 2010; Vialet-Chabrand et al., 2016). Greater focus in future modeling efforts attempting to scale from the leaf to the canopy level should be given to the inclusion and integration of temporal stomatal dynamics to fluctuations in environmental signals (Vico et al., 2011; Vialet-Chabrand et al., 2013) to predict the impact of large-scale heterogeneity in stomatal traits on water and CO₂ fluxes through the canopy, ecosystem, and global scales. Furthermore, as stomata are exposed to constant fluctuations over the diurnal period, it is often the speed of the stomatal response that is critical in determining CO₂ uptake and transpiration dynamics over the course of the day (McAusland et al., 2016; Vialet-Chabrand et al., 2016) rather than the steady-state values that are often the basis of many existing models. Here, we will review the existing dynamic models and the advantages and disadvantages of their use and predictive power while also discussing the incorporation of dynamic models for greater accuracy in predicting stomatal impacts on A, g_s, and W_i in a natural environment.

Modeling the Temporal Response of g_s to Changes in Light Intensity

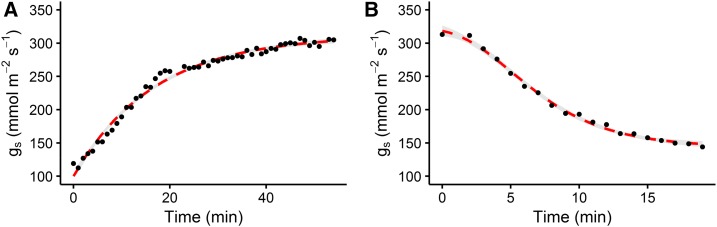
In the early 1970s, temporal responses of g_s were examined to determine the degree of limitation on A and the regulation of water loss (Woods and Turner, 1971; Davies and Kozlowski, 1974; Horie, 1978). Most of these early studies were based on step increases and decreases in light intensity, revealing a slow exponential or sigmoidal variation in g_s with time (Fig. 1). The response of g_s to a step change in light intensity was initially evaluated as the time for g_s to reach the new steady state (G_s) at the new light level or a percentage of this value as an estimator of the rapidity of response (Woods and Turner, 1971; Davies and Kozlowski, 1974; Grantz and Zeiger, 1986; Dumont et al., 2013). More recently, the rapidity of response has been estimated using a regression fit to the linear part of the g_s response, providing an estimate of the maximum rate of g_s increase (Tinoco-Ojanguren and Pearcy, 1992; Fay and Knapp, 1995; Naumburg et al., 2001; Drake et al., 2013). Temporal responses of g_s assessed using these approaches are prone to errors, as they are largely dependent on the estimation of G_s that may never be reached and the linearity of the initial part of the curve. The lack of a standard method to estimate the temporal response of g_s, (e.g. in the choice of the linear part of the curve) prevents a direct comparison of results from different studies. A more robust approach is to use normalized observations of g_s between the initial and final G_s (Laffray et al., 1982; Iino et al., 1985; Barradas et al., 1994; Mencuccini et al., 2000; Drake et al., 2013). This approach not only provides a visual representation of the differences in temporal g_s responses but also is independent of the magnitude of the g_s response, although it is unable to summarize the overall response in one descriptive statistic. Moreover, if a steady state is not reached during the measurement period, it is difficult to normalize data.

Figure 1.

Application of an exponential model (A) and a sigmoidal model (B; red dashed lines) on the temporal response of g_s (black dots) in Arabidopsis (Columbia-0 [Col-0]) to a step change in light intensity (from 100 to 1,000 µmol m⁻² s⁻¹ and from 1,000 to 100 µmol m⁻² s⁻¹, respectively). Gas-exchange measurements of g_s were recorded at 60-s intervals; leaf temperature was maintained at 25°C, and leaf VPD was maintained at 1 kPa.

Dynamic Models of g_s

An alternative to these earlier error-prone approaches is to fit a model to the temporal response of g_s following a step change in light intensity and determine a set of parameter values to describe and enable an evaluation of specific parts of the response curve. In general, such models require the following parameters: an initial and final value of g_s and a time constant. These parameters are targets, which means that if G_s is not reached during the response, the model can constrain the parameter value based on the shape of the response curve. Parameter values can be adjusted using a statistical method that provides the best set of values based on the comparison of the observations and the model outputs.

Typically, two empirical models based on the shape of the variation of g_s are commonly used, an exponential and a sigmoidal model. For both models, a set of differential equations and associated analytical solutions are available. To date, a large number of studies have used the analytical equations of the exponential response of g_s (Horie, 1978; Knapp, 1993; Whitehead and Teskey, 1995; Naumburg and Ellsworth, 2000; Franks and Farquhar, 2001, 2007; Naumburg et al., 2001; Vico et al., 2011; Martins et al., 2016; Qu et al., 2016) that can be formulated for an increase (Eq. 1) or decrease (Eq. 2) in g_s:

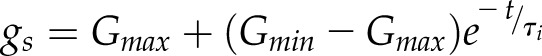(1)

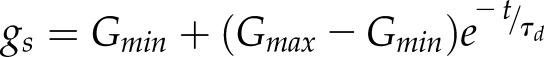(2)

where G_min and G_max represent the minimum and maximum steady state g_s, τ_i and τ_d represent the time constants for the increase and decrease in g_s, and t is the time at which g_s is estimated starting from time 0. In this model, the time constants represent the time required to reach 63% of the total variation (when 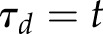,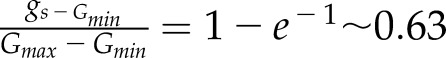). The large number of studies using the exponential model is due to its ease of use and the fact that most of the observed temporal responses of g_s have an exponential shape.

A delay in the increase in g_s responses after a step increase in light has been reported for several species (Barradas et al., 1994; Naumburg and Ellsworth, 2000; Drake et al., 2013; Elliott-Kingston et al., 2016; McAusland et al., 2016), and the shape of this type of response can be described by a sigmoidal equation:

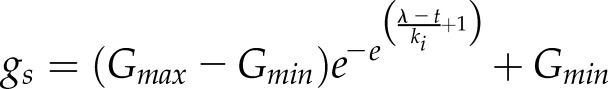(3)

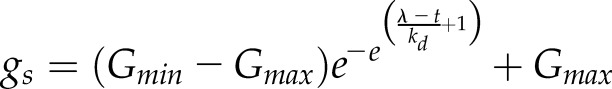(4)

where k_i and k_d represent the time constants for the increase (Eq. 3) or decrease (Eq. 4) of g_s and λ is the initial lag time. Time constants k_i and k_d do not directly represent a time to reach a percentage of G_s but also depend on λ. However, the time to reach any value of g_s can be calculated by solving the previous equation as a function of time:

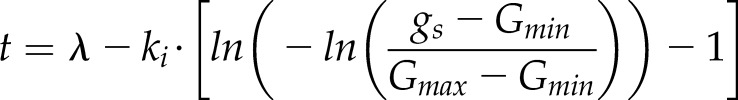(5)

Using Equation 5, the equivalence between the exponential and sigmoidal time constants can be written as:

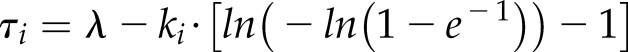(6)

where τ represents the time to reach 63% of the total g_s variation including the initial lag time.

Another interesting property that has been used in numerous studies to describe the speed of stomatal response is the maximum slope of g_s increase, which is calculated based on the previously described parameters:

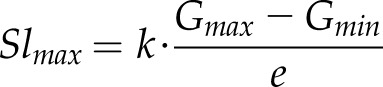(7)

Equation 7 relates the effect on g_s of stomatal density (approximated by G) and the speed of response of stomata (estimated by k), highlighting the importance of differences in stomatal density when drawing conclusions from differences in Sl_max. It should be kept in mind that, as mentioned previously, the scaling up from stoma to leaf level is not a linear process, and caution should be taken when interpreting the temporal response of g_s in terms of stomatal behavior (Kaiser and Kappen, 2001; Vialet-Chabrand et al., 2016).

Both the exponential (Fig. 1A) and sigmoidal (Fig. 1B) models can be fitted on data collected using a generic protocol that consists of a step increase in light intensity from 100 to 1,000 µmol m⁻² s⁻¹ while other environmental variables are held constant (e.g. relative humidity). This generic protocol has been used in numerous publications and can be adapted depending on the species. Although a step change in light intensity often is used as the standard method to assess temporal responses in g_s, this approach is not fully representative of natural environmental variation but is close to what a plant may experience during a sunfleck in the field. We provide a curve-fitting routine in Microsoft Excel to illustrate the use of the exponential and sigmodal models described above in an accessible format (Supplemental File S1). Despite differences in timing or light intensities, the parameters derived from this protocol can be compared to characterize the differences in the temporal response of g_s. Under a continuously changing light environment, the analytical models presented above can be biased, as they assume a constant G_s between each calculated time point. In the case of a dynamic light environment, differential equations would be preferred for their accurate and continuous descriptions of the g_s response. A differential equation describing an exponential response of g_s has been described previously (Horie, 1978; Noe and Giersch, 2004; Vico et al., 2011) but requires a larger number of steps to be solved and, therefore, has rarely been used (Kirschbaum et al., 1988; Noe and Giersch, 2004; Vialet-Chabrand et al., 2016):

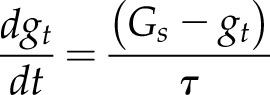(8)

Alternatively, a differential equation for a sigmoidal variation of g_s can be used (Vialet-Chabrand et al., 2013; Moualeu-Ngangue et al., 2016), providing a control on the initial lag experienced by stomata after a change in light intensity:

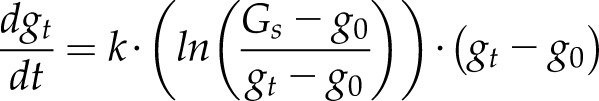(9)

Alternative, more complex equations than Equation 8 have been proposed by Kirschbaum et al. (1988), but they can be more difficult to parameterize due to their large number of parameters. The use of a differential equation required the calculation of the steady-state target G_s at any point of time, so Vialet-Chabrand et al. (2013) proposed the use of a spline function to estimate the light intensity (or any environmental variable) continuously and then use of these values to predict G_s using any already available steady-state model. Therefore, this approach to model the temporal response of g_s can be used in existing steady-state g_s models to predict the transient states of g_s resulting from the previous variations in light intensity.

In many studies, the temporal response of g_s has been associated with stomatal behavior and focused on the rapidity of stomatal movements (Franks and Farquhar, 2007; Drake et al., 2013; Raven, 2014). However, it is important to note that the rapidity of stomatal movements is not necessarily correlated to the rapidity of the variations of g_s (Vialet-Chabrand et al., 2016). For example, a higher stomatal density can result in a higher rate of g_s increase (Sl_max) without changes in stomatal behavior (McAusland et al., 2016). Both anatomical traits (e.g. stomatal density and size) and biochemical traits (e.g. number and regulation of ion channels) describing stomatal behavior need to be considered to fully understand the kinetics of g_s responses following a change in light intensity or any other environmental parameter. To this extent, empirical analysis of g_s also may be extracted from mechanistic models of guard cells, notably OnGuard, which yields outputs in stomatal aperture that connect directly to the underlying processes of solute transport and metabolism (Chen et al., 2012; Hills et al., 2012; Wang et al., 2012). Indeed, Wang et al. (2014) have used this platform to undertake a study of stomatal kinetics, incorporating a first-order sensitivity analysis of the dependence on individual ion channels and pumps at the plasma membrane and tonoplast. Their study yielded a number of unexpected results, as noted below.

An Example of Dynamic Modeling of g_s

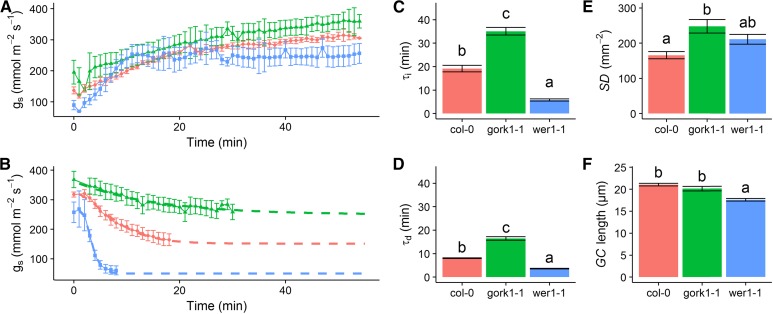
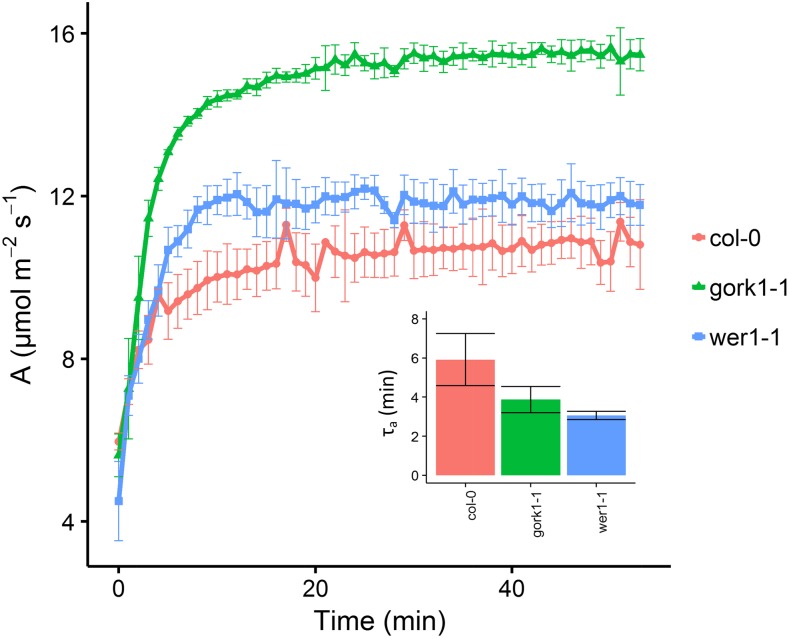
To illustrate the use of models to describe temporal g_s responses and the effect of physical and functional stomatal attributes, we compared the rapidity of the temporal response of g_s in two Arabidopsis (Arabidopsis thaliana) genotypes and ecotype Col-0, one with altered stomatal distribution (wer1-1; Lee and Schiefelbein, 1999) and the second with impaired stomatal closure (gork1-1; Hosy et al., 2003). Compared with Col-0, the ectopic stomata of wer1-1 resulted in a faster stomatal response, as illustrated by the lower G_s (Fig. 2, A and B) and lower τ_i and τ_d (Fig. 2, C and D). The ectopic anatomy of the wer1-1 stomata potentially allows faster pore opening, as there is no back pressure from the surrounding epidermal cells because the stomatal guard cells are above and not in line with the epidermal cells, resulting in faster movements for the same energy cost. This change in stomatal anatomy also leads to a lower G_s compared with the wild-type control, although the mechanism for this is unknown and needs further investigation. As shown previously by Hosy et al. (2003), plants with impaired outward K⁺ channels (gork1-1) have greater τ_i and τ_d and higher G_s, resulting in a large unnecessary water loss during stomatal closure but little effect on stomatal limitation of A due to the relatively high values of g_s. The strong reduction of the outwardly rectifying K⁺ channel activity in the guard cell membrane prevents K⁺ release and increases the stomatal aperture by maintaining membrane depolarization at membrane potentials more positive than the K⁺ equilibrium potential. This imbalance in osmoregulation induced a slow stomatal response by potentially slowing down K⁺ uptake. Although there were small but significant differences in anatomical features such as stomatal density (Fig. 2E) and guard cell length (Fig. 2F), they cannot explain the different temporal responses of g_s in these plants, highlighting the importance of other parameters, such as the biochemistry and mechanics of stomatal movement as described above. The same conclusions can be drawn, for example, from studies of slac1 (Wang et al., 2012), amy3 and bam1 (Horrer et al., 2016), and other mutant and transgenic plants (Eisenach and de Angeli, 2017; Jezek and Blatt, 2017; Lunn and Santelia, 2017). These findings illustrate the plasticity of temporal g_s responses and the potential impact that manipulating the speed of stomatal responses could have on A and WUE. For example, the fast g_s response in the wer1-1 plants reduced g_s limitation of A under an increase in light (Figs. 2A and 3) and reduced potential water loss when subjected to a decrease in light (Fig. 2B). These plants exhibited a potential for increased/greater synchronization between A and g_s (Fig. 3), which may lead to higher WUE over the course of the day (McAusland et al., 2016).

Figure 2.

Temporal response of g_s in Arabidopsis ecotypes (Col-0) and mutants (gork1-1 and wer1-1) following a step change in light intensity (from 100 to 1,000 µmol m⁻² s⁻¹ [A] and from 1,000 to 100 µmol m⁻² s⁻¹ [B]). Gas-exchange measurements of g_s were recorded at 60-s intervals; leaf temperature was maintained at 25°C, and leaf VPD was maintained at 1 kPa. Time constants for an (C) increase (τ_i) and (D) decrease (τ_d) in g_s were derived from the exponential model described in the text; (E) SD, stomatal density; (F) GC, guard cell. Letters represented the results of Tukey’s posthoc comparisons of group means.

Figure 3.

Temporal response of A in Arabidopsis (Col-0, gork1-1, and wer1-1) to a step change in light intensity (from 100 to 1,000 µmol m⁻² s⁻¹). Insert graph, the time constant (τ_a) to reach 63% of the steady-state A under 1,000 µmol m⁻² s⁻¹ light indicates the temporal limitation of A. Gas exchange was recorded at 60-s intervals; leaf temperature was maintained at 25°C, and leaf VPD was maintained at 1 kPa.

CONCLUSION

Despite stomatal behavior occurring at the microscale, it is important to recognize the impact they have on cycles of carbon and water in large-scale global systems. Although stomata typically occupy only a small portion of the leaf surface (0.3%–5%), they are known to control approximately 95% of all gas exchange between the leaf and environment, and estimations show that 98% of all water taken up through the roots may be transpired through stomatal pores (Morison, 2003), potentially translating to 60% of all terrestrial precipitation (Katul et al., 2012). Indeed, most crop plants will transpire over twice their fresh weight in water every day (Chaumont and Tyerman, 2014). With this in mind, stomata represent important targets for manipulating crop photosynthetic productivity and water use, which is particularly important considering that the allocation of fresh water resources is becoming a significant global concern. As highlighted in this review, the importance of the temporal response of g_s is largely unknown and underestimated, and understanding this variation will aid future scaling efforts from individual stoma to leaf and canopy levels. What is apparent is the lack of quantitative data on the rapidity of the stomatal response under different environmental conditions, making it difficult to describe the mechanisms of guard cell movement and assess the impact of uncoordinated responses on leaf-level gas exchange. By integrating the dynamic or stomatal responses to changing environmental conditions, and taking account of different stomatal morphology as well as sensing and signaling systems, we may be able to maximize the benefit of photosynthesis (in terms of carbon gain) relative to the cost of water and translate these findings into more sustainable crop production systems for the future.

Supplemental Data

The following supplemental materials are available.

• Supplemental File S1. GS_Fit.xlsm.

Glossary

WUE

water use efficiency

VPD

vapor pressure deficit

PPFD

photosynthetic photon flux density

Col-0

Columbia-0