Stomatal Function across Temporal and Spatial Scales: Deep-Time Trends, Land-Atmosphere Coupling and Global Models^,

Abstract

Simulating global fluxes of water, carbon, and energy at the land surface requires accurate and versatile models of stomatal conductance, currently represented by structurally similar and interchangeable forms that share weaknesses at environmental extremes.

The colonization of land by plants and their interaction with biogeochemical and atmospheric processes transformed continental climate and hydrology. Stomata, which evolved to optimize the biological economics of plant carbon uptake in exchange for water loss, play a crucial role in large-scale environmental processes by maintaining a connection between deep soil water reservoirs and the atmosphere, regulating terrestrial carbon sinks and altering surface energy balance as they respond to environmental changes. Stomatal feedback control of leaf gas exchange is observed at multiple temporal and spatial scales, but accurately simulating this dynamic behavior remains challenging, particularly for extreme environmental conditions, including drought. Integration of a more realistic representation of stomatal conductance and its regulation of leaf gas exchange in global models is improving global simulations of carbon, water, and energy fluxes, and these simulations in turn highlight some of the limitations with current leaf-scale models. Our analysis of current leaf-scale models of stomatal conductance representing empirical-based and optimization-based approaches reveals close structural similarities that result in virtually indistinguishable simulations of leaf, canopy, and global fluxes. While acknowledging these similarities, future efforts must focus on more accurate parameterization of stomatal conductance models, informed by studies at multiple temporal and spatial scales, including molecular, fossil, geological, leaf, canopy, and landscape.

Stomata first appeared more than 410 million years ago in rudimentary terrestrial plants (Edwards et al., 1998; Raven, 2002; Chater et al., 2016). From then on, they have significantly influenced the fluxes of carbon, water, and energy at the land surface (Berry et al., 2010). After gaining a foothold on land in the late Silurian (Edwards, 1998), the evolution and spread of vascular plants drove one of the most dramatic global climate change events in Earth’s history.

The role of plants in changing Earth’s climate was 2-fold: (1) the proliferation of deep-rooting systems and the uptake of nutrients throughout the Devonian enhanced the weathering of Ca-Mg silicate minerals, which facilitated the large-scale transfer of CO₂ from the atmosphere to marine carbonates; and (2) unprecedented production of lignin-rich, decay-resistant plant structural material, in conjunction with tectonic basins and wet tropical climates, sequestered massive amounts of carbon in vast coal deposits (Berner, 1997, 2005). The resulting massive drawdown in global atmospheric CO₂ concentration from many times that of today, via its reduction of the greenhouse effect, is likely to have contributed significantly to the Permo-Carboniferous glaciation (Royer et al., 2004; Lowry et al., 2014), the most extensive and longest lived glaciation since that time (Crowell, 1978; Scheffler et al., 2003; Montañez and Poulsen, 2013). Ultimately, strong negative feedbacks involving the limitation of terrestrial plant productivity and weathering by low CO₂ are likely to have stabilized minimum atmospheric CO₂ concentrations above the threshold for severe icehouse conditions (Pagani et al., 2009; Beerling et al., 2012). These megacycles in global vegetation productivity and atmospheric CO₂ concentration also are imprinted in the record of plant genome size evolution (Franks et al., 2012a).

The colonization of land by plants and extensive greening of the continents marked a dramatic shift in global water and carbon cycles that moderated continental climates and supported a diversity of terrestrial ecosystems (Kleidon et al., 2000; Beerling, 2007; Berry et al., 2010). Stomata played a crucial role in this by maintaining the flow of water from deep soil reservoirs back to the atmosphere, enhancing continental water cycling and cooling of the climate (Berry et al., 2010), a process that continues across terrestrial biomes today (Bonan et al., 1992; Snyder et al., 2004; Feddema et al., 2005; Bala et al., 2007; Arneth et al., 2010).

Under current increasing atmospheric CO₂ concentration, stomata continue to influence climate as a result of their primary role in optimizing plant water use. Stomatal closure in response to elevated CO₂ is a water-conserving mechanism that reduces transpiration but, as a consequence, increases canopy temperature. This physiological forcing adds to the radiative forcing effect of increasing atmospheric CO₂ concentration on climate (Sellers et al., 1996a; Betts et al., 1997; Cao et al., 2010). The potential magnitude of physiological climate forcing varies substantially from tropical to temperate to boreal landscapes (Bonan, 2008). However, its mechanism is not fully understood, particularly with regard to the role of vegetation in land-atmosphere coupling (Andrews et al., 2011; Berg et al., 2016; Byrne and O’Gorman, 2016).

Owing to the physical and chemical resilience of the guard cell wall and cuticle, stomata are well preserved in fossil plant remains through at least the last 410 million years of the geologic record (Beerling and Woodward, 1997). This resource has proven to be a valuable key to unlocking the history of vegetation-climate coevolution through the Phanerozoic because it has enabled reconstruction of the evolution of plant gas-exchange capacity and productivity (Beerling and Woodward, 1997; Franks and Beerling, 2009a) as well as global atmospheric CO₂ concentration (McElwain et al., 1999; Beerling and Royer, 2002; Grein et al., 2011; Franks et al., 2014; Montañez et al., 2016), the latter a critical boundary condition for simulating paleoclimates using global climate models (Kiehl and Shields, 2013; Meissner et al., 2014; Upchurch et al., 2015).

Despite these advances, the record of Earth’s vegetation-climate coevolution is incomplete, with significant knowledge gaps remaining at some of the key periods of global transition (Montañez et al., 2016). Next-generation stomatal gas-exchange CO₂ proxy models are now helping to reduce uncertainty in reconstructed paleoatmospheric CO₂ concentration (Franks et al., 2014). Results from these studies are revising paleo-CO₂ estimates that were once widely disparate (e.g. 200–2,800 µmol mol⁻¹ for the Paleocene-Eocene thermal maximum; McInerney and Wing, 2011) to well-constrained values that are more compatible with global paleoclimate simulations (Meissner et al., 2014; Upchurch et al., 2015). However, current paleo-CO₂ proxy methods and paleoclimate simulations require refinement and improvement to achieve better agreement across studies and to reduce uncertainty in model outputs.

The scales of stomatal influence are illustrated in Figure 1, with examples of some of the quantities involved and some of the tools applied to different spatial and temporal scales of study. Together with the diversity of technologies involved in data collection at multiple scales, robust, well-validated physiological models describing the complex behavior of stomata at the leaf level are essential for interpretation and simulation. Understanding and predicting larger scale carbon, water, and energy cycles requires accurate estimates of the leaf diffusive (stomatal) conductances to water vapor and CO₂ (g_w and g_c, respectively [definitions for these and other terms are given in Table I]) using stomatal conductance models. Despite considerable progress in the development and application of these models, theoretical questions remain about some of the most basic stomatal sensitivities to environmental variables, such as the response to CO₂ and water deficit (Brodribb and McAdam, 2011; Chater et al., 2011; Ruszala et al., 2011; Franks, 2013; Lind et al., 2015; Franks and Britton-Harper, 2016).

Figure 1.

The scales of influence of stomata. Across temporal and spatial scales of study, there is a progression in the tools and technologies employed. Examples illustrated are leaf gas-exchange chamber, eddy flux tower, satellite, supercomputer, and fossils, the latter a form of deep-time climate data logger. Illustrated also are examples of the influence of stomatal feedback responses to perturbations at all scales. Quantities represented are change in net CO₂ assimilation rate (ΔA), change in net primary productivity (ΔNPP), change in global gross primary productivity (ΔGPP), and change in global surface temperature (ΔTs). The typical relative direction of change is illustrated with plus and minus symbols. Note the positive (amplifying) feedback effect of stomata on ΔTs (top right).

Table I. List of symbols with description and units.

Symbol	Description	Units
A	Net CO2 assimilation rate	μmol m−2 s−1
Ac	RuBP carboxylation-limited CO2 assimilation rate	μmol m−2 s−1
Aj	RuBP regeneration-limited CO2 assimilation rate	μmol m−2 s−1
A/E	Water-use efficiency	mmol CO2 mol−1 water
ca	CO2 concentration of the atmosphere	μmol mol−1
ci/ca	Ratio of intercellular to atmospheric CO2 concentration	Dimensionless
ci	Leaf intercellular CO2 concentration	μmol mol−1
cs	CO2 concentration at the leaf surface	μmol mol−1
D	Stomatal density	mm−2
Ds	Leaf-to-air vapor pressure difference at the leaf surface	kPa
D0	Fitted parameter in Equation 2	kPa
E	Transpiration rate	mol m−2 s−1
gbc	Leaf boundary layer conductance to CO2	mol m−2 s−1
gc	Stomatal conductance to CO2	mol m−2 s−1
gc(max)	Maximum stomatal conductance to CO2	mol m−2 s−1
gw	Stomatal conductance to water vapor	mol m−2 s−1
gw(max)	Maximum stomatal conductance to water vapor	mol m−2 s−1
g0	Intercept in Equations 1, 2, and 3, representing minimum gw	mol m−2 s−1
g1	Slope in Equation 1 (a fitted parameter)	Dimensionless
g1M	Fitted parameter in Equation 3	(kPa)0.5
H	Relative humidity at the leaf surface (as a fraction)	Dimensionless
Jmax	Maximum potential electron transport rate	μmol m−2 s−1
Rd	Leaf respiration rate	μmol m−2 s−1
S	Stomatal size	μm2
Vcmax	Maximum RuBP carboxylation rate	μmol m−2 s−1
∂A/∂gw	Sensitivity of A to gw	mmol mol−1
∂E/∂gw	Sensitivity of E to gw	mmol mol−1
∂E/∂A	Sensitivity of E to A, or gain ratio	mmol water μmol−1 CO2
Γ	CO2 compensation point including respiration	μmol mol−1
Γ*	CO2 compensation point without dark respiration	μmol mol−1
λ	Marginal water cost of leaf carbon	mmol water μmol−1 CO2

One universally recognized feature across all scales of stomatal functioning is their role as feedback regulators (Fig. 1; see discussion in Franks et al., 2013). Importantly, stomata behave as both negative and positive feedback elements, depending on the process. In their primary role of maintaining leaf hydration and optimizing the biological economics of photosynthesis, stomata are finely tuned negative feedback control systems. But, as noted above, the effects of this negative feedback control at the leaf level are manifested as a positive feedback or forcing of climate processes at the landscape scale. Accurately accounting for the effects of stomatal physiology at larger scales remains a challenge.

Here, we provide an update on stomatal function and patterns of change across temporal and spatial scales, with an emphasis on methods used to account for the role of stomata when simulating global carbon, water, and energy fluxes in global models. The temporal scale spans seasonal to evolutionary adaptation over millions of years, and the spatial scale spans leaf to globe.

STOMATAL SIZE, DENSITY, AND CONDUCTANCE THROUGH DEEP TIME

The fossil record reveals strong patterns of change in stomatal morphological features through major geological periods (Edwards et al., 1998; Franks and Beerling, 2009b). The implications from this, based on the well-established coupling between vegetation and climate (Bonan, 2016) and the influence of stomatal morphology on leaf gas exchange (Franks and Farquhar, 2007), are that these patterns reflect coordinated shifts in global vegetation and climate. One challenge, therefore, has been to understand the driving forces and mechanisms behind these patterns, particularly in the context of what they can reveal about the current phase of Earth’s environmental transition.

Some of the earliest insights came from the observation that stomatal density (D; number per unit of area) in leaf material preserved over the last two centuries is negatively correlated with the increase in atmospheric CO₂ concentration (c_a) over that time (Woodward, 1987). It is now well established from controlled-environment studies at elevated and subambient c_a that, over time frames as short as the development and expansion of a leaf, plants can adjust D in response to a sustained change in c_a. This adaptation is usually in the direction that would tend to counteract the physiological effects of the change in c_a (e.g. higher D with lower c_a increases stomatal conductance to counteract the initial drop in CO₂ assimilation rate; Franks et al., 2012b, 2013). What remains unclear about this simple principle is how to characterize this sensitivity quantitatively for the purpose of simulation or prediction.

Modeling the response of D to change in c_a has proven difficult. At developmental time scales, there are strong species-specific differences in sensitivity, including cases of apparent insensitivity (Reid et al., 2003; Tricker et al., 2005; Haworth et al., 2015), as well as nonlinearities in the response over both developmental and evolutionary time scales (Franks et al., 2013). This has been especially problematic in attempts to use the change in D in leaf fossils, alone, as a proxy for change in global mean c_a (Royer, 2014). A detailed theoretical framework for modeling the response of D to c_a has been proposed that uses principles of leaf gas-exchange optimization (Konrad et al., 2008), but this awaits broader implementation and validation.

Early studies suggested that the sensitivity of D to c_a was substantial. For example, Woodward (1987) found that D decreased by 40% to 67% for both historic and growth chamber-simulated change in c_a from 280 to 340 µL L⁻¹, a rate of 66% to 112% per 100 µL L⁻¹, assuming an approximately linear response in this relatively narrow range of c_a. From the many hundreds of studies that have followed, it appears that the sensitivity is usually much less than this, perhaps as little as 2% to 4% per 100 µL L⁻¹ increase in c_a on average (Franks et al., 2012b). This relatively moderate mean sensitivity of D to c_a should be considered in the interpretation of studies involving the manipulation of c_a, particularly where c_a is changed by only a couple of hundred microliters per liter, as in many free-air CO₂ enrichment (FACE) studies.

A key insight to emerge in studying the effects of changing c_a on stomatal density is its coordination with stomatal size (S) and, ultimately, the anatomical maximum diffusive conductance to CO₂ and water vapor [g_c(max) and g_w(max), respectively]. Changes in D appear to be inextricably linked to changes in S, and it is the combination of S and D that determines g_c(max) and g_w(max). There is a consistent negative relationship between S and D at all scales, including leaves within a single species (Franks et al., 2009), across species in a population (Hetherington and Woodward, 2003; Russo et al., 2010), through the fossil record (Franks and Beerling, 2009b), and across mutants of a single species where D is induced to vary by genetic manipulation (Doheny-Adams et al., 2012; Dow et al., 2014; Franks et al., 2015). This negative logarithmic relationship (often represented as a negative linear log-log plot) fundamentally constrains the adaptation and evolution of stomata under forcing by any environmental variable affecting leaf gas exchange. To achieve a new g_c(max) and g_w(max), plants alter S and D within the confines of a general negative logarithmic relationship that optimizes the allocation of leaf epidermal area to gas exchange (de Boer et al., 2016). Fundamentally, selection for higher stomatal conductance is linked to lower S and higher D (Franks and Beerling, 2009b)

The optimization strategy identified by de Boer et al. (2016) has its own set of physical constraints, imposed by the biochemical and mechanical requirements of stomata and the size of the genome that is packed into the nucleus of each guard cell. To be fully functional, stomata need to be separated by at least one epidermal cell, the so-called one-cell-spacing rule (Geisler et al., 2000; Dow et al., 2014), and stomatal guard cells cannot be any smaller than their nucleus. Across vascular plants, much of the greater than 40-fold range in stomatal size (length × width) and, hence, maximum stomatal conductance (Franks and Beerling, 2009b) is linked to the evolution of plant genome size (Beaulieu et al., 2008; Knight and Beaulieu, 2008; Franks et al., 2012a), and angiosperms span the broadest range. This widely observed correlation between stomatal size, guard cell nucleus size, and plant genome size has prompted the hypothesis (yet to be tested comprehensively) that selection for higher or lower stomatal conductance involves coselection for correlated changes in S, D, and genome size (Franks et al., 2012a, 2012b). The role of factors that determine nucleus size and architecture also must be considered, including coiled-coil proteins in the Nuclear Matrix Constituent Protein family (Wang et al., 2013). If genome size does impose a constraint on stomatal size and gas-exchange capacity, then the wide range of angiosperm genome size could be a significant contributing factor in the current dominance of angiosperms across diverse landscapes and climates.

STOMATA EVOLVED AS LAND PLANTS DIVERSIFIED, BUT ALL PLANT DIVISIONS MAY EXHIBIT COMMON STOMATAL CONTROL ATTRIBUTES

One of the most important areas of recent research focus has been the evolution of the stomatal control system, in particular the timing of emergence of active stomatal responses to CO₂ and water deficit as well as mediation by the stress hormone abscisic acid (ABA). This is important because biophysical and molecular models of stomatal control rely upon assumptions about the presence and characteristics of core sensitivities and signaling pathways.

A series of studies have proposed that stomatal sensitivity to CO₂ and ABA evolved first in seed plants (angiosperms and gymnosperms) and are absent in lower vascular plants of more ancient origin, such as ferns and lycophytes (Brodribb et al., 2009; Brodribb and McAdam, 2011, 2013; McAdam and Brodribb, 2012, 2015). These studies hypothesize that, before the evolution of seed plants, stomatal control, particularly in response to water deficit, was largely hydropassive (referred to here as the passive origin model, after Brodribb and McAdam, 2011; also described as the gradualistic model in McAdam and Brodribb, 2012). This hypothesis has been rejected in a number of studies utilizing a variety of methods, including cross-species genetic complementation, bioinformatics, and leaf gas-exchange measurements, which together suggest that active stomatal sensitivity to ABA and CO₂ are traits common to all major land plant divisions (Chater et al., 2011; Ruszala et al., 2011; Lind et al., 2015; Franks and Britton-Harper, 2016; Cai et al., 2017; Chen et al., 2017).

If similar active and passive control elements are identified in all major land plant divisions, this would suggest that they share essentially one stomatal control mechanism (Franks and Britton-Harper, 2016). This universal or general model for stomatal control is illustrated conceptually in Figure 2. In comparison, the passive origin or gradualistic model can be viewed as a variant of the general model in which all of the gene regulatory networks and behaviors associated with the active stomatal response to elevated CO₂ and water deficit are absent from seedless plants (but now updated to include CO₂ sensitivity in ferns and gymnosperms, after Franks and Britton-Harper, 2016; see red colors in Fig. 2). However, some disagreement remains on whether stomatal ABA sensitivity is universal (McAdam et al., 2016).

Figure 2.

Illustrating two current models for the evolution of stomatal control: the general and passive origin (or gradualistic) models. Both models describe the key elements of the stomatal control system and the evolution of these elements as new plant lineages emerged. The major plant divisions, all with stomata, are arranged phylogenetically with respect to their common ancestor (distances not to scale). The main difference between the two models is that the general model incorporates, in some form, all of the core elements of passive and active stomatal control in each plant division, whereas the passive origin (or gradualistic) model assumes that certain active stomatal control elements, including sensitivity to elevated CO₂ and ABA, evolved first in angiosperms (possibly gymnosperms in the case of ABA sensitivity) and are absent in all other divisions. Colors represent genes, gene families, or gene regulatory networks involved in discrete elements of the stomatal control system and their respective feedback control loops in the regulation of stomatal conductance; different color hues represent homologs or other variants resulting from evolutionary processes: black = active response to light; blue = passive response to water potential; green = active response to water potential (including changes imposed by vapor pressure difference); yellow = active ABA response; and red = active response to elevated CO₂.

A general model incorporating active and passive control in all land plants does not imply or predict identical or uniform stomatal behavior. It does, however, incorporate the operation of similar genetic systems, molecular signaling pathways, and feedback control loops in stomata of nonangiosperms as well as angiosperms. All of these elements will have been subjected to natural selection as land plants diversified, and, as a result, many will exhibit altered characteristics among plant clades. However, like the shared basic form and mechanical function of stomata in all land plant divisions (two guard cells that bend apart with increased turgor to create an aperture for gas exchange), a general stomatal control model applies a basic mechanistic framework to the subcellular and extracellular processes that govern stomatal aperture. Further definitive genic and physiological information is needed to fully characterize the origins and nature of passive and active stomatal control across the diversity of vascular plants.

MODELING STOMATAL CONDUCTANCE AT ALL SCALES IS UNDERPINNED BY AN ACCURATE MECHANISTIC UNDERSTANDING

Predicting and manipulating plant gas exchange requires a mechanistic understanding of the process. Goal-driven manipulation (genetic, biochemical, or otherwise) of the behavior of stomata for the purpose of modifying plant gas exchange requires some understanding of the stomatal control mechanism and its elements (genes, signaling networks, internal conductances, etc.). In turn, accurate mechanistic models of stomatal function built from observations of cellular processes can inform the behavior of higher order leaf gas-exchange processes. An example is the OnGuard computational platform for kinetic modeling of guard cell physiology (Hills et al., 2012). Built from detailed observations of guard cell biophysical and kinetic processes, OnGuard has been shown not only to simulate the behavior of stomata but to predict previously unrealized biophysical processes within the guard cell that were subsequently verified experimentally, thus improving the understanding of higher order stomatal function (Chen et al., 2012; Wang et al., 2014). Application of this approach more generally across plant divisions depends on accurate characterization of the subcellular processes governing stomatal behavior in all plant divisions. If some of these processes are found to be lacking in certain plants, then the configuration and broader application of models like OnGuard will have to be revised.

Stomatal conductance models applied to larger spatial scales fall into three broad categories: semiempirical (Jarvis, 1976; Ball et al., 1987), semimechanistic (Buckley et al., 2003), and semioptimization (Lloyd, 1991; Katul et al., 2009; Medlyn et al., 2011). The prefix semi applies because empirical stomatal conductance models are actually founded on solid physiological theory, and all practical applications of mechanistic and optimization models require empirical or other mathematical simplifications, so, in practice, none of the models fits purely into one category. Regardless of classification, each approach has delivered considerable success, but there is now a growing interest in reexamining the merits of these approaches and exploring possible improvements, with particular emphasis on optimization.

Although several innovative studies have applied optimization theory to model plant gas exchange (Lloyd and Farquhar, 1994; Buckley, 2008; Katul et al., 2010; Medlyn et al., 2011; Bonan et al., 2014), it has not been as widely adopted as might have been expected from such an elegant theory. Stomatal control of leaf gas exchange was formulated in terms of optimization theory almost four decades ago (Cowan and Farquhar, 1977), but stomatal control has been modeled predominantly using semiempirical or hybrid mechanistic-empirical approaches (Damour et al., 2010). One difficulty with the practical application of optimization theory is quantifying the ratio of sensitivities of the rates of transpiration (E) and CO₂ assimilation (A) to changes in stomatal conductance to water vapor (g_w), defined as the gain ratio (∂E/∂g_w)/(∂A/∂g_w), or simply ∂E/∂A (Farquhar et al., 1980a). Stomatal conductance behaves optimally when ∂E/∂A is maintained at some constant value, λ. But what determines λ, or what should it be? Stomatal optimization theory cannot provide these answers, it only allows us to determine whether the plant has achieved a given requirement of photosynthetic assimilate with the least possible transpirational loss of water in an environment with certain statistical properties (Cowan and Farquhar, 1977). Cowan (2002) remarked on the potentially indefinable nature of this problem, which takes the form of a fruitless search for optimal λ, appealing to ever-higher levels of plant organization and requiring increasingly dubious simplifications to make the problem tractable.

As a way forward, methods have been devised for prescribing or estimating λ for use in gas-exchange models employing stomatal optimization, but this requires some empirical or mechanistic insight into the nature of E, A, and g_w in the plant or vegetation of interest as well as a number of simplifications that may be unrealistic and/or inconsistent with the original Cowan-Farquhar optimization theory (Buckley et al., 2017). This is somewhat analogous to prescribing c_i/c_a (the ratio of intercellular to atmospheric CO₂ concentration) for a mechanistic model or the slope parameter g₁ in the empirically based Ball-Berry (BB) model (Ball et al., 1987; see Eq. 1 below). The widely observed relative constancy of c_i/c_a for a leaf under typical daily conditions, a feature predicted by the optimal control of stomatal conductance for some conditions, has been usefully applied in the modeling of plant gas exchange, including over geological time (Franks et al., 2014). Note that c_i/c_a does exhibit some systematic variation: it declines with water deficit (Farquhar et al., 1989), and across species, it tends to be higher in plants with greater photosynthetic capacity (Franks and Farquhar, 1999). Although c_i/c_a is mechanistically defined and readily measured, as with λ it is not clear what ultimately determines c_i/c_a. Furthermore, for any value of λ, the trajectories of E, A, and g_w depend on plant metabolic and biophysical attributes that, for the purpose of simulation or prediction, must be defined mechanistically or empirically and calibrated for the plant or vegetation of interest. Errors in the characterization of these traits in different plant functional types will limit the capacity of optimization-type stomatal models to simulate or predict plant gas exchange. Therefore, caution must be used when assessing the benefits of optimization approaches compared with other methods.

STOMATA IN GLOBAL MODELS: EMPIRICAL AND OPTIMIZATION APPROACHES ARE STRUCTURALLY SIMILAR AND CAN PROVIDE IDENTICAL OUTPUTS

Land surface models simulate the fluxes of momentum, energy, moisture, and CO₂ between the land and atmosphere. These models, when coupled with models of atmospheric general circulation, ocean general circulation, and sea ice, form the terrestrial component of Earth system models. Central to Earth system models is the regulation of transpiration and photosynthesis by stomata.

Early versions of land surface models (Dickinson et al., 1986; Sellers et al., 1986) used a maximum stomatal conductance that was multiplicatively scaled for photosynthetically active radiation, temperature, vapor pressure deficit, soil water, and atmospheric CO₂ concentration using the framework of Jarvis (1976; see the commentary on early work by Jarvis in Beerling, 2015). Subsequent land surface models utilize empirical relationships between A and g_w to model stomatal conductance. In the BB model (Ball et al., 1987), for example,

(1)

where A is net CO₂ assimilation rate (μmol CO₂ m^–2 s^–1), c_s is the atmospheric CO₂ concentration at the leaf surface (μmol mol^–1), H is the relative humidity (expressed as a fraction) at the leaf surface, and stomatal conductance g_w has units (mol water m^–2 s^–1). The slope parameter g₁ (dimensionless) relating g_w to AH/c_s is obtained by fitting the equation to leaf gas-exchange data, and the intercept of this regression, g₀, which is usually close to the origin, represents a minimum conductance (mol water m^–2 s^–1).

The significance of g₁ is sometimes lost in referring to the BB model as an empirical model. However, it is readily apparent from Equation 1 that g₁ is largely representative of the ratio g_w/A, the reciprocal of intrinsic water-use efficiency, A/g_w (Farquhar et al., 1989; Feng, 1999), and, therefore, also is related to actual water-use efficiency, A/E. Therefore, it might be expected that plants with characteristically higher A/E will exhibit lower g₁, and this has been observed (Kaminski et al., 2015). The quantity g₁, therefore, embodies the physiological traits that determine plant water-use efficiency.

The BB stomatal model was introduced into land surface models in the mid-1990s (Bonan, 1995; Sellers et al., 1996b; Cox et al., 1998) and is now commonly used to simulate stomatal conductance. To more accurately account for A as c_s approaches zero, Leuning (1990) modified the BB equation by replacing c_s with c_s – Γ, where Γ is the CO₂ compensation point for photosynthesis (including respiration in the light). Also, Equation 1 simulates a linear variation in g_w with change in humidity, so to simulate the often observed nonlinear variation in g_w with change in humidity, Leuning (1995) replaced H in Equation 1 with (1 + D_s/D₀)^–1,

(2)

where D_s is the vapor pressure deficit at the leaf surface, D₀ is an empirical parameter, and g_1L (dimensionless) is the equivalent of g₁ in Equation 1, although of different magnitude for the same conditions. Some models use this form of the BB equation (e.g. the Australian CABLE model; Wang et al., 2011).

Medlyn et al. (2011) introduced a third variant of Equation 1, hereafter abbreviated as the MED model,

(3)

where g_1M is a fitted parameter similar to g₁ in Equation 1, although of different magnitude for the same conditions, and with units that depend on those used for D_s: if D_s has partial pressure units (kPa), then g_1M has units (kPa)^0.5; if D_s has mole fraction units (mmol mol⁻¹), then g_1M has units (mmol mol⁻¹)^0.5. It should be noted that, unlike the straightforward determination of g₁ by linear regression, determining g_1M by fitting Equation 3 to data is a more complex procedure on account of nonlinearity. In Equation 3, g_w varies with humidity in a similar fashion to Equation 2, but as the inverse of the square root of D_s, as predicted by optimal stomatal behavior in response to D_s (see Appendix in Lloyd, 1991). Medlyn et al. (2011) define g_1M as,

(4)

where Γ* is the CO₂ compensation point for photosynthesis without dark respiration, with units (μmol mol⁻¹), and λ is as defined earlier, with units (mmol water μmol⁻¹ CO₂), following the original definition in terms of ∂E/∂A by Cowan and Farquhar (1977), which was also adopted by Medlyn et al. (2011). Note that, in the format of Equation 4, g_1M has units (mmol mol⁻¹)^0.5, but this can be converted to (kPa)^0.5 by dividing by √10, assuming atmospheric pressure of ∼100 kPa. It is useful to note also that, for similar conditions of temperature and over a moderate range of relative humidity (∼40%–80%), g₁ and g_1M are approximately related by

(5)

The MED model relies upon several simplifications; most crucial is that it represents only the condition of ribulose 1,5-bisphosphate (RuBP) regeneration-limited photosynthesis. Medlyn et al. (2011) justify this by arguing, on the basis of observations, that stomata appear to behave as if to optimize RuBP regeneration-limited photosynthesis. Cowan and Farquhar (1977) also remarked on this puzzling behavior and noted that, whatever the physiological mechanism is for maintaining λ constant, the apparent tendency of stomata to optimize only RuBP regeneration-limited photosynthesis suggests that plants do not sense and respond to ∂E/∂A itself. This is a crucial insight that highlights the difficulty in describing λ in terms of the molecular signaling processes and actuating mechanisms driving stomatal control. The specificity of the MED model to the optimization of RuBP regeneration-limited photosynthesis is an important characteristic to consider when comparing the output of the MED model with a full water-use efficiency optimization model, as discussed below.

The significance of the MED model is that it is derived by combining the standard leaf diffusion equations with an equation for optimum leaf internal CO₂ concentration, c_i, in terms of the optimization criterion λ (Arneth et al., 2002), thereby linking g₁ to λ (as well as Γ*, which is temperature dependent). This connection is intuitive because g₁, λ, and, therefore, g_1M are all indexes of plant water-use efficiency (or more precisely its reciprocal, E/A, as traditionally defined). However, compared with the BB model, the MED model offers a broader theoretical framework for developing predictive tools and testable hypotheses around plant water-use efficiency and its optimization. Fundamentally, though, the BB and MED models share the same physiological foundations.

Although the BB equation, and its variants (Eqs. 1–3), are based on a simple linear approximation of the relationship between g_w and A, its implementation in land surface models is complex. This first requires an estimate of A, which for C₃ plants is commonly represented using the Farquhar et al. (1980b) photosynthesis model. In that model

(6)

where A_c is the Rubisco-limited CO₂ assimilation rate, A_j is the RuBP regeneration-limited CO₂ assimilation rate, and R_d is the leaf respiration rate. The rates A_c and A_j depend on c_i, which itself depends on A and g_w through the leaf CO₂ diffusion equation

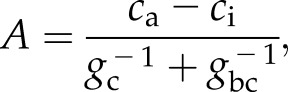(7)

where g_bc is the leaf boundary layer conductance to CO₂ and g_c is the stomatal conductance to CO₂, equivalent to g_w/1.6 (Farquhar and Sharkey, 1982). This results in a system of three equations with three unknowns (A, g_w, and c_i). A further complication is that D_s and c_s, which are specific to the leaf surface, differ slightly from their values in the ambient air at some distance away from the leaf surface. This difference is determined by the boundary layer conductances to water and CO₂, respectively. Some models simplify the calculations by assuming an infinite boundary layer conductance, which effectively makes the values for humidity and CO₂ concentration at the leaf surface the same as those of ambient air. In this case, an analytical solution for g_w can be obtained for C₃ photosynthesis (Leuning, 1990). The solution finds the c_i that satisfies the equation set, which is then used to calculate A and g_w. The equation set must be solved twice, once to obtain c_i for the Rubisco-limited photosynthetic rate and again for the RuBP regeneration-limited rate. However, yet another complication is that the solution depends on leaf temperature (through D_s and also through metabolic parameters in the photosynthesis model) but leaf temperature depends on g_w. Iterative numerical solutions are needed to account for these dependences (Collatz et al., 1991).

An ongoing research topic is the extent to which the empirical-based BB-style equations represent more fundamental principles of water-use efficiency optimization. This theory, as postulated by Cowan and Farquhar (1977), states that optimization is achieved if

(8)

where λ remains constant. An equation for g_w can be obtained from this relationship with A expressed in terms of the Farquhar et al. (1980b) photosynthesis model, but the form of the equation varies with the Rubisco and RuBP regeneration-limited rates of A (Arneth et al., 2002; Buckley et al., 2002; Katul et al., 2010; Medlyn et al., 2011; Vico et al., 2013; Buckley and Schymanski, 2014; Buckley et al., 2017). Although the utility of water-use efficiency optimization has been demonstrated in leaf gas-exchange studies, it has not been implemented directly in land surface models. One exception is the community land model (CLM), in which Bonan et al. (2014) evaluated a water-use efficiency optimization stomatal model at several forest sites. That study found that, without soil moisture stress, CLM simulations using the optimization-type stomatal conductance model performed similarly to those using the traditional BB stomatal conductance model, but the optimization approach improved the quality of CLM simulations under soil moisture stress.

Another important question is the relative significance of g₁, g_1M, and λ as diagnostic or physiologically descriptive traits. The ratio c_i/c_a, measured under normal (light-saturated) conditions of leaf gas exchange or as a time-integrated value from carbon isotope discrimination (Δ¹³C) in plant material, has long been recognized as an index of plant water-use efficiency. A decline in c_i/c_a [and Δ¹³C; i.e. an increase in (1– c_i/c_a)] is equivalent to an increase in A/E if c_s and D_s are constant (Farquhar et al., 1989). Assuming that g₀ ≈ 0, the approximate relationship of mean c_i/c_a to g₁ in terms of H is

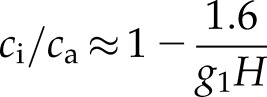(9)

and to g_1M in terms of D_s is

(10)

The values for g₁, g_1M, and λ have been shown to vary severalfold across plant species, communities, and biomes (Lloyd and Farquhar, 1994; Baldocchi and Xu, 2005; Lin et al., 2015). The range of c_i/c_a is more conservative (Franks et al., 2013), but within these narrow limits, there is a systematic global trend toward lower c_i/c_a (increased water-use efficiency) with lower mean annual precipitation, as indicated by lower Δ¹³C (Diefendorf et al., 2010). These ranges of variability are consistent with long-established differences in gas-exchange capacity and water-use efficiency across species (Schulze et al., 1994).

The primary explanation for this variability is illustrated in Figure 3A, which shows the global relationship between A and g_w for C₃ plants at current day (or near current day) atmospheric CO₂ concentration. A globally constant g₁, g_1M, λ, or c_i/c_a would require a constant ratio of A/g_w, but for C₃ plants globally, the mean ratio A/g_w decreases with increasing mean g_w (Fig. 3A). The pattern is not as pronounced for C₄ species, which, because of their internal CO₂-concentrating mechanism, typically maintain higher A than C₃ species for the same g_w. Therefore, C₃ plants with higher capacity for photosynthesis tend to exhibit lower A/g_w and higher g₁, g_1M, λ, and c_i/c_a. An example is shown in Figure 3B, where mean (1 − c_i/c_a), an indicator of water-use efficiency, decreases with mean g_w globally across C₃ plants.

Figure 3.

Global trends in leaf gas-exchange capacity and water-use efficiency. Each data point is an individual leaf-level measurement from raw data compiled by Lin et al. (2015). A, Global nonlinear relationship between CO₂ assimilation rate (A) and stomatal conductance to water vapor (g_w) for 276 species with C3 photosynthesis from all major biomes. Note that measurements are for ambient atmospheric CO₂ concentration (±60 µL L⁻¹) and cover a broad range of leaf temperature (5°C–45°C). The fitted line is y = a − bc^x, where a = 40, b = 40, c = 0.19, n = 14,001, r² = 0.77, P = 0. B, Global decline in mean 1 – c_i/c_a, representing water-use efficiency, with increasing mean g_w, for species in A, using measurements above photosynthesis-saturating light (greater than 800 μmol m⁻² s⁻¹ photosynthetically active radiation). The fitted line is y = 0.144x^–0.38, n = 6,784, r² = 0.5, P = 0. C, Mean g₁ values obtained by fitting the BB model (Eq. 1, assuming g₀ = 0 and c_s ≈ c_a, as in Lin et al., 2015) to subsets of the data from Lin et al. (2015), representing C3 plants (as in A) and C4 plants from a temperate semiarid biome. Data sampled are for the relative humidity (H) range 0.1 to 0.9. Fitted lines are as follows: C3 plants, y = 12.7x, n = 12,521, r² = 0.87, P = 0, solid red line; C4 plants, y = 5.23x, n = 599, 27 species, r² = 0.86, P = 0, dashed red line. D, Mean g₁ values obtained as in C for subsets of the C3 plants, showing different biome-specific g₁ values. Fitted lines are as follows: C3 temperate biome, y = 13x, n = 11,010, 74 species, r² = 0.89, P = 0, green line; boreal biome, y = 7.8, n = 492, five species, r² = 0.95, P = 0, blue line.

Remarkably, when the BB model (Eq. 1) is applied to the pooled data for C3 plants from all major biomes, represented by 276 species of trees, shrubs, grasses, and crops, a single g₁ value of 12.7 captures the gas-exchange behavior of global vegetation exceptionally well (Fig. 3C). It is for this reason that recent versions of CLM have, for convenience, applied a single value for g₁ in global simulations. In CLM4.5, g₁ = 9 for C3 plants and g₁ = 4 for C4 plants (Bonan et al., 2011; Oleson et al., 2013), following Sellers et al. (1996b). A similar approach has been taken with CABLE, in which a single value of g_1L is applied (De Kauwe et al., 2015; Kala et al., 2015). CABLE also has been implemented with Equation 3 for g_w and assigning g_1M values according to the plant functional types in Lin et al. (2015). It is relatively straightforward to apply this approach also to CLM. Some potential values of g₁ specific to global biomes are illustrated in Figure 3D, comparing C3 temperate and boreal biomes. Using Equations 4, 5, and 9, it is possible to determine approximate equivalent values of λ, g₁, and mean c_i/c_a for corresponding values of g_1M, as shown in Table II. These four different indicators of water-use efficiency, therefore, share similar potential for use as calibrating elements in global models.

Table II. Interchangeable water-use efficiency indexes.

Values for g_1M (see Eq. 3) are shown for different plant functional types, as used when implementing the Medlyn et al. (2011) stomatal model in CABLE (De Kauwe et al., 2015; Kala et al., 2015) and in the CLM4.5 simulations in Figures 9 and 10 below. These values are based on those given by Lin et al. (2015) but differ slightly in some cases. Equivalent approximate values are derived from g_1M for λ, g₁, and mean c_i/c_a using Equations 4, 5, and 9 (25°C, H = 0.8, Γ* = 40 μmol mol⁻¹). In the model implementation, g₀ = 0, as was the case for Lin et al. (2015) when determining g_1M from gas-exchange data. Plant types with lower values for g_1M, g₁, λ, or c_i/c_a have comparatively higher water-use efficiency.

Plant Type	g1M	g1	λ	ci/ca
	kPa0.5		mmol water μmol−1 CO2
C3 crop	5.79	16.5	4.47	0.88
C3 grass	5.25	15.1	3.68	0.87
Shrub	4.70	13.8	2.95	0.85
Deciduous broadleaf tree	4.45	13.1	2.64	0.85
Evergreen broadleaf tree	4.12	12.3	2.26	0.84
Evergreen needleleaf tree	2.35	7.88	0.74	0.75
Deciduous needleleaf tree	2.35	7.88	0.74	0.75
Arctic tundra	2.22	7.55	0.66	0.74
C4 grass	1.62	6.05	0.35	0.67

Leaf-Scale Simulations

Leaf-scale simulations illustrate the similarities and differences among the various stomatal models. Figure 4 shows simulations of g_w for the BB model as implemented in CLM4.5 using the global mean g₁ of 9 for all C₃ plants (Bonan et al., 2011). Also shown is the equivalent implementation of the MED model (Medlyn et al., 2011), with g_1M = 4.45 (kPa)^0.5 for broadleaf deciduous trees (Table II), and a water-use efficiency optimization (WUE) model (Bonan et al., 2014), with λ = 1.33 mmol water µmol⁻¹ CO₂, which was evaluated by Bonan et al. (2014) for several broadleaf deciduous forests. An important point with regard to these simulations is that, although the equation for g_w in the MED model (Eq. 3) was derived for the condition of RuBP regeneration-limited CO₂ assimilation (A_j), when implemented in land surface models, A is commonly calculated as in Equation 6 (i.e. the minimum of A_c and A_j).

Figure 4.

Simulations of leaf stomatal conductance, g_w, in response to photosynthetically active radiation (A), ambient CO₂ concentration at the leaf surface, c_s (B), vapor pressure deficit at the leaf surface at 101 kPa atmospheric pressure, D_s (C), and leaf temperature (D). Shown are results for the BB model (Eq. 1; Ball et al., 1987), with g₀ = 0.01 mol m⁻² s⁻¹ and g₁ = 9; the MED model (Eq. 3; Medlyn et al., 2011), with g₀ = 0 mol m⁻² s⁻¹ and g_1M = 4.45 (kPa)^0.5; and the WUE model (Bonan et al., 2014), with λ = 1.33 mmol water µmol⁻¹ CO₂. All simulations used the Farquhar et al. (1980b) photosynthesis model as implemented in CLM4.5 (Bonan et al., 2011) with parameter values for the broadleaf deciduous tree plant functional type. The ratio of potential electron transport rate to maximum RuBP carboxylation rate, J_max/V_cmax, is 1.67 (at 25°C). Standard conditions for the simulations were as follows: c_a = 380 µmol mol⁻¹, photosynthetically active radiation = 2,000 µmol m⁻² s⁻¹ (or 0–2,000 µmol m⁻² s⁻¹ for g_w light responses), relative humidity = 0.8, air temperature = 25°C, and leaf temperature = 25°C. Environmental factors were varied individually. For the temperature simulation, vapor pressure was adjusted so that relative humidity remained constant (80%) or vapor pressure deficit remained constant (0.6 kPa) depending on the model. For these simulations, boundary layer conductance was 2 mol m⁻² s⁻¹, so D_s is comparable to leaf-to-air vapor pressure difference.

All three models show similar functional responses of stomatal conductance to light, CO₂, and temperature (Fig. 4, A, B, and D), although BB in this configuration has considerably lower stomatal conductance compared with the other two models. In all three models, stomatal conductance decreases with atmospheric CO₂ concentrations less than about 300 µL L⁻¹, as has been noted by others (Buckley et al., 2017). The model outputs in this case differ in their overall response to D_s (Fig. 4C). The BB simulation has a linear decline in stomatal conductance with increasing D_s, while MED and WUE have considerably higher stomatal conductance at low D_s, but this diminishes exponentially as D_s increases.

The differences in g_w simulated with the BB and MED models in Figure 4 result primarily from the prescribed values for g₁ and g_1M (9 and 4.45, respectively). When g_1M is reduced to 2.8 (kPa)^0.5 in MED and g₁ is maintained at 9 in BB, the responses of g_w to light, CO₂, and temperature are nearly identical between the two models (Fig. 5, A, B, and D). Note that a g_1M of 2.8 (kPa)^0.5 is equivalent to a g₁ of 9, using Equation 5. Also, with these adjustments, the stomatal responses to D_s are nearly identical over the range 0.5 to 2 kPa (Fig. 5C). However, MED maintains a much larger stomatal conductance at low D_s compared with BB and higher stomatal conductance at larger D_s. For D_s < 0.5 kPa, MED has a much larger sensitivity to D_s than BB. For D_s > 1.75 kPa, MED is nearly invariant with D_s. In the WUE model, decreasing λ from 1.33 mmol water µmol⁻¹ CO₂ in the default simulation (Fig. 4) to 0.714 mmol water µmol⁻¹ CO₂ matches the WUE model output with the BB and MED models for light (Fig. 5A) and closely matches the WUE model with the MED model for D_s (Fig. 5C). The CO₂ response of the WUE model closely matches BB and MED model simulations at CO₂ concentrations greater than 300 µL L⁻¹ but diverges slightly from those models at lower CO₂. Buckley et al. (2017) also showed that the BB, MED, and an optimization model similar to the WUE model here can be formulated to produce similar results. The light, CO₂, and D_s simulations shown in Figure 5 are at a constant leaf temperature (25°C). When leaf temperature varies, the temperature response of g_w in the WUE model closely matches BB and MED (Fig. 5D), but only if (see Eq. 4; i.e. λ decreases with temperature according to the temperature dependence of Γ*).

Figure 5.

Using comparable g₁ and g_1M values results in similar outputs for the BB and MED models. Conditions were as in Figure 4, but with g_1M = 2.8 (kPa)^0.5 for MED and λ = 0.714 mmol water µmol⁻¹ CO₂ for WUE.

Although the BB and MED stomatal responses to CO₂ are similar, the WUE model estimates lower stomatal conductance with CO₂ concentrations less than 300 µL L⁻¹ (Fig. 5B). The results shown in Figures 4 and 5 are with a ratio of maximum potential electron transport rate to maximum RuBP carboxylation rate, J_max/V_cmax, of 1.67 (at 25°C). Decreasing the ratio J_max/V_cmax to 1.3 (at 25°C) and increasing λ slightly (from 0.714 to 0.909 mmol water µmol⁻¹ CO₂ at 25°C) produces closer agreement among the three models for the response of g_w to CO₂ (Fig. 6B) while maintaining the same close agreement among the models for g_w response to light, D_s, and temperature (compare Fig. 5, A, C, and D, with Fig. 6, A, C, and D). The lower J_max/V_cmax ratio had little effect on the BB and MED model simulations, but in combination with the higher λ, it shifted the WUE model CO₂ curve to the left (compare Figs. 5B and 6B). This is because the lower J_max/V_cmax ratio places A in the RuBP regeneration-limited region of operation at a lower CO₂ concentration (Farquhar et al., 1980b), which aligns better with models like MED that represent g_w in terms of RuBP regeneration-limited photosynthesis. Simulations with J_max/V_cmax = 2 (at 25°C) further highlight this effect: in all three models, higher J_max/V_cmax shifts the CO₂ response curve for g_w to the right (Fig. 7).

Figure 6.

Effects of reducing J_max/V_cmax and increasing λ. Conditions were as in Figure 5, but J_max/V_cmax was reduced to 1.3 (at 25°C) and λ was increased slightly (from 0.714 to 0.909 mmol water µmol⁻¹ CO₂ at 25°C).

Figure 7.

Influence of J_max/V_cmax on stomatal sensitivity to CO₂. Conditions were as in Figure 6, but with either J_max/V_cmax = 1.3 or 2 for the BB, MED, and WUE models.

The simulations in Figure 7 predict that stomatal sensitivity to an increase in atmospheric CO₂ concentration from 370 to 570 µL L⁻¹ declines with higher J_max/V_cmax. With J_max/V_cmax = 1.67, g_w declines by 16% to 20% (Figs. 4B and 5B; Table III). This is consistent with an approximately 20% reduction seen in free-air CO₂ enrichment studies as CO₂ increases from 370 to 570 µL L⁻¹ (Ainsworth and Rogers, 2007). With J_max/V_cmax = 1.3, the decline in stomatal conductance increases to 21% to 22% (Fig. 6B; Table III). With J_max/V_cmax = 2, the decline in stomatal conductance is only 6% to 12% over the same range of atmospheric CO₂ concentration (Fig. 7; Table III), but at higher CO₂ concentration, the decline is steeper. These results show that, for all models, the observed decline in g_w with elevated CO₂ is significantly influenced by the ratio J_max/V_cmax. They also highlight the potential influence of J_max/V_cmax and its plasticity in plants growing under different atmospheric CO₂ concentrations on the sensitivity of g_w to CO₂.

Table III. Stomatal sensitivity to CO₂.

Change in stomatal conductance (%) with an increase in atmospheric CO₂ concentration from 370 to 570 µL L⁻¹ is shown for simulations using three different stomatal conductance models (BB, MED, and WUE), as configured for Figures 4 to 7.

Figure (Jmax/Vcmax)	BB (g1)	MED (g1M)	WUE (λ)
4 (1.67)	−16 (9)	−19 (4.45)	−20 (1.330)
5 (1.67)	−16 (9)	−16 (2.80)	−17 (0.714)
6 (1.30)	−21 (9)	−22 (2.80)	−22 (0.909)
7 (2.00)	−11 (9)	−12 (2.80)	−6 (0.909)

Note that, in the simulations from the WUE model shown in Figures 4 to 7, photosynthesis is modeled as the colimited A_c and A_j rates. The effect of this colimitation is to smooth the transition between the A_c and A_j rates. Without colimitation, there is a sharp transition in stomatal conductance over a specific narrow range of atmospheric CO₂ concentration, seen prominently in high light. Buckley et al. (2017) found a similar discontinuity and suggested that it was an artifact in the optimization solution resulting from the characteristics of the Farquhar et al. (1980b) photosynthesis model that strictly represents photosynthesis at the scale of the chloroplast. The smooth CO₂ response curve for g_w obtained with the colimitation solution of water-use efficiency optimization is more physiologically representative of leaf and larger scales where the behavior of many millions of chloroplasts in slightly different microenvironments is integrated.

Canopy-Scale Simulations

Canopy-scale simulations with the BB, MED, and WUE models for a broadleaf deciduous forest further highlight the similarities among the models. Bonan et al. (2014) developed a multilayer canopy flux parameterization for use with CLM4.5 and evaluated the model at three broadleaf deciduous forest eddy covariance flux tower sites. We tested the three stomatal models (BB, MED, and WUE) in this framework in comparison with measured latent heat flux at Harvard Forest (US-Ha1 in Bonan et al., 2014). The BB model with g₁ = 9 underestimates midday latent heat flux compared with observations (Fig. 8A), MED [with the default g_1M = 4.45 (kPa)^0.5] simulates higher midday latent heat flux than the BB model and better matches the observations (Fig. 8B), and the WUE model (with the default λ = 1.33 mmol water μmol⁻¹ CO₂) also simulates higher midday latent heat flux, fitting the data somewhere between the BB and MED models. This result is consistent with the leaf simulations shown in Figure 4, but all three model simulations when compared with the Harvard Forest data are within the observational uncertainty (blue shaded regions in Fig. 8).

Figure 8.

Comparison of canopy-scale simulations of latent heat flux, using the BB, MED, and WUE models, against flux tower data collected above the Harvard Forest study site, the Ameriflux network site US-Ha1 as described by Bonan et al. (2014). A, BB model with g₁ = 9. B, MED model with the default g_1M = 4.45 (kPa)^0.5. C, WUE model with the default λ = 1.33 mmol water μmol⁻¹ CO₂. D, BB model with g₁ increased from 9 to 13. E, MED model with g_1M reduced from 4.45 to 2.8 (kPa)^0.5. F, WUE model with λ reduced from 1.33 to 0.714 mmol water μmol⁻¹ CO₂. The blue shaded area is the 95% confidence interval for the flux tower data; the blue line is the mean for the flux tower data; and the red line is the simulated value from the BB, MED, or WUE model.

Increasing g₁ in the BB model to 13 (to compare with g_1M = 4.45), decreasing g_1M in the MED model to 2.8 (kPa)^0.5 (to compare with g₁ = 9), and decreasing λ in the WUE model to 0.714 mmol water μmol⁻¹ CO₂ (to compare with g₁ = 9) allows a more realistic comparison between the models. With a g₁ value that aligns with the original g_1M value used in the MED model, the fit of the BB model simulation to the data improved and was almost identical to the well-fitting MED model simulation (compare Fig. 8, B and D). With g_1M and λ values adjusted to correspond with the g₁ value of 9 for the original poorly fitting simulation from the BB model, both the MED and WUE model simulations were degraded to similarly poor fits (compare Fig. 8, A with E and F). Therefore, it is evident that comparable parameterization of g₁, g_1M, and λ in the BB, MED, and WUE models, and in particular the BB and MED models, within the CLM4.5 land surface model can yield similarly good or poor fits to canopy-scale data from flux towers.

Global Simulations

Global simulations with the BB and MED models in CLM4.5 illustrate the potential influence that differences in the parameterization of g₁ and g_1M, respectively, can have on estimates of water cycle and carbon cycle fluxes. To explore this, we ran simulations using satellite phenology and atmospheric forcing data for 1991 to 2010 taken from the combined Climatic Research Unit and National Center for Environment Prediction (CRU-NCEP) data set (Le Quéré et al., 2016). Overall, there is good agreement between CLM4.5 simulations using either the MED or BB stomatal conductance model (see light yellow areas in Figs. 9 and 10), but some regions show notable differences. CLM4.5 simulations using MED with the prescribed g_1M values for different plant types (Table II), relative to simulations using BB with a single prescribed global g₁ value of 9 for C3 plants and 4 for C4 plants, result in reduced gross primary productivity during summer in the western United States, north/central Asia, Europe, southern South America, and southern Australia (Fig. 9, A and C). In association, surface runoff during summer is lower in the eastern United States, northern Europe, southern Africa, and northern Australia (Fig. 9, B and D). Also, with this configuration, MED increases transpiration relative to BB in the tropics so that runoff decreases. Comparably large differences were seen with implementation of the MED model for g_w in CABLE (De Kauwe et al., 2015; Kala et al., 2015). Global simulations with JSBACH also showed differences, but neither the BB nor MED model reduces biases in model outputs (Knauer et al., 2015). In our simulations, these differences are reduced substantially when plant types in CLM4.5 simulations using the BB stomatal conductance model are assigned different g₁ values that correspond with the g_1M values for each plant type (Table II) rather than a single g₁ value of 9 for C3 plants (compare Fig. 9, A and C, with Fig. 10, A and C, respectively; and compare Fig. 9, B and D, with Fig. 10, B and D, respectively). The tropics are an exception, where transpiration increases further so that MED has higher surface runoff compared with the simulations using modified BB g₁ values (see orange-red shading in Fig. 10, B and D). As with our analyses for the leaf and canopy scales (Figs. 4–8), these global simulations show that vegetation models incorporating either the BB or MED model for stomatal conductance can produce similar outputs if the respective g₁ or g_1M parameters are assigned comparable values for similar plant types. In summary, the implementation of both empirical-based and optimization-based models of g_w in global land surface models results in equally good fits to observations; therefore, both methods are equally justified.

Figure 9.

Effects of stomatal model parameterization on global simulations. Simulations were compared in the CLM4.5 global model incorporating the Medlyn et al. (2011) stomatal conductance model (MED; Eq. 3), configured with g_1M values listed in Table II, against CLM4.5 simulations using the BB stomatal conductance model (BB; Eq. 1), configured with a global mean g₁ value of 9 for C3 plants and 4 for C4 plants. The difference is calculated as 100(MED − BB)/BB. Data were generated by CLM4.5 using satellite phenology and Climatic Research Unit and National Center for Environment Prediction (CRU-NCEP) atmospheric forcing data for 1991 to 2010. A and B, Mean gross primary productivity (GPP) and total surface runoff (Q), respectively, for 3 months of the peak northern hemisphere summer growing season (June–August; JJA). C and D, As in A and B, but for the southern hemisphere summer growing season (December–February; DJF). To aid comparison, winter hemispheres are shaded translucent gray.

Figure 10.

Similar parameterization of stomatal conductance models results in similar global simulations. The comparison of global simulations was as in Figure 9, except that instead of using a single mean g₁ value of 9 for simulations with the BB stomatal conductance model, different plant types were assigned individual values for g₁, derived from the g_1M values for those plant types using Equation 5 (Table II). This further improved the similarity between CLM4.5 simulations using either the BB or MED stomatal conductance model.

Accounting for Drought

The BB and MED style of stomatal conductance models is appropriate for well-watered soils in the absence of soil moisture stress. Less is known about how to represent stomatal closure in dry soils. Some models impose diffusive limitations in response to soil drying by reducing g₁, consistent with a shift to higher water-use efficiency or, at a more fundamental physiological level, reduced stomatal conductance under drought. Other models impose biochemical limitations and indirectly reduce stomatal conductance by reducing A as soil moisture stress increases (the models explicitly scale g_w with A; otherwise, water-use efficiency would decrease rather than increase with increased biochemical limitation on A). Neither approach can entirely replicate observations (Damour et al., 2010; Egea et al., 2011; De Kauwe et al., 2013), and possibly both diffusive and biochemical limitations must be considered (Zhou et al., 2013). There is also uncertainty about the form of the soil moisture stress function (Verhoef and Egea, 2014). As a result, there is considerable ongoing model development to implement in land surface models the process of plant water uptake and the effects of plant hydraulic stress on stomata (Bonan et al., 2014; Christoffersen et al., 2016; Xu et al., 2016).

CONCLUSION

The role of stomata in Earth system processes and the coevolution of this relationship have become increasingly apparent with new knowledge and better integration of geological, evolutionary, physiological, and global simulation data. Questions and challenges remain at each scale of investigation, but increasingly, there is a role for studies at one scale to inform another. Advances at the molecular level are addressing questions about the function and, in some cases, the mere presence of core elements of the stomatal conductance control mechanism and its behavior under multiple and often conflicting environmental signals (see Outstanding Questions). The integration of more realistic representation of stomatal conductance and its regulation of leaf gas exchange in global models is improving global simulations of carbon, water, and energy fluxes, and these simulations combined with observations in turn highlight some of the limitations with current leaf-scale models. Our analysis here of current leaf-scale models of stomatal conductance representing empirical-based or optimization-based approaches reveals close structural similarities that make them virtually interchangeable and indistinguishable in simulations of leaf, canopy, and global fluxes.

Glossary

ABA

abscisic acid

BB

Ball-Berry

MED

Medlyn

RuBP

ribulose 1,5-bisphosphate

CLM

community land model

WUE

water-use efficiency optimization