Semi-Supervised Pattern Classification: Application to Structural MRI of Alzheimer’s Disease

Abstract

This paper presents an image-based classification method, and applies it to classification of brain MRI scans of individuals with Mild Cognitive Impairment (MCI). The high dimensionality of the image data is reduced using nonlinear manifold learning techniques, thereby yielding a low-dimensional embedding. Features of the embedding are used in conjunction with a semi-supervised classifier, which utilizes both labeled and unlabeled images to boost performance. The method is applied to 237 scans of MCI patients in order to predict conversion from MCI to Alzheimer’s Disease. Experimental results demonstrate better prediction accuracy compared to a state-of-the-art method.

I. Introduction

Alzheimer’s disease (AD) is the most common form of dementia [1]. To date, AD is generally detected at a late stage at which treatment can only slow the progression of cognitive decline. Hence, clinicians are interested in tests for reliable and early detection of AD to improve preventive and disease-modifying therapies. This is especially important in individuals with mild cognitive impairment (MCI), who have high risk to develop AD in the near future.

Among large-scale AD biomarker trials, structural imaging shows great potential in characterizing AD. Many imaging studies have found cortical/hippocampal volume loss in advanced AD [2]. Most of the earlier studies were based on volumetric measurements of manually segmented region of interest (ROI) such as hippocampus. However, such volumetric measurement methods have not shown high sensitivity and specificity in diagnosis of individuals because the spatial pattern of AD pathology is complex and hand-drawn ROIs are not easily reproducible. Voxel-based morphometry (VBM) [3] has been proposed to transcend the limitation of ROI-based approaches. VBM measures the spatial distribution of brain atrophy in AD by evaluating the entire image region instead of making a priori assumptions about specific ROI. While VBM is often applied to measuring group differences, it is of limited use for classifying individuals.

In order to overcome these limitations, high-dimensional pattern classification methods have been proposed in the recent literatures [4], [5]. Unlike VBM, high-dimensional pattern classification methods consider relations between multiple brain regions. The combinations of measurements from many different regions can potentially build patterns of high discriminative power, since no single brain region has sufficient sensitivity and specificity due to inter-subject variability. However, the methods have two fundamental limitations with respect to medical imaging applications. First, the dimensionality of medical images is high relative to the limited sample size. For instance, the number of voxels in medical images is typically more than a million, but the number of subjects is limited to hundreds. Second, class labels for medical images are often only partially available. For example, MCI subjects may deviate from the normal population and may be diagnosed with AD in future follow-up scans; class labels of such subjects are not very well-defined when a patient first presents cognitive symptoms. As a result, traditional supervised approaches may fail to discover categories at finer granularity levels and reflect the underlying data distribution. In this paper, we address the high dimensionality issue via nonlinear dimensionality reduction of the image data and the ambiguous label issue via semi-supervised learning.

We perform dimensionality reduction via manifold learning. Manifold learning techniques embed high dimensional data into a lower dimensional space. The resulting embedding coordinates can be used as lower dimensional features to compare data sets. We address the second issue of ambiguous labeling via a semi-supervised learning approach [6]. Semi-supervised learning trains a classifier on labeled and unlabeled data, which has shown for certain applications to increase the accuracy over only training the classifier on labeled data.

In Section 2, we present our general framework for semi-supervised disease classification. In Section 3, we validate our classification method by applying it to a data set consisting of 237 MCI from which 68 patient convert to AD at a follow-up. We conclude with a discussion of the method in Section 4.

II. Semi-Supervised Disease Classifier

Our semi-supervised disease classifier is composed of three components. We first extract morphological features for each subject from the given brain tissue segmentations of the patients medical scan image. We then use the morphological features to learn a low-dimensional embedding via a manifold learning technique targeted towards dimensionality reduction. Each scan is now represented by coordinates in the low-dimensional embedding. We then apply these coordinates to a semi-supervised classifier to produce the class label. In followings, we will explain each component in detail.

A. Feature extraction

We use the RAVENS maps as a feature characterizing the images [7]. RAVENS maps are the results of deformable registration of brain images to a common template while generating maps that are proportional to each individual’s regional brain volumes, which are reduced in AD.

Suppose S_k denotes the segmented image for tissue k (for structural images, gray matter, white matter and CSF) in the individual image S : Ω_S → R and T : Ω_T → R the template to be registered. Then a RAVENS map, ${\mathcal{D}}_k:{\Omega }_T\to {\Omega }_T$, for tissue k is defined as:

$${\mathcal{D}}_k(x):=J(h(x))S_k(h(x))$$

with h being the deformation map from Ω_S to Ω_T and J(h(x)) is the Jacobian determinant of h at voxel x.

We create the RAVENS map by registering the each structural MRI scan to the stereotaxic brain atlas [8] using HAMMER algorithm [9]. To reduce the noise, the RAVENS maps are smoothed using Gaussian kernel. We only make use of the RAVENS map in the gray matter, ${\mathcal{D}}_{GM}$, as AD mostly impacts this tissue.

B. Dimensionality reduction

The dimensionality of RAVENS maps is relatively high compared to the limited sample size. Hence, we propose to use the ISOMAP algorithm for dimensionality reduction [10]. In order to apply the ISOMAP algorithm, we represent the data as a graph whose vertex corresponds to the image samples. First, we define the edge length d(i, j) between two subjects i and j as a L2 distance of RAVENS maps:

$$d(i,j):={{\displaystyle \sum _{x\in {\mathrm{\Omega }}_T}\left({\mathcal{D}}_{GM}^i(x)-{\mathcal{D}}_{GM}^j(x)\right)}}^2,$$

where ${\mathcal{D}}_{GM}^i$ and ${\mathcal{D}}_{GM}^j$ from the previous section are the RAVENS maps for subject i and j, respectively. Then, we construct a connected kNN graph based on the edge lengths d(i, j). From the kNN graph, we can find the geodesics (shortest paths on the graph) between all pairs of subjects. By solving eigenvalue problems of the geodesics, we can learn a low-dimensional embedding of the data that best preserves the neighborhood relationship in a manifold space. We use these embedding coordinates as a feature that represents each subject.

C. Semi-supervised pattern classification

These coordinates are fed into a classifier to produce a class label. Since the class labels for medical images are only partially available, it is useful to adopt semi-supervised classification methods that make use of both labeled and unlabeled data for training. Semi-supervised classification methods can produce improvement in learning accuracy when unlabeled data are used in conjunction with a small amount of labeled data. Among semi-supervised classification methods, we select the linear Laplacian support vector machine (LapSVM) [11].

Let z be the coordinates computed in the previous section and y ∈ {−1, 1} be the diagnosis of the subject. We then apply LapSVM to l labeled examples ${\left\{z_i,y_i\right\}}_{i=1}^l$ and u unlabeled examples ${\left\{z_i\right\}}_{i=l+1}^{l+u}$. In our application, we consider Alzheimer Disease (AD) as a positive class, Normal Control (CN) as a negative class, and MCI as unlabeled data. Then, we are interested in finding a function f(z) = sign(w^T z+b) given by a weight vector w and a threshold b. In order to find f, we need to solve the following optimization problem in the manifold regularization framework [6]:

$$\begin{array}{r}(w^{\ast },b^{\ast })=\arg \underset{w,b}{min}{\gamma }_A{w}^{T}w+{\gamma }_I{w}^T{Z}^T\mathit{LZw}\\ +\frac{1}{l}{\displaystyle \sum _{i=1}^{l}V(y_i,w^T{z}_i+b)},\end{array}$$ (1)

where γ_A is a weighting parameter for the ambient space norm, γ_I is a weighting parameter for the intrinsic space norm, L is the graph Laplacian, Z = [z₁, z_2, …z_l+u]^T is the data matrix and V is a loss function. The L encodes information relating to all pairwise relations between the images. Therefore, the second term in Eqn. 1 promotes smoothness of class labels on the graph. We can rewrite the formulation as following:

$$(w^{\ast },b^{\ast })=\arg \underset{w,b}{min}{w}^T{C}^{2}w+\frac{1}{l}{\displaystyle \sum _{i=1}^{l}V(y_i,w^T{z}_i+b),}$$

where C² = γ_AI + γ_IZ^TLZ. By changing variables $\stackrel{\sim }{w}=Cw$ and $\stackrel{\sim }{z}=C^{-1}z$, we can convert the problem into a standard SVM.

We use this linear LapSVM to predict MCI to AD conversion. We select the model parameters γ_A and γ_I by grid search using cross-validation. By applying linear LapSVM, we assign the label (AD/CN) to each individual MCI subject. Because target function f is smooth with respect to the affinity graph constructed from labeled and unlabeled data through the graph Laplacian L, we can differentiate near-AD MCI subjects who have more risk to develop AD from other MCI subjects.

III. Classifying MCI

We evaluate our method by applying it on a subset of Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset. The dataset consisted of structural MRI scans of 53 Alzheimer’s (AD), 237 Mild Cognitive Impairment (MCI), and 63 Normal Control (CN) subjects at the baseline time point. Among 237 MCI subjects, 68 patients converted to AD in 15 follow-up months (cMCI) and 169 subjects have not converted yet (ncMCI). Then we conducted the semi-supervised classification with embedding coordinates on this dataset. For cross-validation, the labeled subjects were divided into ten folds (9/10 for training and 1/10 for testing) and the MCI subjects were shared as unlabeled data across folds. The trained classifier was applied to all baseline scans of the MCI patients resulting in a label for each MCI subject. The predicted labels for individual MCI subjects were compared to the diagnosis given at 15 month follow-ups. To have a reference point, we also fed our embedding features to linear support vector machine classifier. In addition, we performed classification using COMPARE [12] algorithm, which has been previously used to predict MCI to AD conversion on the same sample.

A. Low-dimensional embedding

First, we plotted the embedding coordinates for AD, MCI and CN subjects. We used the first two features from ISOMAP algorithm to embed all images into a 2D coordinate system. The results of embedding coordinates are displayed in Figure 1. Since image features are in very high-dimensional space, it is practically impossible to visualize the features. However, if we confine our low-dimensional embedding to 2D Euclidean space, we can visualize the features that represent the data. It is worth noting that the actual feature dimension used for classification was 46. AD (red circle) and CN (blue circle) subjects are located at separate regions. cMCI (red upward triangle) subjects and ncMCI (blue downward triangle) subjects are mainly positioned at nearby AD subjects and CN subjects, respectively. Therefore, these embedding coordinates can have high discriminative power with linear classifier. The mid-axial slice for chosen example subjects is also displayed in Figure 1. The embedding conveniently summarizes the change in ventricle size as the most dominant parameter. These types of observations support the impression that neighborhoods in the embedding coordinates represent images that are similar in terms of gray matter tissue density.

Figure 1.

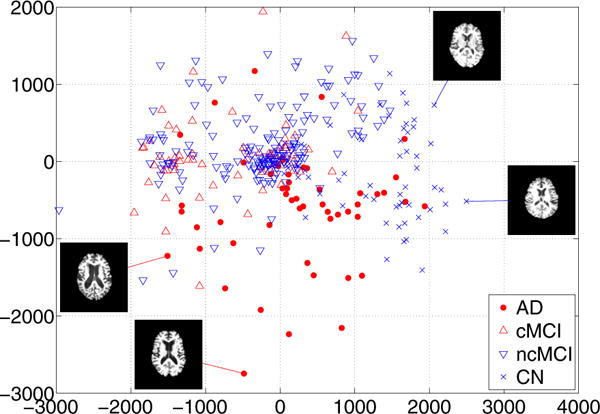
Two-dimensional embedding of all subjects. Only a subset of the samples is shown to avoid clutter.

B. Classification accuracy

After learning low-dimensional embeddings, the embedding coordinates are fed into linear Laplacian support vector machine classifier (LapSVM) and linear support vector machine classifier (SVM). In addition, we performed COMPARE classification method, which feeds brain regional features into SVM. For brevity, Embedding+LapSVM indicates that embedding coordinates are fed into semi-supervised classifier, Embedding+SVM denotes that embedding coordinates are fed into supervised classifier, and COMPARE+SVM represents that regional features are fed into supervised classifier. Table I shows the recall rates for the binary classification between positive cMCI and negative ncMCI. Compared to COMPARE+SVM, Embedding+SVM achieves comparable sensitivity (88.2%) but higher specificity (42%) and classification accuracy (55.3%). This result indicates that embedding coordinates improve the accuracy of our classifiers compared to regional features in COMPARE. Second, we compared Embedding+LapSVM with Embedding+SVM to investiage the affect of semi-supervised classifier. Embedding+LapSVM achieves higher sensitivity (94.1%) and accuracy (56.1%) but lower specificity (40.8%) than Embedding+SVM. It is worth noting that classification of MCI subjects was not anticipated to yield high specificity because the majority of MCI subjects are likely to convert in the later follow-up. This short follow-up period (15 months) is not sufficient to characterize converters. As these patients are follow-up for longer periods, we anticipate our classification rates to increase significantly. Considering this fact that class labels for ncMCI subjects are vague, LapSVM is superior to SVM since LapSVM achieves higher sensitivity than SVM.

Table I.

Recall rates between cMCI versus ncMCI

	Sensitivity(%)	Specificity(%)	Accuracy(%)
Embedding+LapSVM	94.1	40.8	56.1
Embedding+SVM	88.2	42	55.3
COMPARE+SVM	89.8	37	52.3

To further compare the methods, we plot the receiver operating characteristic (ROC) curves in Figure 2. The area under the ROC curve (AUC) for Embedding+LapSVM is 0.73, for Embedding+SVM is 0.71, and for COMPARE+SVM is 0.66. This figure shows that embedding coordinates improve the AUC. In addition, we can even further increase the AUC by using our semi-supervised classifier over a fully supervised classifier.

Figure 2.

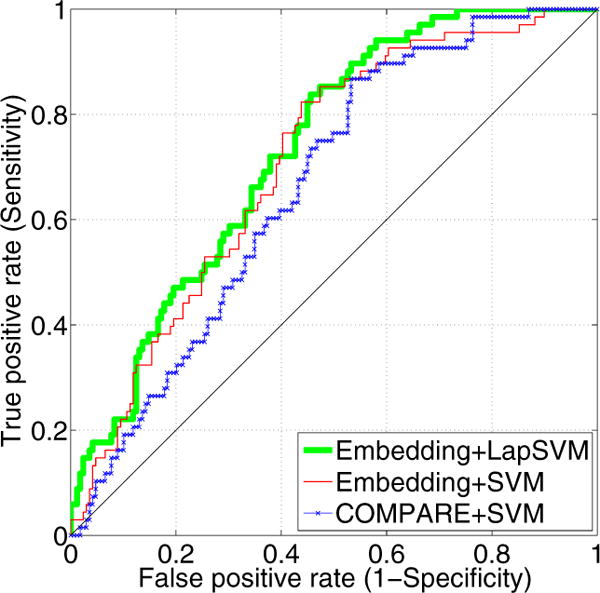
The ROC curve of the prediction accuracy between cMCI versus ncMCI

C. Group comparisons via voxel-based analysis

In order to visualize the regional pattern of atrophy that drives classification, we performed the voxel-based group comparisons between positively and negatively classified subjects. Figure 3 shows t statistics thresholded at p = 0.01 level in different coronal cuts. This figure shows significant reduction of gray matter tissue in cMCI compared to ncMCI. Hippocampus, amygdala and entorhinal cortex regions, which are generally implicated in AD, are highlighted (red/yellow colors). This implies that our classification method can precisely localize the region of gray matter atrophy in cMCI subjects compared to ncMCI subjects.

Figure 3.

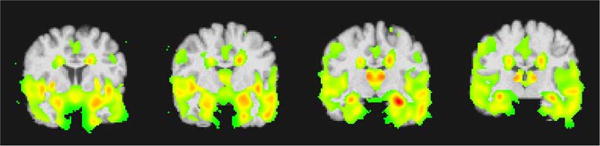
t statistics between cMCI and ncMCI. T-maps were thresholded at the p = 0.01 level.

IV. Conclusion

We presented a disease classification framework to predict the conversion from MCI to AD. Mass-preserving morphological descriptors was used to extract features from structural MRI and dimensionality of features was reduced by using a manifold learning technique. Reduced features were fed into the semi-supervised classifier to incorporate information of unlabeled data. Our disease classification method outperforms a state-of-the-art MCI to AD prediction method, in terms of classifier accuracy and area under curves. We believe this improved performance was due to manifold learning and semi-supervised classification methods that encode all pairwise relations between images.