Multi‐component diffusion characterization of radiation‐induced white matter damage

Abstract

Purpose

We used multi‐b‐value diffusion models to characterize microstructural white matter changes after brain radiation into fast and slow components, in order to better understand the pathophysiology of radiation‐induced tissue damage.

Methods

Fourteen patients were included in this retrospective analysis with imaging prior to, and at 1, 4–5, and 9–10 months after radiotherapy (RT). Diffusion signal decay within brain white matter was fit to a biexponential model to separate changes within the slow and fast components. Linear mixed‐effects models were used to obtain estimates of the effect of radiation dose and time on the model parameters.

Results

We found an increase of 0.11 × 10⁻⁴ and 0.14 × 10⁻⁴ mm²/s in the fast diffusion coefficient per unit dose–time (Gy‐month) in the longitudinal and transverse directions, respectively. By contrast, the longitudinal slow diffusion coefficient decreased independently of dose, by 0.18 × 10⁻⁴, 0.16 × 10⁻⁴, and 0.098 × 10⁻⁴ mm²/s at 1, 4, and 9 months post‐RT, respectively.

Conclusions

Radiation‐induced white matter changes in the first year following RT are driven by dose‐dependent increases in the fast component and dose‐independent decreases in the slow component.

1. Introduction

Incidental irradiation of normal brain tissue during fractionated radiation therapy (RT) for brain tumors is linked to deficits in several cognitive processes, including memory and executive functioning.¹ Subcortical white matter is critical to many of these functions and has thus been the focus of numerous RT‐related brain injury studies.^{2, 3, 4} Diffusion MRI, which is based on the diffusion of water molecules in tissue, can noninvasively quantify microstructural changes within white matter with greater sensitivity than structural MRI.⁵ Changes in diffusion parameters after radiotherapy have been attributed to disrupted axonal integrity (demyelination, degradation) and vascular permeability^{2, 6} and have been correlated with cognitive decline.²

Previous diffusion MRI studies of radiation change typically model the diffusion signal decay as a monoexponential function.^{2, 5, 6} Diffusion weightings, or b‐values, up to 1000 s/mm² are used as standard values. Advances in gradient performance at high (greater than 1500 s/mm²) b‐values have revealed that the signal decay is no longer adequately described by a monoexponential function.⁷ Instead, the decay can be described by a two‐component model of fast and slow‐moving water.^{7, 8} The two components are thought to represent water molecules in different physiochemical states, and be influenced by such processes as macromolecular water binding, viscosity, and compartmentalization.⁹

In this study, we implement a two‐component diffusion model to characterize changes in white matter up to 10 months after RT. The model is tested to ensure that two components are needed to effectively describe the signal decay up to a b‐value of 4000 s/mm². The model parameters are then used to separate differences in time‐ and dose‐dependent changes in fast and slow components. Multicomponent modeling of radiation‐induced white matter damage may not only improve our understanding of the underlying etiology but also provide improved imaging biomarkers for identification.

2. Material and methods

2.A. Patients

From January 2011 to December 2013, 32 patients with primary high‐grade glioma treated with fractionated brain RT underwent imaging at the Moore's Cancer Center at the University of California San Diego. From this group, 14 patients were selected who had the required imaging time points: pre‐RT, 1 month post‐RT, 4–5 months post‐RT, and 9–10 months post‐RT. The cohort consisted of nine males and five females with a median age of 59 yr (range: 40–84). All patients were diagnosed with glioblastoma. Twelve patients were treated to a prescribed dose of 60 Gy in 30 fractions, one patient was treated to 59.4 Gy in 33 fractions, and one patient was treated to 40.05 Gy in 15 fractions. Dose maps of patients treated with schedules other than 30 fractions (n = 2) were converted into an equivalent total dose in 30 fractions using $\mathit{\alpha }/\mathit{\beta }$ = 2 Gy.¹⁰ The median time interval between pre‐RT imaging and start of radiotherapy was 12 days (range: 1–19). Two patients had intervening surgeries due to tumor recurrence. The most common (29 of 31, 93%) chemotherapy treatment was concurrent and adjuvant Temozolomide. Tumor, tumor bed, and all surgical cavities were manually censored from analysis. This study was approved by our institutional review board.

2.B. MR imaging

MR imaging was performed on a 3 T Signa Excite HDx scanner (GE Healthcare, Milwaukee, Wisconsin, USA) equipped with an eight‐channel head coil. The imaging protocol included pre‐ and post‐contrast 3D volumetric T1‐weighted inversion recovery spoiled gradient‐echo sequence (TE, 2.8 ms; TR, 6.5 ms; TI, 450 ms; matrix – rows x columns x slices, 256 × 256 × 166; resolution (mm), 0.9375 × 0.9375 × 1.2) and a 3D T2‐weighted FLAIR sequence (TE, 126 ms; TR, 6000 ms; TI, 1863 ms; matrix, 256 × 256 × 170; resolution (mm), 0.9375 × 0.9375 × 1.2). Diffusion data (TE, 97 ms; TR, 1700 ms, diffusion time, ~90 ms; matrix, 128 × 128 × 48; resolution (mm), 1.875 × 1.875 × 2.5) were acquired with b = 0, 500, 1500, and 4000 s/mm². One instance of the non‐diffusion weighted images (b = 0 s/mm²) was acquired, while 6, 6, and 15 unique gradient directions were acquired for b = 500, 1500, and 4000 s/mm², respectively. The gradient directions are selected according to the method¹¹ of using Coulomb forces to generate roughly evenly distributed points on a unit sphere.

2.C. Image processing and longitudinal registration

All image data were preprocessed using in‐house algorithms developed in MATLAB (Mathworks, Natick, Massachusetts, USA). Structural scans were corrected for distortions attributed to gradient nonlinearities.¹² Diffusion data were corrected for spatial distortions associated with susceptibility and eddy currents,^{13, 14} and rigidly registered to the anatomic scans by the use of mutual information.¹⁵ The pre‐RT T1‐weighted precontrast images were rigidly coregistered to the treatment‐planning CT images. The registered images were visually inspected for accuracy, after which the transformation matrix was used to resample the radiation dose maps (calculated on the treatment‐planning CT) to the pre‐RT MR imaging space. Rigid body registration of the pre‐RT B0 (b = 0) volume and each of the post‐RT (1,4, and 9 month) B0 volumes were used to establish correspondence between the time points. All imaging data, including structural and diffusion scans, from pre‐RT and post‐RT time points and treatment‐planning radiation dose maps were subsequently resampled into baseline pre‐RT diffusion space.

2.D. Region of interest

Normal‐appearing white matter masks were generated from the pre‐RT T1 precontrast scans using automatic segmentation software,¹⁶ and visually inspected for accuracy. The masks were eroded so that only voxels whose six face neighbors were marked as white matter were considered for further analysis. The dose at each white matter voxel was calculated by rounding down the radiation dose at that location to the nearest 10 Gy. White matter voxels receiving greater than or equal to prescription dose were excluded to limit the analysis to regions outside of the planning target volume, and thus normal‐appearing white matter. Surgical scars, tumors, tumor beds, and resection cavities were also censored from analysis.

2.E. Diffusion tensor metrics at b‐value of 1500 s/mm²

Fractional anisotropy and mean diffusivity values were calculated from the diffusion data obtained at a b‐value of 1500 s/mm² to identify trends comparable to those previously reported in the literature (typically at a b‐value of 1000 s/mm²). For every patient and at each time point, data from the six diffusion directions obtained at b = 1500 s/mm², along with b = 0 was used to fit the tensor parameters at each voxel using a linear least squares approach. Average absolute changes in fractional anisotropy and mean diffusivity were then calculated from all voxels across all patients receiving a given dose. One‐sample t‐tests were used to determine whether the average changes in mean diffusivity and fractional anisotropy at the final post‐RT time point were statistically significant.

2.F. Modeling of multi‐b diffusion data

Three diffusion models were compared to fit the full diffusion data (b = 0, 500, 1500, 4000 s/mm²):

1. A monoexponential model consisting of a single component with a longitudinal and transverse apparent diffusion coefficient (ADC) (M₁).

2. A biexponential model with an additional second component with a single longitudinal ADC, where the transverse ADC has been set to 0 (M₂).

3. A biexponential model where both the longitudinal and transverse ADC of the second component are free parameters (M₃).

The three models are formulated as:

$$M_1:X=S^f{e}^{-b[AD{C}_L^f\times {\left(q·q_1\right)}^2+AD{C}_T^f\times (1-{\left(q·q_1\right)}^2)]}$$

$$M_2:X=S^f{e}^{-b[AD{C}_L^f\times {\left(q·q_1\right)}^2+AD{C}_T^f\times \left(1-{\left(q·q_1\right)}^2\right)]}+S^s{e}^{-b[AD{C}_L^s\times {\left(q·q_1\right)}^2]}$$

$$M_3:X=S^f{e}^{-b[AD{C}_L^f\times {\left(q·q_1\right)}^2+AD{C}_T^f\times \left(1-{\left(q·q_1\right)}^2\right)]}+S^s{e}^{-b[AD{C}_L^s\times {\left(q·q_1\right)}^2+AD{C}_T^s\times (1-{\left(q·q_1\right)}^2)]}$$

where X is the observed signal, S is the signal contribution from each component; the superscripts f (fast) and s (slow) refer to the two component; the subscripts L (longitudinal) and T (transverse) refer to the diffusion directions; q is the normalized gradient direction; and q₁ is the primary eigenvector obtained from a tensor fit of the b = 4000 s/mm² diffusion data using a linear least squares approach. It is important to note that ADC, in this instance, refers only to the parameterization of the observed signal decay, and does not carry any additional connotations regarding free vs. restricted diffusion. The model parameters were estimated using the nonlinear curve fitting toolbox provided by MATLAB. The models were compared using the F‐test to determine whether the more complex models with additional parameters were able to improve the fit of the observed signal, and a best‐fit model was chosen for further analysis.

2.G. Changes in model parameters with radiation dose

Model parameters were estimated for each patient at each time point, pre‐ and post‐RT. Voxels within the same dose level (0–9, 10–19, 20–29…Gy) were grouped together and the model parameters (ADC, signal contributions) were estimated using the grouped voxel data. In reporting the signal contribution estimates, a single metric referred to as the slow signal fraction, SF _s :

$$S{F}_s=S^s/(S^s+S^f)$$

was used. SF _s is a summary metric that represents the fraction of the total diffusion signal attributed to the slow component.

2.H. Mixed‐effects modeling of changes in diffusion parameters

Mixed effect models were used to obtain estimates of the changes in diffusion parameters with dose and time, after accounting for repeated measures by patient.¹⁷ The data was prepared in long format, whereby each row of the data set contained the diffusion parameters of interest for a unique combination of patient, time, and dose. The changes in each of the parameters were fit as a linear function of time (continuous, in months) and the interaction between dose (continuous, in Gy) and time. To control for correlated observations within patients, we tested a subject specific random slope for time and the dose–time interaction term. The Wilkinson notation for the models is shown below.

$$\mathrm{\Delta }X\widetilde{+}dose:time+(0+time+dose:time|patient)$$

ΔX represents the change in the parameter, and the expression within the parentheses represents the random effect. The model does not include an intercept, which is represented by the “0” in the expression. With the addition of each random effects term, the model was tested using a likelihood ratio test. Main effects and interaction terms were considered significant at p < 0.05. Statistical analyses were performed using R environment for statistical computing (“lme4” package, version 1.1–7).

3. Results

3.A. Diffusion tensor metrics at b‐value of 1500 s/mm²

The average number of voxels per patient available for analysis was 13,434 [range: 9,227–16,962]. Changes in mean diffusivity using the diffusion data at a b‐value of 1500 s/mm² are shown in Fig. 1(a). The diffusion metrics were averaged across all voxels within that dose level and across all patients. The values are normalized against those prior to radiation therapy (time of 0 months). Mean diffusivity is found to increase over time. At the final post‐RT time point, the average change in mean diffusivity at 0, 10, 20, 30, 40, 50, and 60 Gy was 0.24 (p = 0.03), 0.51 (p = 0.005), 0.58 (p = 0.002), 1.3 (p < 0.001), 1.9 (p < 0.001), and 3.0 (p < 0.001) × 10⁻⁴ mm²/s, respectively. Concurrently, fractional anisotropy, shown in Fig. 1(b), is found to decrease with time. At the final post‐RT time point, the average change in fractional anisotropy at 0, 10, 20, 30, 40, 50, and 60 Gy was −0.053 (p < 0.001), −0.051 (p < 0.001), −0.055 (p < 0.001), −0.086 (p < 0.001), −0.10 (p < 0.001), and −0.12 (p < 0.001), respectively.

Figure 1.

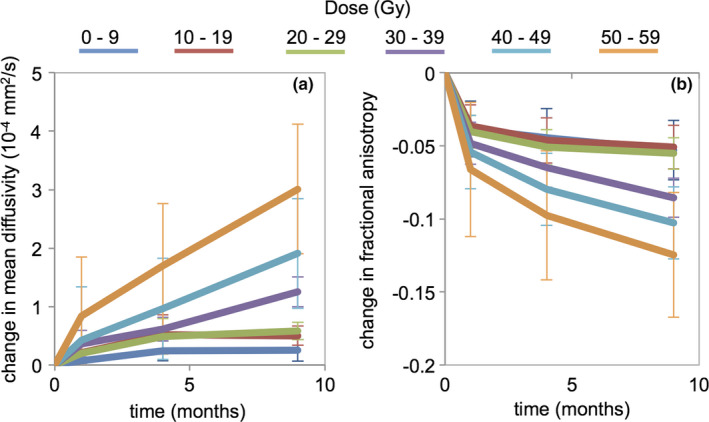
Changes in (a) mean diffusivity and (b) fractional anisotropy relative to pre‐RT baseline (0 months). Metrics were calculated using diffusion tensor fits at b = 1500 s/mm² for various dose levels. Error bars represent standard errors. [Color figure can be viewed at wileyonlinelibrary.com]

3.B. Comparison of mono and biexponential models

A total of 226,500 voxels were tested across all the patients at all four time points to compare the monoexponential (M₁), biexponential with longitudinal direction (M₂), and full biexponential models (M₃) using the F‐test. In the comparison between M₁ and M₂, the null hypothesis that the reduced (monoexponential) model is adequate to explain the variance in the data was rejected in 97.5% of voxels at a p = 0.01. Alternatively, in the comparison between M₂ and M₃, the null hypothesis that the reduced model (biexponential with longitudinal) is adequate was rejected in 8.2% of voxels at p = 0.01. Given the large proportion of voxels for which a biexponential model with a single longitudinal diffusion coefficient (M₂) fit the data adequately, this model was chosen for further analyses.

3.C. Changes in model parameters with radiation therapy

Figure 2 shows an example patient with an anatomic T1‐weighted precontrast image, radiation dose distribution, white matter mask, and maps of changes in each of the four diffusion parameters from M₂ at each of the three post‐RT time points. The diffusion metrics are normalized against those prior to radiation therapy (time of 0 months). An initial decrease in longitudinal fast ADC is observed at 1 month post‐RT, before the metric shows increases relative to baseline at 4 and 9 months. The transverse ADC of the fast component shows a steady increase across all post‐RT time points, with the greatest change observed in the highest dose region. In contrast, the longitudinal ADC of the slow component demonstrated decreased values compared to baseline at all time points, with the greatest change observed immediately post‐RT in the lower dose regions. SF _s also demonstrated decreased values, with the greatest change observed in the highest dose region.

Figure 2.

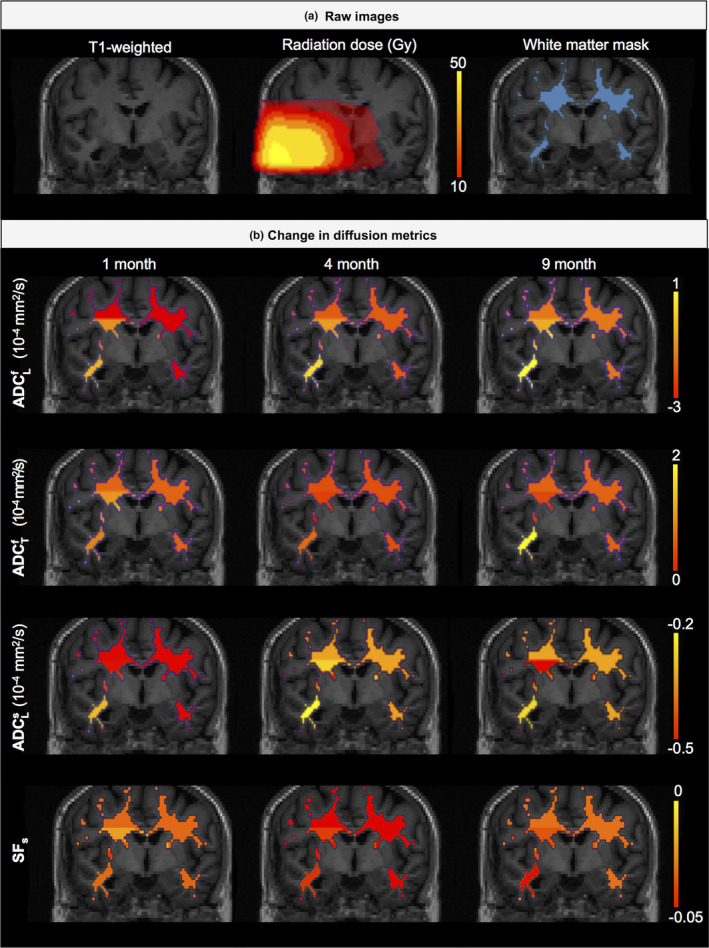
Example of T1‐weighted, radiation dose distribution, white matter mask, and maps of changes in diffusion metrics in a patient. [Color figure can be viewed at wileyonlinelibrary.com]

Average changes in the estimated parameters from M₂ across all patients are shown graphically in Figs. 3(a)–3(d). Overall, the fast ADC estimates increase with dose and time. Nine months after the completion of radiotherapy, the ADC of the fast component had increased by 4 × 10⁻⁴ mm²/s [95%CI: 2, 6 × 10⁻⁴] and 6.7 × 10⁻⁴ mm²/s [4.4, 8.8 × 10⁻⁴] in the longitudinal and transverse directions, respectively. In contrast, the slow ADC had decreased in the same time frame, with a reduced separation between the time–response curves for the various dose levels. In addition, the shape of the dose–response curves also suggests a nonlinear change with respect to time. SF _s decreased with time and dose with a similar dose dependency to the ADC of the slow component.

Figure 3.

Changes in two‐component diffusion parameter relative to pre‐RT baseline (0 months). Error bars represent standard errors. Changes in (a) fast longitudinal, (b) fast transverse, (c) slow longitudinal ADC, and (d) slow signal fraction are shown as a function of time and radiation dose. [Color figure can be viewed at wileyonlinelibrary.com]

3.D. Mixed‐effects modeling of changes in diffusion parameters

Fixed effect estimates from mixed modeling of the changes in model‐derived ADC parameters are shown in Table 1. For each of the three ADC parameters obtained from M₂, the effect size of time, and dose–time interaction term are shown, along with 95% confidence intervals. The dose–time interaction term was significantly associated (p < 0.05) with $AD{C}_L^f$ $AD{C}_T^f$. The estimate was used to generate the marginal effect of time at each of the dose levels.

Table 1.

Parameters derived from mixed modeling of the changes in two‐component diffusion parameters

Parameter	Effect size [95% confidence interval]	p‐value
$AD{C}_L^f$	Time: −0.055 × 10−4 [−0.19, 0.076 × 10−4]	0.41
	Time x dose: 0.11 × 10−4 [0.050, 0.16 × 10−4]	< 0.01
$AD{C}_T^f$	Time: 0.077 × 10−4 [−0.048, 0.20 × 10−4]	0.23
	Time x dose: 0.14 × 10−4 [0.091,0.19 × 10−4]	< 0.01
$AD{C}_L^s$	Time:
	1 month: −0.18 × 10−4 [−0.27, −0.10 × 10−4]	< 0.01
	4 month: −0.16 × 10−4 [−0.25, −0.068 × 10−4]	< 0.01
	9 month: −0.098 × 10−4 [−0.19, −0.010 × 10−4]	0.029
SF s	Time: −0.0026 [−0.0037, −0.0015]	< 0.01
	Time x dose: −0.0016 [−0.0023, −0.0009]	< 0.01

The dose–time interaction was not significantly associated with $AD{C}_L^s$, and was therefore removed from the model. Using time as a continuous variable, the monthly change in $AD{C}_L^s$, irrespective of dose, is −0.018 × 10⁻⁴ mm²/s [−0.031, −0.0043 × 10⁻⁴]. An alternate model, using time as a categorical variable, was tested to probe a potential nonlinear relationship between $AD{C}_L^s$ and time. In this case, an estimate of the average change in $AD{C}_L^s$ is obtained for each time point, along with 95% confidence intervals. Dose was excluded from the alternate model as it was not significantly associated with $AD{C}_L^s$ (p > 0.05). Using Akaike information criterion,¹⁸ the alternate model was selected as the preferred model to explain the relationship between $AD{C}_L^s$ and time. Both time and the interaction between time and dose were significantly associated with the change in SF _s .

4. Discussion

Using biexponential modeling of diffusion data in the brain, we found changes in both the fast and slow components of water after radiotherapy. The increases in fast ADC are mediated by both time and dose; larger effects are seen after 9 months and in regions of the brain receiving higher doses. Similar trends were observed in mean diffusivity, calculated using a single tensor at a b‐value of 1500 s/mm² as well as in the literature.⁵ By comparison, the decreases in slow ADC are found to show little variation with dose, and solely dependent on the progression of time. Interestingly, the reduction in slow signal fraction was found to be strongly dose‐dependent and is therefore likely to be driven by the increase in the signal contribution (and ADC) of the fast component.

The origin of the fast and slow components remains unclear.¹⁹ Some have suggested the two components correspond to extra‐ and intra‐axonal compartments of water, respectively.⁸ Others have attributed the slow diffusion to membrane‐ and macromolecule‐bound water molecules, while the fast diffusion consists of the remaining extra‐ and intracellular water.²⁰ Irrespective of interpretation, our work suggests that the fast pool of water is more sensitive to radiation dose, compared to the slow pool. Previous work has suggested that radiation effects on diffusion parameters, derived from a single tensor, transition from focal and dose‐dependent to diffuse and dose‐independent, 32 weeks after the start of RT.⁵ Our results would suggest that this transition to dose‐independent diffuse changes might be driven by the slow diffusion component.

The mechanisms underlying changes in model parameters can be hypothesized using physiological processes classically associated with radiation‐related white matter injury (see Fig. S1). These include edema, increased vascular permeability from a breakdown of the blood–brain barrier or inflammation, demyelination, and axonal degeneration. Vasogenic edema, for example, is more likely to influence the fast diffusion component²¹ and may contribute to the increase in ADC and signal contribution of this component. The differential effect of each of these processes on the fast and slow diffusion components is beyond the scope of this study, but remains an exciting avenue of research that is best suited for preclinical models.

This study does have limitations to consider. The patient sample size is small; however, more than 10,000 voxels were used on average per patient, to estimate the dose‐ and time‐dependent parameters. The study is retrospective with potential for selection bias. Patients were selected for availability of imaging within four specific time windows. Change in diffusion parameters may also be affected by chemotherapy²² and tumor infiltration.²³ The individual contribution of each of these effects will require further study. Some patients underwent intervening surgery between time points, although all of these regions were manually censored from analyses. Two patients were treated with adjuvant bevacizumab, which may influence the diffusion parameter estimates. In addition, the biexponential model of diffusion used in this study consisted of a slow component with a single identifiable longitudinal ADC, parallel to the primary direction of the axon. The transverse ADC of the intra‐axonal slow water is essentially assumed to be 0. This should not be interpreted that such a component does not exist, but that this component cannot be detected reliably within the constraints of our imaging protocol and the diffusion model. In addition, several studies have demonstrated the importance of the selection of b‐values and gradient sampling schemes on the robust estimation of diffusion model parameters.^{24, 25} However, the benefits of increasing the number of b‐values or gradient directions on model parameter estimation must be weighed against the cost of increased scan time, which is a particularly important tradeoff within the clinical setting. Thus, a rigorous determination of the optimal experimental setup to detect changes in the diffusion properties of white matter after radiation is warranted.

5. Conclusions

We have implemented a two‐component water diffusion model in the study of radiation‐induced changes in cerebral white matter. Dose‐ and time‐dependent increases in ADC were observed in the fast component, whereas a dose‐independent decrease in ADC was observed in the slow component. Future studies correlating the changes in two‐component diffusion parameters with histopathological features and cognitive dysfunction may help us elucidate the clinical importance of fast and slow component changes within the white matter of the brain after RT, and are underway at our institution.

Funding

This work was partially supported by the following grants: National Institutes of Health Grant #1KL2TR001444 (JAH‐G), #UL1TR000100 (JAH‐G), R01NS065838 (C.R.M.), RC2 DA29475 (A.M.D.), and EB00790‐06 (A.M.D.), American Cancer Society Pilot Award ACS‐IRG #70‐002 (JAH‐G), American Cancer Society Research Scholar Grant RSG‐15‐229‐01‐CCE (CRM) and National Science Foundation Grant 1430082 (NSW).

Conflict of interest

N.P., T.M.S., and J.H.G. report grants from Varian Medical Systems, unrelated to the current work. V.M. reports personal fees and non‐financial support from Varian Medical Systems. A.M.D reports that he is a Founder of and holds equity in CorTechs Labs, Inc, and serves on its Scientific Advisory Board. He is a member of the Scientific Advisory Board of Human Longevity, Inc. and receives funding through research agreements with General Electric Healthcare and Medtronic, Inc.

Supporting information

Fig. S1: Possible mechanisms for changes in diffusion parameters after radiation therapy including edema, increased vascular permeability, and axonal injury