Interplay between Hydrogen Bonding and Vibrational Coupling in Liquid N-Methylacetamide

Abstract

Intrinsically disordered proteins play an important role in biology, and unraveling their labile structure presents a vital challenge. However, the dynamical structure of such proteins thwarts their study by standard techniques such as X-ray diffraction and NMR spectroscopy. Here, we use a neat liquid composed of N-methylacetamide molecules as a model system to elucidate dynamical and structural properties similar to those one can expect to see in intrinsically disordered proteins. To examine the structural dynamics in the neat liquid, we combine molecular dynamics, response-function-based spectral simulations, and two-dimensional polarization-resolved infrared spectroscopy in the amide I (CO stretch) region. The two-dimensional spectra reveal a delicate interplay between hydrogen bonding and intermolecular vibrational coupling effects, observed through a fast anisotropy decay. The present study constitutes a general platform for understanding the structure and dynamics of highly disordered proteins.

Proteins, the engines of life, control essentially all of the processes that occur in cells. Well-defined structural parts of proteins are responsible for their biological activity. These systems have been extensively studied with molecular dynamics (MD) and spectroscopic modeling. However, more recently, it has been discovered that intrinsically disordered proteins (IDPs) can also have important biological functions, such as signaling and DNA translation/transcription.¹⁻⁴ IDPs are characterized by weaker interactions, low quantities of bulky side chains, and sequence simplicity. The intrinsic disorder results in lower structural stability and in an absence of well-defined secondary structure domains. This provides new challenges to MD and spectroscopic modeling as the low structural stability allows rapid fluctuations between different conformations, which is crucial for their function. To benchmark the modeling of such systems, we utilize a small-molecule mimic, N-methylacetamide (NMA),⁵⁻⁸ as it is composed of a single peptide bond. In the dynamically disordered hydrogen-bonded bulk liquid, the NMA molecules interact with each other in a way similar to IDPs. The molecules have one hydrogen-bond-accepting oxygen atom and one donating hydrogen atom, as each peptide unit in the protein backbone, which allows fast forming and breaking of hydrogen bonds.

Nuclear magnetic resonance (NMR) and X-ray crystallography methods are powerful tools to determine structure and dynamics of most biological systems. Nonetheless, the main limitation of these techniques is rooted in the fact that they are not well suited to probe subnanosecond dynamics. Two-dimensional infrared spectroscopy (2D-IR) has been used as a novel method to probe the transient structure of biological systems,⁸⁻¹³ thus providing dynamical and structural information on femto- to pico- and nanosecond time scales. The amide I mode, dominated by the CO stretch and NH bending, is the most probed mode in 2D-IR spectroscopy of proteins due to its strong absorbance and high sensitivity to hydrogen bonding and secondary structure.^3,14 Nevertheless, the distribution of different hydrogen bonding environments and vibrational delocalization phenomena arising from intermolecular vibrational coupling result in strongly congested spectra, which are challenging to interpret. Theoretical methods developed recently are of great support to overcome this limitation.¹⁵⁻²⁷ The combination of classical MD with response function methods, due to their low computational cost and high accuracy, has become a powerful tool to model 2D-IR spectra.^{4,16,20,28−30} Conceptually, a time-dependent Hamiltonian containing the site frequencies and the couplings between the molecular sites derived from MD simulations is generated using electrostatic maps.^{7,18,21,22,29,31} This information is converted to 2D spectra using response-function-based calculations,^32,33 which in combination with experimental results are used to disentangle different contributions to spectral shapes and dynamics.

In the current Letter, unlike in many other previous studies,^{7,8,24,29,34−38} we use bulk NMA as opposed to NMA molecules diluted in different solvents, which provides direct insight into the interactions and dynamics in this liquid. Previously, neat liquids of molecules each containing a peptide unit were also studied with 2D-IR.^10,39 The first molecule, N,N-dimethylformamide,³⁹ has one hydrogen-bond-accepting oxygen atom but no donating hydrogen atom and thus does not form hydrogen bonds as a the NMA liquid studied herein. The second molecule, formamide,¹⁰ has one hydrogen-bond-accepting oxygen atom and two donating hydrogen atoms, which results in more branched structures than in peptides.

The goal of this Letter is to investigate the structure and dynamics of liquid NMA as a first step toward using 2D-IR to study IDPs/peptides. We use 2D-IR spectroscopy on the NMA amide I mode combining theoretical predictions with experimental data. We unravel the contributions of hydrogen bonding and vibrational delocalization over multiple peptide units to the amide I vibration spectrum. Our findings reveal that even in highly disordered systems one can expect to find highly delocalized amide I vibrations while the hydrogen bond exchange is still relatively slow.

The experimental and theoretical FTIR spectra of neat liquid NMA (Figure 1) are quite similar. They both exhibit the main band at 1655 cm^–1 and sub-bands at ∼1695 or ∼1685 cm^–1 for theory and experiment, respectively. In the experiment, a low-frequency shoulder is also observed at ∼1635 cm^–1. This is attributed to the H–O–H bend absorption of residual water (<5% molar) in the sample (see the SI for details). This mode was not included in the spectral modeling nor will it be considered in the rest of the Letter.

Figure 1.

Experimental (black line) and theoretical (blue line) FTIR spectra of liquid NMA at 300 K. The magenta line shows the theoretical FTIR spectrum with couplings between amide I units set to zero. The additional shoulder at around ∼1635 cm^–1 in the experimental spectrum corresponds to the water bending mode. All spectra are normalized to the height of the main peak.

To disentangle the origin of the two NMA bands, we first performed spectral calculations omitting the intermolecular vibrational couplings given by the electrostatic coupling between the amide I units (details given in the Theoretical Methods section), thus obtaining a FTIR spectrum of uncoupled NMAs (Figure 1). By comparison of the coupled and uncoupled theoretical spectra, it is clear that the intermolecular vibrational coupling lead to a ∼ 17 cm^–1 red shift of the main band, which is consistent with a similar effect in β-sheets,^16,40 and an overall broadening of the spectrum. Both spectra clearly have at least two components contributing.

To unravel the different NMA substructures underlying the spectral features, we characterized the NMA molecules according to their hydrogen bond configuration (Figure 2). We employed a criterion similar in spirit to that of the most commonly used hydrogen bonding criterion, which is defined in terms of the distance between atoms in the accepting and donating groups as well as an angle involving two atoms of the hydrogen donor.⁴¹ Namely, the distance between the oxygen atom of the accepting group and the nitrogen of the donating group is used, along with the angle between the carbon (accepting), oxygen (accepting), and nitrogen (donating) atoms (Figure 2a). This criterion allows for a better structure–frequency relationship than the more traditional donor-centered hydrogen bonding criterion.⁴¹ This is because the frequency shift of the amide I depends largely on the electric field exerted by the surrounding molecules on the NMA molecules along the CO bond, for which the oxygen acts as a hydrogen bond acceptor.

Figure 2.

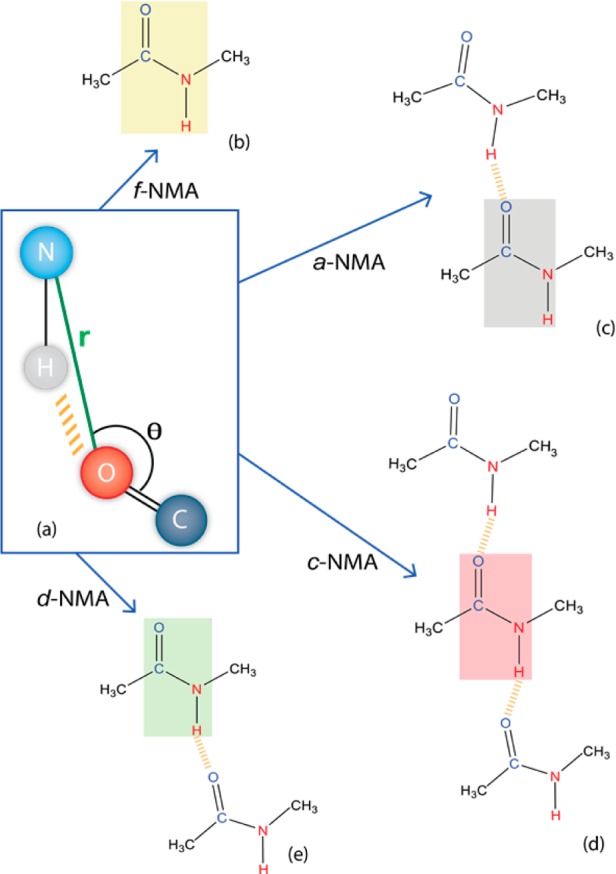
Schematic drawings of the different NMA species categorized with a hydrogen bonding configuration criterion (a), where an r_NO distance smaller than 3.5 Å and an angle θ larger than 120° are used to ascribe a hydrogen bond. The colored rectangles highlight the categorized NMA molecules, while the other molecules are the hydrogen bond partners. The four main species identified are (b) f-NMA: NMA with no hydrogen bonds, (c) a-NMA: accepting NMA, (d) c-NMA: chain of hydrogen-bonded NMA molecules, and (e) d-NMA: donating NMA.

Four main NMA species have been distinguished. The most abundant species (42%) is a hydrogen-bonded chain (c-NMA) (Figure 2d) resembling the cross-strand configurations found in intrinsically disordered peptides.⁴ This structure is followed in abundance by the substructures in which NMA is interacting with one other NMA either by the accepting (a-NMA, 20%) or the donating (d-NMA, 20%) group and a free NMA configuration (f-NMA, 10%) that does not directly hydrogen bond with other molecules (Figure 2). The remaining 8% of the configurations involve different types of bifurcated states, where the NMA molecule either accepts or donates two hydrogen bonds; these states do not play any substantial role due to their scarcity.

To understand in which species the intermolecular vibrational couplings are most pronounced, we calculated the linear spectra in the static approximation for each of the four species independently for both the uncoupled (Figure 3a) and coupled (Figure 3b) cases.

Figure 3.

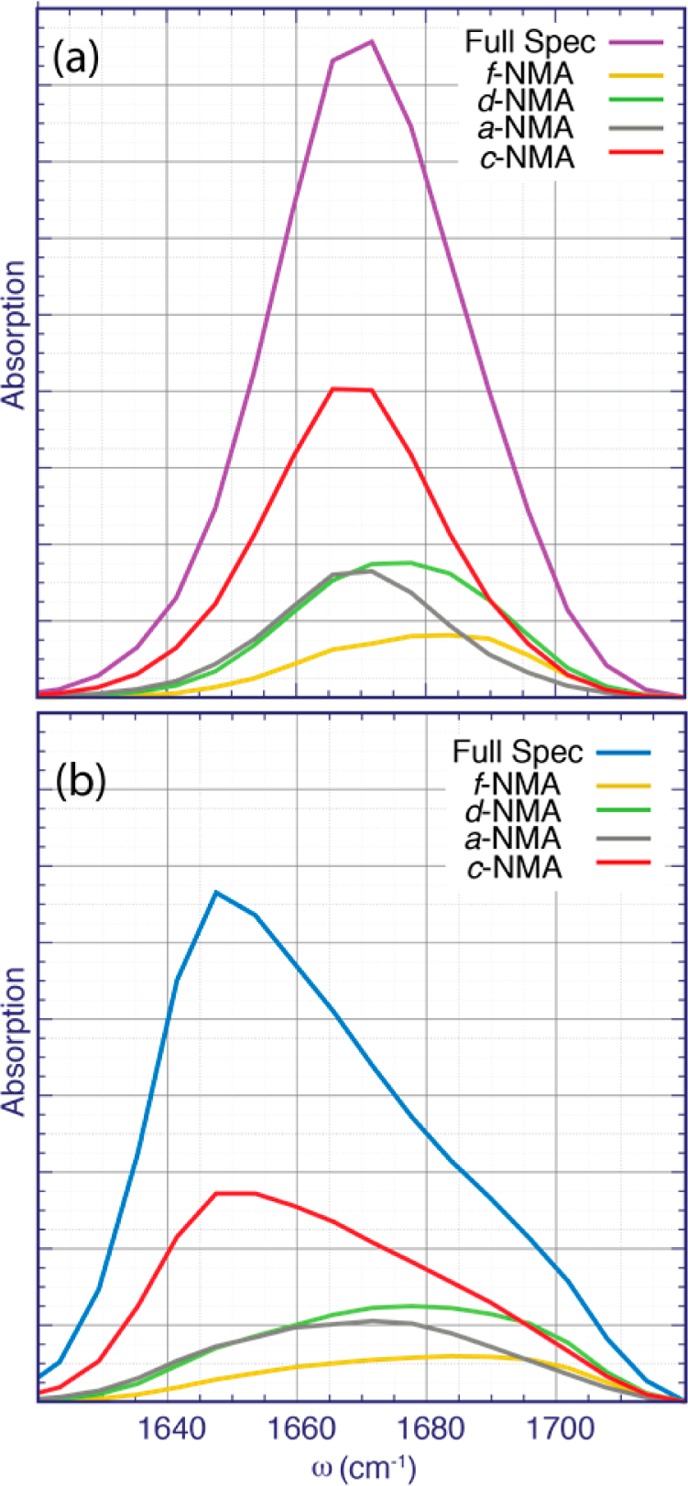
Linear spectra calculated in the static approximation for the different hydrogen-bonded species of NMA. In (a), the vibrational couplings are set to zero, and in (b), the full vibrational Hamiltonian for the given subset of molecules is included.

For the spectra where the vibrational couplings are neglected (Figure3a), the c-NMA and a-NMA species, which both accept a hydrogen bond, absorb in the red flank of the spectrum, while the d-NMA and the f-NMA, which do not accept a hydrogen bond, absorb in the blue region of the spectrum. For the coupled-case spectra (Figure 3b), the peaks of the species accepting hydrogen bonds are red-shifted due to the vibrational coupling for c-NMA and, to a lesser extent, a-NMA. Noteworthy, there is a shoulder in the c-NMA spectrum at ∼1695 cm^–1 in the coupled case that is not present in the uncoupled case (red line in Figure 3). This suggests that this shoulder originates from vibrational couplings among different c-NMA molecules and from f-NMA and a-NMA absorption.

2D-IR experimental and theoretical spectra shown in Figure 4 are in good agreement, apart from the shoulder on the red side of the experimental spectra arising from the water bend (see also Figure S1). In both cases, the diagonally elongated spectra are composed of two peaks with central frequencies of ∼1655 cm^–1 and ∼1685 or ∼1695 cm^–1, experiment and theory, respectively. Note that the subpeak at 1685 cm^–1 identified previously in the linear absorption spectra (Figure 1) is much clearer resolved in the 2D-IR spectra because of diagonal elongation.

Figure 4.

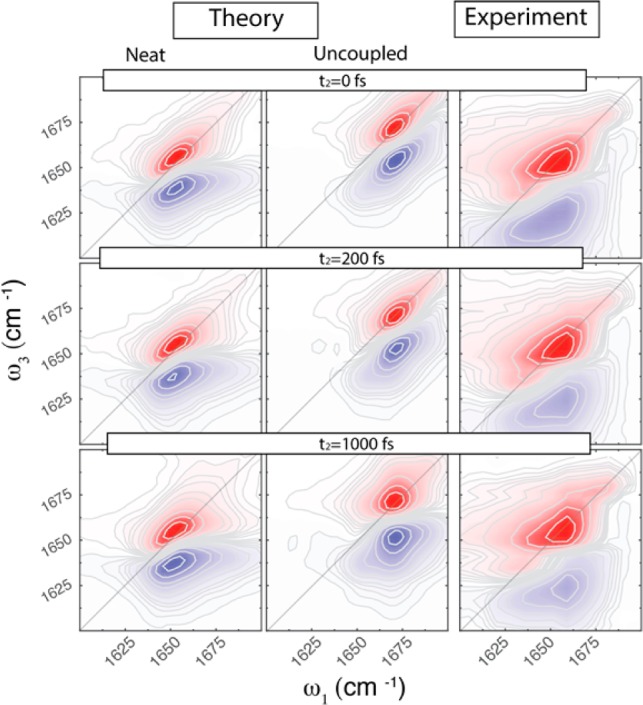
2D-IR parallel polarization spectra of bulk NMA for different waiting times: theoretical NMA (left panels), uncoupled NMA (middle panels), and experimental (right panels) spectra at different waiting times t₂. Equidistant contour lines are drawn with 10% steps from the maximum; red colors indicate bleach, while blue colors indicate absorption.

The anisotropy decay of neat NMA (Figure 5a) was extracted from the parallel and perpendicular polarized 2D-IR spectra (Figures S7 and S8 in the SI) at the position of the main peak. Both theoretical and experimental anisotropy transients decay considerably faster than the anisotropy of the uncoupled case. The latter matches very well with the rotational correlation function (Figure 5b, yellow line), thereby demonstrating the purely orientational origin of the decay on a 20 ps time scale (see Table S1 in the SI for the fitting parameters). This immediately suggests that the anisotropy is affected by vibrational coupling that results in population migration from one oscillator to another, thereby accelerating the anisotropy decay.^27,42,43 The experimental anisotropy starts below 0.4, which is most likely related to the finite pulse duration, which was not included in the theory.

Figure 5.

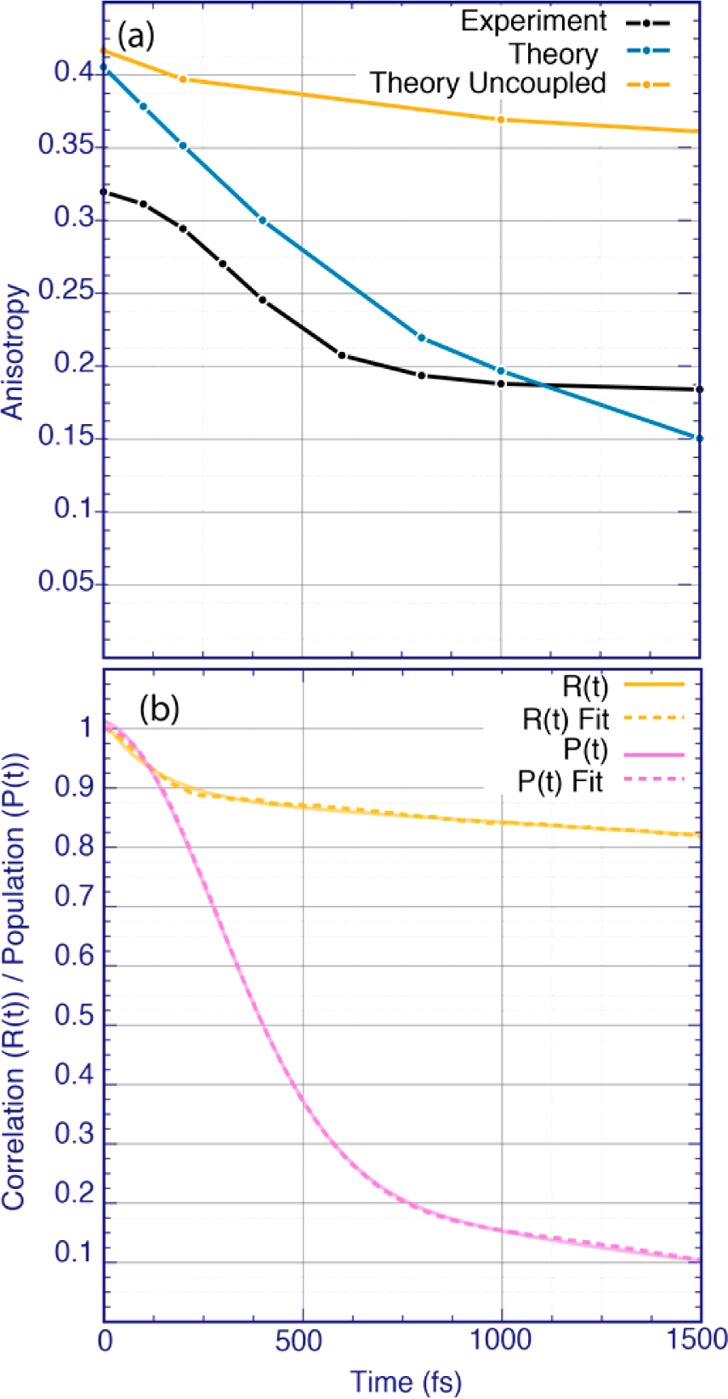
(a) Anisotropy decay for the main absorption peak integrated over the frequency ranges (1651 < ω₁ < 1661 cm^–1, 1647 < ω₃ < 1662 cm^–1) for both theory and experimental spectra. For the uncoupled spectra, the anisotropy decay was integrated over the main peak frequency range (1668 < ω₁ < 1674 cm^–1, 1668 < ω₃ < 1674 cm^–1). (b) Orientational correlation function (yellow line) and population transfer dynamics (purple line), calculated using eqs S9 and S1, respectively. The data of panel (b) were fitted to a biexponential function for the orientational correlation function and to a sum of a Gaussian and an exponential decay for the population transfer. The fits are shown by dashed lines, and the parameters are provided in Table S1 of the SI.

Next, we calculated the population transfer defined as the probability that a molecule excited at time zero will still be excited at time t (see Figure 5b). The population dynamics consists of a fast part resulting in Gaussian decay with a time scale of 400 fs and a slower part resulting in an exponential decay of 1.3 ps. This suggests that the population transfer between hydrogen-bonded molecules is dominated by fast Gaussian decay, while transfer involving the non-hydrogen-bonded species is exponential and occurs on the slower time scale. This demonstrates that the vibrational excitation moves along the hydrogen-bonded chains (see Figure 2d), which largely preserves the orientation of the transition dipole despite movement of the vibrational excitation. This alignment was quantified by calculating the joint angular–radial distribution function for the CO bonds (see SI Figure S9). We further found that typical couplings along the chains amount to −7.5 cm^–1, while couplings between NMA molecules in different chains in close proximity to each other are typically around −2.5 cm^–1. This means that even the coupling is a through-space electrostatic effect; the coupling along the hydrogen bonds is 3 times larger than between chains, which leads to more efficient delocalization of the vibrational modes along the hydrogen bond chains than between chains. Note that a similar effect was previously discussed for the amide-A vibration of neat NMA;⁴⁴ however, the population transfer in that case was much slower.

Our conclusion on the extent of vibrational delocalization is further corroborated by the inverse participation ratio⁴⁵ in the static limit, which is a measure of the delocalization of the vibrational mode in the system. We find that on average the vibration is delocalized over 42 molecules despite the orientational disorder in the liquid. This is larger than values previously reported for normal proteins, ranging from 4 to 23,^8,46 which can be understood by the finite size of the proteins and the fact that these proteins also contain bulky side chains diluting the density of amide I modes. In a previous study on N,N-dimethylacetamide³⁹ the inverse participation ratio was determined for simulation boxes with different sizes, demonstrating that this quantity depends strongly on the size of the system and that one needs to be cautious with the interpretation of this number for three-dimensional systems. The fact that the effects of vibrational coupling are stronger in the c-NMA and a-NMA configurations, as seen in Figure 3, further demonstrates that the hydrogen bonding facilitates the strong vibrational delocalization.

Finally, we comment on the discrepancies between experimental and theoretical data. While the qualitative agreement between theory and experiment is reasonable, the calculated anisotropy decay is slightly different from the experimental one, and the high-frequency peak positions are different also. This indicates that the couplings predicted in our model are somewhat too large. This agrees well with previous findings using the same coupling model.⁴⁷ The presence of the water bend in the experiment does not affect the main amide I peak significantly (see the SI for details); however, the overtone peak region below the main peak in the 2DIR spectra might be contaminated with the water bend response.

In this Letter, we have investigated both experimentally and theoretically the structure and dynamics of bulk NMA using linear and 2D-IR spectroscopy. The main spectroscopic features from both approaches agree very well, enabling interpretation in terms of hydrogen bonding and population transfer from the simulations. We find that NMA aggregation involves four main hydrogen bonding structures, of which the chain structure is most abundant. The main absorption band is red-shifted due to intermolecular vibrational coupling. The high-frequency shoulder contains a contribution from both a coupling-induced sub-band of the c-NMA hydrogen bond species and the main absorption of the d-NMA and f-NMA species. The anisotropy decay of the main band is much faster than the orientational relaxation due to population transfer but is still considerably slower than the population transfer. This demonstrates a delicate interplay between coupling effects and angular correlations of the hydrogen-bonded amide I oscillators even in disordered liquid NMA.

2D-IR anisotropic spectroscopy has proven to be a powerful tool to unravel the interplay between hydrogen bonding vibrational delocalization in liquid NMA. The present study serves as an important benchmark for the models for the structure and dynamics used to unravel spectral signatures of highly disordered systems.

Theoretical Methods

MD simulations were performed with the GROMACS suite version 4.6.1⁴⁸ using the OPLS-AA⁴⁹ force field to describe 343 NMA molecules. After an initial energy minimization, a constant-pressure equilibration of 1 ns at 300 K using a Berendsen barostat,⁵⁰ with an inverse time constant of 0.2 ps^–1, was done. This was followed by a constant-volume equilibration of 1 ns at 300 K at the equilibrium density. A constant-volume production run of 1 ns at 300 K was performed, and the coordinates were stored at each 10 fs for analysis and spectral modeling. For all simulations, a 1 fs time step was used, and the temperature was kept constant using the Berendsen thermostat.⁵⁰ Here, a 1.1 nm cutoff was used for both Lennard-Jones and Coulomb interactions. The latter were treated using the particle mesh Ewald method, with a grid step of 0.16 nm and a convergence of 10^–5.⁵¹ The truncation of the Lennard-Jones interactions was compensated by introducing analytical corrections to pressure and potential energy.⁵² All bonds were constrained using the LINCS algorithm.⁵³ The radial distribution functions of the liquid were calculated for all simulations and are in agreement with those previously obtained.⁴⁹ Furthermore, the joint angular–radial distribution function for the CO bonds was calculated to quantify the angular ordering (see SI Figure S9).

The time-dependent vibrational Hamiltonian for the amide I modes was constructed from the snapshots stored from the MD production run. This Hamiltonian has the form^8,15,54

1

Here, B_i^† and B_i are the bosonic creation and annihilation operators, ω_i(t) is the time-dependent fundamental amide I frequency for the ith molecule, and μ⃗_i(t) is the corresponding transition dipole. The anharmonicity, Δ_i, was kept constant at 16 cm^–1.⁸ The site frequencies of the amide I, ω_i(t), were calculated using the Jansen electrostatic map,²⁹ which relates the electrostatic field and gradient generated by the point charges of the MD force field with the frequency, and the transition dipoles. The long-range intermolecular couplings between the different amide I units were calculated using the transition charge coupling (TCC) model,²⁸ where a charge, q_n, a transition charge, dq_n, and a normal-mode coordinate, ν⃗_ni, are assigned to each atom of the amide one I unit. The TCC model has the form

2

Here, the subscripts n and m, number the atoms, which belong to different amide I modes at molecules i and j, respectively. The distance vector between two atoms in the involved molecules is given by r⃗_nimj. This vibrational Hamiltonian mapping was demonstrated to work well in combination with the OPLS-AA force field in a recent benchmark study for proteins.²⁶

The spectra were calculated using the Numerical Integration of Schrödinger Equation (NISE) method.^20,55 Here, the time-dependent Schrödinger equation is solved numerically for the time-dependent amide I Hamiltonian. The first- and third-order response functions were calculated and the linear absorption and 2D-IR spectra were obtained from Fourier transforms of these response functions (see eqs S3 and S4 in the SI). We used coherence times from 0 to 1.25 ps and a lifetime of 1.8 ps for apodization. The response functions were calculated from starting configurations spaced by 2 ps along the trajectory, giving an ensemble average over 500 realizations. For analysis purposes, linear spectra were also calculated in the static approximation, where the effect of motional narrowing is neglected.

Experimental Section

N-methylacetamide (NMA) with purity of ≥99% was obtained from Sigma-Aldrich and used without any further purification. NMA is a solid under the room temperature of ∼22 °C (the melting point is 28 °C⁵⁶); therefore, it was placed on a heat plate at a temperature of 40 °C until it was melted completely. After that, an NMA droplet of ∼1.4 μL was squeezed between two 1 mm thick CaF₂ windows, which were preheated to T = 40 °C. The NMA sample thickness was ∼2.5 μm assuming that the NMA droplet was spread uniformly between the 1 in. diameter CaF₂ windows. The sample preparation was performed under a nitrogen atmosphere to avoid any contact with air moisture; after preparation, the sample was placed in a nitrogen-filled sample holder. During the experiments, the temperature of the sample was controlled by a thermocouple and maintained at 30.5 ± 1 °C by a thermostat. The water content in the experimental samples did not exceed 5% molar (see the SI).

The IR absorption spectra were recorded with a FTIR spectrometer Vertex-70 purged with dry nitrogen, with 4 cm^–1 spectral resolution. The maximal optical density of the sample was measured as OD ≈ 0.6 at the central frequency of the amide I mode (1656 cm^–1).

A collinear 2D-IR setup, based on the interferometer platform described in ref (57), was used. In short, 25 μJ, 150 fs IR pulses (70 cm^–1 fwhm spectral width), centered at 1640 cm^–1, were split into pump (90% of the total intensity), probe, and reference beams. The reference pulse was advanced with respect to the pump beam by 40 ps. A wobbler in the pump beam path generated a −π, 0, +π, 0 phase sequence⁵⁸ for each subsequent pulse at a 1 kHz repetition rate to remove sample scattering. Before the sample cell, the polarization of the pump beam was rotated by 45° by a halfwave plate. After the sample cell, a movable polarizer selected either the parallel or perpendicular polarization of the probe/reference beams. The probe light was dispersed by a polychromator (Newport Oriel MS 260i) onto one array of a × 32 pixel MCT array (Infrared Associates) to create the ω₃ dimension. The second array was used for detection of the reference spectrum over which the probe spectrum was normalized at each laser shot. With two polychromator settings, a combined spectral window of 150 cm^–1 was achieved. The delay between the two pump pulses, t₁, was scanned up to 2 ps using a st scanning approach.⁵⁷ The waiting time between the later pump pulse and the probe, t₂, was set at different values to study the system dynamics. The 2D signal was averaged over the wobbler-generated phase sequence to extract the nonlinear response related to all three pulses (two pumps and the probe), zero-padded to 4 ps, and Fourier-transformed to obtain the ω₁ dimension with the phase correction applied.⁵⁹

For the pump–probe measurements, one of the pump pulses was blocked and a chopper was installed in the other pump beam. The amide mode lifetime was obtained as 450 ± 100 fs,while the thermalization time of the hot ground state was measured as 5 ± 1 ps (see the SI for details). These two values provide an erimental window of ∼2 ps for 2D-IR spectroscopy.

The whole interferometer was constantly purged with dry air. The whole measuring cycle lasted for ∼16 h.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b00731.

• Experimental details, the theoretical background, additional data from both theory and experiment, and analysis and fits (PDF)

The authors declare no competing financial interest.