Evaluation of the metabolic rate based on the recording of the heart rate

Abstract

The assessment of harsh working conditions requires a correct evaluation of the metabolic rate. This paper revises the basis described in the ISO 8996 standard for the evaluation of the metabolic rate at a work station from the recording of the heart rate of a worker during a representative period of time. From a review of the literature, formulas different from those given in the standard are proposed to estimate the maximum working capacity, the maximum heart rate, the heart rate and the metabolic rate at rest and the relation (HR vs. M) at the basis of the estimation of the equivalent metabolic rate, as a function of the age, height and weight of the person. A Monte Carlo simulation is used to determine, from the approximations of these parameters and formulas, the imprecision of the estimated equivalent metabolic rate. The results show that the standard deviation of this estimate varies from 10 to 15%.

Introduction

Work physiology was a subject of intense research during the years 1960–1980, but then disappeared almost from the publications and congresses in favour of ‘modern’ subjects such as musculoskeletal disorders¹⁾ and the psychosocial factors²⁾ during the years ’90. While it is true that, in the countries said to be developed, the working conditions changed a lot, it is obviously not the case universally as demonstrated by the statistics of fatal industrial accidents reported by Takala³⁾. These ‘modern’ subjects are indeed essential and concerns about the psychosocial work environment constitute a significant evolution in Occupational Health from merely the absence of impairments and diseases, towards wellbeing. However, it would be an awful error, in the so called developed countries, but especially in the developing countries, to consider that the common problems of industrial hygiene are once for all resolved.

The use of the health and safety standards of the countries known as ‘developed’ in other countries raises problem in general, but it is particularly true regarding work physiology and performance in hot conditions. It is remarkable that all the ISO standards concerning the thermal environments were developed based on studies conducted exclusively in developed countries and it can be questioned whether they are really applicable for populations with particular characteristics of morphology, food and living conditions⁴⁾.

All these standards start from the heat balance equation which indicates that the heat produced in the body–the metabolism–has to be evacuated from that body to maintain it at a constant temperature. The ISO standard on metabolic rate (ISO 8996)⁵⁾ concerns the main part of this heat balance, the metabolic rate. Errors on the evaluation of the metabolic rate will obviously result in errors in the evaluation of the comfort-discomfort and the predicted heat stress or strain.

ISO Standard 8996 was first published in 1990, mainly based on the work by Spitzer, Hettinger and Kaminsky⁶⁾ published in 1982, itself based on data collected in the years 1960 to 1975 essentially in Germany. It was deeply revised in 2004 regarding its structure, but still based on the same old data. It is now in revision again in order to update the information and, in particular, to make it more applicable to any population, instead of to the workers populations of the Western countries implicitly considered in the previous versions. The standard presents 4 levels of methods to estimate the metabolic rate.

At the level 1, two simple methods are presented to roughly characterize the mean workload for a given occupation or for a given activity. The first one is a classification according to the kind of activity and is used as such in several standards, such as the WBGT standard (ISO 7243)⁷⁾. The second method is giving average metabolic rate for several occupations: as the nature and the strenuousness of the work of blast furnace workers, machine moulders, but also butchers, gardeners or secretaries has changed, sometimes considerably, in the last decades, the corresponding average metabolic rates are no longer valid and, as new data are not available, this second method has to be withdrawn.

At level 2, a procedure is described to recognize the different activities of a given worker during a representative period of time, to estimate the average metabolic rate for each of them, to record the sequence of activities with time, and compute the time-weighted average metabolic rate. This procedure may lead to very large errors depending upon the complexity of the job, the knowledge of the working conditions by the observer and his ability to recognize the different activities and evaluate their corresponding metabolic rate.

The method of Level 3 of the standard is the estimation of the metabolic rate from recordings of heart rate.

The general formula is:

$$\mathrm{M}=\frac{(\mathrm{M}\mathrm{W}\mathrm{C}-{\mathrm{M}}_0)}{(\mathrm{H}{\mathrm{R}}_{max}-\mathrm{H}{\mathrm{R}}_0)}(\mathrm{H}{\mathrm{R}}_{\mathrm{w}\mathrm{m}}-\mathrm{H}{\mathrm{R}}_0)+{\mathrm{M}}_0$$ (1)

Where

MWC is the maximal work capacity, in watts per kg of body weight or in watts;

M₀ is the resting metabolic rate, in watts per kg or in watts

HR_max is the maximum heart rate, in beats per minute (bpm);

HR₀ is the heart rate at the rest, in bpm;

HR_wm is the average heart rate observed during the observed period of time, in bpm;

M is the corresponding metabolic rate, in watts per kg or in watts.

As heart rate recorders are presently very popular and cheap, this method has become the least bad method to estimate routinely the metabolic rate.

The formulas to estimate MWC and HR_max in the 2004 edition of the standard were those derived by Gillet⁸⁾ in a study of 60 Belgian steel workers in 1982. As this sample may not be considered a priori representative of the population in all parts of the world, a review of the scientific literature will be done in order to determine the best formulas for the estimation (with related precisions) of the basic parameters: MWC, M₀, HR_max and HR₀.

In addition, the standard indicates also that the precision of this method would be approximately 10%. The reference of this value is unknown as well as what it really means. This is an important issue as this greatly influences the precision of the evaluation of comfort and stress indices^{9, 10)}. This also needed to be reanalysed and will be done using a Monte Carlo simulation.

Finally, a revised version of the method of evaluation of the metabolic rate from a recording of HR at the workplace will be proposed.

Evaluation and Precision of the Basic Parameters

Evaluation and precision of the maximal work capacity MWC, in watts per kg of body weight

The maximum capacity of work (MWC) is the expression in watts of the maximum oxygen consumption (VO_2max) which is the maximum quantity of oxygen per unit of time that a person can consume under maximum conditions of her/his cardiovascular possibilities.

This VO_2max quantity, and consequently the MWC, can be evaluated by means of a cardiac stress test where the subject is invited to produce an increasing effort, in general on an ergonomic bicycle or treadmill, until reaching exhaustion. Such cardiac stress tests raise health risks and can only be performed under strict medical surveillance. Therefore they cannot be carried out in the large majority of field studies and it is necessary to fall back on submaximal effort tests, even on formulas of prediction according to the characteristics of the subject.

Malchaire and Mairiaux¹¹⁾ compared the results of various methods of indirect evaluation with the values recorded during full cardiac stress tests and showed the progressive reduction of the correlation coefficient (R) as and when the method deviates from the reference stress test. However, the various methods returned individual variations (± standard deviation SD) relatively concordant of about 12.5%.

Very many studies^{8, 12, 13, 14, 15, 16, 17)} sought to determine the relationship between the MWC (in watts) and individual characteristics. Nearly all adopted a relation depending upon the age, A, and the weight, W_b, with the following algebraic structure:

$$\text{MWC }=\left(\text{b }-\text{ a }\times \text{ A}\right)\times {\text{ W}}_{\text{b}}$$ (2)

where a and b are the intercept and the slope of the linear regression, respectively.

Table 1 summarizes the formulas reported in seven significant studies published in the last 40 yr.

Table 1. Relations for the prediction of MWC (W/kg) as a function of age according to MWC = b – a × A, reported in 7 significant studies in the last 40 yr.

Study	Characteristics	Men		Precision	Women		Precision
		b	a		b	a
Bugajska et al.12)	—	21.40	0.18	SD=3.7	19.50	0.18	SD=3.1
Fitzgerald et al.13)	Active	—	—	—	18.80	0.15	—
	Sedentary	—	—	—	15.25	0.12	—
Tanaka et al.14)	Sedentary	—	—	—	19.50	0.20	R=0.8
Dehn and Bruce15)	Sedentary	17.38	0.097	—	—	—	—
	Active	19.69	0.14	—	—	—	—
Wilson and Tanaka16)	Sedentary	18.86	0.14	—	—	—	—
	Active	21.37	0.14	—	—	—	—
Gillet Y.8)	—	18.00	0.10	—	14.50	0.10	—
Mean values		19.45	0.133		17.51	0.15

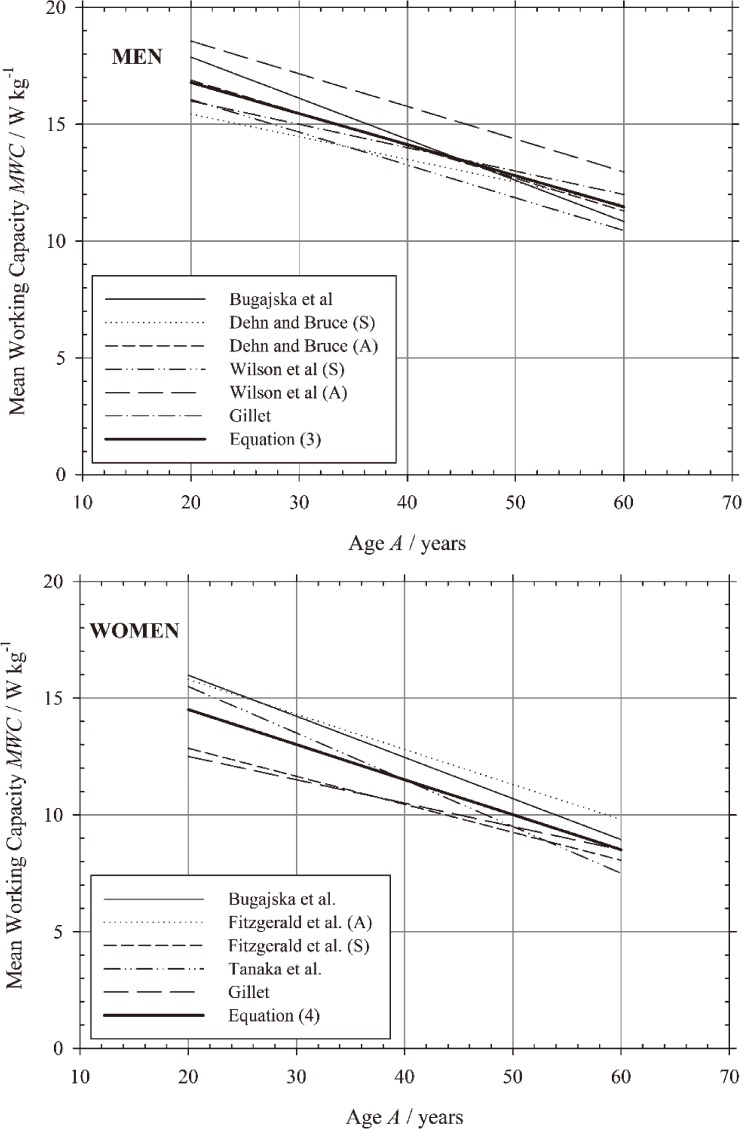
Figure 1 illustrates these formulas of Table 1 for men and women aged from 20 to 60 yr. Although the seven studies were based on very different number of subjects and therefore do not have the same statistical weight, we propose to adopt the mean values for both coefficients. The formulas are then the following ones:

Fig. 1.

Comparison of the prediction formulas of the MWC (W/kg) for women and men.

• for men:

$$\text{MWC }=\text{ 19}.\text{45 }-0.\text{133 }\times \text{ A W}/\text{kg}$$ (3)

• for women:

$$\text{MWC }=\text{ 17}.\text{51 }-0.\text{15}0\times \text{ A W}/\text{kg}$$ (4)

Equations (3) and (4) seem slightly better than those proposed by Gillet⁸⁾, taken over by Malchaire¹⁷⁾ and adopted in the ISO 8996 Standard⁵⁾ in 2004, that estimate the MWC in watts according to the weight raised at the power 0.666. The increase of precision given by these formulas, already meagre in original study (the author reported a correlation coefficient of 0.63 instead of 0.61 when using simply the weight) is all the more insignificant in view of Fig. 1 that shows estimates of MWC varying on average approximately by 23% for men and 12% for women. The standard deviation SD_MWC = 12.5% reported by Malchaire and Mairiaux¹¹⁾ thus appears acceptable, more especially as the coefficient of correlation (0.581) is definitely lower than those reported (when reported!) by the various studies listed in Table 1.

Evaluation and precision of the maximal work capacity in watts

Formulas 3 and 4 allow estimating the MWC in W/kg. The derivation of the metabolic rate from heart rate requires the knowledge of the MWC in watts. Thus, it remains to determine the weight to take into account.

The majority of the studies reported in table 1 mentioned that each subject took a medical examination, sometimes with ECG, but they did not indicate whether a selection was really carried out and on what bases. One study only¹⁴⁾ mentioned the exclusion of subjects with a body mass index BMI = W_b / H_b² greater than 35 kg/m². This means that, in most cases, the actual weight of the person was used as input value in their correlation studies and, consequently, that the MWC can be estimated from the actual weight and not from a ‘lean’ weight as recommended¹⁸⁾. However, the age and weight of the experimental subjects suggest that they were, as very often, students, who usually are not (yet) overweight and therefore are not representative of the general population. Then, the knowledge of the ‘ideal’ weight W_bid of the subject should make it possible for the observer to judge whether the actual weight can be validly used to evaluate the MWC.

Formulas for estimating the ‘ideal’ weight were proposed by Creff¹⁹⁾ (as quoted in Pai and Paloucek²⁰⁾) seeking to take account of the morphology of the subject:

• for ‘normal’ morphology:

$${\text{W}}_{\text{bid},\text{n}}=0.\text{9}\times \left({\text{H}}_{\text{b}}+\text{A}/\text{1}0-\text{1}00\right)$$ (5)

• for ‘slender’ morphology:

$${\text{W}}_{\text{bid}}={\text{ W}}_{\text{bid},\text{n}}\times 0.\text{9}$$ (6)

• for ‘broad’ morphology:

$${\text{W}}_{\text{bid}}={\text{ W}}_{\text{bid},\text{n}}\times \text{ 1}.\text{1}$$ (7)

The formula for ‘normal’ morphology gives ‘ideal’ weight somewhat greater than the formula proposed by Lorentz in 1928 (see de Saint Pol²¹⁾):

• for men:

$${\text{W}}_{\text{bid},\text{m}}=0.\text{75 }\times {\text{ H}}_{\text{b}}-\text{ 62}.\text{5}$$ (8)

• for women:

$${\text{W}}_{\text{bid},\text{w}}=\text{ 1}0+0.\text{8 }\times {\text{ W}}_{\text{bid},\text{m}}$$ (9)

It is proposed to adopt the more recent Creff’s formula, while adopting the reduction for women of equation 9.

However, the use of these formulas rests upon the distinction between the persons ‘normal’, ‘broad’ and ‘slender’. As suggested by Monerot-Dumaine²²⁾ the morphology class can be determined on the basis of the size of the wrist, which is a good indicator of skeletal mass and frame size. According to the most recent anthropometric database²³⁾, the percentiles 25 and 75% of the distribution of wrist breadth (measured at the stylion landmark) in the general population in the USA are 5.7 and 6.2 cm for men and 5 to 5.4 cm for women and do not vary greatly according to the ethnical groups (in the USA) . We suggest therefore that people with a wrist breath between these values be considered to have a ‘normal’ morphology and that the ‘slender’ and ‘broad’ groups be defined as those with wrist breadth respectively lower than these 25% percentiles and greater than these 75% percentiles.

The ‘ideal’ weight estimated from these formulas has for sole purpose to assist the observer to decide what weight to take into account for estimating the MWC of the person who he can interrogate concerning his general health, his eating and drinking habits, his physical activities etc. If it appears that the subject is having regular physical activities and a healthy diet, the actual weight might be the best value to use to estimate the MWC. On the contrary, for a sedentary and obese person, the ‘ideal’ weight might be chosen.

It appears reasonable to assume that the uncertainty on the weight adopted for this evaluation is ± 5 kg, that is that the observer is sure that the correct value is at 95% of probability in the range of the adopted weight ± 5 kg, with SD_Wb=2.5 kg.

Evaluation and precision of the resting metabolic rate

The basal metabolic rate M_b is defined as the minimal energy rate expenditure to sustain the functioning of the vital organs when the subject is at complete rest, that is, 12 h after eating, after a restful sleep, lying and in a state of complete mental and physical relaxation²⁴⁾. The many studies about M_b expressed it in watts and showed that it increases with the size and body mass of the subject and decreases with age. Prediction formulas abound, the most well-known being those proposed by Harris and Benedict²⁴⁾:

• for men:

$$\begin{array}{l}{\text{M}}_{\text{b},\text{m}}=\text{ 3}.\text{2 }+0.\text{666 }\times {\text{ W}}_{\text{b}}+0.\text{242}\\ \times {\text{ H}}_{\text{b}}-0.\text{327 }\times \text{ A}\end{array}$$ (10)

• for women:

$$\begin{array}{l}{\text{M}}_{\text{b},\text{w}}=\text{ 31}.\text{7 }+0.\text{463 }\times {\text{ W}}_{\text{b}}+0.0\text{9}0 \\ \times {\text{ H}}_{\text{b}}-0.\text{226 }\times \text{ A}\end{array}$$ (11)

At present, the formulas most generally quoted are those of Mifflin et al.²⁵⁾,

• for men:

$$\begin{array}{l}{\text{M}}_{\text{b},\text{m}}=0.\text{2 }+0.\text{484 }\times {\text{ W}}_{\text{b}}+0.\text{3}0\text{3} \\ \times {\text{ H}}_{\text{b}}-0.\text{238 }\times \text{ A}\end{array}$$ (12)

• for women:

$${\text{M}}_{\text{b},\text{w}}={\text{ M}}_{\text{b},\text{m}}-\text{ 8}$$ (13)

and those of Black et al.²⁶⁾:

• for men:

$${\text{M}}_{\text{b},\text{m}}=\text{ 1}.\text{255 }\times {{\text{ W}}_{\text{b}}}^{\text{0.48}}\times {{\text{ H}}_{\text{b}}}^{\text{0.5}}\times {\text{ A}}^{-0.\text{13}}$$ (14)

• for women:

$${\text{M}}_{\text{b},\text{w}}={\text{ M}}_{\text{b},\text{m}}\times 0.\text{888}$$ (15)

In the field of the ergonomics of thermal environments, heat exchange being done primarily by convection, radiation and evaporation on the surface of the skin, calculations are carried out per unit of body surface area, i.e. in W/m². The body surface area is given by the formula of Dubois and Dubois²⁷⁾:

$${\text{A}}_{\text{b}}=0.00\text{7184 }\times {{\text{ W}}_{\text{b}}}^{\text{0.425}}\times {{\text{ H}}_{\text{b}}}^{\text{0.725}}$$ (16)

Table 2 gives the minimal, maximum and average values as well as the standard deviations and coefficients of variation of the basal metabolisms in W and W/m², evaluated by formulas 12 and 14 above for men with body masses from 50 to 100 kg, heights from 150 to 190 cm and ages from 20 to 60 yr. Were eliminated the unusual combinations such as 50 kg and more than 170 cm or 100 kg and less than 160 cm.

Table 2. Minimal, maximum and average values as well as standard deviations and coefficients of variation of the basal metabolisms in W and W/m², evaluated by the formulas of Mifflin et al.²⁵⁾ and Black et al.²⁶⁾ for body masses from 50 to 100 kg, heights from 150 to 180 cm and ages from 20 to 60 yr (men) and for body masses from 50 to 90 kg, heights from 150 to 175 cm and ages from 20 to 60 yr (women).

	Men					Women
	Mifflin et al.25) Formula (12)		Black et al.26) Formula (14)			Mifflin et al.25) Formula (13)	Black et al.26) Formula (15)
	W	W/m2	W	W/m2		W/m2	W/m2
Minimum	55.6	38.8	59.0	39.5		33.2	35.0
Maximum	101.4	45.8	106.9	48.7		41.8	43.2
Mean	78.6	42.3	80.8	43.5		37.9	38.6
Standard deviation	10.4	1.9	10.9	2.4		2.0	2.1
Coefficient of variation	0.133	0.045	0.135	0.054		0.053	0.054

The differences in basal metabolic rate are very marked between a minimum (for a subject young (20 yr), tall (180 cm) and heavy (100 kg)) and a maximum (for a person older (60 yr), smaller (150 cm) and lighter (50 kg). In absolute value, M_b in watts varies almost by a factor of 2. On the other hand, brought back to the body surface area, it varies relatively little: the standard deviation is reduced by a factor of about 5 and the coefficient of variation, reduced by about a factor of 2, becomes approximately 5%.

In practice, the basal metabolic rate may thus be regarded as a constant when expressed in W/m² and the most acceptable value seems to be the average of the mean values obtained by the two formulas selected above, that is, 43 W/m² with a standard deviation of 2.2 W/m². The difference of 3 to 5.6 W/m² with the minimum and maximum values reported in Table 2 will not lead to very significant differences when one will calculate the PMV-PPD indices^{9, 28)} or the duration limits of exposure according to the Predicted Heat Strain (PHS) approach for hot working conditions^{10, 29)} or also the Required Clothing Insulation (IREQ) approach in case of cold working conditions³⁰⁾. This value is quite close to the figure of 46 W/m² given for a ‘reclining’ person in the ISO 7730 standard²⁸⁾.

Table 2 reports the same statistics of the basal metabolisms in W/m², evaluated by formulas (13) and (15) for women and makes it possible to conclude that the basal metabolic rate for women is on average of the order of 38 ± 2.1 W/m², that is some 5 W/m² lower than for men.

The basal metabolic rate (M_b or BMR) is to be distinguished from the resting metabolic rate (RMR), which is the energy expenditure of a subject at rest in usual conditions.

The conditions of this definition are however not as rigorous as for the basal metabolism, so that an accurate estimate does not appear possible. RMR is greater than BMR “due to increases in energy expenditure caused by recent food intake or by the delayed effect of recently completed physical activity”³¹⁾. These authors estimate this increase to be equal to 10 to 20%. In their study with 6 male subjects 20 years old, of mean height of 175 cm and mean weight of 70 kg (1.86 m² in body surface area) Garg et al.³²⁾ reported metabolic values, in watts, on average equal to 1.60 and 1.67 times the body mass respectively when seated and upright, that is 112 W and 117 W respectively for a subject of 70 kg, or 60 and 63 W/m² by taking account of the body dimensions of the studied subjects. The resting metabolic rate would correspond consequently to approximately 1.4 times the basal metabolism. This value corresponds to what is given in the report of the World Health Organization³³⁾: M₀ = 1.5 M_b and somewhat higher than the often cited value of 105 watts for a man and 95 watts for a woman, in particular reported by Spitzer et al.⁶⁾. One can thus conclude that the resting metabolic rate can be estimated equal to 60 W/m² for men and to 53 W/m² for women.

As the conditions of evaluation of the metabolic rate ‘at rest’ are not standardized, its imprecision is higher than that considered for the basal metabolism. Garg et al.³²⁾ reported standard deviations of about 12% of the resting metabolic rate, so that it appears logical to admit an imprecision (standard deviation SD_Mo) of 60 × 0.12 ≈ 7 W/m² for both women and men.

Evaluation and precision of the maximum heart rate, HR_max

It is usually considered that the maximum heart rate decreases with age according to (220–A). Robergs and Landwehr³⁴⁾ published an article entitled: ‘The surprising history of the “HR_max = 220-age” equation’ where they re-examine 38 univariate formulas (function of age only) of prediction of HR_max proposed during the last 80 yr. All these formulas strongly approach the formula (208 − 0.7 × A) and do not differ significantly from it considering the low to very low correlation coefficients obtained. This study appears definitive and it seems useless to return to the background documents. The conclusions of the authors are however debatable:

(1) ‘The most precise expression is that of Inbar et al.³⁵⁾: HR_max = 205.8 − 0.685 × A. However the estimation error is very large: SD = 6.4 bpm’. It is true that this expression is based on a very large study with 1,424 subjects, and gives a correlation coefficient of 0.67. However a study quite as large³⁶⁾ led to the expression (207 − 0.64 × A) with a correlation coefficient definitely lower (R = 0.42). The fact that the Inbar correlation coefficient is greater is likely due to the fact that the studied group was more homogeneous as for the other factors unknown to date that determine this HR_max. In no case, it can be alleged on this basis that the expression is more accurate. The differences between HR_max estimated by the Inbar formula and the general formula (208 − 0.7 × A) being lower than 2 bpm for ages higher than 20 yr, this general formula, which does not give the illusion of a high degree of precision, will be adopted.

(2) ‘Additional research is necessary to develop multiple regressions for various populations and various modes of exercises.’ It is rather remarkable to observe from the Robergs and Landwehr review³⁴⁾, that no statistically significant difference was noted for 80 yr between men and women, between sedentary, active and trained subjects, between Hispanic and Caucasian subjects, between subjects in good health and less good health (among whom hypertensive, but not those with cardiac diseases). In addition, the only multivariate models³⁷⁾ explained at best 86% of the total variance instead of 72% for the simple linear regression. This increase hardly appears important in practice and, the results being considerably function of the studied group and not very reproducible, it cannot be asserted that better general multivariate models will ever be developed.

We will conclude from this review of the literature that HR_max can be predicted by the simple relation:

$${\text{HR}}_{\text{max}}=\text{ 2}0\text{8 }-0.\text{7 }\times \text{ A}$$ (17)

but that the imprecision of the prediction is considerable: SD_HRmax = 11 bpm

Evaluation and precision of the heart rate at rest, HR₀

The heart rate of rest HR₀ is difficult to define accurately³⁸⁾. When a calibration cardiac stress test was carried out, the heart rate to consider is that corresponding to the resting metabolic rate. In cases where the subject had, at the low levels, an important elevation due to stress or mental load, this value is determined by extrapolation of the (M vs. HR) relation noted on the levels of high efforts. In the majority of cases however, as said, a cardiac stress test is not carried out and the heart rate at rest must be estimated directly. Various values can be selected:

• An average value such as 70 bpm in all cases: however it is obvious that HR₀ varies greatly between and within individuals. As discussed below (Fig. 2), this would lead to large under or over estimation of the metabolic rate when HR₀ is respectively larger or smaller than this value.

• The HR observed at rest, sitting, at the beginning of the recording: however Malchaire et al.⁴⁰⁾ showed that this value is systematically higher than the values discussed hereafter, this elevation being due to the state of nervousness of the subjects little accustomed to these recordings. This led Meyer et al.³⁹⁾ to recommend that be organized a pause sitting without speaking during at least 5 min during any HR recording at the work station.

• The minimal HR observed during work: this value can be completely occasional and influenced by errors of measurement or recording.

• The HR exceeded during 99% of the working time (HR₉₉) as suggested by Malchaire et al.^{17, 40)}, i.e. the value below which the HR is during approximately 5 min over the 8 work h. This value is less influenced by measurement errors and will generally be close to that observed on average during the rest period recommended by Meyer et al.³⁹⁾, or that recorded during the meal pauses during the day. It remains to the observer to check that possible HR increases of thermal origin are negligible or are taken into account.

• The HR exceeded during 90% of the time HR₉₀ suggested by Gaudemaris et al.³⁸⁾, i.e. below which the HR is during approximately 48 min over the 8 work h. This value will be much more influenced by the nature of work than HR₉₉.

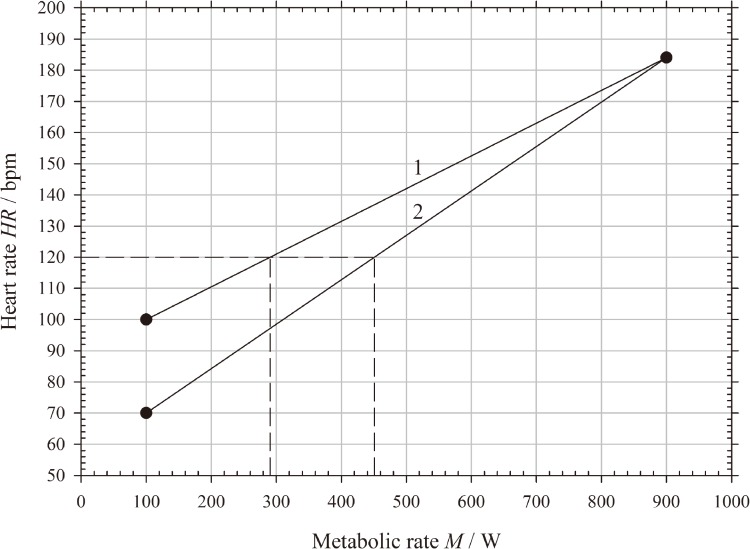
Fig. 2.

Comparison of the (M vs. HR) relationships on 2 hypothetical occasions for the same subject.

HR₉₉ thus seems the most logical choice.

This choice of HR₀ independently of the MWC poses problem when the same subject is recorded on several occasions in the interval of a few days and that the HR₉₉ are strongly different. In this case, the computed relations (M vs. HR) are different as illustrated hypothetically in Fig. 2 and the same HR_wm, for example 120 bpm, will correspond to different metabolic rates: in the example: 300 and 450 W.

This appears acceptable, a rise in HR from 70 to 120 bpm being logically due to a greater metabolic rate (450 W) than a rise from 100 to 120 bpm in the second work condition. The interpretation using the (M vs. HR) relationship derived from a cardiac stress test, as an example relation 2, would have given in both cases the same value for the metabolic rate of work, 450 W, and the increases from 70 to 120 bpm and from 100 to 120 bpm during the 2 observations would have been interpreted as due to the same metabolic rate. It should thus be concluded that the use of the HR₉₉ drawn from the recording to be analysed is preferable to any other HR₀ value.

It remains to determine at which metabolic rate this HR₉₉ has to be associated for the calculation of the (HR vs. M) relationship. If the recommendation of Meyer et al.³⁹⁾ was followed, the corresponding metabolic rate can be taken equal to the resting metabolic rate discussed previously, that is to 60 W/m² for men and 53 W/m² for women, with a standard deviation SD_M0 of 7 W/m². These values are translated into watts by multiplying by the body surface of the subject. In all other cases, it is up to the observer to appreciate the corresponding metabolic rate and its uncertainty.

Evaluation and precision of the average heart rate at work, HR_wm

As discussed in the above section, the MWC is ideally evaluated during a cardiac stress test on a bicycle or a treadmill where the efforts are purely dynamic. In industrial situations, such dynamic efforts are primarily related to displacements and alternating movements of the limbs allowing blood circulation. In most cases however, the worker has to carry out static efforts with the muscles contracted without movements: load lifting, pushing, pulling, etc. In these cases, the cardiovascular constraint is definitely higher: HR increases greater than that related to the oxygen uptake increase and increases not only in the systolic pressure, but also in the diastolic pressure. As an example, Gálvez et al.⁴¹⁾ reported HR elevations of about 20 and 38 bpm in the case of gripping efforts equal to 20% and 50% of the maximum voluntary force. In industrial situation, it is impossible to estimate this HR increase of isometric origin, considering the difficulty of quantifying these isometric efforts and the great inter-individual variability (SD = 6 bpm) under the controlled conditions of the study of Gálvez et al.⁴¹⁾. The heart rate is also raised in association of an increase in core temperature in case of thermal strain. This increase is estimated to be in average equal to 33 bpm per degree of increase of the central temperature⁴²⁾. Again, this correspondence is very variable, from 21 to 46 bpm/°C. The HR is also raised by other factors such as stress, unexpected events, fear etc. Finally it varies according to the circadian rhythm, with again major inter-individual differences⁴³⁾. The heart rate at a given time can thus be regarded as being:

$$\text{HR }={\text{ HR}}_{\text{M}}+\Theta$$ (18)

where:

• HR_M = HR₀ + ΔHR_M is the component in relation to the energy expenditure through dynamic efforts;

• Θ = ΔHR_S + ΔHR_Th + ΔHR_N + ΔHR_ε the component in relation to the other factors with:

• HR₀ = the HR at rest, under neutral thermal conditions;

• ΔHR_M = the HR increase due to the dynamic muscular load, under neutral thermal conditions;

• ΔHR_S = the HR increase due to static muscular work;

• ΔHR_Th = the HR increase associated with the increase in core temperature;

• ΔHR_N = the HR increase associated to mental effects;

• ΔHR_ε = the residual component of the instantaneous heart rate.

In practice, it is not possible to estimate the component Θ, so that it involves an over-estimation of the HR_wm and consequently of the rate of energy expenditure. This estimation is particularly difficult to do as the HR increases are not simply additive, but often multiplicative. In order to recognize this over-estimate, Malchaire et al.⁴⁰⁾ proposed to qualify the estimated metabolic rate of ‘equivalent’ M_eq, and to define it as “the metabolic rate which, during a purely dynamic test, would have been associated to the actual HR_wm value”. M_eq is thus an overestimation of the actual metabolic rate, it is a better estimate of the painfulness of the job performed⁴⁰⁾.

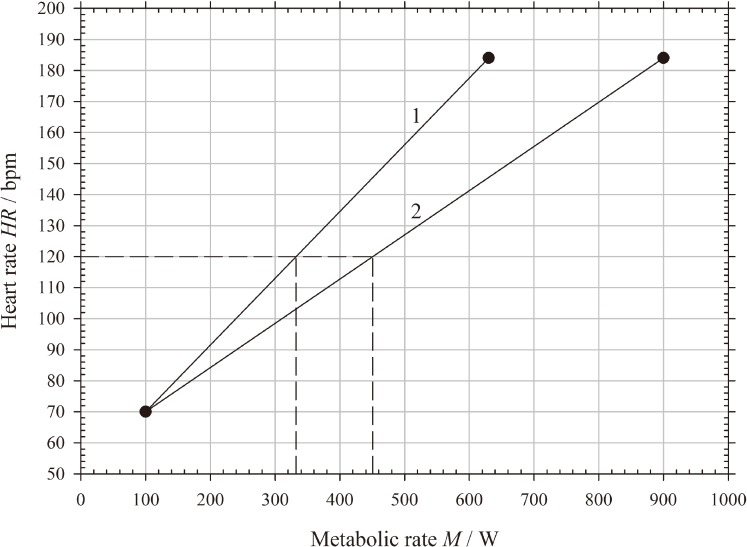
The last question relates to the relevance of the (M vs. HR) relation directly or indirectly derived from a cardiac stress test using the great muscular group of the legs, in the case of a working activity carried out with the upper limbs. Studies showed that the VO_2max during manual crank efforts was 23%⁴⁴⁾ to 30%⁴⁵⁾ lower than that measured for the same HR value during a cardiac stress test on bicycle or treadmill. So, as an example in Fig. 3, the (M vs. HR) relation derived from the cardiac stress test would be line 2 (MWC_legs = 900 W, HR_max = 182 bpm), while it could be line 1 in case of efforts done primarily with the arms (MWC_arms = 900 × 0.7 = 630 W, HR_max = 182 bpm). It results from it that, again, the equivalent metabolic rate will be an over-estimation of the real energy expenditure: a HR_wm of 120 bpm should correspond to 350 W, but will lead to M_eq = 450 W.

Fig. 3.

Example of over-estimation of the average metabolic rate at work in the hypothetical case of efforts primarily done with the arms (line 1), when using the general expression (HR–M) more valid for efforts performed with the legs (line 2).

Precision of the Estimate of the Equivalent Metabolic Rate

The Monte Carlo simulation method

As described by Mahadevan⁴⁶⁾, a Monte Carlo simulation ‘is a numerical experimentation technique to obtain statistics of the output variables of a system computational model, given the statistics of the input variables’.

First a combination of values of age A, height H_b, weight W_b, HR at rest HR₀ and average HR at work HR_wm is selected. Then the equivalent metabolic rate is computed according to the following procedure:

1. to draw at random 4 values in a Gauss normal distribution: t₁, t₂, t₃, t₄.

2. from the values of A, H_b, W_br, to evaluate the parameters MWC (in W/kg), M₀ (in W) and HR_max and their respective standard deviations SD_MWC, SD_M0, SD_HRmax.

3. to compute the random values of the 4 parameters by:

– W_br = W_b + t₁ × 2.5

– MWC_r = (MWC + t₂ × 0.125 × MWC) × W_br

– M_0r = M₀ + t₃ × SD_M0 × A_b

– HR_maxr = HR_max + t₄ × SD_HRmax

4. to compute the (M vs. HR) relation from the estimated MWC_r, M_0r, HR_maxr and HR₀.

5. to compute the equivalent metabolic rate corresponding to 4 values of mean heart rate HR_wm (90, 110, 130, 150 bpm).

This procedure was repeated for 100 values of t₁, t₂, t₃ and t₄ and the average and standard deviation of the 100 million of M_eq estimates were computed.

The procedure was repeated for 3 values of each of the primary parameters, chosen to cover the common range (except the extremes) of age (25, 40 and 55 yr), of height (160, 175 and 190 cm), of weight (60, 75 and 90 kg) and of resting HR (65, 75 and 85). The whole process resulted therefore in 324 values of metabolic rate and corresponding standard deviations.

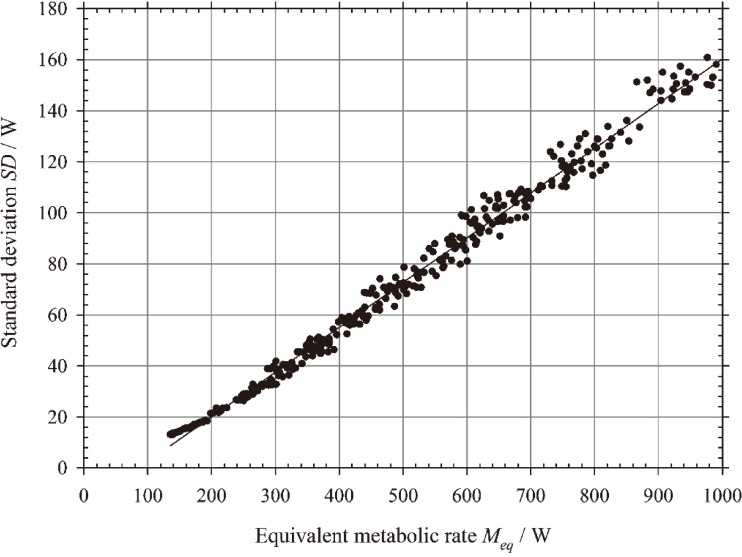
Figure 4 illustrates the relation between the standard deviation and the equivalent metabolic rate in these 324 combinations. The standard deviation varies linearly as a function of the metabolic rate according to the following expression:

$$\text{SD }=0,\text{175 }\times {\text{ M}}_{\text{eq}}–\text{ 15}.0$$ (19)

the correlation coefficient being very high and equal to 0.995. Table 3 gives the coefficients de variation of M_eq for values in the range 100 to 700 watts This result confirms the information given in the standard ISO 8996 of a precision of ± 10% for metabolic rates around 200 watts (light work) but the imprecision is greater and reaches ± 15% for high M_eq values. That means however that for subject of MWC = 1,000 W, the confidence interval (C.I.) at 95% of a M_eq is rather considerable: thus

Fig. 4.

Standard deviations of the equivalent metabolic rate as a function of this M_eq obtained through Monte Carlo simulations in 216 combinations of age, weight, height, resting heart rate and average heart rate at work.

Table 3. Coefficient of variation of the equivalent metabolic rate for values in the range 100 to 700 watts.

Meq (W)	100	200	300	400	500	600	700
SD (W)	3	20	38	55	73	90	108
CV (%)	2.5%	10.0%	12.5%	13.8%	14.5%	15.0%	15.4%

• for M_eq = 250 W:  C.I. = [195 ; 305]

• for M_eq = 500 W:  C.I. = [355 ; 645]

Revised Procedure for the Estimation of the Average Metabolic Rate from A Recording of the Heart Rate at A Work Station

The results of the study make it possible to modify the procedure of analysis of the recordings of HR at a work station described in ISO 8996.

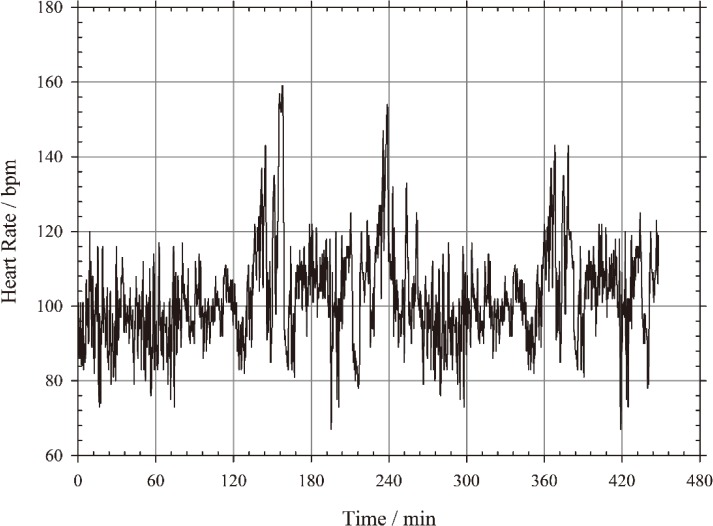
The modified procedure will be illustrated using the HR recording during one day’s work (8 h) in the summer season for a male subject 34 years old, 81 kg and 170 cm, working in a brickyard⁸⁾ (Fig. 5). HR was recorded during 448 min and it can be assumed that this sample is representative of a normal work day of 480 min. The average heart rate during the 7 h 28 min of observation was equal to HR_wm = 102 bpm. The work involved some static work: its effect is impossible to estimate and the concept of ‘equivalent’ metabolic rate is in this case particularly justified. On the contrary, the HR recording did not show any overall trend of elevation of HR and therefore the thermal effect can be neglected.

Fig. 5.

Profile of HR recorded for a male subject in the summer season at a work station in a brickyard.

The subject never smoked and did not play any sport. His wrist breadth was 7 cm, which classifies him in the ‘broad’ morphological group.

His body mass index is: BMI = W_b / H_b² = 28.0 kg/m² and his ‘ideal’ weight is estimated using Creff’s formula equal to: 1.1× 0.9 × (H_b + A / 10 − 100) = 72.7 kg. The subject appears to be a little overweight so his ‘ideal’ weight will be used for the evaluation of his maximum work capacity.

It is the possible to estimate successively:

• the MWC: MWC = (19.45 − 0.133 × A) × W_b = 1,085 W

• The maximum heart rate: HR_max = 208 − 0.7 × A = 184 bpm

• The body surface: A_b = 0.007184 × W^0.425 × H_b ^0.725 = 2.06 m²

• The resting metabolic rate: M₀ = 60 × A_b = 124 W

And, as the HR exceeded during 99% of time was equal to 76 bpm.

• The slope of the (M vs. HR) relation: a = (MWC − M₀) / (HR_max − HR₉₉) = 8.92

• The intersection: b = M₀ − HR₉₉ × a = − 620

• The equivalent metabolic rate: M_eq = a × HR_wm + b = 352 W

• The precision of this estimate: SD = 0.175 × M_eq − 15.0 = 47 W

Discussion

The first uncertainty in the evaluation of the work load in a work situation comes from the representativeness of the period of time during which the observation is made. The representativeness of a day shift might be illusory as, in some work situations, the tasks are varying from one d to another depending, as examples, on the nature of the work, the number of workers and the fluctuations in production. When the observed period of observation is poorly representative of the overall exposure, the conclusions are simply questionable from the start.

If the observation period was representative in the example given above, M_eq=350 watts must be considered as the best estimate of the metabolic rate in the observed work situation, not only for the worker, but also for his colleagues and it should therefore be concluded that the average workload is ‘heavy’ in absolute according to the classification adopted at stage 1, Screening, of ISO 8996 Standard and for the WBGT index^{7, 47)}. For the observed subject with a MWC of 1,085 watts, it is indeed heavy in relative terms (32% of MWC) and marginally compatible with an 8-h work period in continuous. For another subject with a MWC of 800 watts, this M_eq would represent a ‘very heavy’ work (47.5% of the MWC) and be unacceptable at short term. In order to be sure at 95% to protect the exposed workers, the metabolic rate to consider should not be this mean value but the mean plus 2 standard deviations, that is, in the present case, 450 watts. With this assumption, the working conditions should be considered to be unacceptable for both workers and likely for all.

It must be finally stressed how complex is the estimation of the energy requirement at a work station, how difficult it is to identify a representative observation period, how numerous are the assumptions to be made concerning the choice of the observed worker, the resting metabolic rate and heart rate, as well as the body weight to take into account, how important can be the influence of the isometric efforts, the mental load, even the stress caused by the observation. The confidence interval of the final result, M_eq, might therefore be much greater than ± 2 standard deviations and be simply so large that the evaluation is not only meaningless but unfortunately totally misleading, if the interpretation is not based on observations on several people and in several occasions: the modern equipment for recording heart rate makes this easy and affordable.

All the estimations illustrated in the section above can easily be done with a simple computer program, or with an app for smartphones or tablets. Such a program or app can however be easily misused and it is hope that it will only be used by trained people mastering completely the complexity of the evaluation and observing scrupulously the recommendations.

ISO 8996 describes at level 2, Observation, a time and motion study where the observer must determine as a function of time the sequence of activities, assign a metabolic rate value to each of these activities and compute the time weighted average of these metabolic values. With this method, the errors come from: 1) a lack of representativeness of the observation period (usually shorter than when recording the heart rate); 2) the accuracy of the time study and the validity of the definition of the activities and of the corresponding metabolic rate values; 3) the accuracy of these metabolic values themselves. ISO 8996 proposes to estimate these metabolic rates as a function of the work intensity and the body segments with which it is performed. Our experience with students has shown very large differences between observers in the recognition of the work intensities (defined in subjective terms) and the body segments involved. The ISO standard claims that this method is presenting a high error risk and a precision of ± 20%. A very large study comparing the evaluation by a large number of observers (of different backgrounds) in several varied work stations would be necessary to verify this precision. This has apparently never been done and it is reasonable to think that the uncertainty of the estimates is much greater than when using the heart rate methods as discussed above.

Conclusions

The present study was aimed at re-examining the bases of the methodology presented in the International Standard ISO 8996 for the evaluation of the metabolic rate at work from a continuous recording of the heart rate during a representative period of time and to check the assertion of a precision of 10% for this evaluation. The study made it possible to select a set of formulas allowing to estimate the maximum working capacity, the resting metabolic rate, the heart rates of rest and maximum, and to quantify their reliability. The methodology of analysis of a HR recording at a work station and estimation of the metabolic rate has been modified and it is intended to revise the formulas of the ISO 8996 standard accordingly. Using a Monte Carlo simulation, it was possible to verify that the standard deviation of the equivalent metabolic rate evaluated by this modified method is of the order of magnitude of 10% to 14% as announced in the standard. Although this uncertainty is quite large, it can reasonably be considered that this method provides more reliable results than other methods that can be use in practice in the field, provided that it is carried out by people mastering the complexity of the underlying physiological concepts.

Symbols

A	Age	yr
a	Slope of a linear relationship	W/(kg·yr)
Ab	Body surface area	m2
b	Intercept of a linear relationship	W/kg
BMI	Body mass index	kg/m2
CV	Coefficient of variation	–
Hb	Height of the subject	cm
HR0	Heart rate at rest	bpm
HR90	HR value exceeded during 90% of the duration of the HR recording	bpm
HR99	HR value exceeded during 99% of the duration of the HR recording	bpm
HRM	HR value in case of purely dynamic efforts	bpm
HRmax	Maximum heart rate	bpm
HRwm	Average heart rate at work during the observation period	bpm
M0	Metabolic rate at rest	W or W/m2
Mb or BMR	Basal metabolic rate	W or W/m2
Meq	Equivalent metabolic rate	W
MWC	Maximum working capacity	W
R	Correlation coefficient	–
RMR	Resting metabolic rate	W or W/m2
SD	Standard deviation	–
SDHRmax	Standard deviation of HRmax	bpm
SDMo	Standard deviation of M0	W or W/m2
SDMWC	Standard deviation of MWC	W or W/m2
SDWb	Standard deviation of Wb	kg
t1, t2, t3, t4	Radom values in a Gauss normal distribution
VO2max	Maximum oxygen consumption	l/min
Wb	Body mass	kg
Wbid	Ideal body mass	kg
Wbid,m	Ideal body mass of men	kg
Wbid,w	Ideal body mass of women	kg
ΔHRM	HR increase due to the dynamic muscular load, under neutral thermal conditions	bpm
ΔHRN	HR increase associated to mental effects	bpm
ΔHRS	HR increase due to static muscular work	bpm
ΔHRTh	HR increase associated with the increase in core temperature	bpm
ΔHRε	residual component of the instantaneous heart rate	bpm
Θ	Sum of the components of heart rate other than from dynamic muscular load	bpm