Rad4 Recognition-at-a-distance: Physical basis of conformation-specific anomalous diffusion of DNA repair proteins

Abstract

Since Robert Brown’s first observations of random walks by pollen particles suspended in solution, the concept of diffusion has been subject to countless theoretical and experimental studies in diverse fields from finance and social sciences, to physics and biology. Diffusive transport of macromolecules in cells is intimately linked to essential cellular functions including nutrient uptake, signal transduction, gene expression, as well as DNA replication and repair. Advancement in experimental techniques has allowed precise measurements of these diffusion processes. Mathematical and physical descriptions and computer simulations have been applied to model complicated biological systems in which anomalous diffusion, in addition to simple Brownian motion, was observed. The purpose of this review is to provide an overview of the major physical models of anomalous diffusion and corresponding experimental evidence on the target search problem faced by DNA-binding proteins, with an emphasis on DNA repair proteins and the role of anomalous diffusion in DNA target recognition.

Diffusive transport lies at the heart of a broad array of cellular processes. A specific topic of interest is how proteins perform diffusion, either one- or three-dimensional, in search of their targets in DNA. Such targets may be a particular DNA sequence in the case of a transcription factor, or a damaged base in the case of a DNA repair enzyme. We preface these discussions by briefly introducing the diffusive process with a historical perspective. To exemplify the target search process, we consider the case of the DNA repair heterodimer Rad4-Rad23, the yeast homolog of human XPC-HR23B that is involved in the initial damage recognition step in nucleotide excision repair, which performs anomalous diffusion on DNA containing UV-induced photoproducts. This is followed by an overview of several well-established physical models and corresponding experimental observations of anomalous diffusion, particularly subdiffusion. We then focus our attention specifically on the diffusive search problem for DNA-binding proteins with cognate target sequences. Finally, we close by discussing working models for one-dimensional apparent anomalous diffusion by proteins in target search on DNA and the broader implications for biological functions.

1. Introduction to Diffusion

1.1 Brownian Motion

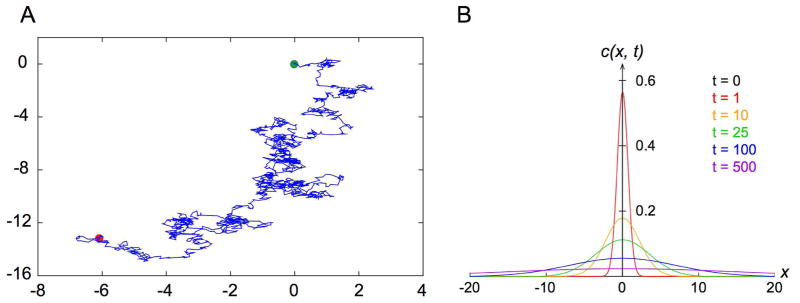
When observing pollen particles from the plant Clarkia pulchella, suspended in solution, through his single lens microscope in June of 1827, Scottish botanist Robert Brown noted their peculiar random jiggling motion (Brown, 1828). He went on to discover the same property of microscopic particles suspended in liquids in other pollen grains, powders of fossil wood, window glass, minerals, rocks, and even a fragment of the Sphinx (Brown, 1828). In a follow up publication, Brown reiterated that such perplexing motion was exhibited by “extremely minute particles of solid matter, whether obtained from organic or inorganic substances, when suspended in pure water, or in some other aqueous fluids,” and that it did not arise from currents in the fluid or as a result of evaporation (Brown, 1829). The random walk of microscopic particles in suspension has since been termed Brownian motion (Figure 1A) in honor of Robert Brown.

Figure 1. Random Walk and Diffusion.

A. Simulated two-dimensional Brownian motion. Green and red dots indicate the start and end of the trajectory, respectively.

B. Plot of the time evolution of the solution c(x, t) Eq. (4) to a one-dimensional Fickian diffusion that starts as a point source at the origin.

1.2 Fickian Diffusion

The first quantitative phenomenological description of macroscopic diffusion was developed by physiologist Adolf Fick in 1855, based on the idea of macroscopic concentrations and fluxes (Fick, 1855). Inspired by Fourier’s law of heat conduction and Ohm’s work on electric conductivity, Fick’s first law proposes that the one-dimensional flux is inversely proportional to the concentration gradient: (1)

$$j=-D\frac{\partial c}{\partial x}$$

where j is the flux in the units of number per unit area per unit time, c the concentration of particles in the units of number per unit volume, x in the units of length, and D the diffusion coefficient in the units of length²/time. By invoking conservation of mass in combination with Fick’s first law and the assumption that the diffusion coefficient D is a constant, we arrive at the law of diffusion in one dimension, or Fick’s second law: (2)

$$\frac{\partial c}{\partial t}=D\frac{{\partial }^{2}c}{{\partial }^{2}x}$$

Consider the case c(x, t) where there the initial concentration at t = 0 is a spike at x = 0, or (3)

$$c(x,0)=N\delta (x)$$

where δ(x) is the Dirac delta function (Phillips et al., 2009). The solution to Fick’s second law then takes the form (4)

$$c(x,t)=\frac{N}{\sqrt{4\pi Dt}}{e}^{-x^2/4Dt}$$

i.e. a zero-mean Gaussian distribution that broadens over time (Figure 1B). For a single particle, it can be shown that (5)

$$\langle x^2(t)\rangle =2Dt$$

This familiar result reflects the well-known linear relationship between time and the mean squared displacement (MSD) of a particle performing a one-dimensional random walk. This should not come as a surprise because the solution c(x, t) is the probability distribution that characterizes the Wiener process, which in turn is the continuum limit of a one-dimensional random walk.

1.3 Einstein’s Theory of Brownian Motion

In 1905, Albert Einstein took a more microscopic approach to the theory of diffusion (Einstein, 1905; Einstein, 1956). Focusing on the behavior of each independent diffusing particle suspended in a liquid, he arrived at the diffusion equation $\frac{\partial f}{\partial t}=D\frac{{\partial }^{2}f}{{\partial }^{2}x}$, its solution for the case of diffusion of n particles from a point source $f(x,t)=\frac{n}{\sqrt{4\pi Dt}}{e}^{-x^2/4Dt}$, as well as the linear dependence of the so-called mean squared displacement (MSD) on time 〈x²(t)〉 = 2Dt. These expressions are indeed equivalent to those from Fick’s second law.

Another important finding presented in the same paper applied to the relation between the diffusion coefficient and other measurable physical quantities in diffusion. By considering a dynamic equilibrium where spherical particles were suspended in liquid and undergoing diffusion as a result of a force acting on them, Einstein derived the well-known Stokes-Einstein relation (6)

$$D=\frac{k_{B}T}{6\pi \eta R}$$

where η is the viscosity of the fluid and R is the radius of the diffusing particle (Einstein, 1956). Its general form, D = μk_BT, where μ is the mobility of the particle, is also called the Einstein-Smoluchowski relation, as independently derived by Marian Smoluchowski in 1906 (von Smoluchowski, 1906).

A more general approach to describe the motion of a Brownian particle of mass m is through the Langevin equation (7)

$$m\frac{d^{2}x(t)}{d{t}^2}=-\gamma \frac{dx(t)}{dt}+\xi (t)$$

where x(t) is the stochastic position of the particle, γ is the friction coefficient (the Stoke drag), and the stochastic term ξ(t) represents a random fluctuating force on the particle (Langevin, 1908). Such ξ(t) has a Gaussian distribution with (8)

$$\langle \xi (t)\rangle =0,\langle \xi (t)\xi (t^{\prime })\rangle =g\delta (t-t^{\prime })$$

It can be shown that ξ(t)dt = dW(t), where dW(t) is a Weiner process by definition. At equilibrium, applying the equipartition theorem yields (9)

$$g=2\gamma k_{B}T$$

and (10)

$$\langle {(x(t)-x_0)}^2\rangle =\frac{2k_{B}T}{\gamma }t=2Dt$$

the Stokes-Einstein relation can be recovered (11)

$$D=\frac{k_{B}T}{\gamma }=\frac{k_{B}T}{6\pi \eta R}$$

Coincidentally, in the same year that Einstein published his paper on the theory of diffusion, the term “random walk” was first used in a letter to Nature titled “The problem of the random walk,” by British statistician Karl Pearson (Pearson, 1905). Pearson was originally interested in the spread of mosquito infestation and framed the problem as a man carrying out a random walk (Figure 1A).

2. Diffusion of a DNA Repair Protein

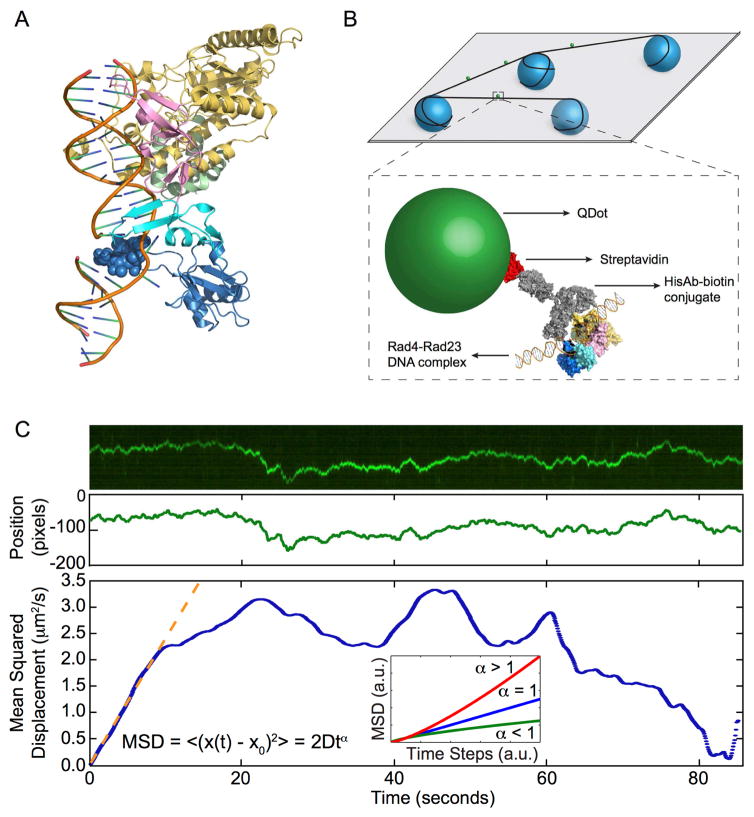
Geared with the basic understanding of diffusion, we shall now illustrate the complexity that could arise in a biological system for the case of diffusive target search by a protein on DNA, where simple diffusion alone does not adequately describe the observed behavior. In a recently published study, we characterized the diffusive behavior of quantum dot-labeled Rad4-Rad23 (the yeast homolog of human XPC-HR23B, Figure 2A), the damage sensor in yeast nucleotide excision repair (NER), using the single-molecule DNA tightrope assay (Kong et al., 2016). It was shown that Rad4-Rad23 utilizes the facilitated diffusion mechanism (See Section 4 for in-depth discussion on the topic) to search for lesions in DNA. More importantly, in addition to one-dimensional random diffusion, we observed and systematically investigated apparent deviations from the simple diffusive behavior by Rad4-Rad23 on DNA, which we termed constrained motion (also called anomalous subdiffusion, see below).

Figure 2. Experimental Set-up and Data Analysis.

A. Co-crystal structure of Rad4-Rad23 bound to DNA containing a CPD-mismatch (PDB ID: 2QSG). Rad23 (green), the transglutaminase homology domain (yellow), β-hairpin domain 1 (pink), β-hairpin domain 2 (cyan), β-hairpin domain 3 (blue). A Rad4 mutant with the entire β-hairpin domain 3 deleted was found to bind specifically to Fl-dT lesions and bend the DNA by approximately 37°. The space-filled seven amino acid tip of β-hairpin domain 3 (blue) was found to be dispensable for specific binding, removal of UV-induced photoproducts and UV survival.

B. Top: Schematics of flow cell and protein conjugation strategy. 5 μm diameter poly-L-lysine coated silica beads (blue) are randomly deposited on a polyethylene glycol treated coverslip (gray). Bottom: DNA (black) is suspended across beads by hydrodynamic flow. His-tagged Rad4-Rad23 (yellow, pink, cyan, and blue) is labeled with streptavidin (red)-coated quantum dot (green) through a His antibody (His-Ab)-biotin conjugate (gray). Adapted from Kong et al., (2016) Mol Cell, 64, 376 – 387 with permission.

C. Top: Representative kymograph of a diffusing particle. Middle: Plot of position, in the units of pixels (1 pixel = 46 nm), versus time, after fitting the light intensity profile at each time point in the kymograph with a one-dimensional Gaussian. Bottom: Plot of mean squared displacement, calculated from Gaussian fitted positions, versus time steps. Orange dashed line is the result of fitting the initial portion of the MSD curve to the equation MSD = 2Dt^α. Inset: three types of 1D diffusion characterized by different α values: superdiffusion (red), random diffusion (blue), and subdiffusion (green).

The evolutionarily conserved NER pathway is responsible for the recognition and repair of bulky and helix-distorting or destabilizing lesions in DNA. As the damage sensor in the yeast NER pathway, Rad4-Rad23 recognizes substrates that include UV-induced 6,4-photoproducts, cisplatin, and fluorescein-modified deoxythymidine (Fl-dT). In this recent study, we sought to elucidate the damage search and recognition mechanism of Rad4-Rad23. Using the previously established single-molecule DNA tightrope technique (Kad et al., 2010), we suspended lesion-containing DNA molecules across 5 μm-diameter poly-L-lysine-coated silica beads that were randomly distributed on a coverslip treated with mPEG-succinimidyl valerate MW-5000. For visualization, Histidine-tagged Rad4-Rad23 was labeled with 655 nm streptavidin-coated quantum dots through a biotin-conjugated anti-His antibody linkage (Figure 2B). Quantum dots were excited with a 488 nm laser at an oblique angle and their emission was collected at ~10 frames per second. Kymographs of one-dimensional diffusion of Rad4-Rad23 on DNA were extracted from each recorded image series. By fitting the intensity profile from kymographs to Gaussians, accurate particle positions were determined with resolutions well beyond the diffraction limit (Figure 2C). The positional accuracy and localization precision of the system are approximately 6 nm and 10 nm, respectively (Ghodke et al., 2014). Time-averaged MSD was calculated from the time series data and fitted to the general expression (12)

$$\mathit{MSD}=\langle x^2(t)\rangle =2D{t}^{\alpha }$$

where α is the anomalous diffusion coefficient (Banks and Fradin, 2005; Bouchaud and Georges, 1990; Havlin and Ben-Avraham, 2002; Saxton and Jacobson, 1997). Compared to Eq. (5) from Fick’s or Einstein’s theory on simple diffusion, in which case α = 1; diffusion is said to be anomalous when α ≠ 1. Slower subdiffusive processes are characterized by α < 1, while α > 1 implies faster super diffusion (Figure 2C inset).

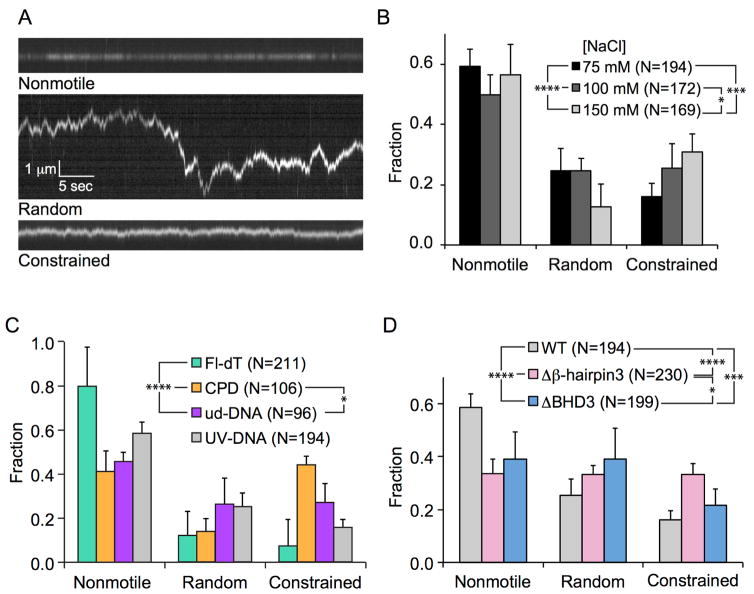
Watching fields of molecules for five minute periods, we observed non-motile Rad4-Rad23, as well as Rad4-Rad23 particles undergoing one-dimensional random diffusion and constrained motion (i.e. apparent subdiffusive motion, 0 < α < 1), on DNA (Figure 3A). This oscillatory motion was between 500 – 1000 bp in either direction around an apparent mid-point. Several aspects of the system were found to influence the extent of subdiffusion. On 20 J/m² UV-irradiated λ-DNA, increased ionic strengths led to more pronounced subdiffusion of wild-type (WT) Rad4-Rad23 (Figure 3B). Using engineered DNA tightropes containing site-specific lesions at regular intervals, we demonstrated that WT Rad4-Rad23 was more prone to constrained motion around cyclobutane pyrimidine dimers (CPDs) that have been biochemically characterized as weakly- or non-interacting (Figure 3C) (Guzder et al., 1998). In order to better understand the structure and function relationship between the putative damage sensing motif (β-hairpin 3) of Rad4 and damage recognition, we constructed differentially truncated variants of Rad4 and found that the Δβ-hairpin3 tip mutant (Δ599–605) lacking the 7 residues at the tip of the β-hairpin 3 (Figure 2A, blue spheres) exhibited the highest amount of subdiffusive motion (Figure 3D). In addition, we also showed that yeast cells expressing the Δβ-hairpin3 tip mutant displayed the same level of UV resistance and removed both UV-induced CPDs and 6–4 photoproducts at the same speed as WT cells.

Figure 3. Subdiffusion of Rad4-Rad23 on DNA.

A. Representative kymographs depicting non-motile (top), random diffusion (middle), and constrained motion (bottom) particles. Scale bars in the middle panel apply to all three kymographs.

B. Distributions of motion types of WT Rad4-Rad23 on UV-irradiated λ-DNA at different salt concentrations. All bar graph data are represented as weighted means ± weighted SDs over four to five independent experimental days (levels of statistical significance *:p ≤ 0.05, **:p ≤ 0.01, ***:p ≤ 0.001, and ****:p ≤ 0.0001).

C. Lesion-dependent distributions of motion types of WT Rad4-Rad23 on DNA damage arrays (Fl-dT, green; CPD, orange; undamaged DNA, purple; UV-irradiated λ-DNA, gray).

D. Distributions of motion types of Rad4 WT and mutants on UV-irradiated λ-DNA (Δβ-hairpin3: Δ599–605, ΔBHD3: Δ541–632).

Adapted from Kong et al., (2016) Mol Cell, 64, 376 – 387 with permission.

Before concluding that this constrained motion was linked to a pattern of anomalous diffusion, we first had to rule out three alternative scenarios that could also explain the observed behavior. High frequency drift due to system noise was considered first and easily ruled out by observing that particles showing subdiffusive behavior were observed alongside other randomly diffusing or non-motile particles bound to the same DNA tightrope. Additionally, the extent of subdiffusion changed in response to either different substrates or protein constructs, indicating that those factors acting as the sole variable between sets of experiments were the cause of change in constrained motion. Systematic noise coming from the microscope stage or intrinsic to the assay platform would have caused global changes in diffusive behavior regardless of other variables. Secondly, it had been noted that apparent anomalous subdiffusion could arise from errors in determining particle positions in single particle tracking experiments (Martin et al., 2002). However, given the error in the tightrope platform combined with measured diffusion coefficients, our measurement times (~1000 s) and lengths of traces used in the fitting process (~10 –100 s) were at least an order of magnitude larger than the characteristic time (~0.1 – 1 s), at which point, according to the arguments raised by Martin et al., the measured anomalous diffusion exponent α_ap approaches within 90% of true α. Finally, we considered the possibility of highly subdiffusive behavior due to the energetic constraint imposed by protein-induced super-helical torsional stress in DNA. We envisioned a DNA unwinding model similar to that of RNA polymerase, which, as it translocates during transcription, generates positive supercoiled waves in front of itself and negative super-helical stress behind (Liu and Wang, 1987). By analogy, we envisioned that β-hairpin 3 of Rad4, which is melted into the DNA in the co-crystal structure (Figure 2A, blue spheres) (Chen et al., 2015; Min and Pavletich, 2007), could remain engaged with DNA during diffusion and cause positive supercoils to build up ahead of the protein in the direction of motion and thus impede further movement. However, our calculations revealed that such a mechanism would only allow Rad4-Rad23 to travel about 50 – 100 bp in either direction with the thermal energy (k_BT) at room temperature, an order of magnitude smaller than observed (500 – 1000 bp) and below our criterion for a particle being considered motile (motion of three pixels, or ~500 bp at 46 nm/pixel).

What then is causing this constrained motion of Rad4-Rad23 around photoproducts in DNA? The answer lies within a thorough understanding of factors that contribute to anomalous diffusion. In the next section we explore the theoretical aspects and physical contributions to anomalous diffusion and give some examples of such behavior in biological systems.

3. Theoretical and Physical Constructs of Anomalous Diffusion

Having described the basic formalism of diffusion, we are now equipped to introduce some of the underlying mechanisms including the mathematical and physical descriptions that contribute to anomalous diffusion. While anomalous diffusion encompasses both subdiffusive and superdiffusive motion, here we focus exclusively on subdiffusion. The following is only a brief explanation and for a much more thorough discussion on anomalous diffusion; interested readers are directed to an excellent recent review of this topic (Metzler et al., 2014).

3.1 Continuous-Time Random Walks

Originally introduced as a stochastic transport model (Montroll and Weiss, 1965) and used to describe motion of charge carriers in amorphous materials (Scher and Montroll, 1975), the continuous-time random walk (CTRW) model can be considered a generalization of regular Brownian motion. Consider the simplest form of a one-dimensional random walk: a particle makes a jump of step size l, to either the left or the right, after a waiting time t. The CTRW generalization of this description requires both step size and waiting time to be random variables, drawn from separate probability distributions. After each step, a new pair of values for l and t are generated from those same distributions, but independent of the values from the previous step. Naturally, when both distributions are well behaved, i.e. finite variance of step lengths and mean waiting times, CTRW describes a simple random walk. However, if we assume a power-law form distribution of waiting times, (13)

$$\psi (t)\propto t^{-1-\alpha }$$

such that for 0 < α < 1, the characteristic waiting time 〈t〉 diverges and the subdiffusive ensemble-averaged MSD takes the form of 〈x²(Δ)〉 ~ Δ^α, where Δ is the lag time (Metzler and Klafter, 2004). Furthermore, the lack of a finite characteristic waiting time also leads to what is known as weak ergodicity breaking among physicists. In the case of diffusion, a process is considered ergodic if the ensemble average of MSD 〈x²(Δ)〉 and time-averaged $\text{MSD}\overline{{\delta }^2(\mathrm{\Delta })}$ are equivalent in the limit of long measurement times, the latter of which is normally derived from time series collected in biophysical single molecule or single particle tracking experiments. For CTRW specifically (Barkai et al., 2012; He et al., 2008; Lubelski et al., 2008), (14)

$$\langle \overline{{\delta }^2(\mathrm{\Delta })}\rangle ~\frac{\mathrm{\Delta }}{t^{1-\alpha }}$$

The dependence of time-averaged $\text{MSD}\langle \overline{{\delta }^2(\mathrm{\Delta })}\rangle$ on measurement time t leads to the observation of aging in the system, such that the time-averaged MSD is smaller if it is measured on a particle that has spent more time undergoing the diffusion process.

Physically, the power-law form of waiting time distribution that results in subdiffusion under the CTRW regime could come from energy traps with exponentially distributed energy wells and their Arrhenius-type escape times (Metzler et al., 2014). CTRW is an attractive model for subdiffusion in biological systems due to the multitude of intermolecular interactions between macromolecules present in the cell that naturally gives rises to energetic traps. Experimentally, CTRW has been shown to accurately model the non-ergodic component of Kv2.1 potassium channels diffusion in two-dimensional plasma membrane, which is caused by transient binding of the potassium channels to the actin cytoskeleton (Weigel et al., 2011). Other experimental evidence lending support to the CTRW model in vivo include observation of subdiffusion of RNA molecules in E. coli (Golding and Cox, 2006), and that of short time behavior of endogenous lipid granules in living fission yeast cells (Jeon et al., 2011).

3.2 Fractional Brownian Motion and Fractional Langevin Equation

Another major stochastic model of anomalous diffusion is called fractional Brownian motion (FBM), described by Mandelbrot and van Ness (Mandelbrot and Van Ness, 1968). FBM is driven by a stationary, fractional Gaussian noise (FGN) with zero mean. Recall that normal diffusion is generated by uncorrelated white noise ξ(t) in Eq. (8); the FGN is time-difference correlated and the correlation takes on a power-law form (15)

$$\langle {\xi }_{\mathit{FGN}}(t)\rangle =0,\langle {\xi }_{\mathit{FGN}}(t){\xi }_{\mathit{FGN}}(t^{\prime })\rangle =\alpha (\alpha -1)K_{\alpha }^{\ast }{\mid t-t^{\prime }\mid }^{\alpha -2}$$

When FGN is anti-correlated (0 < α < 1), FBM describes subdiffusion.

Based on the generalized Langevin equation (Chandler, 1987), and introducing an FGN, as defined in FBM, leads to the fractional Langevin equation (FLE) (Kou and Xie, 2004; Lutz, 2001). Contrary to FBM, FLE with correlated FGN (1 < α <2) leads to FBM-like subdiffusion only in its long time limit (Jeon and Metzler, 2010). Further, in contrast to the characteristic weak ergodicity breaking of CTRW, both FBM and motion governed by FLE have been shown to be ergodic, (i.e., the time averaged MSD converges slowly to the ensemble average), and take on the form of ~t^α with 0 < α < 1 (Deng and Barkai, 2009).

A well-studied FBM/FLE-governed biological system of anomalous diffusion can be found in the subdiffusion of particles in viscoelastic environments, such as the cytoplasm and nucleoplasm of cells, due to effects of molecular crowding (Guigas et al., 2007; Weiss et al., 2004). Evidence from experiments, as well as simulations of particle subdiffusion in artificially crowded solutions, shows that such a process is most consistent with FBM (Ernst et al., 2012; Szymanski and Weiss, 2009; Weiss, 2013). FBM or FLE-governed motion have also been suggested as models for the observed subdiffusion of fluorescently labeled mRNA molecules (Magdziarz et al., 2009), and chromosomal loci in bacterial cells (Weber et al., 2010), and transient subdiffusion of telomeres in U2OS nuclei (Bronstein et al., 2009; Kepten et al., 2011).

3.3 Obstructed Diffusion

Consider a two-dimensional surface (e.g. a biological membrane), randomly decorated with immobile objects (e.g. anchored proteins) that pose obstacles to free diffusion of particles. This is an intuitive example of obstructed diffusion (OD), one of the simplest models of anomalous diffusion. As obstacle concentration increases, the available space for free diffusion decreases and subdiffusion rises. Mathematical modeling of OD is deeply rooted in percolation theory and diffusion in fractal space (Ben-Avraham and Havlin, 2000). Readers are referred to a recent review for more in-depth discussions on the subject (Hofling and Franosch, 2013). At lower obstacle concentrations, subdiffusion is transient before crossing over to normal diffusion. Monte Carlo simulations show that as the obstacle concentration approaches criticality (i.e. the percolation threshold), both crossover time and distance increase, becoming more relevant for observation in biological systems (Saxton, 1994). Therefore, experimental observation of obstructed diffusion would appear anomalous over shorter time periods and normal over longer time periods. Like FBM, OD is also ergodic and stationary (Hofling and Franosch, 2013). Simulations of FBM- and OD-based models agreed favorably with experimentally observed molecular crowding-dependent processive phosphorylation of MAP kinase (Aoki et al., 2011; Hellmann et al., 2012).

3.4 Other Models

Finally, subdiffusion can be modeled by assuming a diffusivity that is either time- or position-dependent, namely the scaled Brownian motion (SBM) (Jeon et al., 2014; Saxton, 2001) and the heterogeneous diffusion process (HDP) (Cherstvy et al., 2013; Cherstvy and Metzler, 2014), respectively. Experimental evidence of the HDP in mammalian cell lines has been established using fluorescence recovery after photobleaching (FRAP) to study freely-diffusing enhanced yellow fluorescent proteins (Kuhn et al., 2011). More recently, patch models have been suggested as a family of HDP to explain CTRW-like non-ergodic subdiffusion that results from heterogeneous diffusivity rather than transient trapping (Massignan et al., 2014). Simulations based on the patch model reproduced the observed non-ergodic subdiffusion of receptor on a live cell membrane, where the receptor motion could also be correlated to its structure (Manzo et al., 2015).

3.5 Subordination

Thus far we have only discussed anomalous diffusion governed solely by a single specific model. However, due to the complexity of biological systems, it is possible that observed behavior is not adequately modeled by any single process. Sometimes, different models are applicable at different time scales. For example, even though endogenous lipid granules in living fission yeast cells undergo short time CTRW subdiffusion, their motion is better described by FBM at longer time scales (Jeon et al., 2011). Other cases require different processes to be combined to form subordination schemes (Blumen et al., 1984; Klafter et al., 1984). Intracellular transport of fluorescently labeled insulin granules was found to be accurately modeled by FBM subordinated to a CTRW (Tabei et al., 2013). Similarly, subordinating the ergodic diffusion on a fractal to a non-ergodic CTRW (Meroz et al., 2010) has been proven appropriate in modeling subdiffusion of Kv2.1 potassium channels in the plasma membrane (Weigel et al., 2011). These subordinated schemes are likely essential in describing biological systems which are inherently complex and heterogeneous. Future investigations are needed for better understanding of which and to what extent underlying biological processes contribute to distinct mechanisms of subdiffusion.

4. The Target Search Problem: Solving the Speed-Stability Paradox

Having discussed some general principles of anomalous diffusion, let us turn to one-dimensional diffusion of proteins on DNA. A question that has inspired biophysics research for the past half century is: how do limited copies of a sequence-specific DNA binding protein (e.g. the lac repressor, LacI, at ~10 molecules/cell) (Kalisky et al., 2007) efficiently locate its target that is buried in a sea of nonspecific sequence (~4.6x10⁶ bp/cell) (Blattner et al., 1997)? The answer appears to be a phenomenon called facilitated diffusion, as described below.

4.1 Facilitated Diffusion

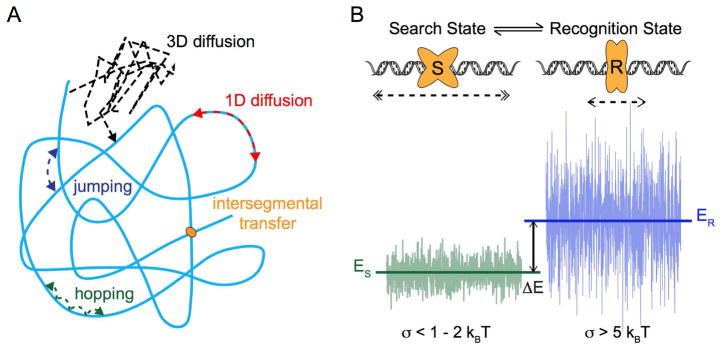
The nature of diffusive transport of DNA binding proteins in the context of target search has been of intense interest for decades and has extensive implications in many different facets of essential cellular processes, ranging from DNA replication and gene regulation to maintenance of genome stability (Kad et al., 2010; Lee et al., 2014a; Redding and Greene, 2013; Tafvizi et al., 2011b). The importance of search dimensionality was first pointed out by Adam and Delbruck, who suggested that the search process can be accelerated by collapsing a three-dimensional search into a one-dimensional search along the DNA (Adam and Delbrück, 1968). The theory was corroborated by the experimental observation that the association rate of the lac repressor to its target is two orders of magnitude faster than three-dimensional diffusion-based predictions according to its size and the viscosity of the media it travels through (Riggs et al., 1970). The concept of facilitated diffusion was subsequently proposed and experimentally studied by von Hippel and colleagues, among others (Berg et al., 1981; von Hippel and Berg, 1989; Winter et al., 1981). In addition to three-dimensional diffusion in solution and one-dimensional sliding on DNA, the facilitated diffusion model also includes microscopic hopping of proteins on DNA, as well as direct intersegmental transfer of a protein between two DNA molecules (Figure 4A).

Figure 4. Target Search on DNA.

A. Schematic of facilitated diffusion. Optimal search strategies combine different modes of protein-DNA interactions, including: 3D diffusion (black), 1D diffusion (red), jumping (blue), hopping (green), and intersegmental transfer. In the case of intersegmental transfer, the protein (orange) binds to two DNA molecules at the same time, releases from the one where it is initially bound, and transfers to the other molecule.

B. Schematic of the two-state model. Protein (orange) is able to switch between two conformational states, S (search) and R (recognition). In S state, protein slides fast (double arrow heads) on DNA with a smooth energy landscape. In R state, protein slides slowly (single arrow heads) over a more rugged energy landscape. The equilibrium constant for transitions between states S and R depends on the energy difference ΔE between mean energies of the two states, E_S and E_R. See text (Section 4.2) for details and references.

Based on the frame work of facilitated diffusion, combining three-dimensional diffusion in solution and one-dimensional sliding on DNA, initial kinetic (Halford and Marko, 2004; Slutsky and Mirny, 2004) and stochastic models (Coppey et al., 2004) were established to address the optimal search strategy. As this field evolved, more recent studies combined other search modes, including hopping, jumping, and intersegmental transfer, with the effects of DNA conformation in their analyses (Eliazar et al., 2007; Foffano et al., 2012; Hu et al., 2006; Lomholt et al., 2005; Lomholt et al., 2009; Loverdo et al., 2009). The effects of macromolecular crowding on facilitated diffusion, as it relates to more physiological conditions in living cells, have also been recently examined (Elf et al., 2007; Li et al., 2009). The latest experimental (Cravens et al., 2015) and theoretical studies (Brackley et al., 2013; Krepel et al., 2016; Liu and Luo, 2014) have shown that crowding environments can lead to altered balance between three-dimensional and one-dimensional diffusion processes, promoting one-dimensional sliding. While the presence of mobile or immobile obstacles on DNA has been shown to effectively slow down one-dimensional sliding (Brackley et al., 2013; Gomez and Klumpp, 2016; Li et al., 2009), this effect could be overcome by hopping on DNA. Even though emphasis in such studies is usually placed on the interplay between three-dimensional and one-dimensional search strategies, with three-dimensional diffusion being modeled as strictly Brownian, the potential for subdiffusion in crowded environments has nonetheless been noted in the context of facilitated diffusion (Bauer and Metzler, 2013; Meroz et al., 2009).

Since the pioneering work by Riggs and coworkers (Riggs et al., 1970), facilitated diffusion has been experimentally observed, both in vitro and in vivo, for a wide host of DNA-binding proteins. A short list of such proteins includes restriction enzymes (Bonnet et al., 2008; Gowers et al., 2005), human transcription factor p53 (Tafvizi et al., 2008), DNA repair proteins (Blainey et al., 2006; Gorman et al., 2012; Kad et al., 2010), and transcriptional repressors such as LacI (Elf et al., 2007; Hammar et al., 2012; Normanno et al., 2015; Ruusala and Crothers, 1992).

4.2 Speed-Stability Paradox

While developing an optimization for target search, Slutsky and Mirny quantitatively formulated the speed-stability paradox of protein-DNA recognition (Slutsky and Mirny, 2004). In brief, it was shown that rapid sliding of proteins on DNA with a sequence-dependent Gaussian-distributed energy landscape is only possible when the landscape is relatively smooth (σ < 1 − 2 k_BT); however, conditions for stable binding necessitate a large variance in energy distribution (σ > 5 k_BT), i.e. a rugged landscape (Mirny et al., 2009). The authors proposed a two-state model as a solution to the paradox (Figure 4B). The idea of a model based on protein conformational changes was first presented by von Hippel and colleagues (Winter et al., 1981). In summary, the protein, or protein-DNA complex in general, adopts two conformations: the recognition (R) state with a rugged energy landscape to allow stable binding and the search (S) state with a fairly smooth landscape to facilitate fast sliding. Such a model was supported by the experimental observation of structural flexibilities in dimeric lac repressor binding to specific and nonspecific DNA (Kalodimos et al., 2004). Quantitatively similar results were also obtained by Hu and Shklovskii through a different approach investigating the effect of energy profile disorder on the enhancement of search rates (Hu and Shklovskii, 2006). More refined and generalized interpretations of the two-state model have also since been discussed (Bauer and Metzler, 2012; Bénichou et al., 2009; Hu et al., 2008; Reingruber and Holcman, 2011; Yu et al., 2013).

The two-state model was elegantly applied in single-molecule studies of p53 searching for DNA binding sites, where it was shown that the C-terminus of the protein allows rapid sliding with a shallow energy surface, while the DNA binding domain interrogates the major groove for specific DNA sequences within a steep energy surface (Leith et al., 2012; Tafvizi et al., 2011a). Fitting the observed diffusion constants to a two-state model indicated that p53 would need to switch between conformations at a minimum rate of 10³/s (Tafvizi et al., 2011a). Other examples that lend support to this model include proteins involved in mismatch repair (Gorman et al., 2007; Gorman et al., 2012) as well as transcription activator-like proteins (Cuculis et al., 2015).

4.3 One-Dimensional (Sub)Diffusion of Protein on DNA

Having described the two-state model as a generally accepted solution to the speed-stability paradox in target search, we now turn to the details of one-dimensional diffusive behavior of a protein on DNA without obstacles. A simple and intuitive way to capture base-sequence-dependent protein-DNA interactions was derived and used to model nonspecific one-dimensional sliding on DNA by Barbi et al. (Barbi et al., 2004a; Barbi et al., 2004b). A model was constructed based on the idea that a sequence-specific protein “reads” the underlying sequence from the DNA major groove while sliding and that recognition is achieved by formation of a specific set of hydrogen bonds between the protein amino acids and the target sequence bases. This approach also assumes that the protein attempts to make the same set of hydrogen bonds on nonspecific sequences as it does at target sites. Protein-DNA interaction at position n was expressed as a 4 × m matrix (D_n), with m being the size of the recognition sequence. The recognition matrix (R) can also be constructed, based on known protein-DNA contacts from structural data, as an m × 4 matrix. The interaction energy landscape at base n, with the implicit assumption that energy contributions from hydrogen bonds are additive, is thus defined as (16)

$$E(n)\propto tr(R·D_n)$$

A case study of T7 RNA polymerase promoter search on T7 DNA with different translocation mechanisms, including one variant of the two-state model, was conducted through simulations. Diffusion was found to be anomalous and subdiffusive for short times and asymptotically approached normal (Barbi et al., 2004b). Furthermore, it was shown that this formulation with energy contributions from discrete hydrogen bonding events could be generalized, which led to Gaussian-distributed interaction energies (σ ~ 2.5 k_BT)and also gave rise to quantitatively similar one-dimensional diffusive behavior as before (Barbi et al., 2004a). Similar transient anomalous subdiffusion due to trapping effects was obtained through another set of Monte Carlo simulations, where diffusion on DNA was modeled as a random walk on a one-dimensional lattice with different models for traps (Saxton, 2007). In such a system, an infinite hierarchy of traps is believed to lead to subdiffusion through a CTRW mechanism. Nonetheless, it was shown that in the generalized case of finite binding site hierarchy, where the target site was represented by the deepest trap, random energy model with a continuous Gaussian distribution (σ = 1.5 k_BT) recapitulated the transient nature of subdiffusion and its crossover to normal diffusive behavior (Saxton, 2007).

At its roots, the speed-stability paradox and its solution are connected to the fact that the one-dimensional diffusive behavior of a protein on DNA is affected by a random potential landscape (Slutsky and Mirny, 2004). For a one-dimensional diffusing particle in a random potential with Gaussian-distributed amplitudes, its diffusion coefficient is proportional to e^−σ2, where σ² denotes the variance of the Gaussian distribution (Zwanzig, 1988), as discussed earlier in the section. The use of a random Gaussian-distributed potential as a continuum approximation of the nonspecific sequence-dependent interaction between a DNA binding protein (e.g. a transcription factor) and the DNA sequence being scanned can be justified by the overall heterogeneity in nucleotide sequence for sufficiently long regions (Lässig, 2007). Inspired by the experimental evidence that binding of the Cro repressor induced bending at both specific and nonspecific sites (Erie et al., 1994), Mirny and colleagues sought to improve the random energy landscape in modeling of one-dimensional diffusion. They argued that there exists a finite-range correlation, whose length scale is on the order of the size of the protein binding domain (Slutsky et al., 2004). It was shown that diffusion in a correlated potential is slower than in an uncorrelated potential, and that the mean first passage time (MFPT) fluctuates more in a correlated potential. When the length scale of diffusion is less than the characteristic distance (N_c), where by definition there is no self-averaging, subdiffusive as well as superdiffusive behavior can occur. Simulations of random walks suggested that as a result of the correlated random potential, proteins could preferentially localize in certain areas of the genome. Diffusion on a correlated random potential was recently revisited by Goychuk and Kharchenko (Goychuk and Kharchenko, 2014). They reasoned that the interaction energies between each base in contact with the protein are additive and that spatial correlation arises because when the protein slides by one base on DNA, the same set of bases remains in contact with the protein, except for the one farthest away from the direction of the movement. Starting with the Langevin equation and the assumption for an exponentially decaying short-range correlation, Goychuk and Kharchenko first showed that such correlation has no effect on the scaling of the diffusion coefficient and that the corresponding diffusion is ergodic in the macroscopic scale. An equation for the mesoscopic subdiffusion was then derived to estimate the physical length scale at which subdiffusion would be expected due to correlations in potential energy. Subdiffusion was shown to be readily macroscopic for a Gaussian potential energy disorder σ ~ 4 – 5 k_BT. Surprisingly, target site location via such subdiffusion was also shown to proceed faster than expected.

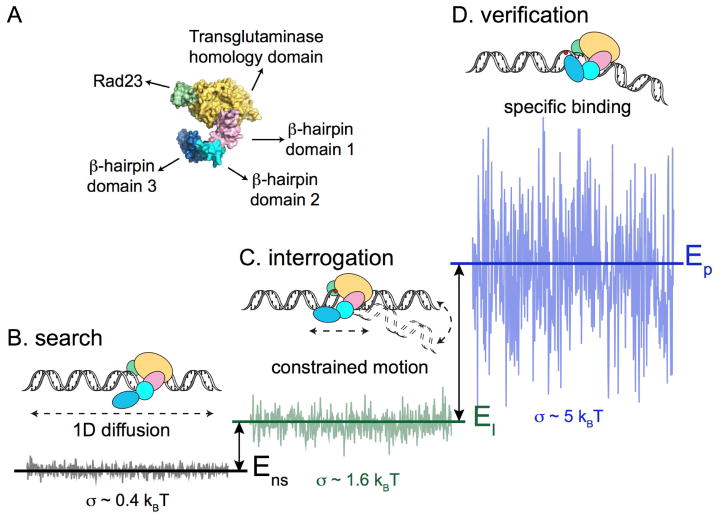
5. Conformation-Driven Constrained Motion of Rad4-Rad23

As discussed above, sequence-specific DNA binding proteins, such as transcription factors and restriction enzymes, have been at the center of many studies on the theoretical modeling of target search. However, parallels can be drawn to proteins that recognize other features of DNA. Such is the case for a wide range of DNA damage sensing proteins. In addition to DNA binding proteins like TRF1 (Lin et al., 2014) and the stromal antigen subunit (SA) SA1 (Lin et al., 2016), DNA repair proteins such as DNA glycosylases (Dunn et al., 2011), UV-damaged DNA-binding proteins (UVDDB) (Ghodke et al., 2014), and endonuclease UvrC from bacterial NER (Hughes et al., 2013) have all been observed to exhibit subdiffusion to some extent. Although not explicitly tested, transient subdiffusion may also be a property of the eukaryotic mismatch repair complex Msh2-Msh6 (Gorman et al., 2007) and restriction enzyme EcoRI (Lee et al., 2014b).

Based on our recent findings on target search by Rad4-Rad23, we propose that one-dimensional constrained motion of proteins on DNA may result from diffusion in a potential energy landscape due to extended protein-DNA interactions and may be a functional form of target recognition in vivo. Notably, factors that affect the extent of observed constrained motion include ionic strength of the solution, type of lesion in DNA, and the presence of β-hairpin 3 of Rad4. Increased constrained motion as a result of the loss of the residues located at the tip of β-hairpin 3 appeared to exhibit a compensatory effect as the protein remained biologically functional in vivo; neither UV resistance nor photoproduct repair was compromised in yeast expressing this mutant. Metzler and colleagues suggested that three-dimensional subdiffusion of transcription factors helps to keep them in the vicinity of their targeted binding sites in DNA and may be beneficial to gene regulation in vivo (Lomholt et al., 2007). We proposed constrained motion by a protein around its target site as a mechanism for “recognition-at-a-distance.” Rad4’s ability to participate in productive NER while undergoing such constrained motion can be thought of as a first responder to arrive at the scene of an accident, namely the ability to direct other emergency personnel around the scene without being physically stationed there at all times. Similar to the Cro repressor, we found, using atomic force microscopy, that Rad4-Rad23 bends DNA to ~42° at both specific and non-specific sites. Applying our estimated roughness of diffusional energy landscape and footprint of Rad4 on DNA based on the co-crystal structure to the one-dimensional subdiffusion as modeled in Section 4.3 (Goychuk and Kharchenko, 2014; Slutsky et al., 2004), subdiffusion may be expected to emerge on the length scale of ~400 – 800 bp, roughly consistent with the observed range of constrained motion (~500 – 1000 bp). Furthermore, we consider the extent of such subdiffusive behavior to be linked to the specific conformation that the protein adopts while interacting with DNA. The strength of correlation in the protein-DNA interaction potential may be influenced by the structural motif(s) that are probing the underlying sequence and the structural integrity of the sequence itself. Most importantly, this one-dimensional subdiffusion, driven by the specific conformation adopted by the protein-DNA complex in general, may represent one intermediate in a generalized two-state model (Figure 5). In the case of Rad4, the protein interacts with UV-irradiated DNA and was observed to form: 1) molecules that show random linear motion with a low barrier of diffusion of ~0.4 k_BT and an anomalous diffusion exponent α ~ 1 (Figure 5B); 2) molecules showing constrained motion with a barrier to free diffusion on DNA of about ~1.6 k_BT and an anomalous diffusion exponent α < 0.8 (Figure 5C); and finally, 3) non-motile complexes that we believe represent stable specific binding complexes (Figure 5D). Since a mutant of Rad4 lacking the entire β-hairpin domain 3 was able to bind specifically to sites of damage and bend the DNA at sites of damage by ~37°, β-hairpin domains 1 and 2 of Rad 4 must make large contact with DNA, and are capable by themselves of transiently bending the DNA (Figure 5C). Presumably this is mediated by the β-hairpin of domain 2. This protein-induced bend would help to increase the energy landscape of the DNA (green) and favor DNA opening, producing a sufficiently steep landscape that can induce constrained motion with an anomalous diffusion exponent α < 1. In this manner, engagement of additional structural motifs on the target recognition path, which goes from freely diffusing on DNA to stably bound recognition complex, could constitute as different intermediates that correspond to increasing levels of ruggedness in the diffusional energy landscape. Thus the correlated potential energy profile from protein-induced DNA bending gives rise to the observed constrained motion. In fact, molecular dynamics simulations and measurements of the free-energy path of Rad4-Rad23 interaction with a mismatched CPD indicated that Rad4’s interaction proceeds via an induced fit model, rather than a structural capture model (Mu et al., 2015). This idea is also consistent with the notion that UVDDB interacts with damaged DNA using a conformational proofreading mechanism (Ghodke et al., 2014).

Figure 5. Conformation-Driven Constrained Motion of Rad4-Rad23.

A. Model for conformation-driven constrained motion of Rad4-Rad23. Domains of Rad4 are as colored and labeled.

B. Rad4-Rad23 diffuses randomly on DNA where non-specific protein-DNA interactions contribute to the smooth energy landscape (σ ~ 0.4 k_BT).

C. Interrogation of DNA through interactions with β-hairpin domains 1 and 2, that most likely includes transient DNA bending, coupled with correlations in potential energy along the DNA due to the presence of lesions, lead to increased ruggedness in the energy landscape (σ ~1.6 k_BT). This constrained motion and subdiffusive behavior emerges on the scale of 500 – 1000 bp, and may represent ‘recognition-at-a-distance.’

D. Specific damage verification and binding is achieved through β-hairpin 3 insertion, which results in a much rougher energy landscape (σ > 5 k_BT). The insertion step occurs spontaneously at highly helix-distorting lesions, or is facilitated when Rad4 is slowed down while undergoing constrained motion near the damage site.

Adapted from Kong et al., (2016) Mol Cell, 64, 376 – 387 with permission.

Despite the wealth of experimental data on anomalous subdiffusion in diverse biological systems, the underlying physical mechanism of such behavior has yet to be fully elucidated. In particular, subdiffusive motion exhibited by proteins while sliding on DNA during target search has not been examined as closely compared to various models of three-dimensional subdiffusion, theoretically or experimentally. Better modeling of the physical basis of such behavior could contribute to greater characterization and understanding of biological systems involving sequence- or structure-specific DNA binding proteins, as well as more precise tuning of known protein-DNA interactions in engineered systems. Advances in imaging techniques and computing technology, single-molecule/single-cell experiments, and simulations based on atomic details of proteins and base-sequence of DNA could provide key insights into solving the puzzle.

Abbreviations

CTRW

Continuous-Time Random Walk

FBM

Fractional Brownian Motion

FGN

Fractional Gaussian Noise

FLE

Fractional Langevin Equation

SBM

Scaled Brownian Motion

HDP

Heterogeneous Diffusion Process

NER

Nucleotide Excision Repair

CPD

Cyclobutane Pyrimidine Dimer

UVDDB

UV-Damaged DNA Binding Protein