SEGMENTATION OF MYOCARDIUM USING DEFORMABLE REGIONS AND GRAPH CUTS

Abstract

Deformable models and graph cuts are two standard image segmentation techniques. Combining some of their benefits, we introduce a new segmentation system for (semi-) automatic delineation of epicardium and endocardium of Left Ventricle of the heart in Magnetic Resonance Images (MRI). Specifically, a temporal information among consecutive phases is exploited via a coupling between deformable models and graph cuts which provides automated accurate cues for graph cuts and also good initialization scheme for deformable model that ultimately leads to more accurate and smooth segmentation results with lower interaction costs than using only graph cut segmentation. In addition, we define deformable model as a region defined by two nested contours and segment epicardium and endocardium in an unified way by optimizing single energy functional. This approach provides inherent coherency among the two contours thus leads to more accurate results than deforming separate contours for each target. We show promising results on the challenging problems of left ventricle segmentation.

1. INTRODUCTION

Cardiovascular disease is now the largest cause of death in the world and most cardiac pathologies involve the left ventricle (LV). Physicians use magnetic resonance imaging (MRI) to for the evaluation of left ventricular functions of the heart. Segmentation of the left ventricle would help the estimation of cardiac functional parameters such as ejection fraction and myocardial mass. The main challenges in LV segmentation are: the overlap of intensity distributions within the cardiac regions; the presence of papillary muscles in the blood pool which causes to partial volume effect between blood pool and myocardium; low intensity contrast between the myocardium and the liver; blur effect observed in the apex slices; and the variation in the thickness of myocardium across the beating cycle. In recent years, significant number of methods have been proposed towards LV segmentation. The methods using graph cuts [1], deformable models [2, 3], morphological operations [4], and shortest path algorithms [5] are some of them. Each of these techniques are state-of-the-art but each have different drawbacks due to high variation in the challenges of segmentation.

In classical graph cut segmentation techniques, consecutive interaction process is required [6, 7, 8, 9] for efficient and accurate segmentation in complex images. With the interaction process, image pixels a priori known to be a part of the object or background have to be introduced as topological constraints. In complex images (i.e myocardium of heart), the amount of time needed for this pixel-accurate work makes image segmentation a particularly frustrating task for users. Thus in a fast and low interaction cost system, the challenge is precise automated initial labeling in order to avoid further interactions. In addition to that, the problem of delineating the boundaries of objects in medical images requires smooth, continues working space. For example, in [10], the graph cuts are interpreted as hyper surfaces or contours in N-D manifolds in discrete image domains; however the problem of finding a smooth boundary separating the regions through the min cut of the graph is not trivial. [10], tries to solve this problem by using ”fine” locally connected grids and it requires increasing the resolution of the connectivity system of the graph from 4, 8 to 256 and even higher resolutions. The result is an approximation and moreover, the computation time is increased since the number of edges in the graph is increased.

In contrast to graph cuts, deformable models [11] solve the segmentation problem in continuous domain using gradient descent optimization. This solves the continuity and smoothness problem indicated above, but in general requires good initialization. Use of global priors such as shape and position learned from training is very common and well known to help gradient descent optimization when good initialization is not provided, but highly nonlinear variation in these features makes the prior based optimization nontrivial. [12] is one of the detailed studies about this topic.

In this work we propose a comprehensive approach by combining several techniques: Graph Cuts, Free Form Deformable regions and image morphology with anatomical properties. We use free form deformable regions and graph cuts as coupled techniques in temporal domain to enhance the segmentation of the myocardium. Such coupling makes it possible to use deformable models for fast segmentation of sequence of images without the need of training; and graph cuts towards automated segmentation without need of iterative interaction. We demonstrate that it is possible to apply combinatorial optimization techniques in combination with variational approaches for segmentation of cardiac MRI using the model of the LV. The following sections describe individual steps of the algorithm in more detail.

2. SEGMENTATION FRAMEWORK USING GRAPH CUT AND DEFORMABLE REGION

We segment Left Ventricle of heart in 2D + time images in a cardiac cycle. Segmentation is started from an initial (end systol) phase of the cardiac cycle and propagated to other phases automatically. Graph cuts and deformable models are energy based object segmentation techniques and are formulated as the optimization of an energy functional of the form:

$$E=\mu E_i+E_b$$ (1)

Typically, E_i represents data term and E_b represents smoothness term. Deformable models optimize the cost function using variational approaches based on gradient descent while graph cuts use combinatorial optimization in finite dimensional space. The target is a continuous contour for a deformable model method or minimum cost cut (subset of weighted edges) of a graph for graph cut method. We use graph cuts for two tasks; 1) segmentation of blood pool region, and 2) rough segmentation of myocardium that is used as initialization for the deformable model method. Deformable models are used for two tasks as well: 1) enhancement of the myocardium segmentation result obtained by graph cuts, 2) providing temporal constraints towards automated pixel labeling for myocardium segmentation that is executed by graph cuts method through consecutive beating hearth images.

2.1. Segmentation of Blood Pool Region via Graph Cuts

Graph cuts require a graph 𝒢 = 〈 𝒱, ℰ 〉 to be constructed with set of nodes 𝒱 and edges ℰ. 𝒱 corresponds to image pixels plus two additional nodes 𝒮 and 𝒯, while ℰ corresponds to union of undirected edges connecting neighboring nodes (image pixels) and undirected edges connecting the two special nodes (𝒮 and 𝒯) to other nodes [6, 9]. Our method starts from end systol (t₀) phase when Blood Pool (bp) is smallest during whole beat cycle. For only (t₀) phase, a quick and easy manual interaction is needed (i.e. paint brushing a few pixels inside and outside of the blood pool region) to initialize background ℬ and object 𝒪 pixels. Edges from 𝒮 to 𝒪^t₀ and from 𝒯 to ℬ^t₀ are created. All edges from these two terminals are referred to as t-links. Under a standard 8-neighborhood system 𝒩, image pixels 𝒱 − {𝒮, 𝒯} are also connected by weighted edges that are called n-links. See Fig. 1(a) for an example initialization. Given the initial seeds ℬ^t₀ and 𝒪^t₀ with image pixels $I_p^{t_0}$, t-links and n-links are constructed and the bp^₀ is extracted via min-cut algorithm that minimizes the cost function.

Fig. 1.

(a) User given ℬ^t₀ and 𝒪^t₀ cues at t₀, (b) a set of bp^t segmentation for t = {−2, −1, 0, 1, 2, 3, 4}. Note here that due to lack of space, t does reflect only the ordering of the actual index number of beat cycle.

$$E=\sum _{e_{ij}\in t-\mathit{links}}{w}_{ij}+\sum _{e_{pq}\in \mathcal{N};p\ne q}{w}_{pq}$$ (2)

which is the homologous functional of Eq. 1. Here w_i,j denote edge cost and they are initialized as follows: w_{i∈𝒪,j=𝒮} and w_{i∈ℬ,j=𝒯} are assigned with a large enough constant ¹ while w_{i∈𝒪,j=𝒯} and w_{i∈ℬ,j=𝒮} are zero. For n-links, a simple intensity gradient such as w_p,q = e^{(−|I_p−I_p|2/σ)} × dist(p, q)⁻¹ is assigned. Here I_p and I_q are intensities at pixels p and q and dist(p, q) is the Euclidean distance. We refer the reader to previous works [6, 9] for more details about the basics of interactive graph cut segmentation. Since, the center of bp^t is guaranteed to be inside the bp^t±1 of the next phase towards end diastol, the centroid of bp^t is propagated with no interaction and used for min-cut segmentations of bt ^t±1 via independently constructed graphs. Fig. 1(b) shows an example set of bp^t segmentation for t = {−2, −1, 0, 1, 2, 3, 4}.

2.2. Rough Segmentation of Myocardium via Graph Cuts

After bp^t is extracted for all cycle, myocardium is assigned as the target object while the blood pool is pushed into the background. The myocardium is segmented fully automatically via graph cuts in the same fashion as described in section 2.1. The ℬ^t₀ and ${\mathcal{O}}_{\mathit{Myo}}^{t_0}$ are initialized with use of morphological operations as follows:

1. bp^t₀ ⊕ se(k^t₀) : Dilate convex hull of blood pool with a disk shaped structuring element of size k^{t₀ 2}.

2. bp^t₀ ⊕ se(k^t₀ − 1): Dilate convex hull of blood pool with a disk shaped structuring element of size k^t₀ − 1

3. Band^t₀ = bp^t₀ ⊕ se(n) : Initialize a band region overlaid on the myocardium with extent n³. (see Fig. 2(a) unmasked gray scale region).

4. ${\mathcal{O}}_{\mathit{Myo}}^{t_0}\equiv [b{p}^{t_0}\oplus se(k^{t_0})]-[b{p}^{t_0}\oplus se(k^{t_0}-1)]$: The object cues are assigned as remainder mask (see Fig. 2(a) red pixels).

5. ℬ^t₀ ≡ The background cues are assigned as the outside of Band^t₀. (see Fig. 2(a) blue pixels).

Fig. 2.

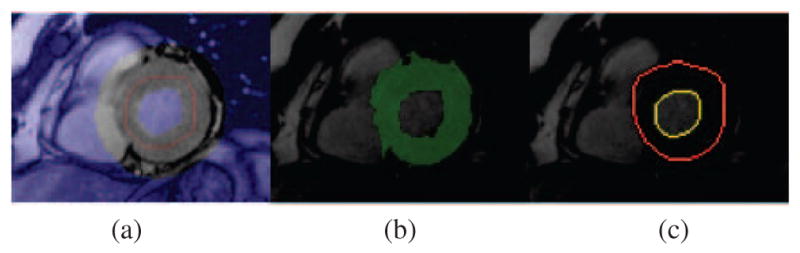
(a) Initialization of myocardium segmentation at t₀, (b) myocardium segmentation via graph cut based on initialization in (a), (c) result obtained after deformable region segmentation that is initialized by (b).

Note here that, Band^t₀ is the free pixels region that are going to be assigned {0, 1} values after graph cut segmentation. Details of the computation / update scheme of Band^t and se(k^t) will be explained in section 2.4. The free pixels in the band region are cut out according to the min-cut of a graph that is constructed with ${\mathcal{O}}_{\mathit{Myo}}^{t_0}$ and ℬ^t₀. An example illustration of resulting rough myocardium segmentation is shown in Fig. 2(b).

2.3. Enhancing Graph Cut Segmentation via Deformable Region

In our framework we follow [11], and the evolving model shape is embedded implicitly as the zero level set of a higher dimensional space of Euclidean distance transform function Φ_ℳ. The deformation of the model is done via space warping technique the Free Form Deformations (FFD) [13]. The main idea in FFD is to deform an object by manipulating a regular control lattice overlaid on its volumetric embedding space based on the computed forces. The rough segmentation of myocardium, obtained via graph cuts, is used as initialization of a FFD region and FFD region is run for a couple of iterations until convergence, under the forces provided by maximum likelihood (ML) intensity E_i data term as in [11]. The E_i data term constrains the model to deform toward areas where the pixel probabilities of belonging to the model interior intensity distribution are high and is formalized by maximizing the log-likelihood of a pixel.

$$E_i=\frac{1}{V}\int \int logP(I\mid {\mathrm{\Phi }}_{ℳ})ds$$ (3)

Here, P(.|.) is computed using Gaussian kernel and Φ_ℳ is the implicit representation of the model as zero level of a higher dimensional distance function. We refer the reader [11] for more details. Different from [11], we define the shape of the deformable model as a donut-shape like chamber and deform the inner and outer contours with a single cost function optimization. This makes the segmentation of endocardium (endo) and epicardium (epi) of heart possible to be done in a unified way, which saves computation time and provides inherent smoothness constraint between them since the control points of FFD are common for both of the contours. Note here that, the smoothness constraint between the contours comes implicitly, since FFD guarantees C¹ continuity at control points and C² continuity everywhere else [13]. Endocardium and epicardium of the heart are computed from this deformation region. Since graph cut result is a very good initialization, FFD region snaps to the true region of the myocardium quickly. In Fig. 2(c), one can see an illustration of myocardium segmentation that is obtained using deformable regions.

2.4. Myocardium Segmentation in Whole Cardiac Cycle Using Temporal Coupling of Graph Cut and Deformable Region

In this section, we explain how Band ^t and se(k^t) are computed automatically when prior segmentation of myocardium is available (for all but the first phase). For a phase t ≠ 0, before computing ${\mathcal{O}}_{\mathit{Myo}}^t$ and ℬ^t pixels, Band and k parameters are updated as follows:

$$k^t=\{\begin{array}{ll}(1-\alpha )·\mathit{minDist}+\alpha ·\mathit{maxDist}\hfill & \text{if}\mathit{avgDist}<k^{t-1},\hfill \\ k^{t-1}\hfill & \text{otherwise}\hfill \end{array}$$

Here, minDist, maxDist and avgDist are minimum, maximum and average perpendicular distances between the points on the bp^t boundary and epi^t−1 contour at phase t − 1. α is a constant weighting parameter.

The extent of Band^t is computed using epi^t−1 (deformable region result) from the prior segmentation and bp^t (graph cut result) from the current phase.

$$\mathit{Band}{(n)}^t=\left\{{\mathrm{\Phi }}_{\mathit{epi}}^{t-1}\ge -3\cap {\mathrm{\Phi }}_{bp}^t\ge 0\right\}$$

Note here Φ is the distance map of a given contour with positive values inside and negative values outside. According to above update scheme the graph cut method tries to increase the goodness of the initialization for the deformable region while deformable region method tries to put better topological (hard) constraints on the graph cut optimization when propagating temporal information from prior segmentations to next phases. Fig. 3 shows the merit of using the temporal coupling between two approaches on a phase t which is closer to end diastol. In the figure, first row left image represents a myocardium initialization (red pixels) based on bp^t only by morphological operations and the right image shows the final result based on it. The second row demonstrate initialization (red pixels) using epi^t−1 (yellow) from prior segmentation and the bp^t from current phase as described in this section. The right image is the corresponding final segmentation.

Fig. 3.

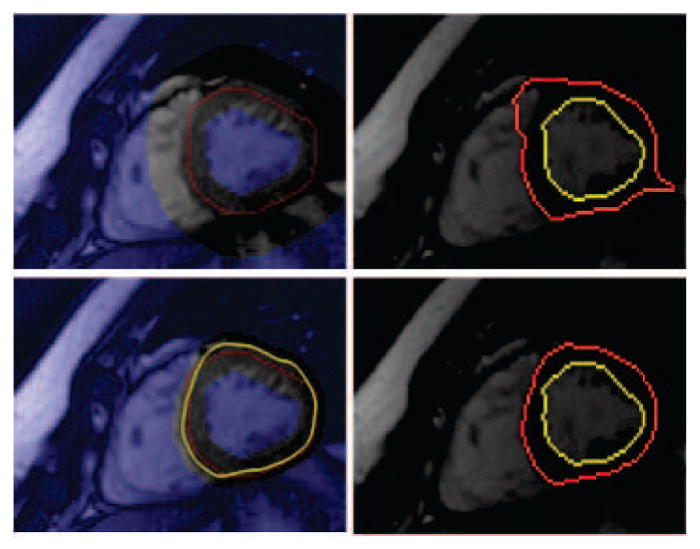
Shows the effect of using temporal constraint. In the first row no prior information is used when initializing the ${\mathcal{O}}_{\mathit{Myo}}^t$ and ℬ^t (left image); whereas on the second row prior epi^t−1 result (yellow) is used. Images in second column show corresponding segmentation results for the initializations. See text.

3. EXPERIMENTS AND RESULTS

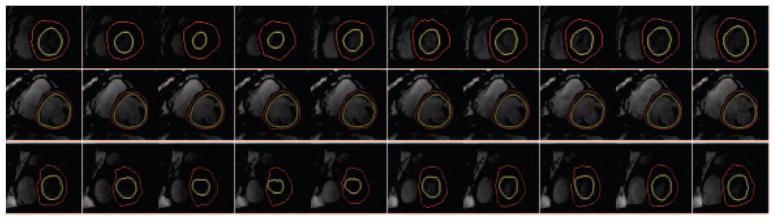
We test our method on public data from MICCAI 2009 Left Ventricle Grand Challenge [14]. As stated in [14], cine steady state free precession (SSFP) MR short axis (SAX) images were obtained with a 1.5T GE Signa MRI. All the images were obtained with a temporal resolution of 20 cardiac phases over the heart cycle, and scanned from the ED phase. They provide ground truth for epicardium and endocardium at end diastol and the endocardium at end systol phase following the convention of including papillary muscles and endocardial trabeculations in the ventricular cavity. Although we segment all phases of cardiac cycle in a given slice we evaluate our results quantitatively only for available ground truths. Our segmentation contours were compared to the ground truth using the evaluation method provided in [14]. We report Dice measure and average perpendicular distance which measures the distance from the automatically segmented contour to the corresponding manually drawn expert contour, averaged over all contour points. The obtained error rates are shown in Table 1. Our proposed method meets the performance of top ranked methods in [14], regarding the average perpendicular distance error of 2.98 ±0.88mm/1.78 ±0.35mm for the endocardium/epicardium, respectively. Besides average scores, we also show performance of our method in specific cases such as ’SC-HYP-07’ and ’SC-HF-I-05’ which have been reported in [5, 2, 4] as difficult cases to segment. Again, the evaluation confirms the stability and reliability of our method. Visual illustrations are also shown in Fig. 4 for entire cardiac cycle of three different cases. First row shows the result on normal (healthy) data while the other two rows shows the epicardium and endocardium results for cases with Ischemic Heart Failure and Hypertrophy, respectively. The speed of the system was measured on core duo laptop (1.83 GHz with 2Gb of RAM) using Matlab environment. Segmentation takes 45 seconds after a quick interaction on the initial phase of a data set of 20 images.

Table 1.

Scores obtained by evaluation method in c.f [14] for the 15 subjects from the validation data sets of the Left Ventricle 2009 Challenge, as well as for 2 difficult to segment data sets ’SC-HYP-07’ and ’SC-HF-I-05’.

Mean/Std	Dice		Dist (mm)
	Endo	Epi	Endo	Epi
’SC-HF-I-05’	0.91	0.92	1.81	1.62
’SC-HYP-07’	0.80	0.91	2.85	1.76
Overall 15 subjects	0.82 ± 0.06	0.91 ± 0.03	2.98 ± 0.88	1.78 ± 0.35

Fig. 4.

Qualitative results for entire cardiac cycle. 1^st row: normal case; 2^nd row: Ischemic Heart Failure case; 3^rd row: Hypertrophy case.

4. CONCLUSIONS AND FUTURE WORKS

We have presented a system to (semi-) automatically segment the left ventricle in cardiac cine MR images. The system takes advantages of using a hybrid method using graph cuts and deformable models such that graph cuts allow quick and easy interaction to create good initializations for deformable models. On the other side, deformable models help making automated cue labeling for graph cuts which creates a chain cycle propagated from initial image to others via temporal information among consecutive phases. We have tested our method on 15 subjects from Miccai Left Ventricle Segmentation Challenge 2009 validation database and reported state-of-the-art results. We have couple of ideas that could next research directions. On deformable models side, segmenting all phases in a unified optimization scheme that involves temporal data cost term would be a useful extension. One could also add more coupling information between endocardium and epicardium during deformation. On graph cuts side, using higher level priors or constraints is possible. One could introduce 3D shape model of LV to increase the accuracy particularly in slices close to apex and basal. Finally, our method also keeps the flexibility of extending the limits of the current interaction scheme allowing more controllability which is also a possible demand from clinicians.