Abstract
Over the past decade, a tremendous amount of resources have been dedicated to the pursuit of developing genomic signatures that effectively match patients with targeted therapies. Although dozens of therapies that target DNA mutations have been developed, the practice of studying single candidate genes has limited our understanding of cancer. Moreover, many studies of multiple-gene signatures have been conducted for the purpose of identifying prognostic risk cohorts, and thus are limited for selecting personalized treatments. Existing statistical methods for treatment selection often model treatment-by-covariate interactions that are difficult to specify, and require prohibitively large patient cohorts. In this article, we describe a Bayesian predictive failure time (BPFT) model for treatment selection that integrates multiple-gene signatures. Our approach relies on a heuristic measure of similarity that determines the extent to which historically treated patients contribute to the outcome prediction of new patients. The similarity measure, which can be obtained from existing clustering methods, imparts robustness to the underlying stochastic data structure, which enhances feasibility in the presence of small samples. Performance of the proposed method is evaluated in simulation studies, and its application is demonstrated through a study of lung squamous cell carcinoma. Our BPFT approach is shown to effectively leverage genomic signatures to match patients to the therapies that are most beneficial for prolonging their survival.
Keywords: Bayesian analysis, genomics, nonexchangeable, personalized medicine, time-to-failure endpoints, unsupervised clustering
1 Introduction
Efforts to develop clinical therapies for cancer patients are transitioning to therapeutic strategies devised to target particular molecular and pathogenic features of the patient’s tumor in place of more conventional one-agent-fits-all therapies1. Through advances in cancer biology that have elucidated the distinct cancer molecular mechanisms exhibited by various types of tumors, some targeted therapies have been sufficiently validated for clinical use. An example is crizotinib for the treatment of patients with non-small-cell lung cancer (NSCLC) that carries an anaplastic lymphoma kinase (ALK) rearrangement2. However, the study of single candidate genes or signaling pathways neglects to capture the extent of complexity inherent to neoplastic diseases and thus has limited our understanding of other areas of oncology3. Consequently, the number of targeted drugs and actionable biomarkers that have been sufficiently validated for clinical use are quite limited when one considers the tremendous amount of resources that have been dedicated over the past decade4. Moreover, when patients present with multiple actionable mutations, which is not uncommon for many cancers5, it becomes difficult to select the “optimal” treatment regime that would yield the best clinical outcome for a particular patient, (i.e., prolonged survival) based on the available data.
Several analytical approaches have been proposed for using patient/disease characteristics to select treatments. Biomarker-driven methods have been devised to match patients with a given mutation to the (expected) most effective treatment5,6,7. These approaches assume that patients are exchangeable within a few biomarker defined subgroups, which may not be adequate to account for the within-subgroup heterogeneity5. This approach is particularly challenging in the presence of rare mutations, since acquiring a large number of patients with a rare mutation is very challenging in practice6,7. Recently, the 21-gene signature developed by Albain et al.8 has demonstrated the clinical utility of adjuvant chemotherapies for women with receptor-positive breast tumors. Treatment selection based on this 21-gene signature may not be optimal, however, because this signature was originally developed as a prognostic biomarker for predicting the risk of disease recurrence or death9,10.
A few advanced statistical methods have been developed for optimal treatment selection with multiple gene signatures based on penalized regression models11,12. These approaches use generalized linear models to characterize treatment-by-covariate interactions and assume that patients are statistically exchangeable within some covariate-defined subgroups. However, the performance of these approaches particularly depends on the correct specification of the treatment-biomarker interaction terms, the specification of which is non-trivial in most settings. Moreover, in the presence of a large set of predictive genomic features, treatment selection based on these approaches requires the estimation of a relatively large number of model parameters, which potentially limits their implementation with the relatively small training sets that are commonplace in clinical cancer studies.
In this article, we propose a Bayesian predictive framework for optimal treatment selection that differs fundamentally from existing methods in two major aspects13. First, instead of assuming full exchangeability, we assume that the extent to which two patients are statistically exchangeable depends on the extent to which their tumors exhibit molecular similarity. In other words, a historically treated patient whose tumor is (conceptually) “70%” molecularly similar to that of the current patient on the basis of the available data contributes to the prediction to the extent of 70% of the influence that would be effectuated under the assumption of full exchangeability. This can be achieved with a power prior model14,15, which is explained in detail in Section 2. Second, pairwise similarity measures based on multi-gene signatures can be derived from any unsupervised clustering method. We assume that this heuristic measure of similarity can fully capture the underlying data structure, which facilitates feasibility for many cancer clinical trials that observe only a limited sample size.
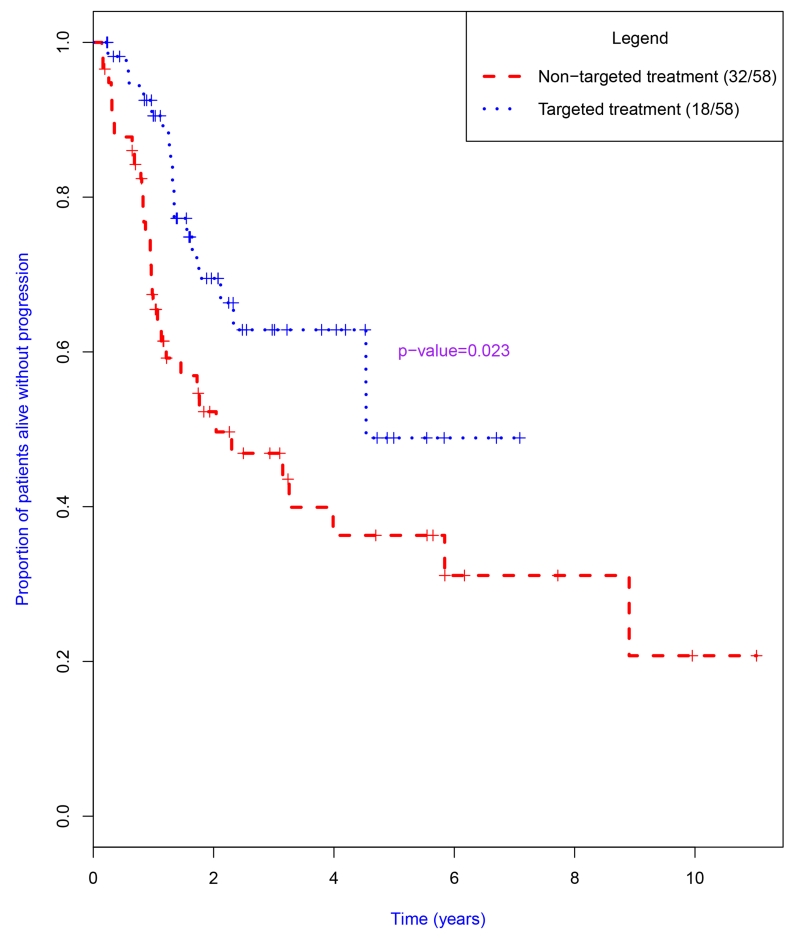
We consider time-to-failure endpoints with treatment allocation strategies that endeavor to prolong the patient’s duration from treatment to disease progression/recurrence or death. We illustrate our approach using a publicly available dataset of lung squamous cell carcinoma (LUSC) from The Cancer Genome Atlas (TCGA) Data Portal. Figure 1 displays the corresponding Kaplan-Meier plots of progression free survival (PFS) durations. For this study, patients treated with the targeted therapy tended to experience prolonged PFS times. Using the proposed method for personalized treatment selection, however, we can identify the set of patients who would benefit from the targeted therapy, and importantly those who would also benefit from the non-targeted treatment strategies.
Figure 1.
Kaplan-Meier plots of progression-free survival durations for patients with lung squamous cell carcinoma; the p-value was calculated using the logrank test. Numbers of events and patients treated with each therapy are provided in the legend as ratios.
The remainder of this article is organized as follows. We first present our Bayesian predictive failure time (BPFT) models for treatment selection. We then evaluate the performances of the proposed method via simulation studies. Thereafter, we present our results from analysis of the TCGA data of LUSC patients. Finally, we close with discussion of potential limitations as well as provide guidance for implementing the method in practice.
2 Bayesian predictive approach for personalized treatment selection
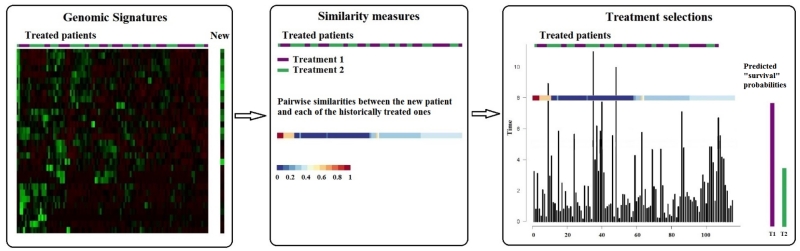
Our proposed approach for personalized treatment selection involves the three sequential components that are depicted in Figure 2. These components are identifying genomic signatures, quantifying tumor similarity and integrating the similarity measure into a Bayesian predictive model for personalized treatment selection. We discuss the details of each component of our modeling procedures in this section.
Figure 2.
Selecting an optimal treatment for a new patient based on genomic signatures and treatment histories of treated patients using our Bayesian approach involves the three components depicted below. Left panel: identify genomic signatures of expression/sequencing data; middle panel: quantify the extent to which the new patient’s tumor exhibits similarity to those previously treated; right panel: integrate the pairwise similarities into the statistical model to predict the probability of prolonging treatment failure beyond time T . The treatment with the highest probability will be recommended for the new patient.
2.1 Predictive genomic signatures
Recent awareness of the general inadequacy of single molecular biomarkers to characterize tumor complexity and heterogeneity, thereby limiting their use to inform treatment selection, has led to an increasing focus on efforts to discover multi-gene signatures that can be used to construct predictive biomarkers. A few examples include the 21-gene signature in breast cancer for adjuvant chemotherapy8,9, the 62-gene signature in pancreatic ductal adenocarcinoma for gemcitabine and erlotinib16, and the 15-gene signature in NSCLC for adjuvant cisplatin/vinorelbine17. In accordance with the aforementioned studies, our approach is founded on the assumption that multi-gene signatures capture enough information to identify distinct actionable cancer molecular features for the specific therapies under consideration. We do not, however, intend to develop such multi-gene signatures, but rather to utilize them to develop personalized treatment selection rules. Our case study demonstrates the approach using multi-gene signatures previously reported in the literature for NSCLC.
2.2 Quantifying tumor similarity with unsupervised clustering
In essence, our approach to personalized treatment selection is based on the assumption that the similarity measure determines the extent to which each historical patient is exchangeable with the current patient. We define the pairwise similarities between the current and the historically treated patients as continuous variables with values in [0, 1], and record these quantities in the matrix of S. A value of Si,k = 0 implies that treated patient i does not contribute to the prediction for the current patient k, while Si,k = 1 implies that patient i contributes to the prediction to an extent that would be achieved under the assumption of statistical exchangeability. Although any clustering method can be used to quantify the similarities, we predominately explore a resampling method based on the consensus clustering (CC) algorithm18. This approach implements an existing clustering algorithm (e.g., k-means) multiple times and resamples both patients and covariates for each run. Results are recorded in the so-called “consensus matrix,” which represents the proportion of times every pair of patients are clustered in the same group. The “consensus matrix” (denoted as S) is what we use to measure the pairwise similarities. For instance, if two patients were clustered in the same group 70 times out of 100 runs, the proportion recorded in the “consensus matrix” would be 0.7. Their molecular similarity would therefore be quantified as 0.7, which is used in the Bayesian statistical model for predicting the probability of prolonging treatment failure beyond time T.
There is a large body of literature pertaining to clustering methods19 that can be used within our framework; however, clustering methods are intrinsically data-driven and their selection depends on the data at hand as well as the investigator’s preference. For example, consensus clustering algorithms have been widely employed in cancer studies of lung adenocarcinoma and glioblastoma20. Another widely utilized clustering method is the nonnegative matrix factorization (NMF) algorithm21, which has been applied to cluster patients with pancreatic ductal adenocarcinoma16. In developing personalized medicine for patients with colon cancer, for example, we may utilize both the NMF and the CC algorithms to quantify the similarities22,23. When such prior knowledge is not available, we may explore existing clustering methods and select the one that yields the best performance, in terms of some pre-specified statistical measures (e.g., log-rank test) obtained from leave-one-out cross-validation analysis; see also Section 4.3 and 4.4.
2.3 Bayesian predictive model for nonexchangeable data
We assume that patients’ tumors are nonexchangeable in the statistical model, such that the extent to which a patient contributes to the prediction of another is determined by their molecular similarity. The approach avoids the need to conduct inference with respect to a complex and potentially misspecified model for which the functional form of the treatment-covariate interactions needs to be determined. In contrast, we propose a Bayesian predictive framework for failure time data that uses power priors to characterize inter-patient similarity based on their genomic profiles.
Let us assume that there are J treatments under investigation. Let δi and ti denote the failure status and duration from treatment to failure or loss to follow-up, respectively, for patient i = 1, … , N. Let nj be the number of patients under the treatment j = 1, … , J such that N = Σjnj. Let 1 – F(ti) and represent survival and density functions for subject i, respectively. For treatment j, the likelihood can be written as , where θj represents the model parameters for treatment j, and D0 represents the observed data (failure times, censoring indicators, and genomic signatures). Let Si,k denote the molecular similarity measure between the historically treated patient i and the current patient k, and Dk represent the genomic data for patient k and the historical data for all patients observed before patient k. Given an initial prior distribution, g(θj), for θj, the posterior distribution can be written as
| (1) |
which is achieved with the concept of a power prior model14,15. The theoretical properties of power priors have been well described24,25. The power prior in (1) is . After the new patient k is enrolled, and that patient’s genomic profile is measured, we can predict the probability of prolonging treatment failure beyond time T under each treatment. The predictive probability under treatment j can be calculated as
| (2) |
where the similarity measure Si,k controls the extent of the ith patient’s contribution to the predictive probability of prolonging treatment failure beyond time T for new patient k. As a special case, assuming that Si,k = 1 for all patients is equivalent to assuming that all patients are exchangeable; see Appendix A for more details. The treatment with the highest predicted probability, p(tk > T, δk = 0|Dk, j), will be recommended. A sensible choice for the duration target, T, is the longest observed follow-up duration26, which was used in our case study of LUSC. To avoid computationally expensive and unnecessarily complex models15, in our implementation we assume that the random patient failure times arise from an exponential distribution. We further assume gamma priors on the model parameters, which results in a closed form of expression for the predictive probability (2). More details of the derivations are provided in Appendix B, along with a brief discussion on how to implement our framework for densities that do not admit a closed form expression of equation (2).
3 Simulation Study
In this section, we evaluate the performance of the proposed BPFT method in comparison with competing approaches. In the interest of maintaining a realistic correlation structure among gene expressions, our simulation studies are based on gene expression data from an actual leukemia trial27. The outcome variables were simulated from a set of survival distributions. We further considered three clustering methods, hierarchical (HC), k-means (KM) and partitioning around medoids (PAM), to measure tumour similarities, and implemented the CC algorithm using the R package ConsensusCluster Plus28,29. For simplicity, we set the duration target time T = 5 for all methods across all scenarios.
For the purpose of comparison, we evaluate the performance of a simplified version of our Bayesian predictive modeling approach where all observations are considered exchangeable, without consideration of the similarity measures. We refer to this approach as the naive method. Another simplified version of our approach assumes exchangeability for all patients within identical clusters obtained from the aforementioned clustering algorithms. We also compare to this approach using a single implementation of the clustering method (unlike CC algorithms which are run multiple times) to yield a similarity matrix which consists of only 1s and 0s. We refer to these methods as BPFT-e in general, or specifically BPFT-eHC, BPFT-eKM and BPFT-ePAM for the clustering methods of HC, KM and PAM, respectively. In addition, we compare our approach with accelerated failure time regression models (RAFT). Specifically, we fit a regression model with treatment, genes and gene-by-treatment interactions as covariates. Thereafter, we utilize this model to calculate the predicted probabilities in (2) under each treatment regime. Again, the optimal treatment regime is the one that attains the highest predicted probability given T . Due to the limited sample size, the RAFT approach is applicable only when the number of genes is relatively small (e.g., ≤ 15). Performance was additionally compared to an adaptive-LASSO penalized regression method recently developed for treatment selection using AFT models. Our simulation study implements this approach (referred to hereafter as OTR) using the R package OT Rselect11. Performance for all methods (BPFT, naive, OTR and RAFT approaches) was compared using various sampling models for the outcomes, as well as differing sets of genes.
3.1 Simulation design
We simulated the data based on actual genomic features (covariate) from a well-known data set of leukemia (http://www.pnas.org/content/101/12/4164.full?tab=ds). This data set contained gene expressions for a total of 5,000 genes among 11 patients diagnosed with acute myelogenous leukemia (AML) and 27 patients diagnosed with acute lymphoblastic leukemia (ALL; 19 ALL-B and 8 ALL-T)21,27. In order to evaluate the properties of the method using a sample size that was comparable to the 116 patients included in our case study (see Section 4), we expanded our leukemia data set to 38×3=114 patients. Specifically, we first clustered the top 700 varied genes (the maximum minus the minimum level of observed gene expression), and selected 95 gene clusters that contained at least three genes. We then calculated gene correlations within each gene group. Assuming that the first three highly correlated genes (referred to as features hereafter) are exchangeable, each patient was duplicated into three. Alternatively, we could have considered generating gene expression data with some well-studied algorithms30. Our approach maintains the complex and heterogeneous structure exhibited in the original leukemia data set, however, which is critical to effectuating meaningful evaluations of performance in the considered cancer genomics settings. Our gene expression data matrix consists of 114 subjects and 95 genes.
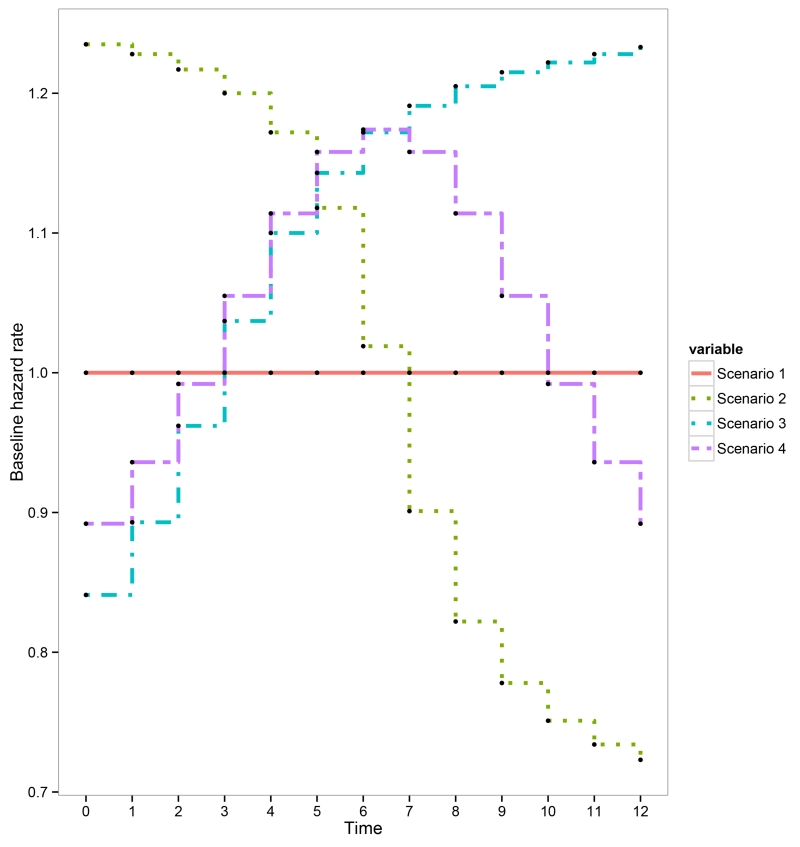
We considered two treatments in the simulation study, and used piecewise constant exponential distributions to generate survival outcomes. For each patient, we determined the true hazard function as λ0(t)exp{−(β0 + β1Zi + β2Ai + β3AiZi)}, where (β0, β1, β2) = (1.7, −0.5, −0.1, 1) were fixed in all scenarios; Ai = {0, 1} represents the treatment and Zi is the second principal component obtained from principal component analysis (PCA) of the 95 selected genes. The Zis were power transformed to avoid unrealistic realizations of the hazard function as well maintain similar hazard function for patients with similar tumour characteristics. For this simulation design, the optimal treatments were A = 0 for the first 24 patients (ALL-T), and A = 1 for all other patients. We considered four piecewise (12 equally spaced time intervals) constant exponential distributions (Figure 5 in Appendix C). These scenarios represent a broad range of hazard functions commonly observed in medical research. Scenario 1 reflects the special case where λ0(t) = 1 for all time intervals (exponential distribution). Scenarios 2-4 were designed to evaluate the performances of the proposed methods in the situation when the model assumptions are violated, i.e., the generated survival outcomes were not exponentially distributed. For each scenario, we generated 100 duplicated data sets for model evaluation.
3.2 Analyzing the simulated data
Selecting genomic signatures
We considered two genomic signatures. First, we considered the signature we used to simulate the outcome variables, i.e., the 95-gene signature. Second, we defined a signature that included the 15 genes with the highest marginal association with the clinical outcome. Specifically, we fitted an AFT regression model with Weibull error terms31 for each gene, including treatment and gene-by-treatment interactions as covariates. Genes were ranked by the p-values of their interaction terms, and the top 15 genes were selected (referred as the 15i-gene signature).
Leave-one-out cross-validation analysis
To avoid overly optimistic results, we conducted leave-one-out cross-validation (LOOCV) analyses. With LOOCV, the patient cohort that is used to train the statistical model and select an optimal treatment excludes the patient for which the prediction is taking place. Therefore, this patient effectively contributes no information to his/her own prediction, which reflects actual clinical practice. For implementation of the RAFT and OTR methods, we used the LOOCV procedure that is similar to that described by Derubeis at al.32. We implemented the proposed BPFT approach by first selecting the optimal number of clusters (rank) via evaluating the 5-year restricted mean survival times (RMSTs) on the training data with one patient excluded. We then predicted the optimal treatment for that patient with the selected rank, and repeated this procedure n = 114 times until all patients were matched to their recommended treatments. Note that all analyses for the BPFT method were based on the exponential survival model presented in Section 2.3.
Simulation results
Since the true optimal treatment is known for each patient in the simulation study, we evaluated the performance of competing methods by comparing the number of patients who were recommended to their corresponding non-optimal/optimal treatment. We observed that in general the proposed methods perform better than the RAFT, OTR and the naive method, where on average, substantially less patients were assigned the non-optimal treatments; see Tables 1 and 2. We also found that the advantages of the proposed methods varied for different similarity measures, i.e., assuming that patients are nonexchangeable generally resulted in fewer non-optimal assignments when compared to methods that assume exchangeability within clusters. Note that, while the OTR method uses penalized estimation to handle high-dimensional data, we encountered numerical issues when all 95 features were included in the prediction model (n=114). We therefore only report results for the OTR methods using the 15i-gene signature. Secondly, we observed comparable results for each method across the four scenarios, which indicates the robustness of our proposed method under various failure time distributions. For example, the average count (CT) of patients who would be wrongly assigned the non-optimal treatments was 1.09 for BPFT (with KM) in scenario 1, while the corresponding numbers were (0.78, 1.45, 1.28) for scenarios 2-4, respectively (Tables 1). Third, results obtained with 95-gene signature were marginally better than those using 15i-gene signature. This is not surprising as both the 95-gene and the 15i-gene signature are highly correlated with the outcomes. These results are also summarized via box plots, see Figures 6 and 7 in Appendix D, which are consistent with the results presented in Tables 1 and 2.
Table 1.
The average number of patients who were recommended to the non-optimal treatments via various treatment selection methods, where small values indicate better results. The outcome variables were simulated with the 95-gene signature, and the data were analyzed using the same set of features. Naive: assumes all patients are exchangeable (similarity measures not used). BPFT: the proposed treatment selection approaches when implemented with clustering methods of HC, PAM and KM. CT: the average counts; and sd: the standard deviation.
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |
|---|---|---|---|---|
| Method | CT (sd) | CT (sd) | CT (sd) | CT (sd) |
| Naive | 24.74 (6.6) | 25.40 (9.4) | 26.02 (11.5) | 26.13 (11.7) |
|
| ||||
| BPFT-eHC | 6.38 (2.2) | 7.36 (4.7) | 6.90 (3.3) | 7.31 (3.5) |
| BPFT-ePAM | 5.84 (6.0) | 3.82 (3.7) | 5.69 (6.6) | 5.27 (6.5) |
| BPFT-eKM | 6.52 (6.0) | 5.48 (5.1) | 6.59 (6.2) | 6.80 (5.8) |
|
| ||||
| BPFT-HC | 4.52 (1.7) | 4.75 (3.8) | 4.75 (3.9) | 4.57 (3.0) |
| BPFT-PAM | 2.66 (3.3) | 2.09 (2.1) | 2.84 (4.7) | 2.96 (4.1) |
| BPFT-KM | 1.09 (2.8) | 0.78 (3.2) | 1.45 (4.6) | 1.28 (2.9) |
Table 2.
The average number of patients who were recommended to non-optimal treatments, where small values indicate better results. The outcome variables were simulated with 95-gene signature, and the data were analyzed using the 15i-gene signature. RAFT: regression based approach with accelerated failure time models. OTR: the adaptive-LASSO penalized regression method. BPFT: the proposed treatment selection approaches when implemented with clustering methods of HC, PAM and KM. CT: the average counts; and sd: the standard deviation.
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | |
|---|---|---|---|---|
| Method | CT (sd) | CT (sd) | CT (sd) | CT (sd) |
| RAFT | 21.25 (7.2) | 21.28 (7.2) | 21.79 (7.6) | 21.12 (7.8) |
|
| ||||
| OTR | 14.66 (12.2) | 15.98 (16.2) | 12.73 (8.8) | 13.86 (8.2) |
|
| ||||
| BPFT-eHC | 6.94 (2.9) | 7.10 (3.7) | 7.50 (4.5) | 7.14 (3.4) |
| BPFT-ePAM | 7.25 (7.2) | 5.40 (5.8) | 6.48 (6.9) | 6.57 (6.6) |
| BPFT-eKM | 7.33 (6.1) | 6.29 (5.4) | 7.00 (6.6) | 6.21 (5.1) |
|
| ||||
| BPFT-HC | 5.04 (2.7) | 5.06 (2.0) | 5.17 (4.4) | 4.94 (3.0) |
| BPFT-PAM | 3.35 (3.4) | 2.89 (3.9) | 4.01 (5.0) | 3.57 (3.8) |
| BPFT-KM | 1.25 (3.0) | 1.04 (3.6) | 1.83 (4.7) | 1.30 (3.1) |
4 A case study for patients with lung squamous cell carcinoma
4.1 The LUSC data
We applied the proposed methods to the publicly available data of LUSC from The Cancer Genome Atlas Data Portal. We downloaded both the clinical and level 3 RNASeqV2 mRNA data from https://tcga-data.nci.nih.gov/tcga/tcgaHome2.jsp. The RNASeqV2 data are read counts, and therefore were transformed by subtracting the mean and dividing by the standard deviation. We focused on a subset of patients who received two therapeutic regimes of targeted (n=60) and non-targeted (n=188) treatments. Since TCGA data are generally observational, to avoid potentially biased estimates of the treatment effects, we matched the data with the baseline covariates of gender, age, tumor stage and initial year of pathological diagnosis (IYPD)33. Specifically, we matched 58 pairs of patients with the 30-day landmark using the R package of MatchIt (with the default settings)34; the resultant standardized differences were −0.037, 0.212, 0.000, and 0.028 for gender, age, tumor stage and IYPD, respectively. All standardized mean differences were less than 0.25, thereby satisfying general standards for effectuating quality matches35. Note that two patients who were administered the targeted drug were excluded due to their short survival time ( ≤ 30 days) after enrollment. The total number of treatment failures was 50 for the matched dataset, with 32 failures occurring in the non-targeted treatment group. The longest follow-up time was 11 years; and the estimated 3-year RMSTs were 2.39 and 1.93 years for patients who received targeted and non-targeted treatments, respectively.
4.2 Selecting genomic signatures
We consider three types of genomic signatures. First, we considered several genomic signatures previously reported in the literature. These signatures were often cross-validated and hence might be viewed as widely robust. However, many of them were developed as prognostic biomarkers that may separate patients into different risk subgroups, and thus may not be optimal for treatment selection9,10. Second, we follow the same procedure as described in Section 3.3 and include the genes with the highest marginal association with the clinical outcome as a signature for data analysis. Third, we considered gene signatures defined by the top varied genes, selected on the basis of the difference in expression/sequencing levels between the maximum and minimum values.
Genomic signatures from existing articles were labeled with the first author’s last name plus the number of the reported genes. Similarly, we used Topi15 and Topi50 to indicate genes that are within the top 15 and 50 statistically significant gene-treatment interactions, respectively, and Topv100, Topv200 and Topv500 to respectively denote the top 100, 200 and 500 varied genes. We investigated a total of 10 signatures, including Topv100, Topv200, Topv500, Topi15, Topi50, Zun15, Sun50A (adenocarcinoma), Sun50S (squamous cell carcinoma), Kaufman13 (squamous cell carcinoma) and Kaufman16 (adenocarcinoma)17,36,37. For BPFT, we explored all signatures with all clustering methods with ranks of 2-15. However, since we only included 116 patients, we only implemented regression methods using the signatures that consist of only a small number of genes ( ≤ 20).
4.3 Model evaluation and comparison
In this section, we describe how to evaluate the predictive performance of BFPT and its competing approaches. This can be done by comparing treatment effects among the stratified subgroups defined by each method38. Specifically, after patients are assigned to their corresponding recommended treatments, they can be stratified into different groups, as shown in the Table 3. Here, a and d represent the patients who actually received the predicted optimal treatments A0 and A1, respectively; whereas b and c represent those who did not receive the predicted optimal treatments. Two levels of comparisons can be conducted, namely the overall comparison of a + d versus b + c and the treatment-level comparison of a versus b and c versus d. The former measures the overall benefit from this model (these results are reported in Section 4.4), and the later identifies patients who may or may not benefit from a certain treatment (these results are reported in Appendix E).
Table 3.
Stratified patient subgroups with the recommended optimal treatments actually received. A0 and A1 represent treatment 1 and 2 respectively; Rec and pred denote the predicted and received treatments, respectively.
| Received | ||
|---|---|---|
|
|
||
| Predicted | A0 | A1 |
| A0 | a= (Rec A0/pred A0) | b= (Rec A1/pred A0) |
|
| ||
| A1 | c= (Rec A0/pred A1) | d= (Rec A1/pred A1) |
There are at least three statistical measures that can be used to compare between-group differences in time-to-failure analysis, namely, the log-rank test, simple nonparametric hazard estimation (Kaplan-Meier) and RMST26. The RMST can be evaluated as the integration of the survival function up to a restricted, clinically relevant follow-up duration τ, which is often pre-specified in the trial protocol or selected to be near the last observed event time26,39. For the case study of LUSC, we set the restricted time τ at 3 years. Note that the restricted time τ is chosen for the purpose of evaluating a treatment selection method, while failure time target T is used within the treatment selection method to compute the “failure time probability”. In other words, we calculate the τ-time RMST using the Kaplan-Meier estimates after we apply the treatment selection methods (with time T ) to stratify patients into treatment-sensitive subgroups. Unlike the τ-time RMST, the T-time survival probabilities may not be directly compared among different approaches (e.g., RAFT versus BPFT) since they are based on different modeling assumptions. It should be noted that these are still valid for comparing among treatments within the same method).
For RAFT, we selected the Weibull AFT models for the sake of simplicity. We used the R package of survival to implement these analyses, and used the package survRM2 to obtain the resulting 95% confidence intervals (CIs)31,40. Aware of conducting multiple tests, we adjusted for multiple comparisons using the conservative Bonferroni method41. Specifically, for a given gene signature, we explored three cluster-based models and therefore conducted 3 hypothesis tests. The significance threshold was set to 0.0167 (0.05/3). We also report the median survival times for the sake of completeness.
4.4 Results
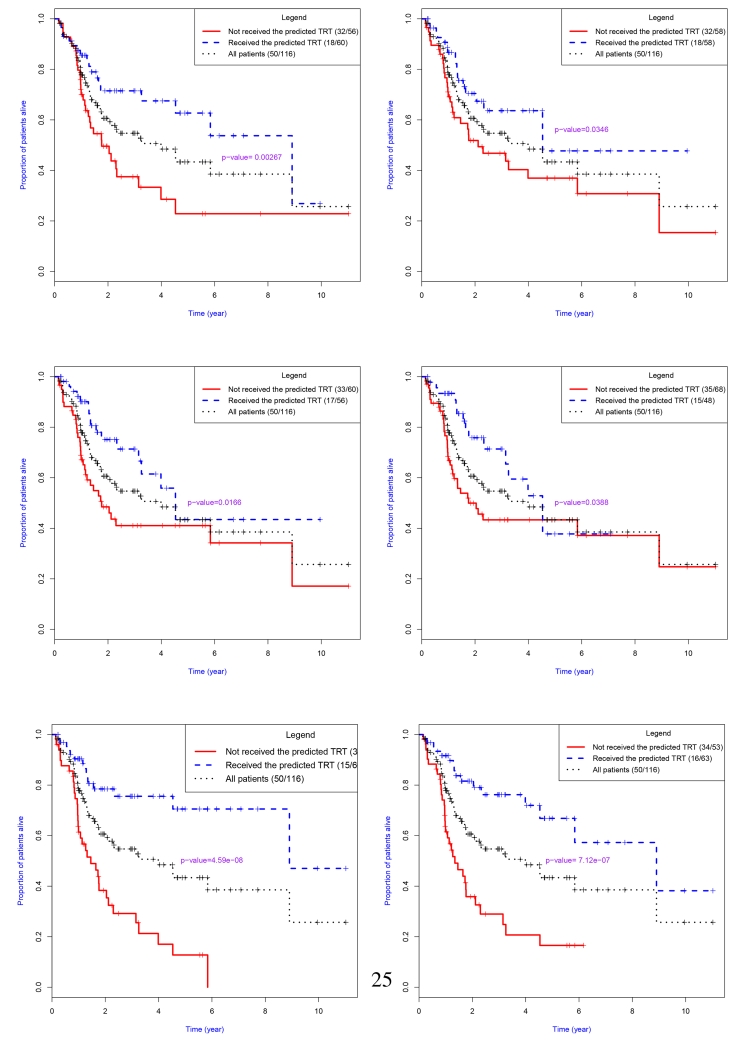
All results are based on LOOCV analyses. The main results of our analyses are summarized in Table 4. For a given gene signature, we only report the results for the clustering method that generated the longest estimated 3-year RMST. On the basis of the results displayed in Table 4, we have several observations. First, we found that some gene signatures worked better than others. For example, the best result of the 3-year RMST was 2.58 (95% CI, 2.36 – 2.80) years, which was obtained from Topi50 using the Bayesian predictive method with PAM. This represents, on average, a 19% prolonged 3-year RMST compared to those obtained from the alternative treatment assignment strategy (2.16 years) of “randomly” allocating both the targeted and non-targeted treatments. We also observed similar results for the signatures of Topi15 and Kaufman13 (using BPFT approaches), and to a lesser extent effectuated improved results for other signatures (Table 4). However, the signatures of Topv100, Topv200, Topv500 and Sun50A failed to effectively identify treatment-sensitive subgroups (results not shown). Second, we found that the BPFT approaches generally performed better than the RAFT methods, which failed to effectively utilize some of the selected gene signatures, such as Kaufman13. For this signature, the RAFT generated results similar to those obtained by the simple “randomization” method. The results are also depicted in the Kaplan-Meier plots in Figure 3 and Figure 4 for BPFT and RAFT, respectively. Due to the lack of model convergence of RAFT in the presence of a large number of genes, Figure 4 does not include the KM plots for the Sun50S and Topi50 signatures. The survival curves for the signatures of Topi15 and Topi50 are well differentiated, indicating substantially improved clinical benefits for patients who received their recommended treatment when compared to those who did not. We also observed that p-values for the BPFT with the two signatures are less than the conservative Bonferroni significant threshold value of 0.0167. Note that results from the OTR and the BPFT-e are presented in Table 5 of Appendix E. We observed that the proposed methods of BPFT and BPFT-e provided close/comparable result; while the OTR method failed to distinguish subgroups of patients on the basis of their optimal treatments. Additional comparisons are presented in Appendix E.
Table 4.
Estimated 3-year restricted mean survival time (RMST) for patients with lung squamous cell carcinoma. Leave-one-out cross-validation analyses were conducted for both the proposed Bayesian predictive failure time (BPFT) methods and the AFT regression (RAFT)-based approaches.
| Signature | Method | Received Recommended Treatment |
Patient No.(event) |
Median | RMST | 0.95CI |
|---|---|---|---|---|---|---|
| Zhu15 | BPFT† | YES‡ | 60 (18) | 8.91 | 2.43 | 2.15 – 2.68 |
| NO§ | 56 (32) | 1.76 | 1.89 | 1.63 – 2.19 | ||
|
| ||||||
| RAFT | YES | 62 (26) | 4.53 | 2.17 | 1.90 – 2.45 | |
| NO | 54 (24) | 3.26 | 2.15 | 1.86 – 2.43 | ||
|
| ||||||
| Sun50S§§ | BPFT | YES | 58 (18) | 4.53 | 2.37 | 2.12 – 2.63 |
| NO | 58 (32) | 2.12 | 1.96 | 1.67 – 2.25 | ||
|
| ||||||
| RAFT | – | – | – | – | – | |
| – | – | – | – | – | ||
|
| ||||||
| Kaufman13* | BPFT | YES | 56 (17) | 4.53 | 2.51 | 2.26 – 2.75 |
| NO | 60 (33) | 1.76 | 1.86 | 1.58 – 2.15 | ||
|
| ||||||
| RAFT | YES | 61 (26) | 3.99 | 2.17 | 1.90 – 2.44 | |
| NO | 55 (24) | 3.26 | 2.15 | 1.85 – 2.44 | ||
|
| ||||||
| Kaufman16** | BPFT | YES | 48 (15) | 4.53 | 2.54 | 2.29 – 2.79 |
| NO | 68 (35) | 1.76 | 1.90 | 1.67 – 2.19 | ||
|
| ||||||
| RAFT | YES | 56 (16) | 5.84 | 2.45 | 2.20 – 2.70 | |
| NO | 60 (34) | 1.76 | 1.91 | 1.63 – 2.17 | ||
|
| ||||||
| Topi15 | BPFT | YES | 66 (15) | 8.91 | 2.54 | 2.32 – 2.77 |
| NO | 50 (35) | 1.46 | 1.68 | 1.38 – 1.97 | ||
|
| ||||||
| RAFT | YES | 65 (22) | 8.91 | 2.40 | 2.16 – 2.64 | |
| NO | 51 (28) | 1.76 | 1.85 | 1.54 – 2.15 | ||
|
| ||||||
| Topi50 | BPFT | YES | 63 (16) | 8.91 | 2.58 | 2.36 – 2.80 |
| NO | 53 (34) | 1.34 | 1.66 | 1.37 – 1.95 | ||
|
| ||||||
| RAFT | – | – | – | – | – | |
| – | – | – | – | – | ||
Results with the longest 3-year RMST using the partitioning around medoids (PAM); k-means (KM) and hierarchical (HC) algorithms;
Received the suggested treatment;
Did not receive the suggested treatment;
43 out of 50 genes were matched;
12 out of 13 genes were matched;
15 out of 16 genes were matched.
Figure 3.
Kaplan-Meier plots of results obtained from treatment allocation strategies developed using the proposed Bayesian predictive failure time (BPFT) methods with different gene signatures. Top: Zhu15, Sun50S; Middle: Kaufman13, Kaufman16; and Bottom: Topi15, Topi50. These results were based on leave-one-out cross-validation and correspond to the results presented in Table 4.
Figure 4.
Kaplan-Meier plots of results obtained from treatment allocation strategies developed using the AFT regression (RAFT) based approaches with different gene signatures. Top: Zhu15, Kaufman13; Bottom: Kaufman16, Topi15. These results were based on leave-one-out cross-validation and correspond to models displayed in Table 4.
We have a few remarks on these results. In our analyses, we set the hyperparameters to α = β = 0.01. We also conducted sensitivity analysis for α = β = {0.5, 0.1, 0.05, 0.005} using the topi50 signature, and found that our approach is robust to that specification, as the prediction results were almost identical. In addition, in assessing the performance of these methods, we recommend evaluating all of the summary measures of the log-rank test, Kaplan-Meier plot and RMST. For example, the BPFT method with the signature of Topi15 generated results for the 3-year RMST that were close to those obtained from Kaufman13, whereas the Topi15 performed better when using the p-values and Kaplan-Meier plots as the criteria (Figure 3). Moreover, the number of genes included in a signature should also be considered carefully. By the principle of Occam’s razor, the signature of Topi15 should be preferred over that of Topi50 as BPFT methods generated very close results with the two signatures yet Topi15 involved fewer genes. Additionally, one must select a clustering algorithm before using the BPFT method to predict the optimal treatment for a future patient. This can be done using the procedure that was discussed in Section 3.2, where we use the training dataset to select the best rank for each patient. Alternatively, we can use the most frequently selected rank in the previously conducted LOOCV analyses, which was rank 10 in our case study using the genomic feature of topi15 (which was chosen as best 72 out of 116 runs).
5 Discussion
We proposed a Bayesian predictive modeling framework for treatment selection with time-to-failure endpoints and a large set of genomic features. To account for cancer tumor heterogeneities and obtain results that have direct clinical interpretations, we derived a strategy for personalized treatment selection that is based on a power prior failure time model14,15,26, wherein the extent to which a patient contributes to the outcome prediction of another is determined by the extent to which their tumors exhibit molecular similarity. We conducted empirical studies to evaluate the performance of our proposed approaches, and applied these methods to a study of LUSC to illustrate their clinical utility for treatment selection. We also described a procedure to select potentially promising genomic signatures for treatment selection. The combination of our Bayesian approach with these genomic signatures and those reported by Kaufman et al.37 revealed the presence of treatment-by-gene interaction effects that elucidate subgroups of patient who might benefit from the targeted/non-targeted regimes. We explored other genomic signatures from the existing literature and applied conventional regression-based approaches, which were less effective at identifying subgroups of patients who might benefit from non-targeted treatments. These results demonstrate the utility of our proposed framework in developing optimal treatment selection rules.
Following advances in high-throughput technology, tremendous resources have been allocated to the development of predictive genomic signatures. There have been additional efforts to establish criteria and guidance for discovery and translation of genomic signatures. For example, a checklist of criteria developed by the US National Cancer Institute covers important issues pertaining to data quality, clinical trial design, and statistical inference42. Our investigation used TCGA data of patients with LUSC, which were obtained from observational studies. We urge researchers to match the observational data, as illustrated in the previous section, and encourage the use of training data from randomized clinical trials. We implemented cross-validation analyses to take into account sample variations of future patients, and demonstrated the extent to which a patient would benefit from the recommended treatments. The clinical utilities of these predictive genomic signatures need to be further validated prior to their use in clinical practice, however.
In this paper we focused on AFT models. Note that for time-to-failure endpoints, statistical methods for personalized treatment selection based on penalized likelihoods have been proposed for Cox models as well12. Although this approach works well with a limited number of covariates12, it is not designed, at least in the current implementation, to handle the large number of genomics covariates we were interested in. We therefore did not compare this method with the other approaches we analyzed in this manuscript.
In this article, we endeavored to develop a statistically sound and computationally efficient method that provides easily interpretable results for personalized treatment selection. There are a few limitations to using the proposed approach, which we intend to resolve in future research. For example, the method’s effectiveness might be impacted by the chosen clustering algorithm, the selection of which is intrinsically data-driven. For a small set of clustering methods, as we considered in this study, the clustering method and ranks may be treated as random factors and modeled simultaneously, which might be useful to overcome their pre-specification. While accommodating all levels of uncertainty is attractive in theory, we expect that implementation of this approach would be challenging and computationally burdensome in practice as model-based clustering does not usually lead to closed form posterior distributions. In addition, the proposed method may not work when applied to a gene signature that includes too many noisy genes. We used regression models (with covariate-by-treatment interactions) to obtain an initial set of candidate signatures using those that showed promise in prior studies. In future work, we intend to explore additional gene signatures, including those that are more biologically oriented37,43. Finally, our current modeling framework does not incorporate clinical prognostic covariates. We are now investigating a more advanced statistical model that simultaneously incorporates both clinical and genomic data.
Acknowledgements
The first author was fully funded by MD Anderson internal funds. The second and third authors were partially supported by the NIH/NCI Cancer Center Support Grant (P30 CA016672), and the third author was also partially supported by the NIH/NCI P50 CA070907-16A1 grant. The authors thank LeeAnn Chastain for editing assistance, two anonymous referees and the editor for providing very constructive comments, and the authors of Wang et al. (2014) for sharing their code.
Appendix A Power priors, non-exchageable data, and treatment selection
Endeavors to establish effective treatment strategies for many cancer subtypes are compounded by the inherent complexity of the disease, whereby collections of cells within the same tumor may exhibit distinct phenotypic and morphological profiles44. Thus, quantitative approaches for applications of precision medicine in oncology are limited by methods that attempt to identify discrete, homogeneous subtypes using models that rely on assumptions of statistical exchangeability which fail to reflect the personalized nature of tumor heterogeneity. By way of contrast, the methodology proposed in this article facilitates personalized treatment selection on the basis of measures of similarity computed from the essential components of tumor heterogeneity. The methodology is founded on a power prior modeling framework that effectively relaxes assumptions of interpatient exchangeability, but rather assumes that the patients represent a nonexchangeable cohort such that their influence or contributions to the outcome prediction of other patients is determined by the similarity measure. Concepts of non- and partial exchangeability have been described by several authors (i.e. see45,46,47 and the references therein). Additionally, several formal definitions of partial exchangeability are available in the Bayesian methodology literature45,48. Moreover, the concept has been considered in the context of Bayesian accelerated failure time models49.
For power prior approaches a power parameter, denoted as a0, is used to quantify the extent to which a historical data cohort D0 influences the estimation of model parameters (θ) on the basis of a current or primary data source D. Ibrahim and Chen referred to a0 as a measure of intercohort heterogeneity14. The power prior is defined as p(θj|D0, a0) ∞ L(θj|D0)a0g(θj) where θj represents model parameters for treatment j, 0 ≤ a0 ≤ 1 is the scalar power parameter and g(θj) is the initial prior for θj. The hyperparameter a0 can be assumed known and thereby fixed on the basis of sensitivity analyses (e.g., a0 = 0, 1), or modeled as random component. The latter approach presents additional complexities for most likelihoods, however, including computational costs25. When multiple M sources of historical data exist D0 = (D01, … , D0M), one can define a vector of power parameters to reflect the contribution of each specific historical source, a0 = (a01, … a0M), resulting in the following prior distribution given the historical data cohorts . The posterior distribution is written as , where L(θj|D) is the likelihood of the current data14. In this article, we consider a special case of M = nj such that each historically treated patient is considered to be an individual “data source” for selecting a treatment strategy for a new patient D = (tk, δk). Replacing a0m with the molecular similarity measure ofSi,k, we can write the power prior as . Let Dk represent the genomic data for patient k and the historical data of D0, the posterior distribution can be written as (1).
As we can see from equation (1), the nonexchangeable data structure is taken into account via the power function such that the likelihood of each of the historically treated patients with exponent Si,k, a heuristic similarity measure obtained from existing clustering methods. If Si,k = 0, the posterior is updated via the initial prior g(θj). Thus, historically treated patients do not contribute to the prediction for the current patient k. On the other hand, if Si,k = 1, each historically treated contributes to the prediction to an extent that would be obtained from assuming that all patients are statistically exchangeable (naive method). Another special case can be accommodated whereby Si,k = 1 or 0 for a distinct subsets of patients. This is equivalent to assuming partial exchangeability defined by Diaconis (1988) as well by Walker and Mallick (1999)45,49; see Section 3 for the method of BPFT-e with this assumption.
Appendix B Predictive T-failure time probability derivation
The predicted probability of prolonging treatment failure beyond time T using the power prior framework follows as, is written as
For exponential models, the density and survival function for subject i are f(ti) = λexp(−λti) and 1 − F(ti) = exp(−λti), respectively. The above equation becomes
With the initial prior of Gamma(α, β) ∞ λα−1exp(−λβ), the power prior predicted survival probability is given as
where for and . The kernel for the integrand is Gamma(), with a normal constant factor of . With a little algebra, we can show that
In contrast, assuming exchangeability is equivalent to assuming that Si,k = 1 for all patients, and thus the predictive probability is reduced to , represents the prediction attained for the naive method that we implemented in our simulation study.
For exponential densities with the conjugate Gamma priors, we showed how to obtain a closed form for the calculation of the predictive failure time probability. This analytical expression greatly eases the implementation of our approaches for treatment selection. At the same time, any proper time-to-failure densities that may better fit/describe the data at hand can be implemented within our framework. Unfortunately, many robust and flexible survival models will not yield closed form expression of the predictive probabilities; moreover, complex survival models require a larger sample size, which makes them not the ideal approach for the applications we are interested in.
When survival models alternative to the exponential distribution are preferred, the predictive distribution can be calculated via Markov chain Monte Carlo (MCMC), or alternative approaches. Note that the quantity in (2) is indeed the power prior predictive probability of prolonging treatment failure beyond time T , whose calculation requires one to integrate out the model parameters θjs from the power prior . In our framework, exchangeability is determined by the similarity measures and incorporated into the prediction using power prior, which consists of the product of an initial prior and power functions that utilize historical data likelihoods as bases and similarity measures as exponents. From this point of view, the model parameters can be sampled from the power prior by means of standard sampling approaches which are described elsewhere15. Given a desired number of samples from the power prior distribution, we can approximate the quantity in (2) with its Monte Carlo estimate, and then assign patients their optimal treatment accordingly.
Appendix C Plots describing the simulation scenarios
Figure 5.
Plots of the baseline hazard rates for our simulation studies. Scenario 1 is a special case where λ0(t) = 1 for all time intervals. In scenario 2, the hazard rates were set to monotonically decreasing. In contrast, we set the hazard rates to be monotonically increasing in scenario 3. Last in scenario 4, we set the hazard rates first monotonically increasing and then monotonically decreasing after time 7.
Appendix D Boxplots for the average number of patients who were assigned to non-optimal treatments
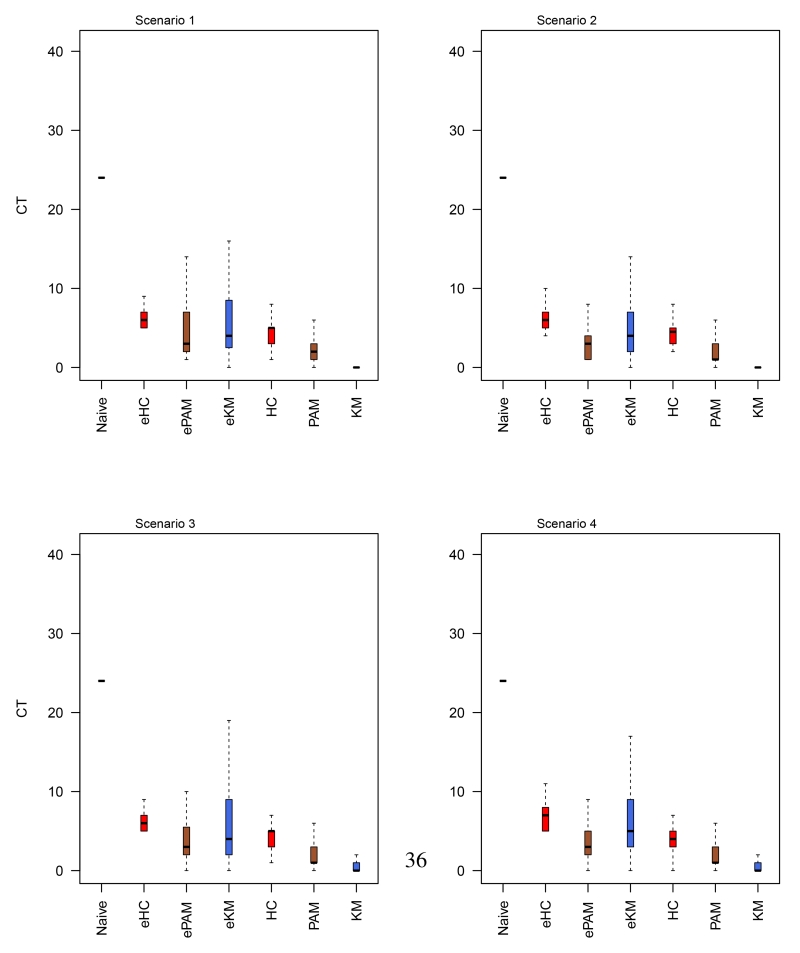
Figure 6.
Box plots of the simulation results for four scenarios based on the 95-gene signature. CT represents the average number of patients who were assigned to non-optimal treatments. We analyzed the data with the naive method and the proposed Bayesian predictive failure time (BPFT) methods with unsupervised clustering based on the consensus clustering approach using hierarchical (HC), k-means (KM) and partitioning around medoids (PAM) algorithms. Clustering approaches were implemented with the LOOCV algorithm described in Section 3.2
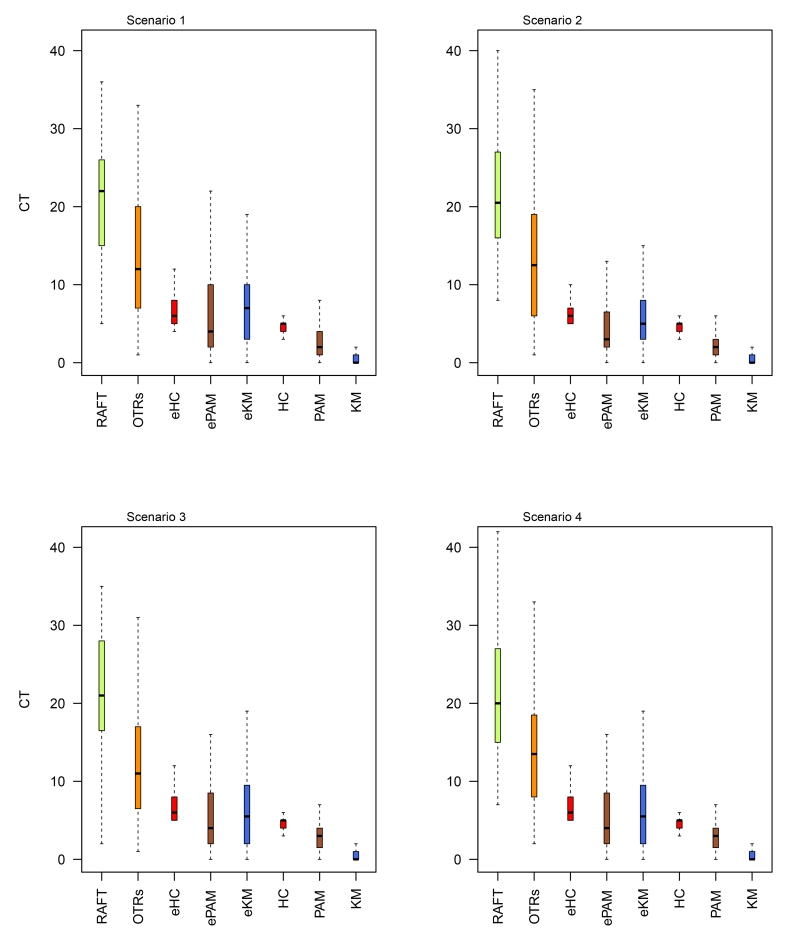
Figure 7.
Box plots of the simulation results for four scenarios based on the signature of 15-feature. CT represents the average number of patients who were assigned to non-optimal treatments. We analyzed the data with the RAFT and the proposed Bayesian predictive failure time (BPFT) methods with unsupervised clustering based on the consensus clustering approach using hierarchical (HC), k-means (KM) and partitioning around medoids (PAM) algorithms. ALL approaches were implemented with the LOOCV algorithm described in Section 3.2
Appendix E Treatment-stratified results for estimation of 3-year RMST
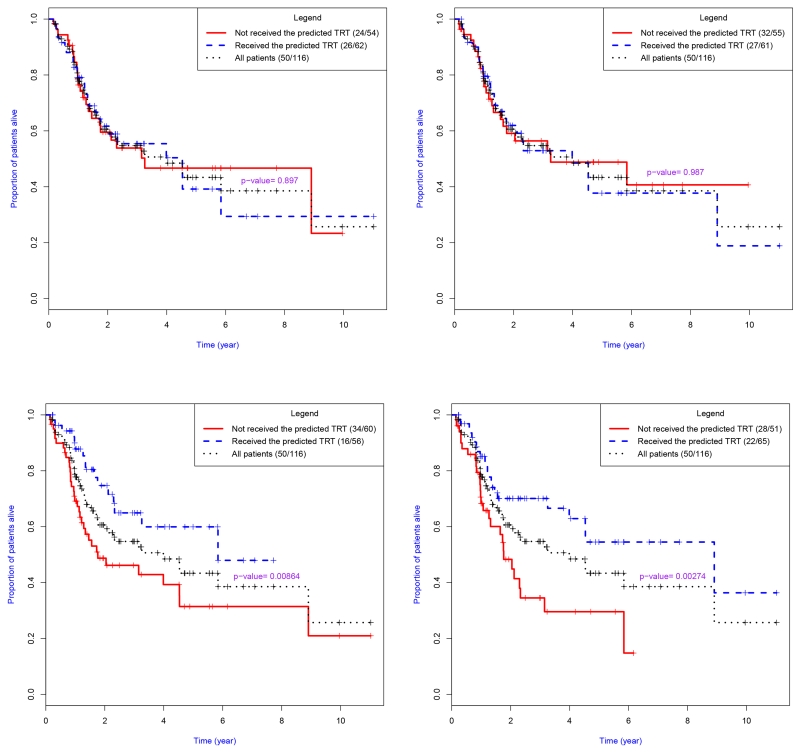
Results from the methods of OTR and BPFT-e are presented in Table 5. We found that results obtained from BPFT-e are generally comparable with those obtained from BPFT. These results are not surprising since model comparisons for the real data analyses are based on the summary measures of RMST whose calculation is determined by the observed survival times. Although in the simulation studies the BPFT-e methods generally assigned several more patients to the non-optimal treatment (with relatively large standard deviations), the summary measure of RMST may not be significantly affected. On the other hand, we found that the OTR methods performed worse than the RAFT method, in that it often failed to select the optimal treatments for all signatures. It has been reported that the OTR method performed worse when the censoring rate is high (e.g.,40%)11. To investigate this, we simulated two additional datasets using the same settings as for scenario 3 with the censoring rates of 15% and 40%, respectively. Note that we set the censoring rate as 0 for the simulation studies in Section 3. The average numbers of patients assigned to the non-optimal treatments were 37.4 (SD=27) and 59.1 (SD=24.8) for the method of OTR with the censoring rates of 15% and 40%, respectively; while the corresponding numbers were 23.0 (SD=8.2) and 27.5 (SD=9) for the method of RAFT, respectively. The reader should note that the original study of OTR utilized a much large patient cohort (n=2137)11, and thus the poor performance of the OTR methods may be due to the relatively small sample size in our study (n=116).
We also evaluated the 3-year restricted mean survival time (RMST) for the targeted therapies based on the subgroup of patients who received the predicted optimal treatment as targeted therapies; and in the same manner calculated the 3-year RMST for the non-targeted therapies. Results obtained using BPFT and RAFT are displayed in Table 6 and Table 7, respectively. Note that results for signatures of Sun50S and Topi50 are not available with the method of RAFT because of their relatively large number of selected genes.
We observed that each method identified a subgroup of patients who might be sensitive to the targeted treatment, i.e., longer 3-year RMSTs for those who received the targeted drugs compared to those who did not. However, for the subgroup of patients who might benefit from the non-targeted treatment, these methods performed substantially different with the combination of different gene signatures. For BPFT with the gene signature of Topi15, the 3-year RMST was estimated as 2.59 years (95% CI, 2.17 – 3.01) for patients for whom the non-targeted therapy was recommended and who received the non-targeted therapy, and 1.9 years (95% CI, 1.40 – 2.39) for those for whom the targeted therapy was recommended, but who received the non-targeted therapy. The corresponding quantities for the RAFT method were estimated as 2.13 years (95% CI, 1.69 – 2.58) and 2.04 years (95% CI, 1.59 – 2.49), respectively. Thus, when compared with the RAFT method, the BPFT method was more efficient at using these data to identify the subgroup of patients who might be sensitive to the non-targeted drugs. We observed similar results for the signatures of Topi50, Kaufman13 and Kaufman16 (Table 6). More importantly, these results demonstrate that the method better leverages the interaction effects between the treatment and the gene signatures, which are the basis for personalized treatment selection.
Table 5.
Results of the estimated 3-year restricted mean survival time (RMST) using the proposed Bayesian predictive failure time methods (assuming exchangeability within estimated clusters, BPFT-e), and the penalized regression based approach (OTR). All results were obtained from Leave-one-out cross-validation analyses.
| Signature | Method | Received Recommended Treatment |
Patient No.(event) |
Median | RMST | 0.95CI |
|---|---|---|---|---|---|---|
| Zhu15 | BPFT-eKM† | YES‡ | 63 (22) | 4.53 | 2.33 | 2.09 – 2.58 |
| NO§ | 53 (28) | 2.30 | 1.97 | 1.66 – 2.27 | ||
| OTR | YES | 60 (25) | 3.15 | 2.11 | 1.82 – 2.39 | |
| NO | 56 (25) | 4.53 | 2.22 | 1.95 – 2.49 | ||
| Sun50S§§ | BPFT-eHC | YES | 59 (22) | 4.53 | 2.34 | 2.10 – 2.59 |
| NO | 57 (28) | 2.30 | 1.96 | 1.65 – 2.27 | ||
| OTR | – | – | – | – | – | |
| – | – | – | – | – | ||
| Kaufman13* | BPFT-eKM | YES | 54 (16) | 4.53 | 2.54 | 2.30 – 2.78 |
| NO | 62 (34) | 1.73 | 1.85 | 1.57 – 2.13 | ||
| OTR | YES | 58 (27) | 2.30 | 1.97 | 1.67 – 2.27 | |
| NO | 58 (23) | 4.53 | 2.34 | 2.09 – 2.59 | ||
| Kaufman16** | BPFT-eHC | YES | 49 (15) | 4.53 | 2.52 | 2.27 – 2.77 |
| NO | 67 (35) | 1.76 | 1.90 | 1.62 – 2.17 | ||
| OTR | YES | 57 (28) | 2.04 | 1.93 | 1.63 – 2.23 | |
| NO | 59 (22) | 4.53 | 2.39 | 2.14 – 2.63 | ||
| Topi15 | BPFT-eKM | YES | 57 (15) | 8.91 | 2.47 | 2.22 – 2.72 |
| NO | 59 (35) | 1.73 | 1.87 | 1.59 – 2.15 | ||
| OTR | YES | 64 (26) | 3.99 | 2.15 | 1.89 – 2.41 | |
| NO | 52 (24) | 3.15 | 2.17 | 1.87 – 2.47 | ||
| Topi50 | BPFT-ePAM | YES | 48 (10) | 8.91 | 2.71 | 2.49 – 2.93 |
| NO | 68 (40) | 1.65 | 1.80 | 1.54 – 2.06 | ||
| OTR | – | – | – | – | – | |
| – | – | – | – | – | ||
Results with the longest 3-year RMST using the partitioning around medoids (PAM); k-means (KM) and hierarchical (HC) algorithms;
Received the suggested treatment;
Did not receive the suggested treatment;
43 out of 50 genes were matched;
12 out of 13 genes were matched;
15 out of 16 genes were matched.
Table 6.
Treatment-stratified results of the estimated 3-year restricted mean survival time (RMST) for patients with lung squamous cell carcinoma. Leave-one-out cross-validation analyses were conducted for the proposed Bayesian predictive failure time (BPFT) models. Results represent the one with the longest 3-year RMST of hierarchical, k-means and partitioning around medoids.
| Signature | Method | Received Recommended Treatment |
Patient No.(event) |
Median | RMST | 0.95CI |
|---|---|---|---|---|---|---|
| Overall | – – | Targeted | 58 (18) | 4.53 | 2.39 | 2.15 – 2.64 |
| Non-targeted | 58 (32) | 2.04 | 1.93 | 1.64 – 2.23 | ||
| Zhu15 | BPFT | Targeted (Y†) | 43 (8) | NA | 2.61 | 2.34 – 2.87 |
| Targeted (N‡) | 41 (22) | 2.04 | 1.90 | 1.55 – 2.24 | ||
| Non-targeted (Y1) | 17 (10) | 3.26 | 2.00 | 1.43 – 2.57 | ||
| Non-targeted (N2) | 15 (10) | 1.76 | 1.86 | 1.43 – 2.29 | ||
| Sun50S§ | BPFT | Targeted (Y) | 53 (15) | 4.53 | 2.43 | 2.17 – 2.70 |
| Targeted (N) | 53 (29) | 2.30 | 1.95 | 1.64 – 2.26 | ||
| Non-targeted (Y) | 5 (3) | 2.04 | 1.77 | 0.85 – 2.69 | ||
| Non-targeted (N) | 5 (3) | 2.12 | 2.21 | 1.58 – 2.83 | ||
| Kaufman13§§ | BPFT | Targeted (Y) | 49 (13) | NA | 2.48 | 2.22 – 2.75 |
| Targeted (N) | 51 (28) | 1.76 | 1.84 | 1.52 – 2.15 | ||
| Non-targeted (Y) | 7 (4) | 3.26 | 2.66 | 2.05 – 3.27 | ||
| Non-targeted (N) | 9 (5) | 2.12 | 2.05 | 1.49 – 2.61 | ||
| Kaufman16* | BPFT | Targeted (Y) | 44 (11) | NA | 2.53 | 2.25 – 2.80 |
| Targeted (N) | 54 (28) | 2.04 | 1.87 | 1.56 – 2.18 | ||
| Non-targeted (Y) | 4 (4) | 3.20 | 2.69 | 2.17 – 3.22 | ||
| Non-targeted (N) | 14 (7) | 1.94 | 2.04 | 1.55 – 2.54 | ||
| Topi15 | BPFT | Targeted (Y) | 48 (11) | NA | 2.53 | 2.26 – 2.79 |
| Targeted (N) | 40 (28) | 1.13 | 1.63 | 1.29 – 1.98 | ||
| Non-targeted (Y) | 18 (4) | NA | 2.59 | 2.17 – 3.01 | ||
| Non-targeted (N) | 10 (7) | 1.76 | 1.90 | 1.40 – 2.39 | ||
| Topi50 | BPFT | Targeted (Y) | 45 (10) | NA | 2.56 | 2.31 – 2.82 |
| Targeted (N) | 40 (26) | 1.13 | 1.61 | 1.27 – 1.95 | ||
| Non-targeted (Y) | 18 (6) | 8.91 | 2.62 | 2.21 – 3.03 | ||
| Non-targeted (N) | 13 (8) | 1.50 | 1.85 | 1.32 – 2.37 | ||
Received the suggested treatment;
Did not receive the suggested treatment;
43 out of 50 genes were matched;
12 out of 13 genes were matched;
15 out of 16 genes were matched.
Table 7.
Treatment-stratified results of the estimated 3-year restricted mean survival time (RMST) for patients with lung squamous cell carcinoma. Leave-one-out cross-validation analyses were conducted for regression (RAFT)-based approaches.
| Signature | Method | Treatment | Patient No.(event) |
Median | RMST | 0.95CI |
|---|---|---|---|---|---|---|
| Overall | – – | Targeted | 58 (18) | 4.53 | 2.39 | 2.15 – 2.64 |
| Non-targeted | 58 (32) | 2.04 | 1.93 | 1.64 – 2.23 | ||
| Zhu15 | RAFT | Targeted (Y†) | 42 (12) | 4.53 | 2.45 | 2.15 – 2.74 |
| Targeted (N‡) | 41 (21) | 3.15 | 2.10 | 1.74 – 2.46 | ||
| Non-targeted | 20 (14) | 1.21 | 1.63 | 1.13 – 2.12 | ||
| Non-targeted | 16 (6) | NA | 2.28 | 1.84 – 2.72 | ||
| Kaufman13§ | RAFT | Targeted (Y) | 35 (12) | 4.53 | 2.38 | 2.07 – 2.70 |
| Targeted (N) | 32 (17) | 2.04 | 1.97 | 1.57 – 2.37 | ||
| Non-targeted (Y) | 26 (15) | 1.73 | 1.89 | 1.46 – 2.32 | ||
| Non-targeted (N) | 23 (6) | NA | 2.42 | 2.03 – 2.80 | ||
| Kaufman16§§ | RAFT | Targeted (Y) | 42 (10) | NA | 2.47 | 2.19 – 2.75 |
| Targeted (N) | 44 (26) | 1.73 | 1.80 | 1.47 – 2.14 | ||
| Non-targeted (Y) | 14 (6) | 3.26 | 2.37 | 1.83 – 2.91 | ||
| Non-targeted (N) | 16 (8) | 4.53 | 2.22 | 1.73 – 2.70 | ||
| Topi15 | RAFT | Targeted (Y) | 42 (10) | NA | 2.56 | 2.28 – 2.83 |
| Targeted (N) | 35 (20) | 1.76 | 1.77 | 1.39 – 2.16 | ||
| Non-targeted (Y) | 23 (12) | 3.99 | 2.13 | 1.69 – 2.58 | ||
| Non-targeted (N) | 16 (8) | 2.12 | 2.04 | 1.59 – 2.49 | ||
Received the suggested treatment;
Did not receive the suggested treatment;
12 out of 13 genes were matched;
15 out of 16 genes were matched.
References
- [1].La Thangue NB, Kerr DJ. Predictive biomarkers: a paradigm shift towards personalized cancer medicine. Nature Reviews Clinical Oncology. 2011;8(10):587–596. doi: 10.1038/nrclinonc.2011.121. [DOI] [PubMed] [Google Scholar]
- [2].Kelloff GJ, Sigman CC. Cancer biomarkers: selecting the right drug for the right patient. Nature Reviews Drug Discovery. 2012;11(3):201–214. doi: 10.1038/nrd3651. [DOI] [PubMed] [Google Scholar]
- [3].Knox SS. From ‘omics’ to complex disease: a systems biology approach to gene-environment interactions in cancer. Cancer Cell International. 2010;10(11):355–364. doi: 10.1186/1475-2867-10-11. doi:10.1186/1475-2867-10-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Kuner R. Lung cancer gene signatures and clinical perspectives. Microarrays. 2013;2(4):318–339. doi: 10.3390/microarrays2040318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Kim ES, Herbst RS, Wistuba II, Lee JJ, Blumenschein GR, Tsao A, Stewart DJ, Hicks ME, Erasmus J, Gupta S, et al. The BATTLE trial: personalizing therapy for lung cancer. Cancer Discovery. 2011;1(1):44–53. doi: 10.1158/2159-8274.CD-10-0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Conley BA, Doroshow JH. Seminars in Oncology. Vol. 41. Elsevier; 2014. Molecular analysis for therapy choice: NCI match; pp. 297–299. [DOI] [PubMed] [Google Scholar]
- [7].Herbst RS, Gandara DR, Hirsch FR, Redman MW, LeBlanc M, Mack PC, Schwartz LH, Vokes E, Ramalingam SS, Bradley JD, et al. Lung master protocol (lung-map)—a biomarker-driven protocol for accelerating development of therapies for squamous cell lung cancer: Swog s1400. Clinical Cancer Research. 2015;21(7):1514–1524. doi: 10.1158/1078-0432.CCR-13-3473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Albain KS, Barlow WE, Shak S, Hortobagyi GN, Livingston RB, Yeh IT, Ravdin P, Bugarini R, Baehner FL, Davidson NE, et al. Prognostic and predictive value of the 21-gene recurrence score assay in a randomized trial of chemotherapy for postmenopausal, node-positive, estrogen receptor-positive breast cancer. The Lancet Oncology. 2010;11(1):55–65. doi: 10.1016/S1470-2045(09)70314-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Paik S, Shak S, Tang G, Kim C, Baker J, Cronin M, Baehner FL, Walker MG, Watson D, Park T, et al. A multigene assay to predict recurrence of tamoxifen-treated, node-negative breast cancer. New England Journal of Medicine. 2004;351(27):2817–2826. doi: 10.1056/NEJMoa041588. [DOI] [PubMed] [Google Scholar]
- [10].Kang C, Janes H, Huang Y. Combining biomarkers to optimize patient treatment recommendations. Biometrics. 2014;70(3):695–707. doi: 10.1111/biom.12191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Geng Y, Zhang HH, Lu W. On optimal treatment regimes selection for mean survival time. Statistics in medicine. 2015;34(7):1169–1184. doi: 10.1002/sim.6397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Wang L, Shen J, Thall PF. A modified adaptive lasso for identifying interactions in the cox model with the heredity constraint. Statistics & probability letters. 2014;93:126–133. doi: 10.1016/j.spl.2014.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ma J, Hobbs BP, Stingo FC. Statistical methods for establishing personalized treatment rules in oncology. BioMed Research International. 2015;2015:1–13. doi: 10.1155/2015/670691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Ibrahim JG, Chen MH. Power prior distributions for regression models. Statistical Science. 2000;15(1):46–60. [Google Scholar]
- [15].Ibrahim JG, Chen MH, Sinha D. Bayesian Survival Analysis. New York, USA; Springer: 2001. [Google Scholar]
- [16].Collisson EA, Sadanandam A, Olson P, Gibb WJ, Truitt M, Gu S, Cooc J, Weinkle J, Kim GE, Jakkula L, et al. Subtypes of pancreatic ductal adenocarcinoma and their differing responses to therapy. Nature Medicine. 2011;17(4):500–503. doi: 10.1038/nm.2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Zhu CQ, Ding K, Strumpf D, Weir BA, Meyerson M, Pennell N, Thomas RK, Naoki K, Ladd-Acosta C, Liu N, et al. Prognostic and predictive gene signature for adjuvant chemotherapy in resected non-small-cell lung cancer. Journal of Clinical Oncology. 2010;28(29):4417–4424. doi: 10.1200/JCO.2009.26.4325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Monti S, Tamayo P, Mesirov J, Golub T. Consensus clustering: a resampling-based method for class discovery and visualization of gene expression microarray data. Machine Learning. 2003;52(1-2):91–118. [Google Scholar]
- [19].Jain AK. Data clustering: 50 years beyond k-means. Pattern Recognition Letters. 2010;31(8):651–666. [Google Scholar]
- [20].Hayes DN, Monti S, Parmigiani G, Gilks CB, Naoki K, Bhattacharjee A, Socinski MA, Perou C, Meyerson M. Gene expression profiling reveals reproducible human lung adenocarcinoma subtypes in multiple independent patient cohorts. Journal of Clinical Oncology. 2006;24(31):5079–5090. doi: 10.1200/JCO.2005.05.1748. [DOI] [PubMed] [Google Scholar]
- [21].Brunet JP, Tamayo P, Golub TR, Mesirov JP. Metagenes and molecular pattern discovery using matrix factorization. Proceedings of the National Academy of Sciences. 2004;101(12):4164–4169. doi: 10.1073/pnas.0308531101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Marisa L, de Reyniès A, Duval A, Selves J, Gaub MP, Vescovo L, Etienne-Grimaldi MC, Schiappa R, Guenot D, Ayadi M, et al. Gene expression classification of colon cancer into molecular subtypes: characterization, validation, and prognostic value. PLoS medicine. 2013;10(5):e1001, 453. doi: 10.1371/journal.pmed.1001453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Sadanandam A, Lyssiotis CA, Homicsko K, Collisson EA, Gibb WJ, Wullschleger S, Ostos LCG, Lannon WA, Grotzinger C, Del Rio M, et al. A colorectal cancer classification system that associates cellular phenotype and responses to therapy. Nature Medicine. 2013;19(5):619–625. doi: 10.1038/nm.3175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Ibrahim JG, Chen MH, Sinha D. On optimality properties of the power prior. Journal of the American Statistical Association. 2003;98(461):204–213. [Google Scholar]
- [25].Ibrahim JG, Chen MH, Gwon Y, Chen F. The power prior: theory and applications. Statistics in medicine. 2015;34(28):3724–3749. doi: 10.1002/sim.6728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Uno H, Claggett B, Tian L, Inoue E, Gallo P, Miyata T, Schrag D, Takeuchi M, Uyama Y, Zhao L, et al. Moving beyond the hazard ratio in quantifying the between-group difference in survival analysis. Journal of Clinical Oncology. 2014;32(22):2380–2385. doi: 10.1200/JCO.2014.55.2208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286(5439):531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- [28].R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; Vienna, Austria: 2013. URL http://www.R-project.org/ [Google Scholar]
- [29].Wilkerson MD, Hayes DN. Consensusclusterplus: a class discovery tool with confidence assessments and item tracking. Bioinformatics. 2010;26(12):1572–1573. doi: 10.1093/bioinformatics/btq170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Qiu W, Joe H. clusterGeneration: Random Cluster Generation (with Specified Degree of Separation) 2015 URL http://CRAN.R-project.org/package=clusterGeneration. R package version 1.3.4.
- [31].Therneau TM. A Package for Survival Analysis in S. 2015 URL http://CRAN.R-project.org/package=survival. version 2.38.
- [32].DeRubeis RJ, Cohen ZD, Forand NR, Fournier JC, Gelfand LA, Lorenzo-Luaces L. The personalized advantage index: Translating research on prediction into individualized treatment recommendations. a demonstration. PloS One. 2014;9(1):e83–875. doi: 10.1371/journal.pone.0083875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].d’Agostino RB. Tutorial in biostatistics: propensity score methods for bias reduction in the comparison of a treatment to a non-randomized control group. Statistics in Medicine. 1998;17(19):2265–2281. doi: 10.1002/(sici)1097-0258(19981015)17:19<2265::aid-sim918>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- [34].Ho DE, Imai K, King G, Stuart EA. MatchIt: Nonparametric preprocessing for parametric causal inference. Journal of Statistical Software. 2011;42(8):1–28. URL http://www.jstatsoft.org/v42/i08/ [Google Scholar]
- [35].Imai K, King G, Stuart EA. Misunderstandings between experimentalists and observation-alists about causal inference. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2008;171(2):481–502. [Google Scholar]
- [36].Sun Z, Wigle DA, Yang P. Non-overlapping and non-cell-type-specific gene expression signatures predict lung cancer survival. Journal of Clinical Oncology. 2008;26(6):877–883. doi: 10.1200/JCO.2007.13.1516. [DOI] [PubMed] [Google Scholar]
- [37].Kaufman JM, Amann JM, Park K, Arasada RR, Li H, Shyr Y, Carbone DP. Lkb1 loss induces characteristic patterns of gene expression in human tumors associated with nrf2 activation and attenuation of pi3k-akt. Journal of Thoracic Oncology. 2014;9(6):794. doi: 10.1097/JTO.0000000000000173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Song X, Pepe MS. Evaluating markers for selecting a patient’s treatment. Biometrics. 2004;60(4):874–883. doi: 10.1111/j.0006-341X.2004.00242.x. [DOI] [PubMed] [Google Scholar]
- [39].Royston P, Parmar MK. The use of restricted mean survival time to estimate the treatment effect in randomized clinical trials when the proportional hazards assumption is in doubt. Statistics in Medicine. 2011;30(19):2409–2421. doi: 10.1002/sim.4274. [DOI] [PubMed] [Google Scholar]
- [40].Uno H, Tian L, Cronin A, Battioui C. survRM2: Comparing Restricted Mean Survival Time. 2015 URL http://CRAN.R-project.org/package=survRM2. R package version 1.0-1.
- [41].Bender R, Lange S. Adjusting for multiple testing—when and how? Journal of Clinical Epidemiology. 2001;54(4):343–349. doi: 10.1016/s0895-4356(00)00314-0. [DOI] [PubMed] [Google Scholar]
- [42].McShane LM, Cavenagh MM, Lively TG, Eberhard DA, Bigbee WL, Williams PM, Mesirov JP, Polley MYC, Kim KY, Tricoli JV, et al. Criteria for the use of omics-based predictors in clinical trials. Nature. 2013;502(7471):317–320. doi: 10.1038/nature12564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Buettner R, Wolf J, Thomas RK. Lessons learned from lung cancer genomics: the emerging concept of individualized diagnostics and treatment. Journal of Clinical Oncology. 2013;31(15):1858–1865. doi: 10.1200/JCO.2012.45.9867. [DOI] [PubMed] [Google Scholar]
- [44].Marte B. Tumour heterogeneity. Nature. 2013;501(7467):327–327. doi: 10.1038/501327a. [DOI] [PubMed] [Google Scholar]
- [45].Diaconis P. Recent progress on de finetti’s notions of exchangeability. Bayesian statistics. 1988;3:111–125. [Google Scholar]
- [46].Lauritzen S. Sufficiency, Partial Exchangeability, and Exponential Families. 2007 http://www.stats.ox.ac.uk/~steffen/teaching/grad/partial.pdf.
- [47].Leon-Novelo L, Bekele BN, Müller P, Quintana F, Wathen K. Borrowing strength with nonexchangeable priors over subpopulations. Biometrics. 2012;68(2):550–558. doi: 10.1111/j.1541-0420.2011.01693.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Bernardo JM, Smith AF. Bayesian theory. John Wiley & Sons; West Susex, England: 2001. [Google Scholar]
- [49].Walker S, Mallick BK. A bayesian semiparametric accelerated failure time model. Biometrics. 1999;55(2):477–483. doi: 10.1111/j.0006-341x.1999.00477.x. [DOI] [PubMed] [Google Scholar]