Simultaneous Tumor Segmentation, Image Restoration, and Blur Kernel Estimation in PET Using Multiple Regularizations

Abstract

Accurate tumor segmentation from PET images is crucial in many radiation oncology applications. Among others, partial volume effect (PVE) is recognized as one of the most important factors degrading imaging quality and segmentation accuracy in PET. Taking into account that image restoration and tumor segmentation are tightly coupled and can promote each other, we proposed a variational method to solve both problems simultaneously in this study. The proposed method integrated total variation (TV) semi-blind de-convolution and Mumford-Shah segmentation with multiple regularizations. Unlike many existing energy minimization methods using either TV or L₂ regularization, the proposed method employed TV regularization over tumor edges to preserve edge information, and L₂ regularization inside tumor regions to preserve the smooth change of the metabolic uptake in a PET image. The blur kernel was modeled as anisotropic Gaussian to address the resolution difference in transverse and axial directions commonly seen in a clinic PET scanner. The energy functional was rephrased using the Γ-convergence approximation and was iteratively optimized using the alternating minimization (AM) algorithm. The performance of the proposed method was validated on a physical phantom and two clinic datasets with non-Hodgkin’s lymphoma and esophageal cancer, respectively. Experimental results demonstrated that the proposed method had high performance for simultaneous image restoration, tumor segmentation and scanner blur kernel estimation. Particularly, the recovery coefficients (RC) of the restored images of the proposed method in the phantom study were close to 1, indicating an efficient recovery of the original blurred images; for segmentation the proposed method achieved average dice similarity indexes (DSIs) of 0.79 and 0.80 for two clinic datasets, respectively; and the relative errors of the estimated blur kernel widths were less than 19% in the transversal direction and 7% in the axial direction.

1. Introduction

Positron emission tomography (PET) with ¹⁸F-fluorodeoxyglucose (FDG) plays an important role in cancer diagnosis, staging, treatment planning and outcome assessment (Juweid and Cheson, 2006; Rohren et al., 2004). PET imaging can provide functional and metabolic information of the human body, and allows earlier diagnosis and better management of oncology patients, compared to anatomical imaging techniques such as magnetic resonance imaging (MRI) and computed tomography (CT).

Many oncology applications using PET rely on accurate tumor segmentation (Zaidi and El Naqa, 2010). For example, in radiation therapy treatment planning an accurate delineation of tumor can ensure the maximum amount of dose delivered to the cancer cells in the tumor and potentially reduce side effects to surrounding healthy tissues (Pan and Mawlawi, 2008); it is known that spatial-temporal PET features extracted from pre- and post-treatment PET images are useful predictors of pathologic tumor response to neoadjuvant chemoradiation therapy, and most of these features rely on accurate delineation of the tumor regions (Tan et al., 2013).

In the past decades, a number of automatic and semiautomatic approaches have been proposed for PET tumor segmentation (Foster et al., 2014; Zaidi and El Naqa, 2010). Thresholding with a fixed percentage such as 42% or 50% of the maximum standardized uptake value (SUV_max) in the tumor region are the most frequently used one in clinic oncology using PET. However, the optimum threshold varies greatly with many factors such as tumor size and shape, image noise and contrast, and others (Biehl et al., 2006; Erdi et al., 1997; Hatt et al., 2011a; Hatt et al., 2011b). A fixed threshold may not always work well for different PET images. Various advanced methods were also used for tumor delineation in PET imaging, such as the stochastic modelling-based methods (Aristophanous et al., 2007; Hatt et al., 2009), learning-based methods (Belhassen and Zaidi, 2010; Kerhet et al., 2009), deformable models (Hsu et al., 2008; Li et al., 2008), Graph-based methods (Bađc et al., 2011), etc. Some of these methods were adopted directly from the general field of computer vision and image processing, without considering the characteristics of the PET images.

Many degrading factors can affect image quality and quantitative metabolic assessment in PET imaging. Among others, the partial volume effect (PVE) is recognized as one of the most important degrading factors, due to the limited spatial resolution of PET scanners, especially for tumors with small sizes (Pan and Mawlawi, 2008; Zaidi and El Naqa, 2010). PVE renders an object boundary blurry in PET imaging (Pan and Mawlawi, 2008), which seriously affect the tumor segmentation accuracy. To remedy this problem, some specifically designed segmentation methods have been proposed for PET images.

In order to calculate a reasonable threshold for tumor segmentation in PET, adaptive thresholding methods have been proposed (Biehl et al., 2006; Daisne et al., 2003; Drever et al., 2006; Erdi et al., 1997; Jentzen et al., 2007; Nestle et al., 2005; Schaefer et al., 2008). Rather than a direct consideration of PVE, these methods computed the optimal threshold using different image features, such as the source-to-background ratio (SBR), full width at half maximum (FWHM), mean background intensity, mean lesion intensity, and volume size (Foster et al., 2014). Generally, these methods required prior calibrations, and their parameters needed to be re-optimized through phantom experiments for a new scanner and different image reconstruction and correction algorithms. Tan et al. (2015) showed that the problem to calculate the optimal threshold for PET tumor segmentation is itself ill-posed, or undetermined. Another major limitation of thresholding methods is that these methods might not work well for tumors with heterogeneous metabolic uptake.

Some other segmentation methods considering PVE have also been studied for PET in the past several years (De Bernardi et al., 2009; El Naqa et al., 2004; Geets et al., 2007; Li et al., 2008; Riddell et al., 1999). Most of these methods recovered the ‘clean’ image first by partial volume correction (PVC) techniques, and the tumors were then delineated on the recovered image (Geets et al., 2007). Various PVC methods have been developed for PET imaging. Srinivas et al. (2009) provided a practical look-up table based on recovery coefficient (RC) for the PVC of spherical lesions. Brix et al. (1997) put forward a reconstruction-based PVC method. This method incorporated scanner characteristics into the process of iterative image reconstruction to improve the spatial resolution of a whole-body PET system. Rousset et al. (1998) designed a geometric transfer matrix (GTM) method to correct PVE for PET brain imaging. The GTM method modeled the geometric interactions between the PET system and the brain activity distribution. Moreover, some de-convolution based image restoration methods have been used for PVE correction (Barbee et al., 2010; Boussion et al., 2009; Kirov et al., 2008; Teo et al., 2007; Tohka and Reilhac, 2008). Teo et al. (2007) proposed an iterative de-convolution technique based on Van Cittert’s method (Van Cittert, 1931) to correct PVE. Tohka and Reilhac (2008) studied three iterative de-convolution algorithms for PVC. The three de-convolution methods included Richardson–Lucy (Lucy, 1974; Richardson, 1972), reblurred Van Cittert iteration according to Carasso (1999), and reblurred Van Cittert iteration with the total variation (TV) regularization (Rudin et al., 1992). Kirov et al. (2008) presented a post-reconstruction PVE correction based on iterative de-convolution, and further modified the regularization procedure (Alenius and Ruotsalainen, 1997) depending on the local topology of the PET image to avoid an increase in variance. In these de-convolution methods the point spread functions (PSFs) were assumed to be known or measured in advance.

Unlike these existing methods considering image restoration (PVC) and tumor segmentation as two separate processes, in this study we proposed a new variational framework for simultaneous image restoration, tumor segmentation and blur kernel estimation, specifically designed for PET imaging.

The idea of simultaneous image restoration and segmentation is itself not new. Bar et al. (2006) integrated semi-blind image de-convolution (parametric blur-kernel) with Mumford-Shah segmentation in a variational framework for two-dimensional image restoration and segmentation. Zheng and Hellwich (2006) built a blind image de-convolution and segmentation model by extending the Mumford-Shah regularization in the context of Bayesian estimation. A cost term for the estimation of the blur kernels via a newly introduced prior solution space was added to the Mumford-Shah model. Cai (2015) established a multiphase segmentation model by combining the piecewise constant Mumford-Shah segmentation model with a new data fidelity term coming from an image restoration model. This method can be used for noisy, blurred vector-valued images; and the noise type and blur kernel have to be known previously. Ayasso and Mohammad-Djafari (2010) presented a method to simultaneously restore and segment the nondestructive testing images. They studied a family of heterogeneous Gauss–Markov fields with Potts region labels model in a Bayesian estimation framework. Paul et al. (2013) derived a new class of data-fitting energies that coupled image restoration and segmentation using a statistical framework of generalized linear models for two-region segmentation of scalar-valued images. Most of these methods were proposed for general image processing applications in two-dimensionality, and they generally used either TV regularization (Paul et al., 2013) or L₂ regularization (Bar et al., 2006; Zheng and Hellwich, 2006) on the restored image, and used an isotropic Gaussian function to model the PSF (Bar et al., 2006) or assumed that the PSF was already known (Ayasso and Mohammad-Djafari, 2010; Cai, 2015; Paul et al., 2013).

However, these existing methods may not be used directly in PET because a PET image has its own specific properties and the clinic radiation oncology has its own specific requirements for PET image processing as well. First of all, in methods based on the Mumford-Shah model (Bar et al., 2006; Zheng and Hellwich, 2006), the regularization for image intensity was applied to only the non-edge areas, but not to target edges. As a result, the intensity over these un-regularized edges in the restored image was sometimes unstable. Our experimental results have confirmed that, without regularizations over the tumor edges, some abnormal large uptake values can appear in the restored PET image. This might not be a problem for general image processing applications. However, in radiation oncology, it is well-known that the maximum uptake in a tumor region is a widely used feature for cancer diagnosis and treatment outcome prediction (Tan et al., 2013). These abnormal large uptake values on tumor edges might lead to an incorrect interpretation of PET images in patient management. Secondly, existing methods generally used only one single regularization (e.g., TV in (Paul et al., 2013) and L₂ in (Bar et al., 2006; Zheng and Hellwich, 2006)). However, a PET image consists of components with different characteristics, requiring multiple regularizations in the variational segmentation and restoration framework. For example, tumor edges in PET are significantly blurred due to PVE, which asks for regularizations with the advantage of preserving edges such as TV. On the other hand, the metabolic uptake inside the tumor region of a PET image may vary smoothly and is somehow heterogeneous. The TV regularization may not work well for the non-edge component of a typical PET image, because minimizing an objective function with the TV regularization enforces neighboring pixels to have similar uptake values thus tends to produce piecewise constant areas in the restored image (Chan et al., 2000), which is the well-known staircase effect. For the non-edge component, the L₂ regularization should be more appropriate than TV. Thirdly, the clinic PET scanner can have different resolutions in different directions, which asks for an anisotropic PSF model rather than an isotropic one, as used in most existing methods. Last but not the least, most existing methods were implemented and tested on two-dimensional images. The strong spatial correlation among neighboring slices in PET requires three-dimensional (3D) processing.

To the best of our knowledge, there is no published method of simultaneous restoration and segmentation specifically designed for PET images. The proposed method in this study addressed both problems simultaneously by integrating semi-blind de-convolution and Mumford-Shah segmentation model, with regularization terms and blur kernel estimation adapted to PET imaging. The novelty of the proposed method can be summarized as follows:

1. In order to suppress the abnormal large uptake values appearing over edges in the restoration result, regularizations were applied not only to the non-edge component but also to the tumor edge component.

2. Multiple regularizations were employed in the simultaneous restoration and segmentation variational framework, with each regularization adapted to a different image component in PET. Particularly, the TV regularization was used over tumor edges for its good edge-preserving ability, while the L₂ regularization was used inside the tumor region to preserve the smooth change of the metabolic uptake in a PET image.

3. The blur kernel was modeled as anisotropic Gaussian to address the resolution difference in transverse and axial directions of the PET scanner.

4. The algorithm was implemented in three-dimensionality, which made full use of the spatial correlation among neighboring slices and potentially improved the accuracy of restoration and segmentation.

The proposed method was iteratively optimized using an alternating minimization (AM) algorithm. The performance of the proposed method was validated on a physical phantom and two datasets of clinic patients with non-Hodgkin’s lymphoma and esophageal cancer, respectively. Experimental results showed that the proposed method improved the segmentation performance when compared with all other tested methods. The blur kernel estimation and desired restored image can be obtained simultaneously.

2. Methods and materials

2.1. Fundamentals

2.1.1. De-convolution

Let Ω ⊂ ℝ³ be a closed and bounded region and f : Ω → ℝ be a sharp or ideal 3D image defined on Ω. The PET imaging can be expressed as the following model (Boussion et al., 2009; El Naqa et al., 2006)

$$g=f\ast h+n,$$ (1)

where h is the PSF of the scanner, n is the additive noise, g is the observed PET image defined on Ω, and * is the 3D convolution operator. In PET imaging, the noise is mainly caused by inaccurate counting of the photon pairs (Humm et al., 2003), and the noise property is related to the used reconstruction methods (Tong et al., 2010). A common assumption is that overall the noise may be characterized as Gaussian (Ollinger and Fessler, 1997).

Normally, only the blurred image g is given, PSF and the sharp image f are unknown. We may want to recover both the sharp image and PSF, which is known as blind de-convolution. A blind de-convolution problem is ill-posed with respect to both f and h. You and Kaveh (1996) proposed to simultaneously regularize f and h and solved the blind de-convolution problem by minimizing the following energy functional

$$F\left(f,h\right)=\frac{1}{2}{\Vert f\ast h-g\Vert }_{L_2(\mathrm{\Omega })}^2+{\alpha }_1{\int }_{\mathrm{\Omega }}{\left|\nabla f\right|}^{2}dA+{\alpha }_2{\int }_{\mathrm{\Omega }}{\left|\nabla h\right|}^{2}dA,$$ (2)

where α₁ and α₂ are both positive parameters, and dA denotes dxdydz (dx, dy and dz represent the infinitesimal elements of x, y and z, respectively). Unfortunately, one potential drawback of the L₂ regularization in Eq.(2) is that it over-smoothes object edges (Perrone and Favaro, 2014). In view of the superiority of the TV regularization on preserving edges, Chan and Wong (1998) regularized both the recovered image and PSF by TV norm. Their blind de-convolution model can be expressed as

$$F\left(f,h\right)=\frac{1}{2}{\Vert f\ast h-g\Vert }_{L_2(\mathrm{\Omega })}^2+{\alpha }_1{\int }_{\mathrm{\Omega }}\left|\nabla f\right|dA+{\alpha }_2{\int }_{\mathrm{\Omega }}\left|\nabla h\right|dA.$$ (3)

The parameters α₁ and α₂ control the smoothness of the recovered image and PSF, respectively.

2.1.2. Mumford-Shah segmentation

In Ref (Mumford and Shah, 1989), Mumford and Shah proposed an energy minimization method to find an optimal piecewise smooth function f to approximate the observed image g. The energy functional was defined as

$$F(f,K)=\frac{1}{2}{\int }_{\mathrm{\Omega }}{(f-g)}^{2}dA+\beta {\int }_{\mathrm{\Omega }/K}{|\nabla f|}^{2}dA+\alpha {\int }_{K}d\sigma ,$$ (4)

where α and β are both positive parameters, K ⊂ Ω represents the edge set of the objects, Ω/K denotes the non-edge areas of the image, and f : Ω → ℝ is continuous or even differentiable in Ω/K but discontinuous across K. The first term is the fidelity term, which requires f to be an “optimal” piecewise smooth approximation of g; the second term is the piecewise-smoothness term, which forces the solution f to be smooth in Ω/K; the third term stands for the total surface measure of the edge set K, which contributes to the smoothness of the edge set K.

The minimization of Eq.(4) is difficult due to the non-convex property of this functional and the unknown discontinuity edge set K in the integral domains (Scherzer, 2011). Ambrosio and Tortorelli (1990) introduced the Γ-convergence to solve this problem. They approximated an irregular functional F(f, K) by a sequence of regular functionals F_ε (f, v) with a small positive constant ε which meets the equation of $\underset{\epsilon \to 0}{lim}{F}_{\epsilon }\left(f,v\right)=F(f,K)$, and the minimizing of F can thus be replaced by the minimizing of F_ε. A continuous function v was used to represent the so-called edge map, i.e., v(x, y, z) ≈ 0 if (x, y, z) is close to object edges, and v(x, y, z) ≈ 1 if (x, y, z) is far away from object edges. Thus, Eq.(4) can be replaced with the Γ-convergence form:

$$F_{\epsilon }(f,v)=\frac{1}{2}{\int }_{\mathrm{\Omega }}{(f-g)}^{2}dA+\beta {\int }_{\mathrm{\Omega }}{v}^2{\left|\nabla f\right|}^{2}dA+\alpha {\int }_{\mathrm{\Omega }}\left(\epsilon {\left|\nabla v\right|}^2+\frac{1}{4\epsilon }{(v-1)}^2\right)dA.$$ (5)

2.2. Coupling restoration with segmentation

2.2.1. A novel model of simultaneous restoration, segmentation and blur kernel estimation

The blurred edges of a tumor in a PET image can become sharp after using a de-convolution technique, which would be helpful to segmentation; conversely, if the precise contours can be obtained by segmentation, it would be easier to estimate the blur kernel, and thus be helpful to image restoration. Considering that both segmentation and restoration problems can benefit each other, we integrated tumor restoration with segmentation using a variational framework in PET.

The proposed method combined the de-convolution model (Eq.(3)) with the Mumford-Shah segmentation model (Eq.(4)), and utilized multiple regularization terms for the restored image. The blur kernel was constrained to be an anisotropic Gaussian parameterized by different widths in transversal and axial directions to be adapted to the different spatial resolution in different directions of a PET scanner. The TV regularization has the advantage of preserving edge information, but suffers from the well-known staircase effect; the L₂ regularization can avoid staircase effect, but may result in over-smoothed object edges. In view of this, we used the TV regularization over tumor edges and the L₂ regularization in non-edge areas in the restored images. Our functional was defined as

$$F\left(f,K,{\sigma }_1,{\sigma }_2\right)=\frac{1}{2}{\iiint }_{\mathrm{\Omega }}{\left(h_{{\sigma }_1{\sigma }_2}\ast f-g\right)}^2\mathit{dxdydz}+\beta {\iiint }_{\mathrm{\Omega }/K}{\left|\nabla f\right|}^2\mathit{dxdydz}+\eta {\iiint }_K\left|\nabla f\right|\mathit{dxdydz}+\alpha {\int }_{K}d\sigma +\gamma {\iiint }_{\mathrm{\Omega }}{\left|\nabla h_{{\sigma }_1,{\sigma }_2}\right|}^2\mathit{dxdydz}.$$ (6)

It is difficult to minimize the above functional because of the non-convex property and the unknown discontinuity edge set K. We rephrased the proposed model using Γ-convergence approximation:

$$\begin{array}{l}{F}_{\epsilon }\left(f,v,{\sigma }_1,{\sigma }_2\right)=\frac{1}{2}{\iiint }_{\mathrm{\Omega }}{\left(h_{{\sigma }_1,{\sigma }_2}\ast f-g\right)}^2\mathit{dxdydz}+\beta {\iiint }_{\mathrm{\Omega }}{v}^2{\left|\nabla f\right|}^2\mathit{dxdydz}\\ +\eta {\iiint }_{\mathrm{\Omega }}\left(1-v^2\right)\left|\nabla f\right|\mathit{dxdydz}+\alpha {\iiint }_{\mathrm{\Omega }}\left(\epsilon {\left|\nabla v\right|}^2+\frac{{(v-1)}^2}{4\epsilon }\right)\mathit{dxdydz}\\ +\gamma {\iiint }_{\mathrm{\Omega }}{\left|\nabla h_{{\sigma }_1,{\sigma }_2}\right|}^2\mathit{dxdydz},\end{array}$$ (7)

where α, β, η, γ and ε are positive parameters; v represents the edge map; h_σ1,σ2 is an anisotropic Gaussian kernel parameterized by its widths σ₁ (transversal direction) and σ₂ (axial direction):

$$h_{{\sigma }_1,{\sigma }_2}=\frac{1}{{(2\pi )}^{3/2}{\sigma }_1^2{\sigma }_2}{e}^{-\left(\frac{x^2+y^2}{2{\sigma }_1^2}+\frac{z^2}{2{\sigma }_2^2}\right)}.$$ (8)

In order to enhance the robustness and convergence of the algorithm, we imposed the following constraints on h_σ1,σ2 and f:

$$\begin{array}{l}{\iiint }_{\mathrm{\Omega }}{h}_{{\sigma }_1,{\sigma }_2}\left(x,y,z\right)\mathit{dxdydz}=1,\\ h_{{\sigma }_1,{\sigma }_2}\left(x,y,z\right)\ge 0,f\left(x,y,z\right)\ge 0.\end{array}$$ (9)

The first term in Eq.(7) is the data fidelity term which contributes to the approximation of the restored image f and the given blurred image g. The second term in Eq.(7) is a piecewise-smoothness term (L₂ regularization) constraining the smoothness of the non-edge areas; and the third term (TV regularization) in Eq.(7) is the TV regularization for object edges, which contributes to the preservation of edge information. The fourth term in Eq.(7) is used to constrain the length of the edge set. The last term in Eq.(7) represents the regularization of the blur kernel in which the convenient L₂ norm was used because the Gaussian kernel h_σ1,σ2 is a smooth function. This term is necessary to reduce the fundamental ambiguity in the division of the apparent blur between the restored image and the blur kernel (Bar et al., 2006).

2.2.2. Alternating minimization

It can be observed that the objective function (Eq.(7)) is not jointly convex with respect to f, v and h_σ1,σ2, but it is convex with respect to any one of the three functions if the other two are estimated and fixed. In view of the above, the AM algorithm (Chan and Shen, 2005; Chan and Wong, 1998; You and Kaveh, 1996) was used to iteratively optimize the energy functional in our study. The AM algorithm is a classical method for solving composite minimization problems. The basic idea is to minimize the objective function only with respect to one variable and keep the others fixed in each iteration. The convergence of the algorithm was proved in Ref (Chan and Shen, 2005).

In our study, the restored image f was initialized as the blurred image g; the edge function v was initialized with a function of constant 1; σ₁ and σ₂ were initialized to a small number to make the blur kernel h_σ1,σ2 approximate the delta function kernel.

The first and second steps in our AM algorithm were to minimize the objective function (Eq.(7)) with respect to the edge map v and the restored image f. These two steps were achieved by solving the Euler-Lagrange equations subject to Neumann boundary conditions (∂v/∂N=0, ∂f/∂N=0):

$$\frac{\delta F_{\epsilon }}{\delta v}=\left(2\beta {\left|\nabla f\right|}^2-2\eta \left|\nabla f\right|\right)v+\alpha ·\frac{v-1}{2\epsilon }-2\epsilon \alpha {\nabla }^{2}v=0,$$ (10)

$$\frac{\delta F_{\epsilon }}{\delta f}=\left(h_{{\sigma }_1,{\sigma }_2}\ast (f-g\right)\ast h_{{\sigma }_1,{\sigma }_2}\left(-x,-y,-z\right)-2\beta \text{Div}\left(v^2\nabla f\right)-\eta \text{Div}\left(\left(1-v^2\right)\frac{\nabla f}{\left|\nabla f\right|}\right)=0.$$ (11)

The detailed derivation of the two Euler-Lagrange equations is presented in Appendix A.

During the (i+1)^th iteration of the AM algorithm, according to the relationship between the Euler-Lagrange equation (Eq.(10)) and the gradient descent flow, we updated the edge map v by the following iterations

$$v_{t+1}^{i+1}=v_t^{i+1}-{\epsilon }_v\left[\left(2\beta {\left|\nabla f^i\right|}^2-2\eta \left|\nabla f^i\right|\right)v_t^{i+1}+\alpha ·\frac{v_t^{i+1}-1}{2\epsilon }-2\epsilon \alpha {\nabla }^2{v}_t^{i+1}\right],$$ (12)

where the step length ε_v > 0 and t denotes the iteration number of the gradient descent flow. This iteration was repeated until the mismatch of the current and the previous iteration results was less than a predefined small positive constant. Similarly, according to the Euler-Lagrange equation Eq.(11), we updated the restored image f by

$$f_{t+1}^{i+1}=f_t^{i+1}-{\epsilon }_f\left[\left(h_{{\sigma }_1,{\sigma }_2}^i\ast f_t^{i+1}-g\right)\ast h_{{\sigma }_1,{\sigma }_2}^i\left(-x,-y,-z\right)-2\beta \text{Div}\left({(v^{i+1})}^2\nabla f_t^{i+1}\right)-\eta \text{Div}\left(\left(1-{(v^{i+1})}^2\right)\frac{\nabla f_t^{i+1}}{\left|\nabla f_t^{i+1}\right|}\right)\right].$$ (13)

The step length ε_f >0 and the termination condition was the same as the iteration of v. The restored image f was truncated at zero:

$$f^{i+1}\left(x,y,z\right)=\{\begin{array}{ll}{f}^{i+1}\left(x,y,z\right),\hfill & \text{if}{f}^{i+1}\left(x,y,z\right)>0\hfill \\ 0,\hfill & \mathit{otherwise}.\hfill \end{array}$$ (14)

The next step of the AM algorithm was to minimize the objective function (Eq.(7)) with respect to the blur kernel widths σ₁ and σ₂ by solving the following two equations:

$$\frac{\partial F_{\epsilon }}{\partial {\sigma }_1}=\underset{\mathrm{\Omega }}{\iiint }\left[\left(h_{{\sigma }_1,{\sigma }_2}\ast f-g\right)\left(\frac{\partial h_{{\sigma }_1,{\sigma }_2}}{\partial {\sigma }_1}\ast f\right)+\gamma \frac{\partial }{\partial {\sigma }_1}{\left|\nabla h_{{\sigma }_1,{\sigma }_2}\right|}^2\right]\mathit{dxdydz}=0,$$ (15)

$$\frac{\partial F_{\epsilon }}{\partial {\sigma }_2}=\underset{\mathrm{\Omega }}{\iiint }\left[\left(h_{{\sigma }_1,{\sigma }_2}\ast f-g\right)\left(\frac{\partial h_{{\sigma }_1,{\sigma }_2}}{\partial {\sigma }_2}\ast f\right)+\gamma \frac{\partial }{\partial {\sigma }_2}{\left|\nabla h_{{\sigma }_1,{\sigma }_2}\right|}^2\right]\mathit{dxdydz}=0,$$ (16)

where

$$\frac{\partial h_{{\sigma }_1,{\sigma }_2}}{\partial {\sigma }_1}=\frac{1}{{(2\pi )}^{3/2}{\sigma }_1^2{\sigma }_2}{e}^{-\left(\frac{x^2+y^2}{2{\sigma }_1^2}+\frac{z^2}{2{\sigma }_2^2}\right)}\left(\frac{x^2+y^2}{{\sigma }_1^3}-\frac{2}{{\sigma }_1}\right),$$ (17)

$$\frac{\partial h_{{\sigma }_1,{\sigma }_2}}{\partial {\sigma }_2}=\frac{1}{{(2\pi )}^{3/2}{\sigma }_1^2{\sigma }_2}{e}^{-\left(\frac{x^2+y^2}{2{\sigma }_1^2}+\frac{z^2}{2{\sigma }_2^2}\right)}\left(\frac{z^2}{{\sigma }_2^3}-\frac{1}{{\sigma }_2}\right),$$ (18)

and

$$\frac{\partial }{\partial {\sigma }_1}{\left|\nabla h_{{\sigma }_1,{\sigma }_2}\right|}^2=\frac{x^2+y^2}{4{\pi }^3{\sigma }_1^4{\sigma }_2^2}{e}^{-\left(\frac{x^2+y^2}{{\sigma }_1^2}+\frac{z^2}{{\sigma }_2^2}\right)}\left(\frac{x^2+y^4}{{\sigma }_1^7}-\frac{4}{{\sigma }_1^5}\right)+\frac{z^2}{4{\pi }^3{\sigma }_1^4{\sigma }_2^2}{e}^{-\left(\frac{x^2+y^2}{{\sigma }_1^2}+\frac{z^2}{{\sigma }_2^2}\right)}\left(\frac{x^2+y^2}{{\sigma }_1^3{\sigma }_2^4}-\frac{2}{{\sigma }_1{\sigma }_2^4}\right),$$ (19)

$$\frac{\partial }{\partial {\sigma }_2}{\left|\nabla h_{{\sigma }_1,{\sigma }_2}\right|}^2=\frac{x^2+y^2}{4{\pi }^3{\sigma }_1^4{\sigma }_2^2}{e}^{-\left(\frac{x^2+y^2}{{\sigma }_1^2}+\frac{z^2}{{\sigma }_2^2}\right)}\left(\frac{z^2}{{\sigma }_1^4{\sigma }_2^3}-\frac{1}{{\sigma }_1^4{\sigma }_2}\right)+\frac{z^2}{4{\pi }^3{\sigma }_1^4{\sigma }_2^2}{e}^{-\left(\frac{x^2+y^2}{{\sigma }_1^2}+\frac{z^2}{{\sigma }_2^2}\right)}\left(\frac{z^2}{{\sigma }_2^7}-\frac{3}{{\sigma }_2^5}\right).$$ (20)

The detailed derivation of Eqs.(17) and (19) is presented in Appendix B. Eqs.(15) and (16) were solved using the bisection method.

During the (i+1)^th iteration of the AM algorithm, the blur kernel $h_{{\sigma }_1,{\sigma }_2}^{i+1}$ was obtained as:

$$h_{{\sigma }_1,{\sigma }_2}^{i+1}\left(x,y,z\right)=\{\begin{array}{ll}{h}_{{\sigma }_1,{\sigma }_2}^{i+1}\left(x,y,z\right),\hfill & \text{if}{h}_{{\sigma }_1,{\sigma }_2}^{i+1}\left(x,y,z\right)>0\hfill \\ 0,\hfill & \mathit{otherwise},\hfill \end{array}$$ (21)

$$h_{{\sigma }_1,{\sigma }_2}^{i+1}\left(x,y,z\right)=\frac{h_{{\sigma }_1,{\sigma }_2}^{i+1}\left(x,y,z\right)}{{\int }_{\mathrm{\Omega }}{h}_{{\sigma }_1,{\sigma }_2}^{i+1}\left(x,y,z\right)\mathit{dxdydz}}.$$ (22)

The AM algorithm can be summarized as follows:

Initialization: f = g, v = 1, σ1 = σ2 = ε1, σ1prev = σ2prev ≫ 1

Iteration: while (|σ1prev − σ1| > ε2 or |σ2prev − σ2| > ε2) repeat Update the edge map v using the gradient descent algorithm, as in Eq.(12). Update the restored image f using the gradient descent algorithm, as in Eq.(13), and constrain f with Eq.(14). Set σ1prev = σ1, and update σ1 by solving Eq.(15) using the bisection method. Set σ2prev = σ2, and update σ2 by solving Eq.(16) using the bisection method. Update the blur kernel hσ1,σ2 with the new σ1 and σ2 using Eqs.(21) and (22).

end

Here ε₂ was set as a small positive constant to control the degree of convergence of the AM algorithm.

2.3. Validation study

2.3.1. Datasets for validation

The performance of the proposed algorithm was validated on a physical phantom and two clinic datasets with different tumor types and imaged using different scanners. This retrospective study was approved by the University of Maryland Baltimore Institutional Review Board.

In the physical phantom, six spheres used as target volumes were placed inside a cylindrical container to mimic clinical head and neck tumor (Li et al., 2008). The volumes of these six spheres were 20, 16, 12, 6, 1 and 0.5 ml, respectively. These spheres were filled with ¹¹C (half life=20.38 min) solution at an activity concentration of 3.627 μCi/ml as sources and the cylindrical container was filled with ¹⁸F-FDG (half life=109.77 min) solution at an activity concentration of 0.224 μCi/ml as the background. The phantom was scanned continuously on a Biograph-40 True Point/True View (Siemens Medical Solutions Inc., Knoxville, TN) PET/CT scanner for 120 min. The spatial resolution for a point source in the transversal direction and axial direction were 4.5 mm and 5.7 mm (FWHM, at 10 mm from the center of the field of view), respectively. Images were reconstructed using the iterative Ordered Subset Expectation Maximization algorithm (OSEM), and the voxel size was 4.0728×4.0728×2.027 mm³. Because of the different decay rate of ¹¹C and ¹⁸F-FDG, PET images with SBRs of 8:1, 6:1, 4:1 and 2:1, respectively, were obtained for our experiments.

The first clinic dataset was acquired from eleven patients with non-Hodgkin’s lymphoma. Each patient was imaged on a GE Advance PET tomograph (General Electric Medical Systems, Milwaukee, Wisconsin, USA) (Betrouni et al., 2012). The transverse and axial resolution were 3.8 mm and 4.0 mm, respectively, at the center of the field of view (DeGrado et al., 1994). Each patient received the intravenous (IV) injection of a 370MBq activity of ¹⁸F-FDG one hour before the beginning of a whole-body imaging scan. The scanning process consisted of a 5-min emission scan and a 2-min transmission scan (external source of germanium), and the final PET images were reconstructed in transverse slices using the OSEM algorithm with a voxel size of 4.3×4.3×4.3 mm³ (Betrouni et al., 2012). For each PET image, only one tumor was selected for test and each tumor was manually delineated three times by five qualified nuclear medicine physicians (Betrouni et al., 2012). Therefore, each tumor was performed fifteen manual delineations. The ground truth for each tumor was computed using a voting strategy based on the fifteen manual delineations: a voxel was considered as the tumor voxel if and only if it was enclosed in the target region at least eight times.

The second clinic dataset was acquired from twenty patients with esophageal cancer. These patients were subjected to PET/CT scans at University of Maryland Medical Center from 2006 to 2009, and all imaging scans were completed on an integrated 16-slice Gemini PET/CT scanner (Philips Medical Systems, Cleveland, OH). The spatial resolution near the center was about 4.9 mm (FWHM) in both transverse and axial directions (Lodge et al., 2004). Following an institution standard protocol, the patients fasted for at least 4 hours and then received the intravenous injection of 12–14 mCi ¹⁸F-FDG. One hour after the injection, whole-body PET and CT imaging scan was started. PET image were attenuation corrected and reconstructed using a maximum likelihood algorithm. The voxel size of PET and CT images were respectively 4.0×4.0×4.0 mm³ and 0.98×0.98×4.0 mm³. The ground truth were manually delineated by an experienced radiation oncologist using the complementary visual features of PET and CT. The general location and nature of a lesion were determined by the visual interpretation of the PET image and the boundary was determined by both PET and CT images.

For each sphere or tumor, a rectangular region of interest (ROI) was manually defined that encloses the whole selected sphere or tumor. The proposed method and all comparison algorithms were implemented in ROI.

2.3.2. Algorithms for comparison

For comparison, the deformable models — Mumford-Shah (MS) segmentation algorithm (Mumford and Shah, 1989), Active Contours (AC) (Chan and Vese, 2001) and Geodesic Active Contours (GAC) (Caselles et al., 1997), the widely used thresholding methods — 42% and 50% of the SUV_max (42% threshold and 50% threshold) and Otsu automatic thresholding (Otsu, 1975), the clustering algorithm — Fuzzy C-means Clustering (FCM), and graph theory method — Graph Cuts (GC) (Boykov and Funka-Lea, 2006) were also tested in our experiments. In addition, in order to test the effects of the multiple regularizations in our proposed algorithm, the simultaneous restoration and segmentation method (Bar’s method) proposed by Bar et al. (2006) was tested. Note that this method does not use any regularizations on the edge set.

The parameters of all methods were manually optimized. To adjust the parameters of the proposed method, we first chose one image from each dataset. The parameter α controls the length of the object edges. The segmented foreground areas decrease when α increases. For PET images with a large tumor volume, a smaller value should be assigned to α. Parameters β and η control the smoothness of the restored images. When β increases, the restored image becomes smoother. When η decreases, the restored edges become sharper. When the SBR of the PET image is low, β and η should be set to a relative smaller value. The parameter γ controls the width of the Gaussian kernel. A larger γ will lead to a wider kernel. If the observed image is severely blurred, a relative larger value of γ should be better for estimating the blur kernel. We adjusted the values of β, η and γ depending on the restored image, and adjusted α depending on the segmentation result. We evaluated the parameter adjustment according to the accuracy of the segmentation result. When the segmentation accuracy no longer increased, we assumed that the parameters were optimized and the proposed method achieved the best performance. Because the real blur kernels of different images kept unchanged in the same dataset, the resulting β, η and γ were used for the remaining images in the same dataset. Only the parameter α might still need to be adjusted according to the tumor volume. For all three experimental data sets, the parameters of the proposed method were tuned in the following range: α changed between 5×10⁻⁸ and 9×10⁻⁷, β changed between 2×10⁻² and 5×10⁻², η was between 3×10⁻⁴ and 5×10⁻³, γ altered between 10 and 60, ε₁=0.8, and ε₂=10⁻⁴.

2.3.3. Criteria for performances evaluation

The segmentation accuracy of all tested algorithms was evaluated using three criteria.

Dice similarity index (DSI) measures the similarity (spatial overlap) between the segmented and ground truth foreground objects. Denote the segmented foreground objects set as V_A and the ground truth foreground set as V_R. DSI is computed as follows (Dewalle-Vignion et al., 2011; Prieto et al., 2012):

$$\mathit{DSI}(V_A,V_R)=\frac{2\left|V_A\cap V_R\right|}{\left|V_A\right|+\left|V_R\right|},$$ (23)

where |X| represents the size of the set X. A bigger value of DSI indicates a better segmentation. DSI reaches the maximum value 1 if two sets completely overlap, and reaches the minimum value 0 if the two sets have no spatial overlap.

Classification error (CE) measures the spatial location bias of the segmented foreground objects compared to the ground truth foreground (Hatt et al., 2009):

$$CE(V_A,V_R)=\frac{\left|V_{FP}\right|+\left|V_{FN}\right|}{\left|V_R\right|},$$ (24)

where |V_FP| represents the number of false positive errors (background voxels that were wrongly assigned to tumor), |V_FN| represents the number of false negative errors (tumor voxels that were wrongly assigned to background).

Volume error (VE) measures the difference between the segmented foreground volume and the ground truth foreground volume (Dewalle-Vignion et al., 2011):

$$VE(V_A,V_R)=\frac{\mathit{abs}\left(\left|V_A\right|-\left|V_R\right|\right)}{\left|V_R\right|}.$$ (25)

A bigger value of CE and VE means a worse segmentation. The values of CE and VE can be bigger than 1. In order to enhance the observability, all the values bigger than 1 were truncated as 1 in our experiments.

We used the recovery coefficient (RC) to quantify the restoration accuracy. RC is generally used to quantify the degree of blurring of a blurred image and hence can be used to evaluate the restoration accuracy (Geworski et al., 2000; Kessler et al., 1984; Srinivas et al., 2009). RC is defined as:

$$RC=\frac{\mathit{Measured}\mathit{sphere}\mathit{activity}-\mathit{Measured}\mathit{bkg}\mathit{activity}}{\mathit{True}\mathit{sphere}\mathit{activity}-\mathit{True}\mathit{bkg}\mathit{activity}},$$ (26)

where bkg is the abbreviation for background. A smaller RC value means that the image is more blurred. For restored image, the closer the RC gets to 1, the better the restoration result is.

For blur kernel estimation, we calculated the relative errors between the corresponding FWHMs of the estimated blur kernel widths and the real FWHMs of the PET scanner.

3. Results

3.1. A toy simulation

The proposed algorithm was first tested on a toy computer simulation. A non-blurred volume was produced with a uniform background of intensity of 50 and a 3D sphere of uniform activity concentration embedded in its center. Without any loss of generality, the voxel size was set to be 1.0×1.0×1.0 mm³. The sphere radius was set to be 2 mm, 4 mm and 6 mm, respectively. For each radius, three different activity concentrations were set, which made SBR vary as 2:1, 3:1, and 4:1. Each non-blurred volume was convolved with a 3D isotropic Gaussian PSF of FWHM of 4 mm and 6 mm, respectively. A total of 18 blurred volumes were constructed. The task was to restore the non-blurred volume, delineate the sphere, and estimate the PSF, given a blurred volume.

Fig. 1 shows DSIs of tested methods for sphere segmentation, averaged over all 18 blurred volumes. The proposed method (DSI=0.80) was much better than other tested methods according to this evaluation criterion. Bar’s method (DSI=0.74) was the second best among all methods. In those without taking into account PVE, GC (DSI=0.71) and AC (DSI=0.70) were relatively better. The two fixed threshold methods — 42% threshold (DSI=0.25) and 50% threshold (DSI=0.33) performed the worst.

Figure 1.

DSI for sphere segmentation, averaged over all 18 blurred volumes.

Fig. 2 (a) presents DSI as a function of FWHM, averaged over all sphere radii and SBRs. Comparing with the FWHM of 4mm, the FWHM of 6mm made images more blurred. As a result, all tested methods performed worse for the FWHM of 6mm. The proposed method performed the best for both FWHM levels and it was more stable over the change of FWHM. Fig. 2 (b) shows DSI as a function of the sphere radius, and Fig. 2 (c) shows DSI as a function of SBR. The proposed method was robust to the change of both sphere radii and SBRs. Although Bar’s method, Otsu, FCM, AC, GAC and GC algorithms performed almost as well as the proposed method for the largest spheres (6mm), their performance dropped sharply with the decrease of the sphere radius. The two fixed threshold methods were especially sensitive to both sphere radius and SBR.

Figure 2.

(a) DSI at different FWHM levels (averaged over all sphere radii and SBRs); (b) DSI at different sphere radius (averaged over all SBRs and FWHM levels); (c) DSI at different SBRs (averaged over all sphere radii and FWHM levels).

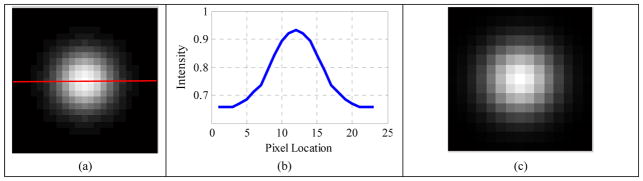
One slice of a blurred volume with FWHM 6mm, SBR 2:1, radius 4mm is shown in Fig. 3 (a). The horizontal profile (Fig. 3 (b)) along the red line in Fig. 3 (a) looks like a Gaussian function, which indicates that the edge of the constructed volume was blurred. The restored image (Fig. 3 (d)), which was almost exactly the same as the ground truth (Fig. 3 (g)), and the corresponding horizontal profile (Fig. 3 (e)) both suggested that the proposed method obtained a good restoration result. The estimated widths of the blur kernel (PSF) were σ₁=2.78 mm (Fig. 3 (h)) and σ₂=2.77 mm (Fig. 3 (i)), which were very close to the true value 2.55 mm (corresponding to the FWHM of 6 mm); and the estimated blur kernel (Fig. 3 (f)) was visually very similar to the true one (Fig. 3 (c)).

Figure 3.

(a) Blurred volume with FWHM 6mm, SBR 2:1, radius 4mm; (b) horizontal profile along the red line in the blurred volume; (c) original Gaussian kernel; (d) restored volume; (e) horizontal profile along the red line in the restored volume; (f) estimated blur kernel; (g) ground truth; (h) convergence curve of σ₁; (i) convergence curve of σ₂.

To quantitatively evaluate the restoration accuracy of the proposed algorithm, RCs of the eighteen blurred volumes and the recovered volumes are listed in Table 1. According to this Table, the original blurred volumes had low RCs (all RCs were less than or equal to 0.65). For fixed FWHM and radius, RC did not vary with SBRs. The blur degree increased when the sphere radius decreased. RCs of the recovered volumes were more close to 1 than those of the original blurred volumes, which suggested the good restoration performance of the proposed method. As expected, the bigger the sphere, the better the restoration effect.

Table 1.

RCs of the original blurred volumes and the recovered volumes of the proposed method, respectively.

FWHM (mm)	SBR	Radius (mm)	Blurred volumes	Recovered volumes (Ours)
			RC	RC
4	2:1	2	0.21	1.38
		4	0.51	1.37
		6	0.65	1.03
	3:1	2	0.21	1.17
		4	0.51	1.17
		6	0.65	0.99
	4:1	2	0.21	1.07
		4	0.51	1.13
		6	0.65	1
6	2:1	2	0.09	1.38
		4	0.32	1.08
		6	0.49	1.06
	3:1	2	0.09	0.92
		4	0.32	1.05
		6	0.49	1.03
	4:1	2	0.09	0.73
		4	0.32	1.03
		6	0.49	0.99

3.2. Experiments on physical phantom

Fig. 4 displays DSI, CE and VE for tested algorithms, averaged over all sphere sizes and SBRs in the physical phantom study. The proposed method performed the best according to the three accuracy evaluation criteria (DSI=0.77, CE=0.41 and VE=0.20). Bar’s method (DSI=0.74, CE=0.44 and VE=0.27) was the second best and followed by FCM (DSI=0.72, CE=0.47 and VE=0.36) and GC method (DSI=0.71, CE=0.54 and VE=0.38). Three thresholding methods (50% and 42% threshold, and Otsu) had worse performance than those advanced ones.

Figure 4.

(a) DSI, (b) CE and (c) VE, for physical phantoms averaged over all spheres and SBRs.

DSIs for six spheres, averaged over four SBRs, is shown in Fig. 5. Quite obviously, the proposed method was the most robust to the change of the sphere size. For example, for the smallest sphere (0.5ml), the proposed method had a DSI of 0.55, while the DSI of Bar’s method was only 0.51 and all other methods were less than 0.4. FCM had a slightly better segmentation result for the three largest spheres than the proposed method. For the three smallest spheres, however, the performance of FCM went down very quickly, and was significantly worse than that of the proposed method.

Figure 5.

DSI for different spheres, averaged over all SBRs.

Fig. 6 displays DSIs at different SBR levels, averaged over all spheres, demonstrating the good robustness of the proposed method over SBR variation. Like in the toy simulation, three thresholding methods — 50% and 42% threshold, and Otsu — were very sensitive to SBR variation. Especially for SBR 2:1, the performances of these three methods deteriorated drastically.

Figure 6.

DSI at different SBR levels, averaged over all sphere sizes.

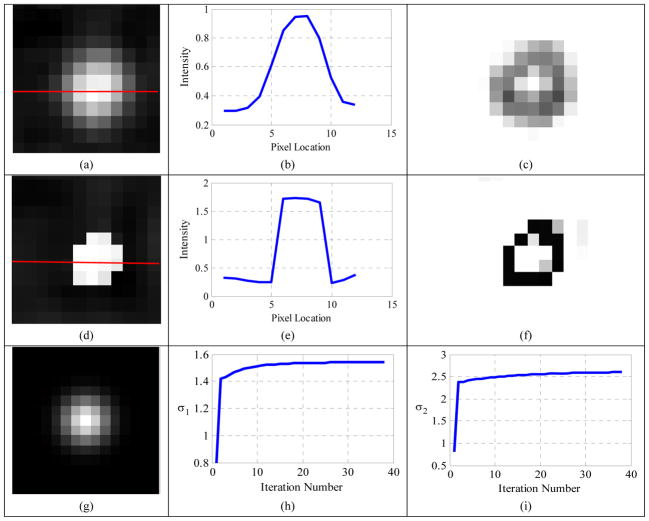
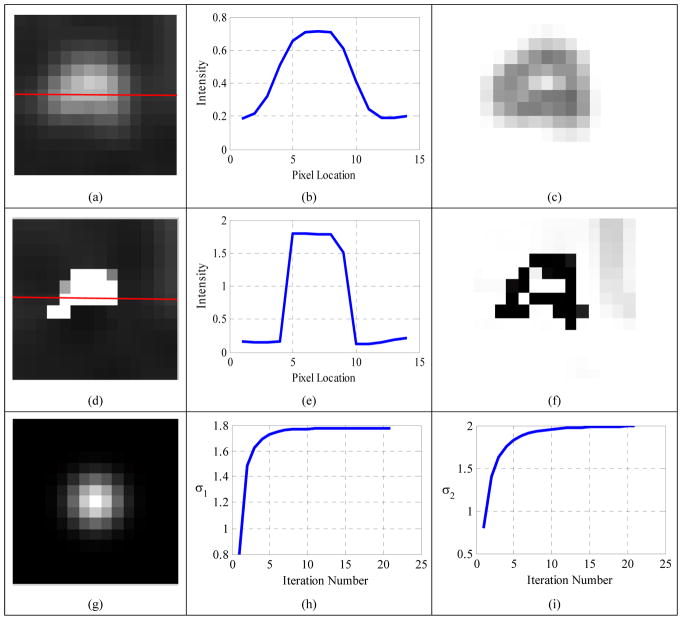
For a visual inspection, results of the proposed method for the 6ml sphere at SBR 4:1 are shown in Fig. 7. The horizontal profile (Fig. 7 (b)) and edge map v (Fig. 7 (c)) of the observed sphere (Fig. 7 (a)) suggested that the original sphere edge had been blurred. The second row of Fig. 7 displays the restored image (Fig. 7(d)) and its horizontal profile (Fig. 7(e)) and the edge map v (Fig. 7(f)), all showing the good restoration effect of the proposed method. The estimated blur kernel widths were 1.54 mm in the transversal direction (σ₁), and 2.60 mm in the axial direction (σ₂), corresponding to FWHMs of 3.63 mm and 6.12 mm, respectively. Both estimated FWHMs were very close to those of the real PET scanner (FWHM=4.5 mm in the transversal direction, and 5.7 mm in the axial direction) and the relative errors were 19% and 7%, respectively.

Figure 7.

(a) Observed 6ml sphere at SBR 4:1; (b) horizontal profile along the red line in the observed sphere; (c) edge map v of the observed sphere; (d) restored image; (e) horizontal profile along the red line in the restored image; (f) edge map v of the restored image; (g) estimated blur kernel (σ₁=1.54 mm, σ₂=2.60 mm); (h) convergence curve of σ₁; (i) convergence curve of σ₂.

In order to observe the restoration effect more clearly, Fig. 8 displays several restoration results. From the third column of this figure it can be seen that, without regularization on the edges, some abnormal high intensities appeared on object edges in the restoration results of Bar’s method, such as the voxels ‘A’, ‘B’ and ‘C’. The intensities of ‘A’, ‘B’ and ‘C’ were 73118, 91223 and 72963, respectively, while the intensities of the remaining voxels in these three slices were less than 35906, 40138 and 42862, respectively. There were not voxels with abnormal intensity in the results of the proposed method, thanks to the TV regularization on object edges.

Figure 8.

(a), (d) and (g): Observed 20ml, 16ml and 12ml spheres at SBR 4:1, respectively; (b), (e) and (h): restored 20ml, 16ml and 12ml spheres obtained by the proposed method, respectively; (c), (f) and (i): the restored 20ml, 16ml and 12ml spheres obtained by Bar’s method, respectively.

Table 2 lists RCs of the original blurred PET images and the recovered images of the proposed method. RCs of the original blurred PET spheres indicated that the blur degree was highly dependent on the sphere volume and only weakly influenced by SBRs, which was consistent with the toy simulation. Since small spheres were more susceptible to PVE, their blur degrees were greater than those of the big spheres. The proposed method could recover the ‘clean’ spheres effectively for both large and small spheres.

Table 2.

RCs of the original blurred PET images and the recovered images of the proposed method, respectively.

SBR	Volume	20 ml	16 ml	12 ml	6 ml	1 ml	0.5 ml
	Method
8:1	Original PET spheres	0.82	0.80	0.75	0.65	0.29	0.16
	Recovered spheres (ours)	1.06	1.07	1.06	1.03	0.86	1.03
6:1	Original PET spheres	0.83	0.81	0.76	0.63	0.27	0.14
	Recovered spheres (ours)	1.07	1.08	1.05	1.09	1.07	1.01
4:1	Original PET spheres	0.83	0.82	0.76	0.64	0.26	0.16
	Recovered spheres (ours)	1.13	1.13	1.15	1.14	1.03	1.08
2:1	Original PET spheres	0.70	0.72	0.65	0.37	0.07	0.01
	Recovered spheres (ours)	1.16	0.93	0.92	1.18	1.69	0.44

3.3. Experiments on non-Hodgkin’s lymphoma

The average DSI, CE and VE of the eleven non-Hodgkin’s lymphoma patients are displayed in Fig. 9. As this figure shows, the proposed method (DSI=0.79, CE=0.41 and VE=0.08) was superior to all other tested methods. FCM (DSI=0.75, CE=0.55 and VE=0.51) performed well according to DSI, but poorly according to CE and VE. The three thresholding methods still performed the worst.

Figure 9.

(a) DSI, (b) CE and (c) VE, averaged over all patients with non-Hodgkin’s lymphoma.

In order to visually inspect the segmentation effect of different methods, Fig. 10 presents the manual contour (closed blue curve in Fig. 10 (a)) and several automatic segmentation results (closed blue curves in Fig. 10 (b–f)) for one patient. For this patient, the proposed method had the most accurate segmentation (Fig. 10 (b), DSI=0.93, CE=0.14 and VE=0.01) and its contour coincided well with the manual contour. The lesions delineated by other methods (Fig. 10 (c–f)) were obviously smaller than the manual contour.

Figure 10.

Visual comparison for one patient with non-Hodgkin’s lymphoma (a) manual Contour, (b) the proposed method (DSI=0.93), (c) 42% thresholding (DSI=0.59), (d) FCM (DSI=0.70), (e) AC (DSI=0.82), and (f) GC (DSI=0.76).

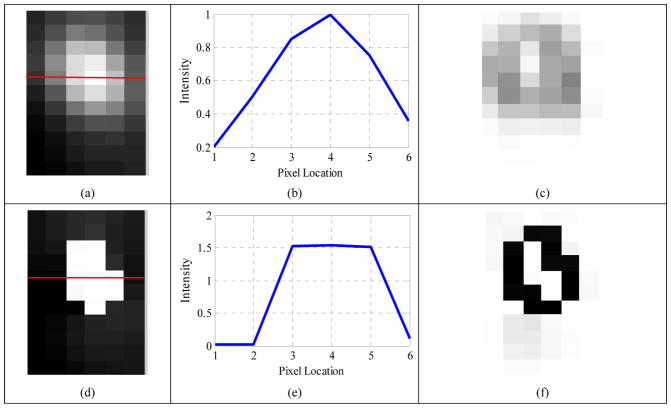
Fig. 11 (a) shows one slice of the original PET image of a non-Hodgkin’s lymphoma patient. The horizontal profile (Fig. 11 (b), along the red line in the original PET image) and the edge map (Fig. 11 (c)) demonstrated that it was difficult to localize the edge for the original PET image. The three images of the second row — Fig. 11 (d–f) — suggested that the proposed method could get a restored result with more clear edges, compared to the original PET image. The estimated blur kernel widths σ₁ (the transversal direction) and σ₂ (the axial direction) converged to 1.43 mm and 1.75 mm, leading to FWHMs of 3.37 mm and 4.12 mm, respectively, which were very close to the real FWHMs (3.8 mm in the transversal direction, and 4.0 mm in the axial direction) with relative errors of 11% and 3%.

Figure 11.

(a) Original PET image (Zoomed in) of a non-Hodgkin’s lymphoma patient; (b) horizontal profile along the red line in the original PET image; (c) edge map of the original PET image; (d) restored image; (e) horizontal profile along the red line in the restored image; (f) edge map of the restored image; (g) the estimated blur kernel (σ₁=1.43 mm, σ₂=1.75 mm); (h) convergence curve of σ₁; (i) convergence curve of σ₂.

Fig. 12 (a) shows one PET image slice of a patient with non-Hodgkin’s lymphoma. Bar’s method still resulted in some abnormal large intensities on object edges, such as voxel ‘A’ in Fig. 12 (c). The intensity (standardized uptake value (SUV)) of ‘A’ was 22.19, while the intensities of other voxels in this slice were less than 11.44.

Figure 12.

(a) One slice of a PET image of a patient with non-Hodgkin’s lymphoma; (b) the restored image obtained by the proposed method; (c) the restored image obtained by Bar’s method.

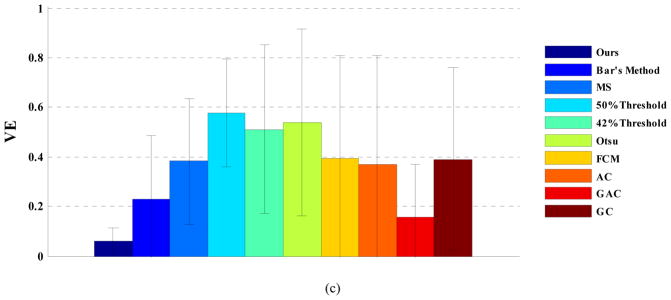
3.4. Experiments on esophageal cancer

Fig. 13 shows the averaged DSI, CE and VE over all patients in the esophageal cancer dataset. Again, the proposed method performed the best with DSI=0.80, CE=0.42, and VE=0.06, followed by GC (DSI=0.75, CE=0.50, VE=0.39), Bar’s method (DSI=0.73, CE=0.53, VE=0.23) and FCM (DSI=0.72, CE=0.43, VE=0.39). For this dataset, 50% threshold (DSI=0.60, CE=0.60, VE=0.58) performed the worst.

Figure 13.

(a) DSI, (b) CE, and (c) VE, averaged over all patients with esophageal cancer.

The manual contour (Fig. 14 (a)) and several automatic segmentation results (Fig. 14 (b–f)) of one patient with esophageal cancer are displayed in Fig. 14. The contour obtained by the proposed method (Fig. 14 (b)) was in good agreement with the manual contour. Other methods performed significantly worse. The 50% threshold (Fig. 14 (c)) and Otsu (Fig. 14 (d)) had only DSI of 0.39 and 0.38, and the lesions delineated by the two methods were obviously smaller than the actual lesion (Fig. 14 (a)).

Figure 14.

Visual comparison (axial view) for one patient with esophageal cancer (a) Manual Contour, (b) the proposed method (DSI=0.87), (c) 50% thresholding (DSI=0.39), (d) Otsu (DSI=0.38), (e) FCM (DSI=0.67), and (f) GC (DSI=0.71).

Fig. 15 displays the results of the proposed method for an esophageal cancer patient. The original PET volume was blurred due to PVE, and it was hard to find tumor edges. The proposed method improved the quality of the blurred PET image, which can be seen from the restored image (Fig. 15 (d)), the corresponding horizontal profile (Fig. 15 (e)) and the edge map v (Fig. 15 (f)). The blur kernel widths σ₁ converged to 1.78 mm which corresponds to FWHM of 4.19 mm in the transversal direction, and σ₂ converged to 1.99 mm which corresponds to FWHM of 4.69 mm in the axial direction. Both estimated FWHMs were very close to the real FWHMs (the real FWHMs in both transversal and axial direction were 4.9 mm) and the relative errors were 14% and 4%, respectively.

Figure 15.

(a) Original PET image (zoomed in) of an esophageal cancer patient; (b) horizontal profile along the red line in the original PET image; (c) edge map of the original PET image; (d) restored image; (e) horizontal profile along the red line in the restored image; (f) edge map of the restored image; (g) the estimated blur kernel (σ₁=1.78 mm, σ₂=1.99 mm); (h) convergence curve of σ₁; (i) convergence curve of σ₂.

Fig. 16 displays the restoration results of the PET images of two esophageal cancer patients. The bright voxels ‘A’ and ‘B’ in Fig. 16 (c) and Fig. 16 (f) were the abnormal large intensities produced by Bar’s method. The intensity (SUV) of ‘A’ and ‘B’ were 66.65 and 22.94, respectively, which were considerably larger than all the other voxels in these two slices. Fortunately, no voxels with abnormal intensity were found in the restored results of the proposed methods.

Figure 16.

(a) and (d): one slice of the PET image of two esophageal cancer patients; (b) and (e): the restored images obtained by the proposed method; (c) and (f): the restored images obtained by Bar’s method.

3.5. Algorithm Robustness

In this section, we examined the robustness of the proposed method to the four parameters (α, β, η and γ) in Eq. (6) and Eq.(7). The experiments were tested with one parameter deviated from the manually tuned value while the other three kept unchanged.

Table 3 lists the segmentation robustness of the proposed method over α, β, η and γ, respectively, in given intervals, for one esophageal patient. As we can see, the segmentation performance of the proposed method is stable in the given intervals to the change of η and γ. For example, the values of DSI and CE kept unchanged when γ changed from 10 to 50. The segmentation accuracy was slightly affected by the parameters α and β. But these effects were still reasonable and acceptable. For example, DSI only changed from 0.83 to 0.90 when α changed by 10 times from 3×10⁻⁸ to 3×10⁻⁷, and the DSI changed from 0.81 to 0.90 when β changed from 2×10⁻² to 6×10⁻².

Table 3.

Segmentation performance of the proposed method with different α, β, η and γ in a given interval.

α	3×10−8	5×10−8	8×10−8	1×10−7	3×10−7
DSI	0.83	0.87	0.89	0.90	0.86
VE	0.30	0.12	0.05	0.05	0.22
CE	0.39	0.26	0.22	0.19	0.25
β	2×10−2	3×10−2	4×10−2	5×10−2	6×10−2
DSI	0.81	0.87	0.89	0.90	0.88
VE	0.30	0.17	0.11	0.05	0.07
CE	0.32	0.23	0.21	0.19	0.24
η	2×10−3	3×10−3	4×10−3	5×10−3	6×10−3
DSI	0.86	0.90	0.89	0.89	0.87
VE	0.06	0.05	0.11	0.12	0.18
CE	0.28	0.19	0.21	0.20	0.24
γ	10	20	30	40	50
DSI	0.90	0.90	0.90	0.90	0.90
VE	0.05	0.05	0.05	0.06	0.05
CE	0.19	0.19	0.19	0.19	0.19

Fig. 17 displays the restored images of the proposed method with different parameters. Compared with the original PET image (Fig. 17 (a)), each set of parameters obtained a clearer restored image. By observing the three images of each column, we can see that the variation of the parameters in the given interval affected the restoration results slightly. The second column (Fig. 17 (b)–(d)) shows that a larger α obtained a restored image with sharper edges but smaller foreground area (tumor area). With the increase of β (Fig. 17 (e)–(g)), the restored image became more smooth. Fig. 17 (h)–(j) shows that a larger η resulted in smoother tumor edges. The parameter γ can adjust the width of the blur kernel. The larger the γ, the bigger the estimated blur kernel widths (σ₁ and σ₂). Only when the corresponding FWHM values of the σ₁ and σ₂ were close to the spatial resolutions of the PET scanner can we achieved the desired results.

Figure 17.

The restored images of the proposed method with different parameters. (a) Original PET image of an esophageal cancer patient; the second column (b)–(d): the restored image with different α; the third column (e)–(g): the restored image with different β; the fourth column (h)–(j): the restored image with different η; the fifth column (k)–(m): the restored image with different γ.

3.6. Execution time

Each iteration of the alternating minimization of the proposed method consists of two gradient descent algorithms and two bisection methods. In the whole iterative process, the most time-consuming part was the gradient descent algorithm due to its disadvantage of the slow convergence. For an image with size of N×N×N, the computational complexity of our algorithm is O(M×N³), where M denotes the iteration number of the AM algorithm. Fortunately, tumor segmentation in radiation oncology was generally conducted in a ROI with small size (small N) rather than the whole PET image. Our current algorithm was implemented in Matlab, and the typical execution time was about several minutes for one patient in our experiments (3.40 GHz CPU, 8GB RAM). The current code still has room to speed up.

4. Discussion

Image restoration and segmentation are both well-known difficult problems in image processing. Due to the limited spatial resolution of clinical PET systems, PET imaging can be largely affected by PVE, especially for tumors with small sizes (Pan and Mawlawi, 2008; Zaidi and El Naqa, 2010). Tumor boundaries are commonly blurred due to PVE (Fig. 8 (a), (d), (g); Fig. 12 (a); Fig. 16 (a), (d)), which affects tumor segmentation accuracy (Soret et al., 2007). One strategy to handle PVE is to correct PVE firstly, and then to segment tumor on the restored image. De-convolution is a widely used method for PVC. However, de-convolution is itself a well-known ill-posed inverse problem. In some circumstances, the system PSF may be unknown, which makes the de-convolution even more difficult. On the contrary, if a precise segmentation result can be available, the blur kernel can be estimated based on the segmentation result, which will be helpful to image de-convolution. As a result, image restoration and segmentation can promote each other, and it is meaningful to integrate the two problems together.

In Ref (Bar et al., 2006), the authors integrated image de-convolution with segmentation in a variational framework. In their model, a piecewise-smoothness term (L₂ regularization) was used to constrain the regions away from object edges, and no constraint was used for the edge set, which sometimes resulted in abnormal large intensity voxels on object edges (Fig. 8 (c), (f), (i); Fig. 12 (c); and Fig. 16 (c), (f)) and further influenced the estimation of the blur kernel and degraded the quality of the restored image.

In this study, we conducted PET image restoration, tumor segmentation and blur kernel estimation simultaneously on a novel variational method. In the proposed method, the restored image was constrained by two regularizations — TV regularization was used over tumor edges and L₂ regularization was used in non-edge regions. The multiple regularizations preserved not only edges but also smooth regions. The experimental results showed that the proposed method could handle PVE and improve segmentation performance. As shown in Figs.1, 4, 9 and 13, the proposed method performed the best according to all the three accuracy evaluation criteria — DSI=0.80, CE=0.43 and VE=0.28 in the toy simulation, DSI=0.77, CE=0.41 and VE=0.20 for the physical phantom, DSI=0.79, CE=0.41 and VE=0.08 for the non-Hodgkin’s lymphoma dataset, and DSI=0.80, CE=0.42 and VE=0.06 for the esophageal cancer dataset — among all tested methods. Figs. 2, 5 and 6 showed that the proposed method was robust to the change of object sizes and SBRs.

Besides the good segmentation performance, the proposed method can effectively estimate the blur kernel (Fig. 3 (f), Fig. 7 (g), Fig. 11 (g), Fig. 15 (g)) and obtain the desired restored image (Fig. 3 (d), Fig. 7 (d), Fig. 11 (d), Fig. 15 (d), Table 1 and Table 2). In the objective functional (Eq.(7)), the blur kernel was constrained to the anisotropic Gaussians parameterized by different widths in transversal (σ₁) and axial (σ₂) directions, as shown in Eq.(8), which can handle PET images with different spatial resolution in different directions and improve the algorithm’s robustness. In the toy simulation, the estimated σ₁ and σ₂ were nearly equal the real values. In physical phantom and clinic datasets experiments, σ₁ (transversal direction) and σ₂ (axial direction) converged to different values and the corresponding FWHM values were very close to those of the real PET scanners. For the restored images, the RCs were close to 1 both in the toy simulation and in the phantom study.

There are four regularization terms in the objective energy functional (Eq.(6)), which was iteratively optimized using the AM algorithm through the Γ-convergence approximation (Eq.(7)). All these four regularization terms are important in the proposed variational framework. The second term in Eqs.(6) and (7) is the L₂ regularization needed for both restoration and segmentation. For image restoration, it constrains the smoothness of the non-edge areas and removes the noise. For segmentation, it plays a crucial role in the evolving of the edge map v which is used to delineate the tumor at last. On tumor edges, the gradient values are high, which made the corresponding values of the edge map v gradually tend to 0 during the minimizing process of the energy functional. Without this term, the proposed model would not be able to achieve tumor segmentation. The third term is the TV regularization applied over target edges. It mainly contributes to preserving and sharpening the tumor edges. If this term was omitted, some abnormal large uptake values would appear on tumor edges. The fourth term is the length regularization term that constrains the length and smoothness of the edge set. If this term was omitted, the target edges in the segmentation result would be jagged and the segmentation accuracy would be reduced. The last term in Eq.(6) and (7) represents the regularization of the blur kernel. If this term was omitted, it would be difficult to control the widths of the blur kernel (Gaussian kernel). The estimation accuracy of the blur kernel may decrease, which would affect the image restoration and further reduce the segmentation accuracy.

Most of existing segmentation algorithms taking into account PVE need to take some prior calibrations through phantom experiments to make the parameters of these methods fit a specific imaging setting, such as some adaptive threshold approaches (Daisne et al., 2003; Drever et al., 2006; Jentzen et al., 2007; Schaefer et al., 2008), or need to know the PSF of the scanner in advance. These methods can be highly system-dependent. Different from these methods, the proposed method needs no prior calibrations or other prior information, and does not depend on the imaging scanners. In this sense, the proposed method is more efficient and has wider applications.

Although the proposed method had a good performance for PET image processing, there are still some issues that need to be resolved in the future. Firstly, the energy functional (Eq.(7)) is non-convex. Therefore, the optimization algorithms can be trapped into local minima and it is a common problem for most variational image processing algorithms. Obtaining the global minimum will be an important and challenging work in our future work. We will study the convex relaxation of the proposed model based on previous researches (Bresson et al., 2007; Chan et al., 2006; Paul et al., 2013), and solve the relaxed convex problem using the alternating split-Bregman (ASB) method (Goldstein et al., 2010; Paul et al., 2013). Secondly, the blur kernel was constrained to Gaussian in this study. Sometimes it may be not accurate. In future work, more types of blur kernel will be studied.

5. Conclusion

In this study, we proposed a novel variational method with multiple regularizations for simultaneous image restoration, tumor segmentation and blur kernel estimation in PET imaging. The alternate usage of the TV and L₂ regularizations can preserve not only edges but also smooth regions. The proposed method can handle PVE and is independent to imaging systems and settings. Experimental results demonstrated that the proposed method had a good segmentation and restoration performance, and could accurately estimate the blur kernel as well.

Appendix A

The detailed mathematical derivations of the Eqs.(10) and (11) corresponding to the objective functional (Eq.(7)) are given in this appendix. In the following derivation, let f(x,y,z) and v(x,y,z) be extended to the whole ℝ³ with the Neumann boundary condition, and h_σ denotes h_σ1,σ2, and the integration element dA denotes dxdydz.

(1) Variation with respect to v

The variation of F_ε with respect to v can be expressed as

$$\begin{array}{l}\frac{\delta F_{\epsilon }}{\delta v}={\frac{\partial }{\partial \lambda }{F}_{\epsilon }\left(v+\lambda \psi \right)|}_{\lambda =0}\\ =\frac{\partial }{\partial \lambda }\{\beta {\int }_{\mathrm{\Omega }}{\left(v+\lambda \psi \right)}^2{\left|\nabla f\right|}^{2}dA+\eta {\int }_{\mathrm{\Omega }}\left(1-{\left(v+\lambda \psi \right)}^2\right)\left|\nabla f\right|dA+{\alpha {\int }_{\mathrm{\Omega }}\left(\epsilon {\left|\nabla \left(v+\lambda \psi \right)\right|}^2+\frac{{(v+\lambda \psi -1)}^2}{4\epsilon }\right)dA\}|}_{\lambda =0}\\ =0.\end{array}$$ (A.1)

Let

$$\begin{array}{c}\frac{\delta F_{\epsilon }^{\mathrm{I}}}{\delta v}={\frac{\partial }{\partial \lambda }\left\{\beta {\int }_{\mathrm{\Omega }}{\left(v+\lambda \psi \right)}^2{\left|\nabla f\right|}^{2}dA\right\}|}_{\lambda =0},\\ \frac{\delta F_{\epsilon }^{\text{II}}}{\delta v}={\frac{\partial }{\partial \lambda }\left\{\eta {\int }_{\mathrm{\Omega }}\left(1-{\left(v+\lambda \psi \right)}^2\right)\left|\nabla f\right|dA\right\}|}_{\lambda =0},\\ \frac{\delta F_{\epsilon }^{\text{III}}}{\delta v}={\frac{\partial }{\partial \lambda }\left\{\alpha {\int }_{\mathrm{\Omega }}\left(\epsilon {\left|\nabla \left(v+\lambda \psi \right)\right|}^2\right)dA\right\}|}_{\lambda =0},\\ \frac{\delta F_{\epsilon }^{\text{IV}}}{\delta v}={\frac{\partial }{\partial \lambda }\left\{\alpha {\int }_{\mathrm{\Omega }}\left(\frac{{(v+\lambda \psi -1)}^2}{4\epsilon }\right)dA\right\}|}_{\lambda =0},\end{array}$$

then

$$\frac{\delta F_{\epsilon }^{\mathrm{I}}}{\delta v}={\left\{\beta {\int }_{\mathrm{\Omega }}2\left(v+\lambda \psi \right)\psi {\left|\nabla f\right|}^{2}dA\right\}|}_{\lambda =0}=2\beta {\int }_{\mathrm{\Omega }}v{\left|\nabla f\right|}^2\psi dA,$$ (A.2)

$$\frac{\delta F_{\epsilon }^{\text{II}}}{\delta v}={\left\{\eta {\int }_{\mathrm{\Omega }}-2\left(v+\lambda \psi \right)\psi {\left|\nabla f\right|}^{2}dA\right\}|}_{\lambda =0}=-2\eta {\int }_{\mathrm{\Omega }}v\left|\nabla f\right|\psi dA,$$ (A.3)

$$\begin{array}{l}\frac{\delta F_{\epsilon }^{\text{III}}}{\delta v}={\left\{\alpha {\int }_{\mathrm{\Omega }}\left(2\epsilon \left(v_x+\lambda {\psi }_x\right){\psi }_x+2\epsilon \left(v_y+\lambda {\psi }_y\right){\psi }_y+2\epsilon \left(v_z+\lambda {\psi }_z\right){\psi }_z\right)dA\right\}|}_{\lambda =0}\\ =2\alpha \epsilon {\int }_{\mathrm{\Omega }}\left(v_x{\psi }_x+v_y{\psi }_y+v_z{\psi }_z\right)dA\\ =2\alpha \epsilon \left\{{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial x}\left(v_x\psi \right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial y}\left(v_y\psi \right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial z}\left(v_z\psi \right)dA-{\int }_{\mathrm{\Omega }}\left(v_{xx}+v_{yy}+v_{zz}\right)\psi dA\right\}.\end{array}$$ (A.4)

By using the divergence theorem, we get

$${\int }_{\mathrm{\Omega }}\frac{\partial }{\partial x}\left(v_x\psi \right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial y}\left(v_y\psi \right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial z}(v_z\psi )dA={\int }_{\partial \mathrm{\Omega }}\psi \nabla \mathit{vdn},$$ (A.5)

where n is the normal vector to the contour. With the Neumann boundary condition:

$$\frac{\partial v}{\partial n}=0,\left(x,y,x\right)\in \partial \mathrm{\Omega },$$

we obtain

$${\int }_{\partial \mathrm{\Omega }}\psi \nabla \mathit{vdn}=0.$$ (A.6)

By substituting Eqs.(A.5) and (A.6) into Eq.(A.4), we have

$$\frac{\delta F_{\epsilon }^{\text{III}}}{\delta v}=-2\alpha \epsilon {\int }_{\mathrm{\Omega }}\left(v_{xx}+v_{yy}+v_{zz}\right)\psi dA=-2\alpha \epsilon {\int }_{\mathrm{\Omega }}{\nabla }^{2}v·\psi dA.$$ (A.7)

$$\frac{\delta F_{\epsilon }^{\text{IV}}}{\delta v}={\left\{\alpha {\int }_{\mathrm{\Omega }}\frac{2}{4\epsilon }\left(v+\lambda \psi -1\right)\psi dA\right\}|}_{\lambda =0}=\alpha {\int }_{\mathrm{\Omega }}\frac{\left(v-1\right)}{2\epsilon }\psi dA.$$ (A.8)

Substituting Eqs.(A.2), (A.3), (A.7) and (A.8) into Eq.(A.1), we have

$$\begin{array}{l}\frac{\delta F_{\epsilon }}{\delta v}=\frac{\delta F_{\epsilon }^{\mathrm{I}}}{\delta v}+\frac{\delta F_{\epsilon }^{\text{II}}}{\delta v}+\frac{\delta F_{\epsilon }^{\text{III}}}{\delta v}+\frac{\delta F_{\epsilon }^{\text{IV}}}{\delta v}\\ ={\int }_{\mathrm{\Omega }}\left(2\beta v{\left|\nabla f\right|}^2-2\eta v\left|\nabla f\right|-2\alpha \epsilon {\nabla }^{2}v+\alpha \frac{\left(v-1\right)}{2\epsilon }\right)\psi dA=0.\end{array}$$ (A.9)

For Eq.(A.9), using the fundamental lemma of calculus of variations, we obtain Eq.(10):

$$\left(2\beta {\left|\nabla f\right|}^2-2\eta \left|\nabla f\right|\right)v+\alpha ·\frac{v-1}{2\epsilon }-2\epsilon \alpha {\nabla }^{2}v=0.$$

(2) Variation with respect to f

The variation of F_ε with respect to f can be expressed as

$$\begin{array}{l}\frac{\delta F_{\epsilon }}{\delta f}={\frac{\partial }{\partial \lambda }{F}_{\epsilon }\left(f+\lambda \varphi \right)|}_{\lambda =0}\\ =\frac{\partial }{\partial \lambda }\{\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(h_{\sigma }\ast \left(f+\lambda \varphi \right)-g\right)}^{2}dA+\beta {\int }_{\mathrm{\Omega }}{v}^2\left({\left(f_x+\lambda {\varphi }_x\right)}^2+{\left(f_y+\lambda {\varphi }_y\right)}^2+{\left(f_z+\lambda {\varphi }_z\right)}^2\right)dA+{\eta {\int }_{\mathrm{\Omega }}\left(1-v^2\right)\sqrt{{\left(f_x+\lambda {\varphi }_x\right)}^2+{\left(f_y+\lambda {\varphi }_y\right)}^2+{\left(f_z+\lambda {\varphi }_z\right)}^2}dA\left\}\right|}_{\lambda =0}\\ =0.\end{array}$$ (A.10)

Let

$$\begin{array}{c}\frac{\delta F_{\epsilon }^{\mathrm{I}}}{\delta f}={\frac{\partial }{\partial \lambda }\left\{\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(h_{\sigma }\ast \left(f+\lambda \varphi \right)-g\right)}^{2}dA\right\}|}_{\lambda =0},\\ \frac{\delta F_{\epsilon }^{\text{II}}}{\delta f}={\frac{\partial }{\partial \lambda }\left\{\beta {\int }_{\mathrm{\Omega }}{v}^2\left({\left(f_x+\lambda {\varphi }_x\right)}^2+{\left(f_y+\lambda {\varphi }_y\right)}^2+{\left(f_z+\lambda {\varphi }_z\right)}^2\right)dA\right\}|}_{\lambda =0},\\ \frac{\delta F_{\epsilon }^{\text{III}}}{\delta f}={\frac{\partial }{\partial \lambda }\left\{\eta {\int }_{\mathrm{\Omega }}\left(1-v^2\right)\sqrt{{\left(f_x+\lambda {\varphi }_x\right)}^2+{\left(f_y+\lambda {\varphi }_y\right)}^2+{\left(f_z+\lambda {\varphi }_z\right)}^2}dA\right\}|}_{\lambda =0},\end{array}$$

then

$$\begin{array}{l}\frac{\delta F_{\epsilon }^{\mathrm{I}}}{\delta f}={\left\{\frac{1}{2}{\int }_{\mathrm{\Omega }}2\left(h_{\sigma }\ast \left(f+\lambda \varphi \right)-g\right)\left(h_{\sigma }\ast \varphi \right)dA\right\}|}_{\lambda =0}\\ ={\int }_{\mathrm{\Omega }}\left(h_{\sigma }\ast f-g\right)\left(h_{\sigma }\ast \varphi \right)dA.\end{array}$$ (A.11)

Let l(x, y, z) = h_σ * f − g, then

$$\begin{array}{l}\frac{\delta F_{\epsilon }^{\mathrm{I}}}{\delta f}={\int }_{\mathrm{\Omega }}l\left(x,y,z\right)\left(h_{\sigma }\ast \varphi \right)dA\\ ={\iiint }_{\mathrm{\Omega }}l\left(x,y,z\right)\left({\iiint }_{\mathrm{\Omega }}{h}_{\sigma }\left(x-x^{\prime },y-y^{\prime },z-z^{\prime }\right)\varphi \left(x^{\prime },y^{\prime },z^{\prime }\right)d{x}^{\prime }d{y}^{\prime }d{z}^{\prime }\right)\mathit{dxdydz}\\ ={\iiint }_{\mathrm{\Omega }}\left({\iiint }_{\mathrm{\Omega }}l\left(x,y,z\right)h_{\sigma }\left(x-x^{\prime },y-y^{\prime },z-z^{\prime }\right)\mathit{dxdydz}\right)\varphi \left(x^{\prime },y^{\prime },z^{\prime }\right)d{x}^{\prime }d{y}^{\prime }d{z}^{\prime }\\ ={\iiint }_{\mathrm{\Omega }}\left(l\left(x,y,z\right)\ast h_{\sigma }\left(-x,-y,-z\right)\right)\varphi \left(x,y,z\right)\mathit{dxdydz}.\end{array}$$ (A.12)

$$\begin{array}{l}\frac{\delta F_{\epsilon }^{\text{II}}}{\delta f}={\left\{\beta {\int }_{\mathrm{\Omega }}{v}^2\left(2\left(f_x+\lambda {\varphi }_x\right){\varphi }_x+2\left(f_y+\lambda {\varphi }_y\right){\varphi }_y+2\left(f_z+\lambda {\varphi }_z\right){\varphi }_z\right)dA\right\}|}_{\lambda =0}\\ =2\beta {\int }_{\mathrm{\Omega }}{v}^2\left(f_x{\varphi }_x+f_y{\varphi }_y+f_z{\varphi }_z\right)dA\\ =2\beta \left\{{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial x}\left(v^2\varphi f_x\right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial y}\left(v^2\varphi f_y\right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial z}\left(v^2\varphi f_z\right)dA-{\int }_{\mathrm{\Omega }}\left(\frac{\partial }{\partial x}\left(v^2{f}_x\right)+\frac{\partial }{\partial y}\left(v^2{f}_y\right)+\frac{\partial }{\partial z}\left(v^2{f}_z\right)\right)\varphi dA\right\}.\end{array}$$ (A.13)

By using the divergence theorem, we get

$${\int }_{\mathrm{\Omega }}\frac{\partial }{\partial x}\left(v^2\varphi f_x\right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial y}\left(v^2\varphi f_y\right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial z}\left(v^2\varphi f_z\right)dA={\int }_{\partial \mathrm{\Omega }}{v}^2\varphi \nabla \mathit{fdn},$$ (A.14)

where n is the normal vector to the contour. With the Neumann boundary condition:

$$\frac{\partial f}{\partial n}=0,\left(x,y,x\right)\in \partial \mathrm{\Omega },$$

we obtain

$${\int }_{\partial \mathrm{\Omega }}{v}^2\varphi \nabla \mathit{fdn}=0.$$ (A.15)

By substituting Eqs.(A.14) and (A.15) into Eq.(A.13), we get

$$\begin{array}{l}\frac{\delta F_{\epsilon }^{\text{II}}}{\delta f}=-2\beta {\int }_{\mathrm{\Omega }}\left(\frac{\partial }{\partial x}\left(v^2{f}_x\right)+\frac{\partial }{\partial y}\left(v^2{f}_y\right)+\frac{\partial }{\partial z}\left(v^2{f}_z\right)\right)\varphi dA\\ =-2\beta {\int }_{\mathrm{\Omega }}\left(\mathit{Div}\left(v^2\nabla f\right)\right)\varphi dA.\end{array}$$ (A.16)

$$\frac{\delta F_{\epsilon }^{\text{III}}}{\delta f}={\left\{\eta {\int }_{\mathrm{\Omega }}\left(1-v^2\right)\frac{\left(f_x+\lambda {\varphi }_x\right){\varphi }_x+\left(f_y+\lambda {\varphi }_y\right){\varphi }_y+\left(f_z+\lambda {\varphi }_z\right){\varphi }_z}{\sqrt{{\left(f_x+\lambda {\varphi }_x\right)}^2+{\left(f_y+\lambda {\varphi }_y\right)}^2+{\left(f_z+\lambda {\varphi }_z\right)}^2}}dA\right\}|}_{\lambda =0}=\eta {\int }_{\mathrm{\Omega }}{\left(1-v\right)}^2\frac{f_x{\varphi }_x+f_y{\varphi }_y+f_z{\varphi }_z}{\sqrt{{\left(f_x\right)}^2+{\left(f_y\right)}^2+{\left(f_z\right)}^2}}dA=\eta \left\{{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial x}\left(\frac{\left(1-v^2\right)\varphi f_x}{\left|\nabla f\right|}\right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial y}\left(\frac{\left(1-v^2\right)\varphi f_y}{\left|\nabla f\right|}\right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial z}\left(\frac{\left(1-v^2\right)\varphi f_z}{\left|\nabla f\right|}\right)dA-{\int }_{\mathrm{\Omega }}\left(\frac{\partial }{\partial x}\left(\frac{\left(1-v^2\right)f_x}{\left|\nabla f\right|}\right)+\frac{\partial }{\partial y}\left(\frac{\left(1-v^2\right)f_y}{\left|\nabla f\right|}\right)+\frac{\partial }{\partial z}\left(\frac{\left(1-v^2\right)f_z}{\left|\nabla f\right|}\right)\right)\varphi dA\right\}.$$ (A.17)

By using the divergence theorem, we get

$${\int }_{\mathrm{\Omega }}\frac{\partial }{\partial x}\left(\frac{\left(1-v^2\right)\varphi f_x}{\left|\nabla f\right|}\right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial y}\left(\frac{\left(1-v^2\right)\varphi f_y}{\left|\nabla f\right|}\right)dA+{\int }_{\mathrm{\Omega }}\frac{\partial }{\partial z}\left(\frac{\left(1-v^2\right)\varphi f_z}{\left|\nabla f\right|}\right)dA={\int }_{\partial \mathrm{\Omega }}\left(1-v^2\right)\varphi \frac{\nabla f}{\left|\nabla f\right|}dn.$$ (A.18)

As with Eq.(A.14), using the Neumann boundary condition, we obtain

$${\int }_{\partial \mathrm{\Omega }}\left(1-v^2\right)\varphi \frac{\nabla f}{\left|\nabla f\right|}dn=0.$$ (A.19)

Substituting Eqs.(A.18) and (A.19) into Eq.(A.17), we obtain

$$\begin{array}{l}\frac{\delta F_{\epsilon }^{\text{III}}}{\delta f}=-\eta {\int }_{\mathrm{\Omega }}\left(\frac{\partial }{\partial x}\left(\frac{\left(1-v^2\right)f_x}{\left|\nabla f\right|}\right)+\frac{\partial }{\partial y}\left(\frac{\left(1-v^2\right)f_y}{\left|\nabla f\right|}\right)+\frac{\partial }{\partial z}\left(\frac{\left(1-v^2\right)f_z}{\left|\nabla f\right|}\right)\right)\varphi dA\\ =-\eta {\int }_{\mathrm{\Omega }}\left(\mathit{Div}\left(\left(1-v^2\right)\frac{\nabla f}{\left|\nabla f\right|}\right)\right)\varphi dA.\end{array}$$ (A.20)

Substituting Eqs.(A.12), (A.16) and (A.20) into Eq.(A.10), we obtain

$$\begin{array}{l}\frac{\delta F_{\epsilon }}{\delta f}=\frac{\delta F_{\epsilon }^{\mathrm{I}}}{\delta f}+\frac{\delta F_{\epsilon }^{\text{II}}}{\delta f}+\frac{\delta F_{\epsilon }^{\text{III}}}{\delta f}\\ ={\int }_{\mathrm{\Omega }}\left(\left(h_{\sigma }\ast f-g\right)\ast h_{\sigma }\left(-x,-y,-z\right)-2\beta \mathit{Div}\left(v^2\nabla f\right)-\eta \mathit{Div}\left(\left(1-v^2\right)\frac{\nabla f}{\left|\nabla f\right|}\right)\right)\varphi dA=0.\end{array}$$ (A.21)

For Eq.(A.21), using the fundamental lemma of calculus of variations, we obtain Eq.(11):

$$\left(h_{\sigma }\ast f-g\right)\ast h_{\sigma }\left(-x,-y,-z\right)-2\beta \text{Div}\left(v^2\nabla f\right)-\eta \text{Div}\left(\left(1-v^2\right)\frac{\nabla f}{\left|\nabla f\right|}\right)=0.$$

Appendix B

In this appendix, we present the detailed derivation of Eqs.(17) and (19).

The anisotropic Gaussian kernel is defined as:

$$h_{{\sigma }_1,{\sigma }_2}=\frac{1}{{(2\pi )}^{3/2}{\sigma }_1^2{\sigma }_2}{e}^{-\left(\frac{x^2+y^2}{2{\sigma }_1^2}+\frac{z^2}{2{\sigma }_2^2}\right)}.$$

Following this definition, Eq.(17) can be obtained using the following steps:

$$\begin{array}{l}\frac{\partial h_{{\sigma }_1,{\sigma }_2}}{\partial {\sigma }_1}=\frac{1}{{(2\pi )}^{3/2}{\sigma }_2}{e}^{-\frac{z^2}{2{\sigma }_2^2}}\frac{\partial }{\partial {\sigma }_1}\left(\frac{1}{{\sigma }_1^2}{e}^{-\frac{x^2+y^2}{2{\sigma }_1^2}}\right)\\ =\frac{1}{{(2\pi )}^{3/2}{\sigma }_2}{e}^{-\frac{z^2}{2{\sigma }_2^2}}\left(\frac{-2}{{\sigma }_1^3}{e}^{-\frac{x^2+y^2}{2{\sigma }_1^2}}+\frac{1}{{\sigma }_1^2}{e}^{-\frac{x^2+y^2}{2{\sigma }_1^2}}\frac{x^2+y^2}{{\sigma }_1^3}\right)\\ =\frac{1}{{(2\pi )}^{3/2}{\sigma }_1^2{\sigma }_2}{e}^{-\left(\frac{x^2+y^2}{2{\sigma }_1^2}+\frac{z^2}{2{\sigma }_2^2}\right)}\left(\frac{x^2+y^2}{{\sigma }_1^3}-\frac{2}{{\sigma }_1}\right).\end{array}$$

Similarly, we can derive Eq.(18).

Eq.(19) can be obtained as:

$$\begin{array}{l}\frac{\partial }{\partial {\sigma }_1}{\left|\nabla h_{{\sigma }_1,{\sigma }_2}\right|}^2=\frac{\partial }{\partial {\sigma }_1}\left({\left(\frac{\partial }{\partial x}{h}_{{\sigma }_1,{\sigma }_2}\right)}^2+{\left(\frac{\partial }{\partial y}{h}_{{\sigma }_1,{\sigma }_2}\right)}^2+{\left(\frac{\partial }{\partial z}{h}_{{\sigma }_1,{\sigma }_2}\right)}^2\right)\\ =\frac{\partial }{\partial {\sigma }_1}\left(\frac{1}{{(2\pi )}^3{\sigma }_1^4{\sigma }_2^2}{e}^{-\left(\frac{x^2+y^2}{{\sigma }_1^2}+\frac{z^2}{{\sigma }_2^2}\right)}\left(\frac{x^2+y^2}{{\sigma }_1^4}+\frac{z^2}{{\sigma }_2^4}\right)\right)\\ =\frac{\partial }{\partial {\sigma }_1}\left(\frac{x^2+y^2}{{(2\pi )}^3{\sigma }_1^8{\sigma }_2^2}{e}^{-\left(\frac{x^2+y^2}{{\sigma }_1^2}+\frac{z^2}{{\sigma }_2^2}\right)}\right)+\frac{\partial }{\partial {\sigma }_1}\left(\frac{z^2}{{(2\pi )}^3{\sigma }_1^4{\sigma }_2^6}{e}^{-\left(\frac{x^2+y^2}{{\sigma }_1^2}+\frac{z^2}{{\sigma }_2^2}\right)}\right)\\ =\frac{x^2+y^2}{4{\pi }^3{\sigma }_1^4{\sigma }_2^2}{e}^{-\left(\frac{x^2+y^2}{{\sigma }_1^2}+\frac{z^2}{{\sigma }_2^2}\right)}\left(\frac{x^2+y^2}{{\sigma }_1^7}-\frac{4}{{\sigma }_1^5}\right)+\frac{z^2}{4{\pi }^3{\sigma }_1^4{\sigma }_2^2}{e}^{-\left(\frac{x^2+y^2}{{\sigma }_1^2}+\frac{z^2}{{\sigma }_2^2}\right)}\left(\frac{x^2+y^2}{{\sigma }_1^3{\sigma }_2^4}-\frac{2}{{\sigma }_1{\sigma }_2^4}\right).\end{array}$$

In the same way, we can derive Eq.(20).