Abstract
Although green tea (Camellia sinensis) (GT) contains a large number of polyphenolic compounds with anti‐oxidative and anti‐proliferative activities, little is known of the pharmacokinetics and tissue dose of tea catechins (TCs) as a chemical mixture in humans. The objectives of this study were to develop and validate a physiologically based pharmacokinetic (PBPK) model of tea catechin mixture (TCM) in rats and humans, and to predict an integrated or total concentration of TCM in the plasma of humans after consuming GT or Polyphenon E (PE). To this end, a PBPK model of epigallocatechin gallate (EGCg) consisting of 13 first‐order, blood flow‐limited tissue compartments was first developed in rats. The rat model was scaled up to humans by replacing its physiological parameters, pharmacokinetic parameters and tissue/blood partition coefficients (PCs) with human‐specific values. Both rat and human EGCg models were then extrapolated to other TCs by substituting its physicochemical parameters, pharmacokinetic parameters, and PCs with catechin‐specific values. Finally, a PBPK model of TCM was constructed by linking three rat (or human) tea catechin models together without including a description for pharmacokinetic interaction between the TCs. The mixture PBPK model accurately predicted the pharmacokinetic behaviors of three individual TCs in the plasma of rats and humans after GT or PE consumption. Model‐predicted total TCM concentration in the plasma was linearly related to the dose consumed by humans. The mixture PBPK model is able to translate an external dose of TCM into internal target tissue doses for future safety assessment and dose‐response analysis studies in humans. The modeling framework as described in this paper is also applicable to the bioactive chemical in other plant‐based health products.
Keywords: PBPK model, tea catechins, systemic dosimetry
Abbreviations
- AUC
area under the concentration‐time curve
- BLPLR
blood/plasma ratio
- BW
body weight
- CBA
catechin in arterial blood
- CBN
catechin in bone
- CBR
catechin in brain
- CBV
catechin in venous blood
- Cexpti
experimental concentration
- CFT
catechin in adipose tissue
- CGT
catechin in gut tissue
- CHR
catechin in heart
- CKD
catechin in kidney
- CL
clearance
- CLG
catechin in lung
- CLV
catechin in liver
- Cmax
peak plasma concentration of tea catechin
- CMS
catechin in muscle
- CO
cardiac output
- Cpredi
model‐predicted concentration
- CRB
catechin in rest of the body
- CSK
catechin in skin
- CSP
catechin in spleen
- EC
epicatechin
- ECg
epicatechin gallate
- EGC
epigallocatechin
- EGCg
epigallocatechin gallate
- EROD
ethoxyresorufin‐O‐deethylase
- F
bioavailability factor
- fup
the fraction unbound in plasma
- fut
the fraction unbound in tissue
- GT
Green tea
- HPLC
high performance liquid chromatograph
- IEF
the inhibitory equivalence factor
- ka, kra, and kf
respectively are absorption, re‐absorption, and fecal excretion rate constants
- LOD
limit of detection
- LSP
Log‐normalized sensitivity parameter
- MAPE
Mean absolute prediction error
- PBPK
physiologically based pharmacokinetic
- PCs
partition coefficients
- PE
Polyphenon E
- PKs
pharmacokinetics
- PO:W
log octanol:water partition coefficient
- PVO:W
log vegetable oil:water partition coefficient
- Rt
residence time of catechin in bile
- TCM
tea catechin mixture
- TCs
tea catechins
- tlag
absorption lag time
- Vn
fractional weight of neutral fat
- Vph,
fractional weight of phospholipids
- Vw
fractional weight of water
Introduction
Green tea (GT), the water extract of Camellia sinensis leaves, consists of a complex mixture of tea catechins (TCs) such as epigallocatechin gallate (EGCg), epigallocatechin (EGC), epicatechin gallate (ECg), and epicatechin (EC) (Fig. 1). Daily consumption of GT is believed to be beneficial to health including prevention of cancer, obesity, diabetes, and cardiovascular diseases (Saito et al. 2009). Thus, Polyphenon E (PE), a standardized GT extract, has been found an effective agent in slowing down the progression of early stage cancer in humans (Shanafelt et al. 2013). Also, a PE ointment has been approved by the US Food and Drug Administration for the treatment of genital warts. However, TCs may cause toxic effects in animals and humans especially when they are administered at high doses, that is, 10–29 mg/kg/day tea‐based diets (Lambert et al. 2007).
Figure 1.

Chemical structures of EGCg, EGC, ECg, and EC.
The pharmacokinetics (PKs) and tissue distribution of TCs have been studied in different animal species including rodents (Chen et al. 1997; Suganuma et al. 1998; Zhu et al. 2000; Cai et al. 2002), dogs (Swezey et al. 2003), and humans (Pietta et al. 1998; Chow et al. 2001; Van Amelsvoort et al. 2001; Lee et al. 2002; Meng et al. 2002). EGCg is the most studied tea catechin because it is the most abundant and potent catechin of GT (Balentine et al. 1997). EGCg is absorbed rapidly by rodents (Kim et al. 2000); peak plasma concentration (C max) usually appears within 3 h after consumption (Chen et al. 1997; Suganuma et al. 1998). About 0.17% and 6% of the consumed EGCg is eliminated in the urine (Zhu et al. 2001) and bile (Kohri et al. 2001a) of rats, respectively. Less than 0.02% and >90% of the EGCg consumed by humans is excreted in the urine (Van Amelsvoort et al. 2001) and feces (Lee et al. 2002), respectively. TCs are metabolized mainly by conjugation with glucuronic acid and sulfate in rats and humans (Kohri et al. 2001a; Meng et al. 2002; Chow et al. 2005) before being excreted into the bile (Kida et al. 2000). The conjugated metabolites may be converted back to the free forms by intestinal bacteria before undergoing entero‐hepatic recycling (Kohri et al. 2001b). Small amounts of TCs also are metabolized by CYP1A2 (Obermeier et al. 1995) and catechol‐O‐methyltransferase (Meng et al. 2002) enzymes. Non‐gallated TCs (e.g., EGC and EC) are more extensively metabolized than gallated TCs (e.g., EGCg and ECg) in rats and humans. The clearance (CL/F) of EGCg, ECG, and EC is 0.061, 0.091, and 0.046 L/min/kg, respectively, in rats (Zhu et al. 2000) but ranges from 0.092 to 0.24 L/min/kg in humans (Chow et al. 2001).
The target organs of GT chemoprevention have been identified in rodents (Yang et al. 2002). However, little is known of the PKs and target organs of a tea catechin mixture (TCM) in humans due to the difficulties and high costs of collecting tissue/organ samples from humans directly. Andersen (1987) has suggested using the physiologically based pharmacokinetic (PBPK) model (IPCS, 2010) to predict the PKs and tissue doses of environmental chemicals in humans. However, only a few PBPK models have been developed for botanical drugs which include soy isoflavone (Schlosser et al. 2006; Law 2007), matrine (Gao and Law 2009), caffeine (Ginsberg et al. 2004), sophoridine (Hu and Huang 1995), and glycyrrhizic acid (Ploeger et al. 2000). Moreover, none of these models are able to predict the PKs and tissue doses of the whole plant in humans because they have been developed with laboratory animals using single marker chemicals of these plants.
The objectives of this study were to develop a PBPK model of TCM for rats and humans after consuming GT or PE, to validate the mixture PBPK model by comparing model simulation with observed data in the literature, and to predict an effect‐based or integrated concentration of TCM in the plasma of humans using C max as the dose surrogate (Andersen 1987; Ito et al. 2004). In the present study, the plasma was used as an illustrative example to predict TCM dose metrics in other organs/tissues. Results of the study showed the mixture PBPK model was able to duplicate the kinetic data of three major tea catechin constituents in the plasma of rats and humans after GT/PE consumption. Moreover, total TCM concentrations in the plasma were related linearly to the dose administered to humans. The modeling approach as described in this paper also is applicable to the bioactive chemical mixtures in other plant‐based natural health products such as traditional medicines, functional foods, and dietary supplements.
Materials and Methods
Sources of experimental data
The empirical data used to develop and validate the PBPK models were taken from previously published pharmacokinetic studies in rats and humans after receiving an oral dose of pure tea catechin or GT/PE formulation. Since we were unable to obtain the original data of these studies, the observed data were read digitally from the publications using DigiMatic® (Windows version 2.2c, FEB Software. Chesterfield, Virginia). The following was a brief summary of the pharmacokinetic studies:
Pharmacokinetic studies in rats
Zhu et al. (2000) studied the PKs of TCs in male Sprague‐Dawley rats (210–230 g) equipped with implanted jugular vein cannuli. Each rat was given an oral dose of PE containing a mixture of EGCg (2500 mg/kg), ECg (650 mg/kg), and EC (250 mg/kg). Blood samples were removed from the jugular cannuli of rats at different time points post‐dosing. The blood samples were centrifuged to separate the plasma from red blood cells. The plasma samples were analyzed for free TCs using a high performance liquid chromatograph (HPLC). Tea catechin concentrations in the plasma samples were plotted against sampling times. The resulting concentration‐time curves were analyzed by the noncompartmental approach. Oral bioavailability of EGCg, ECg, and EC was found to be 0.14, 0.06, and 0.39, respectively; urinary recovery was respectively, 0.17%, 0.25%, and 4.72% of the administered tea catechin doses.
Chen et al. (1997) studied the PKs of TCs in male Sprague‐Dawley rats (310 g) after administering an oral dose of pure EGCg (75 mg/kg) or PE containing a mixture of EGCg (14.6 mg/kg), EGC (13.6 mg/kg) and EC (5.4 mg/kg). Blood samples were removed from the orbital sinus of rats at different time points post‐dosing. The blood samples were centrifuged to separate the plasma from red blood cells. The plasma samples were incubated separately with glucuronidase/sulfatase enzymes at 37°C. The reaction mixture was extracted by ethyl acetate. Total EGCg, EGC or EC concentrations (free catechin plus conjugated metabolites) in ethyl acetate extracts were determined using HPLC and plotted against sampling time. The resulting concentration‐time curves were fitted to the one‐compartment, classical pharmacokinetic model. Results of the study showed the PKs of pure EGCg and crude EGCg were different in the plasma of rats.
Pharmacokinetic studies in humans
Chow et al. (2003) studied the PKs of EGCg in eight healthy human volunteers (72 kg) diagnosed with Fitzpatric type II or III skin problems. Each participant was given an oral dose of pure EGCg (400 mg). Blood samples were collected from the volunteers at 0.5, 1.0, 2.0, 3.5, 5.0, 6.5, 8.0, and 24.0 h post‐dosing and centrifuged to separate the plasma from red blood cells. The plasma samples were extracted by ethyl acetate which was analyzed for free EGCg using an ESA Model 580 HPLC equipped with an ESA 5600 Coulochem electrode array system. The plasma concentration‐time curves were analyzed using the non‐compartment approach (WinNonlin version 2.0. Pharsight Corporation, Cary, N.C. USA).
Chow et al. (2001) studied the PKs of EGCg in human volunteers (75 kg) receiving an oral dose of pure EGCg (400 mg) or a PE preparation containing 400 mg of crude EGCg. Blood samples were collected from the volunteers at different time points post‐dosing and centrifuged to separate the plasma from red blood cells. The plasma samples were extracted by ethyl acetate and quantified using a HPLC. The PK profiles of pure EGCg and crude EGCg in PE were found to be very similar. In a separate study, the PKs of EGCg, EGC, and EC were examined simultaneously in the plasma of humans (72 kg) after consuming PE containing a mixture of EGCg (600 mg), EGC (111 mg), and EC (93 mg). Unchanged EGCg, EGC, and EC in the plasma were determined using a HPLC. Only free or unchanged EGCg, and mainly EGC and EC conjugated metabolites were found in the plasma of humans (Chow et al. 2001). The concentration‐time curves of the TCs were analyzed using the non‐compartmental approach.
Lee et al. (2002) studied the PKs of TCs in the plasma of human volunteers (45–85 kg) after administering an oral dose of pure EGCg (2 mg/kg) or GT solids (20 mg/kg) containing a mixture of EGCg (13.9%), EGC (11.0%), and EC (3.2%). Blood samples were removed from the volunteers at predetermined time points, and centrifuged to separate the plasma from red blood cells. The plasma samples were incubated with β‐glucuronidase and sulfatase, extracted and analyzed by HPLC equipped with a Coulochem electrode array detector. Free EGCg, EGC, and EC concentrations in the plasma samples were determined as a percentage of total concentration (free catechin plus conjugated metabolites) but only at 1 h and 5 h post‐dosing time points. The concentration‐time curves were separately fitted to the one‐compartment, classical pharmacokinetic model. Large inter‐individual differences in pharmacokinetic parameters especially those related to the oral absorption of TCs were observed in the study. Results of the study also confirmed that the pharmacokinetic behaviors of pure EGCg and crude EGCg were very similar in humans (Chow et al. 2001).
Developing PBPK models of individual tea catechins for rats
A PBPK model of EGCg was first developed in rats. The rat EGCg model was then converted to an ECg or EC model by replacing the physicochemical parameters, pharmacokinetic parameters, and tissue/blood partition coefficients (PCs) with values specific for the tea catechin (see Tables 1, 2, 3).
Table 1.
Physicochemical properties and unbound fractions of tea catechins in the plasma of rats
| Parametersa | EGCg | ECg | EGC | EC |
|---|---|---|---|---|
| P O:W | 97.70 | 468 | 4.84 | 3.09 |
| Dvo:w | 5.13 | 29.3 | 0.26 | 0.16 |
| pKa | 7.75 | 7.75 | 9.54 | 9.54 |
| f up b | 0.04 | 0.03 | 0.25 | 0.25 |
| f ut c | 0.08 | 0.06 | 0.40 | 0.40 |
| BLPLRd | 0.91 | 0.99 | 0.88 | 0.88 |
P O:W, log octanol‐water partition coefficient; Dvo:w, log vegetable oil‐water partition coefficient; pKa, ionization constants. P O:W; and pKa are obtained using the ACD/I‐Labs online prediction engine (https://ilab.acdlabs.com/); P VO:W, is calculated from P O:W and pKa according to Poulin and Theil (2002).
f up, the fraction unbound in plasma, is taken from Zhu et al. (2001)
f ut, the fraction unbound in tissue, is calculated using the equation, f ut = 1/[1 + (((1−f up)/f up) × 0.5)] (Poulin and Theil 2002).
BLPLR, the blood/plasma ratios of individual tea catechins in rats, are predicted using tissue composition‐based model (Poulin and Krishnan 1995).
Table 2.
Rat physiological parameters and tissue/blood partition coefficients for PBPK modeling
| Tissues | Blood flowa (% CO) | Tissue volumeb (% BW) | Tissue/blood partition coefficientsc | ||
|---|---|---|---|---|---|
| EGCg | ECg | EC | |||
| Adipose | 7.00 | 7.60 | 0.20 | 0.75 | 0.08 |
| Blood | 8.16 | ||||
| Bone | 12.20 | 4.15 | 1.62 | 4.00 | 0.39 |
| Brain | 2.00 | 0.57 | 3.15 | 7.84 | 0.73 |
| GI tract | 13.10 | 2.70 | 2.04 | 4.82 | 0.63 |
| Heart | 4.90 | 0.33 | 1.27 | 2.65 | 0.62 |
| Kidney | 14.10 | 0.73 | 1.43 | 3.10 | 0.63 |
| Liver | 17.50 | 3.66 | 1.50 | 3.37 | 0.59 |
| Lung | 0.50 | 1.70 | 3.83 | 0.65 | |
| Muscle | 27.80 | 40.40 | 1.02 | 1.97 | 0.59 |
| Skin | 5.80 | 19.00 | 1.79 | 4.23 | 0.55 |
| Spleen | 2.00 | 0.20 | 0.98 | 1.85 | 0.63 |
| Rest of body | 8.70 | 12.00 | 1.00 | 1.00 | 1.00 |
CO (L/h), the cardiac output of rats, is scaled from the allometric equation, CO = 14.0 × (BW)0.75 (Travis 1987) The CO of a 0.4 kg rat is 7.08 L/h. Mean tissue blood flows are adapted from Luttringer et al. (2003) and Davies and Morris (1993).
Table 3.
Pharmacokinetic parameters used to simulate the kinetics of individual tea catechins in rats after consuming a single dose of pure EGCg or PE
| Parametersa | EGCg | ECg | EC |
|---|---|---|---|
| k ac (/min·kg)b | 0.003 | 0.002 | 0.002 |
| F | 0.0003–0.038 | 0.06 | 0.13 |
| tlag (min) | 10.00 | 10.00 | 5.00 |
| R t (min) | 3.00 | 0.30 | 2.00 |
| k rac (/min·kg)b | 0.67 | 0.41 | 13.40 |
| k fc (/min·kg)b | 0.13 | 0.13 | 0.13 |
| CLbc (mL/min·kg)c | 9.13 | 12.60 | 8.70 |
| CLrc (mL/min·kg)d | 0.36 | 0.30 | 4.50 |
The parameters are defined in the text.
Rate constants are scaled from the body weight based on the following equations: k a = k ac(BW)−0.3, k ra = k rac(BW)−0.3, and k f = k fc(BW)−0.3.
CLbc are the scaling coefficients of biliary clearance, CLb which is scaled from body weight using the allometric equation, CLb = CLbc(BW)0.66.
CLrc are the scaling coefficients of renal clearance, CLr which are derived experimentally from rats after receiving an i.v. dose of DGT (Zhu et al. 2001) and scaled to the body weight of rats in the present study using the allometric equation, CLr = CLrc(BW)0.66. The CLr of EGC is assumed equal to EC.
Model structure
Figure 2 shows a schematic for the PBPK model of a single tea catechin in rats or humans: (A) the model consisted of 13 first‐ordered, blood flow‐limited compartments including the lung, kidney, muscle, brain, liver, spleen, gut, bone, skin, heart, fat, blood, and rest of the body. Some of these tissue compartments were identified as the target organs of GT chemoprevention in rats (Yang et al. 2002), (B) individual TCs were absorbed into the blood via the gastrointestinal tract with absorption rate constants (k a). A lag time (tlag) was used to account for the time delay of absorption, (C) TCs were metabolized by the liver mainly to glucuronic acid/sulfate conjugates (Cai et al. 2002) before being excreted into the bile. These conjugated metabolites might be de‐conjugated by microorganisms in the colon and underwent entero‐hepatic recycling. The entero‐hepatic recycling model was modified from Bischoff et al. (1971) and Harrison and Gibaldi (1977). Biliary clearance (CLb) represented both the metabolic and secretory processes of the liver. The residence time (R t) represented the average time these metabolites spent in the bile before being reabsorbed (see Appendix A5). A reabsorption rate constant (k ra) was used to describe the reabsorption of TCs at a location different from the initial absorption sites.
Figure 2.
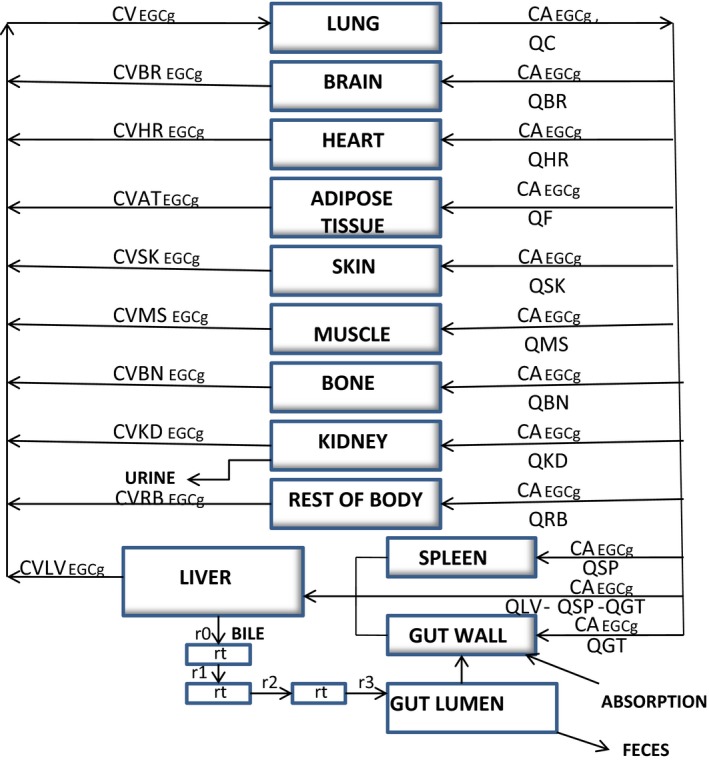
Schematic for the physiologically based pharmacokinetic description of a tea catechin in rats and humans. CA, CV, and Q, respectively, represent arterial concentrations, venous concentrations, and blood flows. The symbols and pharmacokinetic parameters are defined in the Appendix, and Tables 2, 4. The entero‐hepatic recycling sub‐model was adapted from Harrison and Gibaldi (1977) with modification.
Parameterization of PBPK model for rats
Physiological parameters
Tissue volumes and blood flows of rats with an average body weight (BW) of 0.26 kg were taken from the literature (Davies and Morris 1993; Luttringer et al. 2003). Tissue volumes were expressed as the percentage of average BW while blood flows were expressed as the percentage of cardiac output (CO) (Table 1). Gut content was assumed to be 0.014 mL for rats with an average BW of 0.25 kg (Angelo and Pritchard 1987). Physiological parameter values were scaled to the average BW of rats used in the pharmacokinetic study.
Tissue/blood partition coefficients
The tissue/blood PCs of EGCg, ECg, and EC (Table 2) were predicted using the tissue composition‐based equations (Poulin and Krishnan 1995; Poulin et al. 2001; Poulin and Theil 2002):
| (1) |
| (2) |
where P t:b non‐adipose represents non‐adipose tissue/blood PCs, P t:b adipose represents adipose tissue/blood PCs, P o:w represents n‐octanol:water PCs of non‐ionized catechin, D vo:w represents vegetable oil:water distribution for both the non‐ionized and ionized TCs at pH 7.4, V wt, V nt, and V pht are the fractional weight of water, neutral fat, and phospholipids in the tissue, respectively, and V wp, V np, and V php are the corresponding values in the plasma. V wt, V nt, V pht, V wp, V np, and V php were taken from Poulin and Theil (2002). D vo:w was derived from P o:w and pKa according to Poulin and Theil (2002).
The parameters used to implement the tissue composition‐based model (Table 2) were obtained as follows: (1) Log P o:w and pKa for individual TCs were predicted using the ACD/I‐Labs online engine (Advanced Chemistry Development Inc., Toronto, Ontario, Canada. https://ilab.acdlabs.com/). The predicted pKa values were found to be very close to the experimental pKa values which were 7.6, 7.6, >8.5 and >8.7 for EGCg, ECg, EGC, and EC, respectively (Inoue et al. 2002). (2) The BLPLR was calculated based on the theoretical partitioning of individual TCs into the erythrocytes and plasma of rats (Poulin and Krishnan 1995). Thus, BLPLR = (0.37 × Pe + 0.63 × P p)/P p, where P e was the partitioning of the tea catechin into the erythrocytes of rats and P p was the partitioning of the tea catechin in the plasma. Model‐predicted BLPLR were found to be very close to the experimental values which were 0.67, 0.61, and 0.87 for EGCg, ECg and EC, respectively (Zhu et al. 2001). (3) F up and f ut represent the unbound fractions of individual TCs in the plasma and tissue, respectively. The f up of EGCg, ECg, and EC in the plasma of rats were determined experimentally to be 4%, 3% and 25%, respectively (Zhu et al. 2001). The f up of EGC was not available; it was assumed equal to the EC value. The fut was calculated using the equation, f ut = 1/[1 + (((1−f up)/f up) × 0.5)] (Poulin and Theil 2002).
Pharmacokinetic parameters
The k a of EGCg and EC in rats was taken from Chen et al. (1997) study. The k a of ECg was not available; it was assumed equal to that of EC (Table 3). The absorption rate constant scaling coefficients (k ac) were derived from the allometric equation, k ac = k a/(BW)−0.3 (Travis 1987). Renal clearance (CLr) of EGCG, ECg and EC were 0.15, 0.11, and 1.66 mL/min; (Zhu et al. 2000, 2001). The scaling coefficients (Clrc) were derived from CLr using the allometric equation, CLrc = CLr/(BW)0.66 (Chiou et al. 1998) (Table 3). Because TCs were metabolized by the liver and excreted into the bile, biliary clearance (CLb) was assumed equal to hepatic clearance (CLh) which was shown to be 3.74, 3.96, and 5.72 mL/min for EGCG, ECg, and EC, respectively (Zhu et al. 2001). Biliary clearance scaling coefficients (CLbc) were derived using the allometric equation, CLbc = CLb/(BW)0.66 (Chiou et al. 1998). Fecal transport rate constant (k f) (Lutz et al. 1977) was assumed to be 1/transit time in the small intestine as reported by Davies and Morris (1993). Final adjustments were made on the model parameters by fitting the PBPK model to the experimental data of Zhu et al. (2000). No further adjustment was allowed once the parameter values were finalized in Table 3.
Scaling up of rat PBPK models to humans and parameterization of human models
The PBPK model of EGCg in rats (Fig. 2) was scaled up to humans by substituting the physiological parameters, pharmacokinetic parameters such as clearances, and PCs of the rat model with human specific values (Table 4). The human EGCg model was converted to an EGC or EC model by replacing the physicochemical parameters, pharmacokinetic parameters, and PCs with values specific for the tea catechin (Tables 4, 5).
Table 4.
Human physiological parameters and tissue/blood partition coefficients for PBPK modeling
| Tissues | Blood flowa (% CO) | Tissue volumeb(% BW) | Tissue/blood partition coefficientsc | ||
|---|---|---|---|---|---|
| EGCg | EGC | EC | |||
| Adipose | 5.00 | 12.00 | 0.15 | 0.01 | 0.01 |
| Blood | 7.71 | ||||
| Bone | 5.00 | 8.56 | 3.22 | 0.48 | 0.41 |
| Brain | 12.00 | 0.02 | 3.12 | 0.69 | 0.62 |
| GI tract | 17.00 | 1.71 | 2.49 | 0.53 | 0.55 |
| Heart | 4.00 | 0.47 | 1.00 | 0.51 | 0.50 |
| Kidney | 19.00 | 0.44 | 1.38 | 0.56 | 0.53 |
| Liver | 25.00 | 2.57 | 2.05 | 0.59 | 0.55 |
| Lung | 0.76 | 0.57 | 0.51 | 0.51 | |
| Muscle | 17.00 | 40.00 | 1.38 | 0.54 | 0.52 |
| Skin | 5.00 | 3.71 | 1.60 | 0.53 | 0.50 |
| Spleen | 2.00 | 0.26 | 1.40 | 0.56 | 0.54 |
| Rest of body | 8.00 | 21.60 | 1.00 | 1.00 | 1.00 |
CO (L/h) represents the cardiac output of human volunteers; it is scaled from the allometric equation, 16.1 (BW)0.75 (Travis 1987) based on the CO of 390 L/h for a 70 kg human. Mean data on blood flows are adapted from Luttringer et al. (2003).
Table 5.
Pharmacokinetic parameters used to simulate the kinetics of individual tea catechins in humans after consuming a single dose of pure EGCg or PE
| Parametersa | EGCg | EGC | EC |
|---|---|---|---|
| k ac (/h·kg)b | {1.1}[0.85](2.85) | 2.19 | 1.86 |
| F | {0.065}[0.12](0.07) | [0.013](0.052) | [0.01] (0.1) |
| tlag (h) | 0.50 | 0.40 | 0.40 |
| k fc (/h·kg)b | 25.60 | 25.60 | 25.60 |
| R t (h) | 0.03 | 0.03 | 0.03 |
| k rac (/h ·kg)b | 0.18 | 0.18 | 0.18 |
| CLbc (L/h ·kg)c | 2.70 | 0.97 | 1.03 |
| CLrc (L/h ·kg)d | 0.0023 | 0.34 | 0.56 |
The parameters are defined in the text.
Rate constants, k a, k ra, and k f are up‐scaled from rats (see Table 4) using the following allometric equations: k a = k ac (BW)−0.3, k ra = k rac (BW)−0.3, and k f = k fc (BW)−0.3. Values in {}, [] and () brackets are used to simulate Chow et al. (2003), Chow et al. (2001) and Lee et al. (2002) studies, respectively.
CLbc is the scaling coefficient of biliary clearance, CLb is up‐scaled from rats (see Table 3) using the allometric equation, CLb = CLbc(BW)0.66.
The human PBPK model of a single tea catechin was parameterized as follows: (1) human tissue volumes and blood flows to the tissues (Table 4) were taken from the literature (Luttringer et al. 2003). Tissue/blood PCs for humans (Table 4) were predicted using the tissue composition‐based model (Poulin et al. 2001; Poulin and Theil 2002). Gut content was assumed to be 2.1 L (Bischoff et al. 1971), (2) the CLr of a tea catechin (Table 5) was estimated by dividing the amount excreted in the urine with the area under the curve in plasma (AUCplasma). Thus, the CLr of EGCg was derived from the study of Meng et al. (2002) and the CLr of EGC and EC were calculated from the study of Lee et al. (2002). The CLrc of individual TCs were derived from their CLr using the allometric equation, CLrc = CLr/(BW)0.66 (Chiou et al. 1998), (3) the CLbc of individual TCs (Table 5) were scaled up from CLb of rats using allometric equation, CLbc = CLb/(BW)0.66 (Chiou et al. 1998), and (4) human k a, k ra, and k f rate constants (Table 5) were scaled up from rats using the equation, k c = k/(BW)−0.3, where k represented the rate constant, k c represented the scaling coefficient, and BW was the average body weight of human volunteers (Travis 1987). Human BLPLR were assumed equal to those of rats (Table 1). Model parameters that could not be parameterized a prior were optimized by fitting the PBPK model to available experimental data (see Data fitting below). Final physiological and biochemical parameter values were summarized in Tables 4, 5, respectively.
Construction of a PBPK model of tea catechin mixture for rats and humans
A PBPK model of TCM was constructed by linking three different catechin models of rats (or humans) together without accounting for pharmacokinetic interactions between the TCs (Fig. 3). Pharmacokinetic interactions were assumed to be negligible or insignificant among the TCs or between a tea catechin and some unknown chemicals in GT or PE. The assumption of mixture PBPK model was tested by comparing model simulation with the PKs of three catechin constituents in the plasma of rats (or humans) after GT/PE consumption (see Results).
Figure 3.
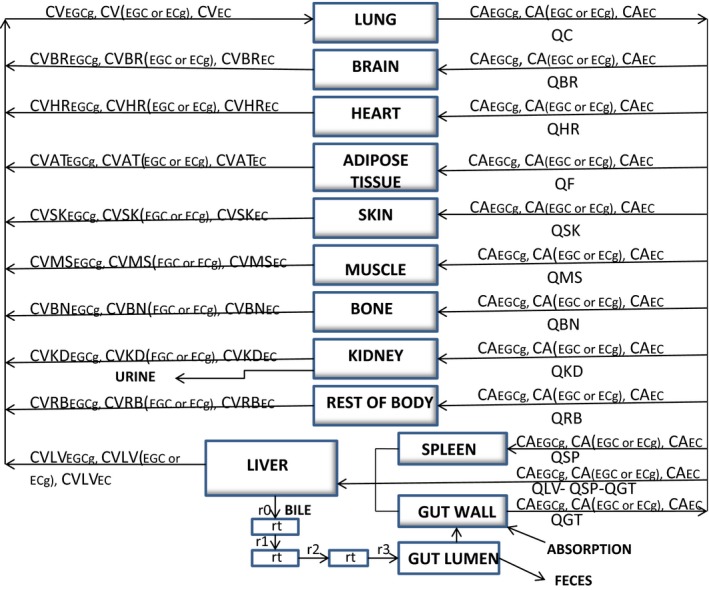
Schematic for the physiologically based pharmacokinetic description of a mixture of tea catechins in rats and humans. CA, CV, and Q, respectively, represent arterial concentrations, venous concentrations and blood flows. The symbols and pharmacokinetic parameters are defined in the Appendix, and Tables 2, 4. The entero‐hepatic recycling sub‐model was adapted from Harrison and Gibaldi (1977) with modification. For the sake of clarity, only the parameters of a single TC was shown in the enterohepatic recycling sub‐model.
Computer simulation and data fitting
Computer simulation
The differential and algebraic equations describing the movement of a single tea catechin (Fig. 2) or a mixture of TCs (Fig. 3) through the body of rats or humans were formulated as a computer program (see Appendix). After incorporating the different parameter values (Tables 1, 2, 3, 4, 5) into the PBPK model, the equations were solved numerically with the aid of AcslXtreme 2.5.0.6 (AEgis Technologies Group, Inc., Orlando, FL).
Data fitting
Model parameters that could not be parameterized a priori were estimated by fitting the initial estimates to the PBPK model with all other parameters fixed at the values listed in Tables 2, 3, 4, 5. Parameter values were adjusted manually at the beginning to test their effects on model simulation. Final adjustment of parameter values to fit the empirical data was carried out using the maximized log likelihood function of AcslXtreme OptStat (AEgis Technologies Group, Inc., Orlando, FL). Upper and lower bound limits on parameter values might be employed during the optimization process. Also, we might sacrifice the best‐fit to a dataset in order to obtain a set of parameter values which described the PKs of all other studies. Final parameter values that are adjusted to available experimental data are listed in Tables 1, 2, 3, 4, 5.
Plasma dosimetry of tea catechin mixture
The C max of individual TCs in a TCM were used as the dose surrogate (Andersen 1987; Ito et al. 2004) to calculate the integrated concentration/dose of TCM in the plasma. Thus, the mixture PBPK model for humans (Fig. 3) was used to predict the C max of individual tea catechin constituents according to the experimental conditions described in Chow et al. (2001, 2005) and Lee et al. (2002) studies. The predicted C max was multiplied by the inhibitory equivalence factor of the tea catechin in inhibiting hepatic 7‐ethoxyresorufin‐O‐deethylase (EROD) activity in vitro (Obermeier et al. 1995). The products of multiplication were added together yielding the integrated concentration/dose of TCM in the plasma (μg EGCg equivalents/mL) of humans after GT/PE consumption. Similarly, the TCM dose metric in externally administered PE/GT was calculated but expressed as μg EGCg equivalents/g of GT/PE. The different steps involved in calculating the dose metrics of TCM were summarized in the following concentration/dose additivity equation (ATSDR, 2004; EPA 2007):
| (3) |
where, TCM concentration/dose is expressed in μg EGCg equivalents/g or mL, C 1 represents the concentration of EGCg in PE or the C max of EGCg in the plasma, Ci represents the ith tea catechin in a TCM, IEF1 represents the inhibitory equivalence factor of EGCg which is assigned a value of 1.00, and IEFi is the inhibitory equivalence factor of the ith tea catechin constituent relative to EGCg. The IEF of EGCg, EGC, ECg, and EC are 1.00, 0.85, 0.45, and 2.21, respectively, since the EROD IC50 are 1175, 1000, 530, and 2600 μmol/L, respectively, in human liver microsomes (Obermeier et al. 1995).
The predicted TCM dose metrics in the plasma of humans from different pharmacokinetic studies were plotted against the administered doses. The plot was subjected to linear regression analysis using the GraphPad Prism Software version 5.04 (San Diego, CA).
Statistical and sensitivity analyses
Mean absolute prediction error
Mean absolute prediction error (MAPE) was used as a measure of good fit between model‐predicted concentration (C predi) and experimental concentration (C expti). It was calculated using the following equation:
| (4) |
where, i represents individual data points and N is the total number of data points. A deviation within a factor of two between predicted and experimental concentration data (i.e., MAPE<50%) was used as the criteria for goodness of fit (Bjorkman et al. 1994).
Log‐normalized sensitivity parameter
Log‐normalized sensitivity parameter (LSP) was used to identify key model parameters that had significant impacts on model prediction. LSP is defined by the following equation (Clewell et al. 1994):
| (5) |
where R is the model output and X is the parameter for which the sensitivity is assessed. This equation quantified the percentage change in an output value as a result of the percentage change in a parameter. The sensitivity analysis was conducted using AcslXtreme 2.5.0.6 (AEgis Technologies Group, Inc., Orlando, FL). The sensitivities of EGCg plasma concentration to tissue/blood partition coefficients and pharmacokinetic parameters were determined in rats (Zhu et al. 2000) and humans (Chow et al. 2001) after consuming a dose of pure or crude EGCg. The LSP of parameters were determined at the last time point of the study using the central difference method (Clewell et al. 1994). A LSP > 1 indicated errors in the input parameter resulted in amplified errors in the model output, which was an undesirable feature of the model.
Results
Development of a PBPK model of EGCg for rats and humans
A PBPK model of EGCg was developed by comparing model simulation with free EGCg concentration‐time data in the plasma of rats after consuming 2500 mg/kg of crude EGCg in PE (Zhu et al. 2000). Figure 4 shows the time course of predicted and observed EGCg concentrations in the plasma.The goodness of fit between predicted and measured data was judged by the 34.9% MAPE which showed predicted EGCg concentrations were within the two‐fold error range of empirical EGCg concentrations. The EGCg model of rats was validated by another set of kinetic data from rats after receiving an oral dose of pure EGCg (75 mg/kg) or crude EGCg (6 mg/kg) in PE (Chen et al. 1997). The EGCg model of rats also was able to duplicate the PKs of pure EGCg and crude EGCg with 17.4% and 14.6% MAPE, respectively (Fig. 5). Simulated concentration‐time curves for pure EGCg appeared parallel to those of crude EGCg. If predicted EGCg concentrations in the plasma were normalized by the administered dose (75 mg/kg for pure EGCg and 6 mg/kg for crude EGCg) before plotting against sampling times, the concentration‐time curve of pure EGCg would be superposable on that of crude EGCg. These results indicated that the concentration‐time curves of pure EGCg and crude EGCg in Figure 5 were indeed parallel to each other (Gabrielsson and Weiner 2000). In other words, the PKs of pure EGCg and crude EGCg were very similar in rats.
Figure 4.
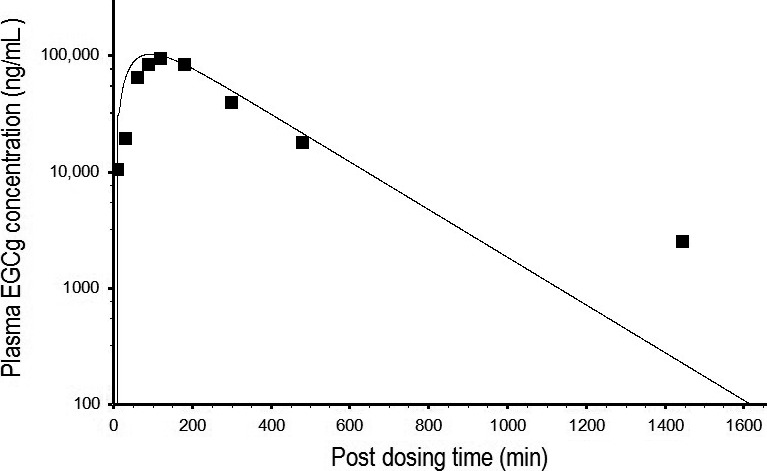
Predicted and measured time course of free EGCg concentrations in the plasma of rats after consuming a single dose of 2500 mg/kg crude EGCg from a PE preparation. ▄ represents mean concentrations of free EGCg (N = 6) at different time points post‐dosing (Zhu et al. 2000). _________ represents model‐simulated concentration‐time curve of free EGCg.
Figure 5.
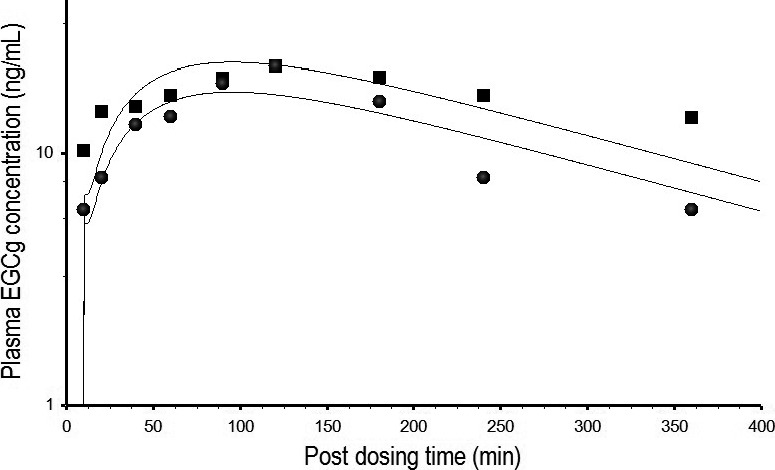
Predicted and measured EGCg concentrations in the plasma of rats after consuming a single dose of pure EGCg (75 mg/kg) or crude EGCg (14.6 mg/kg) from a PE formulation. ▄ and ● represent the time course of total EGCg (free EGCg plus conjugated forms) concentrations in the plasma of rats after consuming pure EGCg and crude EGCG, respectively (Chen et al. 1997). __________ represents model‐simulated concentration‐time curve of free EGCg in the plasma of rats after consuming pure EGCg (upper curve) or crude EGCg (lower curve).
The rat EGCg model was scaled up to humans by replacing the physiological parameters, PCs and pharmacokinetic parameters with human‐specific values (Tables 4, 5). The human EGCg model was calibrated by observed data from Chow et al. (2003) study. Figure 6 shows the predicted and actual kinetic profiles of EGCg in the plasma of humans. The human EGCG model was able to duplicate the observed data since the MAPE between predicted and actual data was only 13.2%. The human EGCg model was validated by another set of kinetic data from humans after consuming 5.33 mg/kg of pure EGCg or 5.33 mg/kg crude EGCg in PE (Chow et al. 2001). The human EGCg model also was able to reproduce the observed data of pure EGCg and crude EGCg with 25.9% and 30.8% MAPE, respectively, although EGCg concentrations were under‐predicted at or close to the 24‐h, post‐dosing time point (Fig. 7). The predicted concentration‐time profiles for pure EGCg and crude EGCg were identical (Fig. 7) because both EGCg formulations contained the same dose (5.33 mg/kg) of EGCg (Chow et al. 2001).
Figure 6.
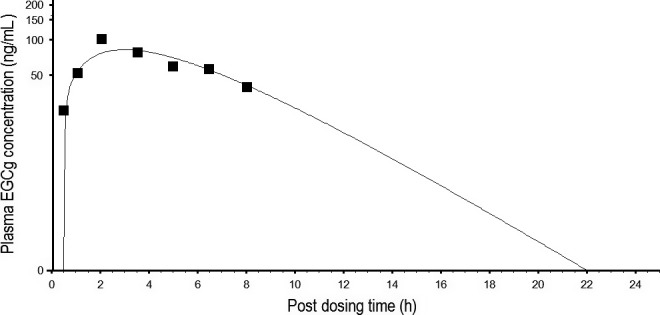
Predicted and measured free EGCg concentrations in the plasma of humans after consuming a single dose of 400 mg pure EGCg. ▄ represents mean concentrations of free EGCg (N = 8) at different time points post‐dosing (Chow et al. 2003). __________ represents model‐simulated concentration‐time curve for free EGCg.
Figure 7.
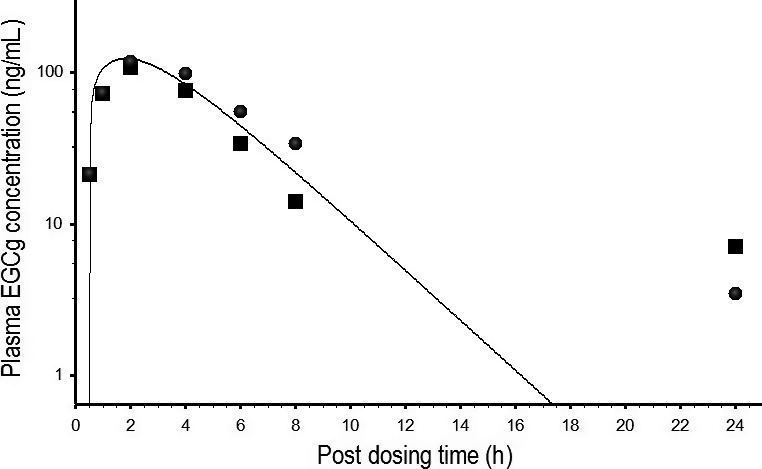
Predicted and measured free EGCg concentrations in the plasma of humans after consuming 400 mg pure EGCg or 400 mg crude EGCg from a PE formulation. ▄ and ● represent mean concentrations of free EGCg (N = 5) in the plasma of humans after consuming pure EGCg and crude EGCg, respectively (Chow et al. 2001). ___________ represents the simulated concentration‐time curves of humans after consuming pure EGCg or crude EGCg; these curves are identical because both EGCg formulations contain the same amount (400 mg) of EGCg (Chow et al. 2001),
Sensitivity analysis of EGCg PBPK model
Table 6 shows the LSP of pharmacokinetic parameters and tissue/blood PCs with respect to EGCg concentrations in the plasma of rats and humans. The LSP of F, BLPLR, and kac in human EGCg model were all >1.0 in absolute values. By contrast, the LSP of tissue/blood PCs, except those of Rms and Rrb, were all <1.0 (Table 6). Similarly, the LSP of F, BLPLR, and BW were >1.0 and the LSP of tissue/blood PCs were <1.0 in rat EGCg model (Table 6).
Table 6.
Log‐normal sensitivity analysis ‐ the effects of pharmacokinetic parameters and partitioning coefficients on plasma EGCg concentration‐time profile
| Pharmacokinetic parametersa | Sensitivity coefficients | Partitioning coefficientsa | Sensitivity coefficients | ||
|---|---|---|---|---|---|
| Ratb | Humanc | Ratb | Humanc | ||
| BW | 10.1 | — | Rbn | — | — |
| BLPLR | –1.1 | –1.1 | Rbr | — | — |
| CLbc | —d | — | Rft | — | — |
| CLrc | — | –0.7 | Rgt | — | — |
| F | 29.4 | 15.2 | Rhr | — | — |
| R t | — | — | Rkd | — | — |
| k ac | — | −4.8 | Rlg | — | — |
| k fc | — | — | Rlv | — | — |
| k rac | — | — | Rms | — | 1.9 |
| tlag | — | 0.8 | Rrb | — | 1.2 |
| Rsk | — | — | |||
| Rsp | — | — | |||
Construction of a PBPK model of tea catechin mixture in rats and humans
The rat EGCg model was extrapolated to an ECg or EC model by replacing the physicochemical parameters, pharmacokinetic parameters, and PCs with ECg‐ or EC‐specific values (Tables 1, 2, 3). A PBPK model of TCM for rats (Fig. 3) was constructed by linking the EGCg, ECg, and EC models together under the assumption of no pharmacokinetic interaction between the TCs. The PBPK model of TCM was calibrated by the kinetic data of rats after receiving an oral dose of PE containing a mixture of EGCg (2500 mg/kg), ECg (650 mg/kg), and EC (250 mg/kg) (Fig. 2 of Zhu et al. 2000). Figure 8 shows the predicted and observed kinetic profiles of EGCg, ECG, and EC in the plasma of rats. The PBPK model of TCM was able to describe the observed data closely since the overall MAPE between predicted and measured data was only 33.9%.
Figure 8.
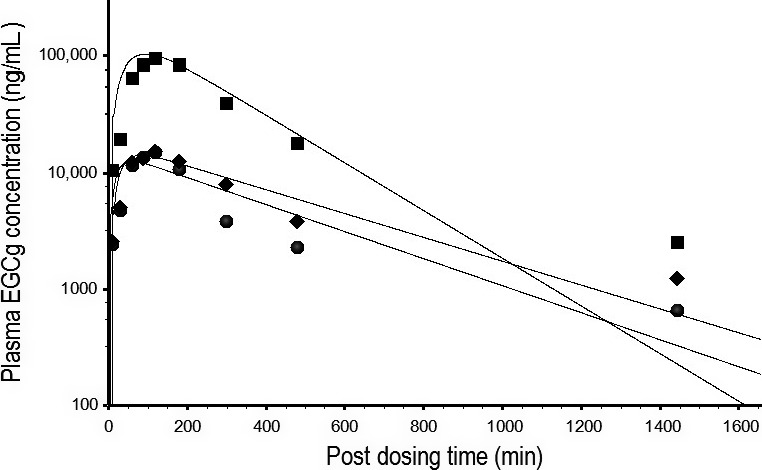
Predicted and measured free EGCg, ECg, and EC concentrations in the plasma of rats after consuming PE containing a mixture of EGCg (2500 mg/kg), ECg (650 mg/kg), and EC (250 mg/kg). ▄, ♦, and ●, respectively, represent mean concentrations (N = 6) of free EGCg, ECg, and EC at different time points post‐dosing (Zhu et al. 2000). ___________ represents model‐simulated concentration‐time curves for free EGCg (top), ECg, (middle), and EC (bottom). Note: the EGCg concentration‐time curve is taken directly from Figure 4 for comparison.
The human EGCg model was extrapolated to an EGC or EC model by substituting the physicochemical parameters, pharmacokinetic parameters, and PCs with EGC‐ or EC‐specific values (Tables 1, 4 and 5). A PBPK model of TCM was constructed for humans (Fig. 3) by linking the EGCg, EGC, and EC models together with no pharmacokinetic interaction between the TCs. The PBPK model of TCM was calibrated with the kinetic data of humans after consuming PE containing a mixture of EGCg (8.3 mg/kg), EGC (1.54 mg/kg), and EC (1.29 mg/kg) (Chow et al. 2001). Figure 9 shows the predicted and observed kinetic profiles of EGCg, EGC, and EC in the plasma of humans. The TCM model was able to reproduce the observed data; the MAPE between predicted and measured concentrations was 29.6%. The TCM model was further validated by comparing model simulation with observed data from humans after consuming GT solids containing a mixture of EGCg (2.78 mg/kg), EGC (2.2 mg/kg), and EC (0.64 mg/kg) (Lee et al. 2002). Figure 10 shows the predicted and actual concentration‐time profiles of the tea catechin constituents in the plasma. The PBPK model was able to describe the observed data closely and the MAPE of the model was just 20.98%.
Figure 9.
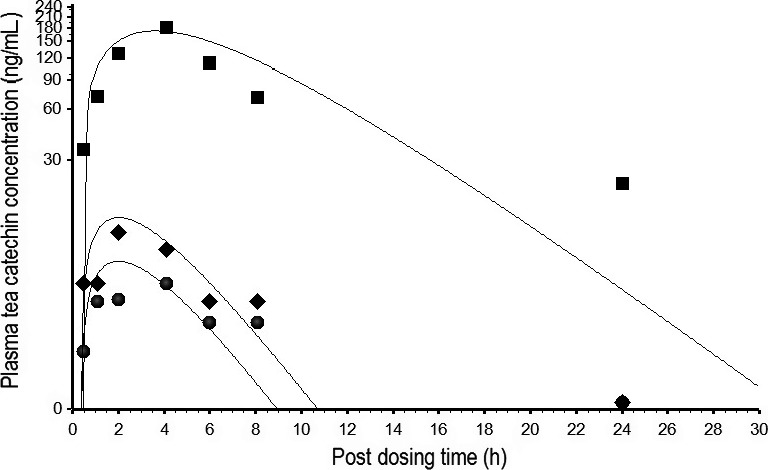
Predicted and measured free EGCg, EGC, and EC concentrations in the plasma of humans after consuming PE containing a mixture of EGCg (8.3 mg/kg), EGC (1.54 mg/kg), and EC (1.29 mg/kg). ▄, ♦, and ●, respectively, represent mean plasma concentrations (N = 5) of EGCg, EGC, and EC at different time points post‐dosing (Chow et al. 2001); __________ represents model‐simulated concentration‐time curves for free EGCg (top), EGC (middle), and EC (bottom).
Figure 10.
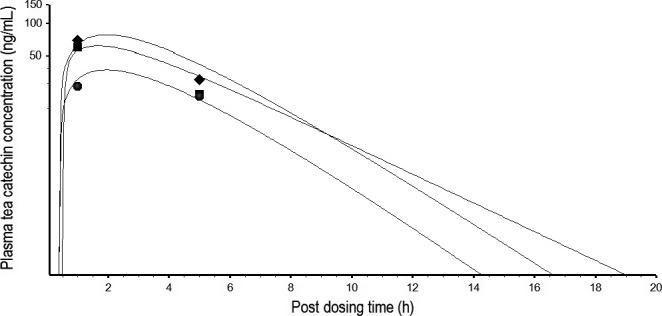
Predicted and measured free EGCg, EGC, and EC concentrations in the plasma of humans after consuming green tea solids containing a mixture of EGCg (2.78 mg/kg), EGC (2.20 mg/kg), and EC (0.64 mg/kg). ♦, ▄, and ●, respectively, represent mean plasma concentrations (N = 5) of EGCg, EGC, and EC at different time points post‐dosing (Lee et al. 2002). _______ represents model‐simulated concentration‐time curves for EGCg (top), EGC (middle), and EC (bottom).
Using model‐predicted Cmax to calculate TCM dosimetry in the plasma of humans
Table 7 (column 2) lists the predicted C max (no bracket) and measured C max (bracketed) of EGCg, EGC, and EC from different pharmacokinetic studies. Predicted Cmax are very close to measured C max except the C max of EGC and EC in Lee et al. (2002) study and the C max of EGCg (1200 mg PE) in Chow et al. (2005) study. The effect‐based or integrated TCM concentrations in the plasma of humans were calculated using the concentration addition approach (ATSDR 2004) which assumed individual tea catechin concentrations in the TCM were additive after adjusting for their inhibition potencies on hepatic EROD activities (Table 7, column 3). When the total TCM concentrations in the plasma of humans were plotted against the administered doses (Table 7, column 4), a straight line with a slope of 0.013 ± 0.003 (R 2 = 0.88) was obtained (Fig. 11).
Table 7.
Using C max as a dose surrogate to predict plasma dosimetry of TCM in humans
| GT solids and PE pharmacokinetic studies in humans | Predicted and actual C max in the plasma (μg/mL) | Total TCM concentration in the plasma (μg EGCg equivalents/mL)d | Administered TCM dose metrics (mg EGCg equivalents/kg)e | ||
|---|---|---|---|---|---|
| EGCG | EGC | EC | |||
| Lee et al. (2002); 20 mg/kg GT solids | 0.06a (0.08)b | 0.07 (0.22)c | 0.04 (0.12)c | 0.20 | 6.06 |
| Chow et al. (2005); 400 mg PE | 0.11 (0.14) | 0.01 (0.02) | 0.01 (0.00) | 0.13 | 8.42 |
| Chow et al. (2001); 600 mg PE | 0.21 (0.17) | 0.02 (0.01) | 0.01 (0.01) | 0.21 | 12.46 |
| Chow et al. (2005); 800 mg PE | 0.21 (0.29) | 0.02 (0.03) | 0.01 (0.00) | 0.25 | 15.71 |
| Chow et al. (2005); 1200 mg PE | 0.35 (0.92)c | 0.04 (0.04) | 0.02 (0.01) | 0.42 | 26.70 |
Values without brackets are predicted C max of unchanged TCs based on PBPK modeling.
Bracketed values are C max from the literature. These C max usually are determined from free tea catechin concentrations except those of Lee et al. (2002) study, which are determined from total tea catechin concentrations (free plus conjugated forms).
Cmax is under‐predicted when compare with the observed value.
Total TCM concentrations are expressed as μg EGCg equivalents/mL plasma; they are calculated using predicted C max and the concentration/dose additivity model (ATSDR, 2004).
Administered dose metrics are expressed as mg EGCg equivalents/kg BW; they are calculated using the concentrations of individual TCs in PE and the additivity model (ATSDR, 2004).
Figure 11.
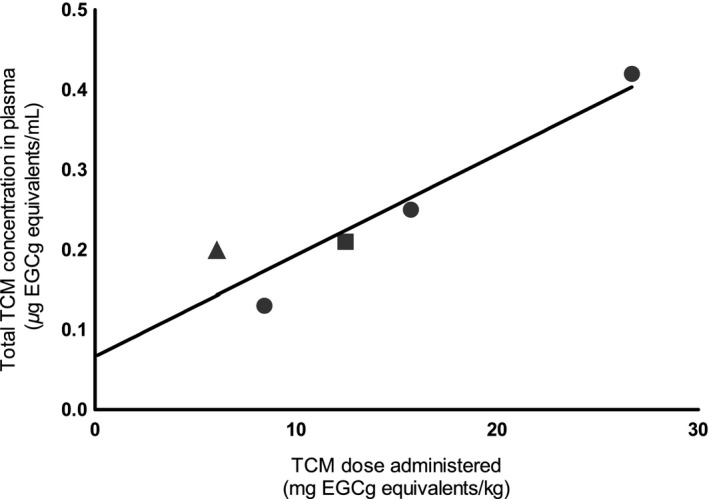
Quantitative relationship between total TCM concentration in plasma and applied dose in humans. TCM dose metrics, expressed in μg EGCg equivalents/mL plasma or g of PE, are calculated using the concentration addition model of ATSDR (2004). ● represents total TCM concentrations in the plasma of humans after consuming 400, 800, or 1200 mg PE (Chow et al. 2005); ▲ and ▄ represent total TCM concentrations in the plasma of humans after consuming 20 mg/kg of green tea solids (Lee et al. 2002) and 600 mg of PE (Chow et al. 2001), respectively.
Discussion
The PBPK model of EGCg (Fig. 2) is able to reproduce the concentration‐time profiles of free EGCg (Fig. 4) as well as total EGCg (free EGCg plus conjugated forms) (Fig. 5) in the plasma of rats. This is unexpected since the PBPK model supposedly is predictive for the kinetics of free EGCg only. The finding that our model is also predictive for the kinetics of total EGCg indicates the presence of free EGCg mainly in the plasma of rats. Thus, although Chen et al. (1997) have analyzed rat plasma samples for total EGCg, they actually measure free EGCg in these samples. Our hypothesis is supported by the following experimental evidence: (1) only free EGCg is found in the plasma of humans after consuming pure EGCg or PE (Chow et al. 2001, 2003; Lee et al. 2002), and (2) little or no EGCg conjugated metabolites are present in the blood of rats because most EGCg is metabolized by bacteria in the intestine (Kohri et al. 2001a).
Model‐simulated pure EGCg and crude EGCg concentration‐time curves are parallel to each other indicating the PKs of these two forms of EGCg are very similar in rats (Fig. 5). In contrast, Chen et al. (1997) have shown that the PKs of pure EGCg and crude EGCg are different in the plasma of rats. The discrepancy in results between our and Chen et al. (1997) studies may be explainable by the different pharmacokinetic approaches used to fit or analyze the empirical data: Chen et al. (1997) have fitted total EGCg concentration‐time curves with data‐based, non‐compartmental analysis yielding inaccurate, composite pharmacokinetic parameter values (Gabrielsson and Weiner 2000). As a result, Chen et al. (1997) may err in concluding that the PKs of pure EGCg and crude EGCg are different in rats. In contrast, the EGCg model (Fig. 2) is developed based on the physiological parameters of rats, and the physicochemical and pharmacokinetic characteristics of EGCg. As such, the predicted concentration‐time profiles are not affected significantly by errors in the empirical data. Andersen (1987) has shown that the PBPK model is better than classical pharmacokinetic approaches in data interpretation. Our results are in agreement with their findings.
We have integrated more than 40 parameters from different sources (Tables 1, 2, 3, 4, 5) to implement the PBPK model of EGCg (see Appendix). The effect of a parameter on model prediction can be quantified using sensitivity coefficient analysis (Clewell et al. 1994). Table 6 shows the LSP of most pharmacokinetic parameters and tissue/blood PCs are <0.5 in absolute values. Thus, errors in estimating the parameters and PCs would not affect significantly the predicted EGCg PKs in rats or humans. In contrast, the LSP of BLPLR, F, k ac, Rms and Rrb in human EGCg model, and the LSP of BLPLR, BW and F in rat EGCg model are >1 in absolute values (Table 6). Thus, small errors in estimating these parameters would impact significantly the predicted plasma concentration‐time profiles of EGCg. Because very few model parameters and PCs show LSP >1, errors in estimating model parameter values would not be significantly amplified in the predicted concentration‐time profiles.
Individual TCs in the TCM are assumed not to interact metabolically with one another in the PBPK model (Fig. 3). This assumption is supported by the following lines of evidence: (1) the PKs of pure EGCg and crude EGCg are similar in the plasma of rats (Fig. 5) and humans (Fig. 7). These results clearly demonstrate crude EGCg does not interact significantly with other TCs or unknown chemicals in GT/PE; (2) the mixture PBPK model is able to reproduce the PKs of three TCs simultaneously in the plasma of rats and humans after GT/PE consumption (Figs. 8, 9, 10). The difference in predicted and actual concentrations is small and probably is related to using reference instead of actual physiological parameters in PBPK modeling (Tables 2, 4) and large variation in empirical data (Zhu et al. 2000; Chow et al. 2001). If there were significant interactions between the TCs, we would observe much larger deviations between model simulation and empirical data; (3) Hong et al. (2001) have reported that systemic tea catechin concentrations in humans are about 5–50 folds less than the effective concentrations of in vitro studies. Tea catechin levels in human plasma (Figs. 8, 9, 10) probably are below the in vivo interaction thresholds since TCs have low oral bioavailabilities (Chow et al. 2005); and (4) hepatic glucuronyltransferase and sulfatase activities are difficult to modulate with chemical treatments. Thus, most drugs or chemicals are weak inhibitors of glucuronyltransferases (Resetar et al. 1991). TCs also are unable to interact with one another by competing for the active sites on catechol‐O‐methyltransferase (Meng et al. 2002), and CYP1A2 enzymes (Obermeier et al. 1995) as these are minor pathways of TCs metabolism.
The mixture PBPK model often under‐predicts the concentrations of TCs in the plasma of rats and humans at or near the 24‐h, post‐dosing time point (Figs. 7, 8, 9). An explanation for under‐predicting the observed data is not available but may be related to the detection limits of the analytical methods in these studies. Since the PBPK model does not have any detection limit, it is capable of predicting TCs at levels much lower than HPLC analysis. Other possible but unlikely explanations for under‐predicting the observed data include the inhibition of efflux transporters in rats and humans since plasma EGCg concentration is increased in humans after daily treatment with a high dose of PE (800 mg) for 4 weeks (Chow et al. 2003). Also, flaws in model structure and inaccurate model parameter values may play important roles in under‐predicting the observed data at or near the 24‐h time point.
A single set of parameter values, except F and kac, has been used successfully to simulate the PKs of a tea catechin in different pharmacokinetic studies (Tables 3, 5). K ac represents the absorption rate constant of TCs while F is the empirical bioavailability factor of the model, which does not equate to the absolute bioavailability of classical pharmacokinetic model (Anderton et al. 2004). Different F and/or k ac values (Tables 3 and 5) are used to simulate the PKs of a tea catechin in different studies because systemic availability of TCs is highly variable in rats (Zhu et al. 2000) and humans (Chow et al. 2001; Lee et al. 2002). F and k ac variation may be related to the fasting/fed conditions of the experimental animals since Chow et al. (2005) have reported that EGCg concentration is higher in the plasma of humans under fasting condition. It is interesting to note that the PCs of gallated TCs (e.g., ECg and EGCg) are larger than non‐gallated TCs (e.g., EGC and EC) (Tables 2). These imply gallated TCs are more widely distributed to the target organs of rats and humans than non‐gallated TCs. Indeed, EGCg is more widely distributed to the target organs of rats than EGC or EC (Chen et al. 1997). Similarly, biliary clearance (CLbc) is larger than renal clearance (CLrc) (Tables 3) indicating TCs are excreted into the bile instead of the urine, a finding which is also reported by Kohri et al. (2001b) after injecting rats i.v. with EGCg.
The effect‐based or integrated concentration of TCM in the plasma of humans is calculated using the Cmax of individual TCs as dose surrogates. Table 7 shows predicted C max are very close to observed C max except the C max of EGC and EC in Lee et al. (2002) study and the C max of EGCg (1200 mg PE) in Chow et al. (2005) study. An explanation for the different predicted and observed C max values in the EGCg study (Chow et al. 2005) is not available. On the other hand, the C max of EGC and EC are under‐predicted because free TCs are predicted by the model whereas both free TCs and their conjugated metabolites are present in the plasma of humans (Lee et al. 2002). Despite the difference in predicted and measured C max (Lee et al. 2002; Chow et al. 2005), total TCM concentration in the plasma is linearly related to the administered dose (Fig. 11). These results also validate the use of first‐order kinetics for tea catechin modeling (Figs. 2, 3).
This is the first study in which a mixture PBPK model is used to predict the PKs and systemic dosimetry of a ternary TCM in humans. The mixture model may be modified to simulate more than three TCs by linking additional tea catechin model(s) to the global model as described in the study of Haddad et al. (1999). The TCM model is a powerful tool for species‐to‐species and dose‐to‐dose extrapolation of pharmacokinetic data (Angelo and Pritchard 1987; Travis 1987). It can be used to estimate an internal tissue concentration/dose of GT/PE for safety assessment and dose‐response analysis. It is also useful in reducing costs and time of a GT/PE clinical study by better planning and study design (IPCS, 2010). The modeling framework as described in this paper is also applicable to plant‐based traditional medicines, functional foods, and dietary supplements.
Disclosure
None declared.
The algebraic and mass balance differential equations which describe the movement of a tea catechin in rats or humans are formulated as a computer program to predict the concentration‐time profile of a tea catechin in arterial blood (CBAc), venous blood (CBVc), lung (CLGc), heart (CHRc), kidney (CKDc), adipose tissue (CFTc), muscle (CMSc), brain (CBRc), liver (CLVc), spleen (CSPc), gut tissue (CGTc), skin (CSKc), bone (CBNc), gut contents (CGCc), and the rest of the body (CRBc) (Figs. 2 and 3).
Non‐eliminating organ
Lung, brain, spleen, muscle, bone, skin, adipose tissue, heart, and the rest of body:
| (A1) |
where, dCc/dt is the rate of catechin concentration change in the non‐eliminating organ; X represents the organ; QX, VX, and RXc represent tissue blood flow, volume, and tissue/blood partition coefficient of the organ, respectively; subscript c represents EGCg, EGC, ECg, or EC. For example,
Lung:
| (A2) |
Eliminating organs
Kidney:
| (A3) |
where, CLrc represents the renal clearance for the tea catechin.
Liver:
| (A4) |
| (A5) |
where, RAMc represents the combined rate of catechin and glucuronide transport from the liver cells into the bile duct; CLbc, the biliary clearance, represents a combination of metabolic and excretory processes of the catechin in the liver; Rtc, the residence time (bile volume/bile flow rate) which is assumed to be equal in each bile duct sub‐compartments; R0 is the transport rate into the first sub‐compartment and ; Rcj is the transport rate from the jth duct sub‐compartment and n = 3 is the optimal number of sub‐compartment for the proposed PBPK model. The mass balance equations describing the time lag of biliary excretion with a series of bile duct sub‐compartments were adapted from Bischoff et al. (1971) with modification.
Gut contents:
| (A6) |
Gut tissue:
| (A7) |
where RAOc is an input function describing the absorption of catechin after oral administration, k ac is a first‐order absorption rate constant from the small intestine, dose represents either the dose of a pure catechin or individual tea catechins in a PE preparation, F c is the apparent or empirical bioavailability factor, and t lagc is the lag time for absorption, k rac is the re‐absorption rate constant of the tea catechin from the colon which is assumed different to the absorption of tea catechin from the small intestine, and k fc is the fecal transport rate constant.
Blood compartment
The total blood volume was divided into a two‐thirds venous pool and one‐third arterial pool.
Arterial blood:
| (A8) |
Venous blood:
| (A9) |
Mixed venous plasma:
| (A10) |
Law F. C. P., Yao M., Bi H.‐C., Lam S.. Physiologically based pharmacokinetic modeling of tea catechin mixture in rats and humans,Pharma Res Per, 5(3), 2017, e00305, doi: 10.1002/prp2.305
Presented in parts at the 10th CSSX Conference and the 3rd ISSX/CSSX Joint International Workshop, Nanjing. China. September, 2012, and the Botanical and Cancer Research: Clinical Trials Workshop. National Cancer Institute, Bethesda, Maryland. USA. July, 2009.
References
- Andersen ME (1987). Tissue dosimetry in risk assessment, or what's the problem here anyway? Pp. 8–23 Pharmacokinetics in risk assessment, drinking water and health. National Academy Press, Washington DC. [Google Scholar]
- Anderton MJ, Manson MM, Verschoyle R, Gescher A, Steward WP, Williams ML, et al. (2004). Physiological modeling of formulated and crystalline 3,3'‐diindolylmethane pharmacokinetics following oral administration in mice. Drug Metab Dispos 32: 632–638. [DOI] [PubMed] [Google Scholar]
- Angelo MJ, Pritchard AB (1987). Route‐to‐route extrapolation of dichloromethane exposure using a physiological pharmacokinetic model Pp. 254–264 Pharmacokinetics in risk assessment: drinking water and health. National Academy Press, Washington, DC. [Google Scholar]
- ATSDR (2004) Guidance manual for the assessment of joint toxic action of chemical mixtures. U.S. Department of Health and Human Services, Public Health Service, Agency for Toxic Substances and Disease Registry.
- Balentine CS, Wiseman SA, Bouwens LC (1997). The chemistry of tea flavonoids. Crit Rev Food Sci Nutr 37: 693–704. [DOI] [PubMed] [Google Scholar]
- Bischoff KB, Dedrick RL, Zaharko DS, Longstreth JA (1971). Methotrexate pharmacokinetics. J Pharm Sci 60: 1128–1133. [DOI] [PubMed] [Google Scholar]
- Bjorkman S, Wada DR, Stanski DR, Ebling WF (1994). Comparative physiological pharmacokinetics of fentanyl and alfentanil in rats and humans based on parametric single‐tissue models. J Pharmacokinet Biopharmaceut 22: 381–410. [DOI] [PubMed] [Google Scholar]
- Cai Y, Anavy ND, Chow SHH (2002). Contribution of presystemic hepatic extraction to the low oral bioavailability of green tea catechins in rats. Drug Metab Dispos 30: 1246–1249. [DOI] [PubMed] [Google Scholar]
- Chen L, Lee MJ, Li H, Yang CS (1997). Absorption, distribution, and elimination of tea polyphenols in rats. Drug Metab Dispos 25: 1045–1050. [PubMed] [Google Scholar]
- Chiou WL, Robbie G, Chung SM, Wu TC, Ma C (1998). Correlation of plasma clearance of 54 extensively metabolized drugs between humans and rats: mean allometric coefficient of 0.66. Pharm Res 15: 1474–1479. [DOI] [PubMed] [Google Scholar]
- Chow HH, Cai Y, Alberts DS, Hakim I, Dorr R, Shahi F, et al. (2001). Phase I pharmacokinetic study of tea polyphenols following single‐dose administration of epigallocatechin gallate and polyphenon. Cancer Epidemiol Biomarkers Prev 10: 53–58. [PubMed] [Google Scholar]
- Chow HH, Cai Y, Hakim IA, Crowell JA, Shahi F, Brooks CA, et al. (2003). Pharmacokinetics and safety of green tea polyphenols after multiple‐dose administration of epigallocatechin gallate and polyphenon E in healthy individuals. Clin Cancer Res 9: 3312–3319. [PubMed] [Google Scholar]
- Chow HH, Hakim IA, Vining DR, Crowell JA, Moore JR, Chew WM, et al. (2005). Effects of dosing condition on the oral bioavailability of green tea catechins after single‐dose administration of Polyphenon E in healthy individuals. Clin Cancer Res 11: 4627–4633. [DOI] [PubMed] [Google Scholar]
- Clewell HJ III, Lee TS, Carpenter RL (1994). Sensitivity of physiologically based pharmacokinetic models to variation in model parameters: methylene chloride. Risk Anal 14: 521–531. [DOI] [PubMed] [Google Scholar]
- Davies B, Morris T (1993). Physiological parameters in laboratory animals and humans. Pharmaceut Res 10: 1093–1095. [DOI] [PubMed] [Google Scholar]
- EPA (2007) Considerations for Developing a Dosimetry‐Based Cumulative Risk Assessment Approach for Mixtures of Environmental Contaminants. U.S. Environmental Protection Agency, National Center for Environmental Assessment, Cincinnati, OH. EPA/600/R‐07/064.
- Gabrielsson J, Weiner D (2000). P. 124 Pharmacokinetic and pharmacodynamic data analysis: concept & application, 3rd ed. Swedish Pharmaceutical Press, Stockholm, Sweden. [Google Scholar]
- Gao GH, Law FCP (2009). Physiologically based pharmacokinetics of matrine in the rat after oral administration of pure chemical and ACAPHA. Drug Metab Dispos 37: 884–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ginsberg G, Hattis D, Russ A, Sonawane B (2004). Physiologically based pharmacokinetic (PBPK) modeling of caffeine and theophylline in neonates and adults: implications for assessing children's risks from environmental agents. J Toxicol Environ Health A 67: 297–329. [DOI] [PubMed] [Google Scholar]
- Haddad S, Tardif R, Charest‐Tardif G, Krishnan K (1999). Physiological modeling of the toxicokinetic interactions in a quaternary mixture of aromatic hydrocarbons. Toxicol Applied Pharmacol 161: 249–257. [DOI] [PubMed] [Google Scholar]
- Harrison LI, Gibaldi M (1977). Physiologically based pharmacokinetic model for digoxin distribution and elimination in the rat. J Pharm Sci 66: 1138–1142. [DOI] [PubMed] [Google Scholar]
- Hong J, Smith TJ, Ho CT, August D, Yang CS (2001). Effects of purified green and black tea polyphenols on cyclooxygenase‐ and lipoxygenase‐dependent metabolism of arachidonic acid in human colon muscosa and colon tumor tissues. Biochem Pharmacol 62: 1176–1183. [DOI] [PubMed] [Google Scholar]
- Hu YZ, Huang SK (1995). Physiological pharmacokinetic modeling of sophoridine. Chin J Pharmacol Toxicol 9: 133–136. [Google Scholar]
- Inoue MB, Inoue M, Fernando Q, Valcic S, Timmermann BN (2002). Potentiometric and 1H NMR studies of complexation of Al(3+) with (‐)‐epigallocatechon gallate, a major active constituent of green tea. J Inorg Biochem 88: 7–13. [DOI] [PubMed] [Google Scholar]
- IPCS , International Programme on Chemical Safety (2010). Characterization and application of physiologically based pharmacokinetic models in risk assessment. World Health Organization, Harmonization Project Document No. 9. Geneva 27, Switzerland. [Google Scholar]
- Ito K, Brown HS, Houston JB (2004). Database analyses for the prediction of in vivo drug‐drug interactions from in vitro data. Br J Clin Pharmacol 57: 473–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kida K, Suzuki M, Matsumoto N, Nanjo F, Hara Y (2000). Identification of biliary metabolites of (‐)‐epigallocatechin gallate in rats. J Agric Food Chem 48: 4151–4155. [DOI] [PubMed] [Google Scholar]
- Kim S, Lee MJ, Hong J, Li C, Smith TJ, Yang GY, et al. (2000). Plasma and tissue levels of tea catechins in rats and mice during chronic consumption of green tea polyphenols. Nutr Cancer 37: 41–48. [DOI] [PubMed] [Google Scholar]
- Kohri T, Matsumoto N, Yamkawa M, Suzuki M, Nanjo F, Hara Y, et al. (2001a). Metabolic fate of (‐)‐[4‐3H]epigallocatechin gallate in rats after oral administration. J Agri Food Chem 49: 4102–4112. [DOI] [PubMed] [Google Scholar]
- Kohri T, Nanjo F, Suzuki M, Seto R, Matsumoto N, Yamakawa M, et al. (2001b). Synthesis of (‐)‐[4‐3H]epigallocatechin gallate and its metabolic fate in rats after intravenous administration. J Agric Food Chem 49: 1042–1048. [DOI] [PubMed] [Google Scholar]
- Lambert JD, Sang SM, Yang CS (2007). Possible controversy over dietary polyphenols: benefits vs Risks. Chem Res Toxicol 20: 583–585. [DOI] [PubMed] [Google Scholar]
- Law FCP (2007) Simulation of soy isoflavone kinetic profiles in rodents and humans using physiologically based pharmacokinetic (PBPK) model. Proceedings of the XI International Congress of Toxicology; 2007 Jul 15–19; Montreal, QC, Canada. Society of Toxicology of Canada, Montreal, QC, Canada.
- Lee MJ, Maliakal P, Chen LS, Meng XF, Bondoc FY, Prabhu S, et al. (2002). Pharmacokinetics of tea catechins after ingestion of green tea and (‐)‐epigallocatechin‐3‐gallate by humans: formation of different metabolites and individual variability. Cancer Epidemiol Biomark Prev 11: 1025–1032. [PubMed] [Google Scholar]
- Luttringer O, Theil FP, Poulin P, Schmitt‐Hoffmann AH, Guentert TW, Lave T (2003). Physiologically‐based pharmacokinetic (PBPK) modeling of disposition of epiroprim in humans. J Pharm Sci 92: 1990–2007. [DOI] [PubMed] [Google Scholar]
- Lutz RJ, Dedrick RL, Matthewa HB, Eling TE, Anderson MW (1977). A preliminary pharmacokinetic model for several chlorinated biphenyls in the rat. Drug Metab Disposit 5: 386–396. [PubMed] [Google Scholar]
- Meng XF, Sang SM, Zhu NQ, Lu H, Sheng SQ, Lee MJ, et al. (2002). Identification and characterization of methylated and ring‐fission metabolites of tea catechins formed in humans, mice, and rats. Chem Res Toxicol 15: 1042–1050. [DOI] [PubMed] [Google Scholar]
- Obermeier MT, White RE, Yang CS (1995). Effects of bioflavonoids on hepatic P450 activities. Xenobiotica 25: 575–584. [DOI] [PubMed] [Google Scholar]
- Pietta PG, Simonetti P, Gardana C, Brusamolino A, Morazzoni P, Bombardelli E (1998). Catechin metabolites after intake of green tea infusion. BioFactors 8: 111–118. [DOI] [PubMed] [Google Scholar]
- Ploeger B, Mensinga T, Sips A, Meulenbelt J, DeJongh J (2000). A human physiologically based model for glycyrrhizic acid, a compound subject to presystemic metabolism and enterohepatic cycling. Pharm Res 17: 1516–1525. [DOI] [PubMed] [Google Scholar]
- Poulin P, Krishnan K (1995). An algorithm for predicting tissue:blood partition coefficient of organic chemicals from n‐octanol:water partition coefficient data. J Toxicol Environ Health 46: 117–129. [DOI] [PubMed] [Google Scholar]
- Poulin P, Theil FP (2002). Prediction of pharmacokinetics prior to in vivo studies. 1. Mechanism‐based prediction of volume of distribution. J Pharm Sci 91: 1358–1370. [DOI] [PubMed] [Google Scholar]
- Poulin P, Schoenlein K, Theil FP (2001). Prediction of adipose tissue:plasma partition coefficients for structurally unrelated drugs. J Pharm Sci 90: 436–447. [DOI] [PubMed] [Google Scholar]
- Resetar A, Minick D, Spector T (1991). Glucurinidation of 3′‐azido‐3′deoxythymidine catalyzed by human liver UDP‐glucuronosyltransferase. Biochem Pharmacol 42: 559–568. [DOI] [PubMed] [Google Scholar]
- Saito ST, Gosmann G, Pungartnik C, Brendel M (2009). Green tea extract – patents and diversity of uses. Recent Pat Food Nutr Agric 1: 203–215. [DOI] [PubMed] [Google Scholar]
- Schlosser PM, Borghoff SJ, Coldham NG, David JA, Ghosh SK (2006). Physiologically‐based pharmacokinetic modeling of genistein in rats. Part I: model development. Risk Anal 26: 483–500. [DOI] [PubMed] [Google Scholar]
- Shanafelt TD, Call TG, Zent CS, Leis JF, LaPlant B, Bowen DA, et al. (2013). Phase 2 trial of daily, oral Polyphenon E in patients with asymptomatic, Rai stage 0 to II chronic lymphocytic leukemia. Cancer 119: 363–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suganuma M, Okabe S, Meng X, Tada Y, Ito H, Fujiki H (1998). Wide distribution of [3H](‐)‐epigallocatechin gallate, a cancer prevention tea ployphenol in mouse tissue. Carcinogenesis 19: 1771–1776. [DOI] [PubMed] [Google Scholar]
- Swezey RR, Aldridge DE, LeValley SE, Crowell JA, Hara Y, Green CE (2003). Absorption, tissue distribution, elimination of 4‐[3H]‐epigallocatechin gallate in beagle dogs. Int J Toxicol 22: 187–193. [DOI] [PubMed] [Google Scholar]
- Travis CC (1987). Interspecies and dose‐route extrapolations, in pharmacokinetics in risk assessment: drinking water and health Vol. 8 National Academy Press, Washington, D.C.. [Google Scholar]
- Van Amelsvoort JMM, van Het Hof KH, Mathot JNJJ, Mulder TPJ, Wiersma A, Tijburg LBM (2001). Plasma concentrations of individual tea catechins after a single oral dose in humans. Xenobiotica 31: 891–901. [DOI] [PubMed] [Google Scholar]
- Yang CS, Maliakal P, Meng X (2002). Inhibition of carcinogenesis by tea. Annul Rev Pharmacol Toxicol 42: 25–54. [DOI] [PubMed] [Google Scholar]
- Zhu M, Chen Y, Li RC (2000). Oral absorption and bioavailability of tea catechins. Planta Med 66: 444–447. [DOI] [PubMed] [Google Scholar]
- Zhu M, Chen Y, Li RC (2001). Pharmacokinetics and system linearity of tea catechins in rat. Xenobiotica 31: 51–60. [DOI] [PubMed] [Google Scholar]


