A three‐parameter two‐state model of receptor function that incorporates affinity, efficacy, and signal amplification

Abstract

A generalized model of receptor function is proposed that relies on the essential assumptions of the minimal two‐state receptor theory (i.e., ligand binding followed by receptor activation), but uses a different parametrization and allows nonlinear response (transduction) for possible signal amplification. For the most general case, three parameters are used: K _d, the classic equilibrium dissociation constant to characterize binding affinity; ε, an intrinsic efficacy to characterize the ability of the bound ligand to activate the receptor (ranging from 0 for an antagonist to 1 for a full agonist); and γ, a gain (amplification) parameter to characterize the nonlinearity of postactivation signal transduction (ranging from 1 for no amplification to infinity). The obtained equation, $E_{/E_{max}}=\frac{\mathit{\epsilon }\mathit{\gamma }\left[\mathrm{L}\right]}{\left(\mathit{\epsilon }\mathit{\gamma }+1-\mathit{\epsilon }\right)\left[\mathrm{L}\right]+K_{\mathrm{d}}}$, resembles that of the operational (Black and Leff) or minimal two‐state (del Castillo‐Katz) models, $E_{/E_{max}}=\frac{\mathit{\tau }\left[\mathrm{L}\right]}{\left(\mathit{\tau }+1\right)\left[\mathrm{L}\right]+K_{\mathrm{d}}}$, with εγ playing a role somewhat similar to that of the τ efficacy parameter of those models, but has several advantages. Its parameters are more intuitive as they are conceptually clearly related to the different steps of binding, activation, and signal transduction (amplification), and they are also better suited for optimization by nonlinear regression. It allows fitting of complex data where receptor binding and response are measured separately and the fractional occupancy and response are mismatched. Unlike the previous models, it is a true generalized model as simplified forms can be reproduced with special cases of its parameters. Such simplified forms can be used on their own to characterize partial agonism, competing partial and full agonists, or signal amplification.

Introduction

Receptor theory

The receptor concept lies at the core of our current mechanism of drug action theories (Maehle et al. 2002; Katzung and Trevor 2014; Rang et al. 2015). It was heralded toward the end of the nineteenth century by the work of Langley (1878‐1879, 1909) and Ehrlich (1885, 1909, 1913) (corpora non agunt nisi fixata). These basic ideas, as expanded and formulated through the twentieth century by Hill (1909, 1910), Clark (1926, 1933), Gaddum (1926, 1937), Schild (1947, 1949), Wyman and Allen (1951), Monod et al. (1965), Ariëns (1954), Stephenson (1956), Del Castillo and Katz (1957), Furchgott (1966), Black and Leff (1983), Black et al. (1985), and others, form the basis of what is known as ‘receptor theory’; see detailed reviews in Jenkinson (2003), Colquhoun (2006), Kenakin (2006, 2008), Ehlert (2015a). They can now also be incorporated in sophisticated pharmacokinetic‐pharmacodynamic (PK‐PD) models for in vivo data ((Danhof et al. 2007) and references therein).

To quantitatively characterize receptor occupancy/activation and to establish a clear functional connection between ligand concentration and the effect produced, pharmacology as a science needs to be based on a receptor theory formulated within a rigorous quantitative framework. The simplest models are based on a straightforward single‐state model that assumes that (1) all ligand‐occupied receptors are active and (2) the effect produced is proportional with the number (concentration) of occupied receptors. The corresponding equations that use binding affinity (K _d) as their parameter (e.g., Clark, Hill, and Gaddum equations) are commonly used as they can provide adequate fitting for a large portion of pharmacological data. On the other hand, most commonly accepted general receptor activation models that are the foundation of our current receptor theory and quantitative pharmacology (Katzung and Trevor 2014; Rang et al. 2015) are two‐state models in which ligand‐occupied and active receptor states do not fully overlap. These more complex receptor activation models, which in addition to binding affinity also employ an efficacy parameter, are needed to be able to describe well‐recognized phenomena that cannot be explained within the framework of simpler, affinity‐only models. Such phenomena include, for example, partial agonism, the existence of receptor reserve (i.e., maximum activation at only partial occupancy), constitutive activity, receptor desensitization, and others (Jenkinson 2003; Colquhoun 2006; Kenakin 2006, 2008).

Cases where constitutive activity does not have to be addressed can be described within the framework of the operational (Black and Leff) or the minimal two‐state (del Castillo‐Katz) model. The corresponding equations, which are mathematically equivalent, use two parameters characterizing affinity (K _d for receptor binding) and efficacy (τ for receptor activation), respectively. They are, however, not widely used as their parameters are not well‐suited for fitting by nonlinear regression (e.g., for full agonists, τ needs to have large values, which are difficult to define accurately), the parameters are not very intuitive (for full or close to full agonists, K _d can have unrealistic values), and the general equation cannot be reduced back to the simpler forms as special cases. Here, a generalized model of receptor function is proposed that relies on the essential assumptions of the minimal two‐state receptor theory (i.e., ligand binding is followed by receptor activation), but uses a different parametrization and allows nonlinear response (transduction) for possible signal amplification. The obtained equation uses more intuitive parameters that are better suited for optimization by nonlinear regression while also being conceptually clearly related to the different steps of binding, activation, and signal transduction (amplification). Furthermore, it results in a true generalized model that, contrary to the previous models, can be reduced back to the simpler forms with special cases of its parameters. A schematic summary of all models discussed here that includes the basic assumptions for ligand binding and receptor activation together with the resulting equations connecting the fractional effect (E _/Emax) to the ligand concentration [L] is shown in Figure 1. To highlight the concepts that led to the formulation of the present model and to place it in the context of other models, a summary description of one‐ and two‐state receptor models together with corresponding equations is included first in the next Background section, followed by a derivation and interpretation of the present model. Because it is well documented that heavy use of equations in the main text is likely to hamper readability and reduce the impact and penetrations of papers in biology‐related fields (Fawcett and Higginson 2012), a set of additional‐related equations and discussion are included as Appendix 1.

Figure 1.

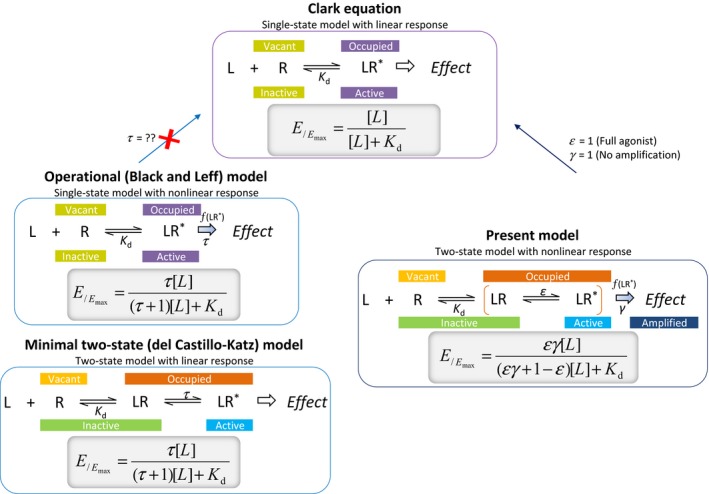
Comparison of the receptor models discussed here. For each model, a schematic illustration of the basic assumption for ligand binding and receptor activation is shown together with the resulting equation describing the fractional effect (E _/Emax) as a function of the ligand concentration [L].

Background: quantitative receptor theory and existing receptor models

Receptor binding

Receptors bind a ligand and transduce this into a functional response. To be able to exert any effect at a given receptor, ligands have to be able to first bind there in a sufficiently potent and specific manner. The strength of the (binding) interaction between a ligand and its receptor is typically characterized via the corresponding equilibrium binding constant, K _d, which is the only parameter used in the simplest quantitative receptor models and a main parameter in all other, more complex models. Typically, a receptor has to show structural specificity in binding its ligand(s) (e.g., stereospecific binding), and the binding should be saturable and limited. Most ligands of pharmacological interest bind in a reversible fashion; irreversible (e.g., covalent) bindings are of interest in a few cases, but will not be considered here.

Receptor occupancy (binding affinity): binding constant and the law of mass action

In its simplest form, binding of a ligand L and receptor R to form a ligand‐receptor complex LR represents a case of a reversible bimolecular association (eq. 1). The classical mass‐action law should hold for the corresponding concentrations, just as for any bimolecular chemical reaction (Silbey et al. 2005).

Here, L, R, and LR denote the ligand, receptor, and their bound complex, respectively, and K _d is the equilibrium dissociation constant of the binding. Corresponding concentrations for each species will be denoted by square brackets, e.g., [L], [R], and [LR]. The equilibrium represented by eq. 1 is, in fact, a dynamic equilibrium with both a forward (L + R→LR) and a backward reaction (L + R←LR), each with its corresponding rate constant k ₁ and k _–1, respectively. According to the law of mass action, one can assume that the rate of the forward reaction (association) is proportional with both [L] and [R], k ₁[L][R], and the rate of the backward reaction (dissociation) is proportional with [LR], k _–1 [LR]. The rate of the reaction (Silbey et al. 2005) is v = –d[L]/dt = d[LR]/dt = k ₁[L][R]–k _–1[LR], which at equilibrium (steady state) becomes zero. Consequently, k ₁[L][R] = k _–1 [LR], and the corresponding equilibrium dissociation constant (K _d) can be expressed as a function of the equilibrium concentrations of the species involved:

$$K_{\mathrm{d}}=\frac{k_{-1}}{k_1}=\frac{[\mathrm{L}]·[\mathrm{R}]}{[\mathrm{LR}]}$$ (2)

It is standard convention to use the equilibrium dissociation constant (K _d) instead of its reciprocal, the association constant (K _a), as it is more intuitive and convenient mainly because it is measured in units of concentration (usually molarity, mol/L). Sometimes, this same quantity (i.e., binding constant measured in concentration units) is denoted as K _a or K _A, but K _d will be used here as it is the constant characterizing the dissociation reaction. The lower K _d, the higher the binding affinity (i.e., more LR complex is formed for the same ligand concentration). For therapeutic xenobiotics, adequate potency is needed to be able to compete with the naturally present ligand(s), to have adequate specificity for the intended target, and to avoid the need for high doses that could be difficult to administer. Hence, activities in the nanomolar (nmol/L) range, or at least in the low micromolar (μmol/L) range, are needed for a compound to be considered as having the potential to become a therapeutically useful drug. Indeed, most existing drugs are quite potent and have affinities in the nanomolar (nmol/L) range: the median value for all marketed small‐molecule drugs is around 20 nmol/L (Overington et al. 2006).

While it is typically not discussed in works related to quantitative receptor theory, it is important to remember that the binding constant K is not just some arbitrary parameter, but a real physicochemical descriptor of the corresponding equilibrium related to the Gibbs‐free energy change (ΔG) of the reaction via the well‐known thermodynamic equation:

$$K_{eq}=e^{-\frac{\mathrm{\Delta }{G}^o}{RT}}$$ (3)

Here, T is the absolute temperature and R is the universal gas constant, R = k _B N _A = 8.314 J/K·mol. Hence, at normal physiological conditions (body temperature, T = 310 K), a drug binding with, for example, 1 nmol/L affinity (K _d = 10^–9 mol/L) requires a free energy of ΔG ⁰ = –RT lnK _d = 53.4 kJ/mol (12.8 kcal/mol) to dissociate from the receptor. For comparison, the average molecular kinetic energy at this temperature is ³/₂ RT = 3.7 kJ/mol, while the energy of an ion–ion interaction between two permanent charges is in the 20–40 kJ/mol range, and that of a dipole–dipole interaction is in the 3–15 kJ/mol range. The relation between K and energy (eq. 3) also means that a 10‐fold change in binding affinity (K _d) requires a change of 5.94 kJ/mol in the binding‐free energy (ΔΔG ⁰).

A main interest is to express occupancy as a function of the ligand concentration [L] present while eliminating the receptor concentrations, which are typically unknown. Since the number (concentration) of total receptors in the system is given (i.e., [R_tot]), this can be done for the fractional occupancy (fraction of receptors occupied), f _ocup = [LR]/[R_tot] by summing up the different forms of the receptor in the system (here, free and occupied) and using the definition of K _d (eq. 2) to link them to the number (concentration) of ligands present:

$$[{\mathrm{R}}_{\mathrm{tot}}]=[\mathrm{R}]+[\mathrm{LR}]=[\mathrm{R}]+\frac{[\mathrm{L}][\mathrm{R}]}{K_{\mathrm{d}}}$$ (4)

This way, the fractional occupancy can be directly connected to the ligand concentration [L]:

$$f_{ocup}=\frac{[\mathrm{LR}]}{[{\mathrm{R}}_{\mathrm{tot}}]}=\frac{[\mathrm{LR}]}{[\mathrm{R}]+[\mathrm{LR}]}=\frac{\frac{[\mathrm{L}][\mathrm{R}]}{K_{\mathrm{d}}}}{[R]\left(1+\frac{[\mathrm{L}]}{K_{\mathrm{d}}}\right)}=\frac{[\mathrm{L}]}{[\mathrm{L}]+K_{\mathrm{d}}}$$ (5)

This is the well‐known Hill‐Langmuir equation, a straightforward result from the law of mass action for binding at a limited number of sites. In pharmacology, it was first introduced by Hill (1909) while investigating Langley's suggestion of “receptive substance”, and it is analogous with the Langmuir absorption isotherm derived for the binding of molecules to a surface (Langmuir 1918). Strictly speaking, [L] in the above equation denotes the concentration of free ligand, but it is usually assumed that the ligand (drug) is present in sufficient excess so that the amount bound is negligible compared to the total amount present, [LR] << [L_tot]. Hence, one can consider the free ligand (drug) concentration as being the same as the total ligand concentration, [L] ≈ [L_tot]. Because, in general, the concentration of total receptors available [R_tot] is much less than [L_tot], [R_tot] << [L_tot], the total fraction of ligands that can be bound is indeed relatively small, [LR] << [L_tot], making [L_tot] = [L] + [LR] ≈ [L] a reasonable approximation. From eq. 5 it is also obvious that K _d is the ligand concentration that results in half of the receptors being occupied: f _ocup = 0.5 at [L] = K _d.

Single‐state receptor models based on affinity alone

Single‐state model with linear response: the Clark equation

To estimate the effect caused by receptor activation following ligand binding (occupancy), the simplest approximation is to assume that all ligand‐occupied receptors are active (denoted by a star R ≡ R*) producing an effect as symbolized by the corresponding arrow in the equation below.

As a further simplification, one can also assume that the biological effect E produced is proportional with the number (concentration) of occupied receptors, [LR] ≡ [LR*]. In other words, E is a simple linear function of [LR*]:

$$E=f([{\mathrm{LR}}^{\ast }])=\mathit{\alpha }[{\mathrm{LR}}^{\ast }];[{\mathrm{LR}}^{\ast }]\equiv [\mathrm{LR}]$$ (7)

As the number of total receptors in the system of interest is always limited (R_tot), the effect is saturable and reaches a maximum when all receptors are occupied, E _max = α[R_tot]. With these assumptions, the fractional effect, E/E _max, produced, which will be denoted as E _/Emax and represents our main interest here, is the same as the fraction of receptors occupied, f _ocup:

$$E_{/E_{\max }}=\frac{E}{E_{max}}=\frac{\mathit{\alpha }[\mathrm{LR}]}{\mathit{\alpha }[{\mathrm{R}}_{\mathrm{tot}}]}=\frac{[\mathrm{LR}]}{[{\mathrm{R}}_{\mathrm{tot}}]}=f_{\mathrm{ocup}}$$ (8)

Hence, it can be connected to the ligand concentration [L] via eq. 5 obtained earlier:

$$E_{/E_{\max }}=f_{\mathrm{ocup}}=\frac{[\mathrm{L}]}{[\mathrm{L}]+K_{\mathrm{d}}}$$ (9)

This is the well‐known Clark equation (Clark 1926, 1933), which is functionally identical with the Hill–Langmuir equation (eq. 5) since, with the present assumptions, the fractional effect produced equals the fractional occupancy. This simple equation can be used for the empirical fitting of most commonly encountered receptor responses, and it is widely used in pharmacology. It is also a direct analog of the Michaelis–Menten equation used in enzyme kinetics (Michaelis and Menten 1913) with E _max replacing v _max and K _d replacing K _MM, the Michaelis–Menten constant. Graphically, the response corresponding to such an equation is a (portion of a) rectangular hyperbola. Most often, however, binding or response data is represented not on a linear scale, that is, as a function of the ligand concentration, E = φ([L]), but on a semi‐log scale, i.e., as a function of log concentration, E = φ(log[L]), resulting in the well‐known sigmoid response function, which has an inflection point at [L] = K _d (e.g., green line in Fig. 2). With the Clark equation (eq. 9), K _d represents the ligand concentration that produces half of the maximal effect, E = E _max/2 at [L] = K _d.

Figure 2.

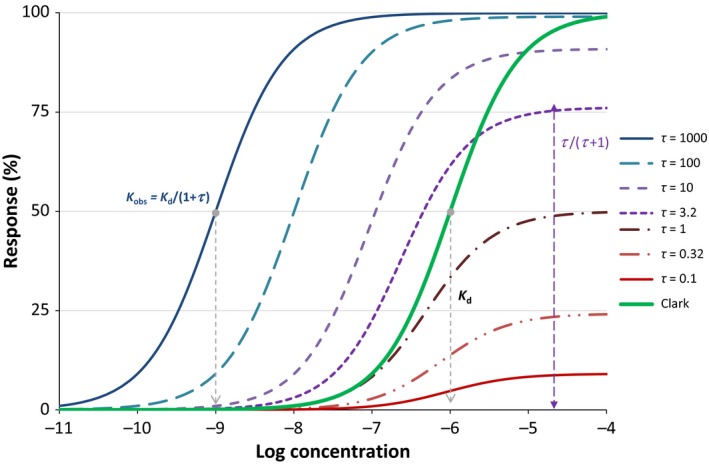
Classic semi‐logarithmic plot illustrating the concentration‐dependent response obtained with the simple Clark equation (eq. 9; green double line) for a ligand with a K _d of 1 μmol/L (10^–6 mol/L) versus the same response obtained with the operational (Black‐Leff) or minimal two‐state (del Castillo‐Katz) model (eq. 14) for the same K _d and different τ values (blue, purple, and red lines). Note that K _obs only corresponds to K _d if τ <<< 1, that is, when there is no response.

Hill and Gaddum equations

In some cases, a more general form, the Hill equation, is used that incorporates an additional parameter the Hill slope, n, to account for deviations from the simple Clark equation caused by more or less abrupt responses, typically attributed to positive (n > 1) or negative (n < 1) cooperativity among binding sites:

$$E_{/E_{\max }}=\frac{{[\mathrm{L}]}^n}{{[\mathrm{L}]}^n+K_{\mathrm{d}}^n}$$ (10)

This function was introduced by Hill (1910, 1913), mostly as an attempt to fit the data and not necessarily as something having a rigorous physical basis (“My object was rather to see whether an equation of this type can satisfy all the observations, than to base any direct physical meaning on n and K” (Colquhoun 2006)). It provides a versatile mathematical function and is often used in pharmacological (Goutelle et al. 2008) or other applications (e.g., Buchwald 2011). The Clark equation (eq. 9), as well as the analogous Michaelis‐Menten equation, represent a special case (n = 1) of the Hill equation. On a semi‐log scale, eq. 10 still results in sigmoid‐like responses, just the transition can be more (n > 1) or less abrupt (n < 1) than with the regular Clark equation corresponding to n = 1. For the regular case (Clark eq., n = 1), transition from almost no effect (~10%) to almost full effect (~90%) requires an approximately two orders of magnitude change in the ligand concentration (i.e., from 0.1K _d to 10K _d; Fig. 2). The case of competitive antagonism and the corresponding Gaddum equation within the formalism of a single‐state affinity‐only receptor model is discussed in Appendix 1.

Receptor models incorporating ligand efficacy

Receptor models based on binding affinity alone represent the simplest approximation. While these forms (i.e., Clark, Hill, and Gaddum equations) are still useful and are sufficient for the empirical fitting of a large portion of pharmacological data, they cannot account for several well‐documented phenomena. One of them is the existence of partial agonists – compounds that can occupy all receptors, yet cannot achieve full activation. Well‐known examples include, for example, prenalterol (vs. adrenaline as full agonist at β‐adrenoceptors), pilocarpine (vs. acetylcholine at muscarinic receptors), and impromidine (vs. histamine at H₂ receptors). It is important to note that there are clear cases where the partial agonist added at sufficiently high concentration to a system with the full agonist already present can displace the full agonist from the receptors and still achieve only partial activity – proving that this is not due to partial occupancy, but partial activation. For example, the case of impromidine and histamine (English et al. 1986) is a frequently used example (Fig. A1), and there are many others in more recent literature (Hoyer and Boddeke 1993; Tadori et al. 2008; Song et al. 2014). At the other end of the spectrum, there is the existence of ‘receptor reserve’ – cases where almost maximal response can be achieved by occupying only a (small) fraction of all receptors. Well‐known extreme cases include, for example, the response of the human calcitonin receptor type 2 to calcitonin (where 20% occupancy already produces close to 100% response) (Chen et al. 1997) and guinea pig ileal response to histamine (where 2% occupancy already produces close to 100% response) (Kenakin and Cook 1976; Adham et al. 1993; Kenakin 2006). Most commonly, these are due to strong signal amplification via second messengers or other systems. Hence, occupied and active receptors do not fully correspond in all cases, and more complex models are needed. Two different models are widely used, but they result in mathematically equivalent equations.

Minimal two‐state model with linear response: del Castillo‐Katz model

For a more general receptor theory, in addition to the parameter characterizing occupancy resulting from binding (affinity), some measure is needed to characterize the ability of the ligand to induce a response at the receptor. The simplest useful model is the minimal two‐state theory (Jenkinson 2003), sometimes also called del Castillo–Katz model (as the corresponding concept was first introduced by them in 1957 (Del Castillo and Katz 1957)). It corresponds to a more general case in which the ‘occupied’ and ‘active’ receptor states no longer fully correspond [cf. eq. 6]:

Here, it is assumed that K _d is similar to the previous definition (eq. 2) and only involves the concentrations of the species involved (L, R, and LR):

$$K_{\mathrm{d}}=\frac{[\mathrm{L}]·[\mathrm{R}]}{[\mathrm{LR}]}$$ (12)

It should be noted that while the definition of K _d here is similar to that given earlier (eq. 2), the previous one (eq. 2) is a macroscopic equilibrium constant that relates to a complete single‐step reaction scheme (eq. 1) and can be measured in an equilibrium‐binding assay, whereas the present one (eq. 12) is a microscopic equilibrium constant that relates to a single step in a multistep reaction scheme and cannot be measured in an equilibrium‐binding assay (eq. 11). While K _d has units in molarity, the equilibrium constant for the second step (activation of the receptor with a bound ligand) is unitless; hence, a different notation with Greek symbols will be used here (τ; replacing what was denoted as E in Jenkinson's description of the model (Jenkinson 2003)). As traditionally defined for this minimal two‐state model, τ _(mtsm) represent the ratio of active to inactive occupied ligand‐receptor complex:

$${\mathit{\tau }}_{(mtsm)}=\frac{[{\mathrm{LR}}^{\ast }]}{[\mathrm{LR}]}$$ (13)

Hence, efficacy as defined here (τ, eq. 13) ranges from 0 for an antagonist that occupies the receptor but produces no activation to infinity (∞) for a full agonist that shift all receptors to the active form. This assumption results in an effect function somewhat similar to the simple Clark equation (eq. 9), but one that also allows for both affinity (via K _d) and efficacy (via τ) (Jenkinson 2003; Colquhoun 2006; Kenakin 2006):

$$E_{/E_{\max }}=\frac{\mathit{\tau }[\mathrm{L}]}{(\mathit{\tau }+1)[\mathrm{L}]+K_{\mathrm{d}}}$$ (14)

A formal derivation can be obtained following the same method that was used earlier for the Clark equation (eq. 9). First, the different forms of the receptor in the system are summed up and the corresponding equilibrium constants are introduced:

$$[{\mathrm{R}}_{\mathrm{tot}}]=[\mathrm{R}]+[\mathrm{LR}]+[{\mathrm{LR}}^{\ast }]=[\mathrm{R}]+\frac{[\mathrm{L}][\mathrm{R}]}{[K_{\mathrm{d}}]}+\mathit{\tau }\frac{[\mathrm{L}][\mathrm{R}]}{[K_{\mathrm{d}}]}=[R]\left\{1+(1+\mathit{\tau })\frac{[\mathrm{L}]}{K_{\mathrm{d}}}\right\}$$ (15)

Since the response is assumed to be linear, the fraction of response can be written as

$$E_{/E_{\max }}=\frac{\mathit{\alpha }[{\mathrm{LR}}^{\ast }]}{\mathit{\alpha }[{\mathrm{R}}_{\mathrm{tot}}]}=\frac{[{\mathrm{LR}}^{\ast }]}{[{\mathrm{R}}_{\mathrm{tot}}]}=\frac{\frac{\mathit{\tau }[\mathrm{L}][\mathit{R}]}{[{\mathrm{K}}_{\mathrm{d}}]}}{[\mathrm{R}]+\frac{[\mathrm{L}][\mathrm{R}]}{[K_{\mathrm{d}}]}+\mathit{\tau }\frac{[\mathrm{L}][\mathrm{R}]}{[K_{\mathrm{d}}]}}=\frac{\mathit{\tau }[\mathrm{L}]}{K_{\mathrm{d}}+(1+\mathit{\tau })[\mathrm{L}]}$$ (16)

This corresponds to the main equation of this model as given in eq. 14. A set of illustrative response functions corresponding to different τ values are shown in Figure 2. Such a general model (eq. 11) that assumes two distinct states of the receptor, so that occupied and active states do not fully overlap, is part of the generally accepted receptor activation model that lies at the foundation of quantitative pharmacological works and is commonly cited in corresponding textbooks (Katzung and Trevor 2014; Rang et al. 2015).

Single‐state model with nonlinear response: operational (Black and Leff) model

Another, different approach is to stay within the framework of a single‐state model (i.e., eq. 6), but assume that the response is nonlinear and not just simply proportional with the number of occupied receptors (Fig. 1). In other words, the effect generated is connected to the number of activated receptors via a transducing function f, and the response function f([LR*] is not linear as it was assumed so far (i.e., eq. 7 no longer holds):

Since in some cases, occupation of only a fraction of total receptors can cause close to maximal response, it makes sense to assume a hyperbolic response where the fractional response is larger than the fractional occupancy. This assumption forms the basis of the operational model introduced by Black and Leff (1983; Black et al. 1985). In this model, all occupied receptors are assumed to be active, but the linear response (eq. 7) is replaced by a hyperbolic response:

$$E=f([{\mathrm{LR}}^{\ast }])=\mathit{\alpha }\frac{[{\mathrm{LR}}^{\ast }]}{[{\mathrm{LR}}^{\ast }]+K_{\mathit{\tau }}};[{\mathrm{LR}}^{\ast }]\equiv [\mathrm{LR}]$$ (18)

This also has a maximum (when all receptors are active). Hence, by using the expression from the law of mass action for [LR] ≡ [LR*] (from eq. 5), the fractional response can be expressed as:

$$\begin{array}{cc}\hfill E_{/E_{\max }}& =\frac{[{\mathrm{LR}}^{\ast }]}{[{\mathrm{LR}}^{\ast }]+K_{\mathit{\tau }}}=\frac{[{\mathrm{R}}_{\mathrm{tot}}]\frac{[\mathrm{L}]}{[\mathrm{L}]+K_{\mathrm{d}}}}{[{\mathrm{R}}_{\mathrm{tot}}]\frac{[\mathrm{L}]}{[\mathrm{L}]+K_{\mathrm{d}}}+K_{\mathit{\tau }}}\hfill \\ & =\frac{[{\mathrm{R}}_{\mathrm{tot}}][\mathrm{L}]}{[{\mathrm{R}}_{\mathrm{tot}}][\mathrm{L}]+[\mathrm{L}]K_{\mathit{\tau }}+K_{\mathrm{d}}{K}_{\mathit{\tau }}}=\frac{\mathit{\tau }[\mathrm{L}]}{(\mathit{\tau }+1)[\mathrm{L}]+{\mathrm{K}}_{\mathrm{d}}}\hfill \end{array}$$ (19)

Here, following the operational model (om) formalism, τ _(om) = [R_tot]/K _τ was introduced in the last step, making it clear that this is mathematically equivalent with the minimal two‐state model (eq. 14). It is noteworthy that even though the minimal two‐state (del Castillo‐Katz) model was mainly introduced to account for partial agonism via partial activation and the operational (Black–Leff) model was mainly introduced to account for receptor reserve via increased effect due to a hyperbolic response function, in the end, they lead to the same equation. Ultimately, this is also a hyperbolic function of [L], just with a modified shape and position. In fact, mathematicians have long known that the function resulting from two (or more) hyperbolic (Langmuir) functions in sequence is also a hyperbolic function, and this has also been clarified in pharmacological applications (Paton and Rothschild 1965; Black and Leff 1983). By slightly rearranging the above form,

$$E_{/E_{\max }}=\frac{\mathit{\tau }}{\mathit{\tau }+1}\frac{[\mathrm{L}]}{[\mathrm{L}]+\frac{K_{\mathrm{d}}}{\mathit{\tau }+1}}$$ (20)

is clear that this is the same type of dependency on ligand concentration [L] as in the Clark equation (eq. 9) just with a lowered maximum, τ/(τ + 1), and a shifted observed activity, K _obs = K _d/(1 + τ). From this, it can also be seen that, in most cases where full response is achieved, τ is essentially an amplification factor: for τ values that produce full response (τ >> 1), τ ≈ τ + 1 essentially shifting the observed curve τ‐fold to the left. In other words, such cases make the activity to appear τ‐fold increased moving the sigmoid response by τ units to the left on a semi‐log scale. The lower K _τ, as compared to [R_tot], the stronger the amplification since τ = [R_tot]/K _τ. Note also that the maximum response of this function is limited as the highest value it can reach even at high ligand concentration (asymptotic limit, E _lim[L]→∞) is τ/(τ + 1), which is always less than unity. This is what causes a limited response (partial agonism) for small τ values (see Fig. 2).

Problems with the existing models

Most current quantitative pharmacological models assume receptor functions along the lines of these two models, with some more complex variations to allow for constitutive activity, receptor desensitization, and other effects, which are not discussed here (Jenkinson 2003; Kenakin 2006). In addition, there are several other current receptor models that build on these concepts (Ehlert et al. 2011; Slack and Hall 2012; Ehlert 2015b; Copeland 2016), and they have been also integrated within PK‐PD models for in vivo data (Danhof et al. 2007). However, there are noticeable disadvantages that hinder the widespread use of the corresponding K _d and τ‐based equation, which is the same for both models (eq. 14, 19). One is that this equation cannot be considered as a straightforward generalization of the Clark (Hill‐Langmuir) equation, and it cannot be reduced back to this simple form: there are no τ values for which eq. 14 converts back to eq. 9 (Fig. 1) so one cannot transition back to this form as a special case of its parameters. Another disadvantage is that K _d for this model is different from the apparent (observed) K (EC₅₀), and its value depends on the value of τ, K _d = K _obs(1 + τ) (see eq. 20). While this should be an important advantage of these models allowing the concentration–response curve to shift from the concentration binding curve, and it has become accepted to use K _d as an empirical parameter not necessarily related to receptor binding as such, it becomes a disadvantage due to the way it has to be achieved. With these models, a ligand can behave as a full agonist (i.e., produce close to maximal activation) only when τ is large enough (τ > 100, see Fig. 2); therefore, all full agonists will need to have K _d values considerably (>100‐fold) higher than the observed K _obs (EC₅₀). Because in this model, K _d shifts depending on the value of the efficacy τ, in some cases, K _d can shift to unrealistically high values for ligand binding, especially as τ is difficult to determine by data fitting (see below). As it has been pointed out, with this model, changes in binding (K _d) and in conformation change (τ) become indistinguishable for very efficacious agonists, making interpretations difficult and cumbersome (Colquhoun 1998).

To highlight a simple example, consider the case of a compound acting on a given receptor for which a K _d (≈EC₅₀) of 1 μmol/L is estimated first using the simple affinity‐only Clark equation. If later another compound is found that produces partial activation requiring the use of the operational model, a τ of >100 needs to be introduced for the first compound to act as a full agonist (i.e., to produce maximal response), which will shift the calculated binding affinity (K _d) at least a 100‐fold (i.e., >100 μmol/L) even though nothing has changed for this compound per se (Fig. A1). Furthermore, for full agonists, the maximal (fractional) response, τ/(τ + 1), needs to have values close to 1, so it is not sensitive to changes in τ. The corresponding large τ values cannot be well‐defined by data fitting, which also makes the linked K _d not well‐defined. Fitting by nonlinear regression might often lead to very large τ values. A specific illustration with extreme shifts that pushes K _d into unrealistic values is shown in Figure A1. Hence, this model is difficult to fit with nonlinear regression, and even if implemented in some software (e.g., GraphPad Prism), it is rarely used and difficult to apply (because it is overparameterized). A further illustration and discussion of related problems is also included later (e.g., Table 1D).

Table 1.

Fitting of data from Figure 7 with the different models discussed here

Model	Parameter	Phenylephrine	Oxymetazoline	Naphazoline	Clonidine	Tolazoline
(A) Experimental data from Ruffolo et al. (1979)
	E max	1.00	0.73	0.48	0.33	0.10
	log ED50	−7.55	−6.77	−8.20	−7.60	−6.64
	log K d 1	−6.46	−6.36	−8.23	−7.66	−6.69
(B) Standard E max (Prism: log[agonist] vs. response ‐ variable slope [four parameters], eq. 9; Hill slope = 1, Bottom = 0)
	Top	99.6 ± 1.26	72.9 ± 1.04	48.0 ± 0.56	33.2 ± 0.70	10.0 ± 1.08
	LogEC50	−7.55 ± 0.035	−6.77 ± 0.029	−8.20 ± 0.027	−7.60 ± 0.047	−6.64 ± 0.174
	r 2	0.9958	0.9978	0.9972	0.9937	0.9491
	SSE	56.25	10.50	4.26	7.52	2.95
(C) Present (Prism implementation of present model, eq. 31 with no amplification γ = 1 [i.e., eq. 26] [n = 1])
	ε	0.996 ± 0.0126	0.729 ± 0.0104	0.480 ± 0.0056	0.332 ± 0.0070	0.100 ± 0.0108
	γ	1	1	1	1	1
	log K d	−7.55 ± 0.035	−6.77 ± 0.029	−8.20 ± 0.027	−7.60 ± 0.047	−6.64 ± 0.174
	r 2	0.9958	0.9978	0.9972	0.9937	0.9491
	SSE	56.25	10.50	4.26	7.52	2.95
(D) Operational model [Prism implementation for partial agonist, eq. 19; n (Hill) = 1, Basal = 0]
	Effectmax	99.58 ± 0.826	99.58 ± 0.826	99.58 ± 0.826	99.58 ± 0.826	99.58 ± 0.826
	logK A	(n.u.)b/~ −1.527 ± 6082	−6.20 ± 0.051	−7.91 ± 0.056	−7.42 ± 0.078	−6.59 ± 0.312
	τ	(n.u.)b/~106.0 b ± too wide	2.731 ± 0.196	0.931 ± 0.042	0.499 ± 0.025	0.112 ± 0.024
	LogEC50	−7.55 ± 0.023/(n.u.)	(not used)	(not used)	(not used)	(not used)
	r 2	0.9958	0.9978	0.9972	0.9937	0.9491
	SSE	56.25	10.50	4.26	7.52	2.95
(E) Present (Prism implementation of present model, eq. 31; K d from experimental [n = 1])
	ε	1	0.1739 ± 0.0274	0.0637 ± 0.0106	0.0369 ± 0.0064	0.0088 ± 0.0022
	γ	11.88 ± 2.02	11.88 ± 2.02	11.88 ± 2.02	11.88 ± 2.02	11.88 ± 2.02
	log K d (from exp.)a	−6.46	−6.36	−8.23	−7.66	−6.69
	↓c
	E max	1.000	0.714	0.447	0.313	0.096
	log EC50(K obs)	−7.53	−6.82	−8.46	−7.81	−6.73
	r 2	0.9957	0.9964	0.9508	0.9736	0.9430
	SSE	57.22	17.21	76.18	31.71	3.30

All fitting were done with models implemented in GraphPad Prism, and in addition to the calculated parameters (shown with their calculated standard errors), descriptors of the quality of fit (correlation coefficient, r ², and sum of squared errors, SSE) are also included.

^aExperimental data, average of log K _A (Table 3) and log K _B (Table 4) from Ruffolo et al. (1979).

^bThe operational model as implemented in GraphPad Prism, does not fit K _A and τ for a full agonist (not used) as well‐defined values cannot be obtained. A set of values were calculated here for illustration by re‐using the data of the full agonist (phenylephrine) as another partial agonist.

^cDerived values for the present model (using eq. 33).

Finally, a hypothesis‐related problematic issue is that while the final equations are mathematically identical, the two models arrive at it from two conceptually different approaches that are both incomplete. The minimal two‐state model, which is now well accepted as a good approach to describe switching of the receptor between active and inactive states, does not formally incorporate nonlinear transduction (signal amplification), which is known to exist. The operational model, allows nonlinear response, but it is a single‐state receptor model that does not formally incorporate the possible existence of active and inactive ligand‐bound receptor states. As a result, these models merge together two different effects in their τ efficacy parameter: the ‘intrinsic’ efficacy of the ligand in activating the receptor, which could be responsible for partial agonism even with a linear response function, and the ‘efficacy’ of the postactivation amplification downstream from the receptor, which can create the appearance of receptor reserve and can be tissue or organ specific.

Present Work: Proposed Receptor Model

Two‐state model with nonlinear response and modified parameterization

The model proposed here is a fully generalized model that still relies on the essential assumptions of the minimal two‐state theory, which reflects our current understanding of receptor pharmacology, that is, ligand binding and receptor activation are two different steps (Katzung and Trevor 2014; Rang et al. 2015). However, it (1) uses an alternative assumption on ligand binding to the inactive and active receptor forms, (2) allows nonlinear (hyperbolic) response following receptor activation to account for signal amplification if needed, and (3) introduces a different parametrization with more intuitive parameters that are also better suited for optimization by nonlinear regression. Its most general form uses three parameters: K _d, the classic equilibrium dissociation constant to characterize binding affinity; ε, an (intrinsic) efficacy to characterize the ability of bound ligand to activate the receptor (0 ≤ ε ≤ 1); and γ, a gain (amplification) parameter to characterize the nonlinearity of postactivation signal transduction (1 ≤ γ ≤ ∞). Accordingly, the overall schematic of the present model is only slightly different from that of the minimal two‐state model (eq. 11) (Fig. 1): it allows binding to/dissociation from both forms of the ligand‐receptor complex (LR and LR*) and incorporates a more general, nonlinear transduction function to describe the dependence of the effect E on the LR* concentration:

Binding parametrization

Regarding receptor binding, we will deviate from the current two‐state model and assume that receptor activation does not affect ligand binding and dissociation, or at least not in a significant manner. The del Castillo–Katz model assumes that binding (or more precisely dissociation, since all models use K _d, the equilibrium dissociation constant) only involves the inactive receptor form, LR. Hence, K _d is defined only in terms of [L], [R], and [LR] (eq. 12). In most cases, however, there is no reason why the ligand could not dissociate from (or bind to) the active receptor, LR*, as well, so that K _d represents an average constant for the ensemble of receptors that the ligand effectively sees. For most protein structures, it is not very likely that the conformation change causing activation of the receptor will completely or even strongly lock the ligand into its binding site. Furthermore, even if there are two somewhat different K _ds for the active (LR*) and the inactive forms (LR), they will only show up as two separate low‐ and high‐affinity steps in the binding curve if the corresponding values differ by close to three orders of magnitude–especially with experimental data that always have some scatter. Otherwise, it will appear as an intermediate affinity with a decreased Hill slope. For example, Figure 3 illustrates ligand binding for a hypothetical case in which 40% of the receptors are in a state with higher affinity (K _d1 = 1 nmol/L) and 60% in a state with lower affinity (K _d2, ranging from 1 to 1000‐fold differences vs. K _d1). The two consecutive steps become clearly separated only at about 1000‐fold difference even in this line‐based graph without any scatter in the data.

Figure 3.

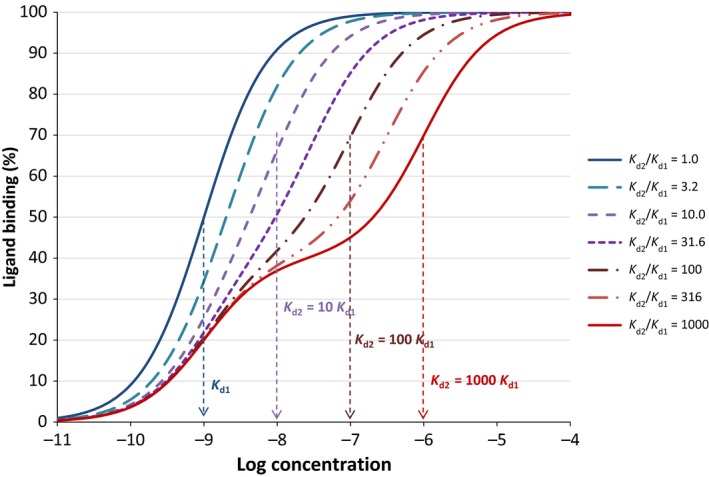
Semi‐logarithmic plot illustrating the concentration‐dependent response obtained for a hypothetical case in which 40% of the receptors are in a state with higher affinity (K _d1 = 1 nmol/L) and 60% in a state with lower affinity (K _d2, which ranges from 1–1000 nmol/L). Even in these theoretical curves with no scatter in the data, the difference is noticeable only if the affinities differ by close to three orders of magnitude (curves with a reddish hue); otherwise, it appears as a single intermediate affinity with decreased Hill slope, n < 1 (curves with blueish or purple hues).

With this assumption that the dissociation constant is similar for the inactive and active ligand‐bound receptor states, the definition of K _d becomes:

$$K_{\mathrm{d}}=\frac{[\mathrm{L}][\mathrm{R}]}{[\mathrm{LR}]+[{\mathrm{LR}}^{\ast }]}$$ (22)

This is somewhat different than the one used previously in the minimal two‐state model (cf. eq. 12), where the denominator only contained the concentration of the inactive LR and not that of all ligand‐bound receptors, [LR] + [LR*]. Ultimately, a main advantage is that with this modified definition, K _d will become independent from the value of the efficacy parameter.

Efficacy parametrization (partial agonism)

To describe receptor activation (‘intrinsic efficacy’), we will also use a slightly different form than the one used in the previous model (cf. eq. 13 for τ) as this will allow a more intuitive final form that is also more suitable for parameter optimization:

$$\mathit{\epsilon }=\frac{[{\mathrm{LR}}^{\ast }]}{[\mathrm{LR}]+[{\mathrm{LR}}^{\ast }]}$$ (23)

Hence, efficacy ε as defined here represents the fraction of ligand‐bound receptors that are active (eq. 23); whereas, τ, as used before, represents the ratio of active to inactive ligand‐bound receptors (eq. 13). Both are unitless, but while τ ranges from 0 to infinity (∞), ε is restricted from 0 to unity (1). With these definitions, ε = τ/(τ + 1). Hence, ε is similar to the intrinsic activity introduced by Ariëns, which is the ratio of the maximum response produced by the partial agonist to that produced by the full agonist (Ariëns 1954), and not to the efficacy as defined by Stephenson, which can have values from 0 to infinity (Stephenson 1956). With the present definition, an antagonist that can occupy all receptors, but produces no effect has zero efficacy, ε = 0, while an agonists that can convert all occupied receptors to active ones has an efficacy of unity, ε = 1. The latter would correspond to a ‘true’ full agonist at the receptor; postreceptor amplification can complicate things as response from a partial agonist can be amplified to a maximum final response (see discussion later). In the present formalism, since K _d is the same for the active and inactive states, binding with high(er) affinity to the active (or inactive) state is replaced by binding and high (or low) efficacy activation.

With these, K _d can be written as follows:

$$K_{\mathrm{d}}=\frac{[\mathrm{L}][\mathrm{R}]}{[\mathrm{LR}]+[{\mathrm{LR}}^{\ast }]}=\frac{[\mathrm{L}][\mathrm{R}]}{[\mathrm{LR}]\left(1+\frac{\mathit{\epsilon }}{1-\mathit{\epsilon }}\right)}=(1-\mathit{\epsilon })\frac{[\mathrm{L}][\mathrm{R}]}{[\mathrm{LR}]}$$ (24)

If, as a first approximation, one assumes linear response, the fractional response (effect) equals the fraction of activated receptors, which can be obtained again via the expression of the total receptors present. The corresponding concentration, [R_tot], is the sum of all free and occupied receptor forms and using eq. 24:

$$\begin{array}{cc}\hfill [{\mathrm{R}}_{\mathrm{tot}}]& =[\mathrm{R}]+[\mathrm{LR}]+[{\mathrm{LR}}^{\ast }]=[\mathrm{R}]+([\mathrm{LR}]+[{\mathrm{LR}}^{\ast }])\hfill \\ & =[\mathrm{R}]\left(1+\frac{[\mathrm{L}]}{K_{\mathrm{d}}}\right)\hfill \end{array}$$ (25)

Hence, the fractional response produced can be expressed as:

$$E_{/E_{\max }}=\frac{[{\mathrm{LR}}^{\ast }]}{[{\mathrm{R}}_{\mathrm{tot}}]}=\frac{\mathit{\epsilon }\frac{[\mathrm{R}][\mathrm{L}]}{K_{\mathrm{d}}}}{[\mathrm{R}]\left(1+\frac{[\mathrm{L}]}{K_{\mathrm{d}}}\right)}=\mathit{\epsilon }\frac{[\mathrm{L}]}{[\mathrm{L}]+K_{\mathrm{d}}}$$ (26)

This is essentially equivalent with a Clark equation that includes a scalable maximum (E _max model), and links the definition of the maximum achievable effect (response) for a partial agonist to a two‐state model. With the slightly different definition of efficacy as used here, ε from eq. 23 versus τ from eq. 13; ε = τ/(τ + 1), ε corresponds to the fraction of maximum activation a partial agonists can achieve as compared to the full agonist. For full agonists, ε = 1, and the above equation corresponds directly to the Clark equation (eq. 9). One advantage of this parametrization is that ε is better suited for optimization via nonlinear regression than τ, which is difficult to define well by data fitting for full agonists where it needs to have large values. A further advantage of the present model is that K _d corresponds completely to the classic model allowing this two‐state model to translate directly into the regular E _max model, which is familiar to most users and also is available to fit as such in all popular nonlinear regression software such as GraphPad Prism.

Gain parametrization (Nonlinear response with signal amplification)

As a final step, signal amplification is incorporated in the model by allowing nonlinear transduction. This is done via a formalism similar to that of the operational model, but with an important modification. One reason for this is to obtain a more convenient parametrization. Another one is that the amplification via the response function as incorporated into the operational model is a limited one: the hyperbolic function used (eq. 18) cannot reach its asymptotic limit as its input [LR*] can only increase up to R_tot and not to infinity. Hence, the amplification approaching the maximum limit, where the hyperbolic function approaches unity, is only possible when K _τ << R_tot; otherwise, a considerable portion of the response function is cut off. An illustration of this using the 3D plot introduced for the operational model (Fig. 2 in (Black and Leff 1983)), but shown here with different K _τ values is provided in Figure A2C versus B. This is the reason why the operational model results in a maximum, τ/(τ + 1), that is always smaller than unity, which is what limits the maximum response for small τ values (see Fig. 2). It is also why the operational model, which was intended to model amplification (hyperbolic response function), can also describe partial activation. Therefore, we will use a hyperbolic response function, but not with [LR*] as its input as done in the operational model, but its odds‐ratio type transform (De Muth 2014), Λ = p/(1–p) = [LR*]/(R_tot–[LR*]). This extends the range of the input from the 0–1 interval, which is the range for [LR*]/R_tot, to the 0–∞ interval. Hence, the response function linking E to [LR*] will be:

$$\begin{array}{cc}\hfill E_{/E_{\max }}& =f([{\mathrm{LR}}^{\ast }])=\frac{\mathrm{\Lambda }}{\mathrm{\Lambda }+\frac{K_{\mathit{\gamma }}}{{\mathrm{R}}_{tot}}}=\frac{\frac{\lfloor {\mathrm{LR}}^{\ast }\rfloor }{{\mathrm{R}}_{\mathrm{tot}}-[{\mathrm{LR}}^{\ast }]}}{\frac{[{\mathrm{LR}}^{\ast }]}{{\mathrm{R}}_{\mathrm{tot}}-[{\mathrm{LR}}^{\ast }]}+\frac{K_{\mathit{\gamma }}}{{\mathrm{R}}_{\mathrm{tot}}}}\hfill \\ & =\frac{[{\mathrm{LR}}^{\ast }]}{\left(1-\frac{K_{\mathit{\gamma }}}{{\mathrm{R}}_{tot}}\right)[{\mathrm{LR}}^{\ast }]+K_{\mathit{\gamma }}}\hfill \end{array}$$ (27)

The resulting function on [LR*] is still an essentially hyperbolic response, particularly for small K _γ (strong amplification). This type of parametrization ensures that the response (effect) generated when all receptors are active ([LR*] = R_tot) always corresponds to E _max (Fig. A2 D,E). Using the form of [LR*] derived for the present model (eq. 26):

$$[{\mathrm{LR}}^{\ast }]=\mathit{\epsilon }{\mathrm{R}}_{\mathrm{tot}}\frac{[\mathrm{L}]}{[\mathrm{L}]+K_{\mathrm{d}}}$$ (28)

we get:

$$\begin{array}{cc}\hfill E_{/E_{\max }}& =\frac{[{\mathrm{LR}}^{\ast }]}{\left(1-\frac{K_{\mathit{\gamma }}}{{\mathrm{R}}_{\mathrm{tot}}}\right)[{\mathrm{LR}}^{\ast }]+K_{\mathit{\gamma }}}\hfill \\ & =\frac{\mathit{\epsilon }{\mathrm{R}}_{\mathrm{tot}}[\mathrm{L}]}{\mathit{\epsilon }{\mathrm{R}}_{\mathrm{tot}}[\mathrm{L}]\left(1-\frac{K_{\mathit{\gamma }}}{{\mathrm{R}}_{\mathrm{tot}}}\right)+K_{\mathit{\gamma }}([\mathrm{L}]+K_{\mathrm{d}})}\hfill \\ & =\frac{[\mathrm{L}]}{[\mathrm{L}]\left(1-\frac{K_{\mathit{\gamma }}}{{\mathrm{R}}_{\mathrm{tot}}}+\frac{K_{\mathit{\gamma }}}{\mathit{\epsilon }{\mathrm{R}}_{\mathrm{tot}}}\right)+\frac{K_{\mathit{\gamma }}{K}_{\mathrm{d}}}{\mathit{\epsilon }{\mathrm{R}}_{\mathrm{tot}}}}\hfill \end{array}$$ (29)

By introducing γ = R_tot/K _γ in a manner similar to that of the operational model, and multiplying with it both sides of the fraction, we obtain the final general form:

$$E_{/E_{\max }}=\frac{\mathit{\gamma }[\mathrm{L}]}{[\mathrm{L}]\left(\mathit{\gamma }-1+\frac{1}{\mathit{\epsilon }}\right)+K_{\mathrm{d}}\frac{1}{\mathit{\epsilon }}}=\frac{\mathit{\epsilon }\mathit{\gamma }[\mathrm{L}]}{(\mathit{\epsilon }\mathit{\gamma }-\mathit{\epsilon }+1)[\mathrm{L}]+K_{\mathrm{d}}}$$ (30)

Here, γ represent an amplification factor (gain), and it is again a unitless parameter. Since it is a gain, for all practical purposes, it has a value larger than unity, γ ≥ 1, in many cases considerably so. A set of illustrative response curves for a fixed value of K _d and different values of ε and γ are shown in Figure 4. Employing the full model (eq. 30) only makes sense if binding (occupancy) and effect can be assessed independently, and if sufficient data can be collected (see, for example, the illustrative data for a series of imidazoline type α‐adrenoceptor agonists causing contraction of an isolated rat aorta discussed in the next section). Reliable fitting of the full model could require a large number of data as, typically, at least 5–10 data points per adjustable parameter are recommended (Knofczynski and Mundfrom 2008; Austin and Steyerberg 2015). For a given drug acting at a specific receptor, affinity (K _d) and (intrinsic) efficacy (ε) should be the same (as long as binding and activation of the receptor are not influenced by the environment), but transduction (signal amplification) could be tissue dependent. Hence, γ, and, in fact, both of its components, R_tot and K _γ, can be tissue dependent.

Figure 4.

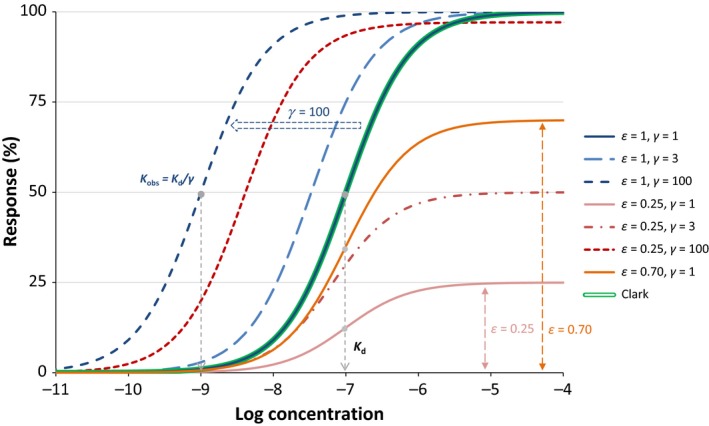
Response curves with the present model (eq. 31) for a ligand of 100 nmol/L affinity (K _d = 10^–7 mol/L) for a full agonist (ε = 1, blue lines) at different amplifications (γ = 1, 3, and 100) and a weak partial agonist (ε = 0.25, red lines) at the same amplifications (γ = 1, 3, and 100). Another partial agonist without amplification is also included (ε = 0.70, γ = 1 orange line) for comparison. Note that with the present model, the basic parametrization (ε = 1, γ = 1) fully reproduces the Clark model (blue and double green lines completely overlap), which could not be done with the previous models (Figure 2). The effect of different post‐activation amplifications on the observed response of a full and a partial agonist is also illustrated in more detail in Figure 6.

Discussion: comparison with other models

While the general equation proposed here has no striking beauty or elegant simplicity, it has several benefits. Rearranging it slightly, makes it clear that it has a form somewhat resembling that of the operational (or del Castillo–Katz) model with τ being replaced by εγ (cf. eq. 14 and 19), but with an additional ε (0 ≤ ε ≤ 1) in the denominator:

$$E_{/E_{\max }}=\frac{\mathit{\epsilon }\mathit{\gamma }[\mathrm{L}]}{(\mathit{\epsilon }\mathit{\gamma }+1-\mathit{\epsilon })[\mathrm{L}]+K_{\mathrm{d}}}$$ (31)

While the overall form is quite similar, the different parametrization provides several advantages. First, all parameters here are straightforward and intuitive, which was not the case with the previous models, where τ was not clearly linked to an intuitive interpretation. Affinity (binding) is characterized by K _d, the binding constant, which is on a molar scale and is now uncoupled from the ability to activate the receptor (efficacy) or the strength of postactivation amplification (gain). Efficacy (ability to activate the receptor) is characterized by ε, which is unitless and ranges from 0 (for an antagonist that produces no activation) to 1 for an agonist that can convert all receptors into the active state. Nonlinear transduction, due to, e.g., postreceptor amplification (gain), is characterized by γ, which is unitless and ranges from 1 (no amplification) to infinity.

A second important advantage is that this general form (eq. 31), contrary to the previous models, is a true generalized model and reduces back to the simplified forms for special cases of its parameters (Fig. 5). For example, if there is no postreceptor amplification (no receptor reserve, that is, no amplification/gain, γ = 1), it reduces back to the equation for partial agonist with an efficiency ε (eq. 26) as ε(γ–1) in the denominator becomes 0. If there is no amplification (γ = 1) and no partial agonism (ε = 1), the equation reduces back to the Clark equation (Fig. 5), which was not the case with the operational model (eq. 19) or the minimal two‐state model (eq. 14). If there is amplification (γ > 1), the response for a full agonist (ε = 1) is a hyperbolic response with a multiplied [L]:

$$E_{/E_{\max }}=\frac{\mathit{\gamma }[\mathrm{L}]}{\mathit{\gamma }[\mathrm{L}]+K_{\mathrm{d}}}$$ (32)

Figure 5.

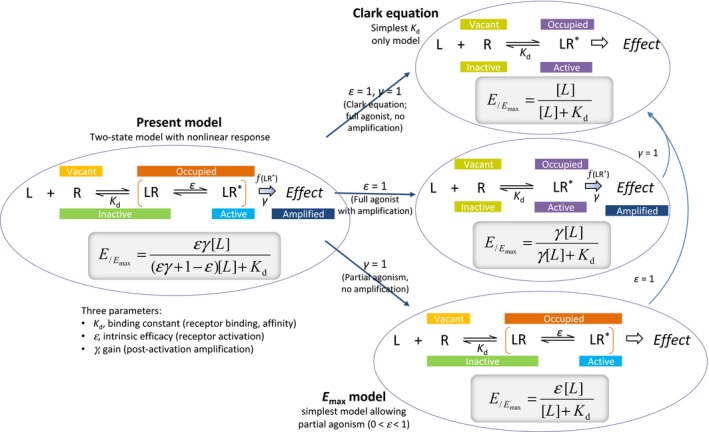
Schematics of receptor binding and effect generation for the present model with its general three‐parameter equation (eq. 31; K _d, ε, γ) (left) and its reduction to simpler forms for special cases of its parameters.

In other words, for a full agonist (at the receptor), γ is a straightforward multiplication factor causing a γ‐fold left‐shift of the sigmoid response function on a semi‐log scale. Hence, for a full agonist, signal amplification causes no change in the shape of the response on semi‐log scale, just a left‐shift so that K _obs = K _d/γ. For a partial agonist, postactivation amplification will increase the maximum response, and a sufficiently strong postreceptor amplification can transform a partial agonist into a full agonist. However, the left shift will be less than that for a full agonist with the same K _d so that the change in the apparent EC₅₀ (K _obs) will be less. An illustration is provided in Figure 6. This can be well seen in a rearranged form of eq. 31

Figure 6.

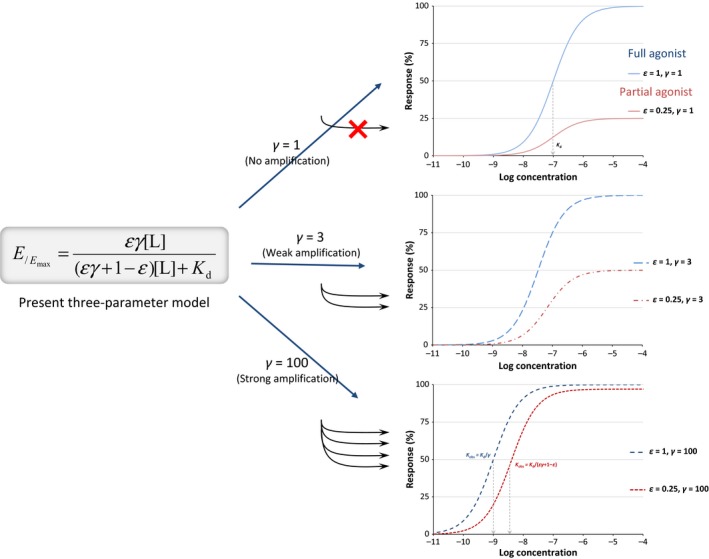
Response curves with the present three‐parameter model (eq. 31) for a ligand of 100 nmol/L binding affinity (K _d = 10^–7 mol/L) that is a full agonist (ε = 1, blue lines) or partial agonist (ε = 0.25, red lines) at different post‐activation amplifications, γ = 1 (no amplification), 3, and 100.

$$E_{/E_{\max }}=\frac{\mathit{\epsilon }\mathit{\gamma }}{(\mathit{\epsilon }\mathit{\gamma }+1-\mathit{\epsilon })}\frac{[\mathrm{L}]}{[\mathrm{L}]+\frac{K_{\mathrm{d}}}{(\mathit{\epsilon }\mathit{\gamma }+1-\mathit{\epsilon })}}$$ (33)

From here, it is clear that K _obs = K _d/(εγ + 1–ε), and the maximum is εγ/(εγ + 1–ε), which can approach unity even with a small ε if γ is large enough. This can account for cases where the mixture of receptor reserve and partial agonism causes complex responses (Adham et al. 1993; Hoyer and Boddeke 1993). Along these lines, it can also account for different responses for the same agonists if they are observed at different vantage points along a stimulus‐response pathway that involves multiple amplification steps (e.g., Fig. 5.2 in (Kenakin 2006)).

To illustrate the possibilities of the present model and its advantage over the previous ones, it is used here (Fig. 7) to fit the dose–response data (contractions of isolated rat aorta) obtained with a series of imidazoline type α‐adrenoceptor agonists that includes phenylephrine, oxymetazoline, naphazoline, clonidine, and tolazoline (Ruffolo et al. 1979). This data is particularly well suited for this, as in addition to response, receptor binding was also assessed separately by two different methods, and it is used as a classic textbook example to illustrate mismatch between fractional receptor occupancy and response (Rang et al. 2015). The response data alone can be fitted well by a standard E _max model (eq. 9), the present model with no amplification (eq. 26, which is essentially the E _max model), and the operational model (eq. 19); they all give identical fits (Fig. 7A; Table 1 B, C, and D). However, while the present model in its simplified form reproduces exactly the E _max and EC₅₀ values of the standard model, the operational model results in a different set of K _A values and some not particularly informative τ parameters, E _max = τ/(τ + 1) (Table 1 B vs. C and D). Notably, in the current implementation of the operational model in Prism, τ and K _A are not calculated for the full agonist (here, phenylephrine) since if it is done, it results in quite meaningless values (it can be done by adding it as another partial agonist, see values in Table 1C). This problem has been discussed earlier. These models can be used for empirical fitting of response data, but none of them offer even a remote possibility to connect the response to the binding data (K _d), which has been determined independently. This can be done, however, with the present general model (eq. 31), and the obtained fit is only slightly less good (Fig. 7B; Table 1). This fit is obtained using the independently derived K _d values for each compound and adjusting only the common γ (gain) and the individual ε (efficacy) parameters. Hence, the present model can do more than just an empirical fit of the response data and can account for complex cases where, depending on the ligand, the fractional response can either exceed or lag behind the fractional occupancy at the same receptor (Fig. 7C).

Figure 7.

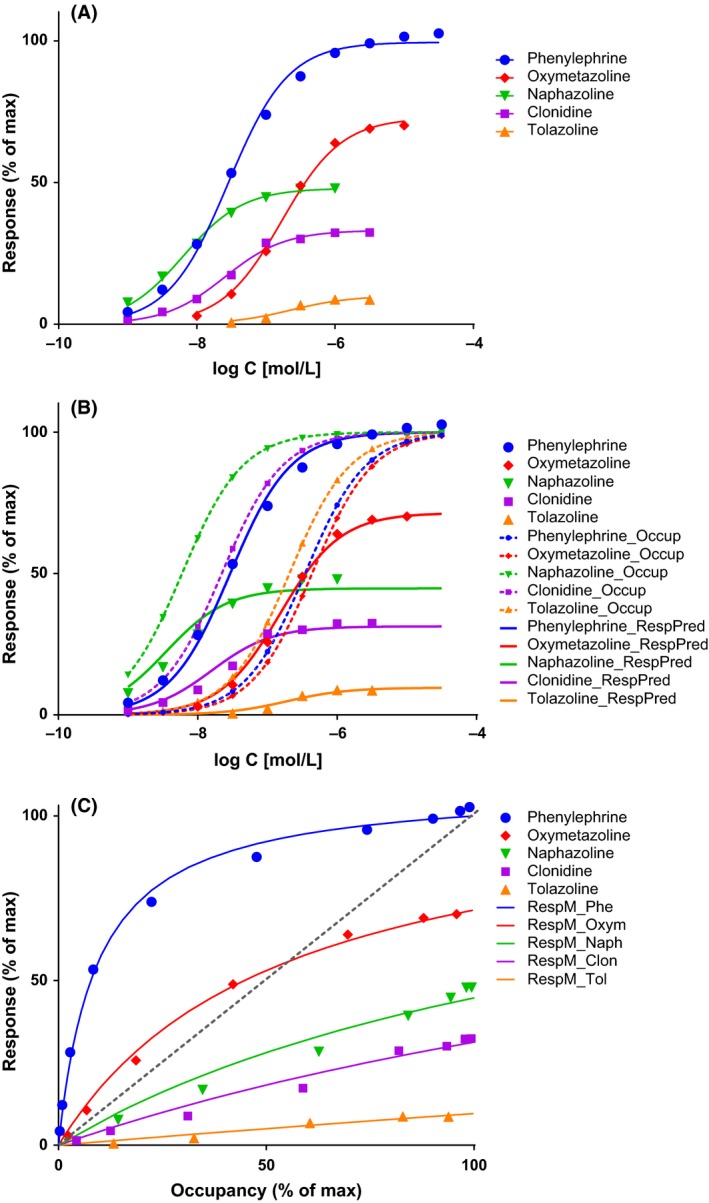
Fit of complex dose–response data obtained with partial agonists where the fractional response can either exceed or lag behind the fractional receptor occupancy. Data are for a series of imidazoline‐type α‐adrenoceptor agonists with response (contraction of isolated rat aorta) shown relative to the maximal one caused by phenylephrine, a full agonist (data after (Ruffolo et al. 1979)). Fractional receptor occupancy values used here are calculated from the average equilibrium dissociation constants (K _d) determined for the receptor binding by two different methods (Ruffolo et al. 1979). (A) Fractional response as a function of log concentration for five compounds (symbols) fitted by three different methods (lines). The three different methods (standard E _max–eq. 9, present model with no amplification–eq. 26, and operational model–eq. 19; see Table 1 B, C, and D) give identical fits and, hence, overlapping lines. (B) Same data fitted with the present model (eq. 31) using the independently derived K _d values for the binding (dotted lines) and fitting the response data by adjusting only the common γ (gain) and the individual ε (efficacy) parameters (Table 1). Fractional receptor occupancy data are also shown as dashed lines to highlight the ability of the model to account for the mismatch between fractional response and occupancy. (C) Fractional response vs. occupancy data for these five compounds (symbols) and their corresponding fit with the present model (curved lines).

The present model can also fit unusual response curve data in different tissues, such as those due to different efficacies resulting from receptor inactivation, just as well as the operational model. For example, the data of guinea‐pig ileum through activation of muscarinic receptors with carbachol and oxotremorine in normal tissue and following inactivation of muscarinic receptor via controlled alkylation (Kenakin and Christopoulos 2011) can be fit slightly better with the present ε and γ based model than with the τ based operational model (Fig. A3). Just as the minimal two‐state or operational models, the present model can also describe competitive partial agonism, which can be considered a generalization of the Gaddum equation for competitive antagonism, and it can do so with more meaningful parameters than the previous models (Appendix 1). The case of impromidine and histamine, a frequently used example (English et al. 1986), is used here to illustrate fitting (Fig. A1). We have also found similar behavior for a partial agonist at the OX40 receptor (Song et al. 2014).

For the present model, an increase in the number of parameters (from two to three) is a small hindrance as model simplification is always an important consideration (George 2000; Myung and Pitt 2004; Buchwald 2005, 2007) and obtaining well‐defined values by fitting requires increased number of (well distributed) data points. However, this disadvantage is compensated on one hand, by the intuitive nature of the parameters, and on the other hand, by the ability to use simplified forms with reduced number of parameters when adequate (Fig. 5). For example, if only partial agonism needs to be addressed, the corresponding equation with only ε as additional parameter can be used (eq. 26). This corresponds fully to the E _max model commonly used for nonlinear regression (e.g., log agonist vs. response model in GraphPad Prism) while still representing a special case of the present general model – something that could not be claimed for the del Castillo–Katz or Black and Leff models. If only a straightforward amplification needs to be addressed for a full agonist (where the effect is left‐shifted compared to occupancy), eq. 32 with only the additional γ gain parameter can be used. Fitting of the full model with all three parameters (K _d, ε, γ) is only needed when both amplification and partial activation have to be addressed (like the cases presented in Figs. 6, 7, and A3), and this requires considerable number of data points to be able to obtain well‐defined values for all parameters.

In conclusion, a three‐parameter two‐state model is proposed here as a simple basis for quantitative receptor theory linking ligand binding and effect generation for cases that do not involve constitutive activity, receptor desensitization, and other more complex effects. While it is undoubtedly a simplification, it can provide quantitative description even in complex cases (e.g., when the generated effect is due to a mixture of interactions between receptor reserves and partial agonism) in a manner similar to the operational (Black and Leff) and the minimal two‐state (del Castillo‐Katz) models. However, contrary to those, for special cases of its parameters, it can be reduced back to simpler models such as the Clark equation or its E _max version providing a straightforward bridge to them from a two‐state receptor model and mathematical forms that are more suitable for fitting by nonlinear regression. Furthermore, in cases where receptor binding and response can be measured separately and they do not overlap, only the present model allows the possibility to connect the response to the binding data (K _d) via its efficacy (ε) and gain (γ) parameters.

Author Contributions

PB is the sole author, he developed the concept, performed the calculations and data fittings, and wrote the manuscript.

Disclosure

The author declares that he has no competing financial interest.

Appendix 1.

Models of Competitive Antagonism and Partial Agonism

Classic single‐state receptor model: Gaddum equation

In the presence of an antagonist, the response produced by the agonist is diminished. In general, various antagonism mechanisms are possible; among those involving the receptor, competitive (orthosteric) and noncompetitive (allosteric) are the two main mechanisms of interest. Competitive antagonists bind at (compete for) the same site as the agonist, which can be envisioned schematically as having an inhibitor‐receptor complex (IR), whose formation competes with that of the ligand‐receptor complex (LR). Staying within the framework of affinity‐only receptor models, one can assume that binding of the ligand produces an effect proportional with the [LR] concentration, whereas binding of the inhibitor produces no effect (i.e., an inactive IR complex). Hence, competitive antagonism can be represented by the following schematics (a generalization of eq. 6):

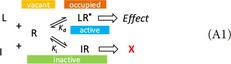
Such antagonists produce an apparent decrease in the affinity of the agonist (right‐shift), characterized by the Gaddum equation:

$$E_{/E_{\max }}=\frac{[\mathrm{L}]}{[\mathrm{L}]+K_{\mathrm{d}}\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)}$$ (A2)

This is, in fact similar to the Clark equation, but with an apparent K _d that is increased. Comparing the two forms (eq. A2 vs. 9), it can be seen that the Gaddum equation has the same functional dependence on [L] just K _d is increased (1 + [I]/K _i) fold resulting in the well‐known right‐shift characteristic for competitive antagonists. Derivation is obtained following the same general procedure. First, the total number (concentration) of receptors can be written as

$$[{\mathrm{R}}_{\mathrm{tot}}]=[\mathrm{R}]+[{\mathrm{LR}}^{\ast }]+[\mathrm{IR}]=[\mathrm{R}]+\frac{[\mathrm{L}][\mathrm{R}]}{[{\mathrm{K}}_{\mathrm{d}}]}+\frac{[\mathrm{I}][\mathrm{R}]}{[{\mathrm{K}}_{\mathrm{i}}]}$$ (A3)

Next, with the assumption of linear response, the fraction of active vs. total receptors leads to the final form of the Gaddum equation:

$$E_{/E_{\max }}=\frac{[{\mathrm{LR}}^{\ast }]}{[{\mathrm{R}}_{\mathrm{tot}}]}=\frac{[{\mathrm{LR}}^{\ast }]}{[\mathrm{R}]+[{\mathrm{LR}}^{\ast }]+[\mathrm{IR}]}=\frac{\frac{[\mathrm{L}][\mathrm{R}]}{K_{\mathrm{d}}}}{[\mathrm{R}]\left(1+\frac{[\mathrm{L}]}{K_{\mathrm{d}}}+\frac{[\mathrm{I}]}{K_{\mathrm{d}}}\right)}=\frac{[\mathrm{L}]}{[\mathrm{L}]+K_{\mathrm{d}}\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)}$$ (A4)

Contrary to a competitive antagonist, noncompetitive antagonists do not bind at (hence, do not compete for) the same site as the agonists. They bind at some different (allosteric) site and modulate the effect of agonist via this binding. Consequently, their effect is not surmountable (i.e., it cannot be overcome by increasing the concentration of the agonist), and they do not cause a right‐shift but, instead, an apparent diminished maximum response. A possible simple model is to assume that the inhibitor I bounds to a separate site of the receptor so that in addition to the ligand‐receptor complex (LR) of eq. 6, IR and ILR complexes can also form, which, however, are nonfunctional and do not produce the (desired) effect E. The resulting equation for the effect indeed reveals a diminished maximum response as a function of the inhibitor concentration [I]:

$$E_{/E_{\max }}=\frac{[\mathrm{L}]}{([\mathrm{L}]+K_{\mathrm{d}})}\frac{1}{\left(1+\frac{[\mathrm{I}]}{K_{\mathrm{i}}}\right)}$$ (A5)

Competitive partial agonism with the minimal two‐state (and operational) model

With models that allow efficacy, competitive agonism can be modeled for cases with competing partial agonist, where both ligands can produce some effect, not just the case of a full agonist competing with an antagonist producing no effect. If two ligands (L₁, L₂) of different affinities (K _d1, K _d2) and efficacies (τ ₁, τ ₂) are present simultaneously competing for binding at the same receptor,

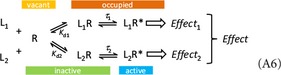
The expression for the total effect is obtained following a procedure similar to the previous ones. First, by using a corresponding equations from the minimal two‐state receptor model (eq. 12, 13) for L₁ and L₂, the total number (concentration) of receptors [R _tot] can be written as:

$$\begin{array}{cc}\hfill [{\mathrm{R}}_{\mathrm{tot}}]& =[\mathrm{R}]+[{\mathrm{L}}_{1}R]+[{\mathrm{L}}_1{R}^{\ast }]+[{\mathrm{L}}_{2}R]+[{\mathrm{L}}_2{\mathrm{R}}^{\ast }]\hfill \\ & =[\mathrm{R}]+\frac{[{\mathrm{L}}_1][\mathrm{R}]}{{\mathrm{K}}_{\mathrm{d}1}}+{\mathit{\tau }}_1\frac{[{\mathrm{L}}_1][\mathrm{R}]}{{\mathrm{K}}_{\mathrm{d}1}}+\frac{[{\mathrm{L}}_2][\mathrm{R}]}{{\mathrm{K}}_{\mathrm{d}2}}+{\mathit{\tau }}_2\frac{[{\mathrm{L}}_2][\mathrm{R}]}{{\mathrm{K}}_{\mathrm{d}2}}\hfill \\ & =[\mathrm{R}]\left\{1+(1+{\mathit{\tau }}_1)\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}+(1+{\mathit{\tau }}_2)\frac{[{\mathrm{L}}_2]}{K_{\mathrm{d}2}}\right\}\hfill \end{array}$$ (A7)

Next, the total effect produced is expressed as a function of the [L₁] and [L₂] concentrations present using the assumptions that the effects E ₁ and E ₂ are proportional with the corresponding [L₁R*] and [L₂R*] concentrations:

$$\begin{array}{cc}\hfill E_{/E_{\max }}& =\frac{[{\mathrm{L}}_1{\mathrm{R}}^{\ast }]+[{\mathrm{L}}_2{\mathrm{R}}^{\ast }]}{[{\mathrm{R}}_{\mathrm{tot}}]}\hfill \\ & =\frac{{\mathit{\tau }}_1\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}+{\mathit{\tau }}_2\frac{[{\mathrm{L}}_2]}{K_{\mathrm{d}2}}}{1+(1+{\mathit{\tau }}_1)\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}+(1+{\mathit{\tau }}_2)\frac{[{\mathrm{L}}_2]}{K_{\mathrm{d}2}}}\hfill \end{array}$$ (A8)

Assuming that the efficacies are different enough (τ ₁ > τ ₂), the partial agonist L₂ can produce either concentration‐dependent activation (when L₁ concentrations are low compared to K _d1) or inactivation (when L₁ concentrations are high compared to K _d1) as illustrated by Figure A1 (see also (Song et al. 2014)). The same equation can be obtained with the formalism of the operational model – see eqs. 6.21 and 6.79 in (Kenakin, 2006). The fully general version of this equation for competing partial agonists can also incorporate a Hill slope, n (see Figure 10.15 and eq. 10.19 in Kenakin 2006):

$$E_{/E_{\max }}=\frac{{\mathit{\tau }}_1^n{\left(\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}\right)}^n+{\mathit{\tau }}_2^n{\left(\frac{[{\mathrm{L}}_2]}{K_{\mathrm{d}2}}\right)}^n}{{\left(1+\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}+\frac{[{\mathrm{L}}_2]}{K_{\mathrm{d}2}}\right)}^n+{\mathit{\tau }}_1^n{\left(\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}\right)}^n+{\mathit{\tau }}_2^n{\left(\frac{[{\mathrm{L}}_2]}{K_{d2}}\right)}^n}$$ (A9)

Competitive partial agonism with the present model

The same problem can be addressed in a similar manner within the formalism of the present model (assuming linear response, γ = 1, for now). If two ligands (L₁, L₂) of different affinities (K _d1, K _d2) and efficacies (ε ₁, ε ₂) are present simultaneously competing for binding at the same receptor, the situation can be summarized below with a slightly modified version of the one used before (eq. A6):

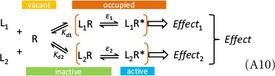
With linear response functions, the total effect can be obtained again as done previously. First, the total number (concentration) of receptors [R_tot] is written as:

$$\begin{array}{cc}\hfill [{\mathrm{R}}_{\mathrm{tot}}]& =[\mathrm{R}]+([{\mathrm{L}}_1\mathrm{R}]+[{\mathrm{L}}_1{\mathrm{R}}^{\ast }])+([{\mathrm{L}}_2\mathrm{R}]+[{\mathrm{L}}_2{\mathrm{R}}^{\ast }])\hfill \\ & =[\mathrm{R}]+\frac{[{\mathrm{L}}_1][\mathrm{R}]}{K_{\mathrm{d}1}}+\frac{[{\mathrm{L}}_2][\mathrm{R}]}{K_{\mathrm{d}2}}=[R]\left\{1+\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}+\frac{[{\mathrm{L}}_2]}{K_{\mathrm{d}2}}\right\}\hfill \end{array}$$ (A11)

Next, the total effect produced is expressed as a function of the [L₁] and [L₂] concentrations present using the assumptions that the effects E ₁ and E ₂ are proportional with the corresponding [L₁R*] and [L₂R*] concentrations:

$$E_{/E_{\max }}=\frac{[{\mathrm{L}}_1{\mathrm{R}}^{\ast }]+[{\mathrm{L}}_2{\mathrm{R}}^{\ast }]}{[{\mathrm{R}}_{\mathrm{tot}}]}=\frac{{\mathit{\epsilon }}_1\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}+{\mathit{\epsilon }}_2\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}2}}}{\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}+\frac{[{\mathrm{L}}_2]}{K_{\mathrm{d}2}}+1}$$ (A12)

This equation replaces eq. A8 of the previous model. As before, if the efficacies are different enough (ε ₁ > ε ₂), the partial agonist L₂ can produce either concentration‐dependent activation (when L₁ concentrations are low compared to K _d1) or inactivation (when L₁ concentrations are high compared to K _d1). A competitive agonist L₂ that produces no effect upon binding, ε ₂ = 0, acts as an antagonist I, and the above equation reproduces the well‐known Gaddum equation (eq. A2) for competitive antagonists (assuming L₁ is a full agonist, ε ₁ = 1, and [L₂] = [I]), which was not possible with the previous models.

$$E_{/E_{\max }}=\frac{\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}}{\frac{[{\mathrm{L}}_1]}{K_{\mathrm{d}1}}+\frac{[{\mathrm{L}}_2]}{K_{\mathrm{d}2}}+1}=\frac{[{\mathrm{L}}_1]}{[{\mathrm{L}}_1]+{\mathrm{K}}_{\mathrm{d}1}\left(1+\frac{[{\mathrm{L}}_2]}{K_{\mathrm{d}2}}\right)}$$ (A13)

Figure A1.

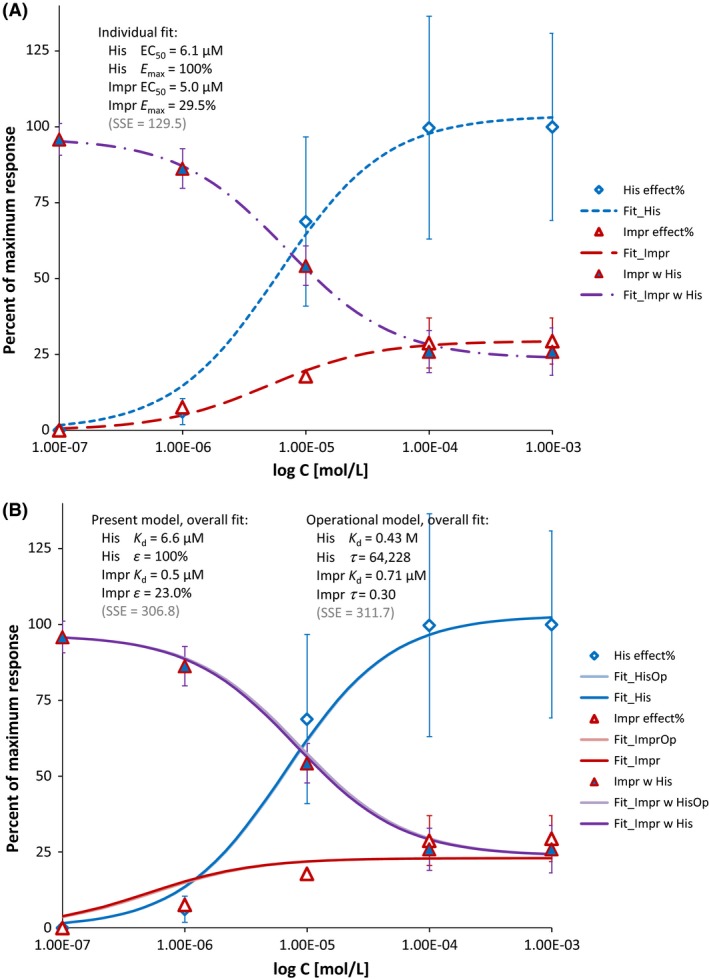
Illustration of full, partial, and competitive partial agonism with the often used example of histamine and impromidine, H2‐receptor agonist acting on isolated ventricular strips from human myocardium; data after (English et al. 1986). Concentration–responses shown are for histamine alone (blue symbols), impromidine alone (red symbols), and impromidine in the presence of a constant concentration (100 μmol/L) of histamine (purple symbols). As a partial agonist, impromidine alone can only produce a maximal response that is far less (~30%) than that obtainable with histamine, and when used in combination, it can displace the full agonist and actually produce a reduction in the overall response. Data were fitted with three individual curves separately using GraphPad Prism (A) and with a single set of parameters using the operational model (eq. 19 and 41) and the present model (eq. 31 and A12, assuming γ = 1 to avoid overparametrization and have the same number of parameters as the operational model) and (B). While the quality of fit in B is essentially identical with both models (overlapping light and dark lines; SSE values of 306.8 versus 311.7 as shown in the graphs), the parameter set of the operational model is quite meaningless especially for histamine (e.g., K _d = 0.43 mol/L due to the large value of τ obtained by fitting). In the meantime, fit of all three curves with the present model using a single set of parameters results in values (B) consistent with those from the individual fit (A).

Figure A2.

3D graphs illustrating the connection between ligand concentration [L] and effect E (purple curves) via the concentration of active ligand‐bound receptors [LR*] (blue curves) and the transduction (response) function generating the effect (red curves). (A) Simple single‐state (Clark) model with linear response and affinity only (K _d) as parameter; (B) operational (Black and Leff) model with high efficacy (high τ, low K _τ) similar to the one shown in the original publication introducing this model (Black and Leff 1983); (C) operational model with low efficacy (low τ, high K _τ; a case not illustrated in the original publication) – note that the response (red line) is below that of the linear one for much of the region and most of the hyperbolic response function is left unused; (D) present model with full agonist (ε = 1) and good amplification (γ >> 1); (E) present model with partial agonist (ε < 1) and low amplification (γ ≈ 1) – note that the response is always larger than the linear one and partial activation / effect is achieved via ε. With the present model, if all receptors are active ([LR*] = R_tot), the response always corresponds to E _max.

Figure A3.

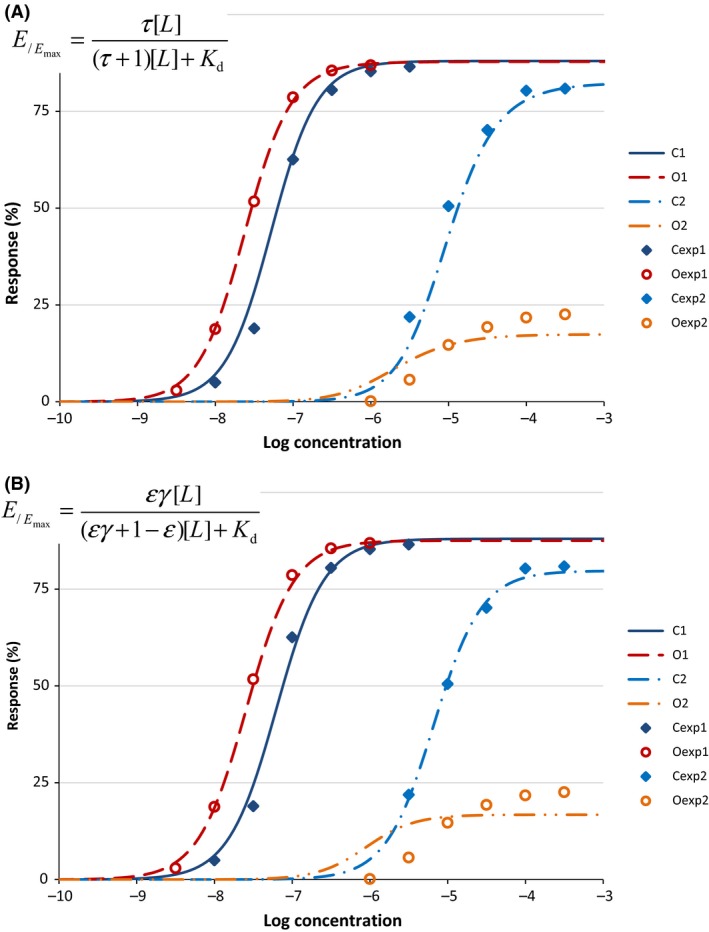
Fit of contraction data of guinea‐pig ileum through activation of muscarinic receptors with carbachol (filled blue diamonds) and oxotremorine (open red circles) in normal tissue (darker colors) and in the same tissue after controlled alkylation of the muscarinic receptor with 1 mmol/L phenoxy‐benzamine for 10 h followed by 2 h drug‐free wash (lighter colors). Data after (Kenakin and Christopoulos 2011) were fitted both with the operational model (A, top, eq. 19) and the present model (B, bottom, eq. 31). Fit requires the assumption that oxotremorine has higher receptor‐binding affinity, but lower efficacy than carbachol. Both gave essentially identical fits with a slightly better fit for the present model as judged by the sum of squared errors (SSE of 278 vs. 331) as well as by the Akaike Information Criteria, a more rigorous model selection criteria used to compare models that have different numbers of parameters (Buchwald 2007) (AIC of 143.4 vs. 145.4).

Table A1. Summary of all parameters used in the present paper

α	Proportionality factor between effect (response) and active receptors in linear models (e.g., Clark equation, eq. 7; minimal two‐state model, eq. 16)
ε	Efficacy parameter for the present model (eq. 28)
γ	Gain (amplification) parameter for the present model (γ = Rtot/K γ, eq. 29 and 30)
k 1, k –1	Rate of forward reaction or backward reaction (law of mass action, eq. 1, 2)
K d	Equilibrium dissociation constant of the receptor binding; defined by eq. 2 for Langmuir‐Hill and Clark equations, eq. 12 for minimal two‐state model, and eq. 23 for present model)
K γ	Constant for the hyperbolic response function of the present model (eq. 27)
K i	Equilibrium dissociation constant for an inhibitor (Gaddum equation, eq. A2)
K obs	Apparent (observed) K for the effect (response), that is, EC50
K τ	Constant for the hyperbolic response function of the operational model (eq. 18)
n	Hill slope (see eq. 10)
Rtot	Total maximum number (concentration) of receptors in the system.
τ	Efficacy parameter in the minimal two‐state model, τ (mtsm) = [LR*]/[LR] (eq. 13) and in the mathematically equivalent operational model, τ (om) = [Rtot]/K τ (eq. 19)

Buchwald P.. A three‐parameter two‐state model of receptor function that incorporates affinity, efficacy, and signal amplification. Pharma Res Per, 5(3), 2017, e00311, doi: 10.1002/prp2.311