Unsupervised classification of petroleum Certified Reference Materials and other fuels by chemometric analysis of gas chromatography-mass spectrometry data

Abstract

As feedstocks transition from conventional oil to unconventional petroleum sources and biomass, it will be necessary to determine whether a particular fuel or fuel blend is suitable for use in engines. Certifying a fuel as safe for use is time-consuming and expensive and must be performed for each new fuel. In principle, suitability of a fuel should be completely determined by its chemical composition. This composition can be probed through use of detailed analytical techniques such as gas chromatography-mass spectroscopy (GC-MS). In traditional analysis, chromatograms would be used to determine the details of the composition. In the approach taken in this paper, the chromatogram is assumed to be entirely representative of the composition of a fuel, and is used directly as the input to an algorithm in order to develop a model that is predictive of a fuel's suitability. When a new fuel is proposed for service, its suitability for any application could then be ascertained by using this model to compare its chromatogram with those of the fuels already known to be suitable for that application.

In this paper, we lay the mathematical and informatics groundwork for a predictive model of hydrocarbon properties. The objective of this work was to develop a reliable model for unsupervised classification of the hydrocarbons as a prelude to developing a predictive model of their engine-relevant physical and chemical properties. A set of hydrocarbons including biodiesel fuels, gasoline, highway and marine diesel fuels, and crude oils was collected and GC-MS profiles obtained. These profiles were then analyzed using multi-way principal components analysis (MPCA), principal factors analysis (PARAFAC), and a self-organizing map (SOM), which is a kind of artificial neural network. It was found that, while MPCA and PARAFAC were able to recover descriptive models of the fuels, their linear nature obscured some of the finer physical details due to the widely varying composition of the fuels. The SOM was able to find a descriptive classification model which has the potential for practical recognition and perhaps prediction of fuel properties.

1 Introduction

The development of alternative fuels has been identified by the United States Office of Science and Technology Policy (OSTP) as a critical need for the transportation industry [1]. It is expected that feedstocks for fuels will transition to some combination of conventional sources, unconventional sources such as tar sands and shale oil [2], and biomass [1]. The substances that are produced from refining these different feedstocks differ in their composition and therefore their suitability for use as fuel may not be known.

Determining whether a fuel is suitable for use in a particular application can be a lengthy and expensive process. This is especially true in aviation, due to the certification required by regulatory bodies such as the United States Federal Aviation Administration (FAA) [1]. In order to certify a new fuel for service, full-scale engine tests must be performed that can consume millions of liters of fuel. In principle, these tests must be conducted for each new fuel that is produced.

Use of technologies such as electric or hybrid powertrains may reduce or eliminate the need for exhaustive fuel certification. However, the OSTP does not anticipate that these technologies will be usable for aviation in the foreseeable future. Furthermore, the same pressures on the aviation industry also affect other transportation industries, even if to a lesser degree. Aviation is, therefore, well-placed to be an industry leader in alternative fuels research and applications.

The FAA has begun a program for new means of certification for alternative jet fuels called the National Jet Fuels Combustion Program [1]. One of the goals of this program is to develop computational models that can be used to certify fuels without the expense of the current process. This research program currently advocates the use of detailed, computationally expensive, numerical simulations to predict engine performance when using a proposed fuel.

In this paper, we propose a different approach: the use of an algorithm to predict performance based on a detailed physiochemical analysis of the fuel. A fuel's performance is in principle entirely determined by its composition, and that composition can be readily determined, or at least probed, by analysis methods such as nuclear magnetic resonance spectroscopy, mass spectrometry, and gas or liquid chromatography. Usually, the output from such an analysis is examined by an expert and then the features of the output are assigned to components of the mixture. In our approach, however, there is no need to identify and quantify each component. Instead, the raw or minimally-processed output from these analysis methods is used directly as an input to an algorithm, trained against a library of known fuels, that will predict the circumstances under which the fuel will be usable.

For the study presented here, a set of hydrocarbons including gasoline, kerosene, highway diesel fuel, marine diesel oil, and biodiesel fuel were collected. Gas chromatography coupled with mass spectrometry (GC-MS) was used to characterize the fuels and the resulting chromatogram was used as input to three chemometric algorithms in order to classify and group the fuels. It was found that the fuels fell into roughly three classes, which were the diesel fuels, kerosenes, and biodiesels. The model generated in this study could be used to determine the similarity of a new fuel to any of these three classes and therefore its suitability for these applications. As the library of suitable fuels grows, the power of the model to classify new substances will grow commensurately.

2 Methods

2.1 Chemometric methods for fuel analysis

GC-MS and its more sophisticated alternative, comprehensive two-dimensional gas chromatography coupled with time-of-flight mass spectrometry (GCxGC-TOFMS), have been the methods of choice for the analysis of fuels. The spectra generated contain a wealth of data about the composition of the fuel. Multivariate analysis methods can help to extract information from the GC-MS [3-6] and GCxGC-TOFMS [7-9] results, and these methods can be used for rapid analysis of fuels [10-13].

Due to the number of compounds present in most fuels and the limited capacity of the chromatographic columns, there is a tendency for GC-MS chromatograms to exhibit raised baseline humps known as unresolved complex mixtures (UCM). This effect has motivated the use of GCxGC-TOFMS for petroleum analysis [14-18]. GCxGC-TOFMS has its disadvantages, however. The instrumentation required is expensive and complex, limiting the number of facilities with access to it. Furthermore, the analysis of GCxGC-TOFMS data is not nearly as mature as GC-MS. Both methods, therefore, remain popular.

Several literature studies have used GC-MS and/or GCxGC-TOFMS as input to advanced analysis algorithms. Pierce and Schale [13] used partial least squares (PLS) to quantify the composition of blends of biodiesel and conventional diesel using GC-MS and GCxGC-TOFMS, discussing the advantage and disadvantage of each method of analysis. Johnson et al. [19] used multi-way chemometric tools to characterize fuel blends by GC-MS, obtaining qualitative and quantitative features for a series of diesel fuel and heavier heating oil blends. Parastar et al. [20] used GCxGC-TOFMS combined with chemometric methods to resolve and quantify mixtures of compounds such as polycyclic aromatic hydrocarbons (PAHs) in heavy fuel oil. Cramer et al. [21] used parallel factor analysis (PARAFAC) and GC-MS to develop an improved peak selection strategy to automatically detect minute compositional changes in fuels. Kehimkar et al. [22] and Freye, et al. [23] applied PLS to rocket kerosene data obtained using GCxGC-TOFMS and GCxGC coupled with flame ionization detection, respectively, to develop multivariate predictive models of fuel composition and engine-relevant fuel properties.

Others studies have used other chemometric techniques to analyze fuel. Dupuy et al. [24] used PCA and soft independent modeling of class analogy classification (SIMCA) combined with near infrared (NIR) spectroscopy to study heavy marine fuels. Pasquini and Bueno [25] used PLS and NIR spectroscopy to predict the true boiling point curve and to estimate the specific gravity of petroleum in refineries. Feng et al. [26] used the least square support vector machine (LS-SVM) and PLS, and NIR spectroscopy for analysis of six diesel fuel properties (i.e., boiling point, cetane number, density, freezing temperature, total aromatics, and viscosity). Yousefinejad et al. [27] classified three types of oil with the use chemometric methods and attenuated total reflectance fourier transform infrared (ATR-FTIR) spectroscopy. Da Silva et al. [28] used near infrared (NIR) and medium infared (MIR) spectra of distillation residue to classify gasoline as with or without additives using PLS, PCA, and linear discriminant analysis.

However, these studies have all relied on a small sets of samples that may not be readily obtainable by researchers wishing to repeat that work. To improve reproducibility, therefore, we would encourage the use of a standard library of fuel samples. Ideally, such a library would be composed of petroleum and unconventional Certified Reference Materials (CRMs) with well-characterized chemometric data. The set of substances used in this study do not necessarily represent such a library, but it is intended to show what such a library might look like.

2.2 Chemometric methods used in this paper

Chemometric methods such as those used in this paper are intended to aid in the analysis and visualization of complex data sets. In such data sets, the variation in the data can often be explained by a relatively few factors within the data space. This is expressed mathematically by the data existing in some low-dimensional subspace. Chemometric methods therefore are designed to find this subspace in order to make the data easier to interpret. In all cases, data with hundreds or thousands of variables are reduced to a few dimensions, usually two or three in order to aid human pattern recognition. The methods used in this study are multi-way principal components analysis (MPCA), parallel factor analysis (PARAFAC), and Kohonen's self-organizing map (SOM). MPCA and PARAFAC are linear classifiers, while SOM is a nonlinear classifier. Each method presents a different way of visualizing the data. MPCA determines those directions in the data space that are responsible for differences between the samples, but does not necessarily help assign physical interpretations to those differences. PARAFAC identifies physical components that are responsible for separating the samples, although these will not correspond to pure substances in this case due to the complexity of the hydrocarbon mixtures. SOM fits a low-dimensional manifold to the data that captures the most variability, but the manifold is nonlinear and therefore the results of the SOM are more difficult to interpret.

2.2.1 Multi-way principal components analysis (MPCA)

Principal components analysis [29] (PCA) reduces the dimensionality of complex data sets by identifying those directions in which the data have the greatest variance. The most common algorithm uses the singular value decomposition, which decomposes an observation matrix X into a set of scores T and loadings W such that T = XW. Each component of W will then describe one of the dimensions of the low-dimensional subspace and will be interpretable as, for instance, a chromatogram. Dimensionality is reduced by retaining only those L components of W that describe more than a certain amount of variance in the data, where L is strictly less than the rank of X.

PCA requires that the data be expressed as a two-way (alternatively, order two) array, meaning a matrix. In order to use PCA on data of higher order, the data must be recast into a two-way array. Employing PCA on such a recast array is multi-way PCA. As a three-way array, X has dimension I × J × K, so it must be unfolded into the two-way array X′ with dimension I × JK. For instance, the GC-MS data considered here are three-way arrays, where the first way represents differing profiles, the second represents the mass spectra, and the third is the elution times. Recast as a two-way array, the first way still represents the differing profiles, while the second has the mass spectra and chromatograms interleaved together. Each component of W, if it is suitably reshaped and added to the sample mean, can be interpreted as a GC-MS profile.

2.2.2 Parallel factor analysis (PARAFAC)

PARAFAC is a multidimensional analogue to PCA [30], decomposing the multiway observation array X into a set of matrices. In the three-way case, each element of X can be expressed in terms of three matrices A, B, and C as x_ijk = Σ_fa_ifb_jfc_kf , with appropriate generalizations to higher orders. The matrix A is of dimension I × F, B is J × F, and C is K × F, where F is the number of factors and is less than the minimum of I, J, and K. The matrices can then be interpreted as a scores matrix, a matrix corresponding to the chromatographic loadings and a matrix corresponding to the mass spectral loadings. The number of factors F in PARAFAC plays the same role as the number of components L in MPCA, and is strictly less than the rank of X.

PARAFAC has an additional advantage over PCA in that, because it is usually solved using a nonlinear optimizer such as alternating least squares, additional constraints can be added such as requiring that all components of A, B, and C be positive.

2.2.3 Kohonen's Self-Organizing Map (SOM)

A self-organizing map [31] is a type of neural network that will project the data into a two-dimensional space based on some notion of closeness. Each node is assigned to a physical location in the two-dimensional map and also to a location in the data space. As with all neural networks, the map is trained on the data using an iterative process. As the learning algorithm runs, each node that is already close to a sample in data space is moved closer to that sample, and nodes close in the map space to that node are moved with it. As long as there are more nodes in the map than there are samples in the training set, each sample will then be assigned to a neighborhood of nodes in the map. The proximity of any two samples on the map corresponds to how similar they are. The SOM has the ability to capture nonlinear relationships among the samples, because a straight line on the map may correspond to a convoluted and nonlinear path through the data space. As a result, however, distances on the map do not translate into distances in the data space except in a nonlinear and integrated sense. Essentially, flexibility is gained at the expense of ease of interpretation.

The nodes in the map can be described by an L × N grid, and each node has a point in the data space assigned to it, in this case a GC-MS profile. Therefore, the SOM can be described as a three-way array M, described by L × N × S elements, with any particular elements M_lns. Because the map represents two spaces, there are two distances that are meaningful between nodes. The first is the Euclidean distance d_E on the map, which for two nodes M_ln and M_op with locations (l,n) and (o,p) is just $d_{\mathrm{E}}^2\left({\mathbf{M}}_{\mathit{\text{ln}}},{\mathbf{M}}_{op}\right)={\left(l-o\right)}^2+{\left(n-p\right)}^2$. The other distance is the distance in the data space, which here we take to be the Hellinger distance, d_H, which for the same two nodes M_ln and M_op is defined as $d_H^2\left({\mathbf{M}}_{\mathit{\text{ln}}},{\mathbf{M}}_{op}\right)=1-\sum \sqrt{M_{\mathit{\text{lns}}}{M}_{\mathit{\text{ops}}}}$. Note that for this expression to be valid, the two spectra must each be normalized so that they sum to 1. The Hellinger distance is 0 if M_ln and M_op have equal values for each component and it is 1 if M_ln is zero everywhere M_op is positive and vice versa.

A SOM is usually interpreted in terms of its unified distance matrix or U-matrix U [32], which is a visual representation of the distance in data space between adjacent nodes on the map. Each element in U is defined as U_2i–1,2j = d_H(M_ij, M_i−1,j), U_2i,2j−1 = d_H (M_ij, M_i,j−1), and U_{2i−1,2j−1} = ½ d_H(M_i−1,j, M_i,j−1)+ ½ d_H(M_i,j, M_i−1,j−1). The even elements U_2i,2j are not defined [32], and here we define them to be the minimum of their eight adjacent elements.

2.3 Chemometric methodology used for the analysis of data

The methodology used in the paper is summarized in Fig. 1. The three-way data array is shown in Fig. 1a. MPCA is then used to determine scores (shown in Fig 1b) and loadings (in Fig. 1c). The results of MPCA are used for variable selection to reduce the computational complexity of the PARAFAC and SOM models, as shown in Figs. 1d (Stage II a) and 1f (Stage II b). Components with the highest loading are chosen for these models. PARAFAC is applied to the reduced data array and used to determine chromatographic loadings, mass spectral loadings, and PARAFAC scores, shown in Fig. 1e, and the SOM is used to generate the two-dimensional map, shown in Fig. 1g.

Figure 1.

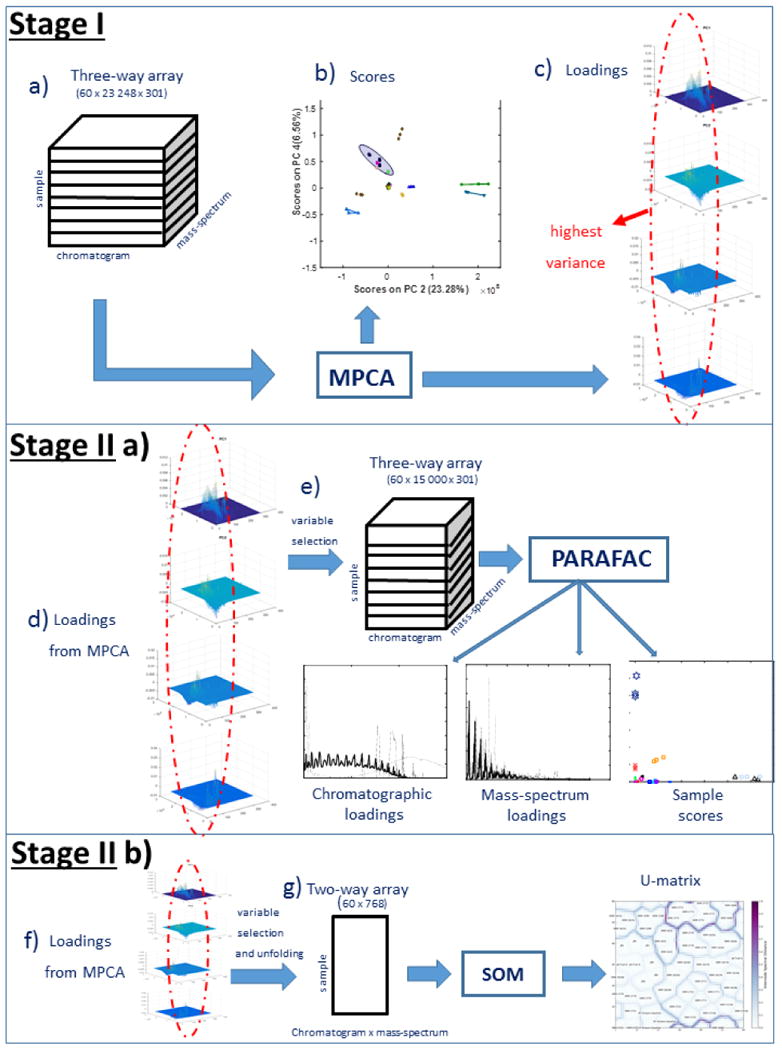
Schematic representation of the MPCA, PARAFAC, and SOM algorithms.

2.4 Experimental procedure

2.4.1 Samples and Materials

The National Institute of Standards and Technology (NIST) provides a number of petroleum-related Certified Reference Materials (CRMs) characterized for various constituents. CRMs provided by NIST are known as Standard Reference Materials (SRMs). Samples of a number of these SRMs were obtained. In addition, gasoline (87 octane) was purchased from a local service station, and three jet fuel samples were provided by the Air Force Research Laboratory. Table 1 lists the sample materials.

Table 1. List of materials analyzed in this study.

Name	Title	Description
SRM 1615	Gas Oil	*certificate not available*
SRM 1616b	Sulfur in Kerosene (Low-Level)	Special low sulfur kerosene (No.1-K) for nonflue-connected applica
SRM 1617b	Sulfur in Kerosene (High-Level)	High sulfur kerosene
SRM 1620c	Sulfur in Residual Fuel Oil (4 %)	Commercial “No. 6” residual fuel oil
SRM 1623c	Sulfur in Residual Fuel Oil (0.3 %)	Commercial “No. 4 (light)” residual fuel oil
SRM 1624d	Sulfur in Diesel Fuel Oil (0.4 %)	Commercial “No. 2 D” distillate fuel oil
SRM 1848	Lubricating Oil Additive	Additive used in manufacture of lubricating oil for gasoline engines
SRM 2299	Sulfur in Gasoline (Reformulated)	Commercial reformulated unleaded gasoline
SRM 2721	Crude Oil (Light-Sour)	Light-sour Texas crude oil
SRM 2722	Crude Oil (Heavy-Sweet)	Heavy-sweet Texas crude oil
SRM 2723b	Sulfur in Diesel Fuel Oil (10 mg/kg)	Commercial “No. 2 D” distillate fuel oil
SRM 2770	Sulfur in Diesel Fuel Oil (40 mg/kg)	Commercial “No. 2 D” distillate fuel oil
SRM 2771	Sulfur in Diesel Fuel Blend Stock	Commercial diesel fuel blend stock
SRM 2772	Biodiesel (Soy-Based)	Commercial 100 % biodiesel produced from soy
SRM 2773	Biodiesel (Animal-Based)	Commercial 100 % biodiesel produced from animal products
SRM 2779	Gulf of Mexico Crude Oil	Collected from 2010 Deepwater Horizon oil site
Gasoline		Commercial 87-octane gasoline sold in 2015
Jet A		Jet fuel from Air Force Research Laboratory (AFRL)
JP5		Jet fuel from AFRL
JP8		Jet fuel from AFRL

SRM 1494 Aliphatic Hydrocarbons in 2,2,4-Trimethylpentane and SRM 2269 Perdeuterated PAH I Solution in Hexane/Toluene were used as internal controls. HPLC grade hexane was used as sample diluent.

2.4.2 Sample preparation

The petroleum samples and SRM 1494 were diluted as follows: 2 mL of hexane, 100 μL of SRM 2269, and 100 μL of the petroleum sample were volumetrically transferred to 4 mL amber vials and sealed. Approximately 1.5 mL of each mixture was then transferred to individual amber autosampler vials for analysis. One vial was prepared for each fuel sample.

2.4.3 GC-MS analysis

The GC-MS analysis was performed using a 0.25 mm (id) × 60 m DB-17MS column (50 % phenylmethylpolysiloxane, 0.25 μm film, [17] (Agilent Technologies, Wilmington, DE). The column was held isothermally at 60 °C for 1 min, ramped at 45 °C per min to 100 °C, held for 10 min, then ramped at 2 °C per min to 290 °C and held for 60 min. All injections were done on-column (1 μL) with helium as the carrier gas at a constant flow rate of 1.2 mL/min. The injection port temperature was held in an oven-track mode (3 °C above the oven temperature), and the auxiliary line temperature was held at 290 °C. Following an 8 min solvent delay, the MS scanned from 50 u to 350 u at 2.48 scans per second with the electron multiplier voltage set to 2000.

SRM 1494 (diluted as described above with SRM 2269 and hexane) was the first sample run to obtain retention times for the aliphatic compounds present in that SRM and for the deuterated compounds present in SRM 2269. Each fuel sample was run in triplicate with one run of hexane after each fuel sample to ensure that there was no carryover.

2.4.4 GC-MS data processing

The retention time for fluoranthene-d₁₂ (one of the components in SRM 2269) was used to check for any retention time shifting over the course of the runs, and the peak area based on the integration of ion 212 was used to assess the dilution of the samples. The retention time and peak area for this deuterated compound remained fairly constant (within 5 %) over the days that it took to run all of the petroleum samples. The Agilent data system was used to generate text files containing retention time, scan, and signal information used in the predictive schemes. Prior to creating the arrays, automated peak integrations were checked and corrected manually to baseline.

2.5 Data analysis and data construction

The data was arranged as a three-way array with dimension 60 × 23248 × 301, for the samples, GC elution times, and mass spectra respectively. This three-way array was then analyzed using a MPCA and PARAFAC models. For the SOM, to reduce computational complexity, principal components analysis was used to reduce the number of active data elements. More details of this selection process can be found in Section 3.3. This results in a two-way array with dimension 60 × 768.

For the construction of the MPCA and PARAFAC models, the PLS toolbox version 3.51 (Eigenvector Research, Manson, WA) was used, running in MATLAB R2015b. Construction of the SOM was performed with the PyMVPA 2.4.2 package, running in Anaconda 4.0.0 with Python 2.7.11. No preprocessing was used beyond the peak alignment verification and manual baseline correction described in Section 2.4.4.

3 Results and Discussion

This study focused on using GC-MS data for the analysis of a wide range of petroleum-based fuels (Table 1) as well as two biodiesels. As suggested in the study by Hupp et al [33], alignment of the chromatograms was checked using the retention time of fluoranthene-d12, a component in SRM 2269 which was added to all samples.

3.1 Multi-way principal components analysis (MPCA)

The data were loaded into PLS-toolbox software as a 23,248 × 301 × 60 array, representing the 23,248 elution times, the 301 masses in the mass spectra, and the 60 samples (20 samples each run in triplicate). For the construction of the MPCA model, the number of principal components was chosen to capture more than 80% of the explained variance [29]. Other methods have been proposed, but generally do not give very different results [29, 34-41].

The samples fall into two superclasses, which essentially splits the biofuels from the petroleum-derived substances. This split is shown in Fig. 2a, which plots the samples with respect to the first three principal components. The confidence ellipse [42] represents the 95% confidence limit for the petroleum class based on the Hotelling T² [43, 44] distance. These substances lie essentially on a two-dimensional surface within this three-dimensional PCA space, and the two biofuels lie along a line extending perpendicularly from this surface. This separation makes chemical sense because biofuels tend to have a relatively invariant composition (composed primarily of fatty acid methyl esters), as compared to petroleum derivatives which can vary significantly depending on the source of the petroleum.

Figure 2.

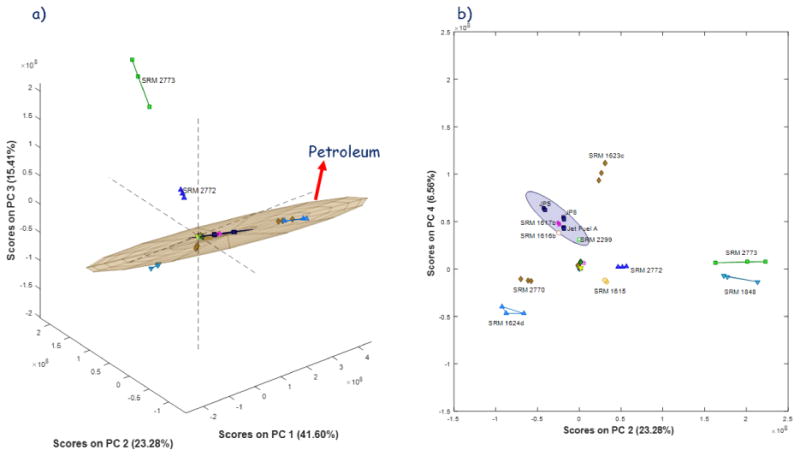
(a) Multiway principal component scores for the first three principal components. The tan region is the ellipse of confidence for the petroleum fuels. (b) MPCA scores for the second and fourth principal components. The grey region is the ellipse of confidence for the jet and kerosene fuels.

Within the petroleum superclass, the jet fuels (JP8, JP5 and Jet Fuel A) can be readily identified as a subclass, as shown in Fig. 2b. This figure shows the score plot using the second and fourth principal components. In the figure, the jet fuels can be seen as a tightly-bundled group surrounded by the ellipse of confidence. In addition to the jet fuels, SRM 1617b, SRM 1616b, and SRM 2299 fall within the ellipse of confidence. This grouping again makes sense because SRM 1616b and SRM 1617b are kerosenes, composed primarily of aliphatics in the C12 to C15 range, and the jet fuels are kerosene-based fuels [45] and consist mostly of aliphatic and aromatic hydrocarbons ranging from C8 to C17 or greater [45]. SRM 2299 is a gasoline composed of short aliphatics from C7 through C11, which is most similar to the jet fuel subclass.

Another point of interest is the proximity of SRM 2770 and SRM 1624d in principal component space. These substances are both diesel fuels with varying amounts of sulfur. SRM 2770 was made by mixing SRM 1624d and SRM 2723a [46-48] to achieve a target sulfur concentration. Thus, the chemical and physical properties of the SRM 2770 are similar to chemical and physical properties of these two substances. It should be noted that SRM 2723a was not available for the GC-MS analysis because it had been superseded by SRM 2723b [49]. If a sample of SRM 2723a had been available, it is likely that the three substances would have fallen essentially on a line. However, SRM 2723b is in the grouping of samples near the origin in the loadings plot in Fig. 2b, suggesting that it is less related to SRMs 1624d and 2770 than might be predicted. All four of these substances are labelled as No. 2 diesel fuels, but this definition is based on physical properties, such as viscosity, flash point, and cetane index, rather than composition [50]. The differences in the classifications highlights the potentially wide chemical variation among petroleum fuels.

3.2 Parallel factor analysis (PARAFAC) model

A limitation of the MPCA model is that the loadings do not have an easy interpretation in terms of chromatographic and mass profiles. The PARAFAC algorithm was designed to generate a model that would have a more straightforward physical interpretation. In principle, PARAFAC would be able to extract GS-MS profiles for the pure components that make up the mixtures, although the complex nature of petroleum distillates makes this ideal state impossible. Even so, PARAFAC is able to isolate a set of basis components, even if that basis set does not actually correspond to a pure substance.

The speed of the algorithm scales poorly with the size of the data matrix and so any amount of variable reduction will have great benefits in computational time. Here, the loadings obtained by the MPCA model, which can be found in Supporting Information Fig. S1, were used for selection of variables. The first four principal components are plotted; there is little information present at elution times greater than about 100 minutes. Removing these elements allowed an increase in computational speed for the construction of the PARAFAC model.

The PARAFAC model was generated using PLS-toolbox. Non-negativity constraints were imposed in the three PARAFAC dimensions, since the true GC-MS values should be strictly positive. A convergence criteria value of 10⁻⁶ and a maximum number of 10000 iterations were used.

According to Skov and Bro [51], PARAFAC will provide a unique solution, but only when the proper number of factors is determined will the unique solution be chemically meaningful. Thus, this step is fundamental to the construction of the model [30]. Various methods are proposed for this choice [52-55]. In this work, the core consistency (CORCONDIA) test [53-55] was used for determining the number of factors, along with heuristics based on chemical knowledge about the problem. The CORCONDIA test provides information about degeneracy between factors, that is, whether two or more factors may be fitting the same feature which would be better described using only one factor. Heuristics must then be applied to determine whether the potential loss of uniqueness in the model is worth the additional degrees of freedom. The core consistencies and the explained variances of the models are seen in Table 2, and a four-factor model was chosen as best representative of this dataset. The core consistency of 99.0% for this model indicates there is no degeneracy in the recovered fuel classes. When five or six factors were used for model building, more than one fuel class was described by the same factor revealing degeneracy in the recovered factors.

Table 2. Core consistencies and the explained variances of the PARAFAC models.

Factors	CORE consistency	Explained variance (%)
1	100	37.9
2	100	42.8
3	100	71.7
4	99	76.6
5	94	80.9
6	81	82.2
7	25	86.3
8	0	86.7

The PARAFAC model divides the substances in a similar manner as the MPCA model. Fig. 3 shows the score plot with respect to the 2^nd through 4^th factors in the PARAFAC model. As was the case for the MPCA model, the biofuel SRMs 2772 and 2773 are separated from the other substances along the 3^rd factor. SRM 1848, which is an additive to lubricating oil, is separated from the other substances along the 2^nd factor. SRM 1623c, a heavy fuel oil, is separated along the 4^th factor, as are the jet fuels and the gasoline SRM 2299. Most other substances lie near the origin of this plot, meaning they are not represented by these three factors.

Figure 3.

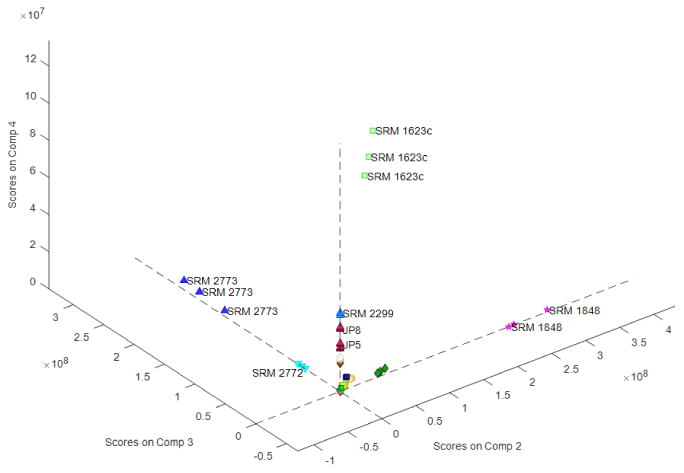
PARAFAC scores for the 2nd through 4th factors in the four-factor PARAFAC model.

In order to show how well the PARAFAC model actually captures these substances, Fig. 4 shows the chromatographic loadings for 2^nd through 4^th factors obtained by the PARAFAC model with experimental chromatograms for SRM 1848, SRM 2773, and SRM 1623c. The corresponding mass spectral loadings are shown in Fig. S2. The results were normalized by the maximum value. The experimental results shown in the figure are the total ion chromatograms averaged over the three replicates for a particular substance. As a measure of goodness-of-fit, the similarity was calculated between the experimental elution profiles and the calculated loading for each factor, as recommended by Amigo et al.[56]. This was calculated as follows:

Figure 4.

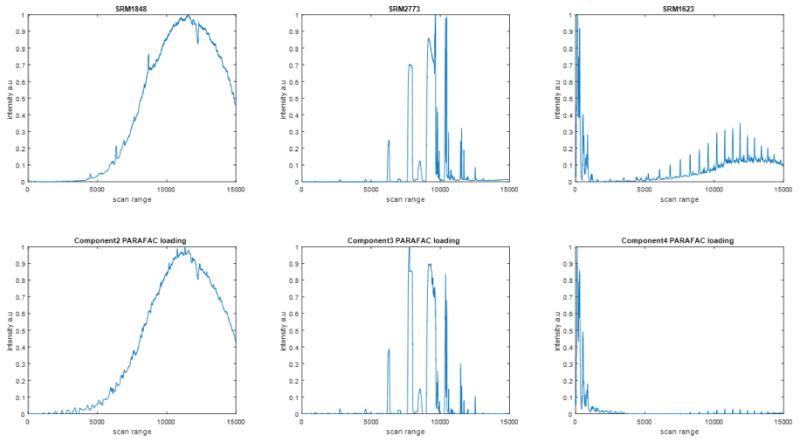
Chromatographic loadings for the 2nd through 4th factors in the four-factor PARAFAC model compared with total ion chromatograms for substances that are representative class members.

$$\mathit{\text{fit}}(\%)=100\times \left(1-\sqrt{\frac{\sum {\left(x_i-\widehat{x_l}\right)}^2}{\sum x_i^2}}\right)$$

where x_i corresponds to the ion intensity and $\widehat{x_l}$ corresponds to the corresponding loading. SRM 1848 showed similarity of 92.9%. SRM 2773 and SRM 1623c showed similarity of 83.3% and 81.4%, respectively. In the case of SRM 1623c, only that part of the chromatogram from 0 to about 80 minutes of elution time was used because there is a deviation from the baseline in the experimental response at longer elution times. The PARAFAC model developed was able to properly capture the chromatographic profile for these three classes.

Since the 2^nd through 4^th PARAFAC factors essentially describe singleton classes. the first PARAFAC component must therefore describe the remaining samples. To help determine whether this is the case, the scores with respect to the first PARAFAC factor for each sample are shown in Fig. 5. The first factor is responsible for the separation of SRM 2770 and SRM 1624d from the other substances. The total ion chromatograms for these substances are shown in Fig. 6, along with the PARAFAC loading for the first factor. Mass spectral loadings are shown in Fig. S3. The loading is constructed from essentially a combination of these two chromatograms, which explains why these two substances have the similar scores for this factor. Again, this result is not terribly surprising, due to the similarities between these two substances as discussed in Section 3.1.

Figure 5.

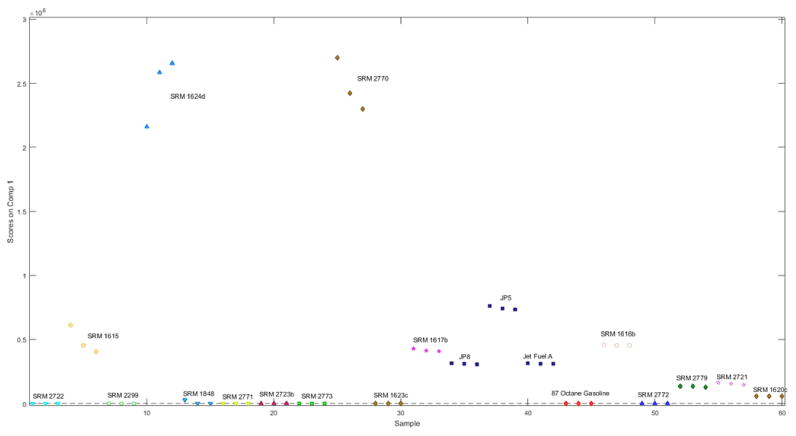
PARAFAC scores for the first factor in the four-factor PARAFAC model.

Figure 6.

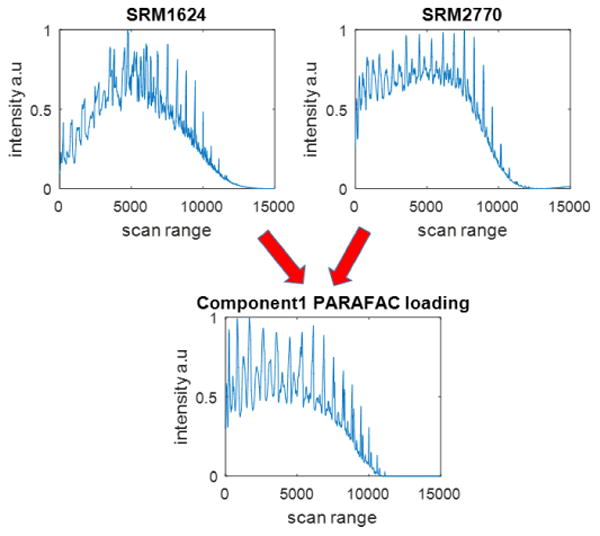
Chromatographic loadings for the first factor in the four-factor PARAFAC model compared with the total ion chromatograms for SRM 2770 and SRM 1624d.

It should be noted, however, that the four PARAFAC components fail to describe most of the substances in the sample set. At first examination, this would appear to be due to underfitting the model, which could be solved by adding more factors. However, as discussed earlier in this section, adding more factors does not add to the model's predictive ability. The loadings for the six-factor are shown in Fig. S4. The fifth factor describes the kerosenes and jet fuels, which was not recovered in the four-factor model, but the sixth factor begins to describe fine differences between the biodiesels. Many samples such as the gasolines and diesels are not recovered even by the six-factor model.

The mass-spectrum loadings obtained by the PARAFAC model can be found in Supporting Information Figs. S2 and S3.

3.3 Kohonen's Self-Organizing Map (SOM)

As mentioned earlier, the MPCA and PARAFAC are linear classifiers, whereas the SOM is a nonlinear classifier that will capture a low-dimensional manifold representing the fuel samples. After the algorithm is complete, the map will represent, albeit in an abstract way, the manifold on which the samples lie.

Using the full data set, each node in the network has, in principle, a complete chromatogram assigned to it, meaning that the self-organizing map will require approximately seven million scalars per node times the number of nodes in the map. In order to reduce the computational complexity, the data space is first reduced using the results from an MPCA model. In this case, the MPCA model is constructed using 10 components and the GC-MS component with the greatest loading is found. Those GC-MS components with loadings greater than 30% of the maximum are selected as active. This reduces each chromatogram from seven million scalars to 786. In this study, the map was chosen to be 60 by 60 nodes, with an initial radius of 60 and a learning rate of 0.5.

The U-matrix for the SOM is shown in Fig. 7a, where the separation among the classes can be seen. This plot shows the distance in the chromatographic space between adjacent nodes and also shows the location of the training samples on the map. Because there are many more nodes in the map than there are samples, each sample is assigned to its own region of the map where each node is very similar to it. The borders between the regions are darker or lighter depending on how different are the samples associated with the regions.

Figure 7.

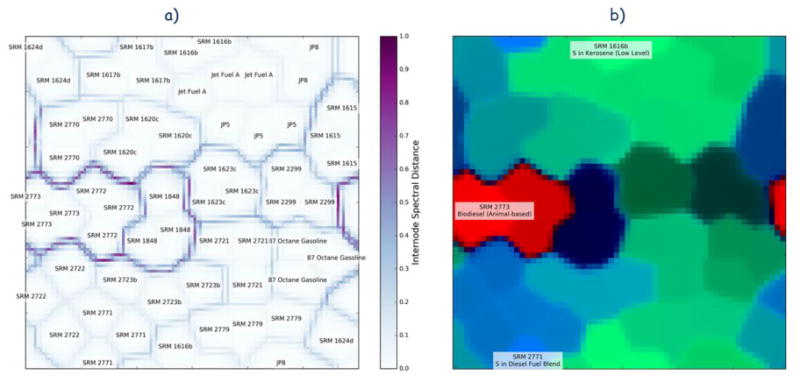
(a) Unified distance matrix for the self-organizing map, with corresponding locations for the sixty samples. (b) False-color map of Hellinger distances from each node to various samples on the map. The red channel corresponds to map nodes closer to SRM 2273, the green channel to SRM 2771, and the blue channel to SRM 1616b. Therefore, nodes that are more red, for instance, will be closer in data space to SRM 2273 and therefore be representative of biodiesels.

As with the other separation models, the biodiesel samples (SRMs 2772 and 2773) are strongly separated from the other samples by the SOM, as evidenced by the dark border that separates their associated region of the map from the rest. In addition, the motor oil additive SRM 1848 is strongly separated into another group. The remaining samples fall into one large group, which is essentially petroleum-derived fuels, with a weak separation between the diesel fuels and kerosene fuels.

To further elucidate these broad categories, we plot the Hellinger distance to every point in the map from three samples in a false-color image in Fig. 7b. The samples are SRM 2273, which is taken to be representative of the biodiesels, SRM 2771 of the kerosenes, and SRM 1616b of the diesels. In this image, the separation among the classes is quite visible, with the biodiesels starkly separated from petroleum fuels and the kerosenes clearly distinct from the diesels. SRM 1848 forms an additional group separate from these three, and the gasolines form a subgroup that is related to, but not entirely the same as, the kerosenes.

The purpose of using a dimensional reduction technique such as MPCA, PARAFAC, or SOM is that the data are presumed to lie on some low-dimensional manifold within the data space. PCA and PARAFAC require that this manifold be linear. If the manifold is not linear, then projections into the PCA or PARAFAC space will not be able to identify patterns and the reduction is unlikely to reveal additional information. For instance, the PARAFAC model discussed in Section 3.2 does not adequately describe many of the fuels, and simply increasing the degrees of freedom available to the model cannot allow it to do so. As discussed in Section 2.3, the SOM fits a manifold to the data that is locally two-dimensional but is able to capture arbitrary structure in the data.

4 Conclusion

A set of petroleum-derived fuels and biofuels were analyzed using gas chromatography coupled with mass spectrometry (GC-MS). The resulting GC-MS chromatograms were analyzed using unsupervised classification algorithms, in particular multiway principal components analysis (MPCA), principal factors analysis (PARAFAC), and a self-organizing map (SOM). All of the classification algorithms were able to generate models that were able to differentiate among the various fuels. In addition, chemically meaningful chromatographic and mass spectral profiles were extracted by PARAFAC.

MPCA and PARAFAC are linear classifiers, while SOM is a nonlinear classifier. Due to the complex nature of the petroleum fuels, the linear classifiers proved to have some difficulty in generating a meaningful separation model. Some of the physical characteristics relevant to the distinction among the fuels proved to be obscured. The SOM, being nonlinear, proved highly able at generating a separation model. However, this flexibility comes at the cost of the model being more difficult to interpret than the linear models.

The results show that GC-MS combined with unsupervised chemometric analysis can be a powerful tool to solve similar analytical problems in which complex mixtures consisting of several hundreds of compounds need to be differentiated through pattern recognition. Furthermore, the combination of GC-MS and chemometric analysis can be employed as a general tool for the differentiation of petroleum-derived and other fuels.

Disclaimer

Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.

Supplementary Material

Figure S1. Principal components loadings for the first four principal components of the MPCA model. The red cylinder indicates those variables that have high loadings in these four principal components. These variables are those which are used for variable selection for the PARAFAC model.

Figure S2. Mass spectral loadings for the 2nd through 4th factors in the four-factor PARAFAC model compared with mass spectra for substances that are representative class members.

Figure S3. Mass spectral loadings for the first factor in the four-factor PARAFAC model compared with the total ion chromatograms for SRM 2770 and SRM 1624d.

Figure S4. PARAFAC scores for the all factors in the six-factor PARAFAC model.