Extension and validation of the GLYCAM force field parameters for modeling glycosaminoglycans

Abstract

Glycosaminoglycans (GAGs) are an important class of carbohydrates that serve critical roles in blood clotting, tissue repair, cell migration and adhesion, and lubrication. The variable sulfation pattern and iduronate ring conformations in GAGs influence their polymeric structure and nature of interaction. This study characterizes several heparin-like GAG disaccharides and tetrasaccharides using NMR and molecular dynamics simulations to assist in the development of parameters for GAGs within the GLYCAM06 force field. The force field additions include parameters and charges for a transferable sulfate group for O- and N-sulfation, neutral (COOH) forms of iduronic and glucuronic acid, and Δ4,5-unsaturated uronate (ΔUA) residues. ΔUA residues frequently arise from the enzymatic digestion of heparin and heparin sulfate. Simulations of disaccharides containing ΔUA reveal that the presence of sulfation on this residue alters the relative populations of ¹H₂ and ²H₁ ring conformations. Simulations of heparin tetrasaccharides containing N-sulfation in place of N-acetylation on glucosamine residues influence the ring conformations of adjacent iduronate residues.

Introduction

Glycosaminoglycans (GAGs) are linear polysaccharides, generally found covalently attached to proteins, forming a protein class called proteoglycans that are widely present on the plasma membrane, in the extracellular matrix, and in secretory granules of all animal cells.¹ GAGs can be classified into five main categories based on the unique composition of the polysaccharide: hyaluronan (HA), heparin/heparan sulfate (HS), chondroitin sulfate (CS), dermatan sulfate (DS), and keratan sulfate (KS). The polysaccharides are typically composed of repeating units of a hexosamine – uronic acid disaccharide. The hexosamine may be an N-sulfated or an N-acetylated glucosamine (HS, HS, and KS) or galactosamine (CA and DS), variably O-sulfated at the 3, 4, and (or) 6 positions. The uronic acid may be a glucuronic acid or an iduronic acid formed as a result of enzymatic epimerization of a glucuronic acid at the C-5 position. These uronic acid moieties may also be 2-O-sulfated. KS lacks uronic acids and instead contains variably sulfated galactose residues, and while most GAGs have a heterogeneous pattern of sulfation, HA is an unsulfated GAG.² GAG–protein interactions are critical in biological processes such as cell adhesion, anticoagulation, regulation of cell growth and proliferation, immobilization of proteins, maintenance of protein concentration gradient in regions of inflammation, viral invasion, and tumor metastasis.^2–8 Each tissue produces a distinctive repertoire of GAGs that interact with proteins in a tissue-specific manner. Most GAG-binding proteins interact with heparin³ because due to structural similarity, it mimics the interaction of these proteins with the widely abundant cell surface HS chains.

GAG sulfation patterns have been demonstrated to modulate biological function, for example in the cases of heparan sulfate in growth factor activation and cellular defense,^5,9 CS growth factor recognition,¹⁰ and synthetic HS in anticoagulant activity.¹¹ Differences in the sulfation pattern also alter the mode of interaction of heparin oligosaccharides with proteins, such as CCL5, where they have been shown to interact selectively with certain residues depending on the degree and pattern of sulfation.¹² This property consequently alters their ability to inhibit the interaction of CCL5 to its receptor CCR1. These sulfation patterns, in addition to altering the charge, also impact the 3D structure of GAG fragments. Nuclear magnetic resonance (NMR) spectroscopy of GAG fragments has shown that sulfation patterns can alter the ring conformations of IdoA^13–15 and nonreducing terminal Δ4,5-unsaturated uronates (ΔUA)^16–18 that typically result from use of bacterial heparin lyase to cleave GAGs. Unsaturated uronate residues are often present in GAG–protein crystal structures and in GAG fragments employed in experimental binding studies. Recently published simulations of HS GAGs have shown that IdoA ring flipping can have a significant impact on the 3D shape of the GAG polymer;¹⁹ however, as noted earlier,²⁰ not all differences in ring puckering lead to an altered overall shape.²¹

The variable levels and patterns of sulfation make the structural analysis of GAGs a challenge. This often limits experimental characterization of GAG structures to composition-based analyses of digested fragments of native GAGs. More detailed analysis, such as by NMR or crystallography, usually employ short, isolated, or synthetic oligomers, where the sulfation patterns are well controlled. Theoretical methods like molecular dynamics (MD) simulations have been widely used^22–24 to augment experimental methods in studying the conformational and binding properties of biomolecules, and the development of an accurate force field is key to the accuracy of these simulations. Molecular simulations employing a consistent and validated force field not only provide a basis for interpreting experimental NMR data but also enable structural analysis of polymers that are either too large for NMR analysis or too complex for routine synthetic preparation. Previously, existing carbohydrate force fields have been augmented in an ad hoc manner for examining specific sulfation patterns²⁵ and only recently have parameters been developed for transferable sulfate moieties.²⁶ In this work, we add two key features to the GLYCAM force field to enable accurate MD simulations of sulfated GAG sequences with AMBER.²⁷ The first addition is the creation of a generalizable sulfate parameter set to model N- and O-sulfation, including new bond, angle, and torsion terms as well as partial atomic charges, consistent with existing GLYCAM partial atomic charges.^28–30 The second is the development of force field parameters for ΔUA residues, which will permit simulation of this nonnaturally occurring residue. In addition, parameters for neutral (NH₂) and protonated (NH₃⁺) glucosamine and protonated glucuronic and iduronic acids have been included.

To test the performance of the new parameters set, MD simulations were performed on variably sulfated GAG disaccharides containing ΔUA residues, and NMR scalar coupling and NOE measurements were collected for comparison with the theoretical data. MD and NMR data were collected for two synthetic GAG tetrasaccharides, with the aim of confirming the accuracy of the MD simulations and examining any influence of sulfation pattern on GAG conformation. The analysis presented here demonstrates that the new force field parameters reproduce the NMR data for a number of GAG fragments, both with and without terminal ΔUA. The simulations confirm the previous observation¹³ that the IdoA ring populates two conformations (¹C₄ 63% and ²S_O 37%) and surprisingly indicate that the terminal GlcA ring does not exclusively adopt the expected ⁴C₁ conformation.

Methods

NMR

NMR spectroscopy was carried out on a spectrometer operating at 18.8 T for disaccharides and 14.0 T for tetrasaccharides, equipped with a Varian Inova console and a 5 mm cryogenically cooled probe. 2,2-Dimethyl-2-silapentane-5-sulfonate (DSS) was included as an internal reference in each sample. NMR samples consisted of 0.5 mg of disaccharide in 100% D₂O buffer containing 20 mmol/L sodium phosphate and 1 mmol/L DSS, pH 6.5. The sample was shimmed to a DSS linewidth of <1 Hz. Proton resonances were assigned using a standard COSY experiment (Varian ChemPack), processed with NMRpipe³¹ and assigned in Sparky.³² 3J-coupling measurements were made from a 1D proton experiment with presaturation to suppress the signal due to any residual H₂O, collected with a spectral width of 9000 Hz and 32k points, processed, and analyzed in MestReNova.

Nuclear Overhauser effects (NOEs) were measured using a standard 2D NOESY experiment (Varian ChemPack) with a mixing time of 0.4 s, 512 increments, and 9000 points for disaccharides and 0.3 s, 512 increments, and 6000 points for tetrasaccharides, processed with NMRpipe. NOE peaks were integrated in NMRViewJ³³ and the distance was calibrated using the distance from the MD simulations between either the H1^B and H2^B or the H2^B and H3^B protons on the disaccharide reducing terminal residue (residue B) for 1–5. Tetrasaccharides 6 and 7 were calibrated using the distance from the MD simulations between the H1 and H5 protons on the glucuronate (residue C), which was shown to be insensitive to fluctuations in ring conformations during the simulations.

Calculation of theoretical NMR properties

Theoretical NOEs were calculated using the isolated spin-pair approximation³⁴ in which NOE intensity is assumed to be proportional to 1/R⁶, where R is the distance between the two spin pairs. Based on previous NMR studies of GAG fragments, it can be assumed that the tetrasaccharides tumble isotropically.^35,36 Three-bond proton–proton scalar couplings (³J_HH) were calculated using a Karplus-like equation developed by Haasnoot et al.³⁷ using the electronegativity values identified by Altona et al.³⁸ (eq. S4.1 and Table S4.3) (see Supplementary material section). Where relevant, experimental ³J_HH couplings were decomposed into populations by least-squares fitting of the contributions from theoretical J values computed for each individual state.³⁹

Molecular mechanics calculations

The SANDER program from the AMBER11 software package was used to compute the molecular mechanic energies associated with the parameter development. None of the one to four nonbonded interactions were scaled, and torsions were restrained at their desired values with a restraint weight of 5000 kcal/mol·rad². A 12 Å cutoff for nonbonded interactions was applied.

MD simulations

Initial structures for performing the MD simulations of the methyl glycosides for ensemble-averaged charge calculation were obtained from quantum mechanics (QM) optimized models. Solutes were solvated with explicit TIP3P waters⁴⁰ with at least a 12 Å buffer between the glycan solute and each edge of the solvated cubic box using the LEaP module of AMER12.²⁷ Counterions were used to neutralize the net charge of each system. Energy minimization was performed under nVT conditions (500 steps steepest descent followed by 24 500 steps of conjugate-gradient minimization). Each system was then heated under nPT conditions for 50 ps, raising the temperature from 0 to 300 K, followed by 100 ps of equilibration while the temperature was maintained at 300 K. All simulations used periodic boundary conditions where the pressure was maintained at 1.0 atm, the external dielectric was set to 1.0, and the system compressibility was set to that of water. The Berendsen thermostat⁴¹ was used for all temperature controls and the SHAKE algorithm⁴² was used to constrain bonds with hydrogens, allowing a 2 fs timestep to be used. Nonbonded scaling factors were set to unity, and a 10.0 Å nonbonded cutoff was employed in all steps. Minimization and equilibration were performed using the PMEMD⁴³ implementation for CPU in AMBER12. Subsequently, production simulations were performed with the PMEMD-Cuda⁴³ implementation for GPUs.

The simulations of heparin disaccharides 1–5 and tetrasaccharides 6 and 7 were performed using a similar protocol, except for the minimization steps. The first minimization step was performed in generalized Born implicit solvent⁴⁴ with an infinite nonbonded cutoff, prior to addition of counterions and explicit solvent. A second minimization step was performed after each system was explicitly solvated and neutralized.

QM calculations

All QM calculations were performed using the Gaussian 09⁴⁵ software package.

Parameter development (partial charges)

Partial atomic charges were derived from the restrained electrostatic potential (RESP) charge fitting methodology.⁴⁶ The ESPs for the small molecules employed in parameter development were computed from the lowest energy conformational state at the HF/cc-pVTZ level of theory with a RESP weight of 0.0005. For anionic monosaccharides, ESPs were computed with diffuse functions at the HF/6-31++G**//HF/6-31++G** level, whereas for neutral and cationic monosaccharides, calculations were performed at the HF/6-31G*//HF/6-31G* level; in each case, a RESP weight of 0.01 was employed to be compatible with GLYCAM06.

Charge models for N- and O-sulfates, glucosamine, and ΔUA were developed using the standard GLYCAM ensemble-averaged charge method.²⁸ The charges were developed for sulfates using 4-O- and 6-O-sulfated β-d-GalNAc and both anomers of N-sulfated α- and β-d-glucosamine (d-GlcNS) using initial glycan geometries extracted from co-crystallized protein–sugar complexes. For the ensemble-averaged charge calculation, an initial QM-optimized structure was used to derive single-point RESP charges and employed for 10–50 ns of MD simulations, as required, for adequate sampling of exocyclic rotamers. From the simulations, 100 evenly spaced snapshots were extracted as a representative ensemble of the 3D structures. Each of these geometries was subjected to QM optimization with all torsion angles frozen in their MD conformation. RESP charges were calculated for each frame and averaged to get the ensemble-averaged charge set for each particular molecule.

The computed charges for the sulfate moieties (SO₃⁻) in both N- and O-sulfates were within statistical variance of each other, allowing the creation of an interchangeable sulfate residue. Examination of the sulfated sugars revealed similar atomic charges on the sulfated and nonsulfated atoms in GLYCAM06.²⁹ The most significant deviation between them was associated with the oxygen or nitrogen atom at the point of sulfate attachment. Consequently, for transferability, the charge on the linking heteroatom was adjusted as necessary to achieve a net integer charge on each sulfated sugar (Table S4.4).

Charges for protonated α- and β-d-glucosamine (GlcNH₃⁺) were similarly developed and found to significantly vary from the GLYCAM charges for α- and β-glucose and N-acetyl-glucosamine, particularly for the ring carbon atoms (Table S4.4). This variation suggests that such analogs require unique charge sets for each monosaccharide, which is not surprising, as the positively charged site is directly adjacent to the sugar ring.

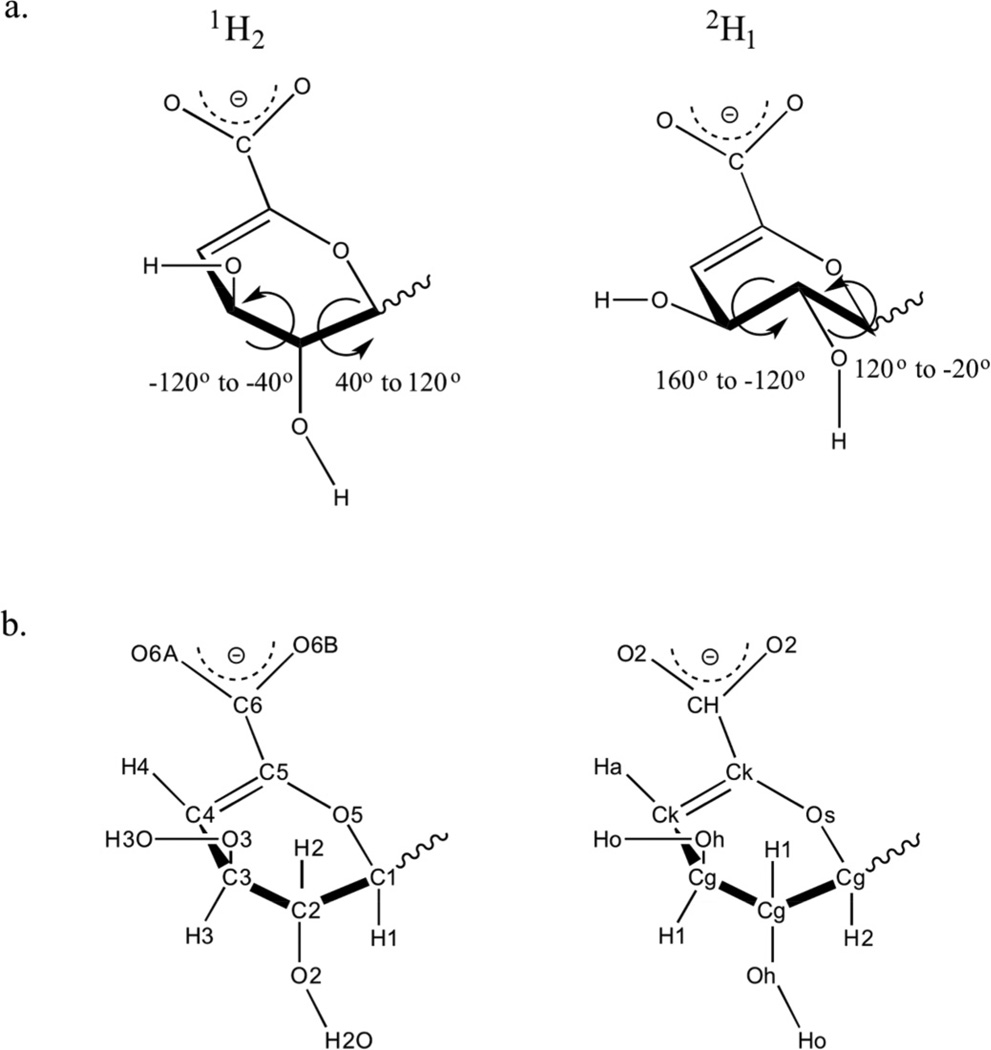
Charges for the ΔUA monomers were obtained by averaging the charges for each of the low-energy half-chair states ¹H₂ and ²H₁ (Fig. 1a; Table S4.4).

Fig. 1.

(a) ΔUA ring conformations with the torsion angle ranges typically associated with H₁–C₁–C₂–H₂ and H₂–C₂-C₃–H₃ atomic sequences. (b) Atom names (left) and atom types (right) employed in GLYCAM for ΔUA.

Parameter development (atom, bond, angle, and torsion parameters)

The GLYCAM06 force field for carbohydrates²⁹ and lipids³⁰ was adapted to include new terms required to model the double bonds found in unsaturated uronic acids. The only new atom type added in this work was the sulfate sulfur atom for which the van der Waals parameters were transferred from the sulfate atom type (S1) found in parm99.⁴⁷ All valence and torsion terms were developed using the hierarchical development procedure outlined in two prior GLYCAM06 publications^29,30 wherein bond terms are developed first followed by angle and torsion terms (Tables S4.1 and S4.2). Small molecules were selected for parameter development such that each contained as few new terms as possible while maintaining an electronic environment relevant to the carbohydrate.²⁹ Equilibrium values for bonds and angles were obtained from the averages of crystal structures found in the Cambridge Structural Database⁴⁸ with molecule IDs HEMKEP, KOCOJ, SRHXGU, MIZFUX, GUVFOS, GUVFEI, GUVFAE, and ZULPIF (Table S4.1); force constants were derived by fitting to QM data computed at the B3LYP/6-31++g(2d,2p)//HF/6-31++g(2d,2p) level.

Torsion potentials were generated for the relevant bonds in the molecules found in Table S4.2. Rotations were sampled in 30° increments with the exception of terms describing double bond rotations in which only 0°, 90°, and 180° orientations were used to characterize the cis/trans relative energies and the barrier height between them. All torsion terms were developed without the use of a phase shift adjustment. Exocyclic torsion terms were developed using tetrahydropyran or its unsaturated analog of ΔUA. In the case of N-sulfate parameters, planarity of the nitrogen atom was maintained during the QM torsion rotation to reflect solution conformations of an sp²-hybridized nitrogen.

In the development of the torsion terms associated with the unsaturated bond, a better fit to experimentally observed rotamer preferences required the use of a higher level of QM theory (second-order Moller–Plesset, MP2) during geometry optimization. This was the case for rotation about the central Cg–Os bond in the Os–Cg–Os–Ck sequence (Fig. 1b), where the terminal Os–Cg bond did not favor the experimentally observed rotamers at the HF level. This behavior was corrected by performing geometry optimizations at the MP2 level. The need for a higher QM level that includes electron correlation may reflect the presence of hyperconjugation between the oxygen atoms (Os) and the unsaturated carbon center (Ck). Having observed a dependence of rotamer preference on the level of QM theory for this term, all other terms were reexamined and found not to show any notable dependence on the QM level. The energy contributions to the barrier for cis/trans rotation in double bonds were distributed equally between heavy and light atom terms, Cg–Ck–Ck–C and Ha–Ck–Ck–C, avoiding the need for improper torsions.³⁰

Tuning torsion terms to reproduce solution populations for ΔUA

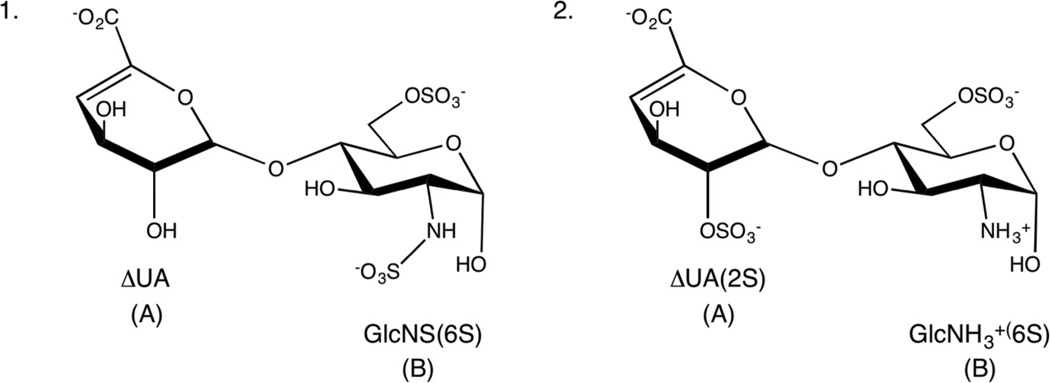
MD simulations (100 ns) with the preliminary parameters were collected for disaccharides 1 and 2 (Fig. 2), which contain ΔUA residues. An analysis of the populations of the ¹H₂ and ²H₁ ring states (¹H₂:²H₁ = 70:30 and 35:65, respectively) showed poor agreement with the NMR-derived populations, 40:60 and 69:31, respectively. As the partial atomic charges in the ΔUA residue had been derived under the assumption of an equal population of half-chair states, this appeared to be a potential source of error. However, the populations from MD simulations, in which the contribution of the partial charges from each half-chair was varied from 0% ¹H₂ to 100% ¹H₂, were relatively insensitive to the atomic charges.

Fig. 2.

Schematic structures of GAG disaccharides (1 and 2), ΔUA monosaccharide (A), and glucosamine residue (B).

Subsequently, the ring torsion terms (Oh–Cg–Cg–Ck (1) and Os–Cg–Cg–Ck (2)) were iteratively adjusted so as to obtain optimal agreement with the NMR populations. MD simulations with the optimized torsion terms yielded average population ratios (¹H₂: ²H₁) for 1 and 2 of 42:58 and 67:33, respectively, that were then in good agreement with experimental values (Table 1). All subsequent simulations employed these parameters.

Table 1.

NMR J couplings and ring state populations for the ΔUA residue in 1 and 2.

	1		2
	NMR	Optimized theoretical	NMR	Optimized theoretical
3J coupling (Hz)a
H1–C1–C2–H2	5.5	4.6	3.4	3.4
H2–C2–C3–H3	4.9	5.0	2.8	3.4
H3–C3–C4–H4	3.8	3.4	4.4	4.4
Population (1H2:2H1)	40:60	42:58	69:31	67:33
NOEs (Å)
H1A–H3B	3.0	4.2	3.1	4.4
H1A–H5B		3.9	2.8	3.9

^aJ couplings for H1–H2, H2–H3, and H3–H4 in the ¹H₂ ring form are 1.7, 1.2, and 5.8 Hz, respectively, and for the ²H₁ form are 6.7, 7.8, and 1.6 Hz, respectively. The J values were independent of the anomeric configuration (α or β) at the reducing terminus.

Results and discussion

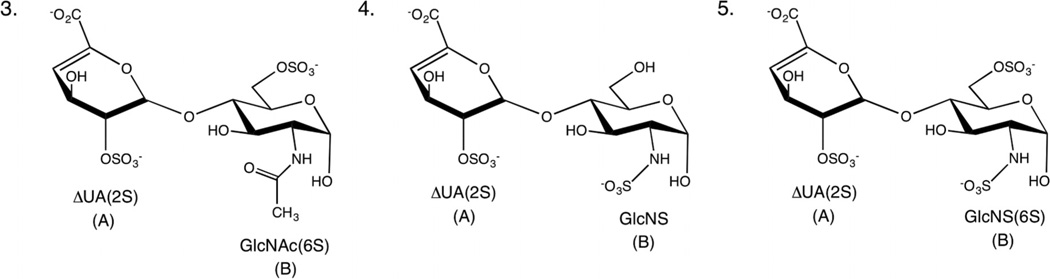
Conformational analysis of ΔUA disaccharides (3–5)

GAG disaccharides 3–5 (Fig. 3) were analyzed using NMR and MD simulations to validate ring conformational populations and glycosidic linkage geometry profiles obtained using the new parameters. Ring conformations and populations were determined from homonuclear ³J_HH couplings, while NOEs were collected to characterize the global 3D shape of these GAG fragments.

Fig. 3.

Schematic structures of GAG disaccharides (3–5).

Ring state populations for the ΔUA residue from MD simulations showed a preference for the ¹H₂ state in all cases, consistent with the populations derived from NMR J couplings (Table 2). Conformational analysis of the ³J couplings for the GlcNx residues (data not shown) was consistent with the ⁴C₁ conformation exclusively.

Table 2.

Experimental observables for residue A of the ΔUA containing disaccharides 3–5.

	3		4		5
Residue A	NMR	Theoretical	NMR	Theoretical	NMR	Theoretical
3J coupling (Hz)a
H1–H2	3.4	2.7	3.0	2.7	3.7	2.9
H2–H3		2.5	2.5	2.5	2.8	2.8
H3–H4	4.7	5.0	4.7	5.0	4.4	4.8
Population (1H2:2H1)	70:30	80:20	76:24	80:20	67:33	76:24
NOEs (Å)
H1A–H3B		3.5	2.7	3.3	2.4	2.9
H1A–H5B		3.5	3.1	3.6		3.3

^aJ couplings for H1–H2, H2–H3, and H3–H4 in the ¹H₂ ring form are 1.7, 1.2, and 5.8 Hz, respectively, and for the 2H1 form are 6.7, 7.8, and 1.6 Hz, respectively. The J values were independent of the anomeric configuration (α or β) at the reducing terminus.

NMR characterization of the glycosidic linkages was provided by an analysis of H1^A–H3^B and H1^A–H5^B proton–proton NOE contacts observed for trans-glycosidic interactions. Comparison of the theoretical- and NMR-derived NOE distances for these protons shows agreement within 0.6 Å in 4 and 5 (Table 2).

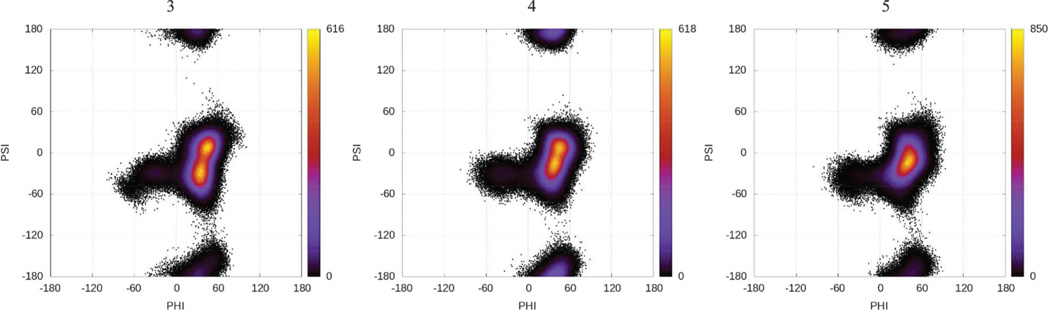
The φ and ψ population distribution heat maps presented in Fig. 4 show that the global minimum from the MD simulations is approximately φ = 50° and ψ = 0° for all of the linkages. Each disaccharide also shows a second stable anti-ψ state near φ = 50° and ψ = 180°.

Fig. 4.

Heat maps for φ versus ψ angles for the glycosidic linkage between A and B for 3, 4, and 5.

Conformational analysis of heparin tetrasaccharides

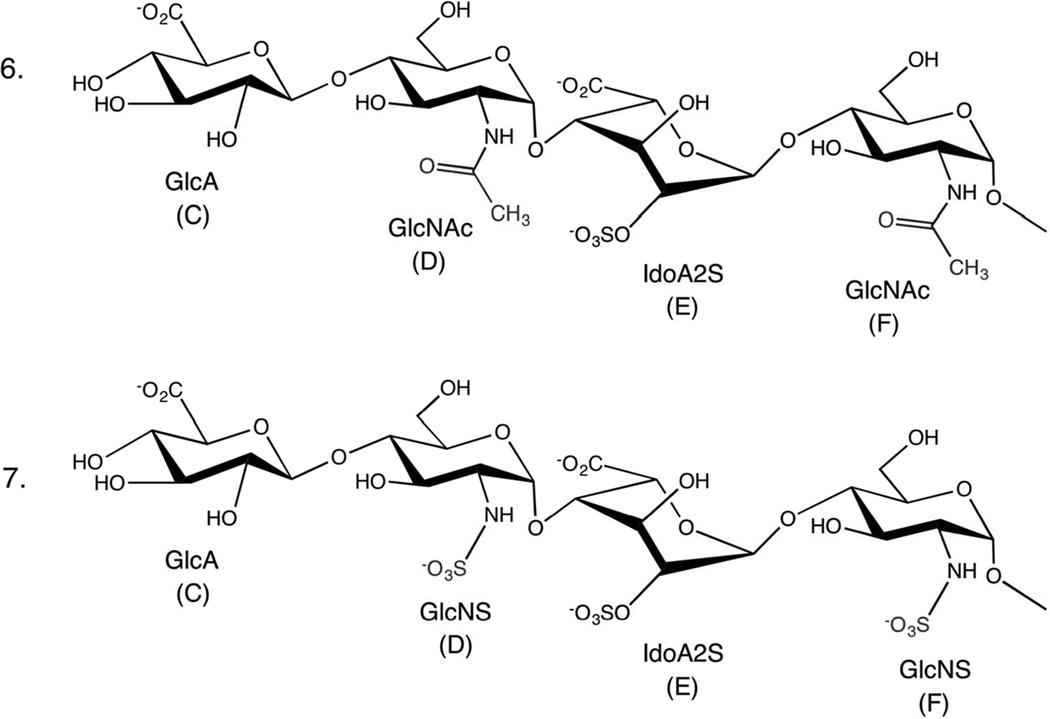
The conformational properties of two synthetic GAG tetrasaccharides, a naturally occurring sequence, 7, and its non-naturally occurring variant, 6, that differ only in the presence (7) or absence (6) of N-sulfation (Fig. 5) were characterized by NMR. To deconvolute the NMR data, MD simulations were performed on 6 and 7 for each of the three common IdoA ring conformations (¹C₄, ²S_O and ⁴C₁) in each tetrasaccharide.

Fig. 5.

Schematic structures of GAG tetrasaccharides (6 and 7). Labels C–F are used to identify the monosaccharide residues.

Ring conformational analysis

During the 1 µs MD simulations, residues C, D, and F each populated only the ⁴C₁ ring conformation, and back-calculation of the J couplings led to agreements with the experimental values within 0.5 Hz for D and F (Table 3). However, the theoretical H1–H2 J values for the terminal C residue (9.8 Hz) in both 6 and 7 were larger than those observed experimentally by almost 2 Hz. Given the otherwise close agreements, this suggests that the MD simulation may not have detected all of the conformations adopted by the C-rings, despite the relatively long simulation time. In the ⁴C₁ conformation, protons H1 and H2 in the β-anomer of the GlcA ring are anti to each other, leading to a large J coupling, whereas in the ¹C₄ conformation, they would be gauche, leading to minimal coupling, and a mixture of approximately 80% ⁴C₁ and 20% ¹C₄ would explain the observed J value in the C residue. However, in the absence of further experimental data, this is not necessarily a unique solution. It is notable that, at least in the case of a fully sulfated GlcA residue, NMR data indicated that the uronate preferred to adopt the ¹C₄ conformation rather than the ⁴C₁.⁴⁹

Table 3.

Theoretical and experimental ³J couplings for 6 and 7.

		6				7
Residue	3J coupling	Theoretical (4C1)a			NMR	Theoretical (4C1)a			NMR
C	H1–H2	9.8			7.9	9.8			7.9
D	H1–H2	3.5			3.6	3.4			3.6
D	H2–H3	10.1			10.6	10.1			10.2
F	H1–H2	3.5			3.6	3.4			3.5
F	H2–H3	10.0			na	10.0			10.2
F	H4–H5	10.0			na	10.0			9.5
Residue	3J coupling	1C4	2SO	4C1	NMR	1C4	2SO	4C1	NMR
E	H1–H2	1.7	8.0	9.9	0.9	1.7	7.9	9.9	3.2
E	H2–H3	1.8	10.0	9.7	na	1.8	10.0	9.7	5.9
E	H3–H4	2.0	6.6	10.0	na	2.0	6.6	10.0	3.7
E	H4–H5	3.4	4.5	4.0	2.4	3.4	4.5	4.0	2.7

^aOnly the ⁴C₁ conformation was sampled during the MD simulations.

Optimal agreement between the experimental and theoretical J values for the IdoA (residue E) ring structure in 7 was achieved using least-squares fitting analysis of the contributions from multiple ring forms, resulting in a population distribution (¹C₄:²S_O) of 63:37 with no contribution from ⁴C₁. The absence of the ⁴C₁ state is supported by NMR data for similar GAGs,^{13,20,21,50,51} which indicate this state to be the least populated of the three, if present at all. A search of the Protein Databank⁵² revealed the ¹C₄ (73%) and ²S_O (24%) states to be the dominant forms of IdoA. For 6, only the ³J_H1H2 and ³J_H4H5 couplings were experimentally observed (0.9 and 2.4 Hz, respectively), and both were below the theoretical values computed from any of the ring conformations. Nevertheless, the small value of the experimental H1–H2 coupling indicates that there cannot be significant amounts of either the ²S_O or ⁴C₁ conformations present.

Interresidue conformational analysis

The theoretical interproton distances (Table 4) showed agreement to within 0.5 Å of the NMR-derived values for all but the distance between protons H1 and H4 (0.8 Å) in residues D and E of 6. The theoretical distances were very similar between the ¹C₄ and ²S_O conformations for the NOEs between residues D and E and E and F, indicating that these IdoA ring conformations do not have a significant influence on the overall shape of the tetrasaccharide. This has previously been determined to be the case in NMR structures of heparin dodecasaccharides.²¹

Table 4.

Theoretical and experimental interring NOE distances (Å) for 6 and 7.

		6			7
C	D	Theoretical		NMR	Theoretical		NMR
H1	H4	2.3		2.8	2.4		2.9
H1	H61/2	2.9		2.8	2.7		2.8
D	E	1C4	2SO	NMR	1C4	2SO	NMR
H1	H2	4.6	4.8	4.2	4.9	4.8	N/A
H1	H3	2.4	2.7	2.5	2.5	2.7	2.7
H1	H4	2.5	2.5	3.3	2.3	2.6	2.7
H5	H4	3.1	3.2	2.7	3.4	3.2	na
E	F	1C4	2SO	NMR	1C4	2SO	NMR
H1	H3	3.2	4.3	na	3.1	3.2	2.6
H1	H4	2.3	2.3	2.7	2.3	2.4	2.6
H1	H61/2	3.0	3.0	2.7	2.9	2.9	2.7

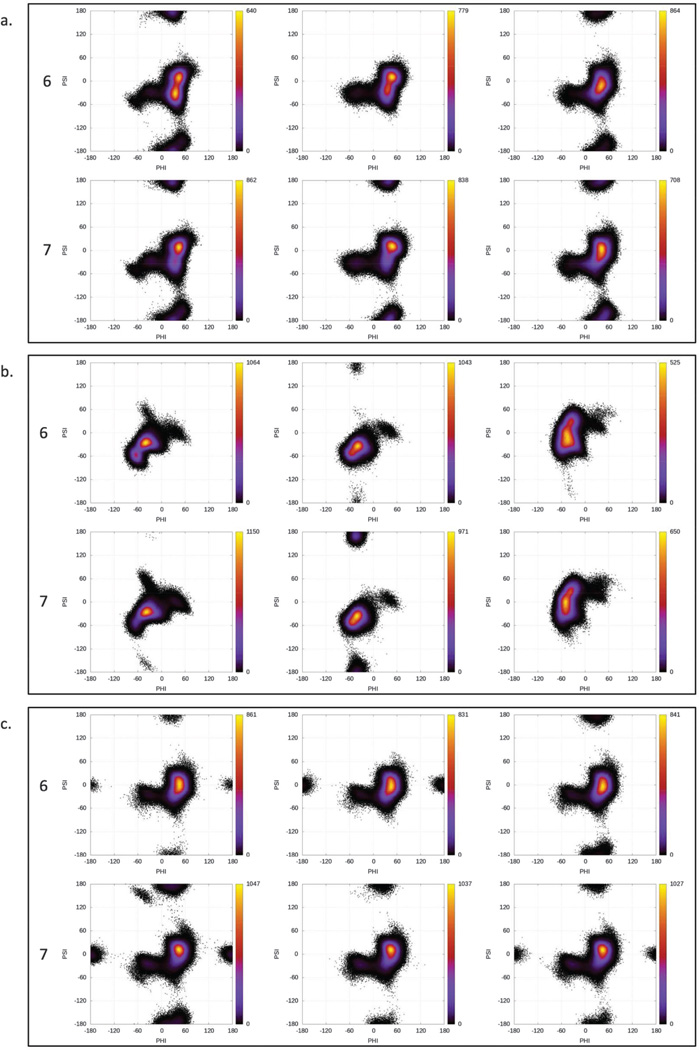
To understand the role of N-sulfation on the glycosidic linkages, heat maps were plotted for the φ versus ψ values for the three glycosidic linkages in each trajectory (Fig. 6). The glycosidic linkages between residues E and F showed very similar distributions for both 6 and 7. In addition to the observed major conformation (φ ≈ 0°−60° and ψ ≈ −60°−60°), this linkage also sampled both the anti-exo (φ ≈ −90°−0° and ψ ≈ −60°−0°) and the anti-ψ (ψ ≈ −150°−+150°) states. Only the simulation of 6 restrained in the ²S_O conformation did not sample the anti-ψ state for this linkage. The percent distribution of each state is presented in Table 5.

Fig. 6.

Heat maps for φ versus ψ angles for the glycosidic linkages between (a) C and D, (b) D and E, and (c) E and F for 6 and 7.

Table 5.

Percent distribution of the φ versus ψ states sampled by the glycosidic linkages during of 6 and 7 during the MD simulations performed with each conformation of IdoA.

Tetrasaccharide	Conformation	Linkage	Exo	Anti-exo	Anti-ψ	Anti-φ
6	1C4	C–D	97.6	2.2	0.1	0.1
		D–E	99.0	1.0	0.0	0.0
		E–F	92.4	2.2	5.4	0.0
	2SO	C–D	97.2	1.9	0.0	0.9
		D–E	99.3	0.7	0.1	0.0
		E–F	97.5	2.5	0.0	0.0
	4C1	C–D	95.9	2.5	1.7	0.0
		D–E	99.3	0.7	0.0	0.0
		E–F	94.8	2.1	3.1	0.0
7	1C4	C–D	87.3	4.1	6.3	2.3
		D–E	94.7	5.3	0.0	0.0
		E–F	87.9	3.9	8.2	0.0
	2SO	C–D	95.0	4.5	0.5	0.0
		D–E	92.6	0.4	7.1	0.0
		E–F	88.1	4.5	7.4	0.0
	4C1	C–D	94.8	4.4	0.5	0.2
		D–E	98.9	1.1	0.0	0.0
		E–F	87.9	3.3	8.8	0.0

The linkage between residues C and D in both 6 and 7 also showed very similar distribution, with an additional sparsely populated anti-φ state (φ ≈ −150° to +150°) for the ¹C₄ conformation. This state was also observed in 7 in the ⁴C₁ simulation, but not in 6. Additionally, the anti-ψ orientation was missing for 6 in ²S_O and anti-φ was missing for 7 in ²S_O. Overall, N-sulfation had little impact on the preferences of the glycosidic linkages, with the possible exception of the E–F linkage in 7, where regardless of the conformation of the IdoA ring, there appeared to be a modest increase in the population of the anti-ψ conformation (bold entries in Table 5).

For the GlcNx (D) and IdoA (E) linkage (Fig. 6b), each ring shape showed a slightly different distribution of glycosidic angles. While the ²S_O conformation showed the tightest distribution around φ ≈ −50° and ψ ≈ −50°, ¹C₄ showed a wider spread of the φ angle and ⁴C₁ a wider spread of the ψ angle. Each of the three also showed a sparsely populated distribution around φ ≈ 40° and ψ ≈ 0°. For the simulation with ²S_O conformation, the D–E linkage also sampled the anti-psi state for both 6 and 7, albeit differing in the percent distribution.

Conclusions

A new parameter set for GAGs containing iduronic acid, ΔUA, sulfate, and protonated glucuronic and iduronic acids has been added to GLYCAM. The development of a transferable sulfate model allows it to be used for multiple attachment points without a need for development of separate charge sets. In addition, development of a single model for ΔUA that reproduces solution conformations permits more accurate modeling of these residues.

The performance of the new parameter set was tested by performing MD simulations on variably sulfated GAG disaccharides containing ΔUA residues and two synthetic GAG tetrasaccharides. NMR scalar coupling and NOE measurements were collected for comparison with the theoretical data, with the aim of verifying the accuracy of the MD simulations and examining any influence of sulfation pattern on GAG conformation.

Unrestrained simulations of ΔUA on timescales that allowed direct parameterization of the ring populations were performed. Analysis of NMR J_HH couplings showed that the conformation populations of the ΔUA ring are largely insensitive to the adjacent sulfation patterns and the N-substituent; however, presence (2–5) or absence (1) of 2-O-sulfation on ΔUA altered the favored geometry.

The most notable effect of sulfation, in the case of GAG tetrasaccharides, was observed on the ring geometries for IdoA. Examination of the NMR data showed that tetrasaccharide 6, which contained 2-O-sulfated IdoA but no N-sulfated glucosamine residues, exclusively favored the ¹C₄ conformation, while 7, which contained two N-sulfated glucosamine residues adjacent to the 2-O-sulfated IdoA, sampled a substantial ²S_O population (37%). While the ring flip dynamics were not captured by this work, long timescale simulations of IdoA using GLYCAM have previously shown experimentally consistent ring populations.⁵³ The ³J_HH coupling analysis also suggested that the terminal GlcA ring may not exclusively adopt the expected ⁴C₁ conformation.

These parameters and related structure files are available for download from the GLYCAM website (www.glycam.org).