OPTIMAL EXPERIMENT DESIGN FOR MAGNETIC RESONANCE FINGERPRINTING

Abstract

Magnetic resonance (MR) fingerprinting is an emerging quantitative MR imaging technique that simultaneously acquires multiple tissue parameters in an efficient experiment. In this work, we present an estimation-theoretic framework to evaluate and design MR fingerprinting experiments. More specifically, we derive the Cramér-Rao bound (CRB), a lower bound on the covariance of any unbiased estimator, to characterize parameter estimation for MR fingerprinting. We then formulate an optimal experiment design problem based on the CRB to choose a set of acquisition parameters (e.g., flip angles and/or repetition times) that maximizes the signal-to-noise ratio efficiency of the resulting experiment. The utility of the proposed approach is validated by numerical studies. Representative results demonstrate that the optimized experiments allow for substantial reduction in the length of an MR fingerprinting acquisition, and substantial improvement in parameter estimation performance.

1. INTRODUCTION

Magnetic resonance (MR) imaging is a powerful and versatile imaging modality that has revolutionized the medicine and biology [1]. Clinical MR imaging applications mostly rely on contrast-weighted images, which are complex functions of intrinsic tissue MR parameters (e.g., spin density, and T₁ and T₂ relaxation times) and extrinsic imperfections arising from pulse sequences and hardware. These images are qualitative in nature, and often have limited sensitivity to tissue physiological and/or pathological variations. This hampers the effectiveness of using MRI for early detection and monitoring of cancer, neurodegenerative diseases, and other pathologies. Although the potential of quantitative imaging has long been recognized, pushing forward towards truly quantitative imaging faces a number of technical challenges. One key challenge is long acquisition time.

Magnetic resonance fingerprinting [2] is a very recent break-through in quantitative MR imaging. It enables simultaneous quantitative measurement of multiple MR tissue parameters (e.g., spin density, and T₁ and T₂ relaxation times) at an ultrafast speed. In contrast to conventional MR relaxometry techniques, a key distinguishing feature of MR fingerprinting is its ingenious use of incoherence in signal excitation and data acquisition. In particular, it employs a series of time-varying quasi-random data acquisition parameters (e.g., flip angles and repetition times) to probe the spin system, producing the temporal incoherence.

Despite the revolutionary concept, several fundamental questions remain unclear about the mechanism of MR fingerprinting. For example, while it has been theoretically established that quasi-random acquisition schemes can have a high probability of success in abstract/asymptotic formulations of the problem [3], it is unclear whether quasi-random acquisition schemes make optimally efficient use of the data acquisition time in real-world experiments. Moreover, MR fingerprinting suffers from a number of practical limitations. For example, the accuracy of the T₂ maps often depends critically on the length of data acquisition, and is much worse than the accuracy of T₁ maps when the acquisition length becomes short [4, 5].

To address the above issues, this work introduces a principled framework to evaluate and optimize MR fingerprinting experiments. Similar to previous approaches (e.g., [6–8]), we use the Cramér-Rao bound (CRB), an estimation-theoretic bound on the variance of any unbiased estimator, as a quality measure for comparing different experiment designs. We further utilize this bound to formulate an optimal experiment design problem that chooses MR fingerprinting acquisition parameters for maximal signal-to-noise (SNR) efficiency. We show representative results to illustrate the effectiveness of the proposed approach.

2. PROPOSED APPROACH

2.1. Data Model

We start by formally describing the data model for MR fingerprinting. Notice that there are a number of data acquisition protocols (e.g., [2, 9]) that can be used to implement MR fingerprinting. As a concrete example, we consider here the signal model for the inversion-recovery balanced steady state free precession (IR-bSSFP) based pulse sequence [2]. Generalization to other acquisition protocols is straightforward.

Let T₁, T₂, M₀ respectively denote the spin-lattice relaxation time, spin-spin relaxation time, and spin density. Given a set of flip angles ${\{{\alpha }_n\}}_{n=1}^N$, RF pulse phases ${\{{\varphi }_n\}}_{n=1}^N$, and repetition times ${\{T{R}_n\}}_{n=1}^N$, the magnetization dynamics Mⁿ(T₁, T₂, M₀) for IR-bSSFP can be described by the following linear difference equation [10]:

$${\mathbf{M}}^n=\mathbf{R}(T_1,T_2,T{R}_n)\mathbf{Q}({\varphi }_n,{\alpha }_n){\mathbf{M}}^{n-1}+\mathbf{b}(T_1,M_0,T{R}_n),$$ (1)

where $\mathbf{b}(T_1,M_0,T{R}_n)={[\begin{array}{ccc}0& 0& (1-e^{-T{R}_n/T_1})M_0\end{array}]}^T$,

$$\begin{array}{l}\mathbf{Q}({\varphi }_n,{\alpha }_n)=\left[\begin{array}{ccc}cos({\varphi }_n)& sin({\varphi }_n)& 0\\ -sin({\varphi }_n)& cos({\varphi }_n)& 0\\ 0& 0& 1\end{array}\right]\\ \left[\begin{array}{ccc}1& 0& 0\\ 0& cos({\alpha }_n)& sin({\alpha }_n)\\ 0& -sin({\alpha }_n)& cos({\alpha }_n)\end{array}\right]\left[\begin{array}{ccc}cos({\varphi }_n)& -sin({\varphi }_n)& 0\\ sin({\varphi }_n)& cos({\varphi }_n)& 0\\ 0& 0& 1\end{array}\right],\\ \mathbf{R}(T_1,T_2,T{R}_n)=\left[\begin{array}{ccc}{e}^{-T{R}_n/T_2}& 0& 0\\ 0& e^{-T{R}_n/T_2}& 0\\ 0& 0& e^{-T{R}_n/T_1}\end{array}\right],\end{array}$$

and n = 1,…, N. Note that off-resonance effects are ignored in (1) for simplicity. Furthermore, assuming that the magnetization is fully relaxed before signal excitation, the initial condition for (1) is given by ${\mathbf{M}}^0={[\begin{array}{ccc}0& 0& M_0\end{array}]}^T$.

With respect to the data model (ignoring the spatial encoding for simplicity), the measured signal sⁿ can be expressed as

$${\mathbf{s}}^n={\mathbf{m}}^n+{\mathbf{z}}^n,$$ (2)

where mⁿ denotes the noise-free magnetization at the nth echo time, and zⁿ ∈ ℝ² ~ 𝒩(0, σ²I) is independent and identically distributed (iid) Gaussian noise. More specifically, given a set of echo times ${\{T{E}_n\}}_{n=1}^N$, mⁿ can be expressed as

$${\mathbf{m}}^n=\mathbf{D}(\gamma )[\mathbf{R}(T_1,T_2,T{E}_n)\mathbf{Q}({\varphi }_n,{\alpha }_n){\mathbf{M}}^{n-1}+\mathbf{b}(T_1,M_0,T{E}_n)],$$ (3)

where

$$\mathbf{D}(\gamma )=\left[\begin{array}{ccc}cos(\gamma )& sin(\gamma )& 0\\ -sin(\gamma )& cos(\gamma )& 0\end{array}\right],$$

and γ denotes the phase of the receiver coil (assumed to be known).

2.2. Cramér-Rao Bound

Here we derive the Cramér-Rao bound (CRB) to characterize parameter estimation with the data model (2). For notational simplicity, denote θ = [T₁, T₂, M₀]^T. From statistical estimation theory, under mild regularity conditions, the CRB provides a lower bound on the covariance of any unbiased estimator θ̂, and this bound can be asymptotically achieved by the maximum likelihood (ML) estimator. Mathematically, the CRB can be expressed as the following information inequality [11]:

$$\mathbb{E}\left\{(\mathbf{\theta }-\widehat{\mathbf{\theta }}){(\mathbf{\theta }-\widehat{\mathbf{\theta }})}^T\right\}\ge \mathbf{C}(\mathbf{\theta })={\mathbf{J}}^{†}(\mathbf{\theta }),$$ (4)

where C(θ) is the CRB matrix, J(θ) is the Fisher information matrix (FIM) given by

$$\mathbf{J}(\mathbf{\theta })=\mathbb{E}\left[\left(\frac{\partial lnP(\{{\mathbf{s}}_n\};\mathbf{\theta })}{\partial \mathbf{\theta }}\right){\left(\frac{\partial lnP(\{{\mathbf{s}}_n\};\mathbf{\theta })}{\partial \mathbf{\theta }}\right)}^T\right],$$ (5)

In P(·) is the log-likelihood function for the data model, and † denotes the pseudo-inverse. For the iid additive Gaussian model in (2), the FIM can be readily derived (see Appendix for more details). Moreover, to obtain the bound on the variance of individual component θ_i, the diagonal entry of C(θ) can be extracted, i.e.,

$$\text{Var}(\widehat{\mathbf{\theta }})\ge {[\mathbf{C}(\mathbf{\theta })]}_{i,i}.$$ (6)

Since the CRB characterizes the smallest possible covariance for any unbiased estimator, for the first time, we have a way to understand the SNR efficiency of a fingerprinting experiment. This has many uses, including understanding the potential reliability of an MR fingerprinting experiment, and figuring out how much acquisition time is necessary to achieve a certain level of quantitative accuracy. Importantly, this also gives us the unique ability to optimize the MR fingerprinting acquisition.

2.3. Optimal Experiment Design

To determine a set of data acquisition parameters ${\{{\alpha }_n,{\varphi }_n,T{R}_n\}}_{n=1}^N$, which maximizes the SNR efficiency of an MR fingerprinting experiment, we formulate the experiment design problem as follows:

$$\begin{array}{c}\underset{{\{{\alpha }_n,{\varphi }_n,T{R}_n\}}_{n=1}^N}{min}{\sum }_{l=1}^L{\sum }_{i=1}^3{\omega }_i\sqrt{{[\mathbf{C}({\mathbf{\theta }}^{(l)})]}_{i,i}}/{\mathbf{\theta }}_i^{(l)}\\ \mathrm{s}.\mathrm{t}.{\sum }_{n=1}^{N}T{R}_n\le T,\\ {\alpha }_n^{min}\le {\alpha }_n\le {\alpha }_n^{max},\\ {\varphi }_n^{min}\le {\varphi }_n\le {\varphi }_n^{max},\\ T{R}_n^{min}\le T{R}_n\le T{R}_n^{max},\end{array}$$ (7)

where T is the pre-specified total acquisition time, [ ${\alpha }_n^{min},{\alpha }_n^{max}$] and [ ${\varphi }_n^{min},{\varphi }_n^{max}$] respectively denote the user-specified ranges for the flip angle and phase of the nth RF pulse, [ $T{R}_n^{min},T{R}_n^{max}$] denotes the range of the nth repetition time, and ω_i s are user-selected weighting parameters that balance the importance of different tissue parameters for experiment design. Notice that in (7), the experiment is designed with respect to a set of representative tissue parameters ${\{{\mathbf{\theta }}^{(l)}\}}_{l=1}^L$. Equation (7) results in a nonconvex optimization problem that often have many spurious local minima. Here, stochastic optimization is applied to obtain a good local minimum.

3. RESULTS

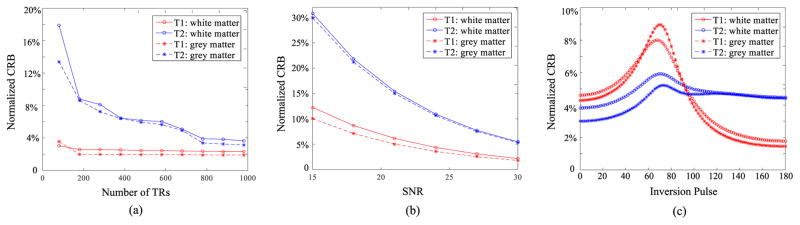
In this section, we demonstrate the utility of applying the CR-B to analyze and optimize MR fingerprinting experiments. We first use the CRB to study the characteristics of the conventional MRF acquisition scheme [2]. More specifically, we calculated the CRBs for two representative tissues from the grey matter and white matter of the brain, whose tissue parameters were set as θ⁽¹⁾ = [700 ms, 60 ms, 0.6] and θ⁽²⁾ = [1000 ms, 102 ms, 0.6], respectively. Fig. 1(a) and (b) respectively plot the normalized CRB with respect to different number of TRs (i.e., acquisition time) and SNRs. As expected, the CRBs reduce with the increase of acquisition time or SNR for both of the tissues. However, it is worth noting that the CRBs for T₂ are much larger than those for T₁, consistent with the empirical observations in the literature [4, 5]. Additionally, Fig. 1(a) shows that the T₁ estimation accuracy rapidly reaches its asymptotic limit within the first 200 TRs, while attaining good accuracy for T₂ requires significantly longer acquisition time. This clearly indicates the sub-optimality of the conventional MR fingerprinting experiment design.

Fig. 1.

The CRB analysis of the conventional MR fingerprinting experiment. (a): normalized CRB versus number of TRs, (b): normalized CRB versus SNRs, and (c): normalized CRB versus different inversion preparation pulses α₁

Given that MR fingerprinting experiments provide large flexibility of choosing different data acquisition parameters (e.g., flip angles and repetition times), it is worth analyzing the impact of these parameters on the estimation accuracy. As an example, we study the role of the initial RF pulse, i.e., α₁, which has typically been chosen as an inversion preparation pulse (180°) in conventional fingerprinting designs. More specifically, we calculated the CRBs for the above two tissues across the full range of possible flip angles. Fig. 1(c) plots the CRB versus the flip angle of the initial pulse. As can be seen, the accuracy of T₁ substantially benefits from the 180° inversion pulse used in the conventional MR experiment, while this inversion pulse can be sub-optimal in terms of the T₂ accuracy.

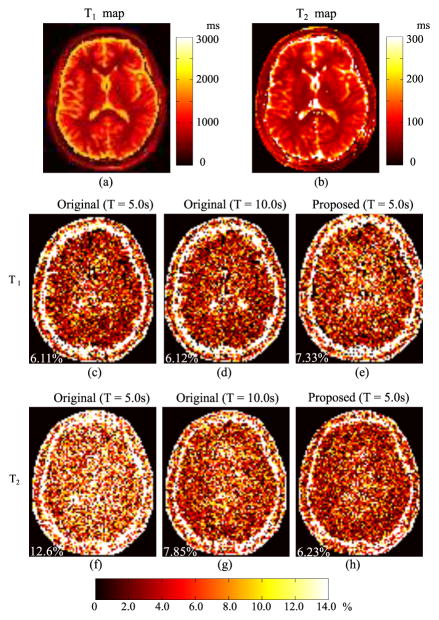
Next, we performed the optimal experiment design based on (7). Assuming that T₁ and T₂ are tissue parameters of interest, we set [ω₁, ω₂, ω₃] = [1, 1, 0]. Furthermore, let T = 5 s, $[{\alpha }_1^{min},{\alpha }_1^{max}]=[0°,180°]$ for α₁, $[{\alpha }_n^{min},{\alpha }_n^{max}]=[0°,60°]$ for other flip angles, $[T{R}_n^{min},T{R}_n^{max}]=[8\text{ms},11\text{ms}]$, and ${\varphi }_n^{min}={\varphi }_n^{max}=0°$. Additionally, we chose seven “training” tissues, listed in Table 1, as θ^(l) to determine the data acquisition parameters. To evaluate the effectiveness of the optimized experiment, we performed simulation studies using a numerical brain phantom with T₁ and T₂ maps shown in Fig. 2 (a) and (b). We performed Bloch simulations to simulate MR fingerprinting acquisitions using the original acquisition parameters and optimized parameters, all with the same acquisition time T = 5 s. In addition, we performed the original experiment with T = 10 s. Fig. 2(c)–(h) shows the error maps associated with the T₁and T₂ reconstructions obtained by the ML approach [4]. As can be seen, compared to the original experiment with T = 5 s, the optimized experiment achieves a similar level of accuracy for the T₁ estimation, while enabling substantial improvement in the T₂ estimation accuracy. When the acquisition time is doubled for the original experiment, the accuracy of T₂ estimation considerably improves, as shown in Fig. 2 (g). Nevertheless, the optimized experiment with T = 5 s still provides a more accurate T2 map than the original one with T = 10 s, indicating the improvement of SNR efficiency offered by the optimized experiment.

Table 1.

T₁ and T₂ values for the training tissue.

Tissue No.	1	2	3	4	5	6	7
T1 (ms)	600	680	750	860	1000	1160	1260
T2 (ms)	65	73	80	90	95	102	110

Fig. 2.

Reconstruction errors associated with the original and optimized MRF experiments. (a)–(b): ground truth T₁ and T₂ maps. (c)–(e): T₁ error maps associated with the original experiment and the optimized experiment. (f)–(h): T₂ error maps associated with the original experiments and and the optimized experiment. Note that the overall NRMSE is labeled at lower left corner of each error map.

4. CONCLUSION

This work presented a principled framework based on the CRB to evaluate and design MR fingerprinting experiments. This framework enables theoretical analysis of the impact of data acquisition parameters, and also provides insights into the inherent limitation of the unbalanced accuracy between T₁ and T₂ estimation. Within this framework, we formulated the optimal experiment design problem that maximizes the SNR efficiency of the resulting experiment. Numerical results demonstrate that the optimized experiments allow for substantial improvement in the T₂ estimation accuracy, while maintaining similar accuracy level for the T₁ estimation. With the optimized experiments, we could potentially reduce acquisition time by a factor of two while preserving or even improving the quantitative accuracy of the experiment.

In future work, it is worth evaluating the robustness of the optimized experiments with in vivo data in which a variety of model mismatches may exist. Moreover, the current experiment design has only been optimized with respect to pulse timing and flip angle parameters. It would be interesting to study the problem of jointly designing k-space trajectories and acquisition parameters, although the associated CRB calculation can be more computationally expensive.

5. APPENDIX

In this appendix, we derive the FIM in (5). First, note that for the iid additive Gaussian model in (2), J_i,_j can be simplified as [11]:

$${\mathbf{J}}_{i,j}=\frac{1}{{\sigma }^2}\sum _{n=1}^N{\left[\frac{\partial {\mathbf{m}}^n(\mathbf{\theta })}{\partial {\mathbf{\theta }}_i}\right]}^T\left[\frac{\partial {\mathbf{m}}^n(\mathbf{\theta })}{\partial {\mathbf{\theta }}_j}\right].$$ (8)

Thus, the FIM calculation reduces to computing the derivative of mⁿ with respect to unknown parameter θ = [T₁, T₂, M₀]^T. Next, we show that such derivative evaluations can be done by solving linear difference equations via simple recursion.

5.1. Derivative with respect to M₀

Taking the derivative with respect to M₀ on both sides of (3) yields

$$\frac{\partial {\mathbf{m}}^n(\mathbf{\theta })}{\partial M_0}=\mathbf{D}(\gamma )\mathbf{R}(T_1,T_2,T{E}_n)\mathbf{Q}({\varphi }_n,{\alpha }_n)\frac{\partial {\mathbf{M}}^{n-1}}{\partial M_0}+\mathbf{D}(\gamma )\frac{\partial \mathbf{b}(T_1,M_0,T{E}_n)}{\partial M_0}.$$ (9)

While calculating $\frac{\partial \mathbf{b}(T_1,M_0,T{E}_n)}{\partial M_0}$ is straightforward, determining $\frac{\partial {\mathbf{M}}^{n-1}}{\partial M_0}$ is a bit more involved. Notice that by invoking the derivative of (1), we can obtain the following linear difference equation:

$$\frac{\partial {\mathbf{M}}^n}{\partial M_0}=\mathbf{R}(T_1,T_2,T{R}_n)\mathbf{Q}({\varphi }_n,{\alpha }_n)\frac{\partial {\mathbf{M}}^{n-1}}{\partial M_0}+\frac{\partial \mathbf{b}(T_1,M_0,T{R}_n)}{\partial M_0}.$$

From this equation, we can determine $\frac{\partial {\mathbf{M}}^{n-1}}{\partial M_0}$ by simple recursion, with the initial condition given by $\frac{\partial {\mathbf{M}}^0}{\partial M_0}={[\begin{array}{ccc}0& 0& 1\end{array}]}^T$.

5.2. Derivative with respect to T₁

Notice that by the chain rule, we have

$$\frac{\partial {\mathbf{m}}^n(\mathbf{\theta })}{\partial T_1}=\mathbf{D}(\gamma )\mathbf{R}(T_1,T_2,T{E}_n)\mathbf{Q}({\varphi }_n,{\alpha }_n)\frac{\partial {\mathbf{M}}^{n-1}}{\partial T_1}+\mathbf{D}(\gamma )\left[\frac{\partial \mathbf{R}(T_1,T_2,T{E}_n)}{\partial T_1}\right]\mathbf{Q}({\varphi }_n,{\alpha }_n){\mathbf{M}}^{n-1}+\mathbf{D}(\gamma )\frac{\partial \mathbf{b}(T_1,M_0,T{E}_n)}{\partial T_1},$$ (10)

with

$$\frac{\partial {\mathbf{M}}^n}{\partial T_1}=\mathbf{R}(T_1,T_2,T{R}_n)\mathbf{Q}({\varphi }_n,{\alpha }_n)\frac{\partial {\mathbf{M}}^{n-1}}{\partial T_1}+\left[\frac{\partial \mathbf{R}(T_1,T_2,T{R}_n)}{\partial T_1}\right]\mathbf{Q}({\varphi }_n,{\alpha }_n){\mathbf{M}}^{n-1}+\frac{\partial \mathbf{b}(T_1,M_0,T{R}_n)}{\partial T_1}.$$

Here the initial condition is $\frac{\partial {\mathbf{M}}^0}{\partial T_1}={[\begin{array}{ccc}0& 0& 0\end{array}]}^T$. Moreover, note that the second term in the right hand side of (10) vanishes, due to the fact

$$\mathbf{D}(\gamma )\left[\frac{\partial \mathbf{R}(T_1,T_2,T{R}_n)}{\partial T_1}\right]=\mathbf{0}.$$

5.3. Derivative with respect to T₂

Similarly, the derivative with respect to T₂ can be calculated as

$$\frac{\partial {\mathbf{m}}^n(\mathbf{\theta })}{\partial T_2}=\mathbf{D}(\gamma )\mathbf{R}(T_1,T_2,T{E}_n)\mathbf{Q}({\varphi }_n,{\alpha }_n)\frac{\partial {\mathbf{M}}^{n-1}}{\partial T_2}+\mathbf{D}(\gamma )\left[\frac{\partial \mathbf{R}(T_1,T_2,T{E}_n)}{\partial T_2}\right]\mathbf{Q}({\varphi }_n,{\alpha }_n){\mathbf{M}}^{n-1},$$ (11)

with

$$\frac{\partial {\mathbf{M}}^n}{\partial T_2}=\mathbf{R}(T_1,T_2,T{R}_n)\mathbf{Q}({\varphi }_n,{\alpha }_n)\frac{\partial {\mathbf{M}}^{n-1}}{\partial T_2}+\left[\frac{\partial \mathbf{R}(T_1,T_2,T{R}_n)}{\partial T_2}\right]\mathbf{Q}({\varphi }_n,{\alpha }_n){\mathbf{M}}^{n-1}$$

and $\frac{\partial {\mathbf{M}}^0}{\partial T_2}={[\begin{array}{ccc}0& 0& 0\end{array}]}^T$.