A Survey of Methods for Time Series Change Point Detection

Abstract

Change points are abrupt variations in time series data. Such abrupt changes may represent transitions that occur between states. Detection of change points is useful in modelling and prediction of time series and is found in application areas such as medical condition monitoring, climate change detection, speech and image analysis, and human activity analysis. This survey article enumerates, categorizes, and compares many of the methods that have been proposed to detect change points in time series. The methods examined include both supervised and unsupervised algorithms that have been introduced and evaluated. We introduce several criteria to compare the algorithms. Finally, we present some grand challenges for the community to consider.

1. INTRODUCTION

Time series analysis has become increasingly important in diverse fields including medicine, aerospace, finance, business, meteorology, and entertainment. Time series data are sequences of measurements over time describing the behavior of systems. These behaviors can change over time due to external events and/or internal systematic changes in dynamics/distribution [1]. Change point detection (CPD) is the problem of finding abrupt changes in data when a property of the time series changes [2]. Segmentation, edge detection, event detection and anomaly detection are similar concepts which are occasionally applied as well as change point detection. Change point detection is closely related to the well-known problem of change point estimation or change point mining [3][4][5]. Unlike CPD, however, change point estimation tries to model and interpret known changes in time series rather than identifying that a change has occurred. The focus of change point estimates is to describe the nature and degree of the known change.

In this paper, we survey the topic of change point detection and examine recent research in this area. CPD has been studied over the last several decades in the fields of data mining, statistics, and computer science. This problem covers a broad range of real-world problems. Here are some motivating examples.

Medical condition monitoring

Continuous monitoring of patient health involves trend detection in physiological variables such as heart rate, electroencephalogram (EEG), and electrocardiogram (ECG) in order to perform automated, real-time monitoring. Research studies investigate change point detection for specific medical issues such as sleep problems, epilepsy, magnetic resonance imaging (MRI) interpretation, and understanding of brain activities [6][7][8][9].

Climate change detection

Climate analysis, monitoring, and prediction methods that utilize change point detection have become increasingly important over the last few decades due to the possible occurrence of climate change and the increase of greenhouse gases in the atmosphere [10][11][12].

Speech recognition

Speech recognition represents the process of converting spoken speech utterances to words or text. Change point detection methods are applied here for audio segmentation and recognizing boundaries between silence, sentences, words, and noise [13][14].

Image analysis

Researchers and practitioners collect image data over time, or video data, for video-based surveillance. The detection of abrupt events, such as security breaches, can be formulated as a change-point problem. Here, the observation at each time point is the digital encoding of an image [15].

Human activity analysis

Detecting activity breakpoints or transitions based on characteristics of observed sensor data from smart homes or mobile devices can be formulated as change point detection. These change points are useful for segmenting activities, interacting with humans while minimizing interruptions, providing activity-aware services, and detecting changes in behavior that provide insights on health status [13–20].

In this survey we will explain the problem of change point detection and explore how different supervised and unsupervised methodologies can be used for detecting change points in time series data. We will compare and contrast investigated techniques based on their cost, limitations, and performance. Finally, we discuss the gaps in the research, summarize challenges that arise for change point applications, and provide suggestions for continuing investigation.

2. BACKGROUND

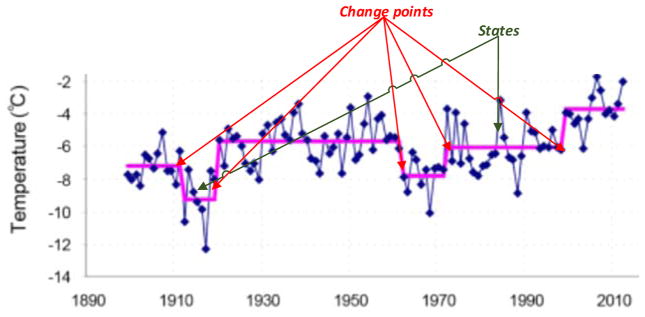
Figure 1 graphs an example time series that contains several change points. The data illustrate long term mean annual temperature trends of Spitsbergen for the period 1899–2010 [16]. The data can be used for climate change detection. This plot highlights the observation that the climate of Spitsbergen went through six different regimes in this period. We refer to these portions of the time series as states of the time series, or periods of time when the parameters governing the process do not change. Two consecutive distinct states are distinguished by a change point. The objective of change point detection is to identify these state borders by discovering the change points.

Figure 1.

Sample time series and change points (horizontal lines indicate separate states).

2.1 Definitions and Problem Formulation

We begin by presenting definitions of key terms that we use throughout this survey.

Definition 1

A time series data stream is an infinite sequence of elements

$$S=\{x_1,\dots ,x_i,\dots \}$$

where x_i is a d-dimensional data vector arriving at time stamp i [17].

Definition 2

A stationary time series is a finite variance process whose statistical properties are all constant over time [18]. This definition assumes that

• The mean value function μ_t = E(x_t) is constant and does not depend on time t.

• The auto covariance function γ(s, t) = cov(x_s, x_t) = E[(x_s − μ_s)(x_t − μ_t)] depends on time stamps s and t only through their time difference, or |s – t|.

Definition 3

Independent and identically distributed (i.i.d.) variables are mutually independent of each other, and are identically distributed in the sense that they are drawn from the same probability distribution. An i.i.d. time series is a special case of a stationary time series.

Definition 4

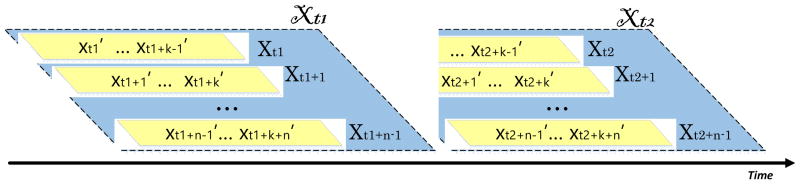
Given a time series T of fixed length m (a subset of a time series data stream) and x_t as a series sample at time t, a matrix WM of all possible subsequences of length k can be built by moving a sliding window of size k across T and placing subsequence X_p = {x_p, x_p+1, … , x_p+k} (Figure 2) in the p^th row of WM. The size of the resulting matrix WM is (m − k + 1) × n [19][20].

Figure 2.

An illustrative example of time series notations.

Definition 5

In a time series, using sliding window X_t as a sample instead of x_t, an interval χ_t with Hankel matrix {X_t, X_t+1, … , X_t+n–1} as shown in Figure 2 will be a set of n retrospective subsequence samples starting at time t [2][21][22].

Definition 6

A change point represents a transition between different states in a process that generates the time series data.

Definition 7

Let {x_m, x_m+1, . . , x_n} be a sequence of time series variables. Change point detection (CPD) can be defined as the problem of hypothesis testing between two alternatives, the null hypothesis H₀: “No change occurs” and the alternative hypothesis H_A: “A change occurs” [23][24]

1. H₀: ℙ_Xm = ⋯ = ℙ_Xk = ⋯ = ℙ_Xn.

2. H_A: There exists m < k^* < n such that ℙ_Xm = ⋯ = ℙ_Xk* ≠ ℙ_Xk*+1 = ⋯ = ℙ_Xn.

   where ℙ_Xi is the probability density function of the sliding window start at point x_i and k^* is a change point.

2.2 Criteria

In the previous section we provide a formal introduction to the traditional change point detection. However, practical application of change point detection introduces a number of new challenges that need to be addressed. Here we introduce and describe some of these challenges.

2.2.1 Online detection

Change point detection algorithms are traditionally classified as “online” or “offline”. Offline algorithms consider the entire data set at once, and look back in time to recognize where the change occurred. The goal of this scenario is generally to identify all of a sequence’s change points in batch mode. In contrast, online, or real-time, algorithms run concurrently with the process they are monitoring, processing each data point as it becomes available, with a goal of detecting a change point as soon as possible after it occurs, ideally before the next data point arrives [25].

In practice, no change point detection algorithm operates in perfect real time because it must inspect new data before determining if a change point occurred between the old and new data points. However, different online algorithms require different amounts of new data before change point detection can occur. Based on this observation we will define a new term to use throughout this paper. We will denote as an ε –real time algorithm an online algorithm which needs at least ε data samples in the new batch of data to be able to find change points. An offline algorithm can then be viewed as ∞ –real time and the completely-online algorithm is 1-real time because for every data point, it can predict whether or not a change point occurs before the new data point. Smaller ε values may lead to stronger, more responsive change point detection algorithms.

2.2.2 Scalability

Real world time series data from sources such as human activities and remote sensing satellites are becoming ever larger in both number of data points and number of dimensions. Change detection methods need to be designed in a computationally efficient manner so that they can scale to massive data sizes [26]. Hence we compare the computational cost of alternative CPD algorithms to determine which one can reach an optimal (or a good enough) solution as fast as possible. One way to compare the computational cost of the algorithms is finding the algorithm is parametric or non-parametric. Distinguishing between parametric and nonparametric approaches is important because nonparametric approaches have demonstrated greater success for massively large datasets. Also, the computational cost of parametric methods is higher than nonparametric approaches and does not scale as well with the size of the dataset [23].

A parametric approach specifies a particular functional form to be learned by the model and then estimates the unknown parameters based on labeled training data. Once the model has been trained the training examples can be discarded. In contrast, nonparametric methods do not make any assumptions about the form of the underlying function. The corresponding price to be paid is that all the available data has to be retained while making the inference [27].

A successful algorithm must trade off decision quality for deliberation cost. One promising approach is to use anytime algorithms [28] which allow the execution to be interrupted at any time and output the best possible solution obtained so far. A similar method is a contract algorithm which also trades off computation time for solution quality but is given the allowable run time in advance as a type of contract agreement. In contrast to an anytime algorithm, a contract algorithm receives its allowable execution time as a specified parameter. If a contract algorithm is interrupted before the allocated time is completed, it might not yield any useful results. An interruptible algorithm (such as an anytime algorithm) is one whose execution time is not given in advance and thus must be prepared to be interrupted at any moment, but it uses available time to continually improve the quality of its solution. In general, every interruptible algorithm is trivially a contract algorithm, but the converse is not true [29].

2.2.3 Algorithm constraints

Approaches to CPD can also be distinguished based on the requirements that are imposed on the input data and the algorithm. These constraints are important in selecting an appropriate technique for detecting change points in a specific data sequence. Constraints related to the nature of the time series data may emanate from the stationarity [30], i.i.d. [31], dimensionality, or continuity of the data [32].

Some of the algorithms require information about the data, such as the number of change points in the data, the number of states in the system, and the features of the system states [33][34]. Another important issue in parametric methods is the degree to which the algorithm is sensitive to the choice of initial parameter values.

2.3 Performance Evaluation

In order to compare alternative CPD algorithms and estimate the expected resulting performance, measures of performance are needed. Many performance metrics have been introduced to evaluate change point detection algorithms based on the type of decisions they make [35]. The output of CPD algorithms can contain the following:

• Change-point yes/no decisions (the algorithm is a binary classifier)

• Change point identification with varying levels of precision (i.e., the =change point occurs within x time units. This type of algorithm utilizes a multi-class classifier or unsupervised learning methods.

• The time of the next change point (or the times of all change points in the series)

In case of the first two types of output, standard methods for evaluating supervised learning algorithms can be utilized to evaluate the performance of the change point detector. A first step at evaluating the performance of a supervised change point learner is to generate a confusion matrix which summarizes the actual and predicted classes. Table 1 illustrates a confusion matrix for a binary change point classifier.

Table 1.

Example confusion matrix. In this example, a change point can be considered the “positive” class while no change point can be considered the “negative” class.

	Classified as change point	Classified as non-change point
True change point	TP	FN
True non-change point	FP	TN

Some of the useful performance metrics that we can employ to evaluate CPD algorithms are summarized below. While these are described in the context of binary classification, they can each be extended to classification of a greater number of classes by providing the measures for each class independently or in combination.

• Accuracy, calculated as the ratio of correctly-classified data points to total data points. This measure provides a high-level idea about the algorithm’s performance. The companion to accuracy is Error Rate, which is computed as 1 - Accuracy. Accuracy and Error Rate do not provide insights on the source of the error or the distribution of error among the different classes. In addition, they are ineffective for evaluating performance in a class-imbalanced dataset, which is typical for change point detection, because they consider different types of classification errors as equally important. Sensitivity and g-mean are useful metrics to utilize in this case.

  $$\text{Accuracy}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{FP}+\text{FN}+\text{TN}}$$
• Sensitivity, also referred to as Recall or the true positive rate (TP Rate). This refers to the portion of a class of interest (Change Points) that was recognized correctly.

  $$\text{Sensitivity}=\text{Recall}=\text{TP}\text{Rate}=\frac{\text{TP}}{\text{TP}+\text{FN}}$$
• G-mean. Change point detection typically results in a learning problem with an imbalanced class distribution because the ratio of changes to total data is small. As a result, G-mean is commonly used as an indicator of CPD performance. This utilizes both Sensitivity and Specificity measures to assess the performance of the algorithm both in terms of the ratio of positive accuracy (Sensitivity) and the ratio of negative accuracy (Specificity).

  $$G-\mathit{mean}=\sqrt{\mathit{Sensitivity}\times \mathit{Specificity}}=\sqrt{\frac{TP}{TP+FN}\times \frac{TN}{FP+TN}}$$
• Precision. This is calculated as the ratio of true positive data points (change points) to total points classified as change points.

  $$\mathit{Precision}=\frac{TP}{TP+FP}$$
• F-measure (also referred to as f-score or f1 score). This measure provides a way to combine Precision and Recall as a measure of the overall effectiveness of a CPD algorithm. F-measure is calculated as a ratio of the weighted importance of Precision and Recall.

  $$F-\mathit{measure}=\frac{{(1+\beta )}^2\times \mathit{Recall}\times \mathit{Precision}}{{\beta }^2\times \mathit{Recall}+\mathit{Precision}}=\frac{{(1+\beta )}^2\times \frac{TP}{TP+FN}\times \frac{TP}{TP+FP}}{{\beta }^2\times \frac{TP}{TP+FN}+\frac{TP}{TP+FP}}$$

• Receiver Operating Characteristics Curve (ROC). ROC-based assessment facilitates explicit analysis of the tradeoff between true positive and false positive rates. This is done by plotting a two-dimensional graph with the false positive rate on the x axis and the true positive rates on the y axis. A CPD algorithm produces a (TP_Rate, FP_Rate) pair that corresponds to a single point in the ROC space. One algorithm can generally be considered as superior to another if its point is closer to the (0,1) coordinate (the upper left corner) than the other. To assess the overall performance of an algorithm, we can look at the Area Under the ROC curve, or AUC. In general, we want the false positive rate to be low and the true positive rate to be high. This means that the closer to 1 the AUC value is, the stronger is the algorithm. Another useful measure that can be derived from the ROC curve is the Equal Error Rate (EER), which is the point where the false positive rate and the false negative rate are equal. This point is kept small by a strong algorithm.

• Precision-Recall Curve (PR Curve). A PRC can also be generated and used to compare alternative CPD algorithms. The PR curve plots precision rate as a function of recall rate. While optimal algorithm performance for an ROC curve is indicated by points in the upper left of the space, optimal performance in the PR space is near the upper right. As with the ROC, the area under a PRC can be computed to compare two algorithms and attempt to optimize CPD performance. The PR curve in particular provides insightful analysis when the class distribution is highly skewed.

If the difference in time between the detected change point (CP) and the actual CP represents the measure of performance (utilizing supervised or unsupervised CPD methods), then the above metrics are not appropriate choices. Evaluating the performance of these algorithms is not as straightforward as for the previous case, because there is no single label against which the performance of the algorithm can be measured. However, a number of useful metrics exist for this case, including:

• Mean absolute error (MAE). This directly measures how close the predicted CP is to the actual CP. The absolute value of the difference between the predicted and actual CP time is summed and normalized over each of the CP points.

  $$\mathit{MAE}=\frac{{\sum }_{i=1}^{\#CP}\mid \mathit{Predicted}(CP)-\mathit{Actual}(CP)\mid }{\#CP}$$
• Mean squared error (MSE) is a well-known alternative to MAE. In this case, because the errors are squared, the resulting measure will be very large if a few dramatic outliers exist in the classified data.

  $$\mathit{MSE}=\frac{{\sum }_{i=1}^{\#CP}{(\mathit{Predicted}(CP)-\mathit{Actual}(CP))}^2}{\#CP}$$
• Mean signed difference (MSD). In addition to calculating the difference between the predicted and actual CP, this measure considers the direction of the error (predicting before or after the actual CP time).

  $$\mathit{MSD}=\frac{{\sum }_{i=1}^{\#CP}(\mathit{Predicted}(CP)-\mathit{Actual}(CP))}{\#CP}$$
• Root mean squared error (RMSE). This aggregates the difference between predicted and actual error and squares each difference to remove the sign factor. The square root is computed of the final estimate to offset the scaling factor of squaring the individual differences.

  $$\mathit{RMSE}=\sqrt{\frac{{\sum }_{i=1}^{\#CP}{(\mathit{Predicted}(CP)-\mathit{Actual}(CP))}^2}{\#CP}}$$
• Normalized root mean squared error (NRMSE). This measure removes the sensitivity of the values to the unit size of the predicted value. NRMSE facilitates more direct comparison of error between different datasets and aids in interpreting the error measures. Two common methods are to normalize the error to the range of the observed CPs or normalize to the mean of the observed CPs.

  $$\begin{array}{c}\mathit{NRSMSE}=\frac{\mathit{RMSE}}{\mathit{MaxLength}(\mathit{Actual}CP)-\mathit{MinLength}(\mathit{Actual}CP)}\\ \mathit{NRMSE}=\frac{\mathit{RMSE}}{\mathit{mean}(\mathit{Actual}CP)}\end{array}$$

3. Review

Many machine learning algorithms have been designed, enhanced, and adapted for change point detection. Here, we provide an overview of the basic algorithms that are commonly applied to the CPD problem. These techniques include both supervised and unsupervised methods, chosen based on the desired outcome of the algorithm.

3.1. Supervised Methods

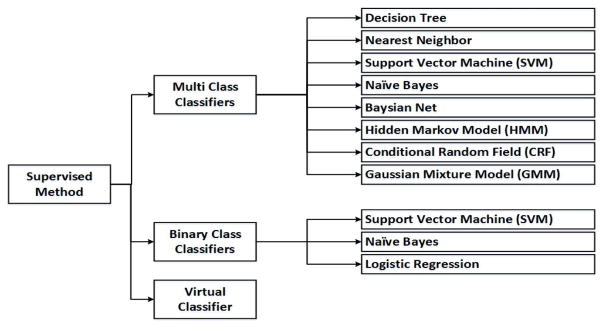
Supervised learning algorithms are machine learning algorithms that learn a mapping from input data to a target attribute of the data, which is usually a class label [35]. Figure 3 provides an overview of supervised methods used in change point detection. When a supervised approach is employed for change point detection, machine learning algorithms can be trained as binary or multi-class classifiers. If the number of states is specified, the change point detection algorithm is trained to find each state boundary. A sliding window moves through the data, considering each possible division between two data points as a possible change point. While this approach has a simpler training phase, a sufficient amount and diversity of training data needs to be provided to represent all of the classes. On the other hand, detecting each class separately provides enough information to find both the nature and the amount of detected change. A variety of classifiers can be used for this learning problem. Examples include decision tree [33][34][36][37], naïve Bayes [33], Bayesian net [34], support vector machine [33][34], nearest neighbor [33][20], hidden Markov model [38][39][33], conditional random field [34], and Gaussian mixture model (GMM) [38][39].

Figure 3.

Supervised methods for change point detection.

An alternative is to treat change point detection as a binary class problem, where all of the possible state transition (change point) sequences represents one class and all of the within-state sequences represents a second class. While only two classes need to be learned in this case, this is a much more complex learning problem if the number of possible types of transitions is large [35]. As with the previous type of supervised approaches, in this learning approach each feature in the input vector indicates a source of possible change. Therefore, any supervised learning algorithm that generates an interpretable model (such as a decision tree or a rule learner) will not only identify a change but also describe the nature of the change. Support vector machines [21][40], naïve Bayes [21], and logistic regression [21] have been tested using this approach. This type of problem will also suffer from extreme class imbalance as there are typically many more within-state sequences than change point sequences.

Another supervised approach is to use a virtual classifier [4]. This method goes beyond just detecting changes to actually interpreting a change that occurs between two consecutive windows. The virtual classifier attaches a hypothetical label (+1) to each sample from the first window and (−1) to each sample from the second window, then trains a virtual classifier (VC) using any supervised method based on the labeled data points. If there is a change point between two windows, they should be correctly classified by the classifier and the classification accuracy p should be significantly higher than random noise p_rand=0.5. In order to test the significance of a change score, the inverse survival function of a binomial distribution is used to determine a critical value, p_critical, at which Bernoulli trials are expected to exceed p_rand with α confidence level. Finally, if p > p_critical, a significant change exists between the two windows. Once the change point is detected, the classifier is retrained using all of the samples in the two neighboring windows. If some features play a dominant role in the classifier, then they are the ones that characterize the difference.

3.2 Unsupervised Methods

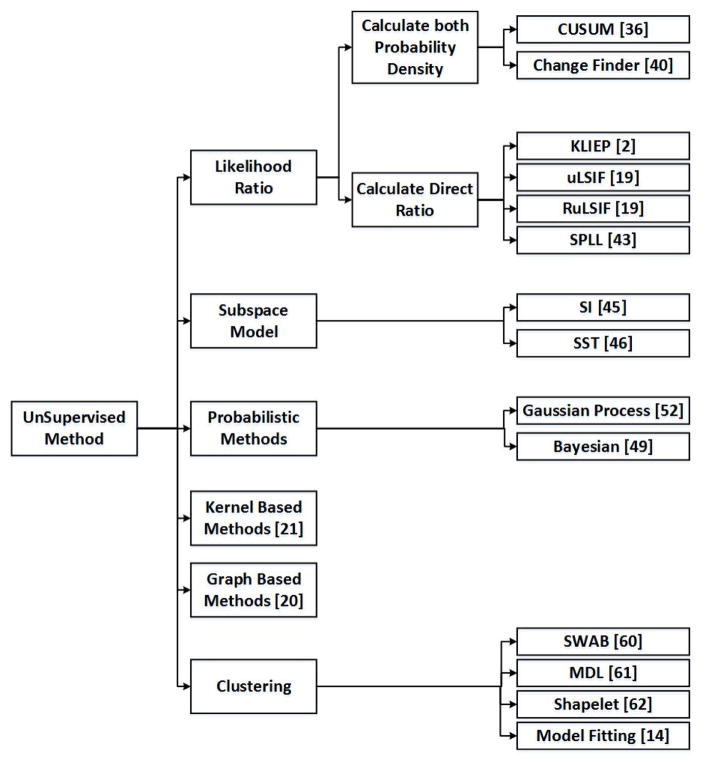
Unsupervised learning algorithms are typically used to discover patterns in unlabeled data. In the context of change point detection, such algorithms can be used to segment time series data, thus finding change points based on statistical features of the data. Unsupervised segmentation is attractive because it may handle a variety of different situations without requiring prior training for each situation. Figure 4 provides an overview of unsupervised methods that have been used for change point detection. Early reported methods utilize likelihood ratio based on the observation that the probability density of two consecutive intervals are the same if they belong to the same state. Another traditional solution is subspace modelling, which represents a time series using state spaces and thus detects change points by predicting the state space parameters. Probabilistic methods estimate probability distributions of the new interval based on the data that has been observed since the previous candidate change point. In contrast, kernel-based methods map observations onto a higher-dimensional feature space and detect change points by comparing the homogeneity of each subsequence. The graph based technique is a newly-introduced method which represents time series observations as a graph and applies statistical tests to detect change points based on this representation. Finally, clustering methods group time series data into their respective states and find changes by identifying differences between features of the states.

Figure 4.

Unsupervised methods for change point detection.

3.2.1 Likelihood Ratio Methods

A typical statistical formulation of change-point detection is to analyze the probability distributions of data before and after a candidate change point, and identify the candidate as a change point if the two distributions are significantly different. In these approaches, the logarithm of the likelihood ratio between two consecutive intervals in time-series data is monitored for detecting change points [2].

This strategy requires two steps. First, the probability density of two consecutive intervals is calculated separately. Second, the ratio of these probability densities is computed. The most familiar change point algorithm is cumulative sum [41][42][43][44], which accumulates deviations relative to a specified target of incoming measurements and indicates that a change point exists when the cumulative sum exceeds a specified threshold.

Change Finder [2][45][22] is another commonly used method which reduces the problem of change point detection into time series-based outlier detection. This method fits an Auto Regression (AR) model onto the data to represent the statistical behavior of the time series and updates its parameter estimates incrementally so that the effect of past examples is gradually discounted. Considering time series xt, we can model the time series using an AR mode of the kth order by:

$$x_t=\omega x_{t-k}^{t-1}+\epsilon$$

where $x_{t-k}^{t-1}=(x_{t-1},x_{t-2},\dots ,x_{t-k})$ are previous observations, ω = (ω₁, … , ω_k) ∈ ℝ^k are constants, and ε is a normal random variable generated according to a Gaussian distribution like white noise. By updating model parameters the probability density function at time t is calculated and we have a sequence of probability densities {p_t: t = 1, 2, … }. Next, an auxiliary time-series y_t is generated by giving a score to each data point. This score function is defined as the average of the log-likelihood, Score(y_t) = − log p_t–1(y_t), or statistical deviation, Score(y_t) = d(p_t–1, p_t), where d(*,*) is provided by any of a number of distance functions including variation distance, Hellinger distance, or quadratic distance. The new time series data represents the difference between each pair of consecutive time series intervals. In order to detect change points, we need to know if there are abrupt changes between two consecutive differences. To do this, one more AR model is fit to the difference-based time series and a new sequence of probability density functions {q_t: t = 1, 2, … } is constructed. The change-point score is defined using aforementioned score function. A higher score indicates a higher possibility of being a change point.

Since these methods rely on pre-designed parametric models and they are less flexible in real-world change point detection scenarios, some recent studies introduce more flexible non-parametric variations by estimating the ratio of probability densities directly without needing to perform density estimation. The rationale of this density-ratio estimation idea is that knowing the two densities implies knowing the density ratio. However, the inverse is not true: knowing the ratio does not necessarily imply knowing the two densities because such decomposition is not unique. Thus, direct density-ratio estimation is substantially simpler than density estimation. Following this idea, methods of direct density-ratio estimation have been developed [2][22]. These methods model the density ratio between two consequent intervals χ and χ′ by a non-parametric Gaussian kernel model as follows:

$$\begin{array}{c}g(\mathcal{X})=\frac{p(\mathcal{X})}{p^{\prime }({\mathcal{X}}^{\prime })}={\sum }_{l=1}^n{\theta }_{l}K(X,X_l)\\ K(X,X^{\prime })=\mathit{exp}\left(-\frac{{\Vert X-X^{\prime }\Vert }^2}{2{\sigma }^2}\right)\end{array}$$

Where p(χ) is the probability distribution of interval χ, θ = (θ₁, … , θ_n)^T are parameters to be learned from data samples, X is a sliding window, and σ > 0 is the kernel parameter. In the training phase, the parameters θ are determined so that the dissimilarity measure is minimized. Given a density-ratio estimator g(χ), an approximator of the dissimilarity measure between two samples χ_t and χ_t+n is calculated in the test phase. The higher the dissimilarity measure is, the more likely the point is a change point [2][22].

A popular choice for the dissimilarity measure is Kullback-Leibler (KL) divergence:

$$KL[p(x)\Vert p^{\prime }(x)]=-\int p^{\prime }(x)\mathit{log}\frac{p(x)}{p^{\prime }(x)}dx$$

The Kullback-Leibler importance estimation procedure (KLIEP) estimates the density ratio using KL divergence. This problem is a convex optimization problem, so the unique global optimal solution θ can be simply obtained, for example, by a gradient projection method. Projected gradient descent moves in the direction of the negative gradient at each step and projects onto the feasible parameter. The resulting approximation of KL divergence is given in the following equation [2][22].

$$\widehat{KL}=\frac{1}{n}{\sum }_{i=1}^n\mathit{log}\widehat{g}(Y_i)$$

Another direct density ratio estimator is uLSIF (Unconstrained Least-Squares Importance Fitting) which uses Pearson (PE) divergence as a dissimilarity measure, shown as:

$$PE[p(x)\Vert p^{\prime }(x)]=\int p^{\prime }(x){\left(\frac{p(x)}{p^{\prime }(x)}-1\right)}^{2}dx$$

As part of the uLSIF training criterion, the density-ratio model is fitted to the true density ratio under the squared loss. An approximator of the PE divergence is as follows [22]:

$$\widehat{PE}=-\frac{1}{2n}{\sum }_{j=1}^n\widehat{g}{(Y_j^{\prime })}^2+\frac{1}{n}{\sum }_{i=1}^n\widehat{g}(Y_i)-\frac{1}{2}$$

Depending on the condition of the second interval density p′ (x), the density-ratio value can be unbounded. To overcome this problem, α -relative PE divergence for 0 ≤ α < 1 is used as a dissimilarity measure in an approach known as Relative uLSIF (RuLSIF). The RuLSIF measure is:

$$P{E}_{\alpha }[p(x)\Vert p^{\prime }(x)]=PE(p(x)\Vert \alpha p(x)+(1-\alpha )p^{\prime }(x))$$

The α-relative density ratio is reduced to a plain density ratio if α = 0, and it tends to be “smoother” as α gets larger. The novelty of RuLSIF is that it is always bounded above by $\frac{1}{\alpha }$, and it has been shown that the convergence rate for estimating the relative density ratio is faster than that of the uLSIF [22][46].

Recently, a Semi-Parametric Log-Likelihood Change Detector (SPLL) [47][48][49] was proposed as a semi-parametric change detector based on Kullback-Leibler statistics. Suppose that the data before the change point (window W₁) come from a Gaussian mixture, p₁(x). The change detection criterion is derived using an upper bound of the log-likelihood of the data in the second window, W₂ using the index of the component with the smallest squared Mahalanobis distance between x and its center. If W₂ does not come from the same distribution of W₁, then the mean of the distances will deviate from n (where n is the dimensionality of the feature space). A value of SPLL that is larger or smaller than a specified range will indicate a change. It is important to note that the accuracy of all of these estimation methods is degraded by data noise [46].

3.2.2 Subspace Model Methods

Another line of research bases change point detection on an analysis of subspaces in which time series sequences are constrained. This approach has a strong connection with a system identification method, which has been thoroughly studied in the area of control theory [2].

One such subspace model method is called subspace identification (SI) [22][50]. SI is based on a state space model of the system which also explicitly considers a noise factor.

$$\begin{array}{l}x(t+1)=Ax(t)+Ke(t)\\ y(t)=Cx(t)+e(t)\end{array}$$

Here C and A are system matrices, e(t) represents system noise and K is the stationary Kalman gain. We are using different notation in subspace methods. Since in these methods x represents model states, we use y as time series.

In system identification, an extended observability matrix is a measure for how well internal states (x(t)) of a system can be inferred by knowledge of its external outputs, (y(t)). Here we use the extended observability matrix as a representation of a subspace in which time series data are constrained.

An extended observability matrix is defined as:

$${\mathrm{O}}_k=[\begin{array}{cccc}{C}^T& {(CA)}^T& \dots & {(C{A}^{k-1})}^T\end{array}]$$

For each interval as described in Section 2.1, SI estimates the observability matrix using LQ factorization and Singular Value Decomposition (SVD) of the normalized conditional covariance. LQ factorization is the orthogonal decomposition of a matrix into lower trapezoidal matrices. The SVD of a matrix A is the factorization of A into the product of three matrices A = UDV^T where the columns of U and V are orthonormal and the matrix D is diagonal with positive real entries. In the next step, the gap between subspaces is calculated and utilized as a measure of the change in the time series sequence. This measure of change, D, can be compared to a specified threshold to determine if the current point is a change point.

$$D={\mathcal{X}}^T\mathcal{X}-{\mathcal{X}}^{T}U{U}^T\mathcal{X}$$

Here χ represents the Hankel matrix of the new interval and U is calculated by the SVD of the estimated extended observability matrix for the previous interval.

The next subspace model method we will discuss is called a Singular Spectrum Transformation (SST) [11][22] [30], which is also based on a state space model. Unlike the SI model, however, it does not consider the system noise. SST will define a trajectory matrix based on an explained Hankel matrix for each window as shown in the following equation:

$$X=\left(\begin{array}{cccc}{y}_1& y_2& \cdots & y_K\\ y_2& y_3& \cdots & y_{K+1}\\ ⋮& ⋮& \ddots & ⋮\\ y_L& y_{L+1}& \cdots & y_N\end{array}\right)$$

where L is the window length and K is the number of windows. The trajectory matrix can be decomposed into submatrices using SVD. These submatrices consist of singular value empirical orthogonal functions, or EOF functions, and principal components. Distance-based change point scores are defined by a comparison between singular spectrums of two trajectory matrices for consecutive intervals.

Although both of these subspace model methods are based on a predefined model, SST does not consider the effect of noise on the system. As a result, it is more sensitive than SI to choices of parameter values and has demonstrated lower accuracies for some datasets [22][50].

3.2.3 Probabilistic Methods

Early Bayesian approaches to change point detection were offline ( ∞ – real time) and were based on retrospective segmentation [51][52]. One of the first approaches to online Bayesian change point detection (BCPD) was introduced under the assumption that a sequence of observations may be divided into non-overlapping states partitions and the data within each state ρ in time series are i.i.d. from some probability distribution P(x_t|η_ρ) [31].

Compared to the previous methods which only consider pairs of consecutive samples, BCPD compares new sliding window features with the estimation based on all previous intervals from the same state. BCPD estimates the posterior distribution by defining an auxiliary variable run-length (r_t) which represents the time that elapsed since the last change point. Given the run length at a time instant t, the run length at the next time point can either reset back to 0 (if a change point occurs at this time) or increase by 1 (if the current state continues for one more time unit). The run length distribution based on Bayes’ theorem can be denoted as:

$$P(r_t\mid x_{1:t})=\frac{{\sum }_{r_{t-1}}P(r_t\mid r_{t-1})P\left(x_t\mid r_{t-1},x_t^{(r)}\right)P(r_{t-1},x_{1:t-1})}{{\sum }_{r_t}P(r_t,x_{1:t})}$$

Where $x_t^{(r)}$ indicates the set of observations associated with the run r_t and P(r_t|r_t–1), $P\left(x_t\mid r_{t-1},x_t^{(r)}\right)$, and P(r_t–1, x_1:t–1) are prior, likelihood, and recursive components of the equation. The conditional prior is nonzero at only two outcomes (r_t = 0 or r_t = r_t–1 + 1) and simplifies the equation.

$$P(r_t\mid r_{t-1})=\{\begin{array}{cc}H(r_{t-1}+1)& if{r}_t=0\\ 1-H(r_{t-1}+1)& if{r}_t=r_{t-1}+1\\ 0& \mathit{otherwise}\end{array}$$

In this equation, $H(\tau )=\frac{P(\tau )}{{\sum }_{t=\tau }^{\infty }P(t)}$ is a hazard function which is defined as the ratio of probability density over the run to the total value of probability densities [31][53][54]. The likelihood term represents the probability that the most recent datum belongs to current run. This is the most challenging term to calculate and it tends to be most computationally efficient when a conjugate exponential model is used [31].

After calculating the run length distribution and updating the corresponding statistics, change point prediction is performed by comparing probability values. If r_t has the highest probability in the distribution, then a change point has occurred and the run length is reset to r_t = 0. If not, the run length is incremented by one, r_t = r_t–1 + 1 [31][53].

This method was later extended to the general case of non i.i.d time series by incorporating the likelihood of different subsequences of data in the equations. In addition, a simplification was introduced that reduces the algorithm complexity from n² to n using a simple approximation. The key idea is to compute the joint probability weights for only a fixed number of nodes, instead of computing these weights at all $\frac{n(n-1)}{2}$ nodes [7].

A Gaussian Process (GP) represents another probabilistic method for stationary time series analysis and prediction [55]. A GP is a generalization of a Gaussian distribution and is defined as a collection of random variables, any finite number of which have a joint Gaussian distribution [56][57]. In this method, time series observations {x_t} are defined as a noisy version of Gaussian distribution function values f(t).

$$x_t=f(t)+{\epsilon }_t$$

In this Gaussian distribution function, ε_t is a noise term, usually assumed to be a Gaussian noise term $\mathcal{N}(0,{\sigma }_n^2)$ and f(t) = 𝒢℘(0, K) is a GP distribution function specified by mean zero and covariance function K. Typically, a covariance function is specified using a set of hyper-parameters. A widely used covariance function is:

$$K(t_1,t_2)={\sigma }^2\mathit{exp}\left(-\frac{{(t_1-t_2)}^2}{2l^2}\right)$$

Given a time series, the GP function can be used to make a normal distribution prediction at time t. The GP Change algorithm uses a Gaussian process to estimate the predictive distribution at time t using observations available through time (t − 1). The algorithm then computes the p-value for the actual observation y_t under the reference distribution, $\mathcal{N}({\widehat{y}}_t,{\widehat{\sigma }}_t^2)$. A threshold α ∈ (0,1) is used to determine when the actual observation does not follow the predictive distribution, which is indicative of a possible state change (and thus a change point) [56]. Using observations available through time t–1 to detect change points instead of using only observations from the last state makes the GP method more complicated and yet more accurate than BCPD.

3.2.4 Kernel Based Methods

Although kernel-based methods are typically utilized as supervised learning techniques, some studies use an unsupervised kernel-based test statistic to test the homogeneity of data in time series past and present sliding windows. These methods map the observations in a reproducing kernel Hilbert space (RKHS) ℋ associated with a reproducing kernel k(. , . ) and a feature map Φ(X) = k(X, . ) [58]. They then use a test statistic based upon the kernel Fisher discriminant ratio as a measure of homogeneity between windows.

Considering two windows of observations, the empirical mean elements and covariance operators for sample X with length n are calculated as:

$$\begin{array}{c}\widehat{\mu }=\frac{1}{n}{\sum }_{l=1}^{n}k(X_l,.)\\ \widehat{\mathrm{\sum }}=\frac{1}{n}\sum _{l=1}^n\{k(X_l,.)-\widehat{\mu }\}\otimes \{k(X_l,.)-\widehat{\mu }\}\end{array}$$

where the tensor product operator u⊗v for all function f ∈ ℋ is defined as (u⊗v)f = 〈v, f〉_ℋu. Now the kernel Fisher discriminant ratio (KFDR) between two samples is defined as [58][24]:

$$\mathit{KFDR}(X_1^{\mathit{length}{n}_1},X_2^{\mathit{length}{n}_2})=\frac{n_1{n}_2}{n_1+n_2}{\langle {\widehat{\mu }}_2-{\widehat{\mu }}_1,{({\widehat{\mathrm{\sum }}}_w+\gamma I)}^{-1}({\widehat{\mu }}_2-{\widehat{\mu }}_1)\rangle }_{\mathcal{H}}$$

where γ is a regularization parameter and

$${\widehat{\mathrm{\sum }}}_w=\frac{n_1}{n_1+n_2}{\widehat{\mathrm{\sum }}}_1+\frac{n_2}{n_1+n_2}{\widehat{\mathrm{\sum }}}_2.$$

The easiest way to determine whether a change point exists between two windows is comparing the KFDR ratio with a threshold value [58]. The other method known as running maximum partition strategy [24] calculates the KFDR ratio between all consequent windows in each interval. Then the maximum ratio will be compared to threshold to detect change point.

A common drawback for kernel-based methods is that they rely heavily on the choice of the kernel function and its parameters, and the problem becomes more severe when the data are in moderate to high dimensional spaces [23].

3.2.5 Graph Based Methods

Several recent studies showed time series can be investigated using graph theory tools. The graph is usually derived from a distance or a generalized dissimilarity on the sample space, with time series observations as nodes and edges connecting observations based on their distance. This graph can be defined based on a minimum spanning tree [59], minimum distance pairing [60], nearest neighbor graph [59][60], or visibility graph [61][62].

A graph based framework for change point detection is a nonparametric approach that applies a two sample test on an equivalent graph to find whether there is a change point within the observations or not. In this method graph G is constructed for each sequence of data. Each possible value of τ as change point time divides the observations into two windows: observations that come before τ and observations that come after τ. The number of edges in the graph G (R_G) that connects observations from these two windows is used as an indicator of a change point, so that smaller edges increase the possibility of change point. Since the value of R_G depends on time t, the standardized function (Z_G) is defined as:

$$Z_G(t)=-\frac{R_G(t)-E[R_G(t)]}{\sqrt{\mathit{VAR}[R_G(t)]}}$$

where E[. ] and VAR[. ] are Expectation and Variance, respectively. The maximum value of Z_G among all data points in the graph is identified as a candidate change point. The change point is accepted if the maxima is greater than a specified threshold [23]. This method is powerful for high dimensional data with fewer parameter assumptions. However, it does not utilize much information from the time series observations themselves, instead relying on defining an appropriate graph structure.

3.2.6 Clustering Methods

From a different perspective, the problem of change point detection can be considered as a clustering problem with a known or unknown number of clusters, such that observations within clusters are identically distributed, and observations between adjacent clusters are not. If a data point at time stamp t belongs to a different cluster than the data point at time stamp t+1, then a change point occurs between the two observations.

One clustering approach used for change point detection combines sliding window and bottom up methods into an algorithm called SWAB (Sliding Window and Bottom-up) [63]. The original bottom-up approach first treats each data point as a separate subsequence, then merges subsequences with an associate merge cost until the stopping criteria is met. In contrast, SWAB maintains a buffer of size w to store enough data for 5 – 6 subsequences. The bottom-up method is applied to the data in the buffer and the leftmost resulting subsequence is reported. The data corresponding to the reported subsequence are removed from the buffer and replaced with the next data in the series.

A second clustering approach groups subsequences based on Minimum Description Length [32]. The description length DL of a time series T of length m is the total number of bits that are required to represent the series, or:

$$DL(T)=m\ast H(T)$$

where H(T) is the entropy of the time series.

MDL-based change point detection is a bottom-up greedy search over the space of clusters which can include subsequences of different lengths and does not require the number of clusters to be specified. This method clusters enumerated motifs instead of all the subsequences.

After finding time series motifs, three search operators are applied: create (create a new cluster), add (add a subsequence to an existing cluster), and merge (merge two clusters). The value of bitsave represents the total number of bits that are saved by applying one of these operators to the time series.

$$\mathit{bitsave}=DL(\mathit{Before})-DL(\mathit{After})$$

The bitsave for each operator is defined as the following:

1. Creating a new cluster C from subsequences A and B

   $$\mathit{bitsave}=DL(A)+DL(B)-\mathit{DLC}(C)$$

   DLC(C) is the number of bits needed to represent all subsequences in cluster C.

2. Adding a subsequence A to an existing cluster C

   $$\mathit{bitsave}=DL(A)+\mathit{DLC}(C)-\mathit{DLC}(C^{\prime })$$

   C′ is the cluster C after including subsequence A.

3. Merging cluster C1 and C2 to a new cluster C

   $$\mathit{bitsave}=\mathit{DLC}(C_1)+\mathit{DLC}(C_2)-\mathit{DLC}(C)$$

The first step creates a new cluster from the motifs and the number of bits saved using this step is calculated. In the next stage of the algorithm, there are two operators available: create or add. The new subsequence can be added to one of the existing clusters or it can be assigned as the only member of a newly-created cluster. To add a subsequence into an existing cluster, the distance between the subsequence and each cluster is calculated to find the cluster nearest to the subsequence. After the search, the nearest cluster is updated to include the subsequence, the number of bits saved is calculated, and the clusters are recorded. After each step, any pair of clusters is allowed to merge if it maximally decreases the description length (increases bitsave). Since the MDL technique requires discrete data, this method is applicable to discretized time series values.

Another way to cluster time series data as a way to find change points using a Shapelet method [64]. An unsupervised-shapelet, or u-shapelet S, is a small pattern in a time series T for which the distance between S and part of time series is much smaller than the distance between S and the rest of the time series. Shapelet-based clustering, which attempts to cluster the data based on the shape of the entire time series, searches for a u-shapelet which can separate and remove a time series subsequence from the rest of the dataset. The algorithm iteratively repeats this search among the remaining data until no data remains to be separated. A greedy search algorithm which attempts to maximize the separation gap between two subsets of data is used to extract u-shapelets. Then any clustering algorithm such as k-means with a Euclidian distance function can be used to cluster the time series and find change points.

Yet another time series clustering approach is Model fitting, in which a change can be considered to occur when a new data item or block of data items do not fit into any of the existing clusters [17]. Assuming a data stream {x₁, … , x_i, … }, change point is occurred after data point x_i, if the following logical expression is true.

$$\mathit{change}={\bigwedge }_{j=1}^k\left[d\left(x_{i+1},\mathit{center}(C_j)\right)>\mathit{radius}(C_j)\right]$$

where d (x_i+1, center(C_j)) is the Euclidian distance between a newly-incoming data point x_i+1 and the center of cluster C_j, radius(C_j) is the radius of cluster j, K is the number of clusters, and ^ is the logical and symbol. The radius of cluster C with n data point and mean value of μ is:

$$\mathit{radius}(C)=\sqrt{\frac{{\sum }_{i=1}^n{(x_i-\mu )}^2}{n}}$$

4. DISCUSSION AND COMPARISON

The previous sections present an overview of change point detection algorithms that are commonly used in the literature. Choosing the most appropriate algorithm a particular dataset depends on which criterion is most important for the application. Here, we compare CPD methods based on several frequently-used criteria.

4.1 Online vs Offline

One important criteria for change point detection is the ability to identify the change point in real time or near-real time. The complete offline algorithms are applicable when processing an entire time series at once, and ε –real time algorithms need to look at least ε data points ahead of the candidate change point. The value of ε depends on the nature of the algorithm and amount of input data that is required for each step. Online algorithms process data within a sliding window with size n. For these approaches, n should be large enough to store the data that is necessary to represent the time series state yet small enough to still meet the epsilon requirement.

Supervised methods

Once they process enough training data, these methods will predict if there is a CP in the current window. Therefore we can state that supervised techniques are n-real time.

Likelihood ratio methods

These methods are based on comparing probability densities between two consequent intervals. When a new retrospective subsequence comes the new calculation will return the result so we can say these methods are n+k-real time.

Subspace Model

New intervals in these techniques are calculated in the same manner as for likelihood methods. As a result, these methods are also n+k-real time.

Probabilistic Methods

These methods rely only upon a single sliding window for detecting CP, so they are n-real time.

Kernel Based Methods

Unsupervised kernel methods are based on sliding windows. However, as with the likelihood ratio methods these need a retrospective subsequence of data, so they are n+k-real time.

Clustering

The SWAB technique is a combination of sliding window and bottom up. SWAB maintains a buffer of size w. Bottom-up is applied to the data in the buffer and the leftmost subsequence is reported. As a result, SWAB is w-real time. MDL-based methods and Shapelet-based methods need to access the entire time series at once, so they are offline or infinity-real time. The model fitting technique depends on a single window and therefore is n-real time.

Graph Based Method

This technique derives a graph from a single window. A change point is reported if it exists within the current window, thus the method is n-real time.

Figure 5 visualizes the relationship between the alternative CPD approaches and their point on the continuum between complete offline and online processing.

Figure 5.

Offline vs. online CPD algorithm comparison.

4.2 Scalability

A second important criteria is the computational cost of change point detection algorithms. The computational cost of the algorithms we survey, where available, are compared in Table 2. Where authors do not provide this information, the comparison has been performed qualitatively based on algorithmic descriptions. In general, as the dimension of the time series increases the nonparametric methods gain power in computational cost and will be less expensive than parametric methods. It is very hard to characterize the cost of supervised methods because there are two complexities involved. These are at the run time of the training stage and the run time of the CP detection stage.

Table 2.

Comparison of CPD algorithm scalability based on sliding window size n. * = estimate based on algorithm.

Category	Method	Parametric/Non Parametric	Computational Cost
Probability Density Ratio	CUSUM	Parametric	O(n2)*
	AR	Parametric	O(n3)*
	KLIEP	Non Parametric	KLIEP< CUSUM ; KLIEP < AR
	uLSIF	Non Parametric	uLSIF < KLIEP
	RuLSIF	Non Parametric	RuLSIF < uLSIF
	SPLL	Semi Parametric	O(n2)*
Subspace Models	SI	Parametric	SI > KLIEP
	SST	Parametric	SST > KLIEP
Probabilistic Method	Bayesian	Parametric	O(n)
	GP	Non Parametric	O(n2)
Kernel Based Methods	KcpA	Non Parametric	O(n3)
Clustering	SWAB		O(Ln)
	MDL
	Shapelet
	Model Fitting
Graph Based Methods		Non Parametric
Multi-Class Classifier	Nearest Neighbor	Non Parametric	= Cost (Training + CP detection)
	HMM	Parametric
	GMM	Parametric
Binary Class Classifier	SVM	Parametric
	Naive Bayes	Parametric
	Logistic Regression	Parametric

To the best of our knowledge no existing CPD algorithm provides an interruptible or contract anytime option. This can be considered an avenue for future research.

4.3 Learning Constraint

Most of the likelihood ratio methods (except SPLL) and all of the subspace model techniques originally were designed for one-dimensional time series. Thus in the case of a d-dimensional time series, these methods merge all of the dimensions together and generate a one-dimensional series with a d-size value vector. Although there is no constraint on time series dimensionality for the other algorithms, increasing the number of dimensions will increase the algorithm’s computational cost.

All of the algorithms accept both discrete and continuous time series input. One exception is the MDL-based method, which work only with discrete input values.

The supervised learning approaches to CPD operate under the assumption that a transition period can be detected independent of the current time series state. In contrast, the unsupervised learning algorithm operates under the assumption that the distribution of time series data changes before and after each change point [21]. While the supervised data frequently outperform unsupervised methods in detecting change points, they depend on sufficient quality and quantity of training data, which is not always accessible for real world data. The multi-class supervised algorithms are the only group that needs to know the number of possible time series states.

In general, non-parametric CPD methods are more robust than parametric ones because the parametric methods rely heavily on the choice of parameters. In addition, the CPD problem becomes more complex for parametric methods when the data has moderate to high dimensionality.

Most unsupervised CPD algorithms operate on limited types of time series data. Some of them are only work for stationary or i.i.d. datasets and others offer parametric versions for non-stationary time series datasets. The corresponding parametric versions use a forgetting factor to remove the effects of older observations. Table 3 summarizes these limitations for the methods that we survey.

Table 3.

Comparison of CPD algorithm limitations.

Category	Method	Time Series Limitation
Probability Density Ratio	CUSUM	No Limitation
	AR	No Limitation
	KLIEP	The parametric version should be used in case of non-stationary time series
	uLSIF	The parametric version should be used in case of non-stationary time series
	RuLSIF	The parametric version should be used in case of non-stationary time series
	SPLL	Time Series should be i.i.d.
Subspace Models	SI	The parametric version should be used in case of non-stationary time series
	SST	Time Series should be Stationary
Probabilistic Method	Bayesian	The original method works only for i.i.d. time series Extended version works for non-i.i.d time series
	GP	Time Series should be Stationary
Kernel Based Methods	KcpA	Time Series should be i.i.d.
Clustering	SWAB	No Limitation
	MDL	No Limitation
	Shapelet	No Limitation
	Model Fitting	No Limitation
Graph Based Methods		Time Series should be i.i.d.
Multi-Class Classifier	Nearest Neighbor	No Limitation
	HMM	No Limitation
	GMM	No Limitation
Binary Class Classifier	SVM	No Limitation
	Naive Bayes	No Limitation
	Logistic Regression	No Limitation

4.4 Performance Evaluation

Several artificial and real-world datasets have been used to measure the performance of CPD algorithms. It is important to notice that an objective comparison of the performance of different CPD methods is very difficult due to the use of these different datasets. Here we try to describe some popular benchmark real-world time series datasets and to compare the reported performance of different CPD methods on these datasets.

A majority of the studies do not provide any comparisons, or in some cases, even measures of performance. For example, there are no available results for the SPLL and clustering methods. Similarly, experimental results for graph-based CPD are available only for different graph structures, to demonstrate the fact that accuracy highly depends on the structure of the graph [23]. Studies that include performance analyses tend to calculate the distance between actual and detected CPs and use discrete metrics like accuracy, precision, and recall to evaluate the algorithms. Table 4 summarizes reported performance from previous studies using the following data sets:

Table 4.

Comparison of CPD algorithm performance based on accuracy (Acc), recall (Rec), Precision (Prec), Error (Err), and Area Under the ROC Curve (AUC).

Method	Dataset 1 [2] [22]	Dataset 2 [2][63][50]	Dataset 3 [58]	Dataset 4 [24]	Dataset 5 [26]	Dataset 6 [21]	Dataset 7 [22]
CUSUM					Acc = 0.75 Rec. = 0.75 Prec. = 0.75
AR	AUC = 0.79 Acc = 0.36	Acc = 0.23					AUC = 0.85
KLIEP	AUC = 0.63 Acc = 0.43	Acc = 0.49					AUC = 0.90
uLSIF	AUC = 0.86						AUC = 0.90
RuLSIF	AUC = 0.94					AUC = 0.89	AUC = 0.97
SI	AUC = 0.76 Acc = 0.39	Acc = 0.47					AUC = 0.94
SST	AUC = 0.76 Acc = 0.44	Acc = 0.46					AUC = 0.87
Bayesian					Acc = 0.50
GP					Acc = 78 Rec. = 0.75 Prec. = 0.82
Kernel			Prec. = 0.89 Rec. =0. 90	Acc = 0.79 ; 0.74; 0.61
SWAB		Max Err < 0.4
B HMM			Prec. = 0.93 Rec. =0. 96
M SVM				Acc = 0.76 ; 0.69; 0.60		AUC = 0.85
M Naive Bayes						AUC = 0.78
M Logistic Regression						AUC = 0.92

Dataset 1: Speech recognition

This is the IPSJ SIG-SLP Corpora and Environments for Noisy Speech Recognition (CENSREC) dataset provided by the National Institute of Informatics (NII) [65]. This dataset records a human voice in a noisy environment. The task is to extract speech sections from recorded signals.

Dataset 2: ECG

This is a respiration dataset found in the UCR Time Series Data Mining Archive [66]. This dataset records patients’ respiration measured by thorax extension as they wake up. The series is manually segmented by a medical expert.

Dataset 3: Speech recognition

This dataset represents soundtracks from popular French 1980s entertainment TV shows (“Le Grand ‘Echiquier”). The dataset comprises roughly three hours of sound track data.

Dataset 4: Brain-Computer Interface Data

Signals acquired during these Brain-Computer Interface (BCI) trial experiments naturally exhibit temporal structure. The corresponding dataset formed the basis of the BCI competition III. Data are acquired during four non-feedback sessions on three normal subjects where each subject was asked to perform different tasks, where time when the subject switches from one task to another are random.

Dataset 5: Iowa Crop Biomass NDVI Data

The NDVI time series data was available as a data product for years 2001 to 2006. In this dataset, observations were made for every sixteen days.

Dataset 6: Smart Home Data

This data represents sensor readings collected in a smart apartment located on the on WSU campus [67]. The apartment is equipped with infrared motion / ambient light sensors, door / ambient temperature sensors, light switch sensors, and power usage sensors. The data is labeled with corresponding human activities and changes naturally occur between the activities.

Dataset 7: Human activity dataset

This is a subset of the Human Activity Sensing Consortium [68] challenge 2011, which provides human activity information collected by portable three-axis accelerometers. The task of change-point detection is to segment the time-series data according to the six behaviors: “stay”, “walk”, “jog”, “skip”, “stair up”, and “stair down”.

In summary, we note that supervised methods tend to be more accurate than unsupervised methods if enough training data exist and the series is stationary. If these conditions are not met, the unsupervised methods are more useful. There is no comprehensive performance comparison among unsupervised methods, but it can be seen from experimental results that RulSIF consistently yields strong accuracy. Because kernel-based methods, subspace models, CUSUM, AR, and clustering methods rely upon parameters to model time series dynamics, they do not exhibit good performance for noisy data, or highly dynamic systems.

Most unsupervised algorithms place constraints on the types of time series methods that can be processed. One notable exception to this is the AR method. In addition, some of these methods have parametric versions for non-stationary data, which makes them sensitive to the choice of parameters. For high-dimension time series data, the likelihood ratio and subspace models are not the best choices, because they cannot directly handle multidimensional data. In this case, graph-based or probabilistic methods are more promising.

5. CONCLUSIONS AND CHALLENGES FOR FUTURE WORK

In this survey, we presented the state of the art in change point detection methods, analyzed their advantages and disadvantages, and summarized challenges that arise for change point detection. Both supervised and supervised method were used in literature to detect changes in time series. Although CPD algorithms have progressed significantly in the last decade, there are still many open challenges.

One important issue for CPD algorithms relates to the need for online algorithms and the detection delay for many existing approaches. In many real world applications, change points are used selecting and executing timely actions, thus finding the change points as soon as possible is crucial. Anytime algorithms can potentially be used to compensate for algorithm delays and adjust the computational time in balance with the quality of the detected change points. Another alternative is to employ methods that need smaller window sizes to calculate change point scores, such as Bayesian methods.

Another open problem is algorithm robustness. Although some discussion does exist about this point and generally non parametric methods are more robust than parametric ones, there is no formal analysis of robustness found in the literature. Finally, for almost all of the methods change detection depends on the window size. Although small windows would detect more local changes compared to large windows, it cannot look ahead of data and will increase cost. Incorporating variable window sizes may provide a good solution to using the best window length for each subsequence.

In many real world data analysis problems, however, the problem of change detection by itself is not of particular interest. For example, a climate change researcher may be interested in finding the amount of change in temperature instead of just detecting that a change occurred. Here, the main interest is the detailed information about the amount and source of change. Some of the existing techniques we surveyed provide information about the amount or source of change, but further work is needed to develop more accurate change analysis or change estimation algorithms. Calculating dissimilarity measures for each feature whenever a change occurs represents one possible solution for finding the change source and the total dissimilarity measure can then be used to conduct a change estimation.

Evaluating the significance of the detected change point is another important open issue for unsupervised methods. Currently, most existing methods compare detect change scores with a threshold value to determine whether change occurs or not. Selecting the optimal threshold value is difficult. These values may be application dependent and they may change over time. Developing statistical method to find significant change point based on previous values may offer greater autonomy and reliability.

Finally, an ongoing challenge for CPD is to handle non-stationary time series. Literature does exist for detecting concept drift, which can be utilized to help with this issue [69][70]. Blending change point detection with concept drift detection is a challenging but important problem, because many real-world datasets are non-stationary and multi-dimensional.