Genome-wide regulatory complexity in yeast promoters: Separation of functionally conserved and neutral sequence

Abstract

To gauge the complexity of gene regulation in yeast, it is essential to know how much promoter sequence is functional. Conservation across species can be a sensitive means of detecting functional sequences, provided that the significance of conservation can be accurately calibrated with the local neutral mutation rate. By analyzing yeast coding and promoter sequences, we find that neutral mutation rates in yeast are uniform genome-wide, in contrast to mammals, where neutral mutation rates vary along chromosomes. We develop an approach that uses this uniform rate to estimate the amount of promoter sequence under purifying selection. This amount is ∼30%, corresponding to roughly 90 bp for a typical promoter. Furthermore, using a hidden Markov model, we are able to separate each promoter into distinct high and low conservation regions. Known regulatory motifs are strongly biased toward high conservation regions, while low conservation regions have mutation rates similar to that of the neutral background. Certain Gene Ontology groupings of genes (e.g., Carbohydrate Metabolism) have large amounts of high conservation sequence, suggesting complexity in their transcriptional regulation. Others (e.g., RNA Processing) have little high conservation sequence and are likely to be simply regulated. The separation of functionally conserved sequence from the neutral background allows us to estimate the complexity of cis-regulation on a genomic scale.

The regulation of gene expression is a universal, yet complex, process in biological systems. In the model organism Saccharomyces cerevisiae, several hundred transcription factors are thought to be involved in the regulation of ∼6000 genes (Gene Ontology Consortium 2000; Dolinski et al. 2004). Much of this regulation is mediated by transcription-factor-binding sites in promoter sequences, making knowledge of these sites essential for understanding the logic of cis-regulation. One promising approach for detecting binding sites is phylogenetic footprinting, the identification of selectively constrained elements by their conservation across species. For example, the genome sequences of S. cerevisiae and several of its close relatives have been used to predict motifs likely to describe transcription-factor-binding sites (Chiang et al. 2003; Cliften et al. 2003; Kellis et al. 2003; Pritsker et al. 2004; Siddharthan et al. 2004; Tanay et al. 2004).

Although a number of transcription factors and binding motifs have been studied in detail, some basic parameters of transcriptional regulation are not known. One important feature that has not been characterized is the amount of functional sequence under purifying selection in yeast promoters. This is crucial for assessing how many transcription factors bind a typical promoter, how prevalent combinatorial control is, and whether regulation is more complex for particular gene families.

Inspection of aligned yeast promoters shows rich structure in conservation patterns. There are blocks of highly conserved sequence, as well as blocks with lower conservation rates. The extent of conservation also varies from promoter to promoter. But do these variations in conservation reflect differences in the complexity of cis-regulation, or simply differences in local neutral mutation processes? Conservation of a sequence does not necessarily imply functionality. Conservation may also be neutral, because of lack of divergence time. Variations in conservation could be explained by regional biases in mutation rates. In mammals, for example, mutation rates are known to vary in blocks several megabases long (Hardison et al. 2003; Chuang and Li 2004), but it is not known whether such regional effects are present in yeast. To determine the amount of functionally conserved sequence in yeast promoters, it is necessary to measure the neutral conservation rates along the genome, as these rates provide the calibration for significance.

In the first section of this paper we determine the local neutral mutation rates by measuring the degree of sequence conservation across the genome, using data from silent site positions in aligned yeast coding sequences (Kellis et al. 2003) from S. cerevisiae, Saccharomyces paradoxus, Saccharomyces bayanus, and Saccharomyces mikatae. Our results indicate that, unlike in mammals, the neutral mutation rate is uniform across the S. cerevisiae genome. We are able to distinguish the small set of genes that deviate from neutral expectations because of codon usage selection.

With knowledge of the neutral mutation rate, it becomes possible to determine what parts of yeast promoters evolve neutrally. In the second section, we show that yeast promoters can be separated into neutral and functionally conserved regions. Using a hidden Markov model (HMM), we are able to distinguish regions of high and low sequence conservation. We find that the conservation rates in the low conservation regions are similar to the neutral mutation rate determined from the silent sites. The highly conserved regions, on the other hand, contain an over-abundance of known transcription-factor-binding sites.

We next estimate the total amount of promoter sequence under selection in all S. cerevisiae promoters. Through an analysis of the frequencies of conserved blocks of different lengths, we find that ∼30% of sites in the promoters are under selection. This result is robust over several different species comparisons.

Finally, we analyze the length of sequence in high conservation regions for each promoter, as this provides a rough measure of how much regulation acts on each gene. We perform a functional analysis of the types of genes having long lengths of high conservation regions, finding several Gene Ontology categories with unusual conservation levels.

Results

Neutral mutation rates are uniform genome-wide

An understanding of neutral mutation rates is important for calibrating the functional significance of sequence conservation between yeast species. To determine neutral rates of conservation, we measured rates of conservation in genes shared among the species S. cerevisiae, S. paradoxus, S. mikatae, and S. bayanus, using data from fourfold degenerate base positions (see Methods). It might be argued that fourfold sites are not appropriate for measuring neutral rates, because codon usage selection affects silent sites in some S. cerevisiae genes. However, as we show below, it is possible to distinguish selective effects from neutral ones by analyzing the distribution of conservation rates and codon usage bias.

Regional biases can have a strong effect on mutation rates, as has been observed in mammals (Hardison et al. 2003; Chuang and Li 2004). Therefore, proper accounting for such biases could potentially be crucial for calibration of phylogenetic footprinting. We tested for regional biases in the yeast genome by first comparing S. cerevisiae to its closest sequenced relative, S. paradoxus, which diverged from it ∼5 million years ago (Myr) (Kellis et al. 2003). We used this closest relative to minimize the possible effects of chromosomal rearrangements, which could obscure regional biases when species are further diverged.

For each gene, we measured the conservation rate as the fraction of shared fourfold sites that are identical in S. cerevisiae and S. paradoxus. Genome-wide, the mode conservation rate at fourfold sites was 0.74. To properly account for finite-length effects, we mapped each rate to a normalized value r, by subtracting the mode conservation rate in the genome and dividing by the standard deviation predicted by an independent sites model (Chuang and Li 2004) (see Methods). We used these normalized rates to test for regional correlations, through an analysis of the autocorrelation function 〈r(0)r(x)〉, where r(0) is the normalized conservation rate of a gene, r(x) is the conservation rate of a gene x base pairs downstream from the first gene, and 〈...〉 indicates an average over all gene pairs separated by a distance x. Distances were measured along the S. cerevisiae coordinate. Since the rates r were normalized around r = 0, we expected 〈r(0)r(x)〉 0 if rates were not correlated at a distance x (see Methods).

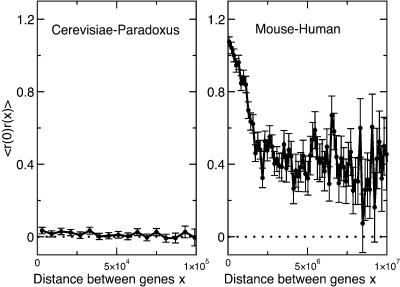
Overall, rate correlations between genes were weak. The autocorrelation function is plotted versus the gene separation x in Figure 1, with data points in bins of width 6000 bp. For almost all distances out to 100 kb, the autocorrelation was not significant. This finding contrasted strongly with the mutation patterns measured between mouse and human, in which rates are much more strongly correlated, and at distances out to several megabases along the human coordinate (Fig. 1, right graph; Chuang and Li 2004).

Figure 1.

Autocorrelation in normalized conservation rates at fourfold sites shared between S. cerevisiae and S. paradoxus. (Left) Rates are not correlated along the S. cerevisiae genome, even for genes as close as several thousand base pairs. The average distance between genes in our data set is ∼3000 bp. (Right) In contrast, mouse-human conservation rates are significantly correlated along the human genome at separations up to several megabases.

We next measured the rates at which silent sites were conserved among all four yeast species, to allow for phylogenetic footprinting using all of the genomes. For each gene shared by all four species, we measured the fraction of fourfold sites in which every species has the same base. Although classifying sites based on four-species data ignores lineage-specific effects, it has the advantage of providing much stronger signal-to-noise than any two-species comparison. Because of this choice of data, we generally use the term “selection” to indicate purifying selection common to all four species. Conversely, we use “neutral” to indicate the absence of such four-species selection. The four-species conservation rates were then normalized, analogously as for the S. cerevisiae-S. paradoxus conservation rates, using the genome-wide mode conservation rate of 0.33. We repeated the autocorrelation analysis using the four-species rates, and again found no significant correlations. For completeness, we tested rate autocorrelations in the comparisons S. cerevisiae-S. mikatae and S. cerevisiae-S. bayanus, in each case finding no correlations.

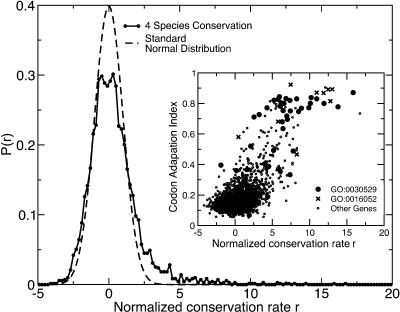
The conclusion that mutation rates are uncorrelated along the yeast genome was further supported by the genome-wide distribution of normalized four-species conservation rates. A useful property of normalized rates is that they should be Gaussian-distributed with unit standard deviation, if all fourfold sites mutate independently at the same rate (see Methods). The observed rate distribution followed the characteristics expected for independently mutating sites, as shown in Figure 2. The main part of the data distribution (around r = 0) had the same center and the same width as the standard Normal distribution. This general adherence to a Normal distribution was also observed in each of the individual comparisons S. cerevisiae-S. paradoxus, S. cerevisiae-S. mikatae, and S. cerevisiae-S. bayanus.

Figure 2.

Distribution of normalized conservation rates based on the fourfold sites in each gene. Conservation among all four species S. cerevisiae, S. paradoxus, S. mikatae, and S. bayanus. Each rate has been normalized based on the distribution expected if each fourfold site in the genome were to have an independent and equal probability of conservation at the genome-wide mode rate. The expected distribution if this hypothesis were true is a standard Normal distribution, which is shown for comparison. (Inset) Normalized conservation rate among four yeast species versus codon adaptation index. Most genes with high conservation rates at their fourfold sites have strong codon usage biases. These genes are largely ribosomal (Gene Ontology category GO:0030529, Ribonucleoprotein Complex) or are associated with energy generation (GO:0016052, Carbohydrate Catabolism).

Although the observed and expected four-species rate distributions were largely similar, the observed distribution had a bias toward high conservation rates. This is evidenced by the long tail at large values of r in Figure 2. This observation suggested that a subset of genes was biased toward high conservation by some secondary effect. We therefore used a Bayesian demixing model (see Supplemental material) to find the best separation of genes into two distributions, where we assumed that fourfold sites in each distribution had either a high or a low mutation rate, depending on the distribution. This model was optimized for the relative number of genes in each distribution, the high rate, and the low rate. From this model we estimated that 92% of the genes mutate neutrally at fourfold degenerate sites. Consistent with the mode conservation rate at fourfold sites, we found a low rate of 0.33. The high rate was 0.53.

The high conservation values for the remaining 8% of the genes were explainable by codon usage selection (Li and Sharp 1987). Genes with high conservation values were observed to have high codon usage bias, as measured by the codon adaptation index (CAI) (Li and Sharp 1987) values for the S. cerevisiae versions of the gene. The Pearson correlation of the normalized substitution rate with CAI (Dolinski et al. 2004) was 0.67 (3568 genes; p <10^-250). Many of the genes having high conservation rate were among the types known to be under codon usage selection, such as ribosomal genes and those involved in carbohydrate metabolism (Fig. 2, inset; Li and Sharp 1987).

Neutral conservation rates in promoters

Promoters, the sequences upstream of coding regions, contain functional elements such as transcription-factor-binding sites. Conservation across species can be an effective way to detect functional elements, although conservation can also be due to shared ancestry. To detect the functional elements, they must be separated from the neutral background.

We used a hidden Markov model (HMM) (Rabiner 1989) to decompose promoters into neutral and selectively constrained regions based on their patterns of conservation, where conservation was defined as sharing of the same base in all four species. Hidden Markov models have previously been applied to several sequence decomposition problems, such as the identification of genes or CpG islands in DNA sequence (Burge and Karlin 1997; Durbin et al. 1998).

Our HMM (see Methods; full details are in the Supplemental material) was designed to identify functional and neutral regions in promoters by breaking the promoters into high conservation regions (HCR) and low conservation regions (LCR). Since neutral rates were found to be uniform, we chose a hidden Markov model with a single set of global parameters, and trained it using a set of 2453 promoter sequences (Kellis et al. 2003) that had four-species alignments. An example of a sequence decomposition is shown in Figure 3. We expected highly conserved regions to correspond to functionally conserved regions, as functional sites are known to cause purifying selection in yeast promoters (Cliften et al. 2003; Kellis et al. 2003). Low conservation regions were expected to correspond to neutrally evolving sequence.

Figure 3.

Example of separation of conserved blocks from the background. The alignment for the promoter of ORF YCL030 (HIS4), where ^* indicates a base conserved across all four species. The gray highlights mark the high conservation regions identified by the hidden Markov model. Low conservation regions are comprised of the remaining sites with sequence data in all four species. Gapped regions (dashes and lowercase letters) were classified separately. Known transcription-factor-binding sites from SCPD (Zhu and Zhang 1999) are labeled.

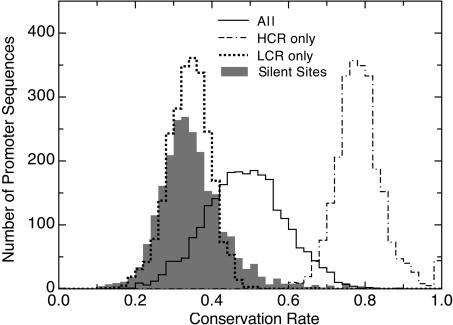
The HCRs and LCRs identified by the HMM had distinct conservation rates (Fig. 4), suggesting qualitatively different behaviors. In all, 34.3% of the total promoter sequence was inside HCRs, with the remainder in LCRs. The clear separation of HCR and LCR conservation rates was not an artifact of the method. To test this, a conservation pattern was generated for every promoter using a uniform mutation model. When the HMM was applied to this synthetic set, no separation of high and low rate regions was observed. Similarly, no separation was observed when the alignment procedure and HMM were applied to a set of synthetically generated promoter sequences (see Supplemental material).

Figure 4.

Distribution of the conservation rate for promoter sequences. The overall conservation rates and the conservation rates within the LCRs and HCRs are calculated for each promoter sequence. Each bin shows how many promoter sequences have the given conservation rate. The distribution of silent site conservation rates in coding sequences, which agrees with the distribution from LCRs, is indicated by the solid bars.

The neutral rates in the LCRs were consistent with the neutral rates obtained from the fourfold site analysis, suggesting that both methods accurately measure the neutral conservation rate. The distribution of conservation rates for the LCRs overlapped well with that of the fourfold sites (solid bars in Fig. 4). The fourfold site median conservation rate was 33%, while the LCR median was 34%. The LCR rates also confirmed the uniformity of the neutral mutation rate. There was no correlation between the normalized conservation rates of the LCRs of each promoter and the fourfold sites of the downstream gene (Pearson correlation = 0.018, p = 0.33).

The HCRs, on the other hand, contained an excess of functional elements. Using a set of regulatory motifs identified computationally by W. Wang, M. Cherry, Y. Nochomovitz, E. Jolly, D. Botstein, and H. Li, (in prep.) from chromatin immunoprecipitation data, we tested whether regulatory motifs were biased toward HCRs over LCRs. While the HCRs covered only 34.3% of the promoter regions, they contained 406 of the 567 motifs in the test set and in our promoters (71.6%). As a control, we randomized the locations of the motifs within their respective promoters. In the random case, only 178 ± 10 motifs were inside HCRs, giving the observed results a p-value of 10^-107. We found similar enrichment when a set of motifs from SCPD (Zhu and Zhang 1999) was used. Out of 234 motifs, 168 (71.8%) overlapped with our HCRs, while only 85 ± 6 overlapped when their locations were randomized. Thus, we found strong overlap of the predicted motifs with our HCR regions, despite the fact that both the SCPD and Wang et al. motif sets were obtained independently of conservation information.

Genome-wide amount of promoter sequence under selection

In the previous section we showed that the fourfold site neutral conservation rate can provide a calibration for detecting the functionally conserved regions within promoters. In this section, we use the neutral rate to calculate the fraction of all promoter sequence that is under purifying selection.

Although a good approximation, the HCRs and LCRs did not always correspond to functional and neutral regions, as the separation by the HMM was imperfect. To precisely evaluate the amount of functional sequence, we therefore used a different approach. The procedure involved counting the numbers of blocks of n consecutive conserved bases in the promoter sequences, which were then compared to neutral expectations. This approach did not infer whether any specific region is functional, instead only predicting the total amount of functional sequence. This method, which we refer to as the Frequency of Conserved Blocks (FCB) method, was more robust than the HMM for inferring the amount of selectively conserved sequence (see Methods).

The FCB method yields an accurate estimate of the amount of functionally conserved sequence subject to two requirements: (1) the frequency distribution of conserved blocks in neutral sequence is known; and (2) this neutral component can be extracted from the real frequency distribution. Both of these requirements could be met for the yeast data set. We were able to generate the conserved n-mer distribution from synthetic neutral sequences of the same lengths as the real promoters using the known neutral conservation rate. We could extract the neutral component of the observed frequency distribution by considering the counts of conserved n-mers at small n. This extraction was based on the assumption that for small n, the conserved n-mer counts would be dominated by the neutral component, because functional conservation would be unlikely to cause isolated conserved bases. The assumption was supported by the neutral conservation rate inferred from the small n counts, which agreed with the rate estimated from gene silent sites (see below).

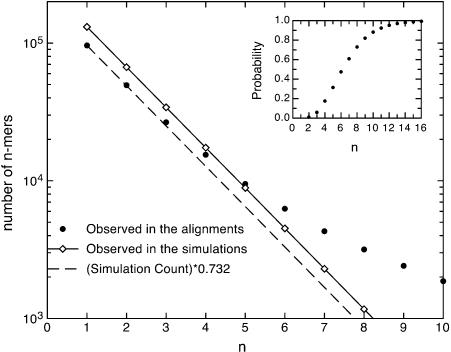
We calculated the amount of promoter sequence selectively conserved among all four species, as well as the amount in the pairwise comparisons of S. cerevisiae to S. paradoxus, S. mikatae, and S. bayanus. The observed conserved n-mer distribution and the simulated neutral distribution for S. cerevisiae-S. bayanus are shown in Figure 5. The neutral distribution decays exponentially, as expected because bases were conserved independently in the synthetic data. The slope of the semilog plot is given by ln γ, where γ is the conservation rate. At small n, the real distribution also decays exponentially and with a slope equal to that of the synthetic neutral data. This indicates that the small n behavior for the real promoters is controlled by the neutrally evolving regions. However, at large n the curves diverge, because of selective effects. We estimated the fraction of the real promoters evolving neutrally by calculating the ratio of conserved n-mers at small n in the real and synthetic data sets. An example is shown in Figure 5. When we normalized the simulated curve using this ratio, the simulated and observed curves matched at small n.

Figure 5.

Distribution of the counts of blocks of n consecutive conserved bases between S. cerevisiae and S. bayanus as a function of n. The solid line is the distribution for simulated neutral sequence. The small n values of the simulated curve and the real curve overlap well when the simulated curve is scaled by a factor 0.732 (dashed line), suggesting that 73% of the promoter sequence evolves neutrally and 27% is under selection. The inset shows the probability that a block conserved between S. cerevisiae and S. bayanus is functional, given its length n.

We obtained the percentage of promoter sequence evolving neutrally using the ratio of conserved singlet (n = 1) counts for several different species comparisons (Table 1). This neutral percentage was calculated 100 times using independent simulations of neutral promoter sequence. The estimated percentages were similar (70%-74%) in all of the pairwise and four-species comparisons. In other words, ∼30% of the promoter sites are under selection in each of these lineages. The robustness of this estimate is remarkable, given that the number count of conserved singlets varies by 2.5-fold over the different comparisons. These similarities in amounts of functional promoter sequence reflect the close phylogeny of these species (divergence times were 5-20 Myr). We also expected that more closely related species would have slightly higher levels of functional conservation, because they should have more shared functional sequences. This trend was, indeed, observed, as shown in Table 1, where the rows are arranged in order of increasing divergence time.

Table 1.

Estimate of the percentage of sites evolving neutrally among various species

Alignment	Estimated neutral conservation rate	Conserved singlet in the alignment	Conserved singlet in the simulation	Estimated percentage evolving neutrally
Saccharomyces cerevisiae/Saccharomyces paradoxus	0.74	41,334	59,218 ± 214	69.8 ± 0.3%
Saccharomyces cerevisiae/Saccharomyces mikatae	0.60	76,392	107,485 ± 283	71.1 ± 0.2%
Saccharomyces cerevisiae/Saccharomyces bayanus	0.52	96,068	131,135 ± 323	73.2 ± 0.2%
Saccharomyces cerevisiae/Saccharomyces paradoxus/Saccharomyces mikatae/Saccharomyces bayanus	0.33	110,011	149,334 ± 356	73.7 ± 0.2%

The separation of the neutral component from the frequency distribution also allows one to calculate the likelihood that a block of n conserved bases is functional. This can be done by comparing the estimated number of neutrally conserved n-mers to the total number of conserved n-mers. For example, for a 6-mer conserved across all four species, the probability that it is functional is 90% (see Methods). The inset in Figure 5 shows the probability of being functional versus n for n-mers conserved between S. cerevisiae and S. bayanus.

Gene-specific selection in promoters

Gene promoters have varying levels of functional conservation. Because the HCRs strongly correlate with known transcription-factor-binding sites, much of this functional conservation is likely to be related to transcriptional regulation, although some other functional features may contribute as well (see Discussion). Thus, the HCRs provide a rough characterization of the transcriptional regulation in each promoter. All HCRs have conservation rates higher than the typical LCR region (Fig. 4). The total length of the HCRs in a promoter can therefore serve as an approximate measure for the cis-transcriptional regulation experienced by the adjacent gene. This measure has a natural, if simplistic, interpretation. It is assumed to be proportional to the number of binding sites in the promoter.

The mode length of HCRs in promoters was found to be 90 bases, although the distribution has a long tail (see Supplemental material). This corresponds to most genes having 15%-25% of their promoter sequence in HCRs. We systematically surveyed all Gene Ontology (GO) (Gene Ontology Consortium 2000) terms to determine if any were biased toward long HCR regions. For each GO term, we calculated the mean length of the HCRs for the associated genes. This mean length was compared to the mean for an equal number of randomly chosen genes, to determine an HCR length z-score z_l (see Methods).

There were several strong outliers with positive z-scores, but fewer for negative z-scores. The GO terms with the largest HCR length biases were those involved in the energy generation (Glucose Catabolism, Alcohol Catabolism) and steroid synthesis (Steroid Metabolism, Sterol Biosynthesis) pathways, suggesting that these types of genes have unusually complex regulation. The GO terms with the shortest HCRs included RNA processing (GO: 0006396) and condensed chromosomes (GO:0000793), although their biases were not as pronounced as for the high z-scores. The full list of GO terms can be found in the Supplemental material.

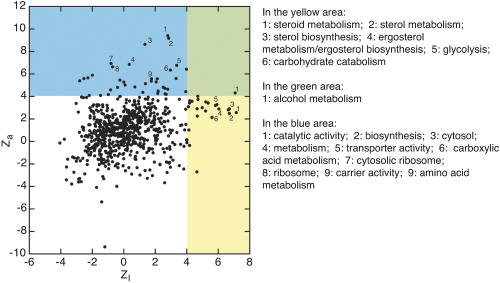
The frequency of amino-acid-changing mutations in genes (K_a) provided an interesting comparison for the amount of HCR sequence (see Methods). These quantities measure the amounts of selective pressure on protein sequence and cis-regulation, respectively. Figure 6 shows each GO term plotted by z_l and the K_a z-score (z_a—larger z_a indicates greater amino acid conservation). The categories of genes with the longest HCR lengths, steroid synthesis genes and energy generation genes, had higher levels of protein sequence conservation than most other categories (yellow region). Protein sequence conservation was correlated on a gene-by-gene basis with HCR length (correlation = 0.10, p-value = 1.3 × 10^-4), suggesting that protein and regulatory evolution can be coupled (Castillo-Davis et al. 2004). However, the correlation was not absolute. The genes with the strongest protein sequence conservation (Catalysis, Basic Biosynthesis, and Ribosomal Genes) were not those having the longest HCR lengths (blue region).

Figure 6.

Enrichment of Gene Ontology categories in terms of their nonsynonymous conservation z_a and lengths of HCR in the promoters z_l. The blue area covers those categories with unusually high nonsynonymous conservation. The yellow shaded area covers those categories that have unusually long conserved blocks in their promoters. The green region indicates GO categories with unusual values along both coordinates.

Discussion

By analyzing sequence conservation patterns at silent sites in yeast coding sequence as well as in promoter sequences, we have made several findings. First, we found that the neutral conservation rate is uniform across yeast genomes (S. cerevisiae, S. paradoxus, S. mikatae, and S. bayanus). This uniformity was found in pairwise comparisons of S. cerevisiae to each of the other species and among all four species collectively.

Knowledge of the uniform neutral conservation rate allowed us to separate functional and neutral sequence. A significant fraction of promoter sequence was under purifying selection. For various species comparisons, the amount of selectively conserved sequence ranged from 26% to 30%. The similarities in amount of functional sequence suggested that lineage-specific functional elements are rare compared to elements common to all four species. More recently diverged species were found to have a slightly larger amount of shared functional sequence. For example, we predicted that S. cerevisiae and S. bayanus, which are diverged by ∼20 Myr (Kellis et al. 2003) have 27% of their promoter sequences functionally conserved. Meanwhile, S. cerevisiae and S. paradoxus, which are diverged by ∼5 Myr (Kellis et al. 2003) have 30% of their promoter sequence functionally conserved. This mere 3% change between these two evolutionary branches suggests that S. cerevisiae is unlikely to have much more than 30% of its promoter sequence functional, even including species-specific elements.

Promoters contained blocks of highly conserved sequence embedded in a background mutating at the uniform neutral rate. Known functional elements were found to be strongly biased to these high conservation regions (HCRs). The HCR blocks were typically 8-20 bases long, although some blocks had as many as 40 consecutive conserved bases. Thus, a typical block may contain one or two protein-binding sites. The typical length of all HCR regions in a promoter was 90 bases, providing an upper bound of ∼10 transcription-factor-binding sites in a promoter, although this number could be mitigated by sites conserved for other reasons. The example of the HIS4 promoter in Figure 3 shows that a major portion of the selectively conserved promoter sequence could plausibly be for transcription factor binding. If so, there are enough potential binding sites for combinatorial control to be prevalent in the genome. In addition, the significant number of long blocks indicates that it may be common for transcription-factor-binding sites to overlap or lie adjacent to one another, which could allow for complex regulatory logic (Buchler et al. 2003).

Genes involved in energy generation and steroid synthesis were found to have the strongest biases toward long HCRs. This suggested that these genes may be subject to complex transcriptional regulation, because the number of transcription-factor-binding sites should increase with the length of HCRs in a promoter, and increased binding sites would allow more specific responses to different cellular conditions. The long HCRs of these genes may be related to the fact that these genes are often members of multiple pathways. For example, ERG10 (YPL028W) is a steroid metabolism gene with 215 HCR sites, and it is involved in nine different KEGG pathways (Kanehisa and Goto 2000). CDC19 (YAL038W) is a glycolysis gene with 394 HCR sites, and it is involved in four different pathways. Energy generation and steroid synthesis genes are each important for fitness—both were found to have above average protein sequence conservation as measured by K_A. One quantitative distinction between these types of genes is their level of silent site conservation. Energy generation genes have high silent conservation rates, which could be an indication of high translation efficiency (Akashi 2004), while we found that steroid synthesis genes are more average in this regard. At the other extreme of promoter sequence conservation, genes with the shortest HCR lengths tended to be involved in RNA processing. This was consistent with the view that RNA processing genes are constitutively expressed, which would require simple transcriptional regulation.

Our observation that the neutral mutation rate is uniform in the yeast genome is in sharp contrast to what is known in mammals, where the rate varies along chromosomes. This result was surprising, because recombination rates vary along the yeast genome (Gerton et al. 2000) and recombination events have been reported to increase local mutation rates (Rattray et al. 2002). However, recombination-associated mutagenesis does not appear to have occurred frequently enough to have had a major impact on the sequences. We found that recombination rates in S. cerevisiae genes, as obtained from Gerton et al. (2000), were not correlated with our four-species normalized conservation rates (3530 genes; r = 0.02, p = 0.18). Since the mechanism for variable rate in mammals is still unknown, we can only speculate on what may be responsible for the difference between yeast and mammals. One nonselective possibility is that yeast chromosomes are too short to have heterogeneity in their mutational environment. For example, in the mouse-human comparison, rate correlations have a typical length scale of several megabases, while most yeast chromosomes are <1 Mb long. Alternatively, a selective possibility is that nonuniform rates create hotspots that provide a benefit in mammals (Cox 1972; Chuang and Li 2004), but not in yeast.

The general approach we followed was to determine the local neutral conservation rate and then to calibrate the separation of functional and neutral sequence in promoters by this rate. This approach was of a qualitatively different nature than those of Kellis et al. (2003) and Cliften et al. (2003), who also analyzed sequence conservation in yeast promoters. Both of these groups searched for sequence motifs of a specified pattern, and then assessed their significance by evaluating the overall conservation rate across all motif occurrences in the genome. By applying bootstrapping-type methods, they were able to determine which motifs of the specified pattern had outlier behavior. In contrast, we analyzed the overall conservation pattern and not specific motifs. By accurately calibrating for the neutral rate of conservation, we were able to decompose the neutral and functionally conserved sequence on a global scale. Our approach was similar in spirit to that taken by the Mouse Sequencing Consortium in estimating the total amount of functional sequence in the human genome (Mouse Genome Sequencing Consortium 2002). They did so by analyzing the distribution of alignment scores for all aligned human-mouse 50-mers and comparing it to a distribution of scores from presumably neutral repeat sequences. Our separation method based on the frequency of conserved blocks has higher resolution, as it is able to evaluate functionally constrained sites a few base pairs in length, and is also robust over different species' divergence times.

Mutational uniformity was a key aspect of our findings, as it justified genome-wide approaches to separating functional from neutral sequence. In addition to the HMM method, it allowed us to apply a novel separation method based on the frequencies of conserved blocks. Despite the fact that the neutral conservation rate differed 2.5-fold among different yeast comparisons, our conserved block method was able to robustly infer similar amounts of selectively conserved sequence in each of these lineages. If uniformity of mutation can be established in other species, it should be possible to apply these separation methods to them as well. For genomes with regional mutation biases, such as mouse and human, it may be possible to apply these methods by breaking up the genome into blocks with internally homogeneous neutral mutation rates.

By measuring the lengths of the HCRs in each promoter, we produced a novel dimension for quantifying selection on yeast genes. Traditionally, selective arguments have been applied to genes based on conservation of their protein sequence (K_A) and/or their silent sites in the coding sequence (K_S). In contrast, the total length of HCRs serves as a measure of regulatory complexity for each gene. Certainly, this is a simplification, as not all functional elements need be conserved across species, and not all of the conserved functional elements need be transcription-factor-binding sites; for example, they could be RNAs (Ludwig 2002; Martens et al. 2004), replication origins, or may be related to translation (Vilardell and Warner 1997; Cliften et al. 2003). However, the strong bias of known transcription-factor-binding sites to HCRs suggests that the HCRs are a useful approximation to regulatory sequence. These HCRs will be beneficial not only for characterizing regulation in each gene promoter, but may also shed light on the evolution of yeast promoters and gene expression.

Decompositions of each promoter into high conservation and low conservation regions are available at http://genome.ucsf.edu/YeastReg.

Methods

Calculation of substitution rates from fourfold sites

We obtained coding sequence data from the data set of Kellis et al. (2003) for each of the four species S. cerevisiae, S. paradoxus, S. bayanus, and S. mikatae. We translated each coding sequence into protein sequence, aligned the protein sequences with their orthologs using CLUSTALW, and then back-translated to determine the aligned coding sequences. In some cases, the coding sequences contained stop codons. In these cases, any sequence following a stop codon was discarded. We used fourfold sites, the third bases of codons for which the amino acid is specified by the first two bases, to analyze mutation rates. If the sequence before a stop codon contained fewer than 20 fourfold sites, the entire sequence was discarded.

For each of the 4541 genes in the data set shared by S. cerevisiae and S. paradoxus, we calculated the fraction of fourfold sites that were identical. For each of the 3571 genes shared by all four species, we calculated the fraction of fourfold sites identical in all species. Fourfold site conservation rates were analyzed because they do not affect amino acid sequence and therefore provide an estimate of neutral conservation processes. These conservation rates were then mapped to normalized values to account for finite-size effects. We defined the normalized substitution rate to be

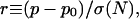(1)

where p is the fourfold conservation rate in the gene, p₀ is the mode conservation rate in the genome, N is the number of fourfold sites, and σ(N) is the standard deviation calculated from a binomial model, equal to . The value of p₀ used in the S. cerevisiae-S. paradoxus comparison was 0.74, which was the mode value from the fourfold sites. The value used for the four-species comparison was 0.33, which was also the mode value. These p₀ values were both consistent with the values inferred from Bayesian demixing.

Although this mutation model is rather simple with respect to base composition, it has several good features: It gives r =0 when the mutation rate is equal to the typical rate in the genome, accounts for fluctuations due to gene length, and predicts a normal distribution for r values if fourfold sites mutate independently with a uniform rate (Chuang and Li 2004).

Mutational uniformity

We considered all pairs of genes on continuous orthologous blocks, starting from the first neighbor up to the 35-th gene downstream. Orthologous block boundaries were defined by genes at which the S. cerevisiae chromosome changes. This allowed us to get hundreds of measurements of r(0)r(x)for x values as large as 100 kb. We binned these data into 50 uniformly spaced groups covering x ∈ [0, 300000] and then averaged over each of these bins to determine the correlation function 〈r(0)r(x)〉, where 〈...〉 indicates an average over all gene pairs in the bin. Error bars were given by the standard deviation of the values in each bin, multiplied by a correction factor of M^-1/2, where M is the number of gene pairs in the bin, because we were interested in the error in the mean. Since the plotted values for each bin are averages over the M gene pairs, our autocorrelation analysis may still report uniformity if there are fewer than M^1/2 gene pairs whose mutation rates are correlated. The number of gene pairs in any bin is proportional to the number of genes in our data set (∼4500 for S. cerevisiae-S. paradoxus), meaning the sensitivity of our autocorrelation analysis is ∼70 gene pairs. The conclusion of uniformity from the autocorrelation analysis is a statement that there are no more than ∼70 pairs of genes (1%-2% of the genome) whose rates are correlated at any given distance.

For randomly sampled gene pairs, the average value of r₁ × r₂ was 0.01. 〈r(0)r(x)〉 values were only considered significant if the lower error bar was above this value. In practice, 0.01 is indistinguishable from 0 for the scale of values in Figure 1. In general, rate correlations were weak along the S. cerevisiae genome. A small (much weaker than the mouse-human autocorrelation) but significant autocorrelation was found out to distances around 20 kb, but this was caused by just a few unusual genes. When medians, rather than means, were used to assess 〈r(0)r(x)〉, this slight autocorrelation vanished. The slight autocorrelation was caused by a block of 12 yeast genes on Chromosome 14 (YNL320-YN323, YNL325-YNL332) with high sequence conservation between S. cerevisiae and S. paradoxus. When these 12 genes were removed, the unusual values disappeared. Furthermore, correlations in the rates of neighboring genes largely vanished (Full data set: Pearson correlation = 0.10, p-value = 3.3 × 10^-12; data set with these genes removed: Pearson correlation = 0.04, p-value = 0.01). Because these genes were a special case, Figure 1 was plotted without them. The reason for high conservation in these genes is not clear, although five are in the Gene Ontology term GO:0008151, Cell Growth/Maintenance.

The rates determined from the four species comparisons also indicated no regional biases in mutation rate. Neighboring genes had only marginal correlation in conservation rate (Pearson correlation = 0.03, p-value = 0.05). Autocorrelation analysis was more complicated than for the S. cerevisiae-S. paradoxus comparison because of the significant number of genes with high four-species conservation rates, as illustrated by the long tail in Figure 2. This caused 〈r(0)r(x)〉 to have a spurious nonzero expectation (∼0.1) at all x. However, we found that when genes with extremely high conservation rates (r ≥ 5, 88 genes) were removed, this effect vanished. After removal, 〈r(0)r(x)〉 had an average value of 0.02 in the region t ∈ (0, 100 kb). Removal of these genes did not correspond to removing any clusters of slowly mutating genes; the median distance between these cold genes was 82 kb (∼30 genes away).

As mentioned in the main text, there was also no correlation between the normalized conservation rates of the LCRs inferred from the HMM and the fourfold sites of their genes. It might be supposed that regional effects could exist for the small group of genes with the highest fourfold conservation rates. However, this was not the case. For those genes with fourfold conservation z-scores >3, there was also no correlation (Pearson correlation r = -0.18; p = 0.1, 195 genes).

We also performed uniformity tests for comparisons of S. cerevisiae-S. mikatae and S. cerevisiae-S. bayanus. For the S. cerevisiae-S. mikatae comparison, neighboring genes had insignificant Pearson correlation in their normalized fourfold substitution rates (r = 0.004; p = 0.80), the median values of the autocorrelation were all within error of zero, and the rate distribution closely followed a Normal distribution. For S. cerevisiae-S. mikatae, these qualities all held true as well (neighboring gene Pearson correlation: r = 0.023; p = 0.10).

Separation of high and low conserved regions with a hidden Markov model

A hidden Markov model (HMM) (Durbin et al. 1998) is a model that assumes that there are hidden states (in our case, the two hidden states are neutral or under selective constraint) at each position in a sequence. The observed sequence values (in our case, these are the conservation patterns along the aligned promoter sequences) are probabilistic outcomes emitted by the hidden states. These emission probabilities, as well as the transition probabilities between hidden states, are unknown parameters that can be learned through an iterative procedure that attempts to maximize the likelihood of the observed sequence as a function of these parameters (Baum 1972). The value of the hidden state at each position can be recovered by considering the sequence of hidden states most likely to have produced the observed sequence values. Our HMM methods follow standard protocols as described in Durbin et al. (1998). Full details of the HMM are provided in the Supplemental materials.

Genome-wide percentage of promoter sites under selection

In the frequencies of conserved blocks (FCB) method, we defined a conserved n-mer to be n consecutive conserved sites flanked by nonconserved sites or gaps. The numbers of conserved n-mers f(n) were used to calculate the percentage of sites under selection. This percentage of sites under selection was determined by comparing the f_obs(n) distribution for the observed data to the f_sim(n) function found for simulated neutrally evolving sequence. Such simulated neutrally evolving sequence was generated using the neutral conservation rate obtained from the fourfold site analysis. In each species comparison, the neutral conservation rate was obtained by Bayesian demixing. For each promoter, we generated a conservation pattern by randomly assigning each site to be conserved with a probability equal to the neutral fourfold conservation rate. The gap positions and the length of each promoter were preserved. This yielded a distribution f_sim(n), which was expected to have the same n-dependence as would be expected for neutrally evolving sequence. However, since f_sim(n) was generated using the full lengths of promoters, it was necessary to separately determine how much of the real promoter sequence followed the f_sim(n) distribution.

An example of the observed distribution and the simulated distribution is shown in Figure 5. At small n, the real and simulated distributions decayed exponentially at nearly the same rate. The slopes for the simulated alignment and observed alignments matched from n = 0 out to n =4 ∼ 6. This implies that the small n statistics in the observed data were dominated by neutral effects. We therefore assumed that f_obs(n = 1) was completely due to the neutral sequence in promoters. This provided a normalization factor for determining the contribution of neutral sequence to f_obs(n). The number of conserved n-mers generated by neutral sequence in the real promoters was estimated as

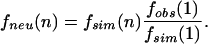Note that this implies the overall fraction of sequence in promoters which is neutral is

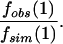It also follows that for a conserved n-mer, the probability that it is functional is

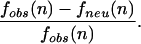We used the FCB method to estimate the amount of functionally conserved sequence, rather than just the HCRs from the HMM, because the FCB method was more robust. In general, the HMM decomposition worked if the neutral and functional conservation rates were sufficiently distinct. This appeared to be the case in the four-species comparison: The amount of predicted functional sequence was similar from the HMM and the conserved n-mer methods, the conservation rates in LCRs overlapped well with the fourfold rates, and the HCR and LCR rate location dependences were consistent with functionality and neutrality, respectively (see Supplemental material). However, the HMM tended to overestimate the amount of functional sequence when species were closely related. The HMM method identified 75% of the promoter sequence as HCR in the S. cerevisiae-S. paradoxus comparison, 50% for the S. cerevisiae-S. mikatae comparison, and 38% for the S. cerevisiae-S. bayanus comparison. On the other hand, the FCB method gave consistent estimates of the amount of functional sequence over a range of species divergences.

z-score in Gene Ontology analysis

For a given type of measurement, for example, the average HCR length, the z-score for each GO category was calculated by comparing the value of the measurement for the genes in the GO category against the values for randomly sampled genes. For example, if a GO category had x genes, a mean m_s and standard deviation σ_s of the measurement s was calculated from 1000 samples of x randomly chosen genes. The z-score for the GO category was then reported as z = (m - m_s)/σ_s, where m was the value of the measurement from the genes in the GO category.

To calculate z_a, the z-score based on amino-acid-changing changes in the coding sequence, we used the K_a values published by Kellis et al. (2003) for the S. cerevisiae-S. bayanus comparison.