Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2017 Jun 5;8:15705. doi: 10.1038/ncomms15705

Single-stage plasma-based correlated energy spread compensation for ultrahigh 6D brightness electron beams

G G Manahan 1,2,a, A F Habib 1,2,3, P Scherkl 1,2, P Delinikolas 1,2, A Beaton 1,2, A Knetsch 3, O Karger 3, G Wittig 3, T Heinemann 1,2,3,4, Z M Sheng 1,2,5, J R Cary 6, D L Bruhwiler 7, J B Rosenzweig 8, B Hidding 1,2,b
PMCID: PMC5465367  PMID: 28580954

Abstract

Plasma photocathode wakefield acceleration combines energy gains of tens of GeV m−1 with generation of ultralow emittance electron bunches, and opens a path towards 5D-brightness orders of magnitude larger than state-of-the-art. This holds great promise for compact accelerator building blocks and advanced light sources. However, an intrinsic by-product of the enormous electric field gradients inherent to plasma accelerators is substantial correlated energy spread—an obstacle for key applications such as free-electron-lasers. Here we show that by releasing an additional tailored escort electron beam at a later phase of the acceleration, when the witness bunch is relativistically stable, the plasma wave can be locally overloaded without compromising the witness bunch normalized emittance. This reverses the effective accelerating gradient, and counter-rotates the accumulated negative longitudinal phase space chirp of the witness bunch. Thereby, the energy spread is reduced by an order of magnitude, thus enabling the production of ultrahigh 6D-brightness beams.

Controlling and improving electron beam parameters are crucial for their application in free electron laser and X-ray sources. Here the authors generate quality electron beams with reduced energy spread from plasma accelerators by using a tailored escort electron bunch with the main accelerating bunch.

Acceleration of electrons in plasma waves harnesses electric fields on the order of tens of GV m−1 (refs 1, 2). This is orders of magnitude larger than in state-of-the-art radiofrequency-driven accelerator systems, and may allow to shrink even high-energy accelerators from km to metre-scale. Plasma accelerators have advanced from the generation of broadband electron distributions to point-like, quasi-monoenergetic electron beams3,4,5,6,7 in the last decade. The so-called Trojan Horse (TH) plasma wakefield acceleration8 and related schemes9,10,11,12 promise a further step change by decoupling the plasma wave excitation from the electron bunch generation in a highly flexible underdense plasma photocathode process. This allows generation and acceleration of transversally ultra-cold electron bunches with normalized transverse emittance down to ɛn≈10−9 mrad. Reaching such low emittance has key significance for many of the most prominent accelerator applications, for example in high-energy colliders for high-energy physics, and for advanced light sources13. In high-energy physics experiments, emittance limits the focusability of particle beams and hence the obtainable luminosity, and in turn the event rate. This is why emittance damping rings are required to reach luminosity goals in colliders14. Obtaining nm-scale normalized emittances without the need for damping rings may therefore open up interesting avenues for high energy physics research. For similar reasons, electron emittance is crucial for light sources based on inverse Compton scattering, as the small spot sizes promote generation of large X-ray or γ-ray fluxes during the scattering process, as well as high-spectral brightness15,16, and for betatron or ion channel laser-based radiation sources17,18,19,20. Ultra-fast transmission electron spectroscopy is another important imaging technique at comparably low-electron energies on the few MeV scale, which likewise profits strongly from decreased transverse electron beam emittance, bunch duration and charge21. The electron beam 5D-brightness B5D≈2Ip/(ɛnx ɛny), where Ip is the peak current and ɛnx,y are the normalized emittances in the transverse (x, y) directions, is a crucial figure of merit which amalgamates the bunch duration, charge and emittance. Emittance and brightness are key performance factors for free-electron lasers (FELs). Progress in this regard, particularly in the development of high brightness photocathode guns for radiofrequency-driven linear accelerators, had paved the way for the realization of research-enabling machines such as hard X-ray FELs22,23,24,25. The inherent ability of plasma accelerators to generate electron bunches with fs-scale durations and multi-kA currents26,27, enhanced by the TH strategy towards nm-scale transverse normalized emittance, suggests unprecedented 5D-brightness values approaching B5D≈1020 A m−2 rad−2 levels. This is order of magnitude brighter than state-of-the-art and may therefore have transformative impact, for example, for the realization of fifth generation light sources28.

However, the enormous accelerating fields in plasma accelerators inherently produce electron bunches with large correlated energy spread. In the strongly nonlinear blowout regime29 of plasma wakefield acceleration, the nearly sawtooth-shaped on-axis longitudinal electric field varies linearly with a steep slope along the co-moving coordinate ξ=z−ct, yielding acceleration gradients of the order of ΔEz∼0.3 MV μm−1 for a plasma wavelength of λp≈100 μm, corresponding to a plasma electron density n0∼1017 cm−3. It results in a negative energy chirp: the energy distribution of the generated bunch is highly correlated to its longitudinal position inside the plasma wake, that is, the head of the bunch accumulates significantly lower energy than its tail during the acceleration process.

The accumulated correlated energy spread is problematic on a number of levels: first, extraction of the electron bunch from the plasma accelerator stage and transport30 can substantially deteriorate the beam emittance due to chromatic effects and non-matched transverse forces31,32,33. Similar effects occur during entry into a plasma stage, and are further multiplied when staged acceleration is required34. Second, the electron energy spread limits the realizability and performance of accelerator applications such as light sources. For instance, to allow proper micro-bunching and high-gain in FELs, the maximum relative energy spread ΔWr.m.s./W, should be less than the Pierce parameter35, ρFEL >ΔWr.m.s./W. Typical values for X-ray FEL's are in the range of ρFEL ∼10−3−10−4. Similarly, for example in case of inverse Compton scattering, low-electron beam emittance combined with small energy spread significantly narrows the on-axis photon radiation bandwidth16. While plasma accelerators produce bunches with comparably strong energy chirps, but inherently short bunch durations on the few-fs-scale, the situation is quite the opposite in state-of-the-art radiofrequency-based accelerators. Here, acceleration in the linac cavities typically leads to inherently monoenergetic bunches with very low correlated and uncorrelated energy spread, but in turn obtaining ultrashort electron bunches on the fs-scale requires magnetic compression techniques. In fact, energy chirps are purposefully generated in order to achieve sufficient compression in magnetic chicanes36,37. Various dechirping techniques are being developed and applied for state-of-the-art accelerators38,39,40 to subsequently improve the energy spread after compression. The electron beam 6D-brightness B6D≈B5D/0.1% ΔWr.m.s./W is used to quantify the combined current, transverse emittance and energy spread25,41.

Here, we show how to obtain electron bunches with ultrahigh 6D-brightness by controlled manipulation of the electron bunch longitudinal phase space inside a single-stage plasma accelerator.

Results

Loaded plasma wake in the 1D nonlinear regime

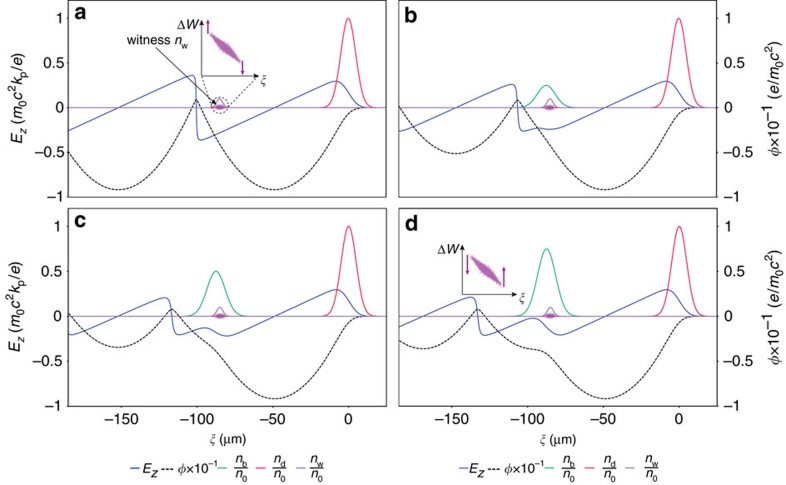
A co-propagating Gaussian electron beam with peak density 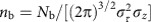Inline graphic, where Nb is the number of electrons and σr, σz are the transverse and longitudinal r.m.s. beam sizes, respectively, can distort the accelerating plasma wakefield via beam loading42,43 if nb becomes similar to the plasma electron density n0. Figure 1 visualizes this for the case of an electron beam driven plasma wakefield accelerator (PWFA) in the nonlinear 1D model44 (see Methods). Hence, the electron density ratio of nb/n0∼1 defines the threshold for overloading the wake. While the TH method allows to release low-emittance electron populations with charge tunable over many orders of magnitude, it is unable to reach the electron density levels required for beam loading without compromising the highest achievable brightness levels. This is due to strong space charge forces during the witness bunch formation, which increases the emittance. However, space charge forces decrease with γ−2 during acceleration, where γ is the relativistic Lorentz factor associated with the accelerating electron beam. To exploit this, an additional electron escort population is released once the witness bunch is relativistically stable, such that the escort overlaps with the witness bunch during the trapping process, but without destroying its emittance. The escort electron population is tuned to a much higher charge values than the witness bunch, for example, by increasing the corresponding photocathode laser intensity and/or its Rayleigh length. The amount of released charge can thus be regulated to flatten the local field (Fig. 1b), or can be further increased to levels such that the escort bunch overloads the wake and thus reverses the slope of Ez locally for the remainder of the acceleration process, as shown in Fig. 1c,d. This allows adjustment of the witness energy chirp by counter-rotation of the longitudinal phase space to arbitrary positive or negative values, or—most important—to minimize it.

Figure 1. Beamloading of the plasma wake in 1D nonlinear regime.

Figure 1

Open in a new tab

On-axis longitudinal electric field Ez (blue line) and electrostatic potential φ (dashed black line) in a plasma wave of density n0=1.1 × 1017 cm−3, driven by a non-evolving electron beam (red curve), propagating to the right. Adding an electron escort beam (green curve) with charge density nb can load the wake and flatten or reverse the electric longitudinal field locally: (a) unloaded case (nb=0), where the position of the witness bunch nw (purple curve) and its resulting energy chirp is indicated schematically, (b) nb/n0=0.5, (c) nb/n0=1.0 and (d) nb/n0=1.5. The results are obtained using the 1D nonlinear fluid model description. The electron witness bunch position and size (purple) is indicated, thus visualizing the electric accelerating field which would be sampled by the witness. The insets in (a,d) are the longitudinal phase spaces of the witness bunch, indicating the phase rotation for the (a) unloaded and (d) loaded cases.

Particle-in-cell simulation of the dechirping technique

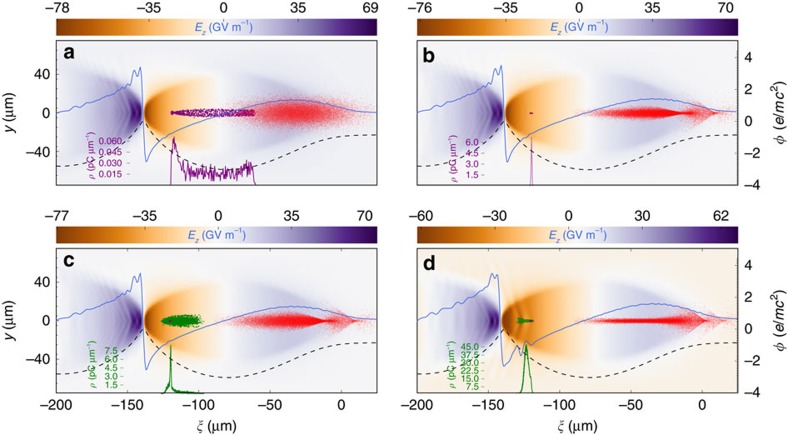
To verify the concept, we performed 3D particle-in-cell simulations (see Methods for details). As shown in Fig. 2a,b, a high 5D-brightness witness bunch (purple) is initially produced in a strong blowout with a longitudinal electric wakefield maximum of Ez,peak≈80 GV m−1 based on pre-ionized lithium plasma (λp≈100 μm), driven by a FACET-II (ref. 45) scale electron bunch (parameters are summarized in Supplementary Table 1). The TH witness bunch release laser pulse with normalized intensity a0,w=0.1, focal spot size wo,w=7 μm and duration τw=25 fs generates the witness (purple) with charge Qw≈5 pC at the beginning of the plasma stage (Fig. 2a). The snapshot in Fig. 2a visualizes the trapping process with the transient longitudinal charge density ρ(ξ) plotted as inset, just before trapping compresses the witness bunch to a length of σw,z≈2 μm, corresponding to a peak current of Ip≈2.0 kA. At a normalized emittance of ɛnx,y≈3.6 × 10−8 mrad, this corresponds to a 5D-brightness of B5D≈3.0 × 1018 A m−2 rad−2.

Figure 2. Numerical simulation of the dechirping process.

Figure 2

Open in a new tab

Three-dimensional particle-in-cell simulation results with VSim63, showing snapshots of the driver beam (red) and the electric field Ez with on-axis lineout (blue solid line), electrostatic on-axis potential φ (black dashed line), and witness (purple) and escort bunch (green) longitudinal charge profiles. In (a) at zacc=0.075 cm, the witness bunch is just being released by the laser pulse ionization front (not shown), in (b) at zacc=1.6 cm, the witness is fully formed and accelerated to W≈500 MeV. In (c) at zacc=1.65 cm, the escort bunch is released and begins to overload the wakefield, and in (d) at zacc=2.4 cm, the escort bunch is fully trapped, overlaps with the witness bunch and has reversed the local accelerating field slope ΔEz/Δz.

When this bunch reaches the energy of W≈500 MeV after an acceleration length of zacc≈1.6 cm, it is relativistically stable and much more immune to space charge forces when compared with the initial bunch during its trapping and formation process (Fig. 2b). Now, the second, more intense, softer focused and longer laser pulse (a0,e=0.11, w0,e=10 μm, τe=80 fs) releases the escort beam with a charge of Qe≈184 pC—more than one order of magnitude compared to the witness bunch. Same holds for escort charge density ρ(ξ) (green) and the corresponding peak current. Trapping of this population in the accelerating phase of the wakefield strongly overloads the wake and reverses the slope of Ez (Fig. 2c,d) locally. The average ionization front position of the laser pulse which releases the escort bunch sweeps over the release position ξ of the witness bunch in the co-moving frame of the wake. Reflecting the intensity dynamics of a co-propagating focusing Gaussian Ti:Sapphire laser pulse with central laser pulse wavelength of λL≈800 nm, the ionization front first starts to appear at the center of the 80 fs Gaussian laser pulse, where the tunnel ionization threshold is reached first. For the used peak intensity value, this happens before the geometric focus in the laboratory frame is reached. During further focusing, the ionization front then moves forward with respect to the Gaussian temporal intensity profile of the laser pulse, which in the co-moving frame means to higher values of ξ with respect to the plasma wake field. It reaches maximum ξ at the geometric focus position of the laser pulse, and then moves back towards the laser pulse intensity center as the pulse diffracts46,47. This single-cycle ionization front phase oscillation is larger in amplitude Δξ, the larger the peak intensity and the larger the Rayleigh length, is also dependent on the laser pulse duration and defines a maximum length of the produced electron bunch and its charge. While for the escort beam, this oscillation amplitude should be large, it should be small for the witness bunch. In case of the witness bunch, this also allows for an estimation of the witness residual energy spread, which will be discussed later. The optimization requirements for the witness bunch (low emittance, small energy spread and high current) and for the escort bunch (high charge, much longer duration than the witness) are therefore substantially different. Fortunately, the inherent flexibility of the scheme allows to tune both bunches independently, and to choose the parameters of the injection lasers in a wide range so that different regimes of ionization front movement can be accessed. The much longer escort Rayleigh length ZR,e=πwe2/λL≈392 μm when compared with the witness ZR,w=πww2/λL≈192 μm, the significantly larger dimensionless light amplitude a0,e=0.11>0.1=a0,w and the longer pulse duration τe=80 fs >τw=25 fs in combination lead to a desired large ionization front phase oscillation amplitude of approximately Δξ≈5 μm as observed in the simulation in case of the escort bunch production, while the ionization front is quasistatic in case of the witness bunch production. The accumulating beam-loading during trapping of the high-charge escort bunch production increasingly distorts not only the electric fields, but also the underlying electrostatic potential φ, as shown in Fig. 1 (dashed black line), and leads to significant elongation of the plasma blowout, as seen in Figs 1 and 2c,d. At the bottom line, the region where the escort bunch overloads the wake—the dechirping region—is much longer than the witness bunch, which can therefore be fully dechirped from head to tail.

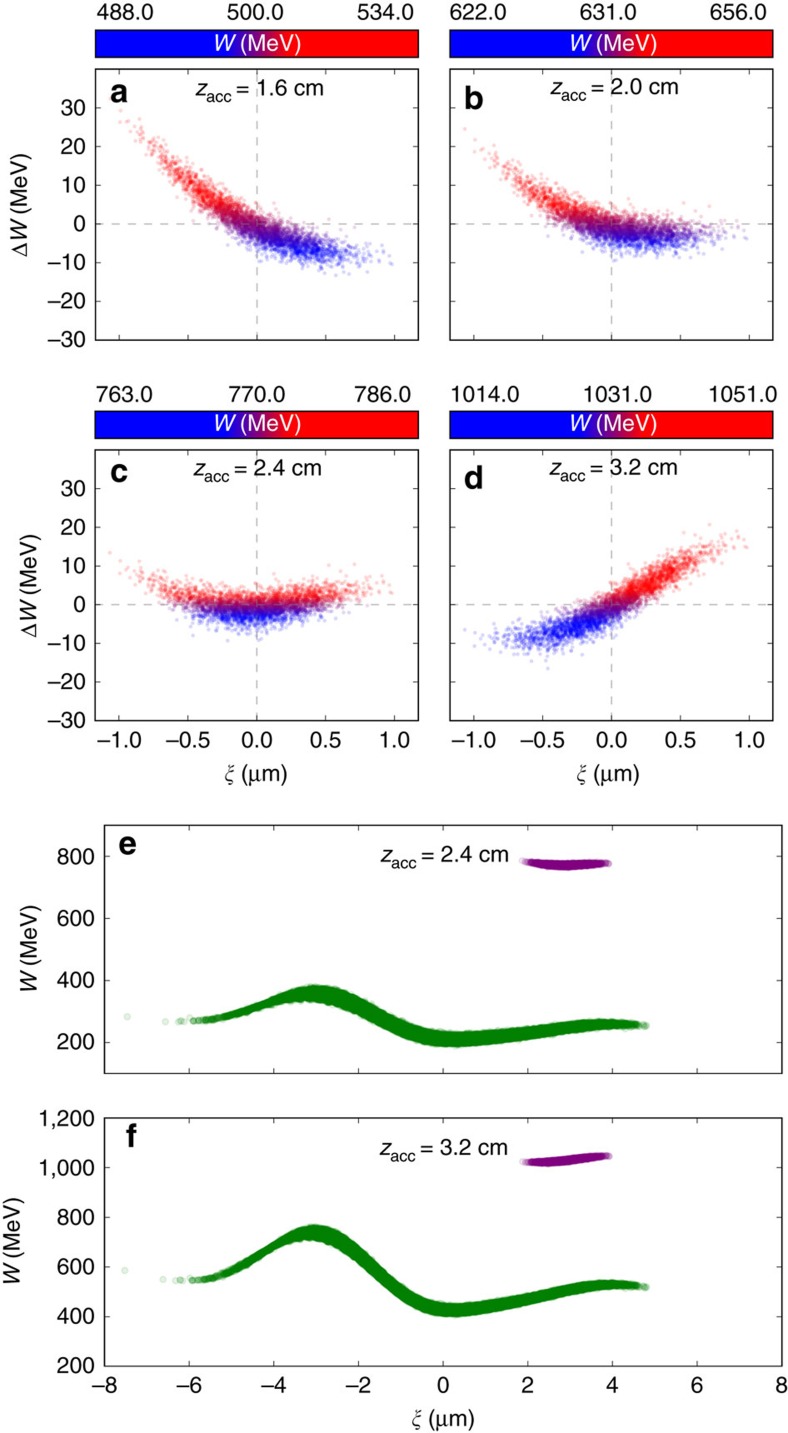
Figure 3 summarizes the corresponding longitudinal phase space evolution associated with the simulation discussed in Fig. 2. Immediately before the escort bunch is generated, the witness bunch exhibits the typical negative chirp, shown in Fig. 3a. This situation corresponds to Fig. 1a (unloaded wake) and Fig. 2b. Once the escort is produced and trapped at around the same position ξ as the previously produced and accelerated witness bunch, however, the locally reversed Ez begins to rotate the longitudinal phase space of the witness bunch counter-clockwise, while the witness bunch in total is further accelerated at slightly reduced level. Consequently, the witness bunch absolute energy spread is reduced strongly and as acceleration progresses the correlated energy spread reduces, reaching a minimum of ΔWr.m.s.≈2.56 MeV at a mean energy of 770 MeV after zacc≈2.4 cm (Fig. 3c). This would be an optimal extraction point for key applications which require minimized energy spread. It is also possible to further rotate the phase space in order to generate positive energy chirps, which corresponds to the situation depicted in Fig. 3d. As shown in Fig. 3e,f, although necessarily spatially overlapping, the witness and escort electron population are at all times strongly separated in energy, which allows straightforward separation.

Figure 3. Witness bunch longitudinal phase space.

Figure 3

Open in a new tab

3D VSim results showing the longitudinal phase space evolution of the witness bunch just before release of the escort bunch (a) after Δzacc≈0.35 cm of dechirping (b) and at zacc≈2.4 cm at optimum dechirping (c). Further counter-clockwise phase-space rotation generates bunches with positive energy chirps (d). (e,f) show the fully dechirped case and the overchirped case, respectively, where the witness (purple) and escort (green) beam are clearly separated by energy.

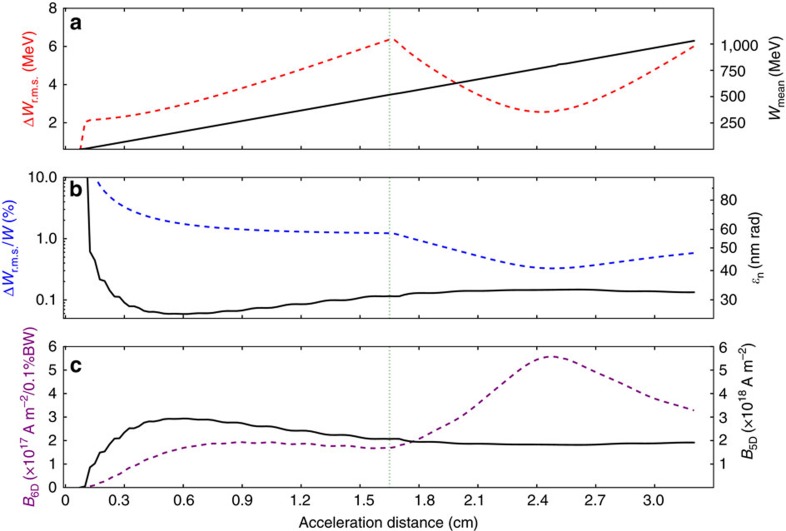
The results of these proof-of-concept simulations for the witness bunch parameters are summarized in Fig. 4. While the mean witness energy W increases linearly (black solid line, right y-axis), the absolute energy spread ΔWr.m.s. (red dashed line, left y-axis) increases significantly up to the escort release point at zacc≈1.6 cm, as expected (Fig. 4a). The ΔEz reversal, generated by the escort bunch, then subsequently reduces the accumulated energy chirp until the minimum energy spread is reached at zacc≈2.4 cm. The active dechirping method includes head and tail of the witness bunch, which increases its efficiency. The minimum total energy spread is approximately the same as at the very beginning of the witness bunch acceleration process at zacc≈0.15 cm. The relative energy spread ΔWr.m.s./W (blue dashed line, left y-axis—note the log scale) reduces from nearly 2% before dechirping sets in, down to a minimum of ∼0.3% at a mean energy of Wmean≈774 MeV, as seen in Fig. 4b. After the compensation of the correlated energy spread, the absolute energy spread ΔWr.m.s. rises again due to continuing phase space rotation, which leads to overcompensation. The witness bunch normalized transverse emittance ɛn (black solid line, right y-axis), is almost unaffected by the escort bunch and continues to stay at tens of nm-rad levels during the longitudinal phase space rotation. Finally, in Fig. 4c the 5D and 6D-brightness evolutions are plotted. The 6D-brightness reaches record values of B6D≈5.5 × 1017 Am−2 rad−2/0.1% ΔWr.m.s./W. Supplementary Movie 1 (with description provided in Supplementary Fig. 1 and Supplementary Note 1) visualizes the concept and the witness parameter evolution. It should be noted that the obtained values are significantly limited by the computational load of the 3D-simulations. At larger plasma wavelengths (thus simulation boxes), with other plasma species, and fully resolved laser pulses, the energy spreads, emittance and brightness values have the potential to be further improved by at least one order of magnitude.

Figure 4. Evolution of the witness bunch parameters.

Figure 4

Open in a new tab

(a) r.m.s. energy spread ΔWr.m.s. and central energy Wmean; (b) relative energy spread ΔWr.m.s./W and normalized transverse emittance ɛn; and (c) 5D- and 6D-brightness. At zacc≈2.4 cm in the lab frame, the optimum dechirping point and hence the maximum 6D-brightness is reached.

Calculation of the residual energy spread

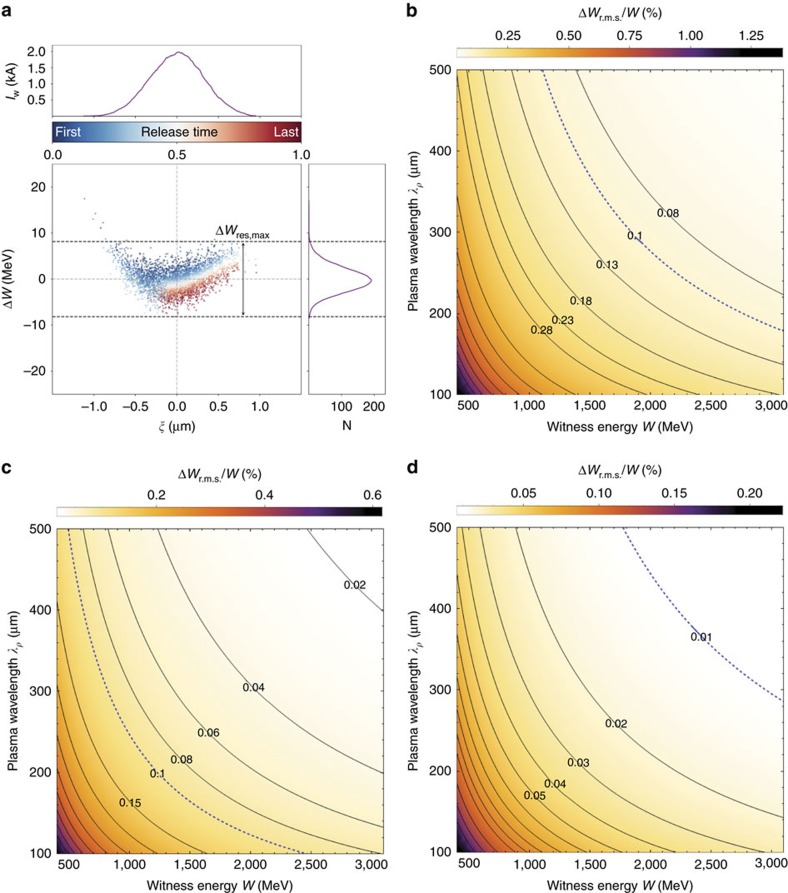
A fully chirp-compensated bunch or other longitudinal phase space shapes can be produced at arbitrary mean energy, as one can either vary the escort charge, its release position and/or the plasma stage length. The inherent residual energy spread of the witness may be approximated based on the different release times of individual witness electrons by the co-propagating laser pulse as ΔWres,r.m.s.≈2π/5 Ez,trap w0,w2/λL (see Methods). Figure 5a visualizes the dechirped bunch of Fig. 3c with a color-coding of the release times, revealing that the electrons which were released first (blue) are accelerated longer and hence gain more energy than electrons born last (red). Using the witness bunch release laser parameters of w0,w=7 μm, λL=800 nm, and an electric accelerating field at trapping position of Ez,trap=33.2 GV m−1 as seen in the simulation, the scaling predicts a ΔWres,r.m.s.≈2.55 MeV. This is in excellent agreement with the minimum energy spread of ΔWres,r.m.s.≈2.56 MeV as retrieved from the simulation.

Figure 5. Residual energy spread from simulation and scaling prediction.

Figure 5

Open in a new tab

Absolute residual witness energy spread from simulation (a) and relative energy spread from scaling predictions (b–d). In (a), the residual energy spread as observed in the PIC-simulation at minimum energy spread position (corresponding to the case depicted in Fig. 3c) is shown with color-coding of laser-released witness electrons, where position 0 indicates the first electron released and position 1 indicates the last electron released. Electrons which are released earlier (blue) are gaining more energy than those released later (red), in accordance with the numerical scaling estimation. b–d show relative energy spread predictions based on the residual energy spread scaling for a witness release laser spot size of w0,w=10 μm (b), w0,w=7 μm (c) and w0,w=4 μm (d) in dependence of witness bunch energy and wavelength of the accelerating plasma wave. Isolines depict the combinations of constant relative energy spread for selected values.

A further simulation was performed at reduced resolution to demonstrate the scalability of the concept to higher electron energies numerically (Supplementary Fig. 2 and Supplementary Note 2). Here, the relative energy spread amounts to ΔWres,r.m.s./Wmean≈0.15% at mean energy of Wmean≈1.6 GeV, and the corresponding slice energy spread is at the 0.1% level. This is likewise in excellent agreement with the residual energy spread scaling. The experimental implications are that strong focusing and operation at longer plasma wavelengths can decrease the residual energy spread. Figure 5b–d shows predictions of a generalized scaling which uses the linear wave-breaking limit as approximation for the electric field accelerating the witness (see Methods). The experimentally relevant relative energy spread, which naturally decreases as ∝ 1/Wmean on top of a minimized residual energy spread ΔWres,r.m.s., is plotted for different values of plasma wavelengths and laser focus sizes w0. For example, the scaling suggests that at λp=500 μm and w0,w=7 μm, a relative energy spread of ΔWres,r.m.s./Wmean≈0.03% can be obtained at an electron energy of Wmean≈2 GeV (see Fig. 5c), and that for w0,w=4 μm, plasma wavelengths of a few hundred μm at energies around 2 GeV and beyond, the relative energy spread can reach values of ΔWres,r.m.s./Wmean <0.01%.

Discussion

A tuneable and flexible scheme for minimization of energy spreads in plasma wakefield accelerators by approximately an order of magnitude is presented. The energy compensation occurs in a single stage at constant plasma density profile—the same stage where witness bunch generation and acceleration take place. This is a far-reaching advantage. First, otherwise extraction of energy-chirped witness bunches from plasma accelerator stages and their transport is highly problematic, and second the minimized energy spread enables a strongly broadened range of applications. While the technique is in principle applicable also for purely (for example, two-color) laser driven schemes, the dephasing-free PWFA with up to metre-scale acceleration in a single-stage and multi- or even tens of GeV energy gains, is of particular interest. The highest impact may be expected from applying the scheme to witness bunches with ultrahigh 5D-brightness, as accessible by the underdense photocathode Trojan Horse scheme. In this case, reduced energy spread is combined with ultrahigh 5D-brightness, leading to unprecedented 6D-brightness values. Experimentally, the production of the escort bunch for chirp control adds no additional qualitative challenges compared to the TH scheme, for which first signatures have recently been observed at SLAC FACET, the Facility for Advanced Accelerator Experimental Tests with its pioneering electron beam driven plasma wakefield accelerator program48. The concept is scalable towards higher energies and can remove correlated energy spread nearly completely, just leaving the minimized residual uncorrelated energy spread. Particular impact of the approach may be expected for light source applications. For example, in inverse Compton scattering setups higher γ-photon beams can be obtained with decreased spectral bandwidth if the electron energy spread can be minimized, or hard X-ray FEL's could be realized experimentally already at few GeV electron energies. The combination of low emittance, ultrahigh brightness and low energy spread may allow to beat the Pellegrini criterion49 and the Pierce parameter ρFEL at the same time, and to achieve ultrahigh gain. The Pellegrini criterion ɛn≤γλr/4π states that the transverse normalized emittance ɛn of the electron beam must be smaller than the obtainable diffraction limited FEL photon beam wavelength λr, which is clearly satisfied at emittance levels of ɛn ≈10−8 mrad in principle even for sub-angstrom hard X-ray FELs. The derived residual energy spread scaling together with scalability to higher energies indicates that relative energy spread levels ΔWr.m.s. /W≈0.01% can be reached at few GeV energy levels, which would be an order of magnitude better than the threshold to satisfy Pierce parameter levels of ρFEL <0.1% as required for a hard X-ray FEL. Electron energies of few GeV can nowadays be reached straightforwardly in a single plasma stage. For example, an electron beam at energy W=3 GeV and with a normalized emittance of ɛn=40 nm and a peak current of Ip≈2.0 kA, dechirped to relative energy spreads of ΔWr.m.s./W≈0.085% (corresponding to a residual energy spread of ΔWres,r.m.s.≈2.56 MeV as seen consistently in the simulations) using the presented method, would be expected to lase strongly in a state-of-the-art undulator with a period length of λu=1.5 cm and undulator parameter K=1.0 to obtain FEL radiation at λr≈0.32 nm. Because of the high-brightness electron beam source, the 1D FEL gain length may hence amount to Lg,1D≈0.6 m, only, potentially allowing very high FEL power levels. With advanced cryogenic undulators which allow for sub-cm undulator periods50, hard X-ray wavelengths may be realizable already at even lower electron energies8. The control over the longitudinal phase space furthermore allows generation of beams with negative or positive chirps in a wide range, or even non-linear chirps by tuning the escort bunch current profile, which may be useful to realize chirped broadband radiation sources, energy tapering51 or (dechirped) multi-color light sources52. It should be noted that our findings, while they may on longer term prove transformative for future light source design and other applications which require extremely high beam quality, do not yet include extraction, capture, separation, transport and potential conditioning of the electron beams. This is beyond the scope of the present manuscript and a subject of future studies.

Finally, operation at long plasma wavelengths does not only allow a further reduction of the residual energy spread, but is also advantageous as regards experimental realization and shot-to-shot stability. If using an electron beam generated by a radiofrequency-based linear accelerator as driver for the plasma stage, the issue of synchronization of the electron beam with a laser pulse system arises. Inversely, this is also a problem which is found for external injection of linac-generated electron beams into laser-driven plasma waves53,54,55, and for pump-probe experiments and free-electron lasers56. In ref. 54, next to phase space rotation and compression in plasma waves, jitter effects are discussed, and in ref. 56, sub-30-fs synchronization has been reported, and improvements to sub-10-fs levels has been suggested. A longitudinal position jitter of ∼3 μm, corresponding to sub-10-fs temporal jitter, in a plasma wave with wavelength λp >300 μm amounts to less than 1%, and a dechirper region length of ∼10 μm suggests that the dechirping could be realized with each shot. In this connection, it suggests itself that the two release laser pulses which produce witness and escort bunches should be taken from the same laser system and parent laser pulse, such that they may inherently have fs or even sub-fs scale synchronization between each other (see Supplementary Fig. 3 and Supplementary Note 3). In all-optical versions of the scheme, in addition, the driver beam would also be produced by a laser system8,10,12,57,58,59,60,61,62, which would allow to harness inherently fs or sub-fs level synchronization. Spatial alignment jitter is in general of lesser concern than synchronization, because it has a reduced impact on trapping positions and hence residual energy spread. Furthermore, operation at larger plasma waves further improves resilience towards spatial positioning jitter, analogously to temporal jitter considerations. We conclude that state-of-the-art technology and methods of spatiotemporal jitter control are sufficient to realize the proposed approach.

Methods

Semi-analytical model of plasma wakes in the 1D nonlinear regime

A simplified 1D fluid model is used to describe the nonlinear wakefield excitation and interaction by the driver, witness and escort beams. The wake is driven by a relativistic electron beam with velocity vd so that vp∼vd∼c, where vp is the phase velocity of the plasma wake. In this relativistic, dephasing-free scenario in quasi-static approximation and assuming a non-evolving driver beam, the resulting quantities are only dependent on the longitudinal coordinate ξ=z−vpt. The Poisson equation can then be simplified44 to 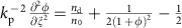Inline graphic, where n0 is the unperturbed background plasma density, kp=2π/λp is the plasma wavenumber corresponding to a plasma wavelength λp=2πc[meɛ0/(n0e2)]1/2, c being the speed of light, me and e are the electron mass and charge, respectively, nd(ξ) is the electron driver charge density, and φ is the scaled electrostatic potential. If additional relativistically co-moving, non-evolving electron witness and escort beams with charge density distributions nw(ξ) and nb(ξ), respectively, are added, the wake changes to 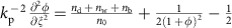Inline graphic. This differential equation is solved numerically (note that in Fig. 1, nw(ξ)/n0=0.2 to account for the much smaller witness bunch charge when compared to the escort), and expressions for the potential φ and the electric field Ez are obtained. The results shown in Fig. 1 are based on this description, and are depicted for lengths σz,d=0.6/kp, σz,w=0.25/kp and σz,b=0.7/kp and different ratios of nb/n0, which is used to inform the amount of charge to be released by the laser pulse generating the escort bunch in the implementation.

3D particle-in-cell simulations

Being guided by the semi-analytical 1D model, 3D particle-in-cell simulations using the VSim code63 have been carried through in order to verify the hypothesis. The driving electron beam is chosen as a Gaussian both in transverse (x,y) and longitudinal (z) direction, with r.m.s. sizes of σx,y=7.5 μm and σz=20 μm, respectively, a normalized emittance of ɛn=5 mm-mrad, central energy of Wd=10 GeV, energy spread ΔWr.m.s.=0.1 GeV and total charge Qd=2 nC. Such energies and current levels are easily within the range of SLAC FACET-II. We chose a plasma density of n0=1.1 × 1017 cm−3, corresponding to a plasma wavelength of λp≈100 μm. In view of the multi-cm-long simulation lengths, and the numerical Cherenkov effect, which is known to have significant ramifications on multi-dimensional relativistic plasma simulations, we use a co-moving simulation box with a grid of 288 × 48 × 48 cells (660 k cells in total), and a cell size of 0.8 μm in longitudinal and 3.2 μm in the transverse directions. We use the optimal time step64,65 and digital smoothing of the gridded currents to minimize the growth rate of numerical Cherenkov noise. Numerical Cherenkov is still significant and accounts for the wiggles in the lineouts of the electric field, as seen in Fig. 2—and for the production of an extra hump behind the escort beam, which leads to a substantially shorter usable length of the dechirping region than one would expect. The numerically usable dechirping length is ∼5 μm long and is adequate for demonstration of the concept; however, the longer physically correct dechirping length (estimated to be ∼10 μm) would allow significantly better results. We use an artificially short plasma wavelength to reduce the computational load, resulting in wakefield and driver field 'hot spots' of very high electric fields. This prohibits the use of H/He mixtures to realize the underdense photocathode PWFA because of He ionization at these hot spots, which impairs the laser-induced helium ionization and also leads to dark current66. Instead, we use a one-component version of the TH based on lithium, where Li is pre-ionized and the further ionization to Li+ is exploited to generate the laser-released bunches. This required setting the focus intensity of the Gaussian laser pulses, operating at a central wavelength of 0.8 μm, to much larger values than in the H/He case, namely to a normalized light amplitude of a0=eE/(meωc)≈0.1, where e and me are the charge and mass of an electron, respectively, ω is the laser frequency and c is the vacuum speed of light, which increases the emittance limits67,68. These choices also increase the longitudinal electric field gradient and hence the chirp of the produced beams. The validation of the scheme using a non-optimal physics scenario in order to reduce computational load leaves substantial room for further optimization of the performance.

Residual energy spread scaling

The total energy spread of the generated electron bunches has a correlated energy spread component and an uncorrelated one. While the longitudinal phase space chirp which is imposed by the strong accelerating field gradient can be removed by the escort bunch technique, the uncorrelated energy spread is a result of the witness bunch generation process. This needs to be minimized, too, and can be estimated as follows. In doing so, one may assume a quasi-static ionization front position of the co-propagating laser pulse which releases the witness bunch. This is justified because of the stronger focusing, lower a0 and shorter laser pulse duration chosen when compared to the escort bunch. A typical effective ionization length for such laser pulses is of the order of 2ZR. Electrons which are released first are trapped first, and therefore experience a longer total acceleration time than electrons released later during the acceleration process. This constitutes a total residual maximum energy spread which can be expressed as ΔWres,max=Wfirst−Wfinal, where Wfirst is the energy gain of the first released witness electron and Wfinal is the energy gain of the last electron released. Figure 5a shows a color-coded longitudinal phase space of the electron witness bunch obtained from the simulation at the position of minimized total energy spread, where electrons born earlier are colored blue and electrons born later are colored red.

Since plasma wakefield acceleration driven by relativistic electron beams is essentially dephasing-free, the residual maximum energy spread can then be approximated as ΔWres,max=2 Ez,trap ZR, where Ez,trap is the accelerating longitudinal electric field at quasistatic trapping position of the witness bunch inside the wake. Taking into account the energy range of two full width at half maximum (FWHM) for the numerical evaluation, which contains approximately 99% of the contributing particles within 2 FWHM≈5σr.m.s., allows to estimate the r.m.s. residual energy spread as ΔWres,r.m.s.≈ΔWres,max/5≈2/5 Ez,trap ZR≈2π/5 Ez,trap w02/λL. Using the witness bunch laser parameters of w0=7 μm, λL=800 nm, and an electric field at trapping position in the simulation of Ez,trap≈33.2 GV m−1, this scaling predicts a ΔWres,r.m.s.≈2.55 MeV, which is in excellent agreement with the minimum energy spread of ΔWres,r.m.s.≈2.56 MeV, as retrieved from the simulation.

The residual energy spread scaling may be generalized by using the linear wave breaking limit E0 [V m−1]≅96 n01/2 [cm−3] as estimation of the electric accelerating field, where n0 is the background plasma density in cm−3. While the peak fields in the strongly nonlinear blowout case can exceed the linear wavebreaking prediction considerably, for reasons of stability and robustness of the acceleration process the trapping position in the nonlinear blowout should be chosen significantly further ahead within the blowout, where the accelerating fields are lower and are more linear. The linear wave breaking limit then is therefore a good approximation. The scaling then generalizes to ΔWres,max≈2π/5 Ez,trap w0,w2/λL≈96 n01/2 [cm−3] 2π/5 w0,w2/λL.

Data availability

Data associated with research published in this paper is available at http://dx.doi.org/10.15129/3563d476-7a65-497c-9c7e-5a1f7a57591f.

Additional information

How to cite this article: Manahan, G. G. et al. Single-stage plasma-based correlated energy spread compensation for ultrahigh 6D brightness electron beams. Nat. Commun. 8, 15705 doi: 10.1038/ncomms15705 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Information

Supplementary Figures, Supplementary Table and Supplementary Notes.

ncomms15705-s1.pdf (794.9KB, pdf)
Supplementary Movie 1

Ultrahigh 6D brightness electron beam generation.

Download video file (10.4MB, mov)

Acknowledgments

This work used computational resources of the National Energy Research Scientific Computing Center, which is supported by DOE DE-AC02-05CH11231, of JURECA (Project hhh36), of HLRN and of Shaheen (Project k1191). A.F.H. is supported by a fellowship within the FIT worldwide programme of the German Academic Exchange Service (DAAD). B.H. acknowledges the support by DFG Emmy-Noether program, and by RadiaBeam Technologies (DOE contract DE-SC0009533). Z.M.S. acknowledges the support by Leverhulme Trust Research Project Grant, the National Basic Research Program of China (Grant No. 2013CBA01504) and NSFC (Grant No. 11421064). B.H. and Z.M.S. acknowledge support of by EPSRC (Grant No. EP/N028694/1), of H2020 EuPRAXIA (Grant No. 653782) and of LASERLAB-EUROPE Grant No. 284464. D.L.B. acknowledges support of the US DOE Office of High Energy Physics under Award No. DE-SC0013855.

Footnotes

The authors are involved in intellectual property development with regard to applications of high 6D-brightness electron beams.

Author contributions G.G.M. and A.F.H. contributed equally to this work. B.H., A.F.H. and G.G.M. conceived the idea and performed the simulations and writing of the manuscript. P.S. and T.H. provided additional figures and contributed to the completion of the manuscript. P.S., P.D., A.B., A.K., O.K., G.W. and T.H. provided PIC simulation support. Z.M.S., J.R.C., D.L.B. and J.B.R. contributed to theoretical, numerical and computational aspects of the concept.

References

  1. Blumenfeld I. et al. Energy doubling of 42 GeV electrons in a metre-scale plasma wakefield accelerator. Nature 445, 741–744 (2007). [DOI] [PubMed] [Google Scholar]
  2. Litos M. et al. High efficiency acceleration of an electron beam in a plasma wakefield accelerator. Nature 515, 92–95 (2014). [DOI] [PubMed] [Google Scholar]
  3. Mangles S. et al. Monoenergetic beams of relativistic electrons from intense laser-plasma interactions. Nature 431, 535–538 (2004). [DOI] [PubMed] [Google Scholar]
  4. Geddes C. D. R. et al. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature 431, 538–541 (2004). [DOI] [PubMed] [Google Scholar]
  5. Faure J. et al. A laser-plasma accelerator producing monoenergetic electron beams. Nature 431, 541–544 (2004). [DOI] [PubMed] [Google Scholar]
  6. Wang X. et al. Quasi-monoenergetic laser-plasma acceleration of electrons to 2 GeV. Nat. Commun. 4, 1988 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Leemans W. P. et al. Multi-GeV electron beams from capillary-discharged-guided subpetawatt laser pulses in the self-trapping regime. Phys. Rev. Lett. 113, 245002 (2014). [DOI] [PubMed] [Google Scholar]
  8. Hidding B. et al. Ultracold electron bunch generation via plasma photocathode emission and acceleration in a beam-driven plasma blowout. Phys. Rev. Lett. 108, 035001 (2012). [DOI] [PubMed] [Google Scholar]
  9. Li F. et al. Generating high-brightness electron beams via ionization injection by transverse colliding lasers in a plasma-wakefield accelerator. Phys. Rev. Lett. 111, 015003 (2013). [DOI] [PubMed] [Google Scholar]
  10. Bourgeois N., Cowley J. & Hooker S. M. Two-pulse ionization injection into Quasilinear Laser Wakefields. Phys. Rev. Lett. 111, 015003 (2013). [DOI] [PubMed] [Google Scholar]
  11. Martinez de la Ossa A., Grebenyuk J., Mehrling T., Schaper L. & Osterhoff J. High-Quality Electron Beams from Beam-Driven Plasma Accelerators by Wakefield-Induced Ionization Injection. Phys. Rev. Lett. 111, 245003 (2013). [DOI] [PubMed] [Google Scholar]
  12. Yu L.-L. et al. Two-color laser-ionization injection. Phys. Rev. Lett. 112, 125001 (2014). [DOI] [PubMed] [Google Scholar]
  13. Kim K.-J. et al. Towards advanced electron beam brightness enhancement and conditioning. Report No. ANL/APS/LS-305 (U.S. Department of Energy, 2003).
  14. Emma P. & Raubenheimer T. Systematic approach to damping ring design. Phys. Rev. ST Accel. Beams 4, 021001 (2001). [Google Scholar]
  15. Graves W. S., Brown W., Kaertner F. X. & Moncton D. E. MIT inverse Compton source concept. Nuclear Instrum. Methods A 608, S103–S105 (2009). [Google Scholar]
  16. Carlsten B. E. et al. High repetition-rate inverse Compton scattering x-ray source driven by a free-electron laser. J. Phys. B: At. Mol. Opt. Phys. 47, 234012 (2014). [Google Scholar]
  17. Whittum D. H., Sessler A. M. & Dawson J. M. Ion-channel laser. Phys. Rev. Lett. 64, 2511 (1990). [DOI] [PubMed] [Google Scholar]
  18. Esarey E., Shadwick B. A., Catravas P. & Leemans W. P. Synchrotron radiation from electron beams in plasma-focusing channels. Phys. Rev. E 65, 056505 (2001). [DOI] [PubMed] [Google Scholar]
  19. Ersfeld B. et al. The ion channel free-electron laser with varying betatron amplitude. New J. Phys. 16, 093025 (2014). [Google Scholar]
  20. Rousse A. et al. Scaling of betatron x-ray radiation. Eur. Phys. J. 45, 391 (2007). [Google Scholar]
  21. Li R. K. & Musumeci P. Single-shot MeV transmission electron microscopy with picosecond temporal resolution. Phys. Rev. Appl. 2, 024003 (2014). [Google Scholar]
  22. Pellegrini C. The history of x-ray free electron lasers. Eur. Phys. J. H 37, 659–708 (2012). [Google Scholar]
  23. Pellegrini C., Marinelli A. & Reiche S. The physics of x-ray free-electron lasers. Rev. Mod. Phys. 88, 015006 (2016). [Google Scholar]
  24. Emma C. et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photon. 4, 641–647 (2010). [Google Scholar]
  25. Di Mitri S. On the importance of electron beam brightness in high gain free electron lasers. Photonics 2, 317–341 (2015). [Google Scholar]
  26. Wiggins S. M. et al. High quality electron beams from a laser wakefield accelerator. Plasma Phys. Control. Fusion 52, 124032 (2010). [Google Scholar]
  27. Lundh O. et al. Few femtosecond, few kiloampere electron bunch produced by a laser-plasma accelerator. Nat. Phys. 7, 219–222 (2011). [Google Scholar]
  28. Hidding B. et al. Ultrahigh brightness bunches from hybrid plasma accelerators as drivers of 5th generation light sources. J. Phys. B: At. Mol. Opt. Phys. 47, 234010 (2014). [Google Scholar]
  29. Rosenzweig J. B., Breizman B., Katsouleas T. & Su J. J. Acceleration and focusing of electrons in two-dimensional nonlinear plasma wake fields. Phys. Rev. A 44, R6189 (1991). [DOI] [PubMed] [Google Scholar]
  30. Antici P. et al. Laser-driven electron beamlines generated by coupling laser-plasma sources with conventional transport systems. J. Appl. Phys. 112, 044902 (2012). [Google Scholar]
  31. Assmann R. & Yokoya K. Transverse beam dynamics in plasma-based linacs. Nucl. Instrum. Methods Phys. Res. A 410, 544–548 (1998). [Google Scholar]
  32. Floettmann K. Some basic features of the beam emittance. Phys. Rev. ST Accel. Beams 6, 034202 (2003). [Google Scholar]
  33. Gholizadeh R. et al. Preservation of beam emittance in the presence of ion motion in future high-energy plasma-wakefield-based colliders. Phys. Rev. Lett. 104, 155001 (2010). [DOI] [PubMed] [Google Scholar]
  34. Mehrling T. et al. Transverse emittance growth in staged laser-wakefield acceleration. Phys. Rev. ST Accel. Beams 15, 111303 (2012). [Google Scholar]
  35. Bonifacio R. et al. Collective instabilities and high gain regime in free electron laser. Optics Commun. 50, 373–378 (1984). [Google Scholar]
  36. Saldin E., Schneidmiller E. A. & Yurkov M. V. An analytical description of longitudinal phase space distortion in magnetic bunch compressors. Nuclear Instrum. Methods A 483, 516–520 (2002). [Google Scholar]
  37. Braun H., Chautard F., Corsini R., Raubenheimer T. O. & Tenenbaum P. Emittance growth during bunch compression in the CTF-II. Phys. Rev. Lett. 84, 658 (2000). [DOI] [PubMed] [Google Scholar]
  38. Emma P. et al. Experimental demonstration of energy-chirp control in relativistic electron bunches using a corrugated pipe. Phys. Rev. Lett. 112, 034801 (2014). [DOI] [PubMed] [Google Scholar]
  39. Zhang Z. et al. Electron beam energy chirp control with a rectangular corrugated structure at the Linac Coherent Light Source. Phys. Rev. ST Accel. Beams 18, 010702 (2015). [Google Scholar]
  40. Antipov T. et al. Experimental demonstration of energy-chirp compensation by a tunable dielectric-based structure. Phys. Rev. Lett. 112, 114801 (2014). [DOI] [PubMed] [Google Scholar]
  41. Di Mitri S. & Cornaccchia M. Electron beam brightness in linac drivers for free-electron lasers. Phys. Rep. 539, 1–48 (2014). [Google Scholar]
  42. Katsouleas T. et al. Beam loading in plasma accelerators. Part. Accel. 22, 81–99 (1987). [Google Scholar]
  43. Tzoufras M. et al. Beam loading in the nonlinear regime of plasma-based acceleration. Phys. Rev. Lett. 101, 145002 (2008). [DOI] [PubMed] [Google Scholar]
  44. Esarey E. et al. Overview of plasma-based accelerator concepts. IEEE Trans. Plasma Sci. 24, 252–288 (1996). [Google Scholar]
  45. Technical Design Report for the FACET-II project at SLAC National Accelerator Laboratory, SLAC-R-1072 (SLAC National Accelerator Laboratory, 2016).
  46. Wood W. M., Siders C. W. & Downer M. C. Femtosecond growth dynamics of an underdense ionization front measured by spectral blueshifting. IEEE Trans. Plasma Sci. 21, 20–33 (1993). [Google Scholar]
  47. Kim K. Y., Alexeev I. & Milchberg H. M. Single-shot measurement of laser-induced double step ionization of helium. Optics Express 10, 1563 (2002). [DOI] [PubMed] [Google Scholar]
  48. Hogan M. J. et al. Plasma wakefield acceleration experiments at FACET. New J. Phys. 12, 055030 (2010). [Google Scholar]
  49. Murphy J. B. & Pellegrini C. Generation of high intensity coherent radiation in the soft xray and vacuum ultraviolet region. J. Opt. Soc. Am. B 2, 259 (1985). [Google Scholar]
  50. O'Shea F. H. et al. Short period, high field cryogenic undulator for extreme performance x-ray free electron lasers. Phys. Rev. ST Accel. Beams 13, 070702 (2010). [Google Scholar]
  51. Saldin E. L., Schneidmiller E. A. & Yurkov M. V. Self-amplified spontaneous emission FEL with energy chirped electorn beam and its application for generation of attosecond pulses. Phys. Rev. ST Accel. Beams 9, 050707 (2006). [Google Scholar]
  52. Zhang Z., Ding Y., Marinelli A. & Huang Z. Longitudinal dynamics of twin electron bunches in the Linac Coherent Light Source. Phys. Rev. ST. Accel. Beams 18, 030702 (2015). [Google Scholar]
  53. Clayton C. E. et al. Ultrahigh-gradient acceleration of injected electrons by laser-excited relativistic electron plasma waves. Phys. Rev. Lett. 70, 37 (1993). [DOI] [PubMed] [Google Scholar]
  54. Ferrario M., Katsouleas T. C., Serafini L. & Ben-Zvi I. Adiabatic plasma buncher. IEEE Trans. Plasma Sci. 28, 1152–1158 (2000). [Google Scholar]
  55. Zeitler B. et al. Merging conventional and laser wakefield accelerators. Proc. SPIE 8779, 877904 (2013).
  56. Schulz S. et al. Femtosecond all-optical synchronization of an X-ray free-electron laser. Nat. Commun. 6, 5938 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Hidding B. et al. Monoenergetic energy doubling in a hybrid laser-plasma wakefield accelerator. Phys. Rev. Lett. 104, 195002 (2010). [DOI] [PubMed] [Google Scholar]
  58. Masson-Laborde P. E. et al. Giga-electronvolt electrons due to a transition from laser wakefield acceleration to plasma wakefield acceleration. Phys. Plasmas 21, 123113 (2014). [Google Scholar]
  59. Chou S. et al. Collective Deceleration of Laser-Driven Electron Bunches. Phys. Rev. Lett 117, 144801 (2016). [DOI] [PubMed] [Google Scholar]
  60. Tsung F. S. et al. Near-GeV energy laser wakefield acceleration of self-injected electrons in a centimetre-scale plasma channel. Phys. Rev. Lett. 93, 185002 (2004). [DOI] [PubMed] [Google Scholar]
  61. Pae K. H., Choi I. W. & Lee J. Self-mode-transition from laser wakefield accelerator to plasma wakefield accelerator of laser-driven plasma-based electron acceleration. Phys. Plasmas 17, 123104 (2016). [Google Scholar]
  62. Kuschel S. et al. Demonstration of passive plasma lensing of a laser wakefield accelerated electron bunch. Phys. Rev. Accel. Beams 19, 071301 (2016). [Google Scholar]
  63. Nieter C. & Cary J. R. VORPAL: A versatile plasma simulation code. J. Comp. Physics 196, 448–478 (2004). [Google Scholar]
  64. Vay J. L., Geddes C. G. R., Cormier-Michel E. & Grote D. P. Numerical methods for instability mitigation in the modeling of laser Wakefield accelerators in a Lorentz-boosted frame. J. Comp. Phys. 230, 15 (2011). [Google Scholar]
  65. Godfrey B. B. & Vay J. L. Numerical stability of relativistic beam multidimensional PIC simulations employing the Esirkepov algorithm. J. Comp. Phys. 248, 33–46 (2013). [Google Scholar]
  66. Manahan G. G. et al. Hot spots and dark current in advanced plasma Wakefield accelerators. Phys. Rev. Accel. Beams 19, 011303 (2016). [Google Scholar]
  67. Xi Y. et al. Hybrid modeling of relativistic underdense plasma photocathode injectors. Phys. Rev. ST Accel. Beams 16, 031303 (2013). [Google Scholar]
  68. Schroeder C. et al. Thermal emittance from ionization-induced trapping in plasma accelerators. Phys. Rev. ST Accel. Beams 17, 101301 (2014). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures, Supplementary Table and Supplementary Notes.

ncomms15705-s1.pdf (794.9KB, pdf)
Supplementary Movie 1

Ultrahigh 6D brightness electron beam generation.

Download video file (10.4MB, mov)

Data Availability Statement

Data associated with research published in this paper is available at http://dx.doi.org/10.15129/3563d476-7a65-497c-9c7e-5a1f7a57591f.

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES