Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2017 Jun 5;8:15766. doi: 10.1038/ncomms15766

New Martian valley network volume estimate consistent with ancient ocean and warm and wet climate

Wei Luo 1,a, Xuezhi Cang 1, Alan D Howard 2
PMCID: PMC5465386  PMID: 28580943

Abstract

The volume of Martian valley network (VN) cavity and the amount of water needed to create the cavity by erosion are of significant importance for understanding the early Martian climate, the style and rate of hydrologic cycling, and the possibility of an ancient ocean. However, previous attempts at estimating these two quantities were based on selected valleys or at local sites using crude estimates of VN length, width and depth. Here we employed an innovative progressive black top hat transformation method to estimate them on a global scale based on the depth of each valley pixel. The conservative estimate of the minimum global VN volume is 1.74 × 1014 m3 and minimum cumulative volume of water required is 6.86 × 1017 m3 (or ∼5 km of global equivalent layer, GEL). Both are much larger than previous estimates and are consistent with an early warm and wet climate with active hydrologic cycling involving an ocean.

To understand the early Martian climate, the volume of the global Martian valley network is required. Here, the authors use a black top hat transformation method and find that the minimum global valley network volume is 1.74 × 1,014 m3 with a minimum cumulative volume of water required of 6.86 × 1,017 m3.

Fluvial landforms such as valley networks (VNs), outflow channels and delta deposits found on Mars offer the best evidence for its past water activities1,2,3. The inventory of water on Mars has been estimated based on a number of different sources, including volatiles from volcanic activities4, geomorphologic traces left by past water activities (from paleolakes and deltas5,6, outflow channels7,8 and VNs9), the hypothesized northern ocean10 and, more recently, the observed deuterium/hydrogen (D/H) enrichment11. VNs on Mars are river-valley-like features that distribute predominantly on the ancient cratered southern highlands and have been long recognized as the best evidence for past water activities7. In the scenario of a warm and wet early Mars climate, the water running through the VNs would eventually flow towards and collect at the topographically low northern plains, forming an ocean covering nearly 1/3 of the surface12,13. However, the ocean hypothesis has also been controversial3. Supporting evidences include the shoreline features identified from remote-sensing images12, delta deposits found at similar elevation14, sediment stratigraphy consistent with distributary environment15, spatial distribution of VN termini near proposed shorelines16 and elemental distribution of K, Th and Fe revealed by Gamma Ray Spectrometer that are consistent with paleo-ocean boundaries17. Evidence against the ocean hypothesis include variations in the identified shoreline elevations of up to a couple of kilometres10,18, low water inventory19 in comparison with the purported ocean volume and large boulders observed on the ocean floor20. The variations in shoreline elevation have been recently explained by later deformation associated with true polar wander21 and tsunami deposits22. The presence of large boulders in the ocean floor could be emplaced by catastrophic mass-transport events similar to those documented within continental margins on Earth23.

The volume of VN cavity and the amount of water needed to create the cavity by erosion are of significant importance for understanding the early Martian climate, the style and rate of hydrologic cycling and the possibility of an ancient ocean10,12,14,24. However, these two quantities on a global scale remain less well constrained. Improving these estimates may provide additional evidence or constraints regarding early Martian climate and the ocean hypothesis. The volume of VNs is most critical, because it is the basis for inferring the volume of water needed to create the VNs. Early attempts at estimating VN volume were primarily conducted at selected local sites based on simple estimates of VN lengths, widths and depths by assuming VN wall slopes9,25,26 or based on the valley area and the average depth27. The results contained large uncertainty due to crude methodology and/or poor data quality. Rosenberg and Head24 recently estimated the cumulative volume of water needed to carve the late Noachian VNs based on a fluid/sediment flux ratio function derived from terrestrial empirical data. Their estimate of the most probable cumulative water volume was 3–100 m global equivalent layer (GEL) and concluded that the Late Noachian Martian climate may have been less wet than previously thought24. However, their volume of VN excavation was based on eight largest VNs analysed in a previous study28, not on all the VNs mapped globally, even though they claimed that the rest of the VNs were small and had negligible contribution to the total global volume. Here we employed an innovative progressive black top hat (PBTH) transformation method to estimate the depth of each valley pixel29, the minimum volume of material that would have been excavated to form the global VNs16,30 and the minimum cumulative volume of water required to do that.

Results

VN cavity volume

The global VN cavity volume estimate based on the topographically derived version of VN16 is (1.74±0.8) × 1014 m3 and that based on the VN that integrates both the topographically derived14 and manually digitized30 VN is (2.23±1.0) × 1014 m3 (Table 1). Both estimates are one order of magnitude larger than that used the Rosenberg and Head study24. The errors in Table 1 were estimated based on propagation of the vertical error (∼45 m) estimated from gridded Mars Orbiter Laser Altimeter (MOLA) digital elevation model (DEM)31. As the horizontal error of MOLA data (∼100 m) is less than the cell size, it would not impact the final volume estimate.

Table 1. Global Martian VN volume estimates based on PBTH method and volume of water required.

  Topographically derived VN16
 Combined VN (topographically derived14 and manually digitized30)
  Volume or mass GEL (m)* Volume or mass GEL (m)*
VVN (MOLA) (1.74±0.8) × 1014 m3 1.20 (2.23±1.0) × 1014 m3 1.54
VVN (HRSC†) (2.31±1.1) × 1014 m3 1.59 (2.96±1.4) × 1014 m3 2.04
Vs=VVN/(1−λ) (3.55±1.6) × 1014 m3 2.45 (4.55±2.1) × 1014 m3 3.14
Ms=Vs × ρs (1.03±0.5) × 1018 kg — (1.32±0.6) × 1018 kg —
Vw=Ms/Ls (6.86±3.2) × 1017 m3 4.74 × 103 (8.80±4.1) × 1017 m3 6.08 × 103
Open in a new tab

GEL, global equivalent layer; HRSC, High/Super Resolution Stereo Colour Imager; Ls, sediment load in water=1.5 kg m−3; MOLA, Mars Orbiter Laser Altimeter; Ms, mass of sediment; PBTH, progressive black top hat; VN, valley network; Vs, volume of sediment; VVN, volume of VN; Vw, volume of water; λ, porosity=0.35; ρs, density of sediment=2,900 kg m−3.

*Errors for GEL are all less than 10−6 m.

†Scaled based on regression line shown in Fig. 3c.

Minimum cumulative volume of water needed to carve the VNs

There are several ways to convert the volume of VNs to the minimum cumulative volume of water needed to carve the VNs, for example, using a simple water-to-sediment ratio9,26 or fluid/sediment flux ratio function empirically derived based on terrestrial data24. As we are only interested in the global scale estimate, we derived the minimum cumulative volume of water by assuming a reasonable sediment load and density of sediment27, and the result is ∼5 km GEL (based topographically derived VN) to ∼6 km GEL (based on combined VN, Table 1). The minimum cumulative volume of water needed to erode the VNs is about 4,000 times the volume of VNs (for both the topography-based VN and the combined VN), suggesting a relative high rate of water recycling involved in excavating the Martian VNs and consistent with a large open water body (ocean).

If we plug in our most conservative VN volume estimate data (1.74 × 1017 m3) into the empirically fitted fluid/sediment flux ratio function of Rosenberg and Head (their equation (4))24, we would also obtain larger cumulative water volume estimates, ranging from 0.6 km GEL (α=60), 1 km GEL (α=35), to 11 km GEL (α=6), depending on the value of α. The parameter α is a function of hydraulic radius, sediment grain size and density, among other things24. Although their favoured range of α is 35–60, they pointed out the range of α for large VNs should be 6–35 (ref. 24). Therefore, cumulative water volumes for all assumed values of α considerably exceed the estimate of Rosenberg and Head24.

Discussion

Our estimates of the VN volume and water volume are based on the following assumptions: (1) the valley shoulder elevations did not change significantly since their formation; (2) the amount of sediments carried into the valleys from elsewhere (for example, from hillslope by sheet flow) was negligible. In addition, the post-formation infill by other processes such as eolian process or mass wasting were deemed minimum and not considered. Thus, the estimated water volume is the minimum cumulative volume of water required to carve the VNs on Mars globally. Yet, this minimum volume of water is larger than the volume of the hypothesized northern ocean (ranging from 156 to 548 m GEL10,14), which suggests that the water must have cycled through the VN system many times (that is, implying an active hydrologic cycle) and the early climate was likely to be wetter than suggested by some previous studies19,24. We realize that not all VNs on Mars drain to the northern ocean. If we only include those VNs that drain to the northern lowlands (based on current topography), our estimate of cumulative water needed to carve them would be 3.32 km GEL (based on the topographically derived VNs), still larger than previous cumulative water volume estimates and the volume of hypothesized ocean, suggesting an active hydrologic cycle. As on Earth, the great amount of water recycling needed to carve VNs would probably require a large open water body (ocean) on Mars contemporaneous with the VN formation, and a warm and wet climate to support the active hydrologic cycle. Without an ocean-sized open body of water, it would be hard to imagine the high rate of water cycling suggested by our new estimates. Given the large inventory of water from the perspective of global VNs, and that the age of most of the Martian VNs is more than three billion years old (carved into the ancient Noachian highlands), the active hydrologic cycle, the warm and wet climate, and the existence of an ocean must have happened early in Martian history.

There is no ground truth to assess the real accuracy of our estimation. However, we can establish the confidence of our estimates by comparing them with those of previous studies at the same locations using similar data, for example, Hoke et al.28 and Matsubara et al.32 (Table 2). As shown in Table 2, our estimates are generally consistent with these previous studies to within one order of magnitude with the ratio of our estimate to theirs ranging from 0.15 to 1.9. The differences are due to different methodologies used in calculating the volume and how the valley areas were defined. Matsubara et al.32 used the 75th percentile elevation within a search radius along the valley as the shoulder elevation and minimum elevation within that search window as the valley bottom elevation to estimate the eroded volume. Their estimates are larger than ours, as their method generally results in valley areas larger than ours. If we convert our VN volume estimate of the Evros and Samara, Parana and Loire Valles (first and last rows of Table 2) into volume of sediments, our numbers would be 2.28 × 1012 and 9.79 × 1012 m3, respectively, much closer to their estimates. Hoke et al.28 estimated the VN volumes based on manually drawn boundary along the outer walls of the visible valleys and measurements of width and length and estimates of depth. The manually drawn VN boundary is likely different from that derived from PBTH method and may be the primary reason for the differences in volume estimates. Applying the Hoke et al.28 method to the same simulated landscape with the same VN boundary29 resulted in a relative accuracy of ∼85% (see Table 3, calculation courtesy of Brian Hynek and William Nelson, University of Colorado, Boulder, personal communication). They have recently improved their methodology by using the Reimman sums and the Simpson rule. Again, using the same simulated landscape and same VN boundary, the improved method resulted in a slightly better relative accuracy than ours (by about 2.7%, see Table 3, calculation courtesy of Brian Hynek and William Nelson, personal communication). However, their new method requires considerably more human intervention and the user still has to provide a valley area boundary, which BPTH method can automatically generate. The small gain in relative accuracy would not make any significant difference in global estimate of the VN volumes.

Table 2. Comparison of VN volume estimates with previous studies.

VN location Volume1 (m3) (Hoke et al.28) Volume2 (m3) (this paper) Vol2/Vol1 Volume3 (m3) (Matsubara et al.32) Vol2/Vol3
12°S, 12°E (Evros) 9.6 × 1012 1.48 × 1012 0.15 3.35 × 1012 0.44
7°S, 3°E 7.2 × 1011 1.38 × 1012 1.91 — —
3°S, 5°E 2.8 × 1011 4.16 × 1011 1.49 — —
0°N, 23°E 1.5 × 1012 7.19 × 1011 0.48 — —
2°N, 34°E (Naktong) 8.5 × 1012 3.01 × 1012 0.36 — —
12°N, 43°E 1.7 × 1012 7.88 × 1011 0.46 — —
6°S, 45°E 2.1 × 1012 7.49 × 1011 0.36 — —
24.9°S 343.7°E (SPL) — 6.36 × 1012   1.39 × 1013 0.46
Open in a new tab

SPL, Samara, Parana, Loire Valles summed; VN, valley network.

Volume1 was from Table 3 of Hoke et al.28, Naktong east and Naktong west were summed here; volume2 was this study based on the combined VN; volume3 was the eroded volume under X ratio=3.2 from Table 3 of Matsubara et al.32.

Table 3. Comparison of volume estimates based on the same simulated landscape29.

  Hoke et al.28 method Reimman-Simpson PBTH ‘Truth'
Volume (m3) 18,562.00 21,716.00 21,109.45 21,940.71
Overall relative accuracy 84.60% 98.98% 96.21% 100.00%
Open in a new tab

PBTH, progressive black top hat; VN, valley network.

Calculation of the first two columns performed by Brian Hynek and William Nelson, University of Colorado, Boulder, using the same VN area boundary.

Thus, we are confident about PBTH method as a robust, accurate and efficient method for estimating the global VN volume. The PBTH method objectively and consistently delineates the VN boundaries and estimates valley depth at pixel level. Because of the automated procedure, we have included all the VNs mapped at the global scale to date. Our results provided an independent source of estimate of global water inventory on Mars. Our result is consistent with a warm and wet early Mars climate and the existence of an ancient northern ocean. If erosion of the VNs required significant chemical or physical weathering to produce transportable sediment, fluvial abrasion of channel beds33 or transport of appreciable quantities of gravel34, the required volume of water may have been many times our conservative estimate.

Existing climate models have not been able to reproduce an early Mars climate sufficient to promote an active hydrological cycle35,36,37 (see also a recent review by Wordworth38 and references therein); this has led to hypotheses suggesting accumulation of thick cold-based ice on the equatorial highlands with VN formation during short-lived episodes of top–down melting39. If true, this argues against an unfrozen ocean. However, an equivalent amount of erosion and equivalent total runoff would still need to be accounted, which may be challenging to achieve under cold climate scenario36. The gap between the geomorphic evidence such as this study, which suggests a warm and wet climate, and the climate models that struggle to get temperature high enough for early Mars36 still requires further study.

Methods

Automation of PBTH method for global Mars application

We set out to conduct a comprehensive global VN volume estimation through developing a method that is robust, accurate and automated. The PBTH method we adopted integrates techniques used in Lidar data analysis and image processing29, which allowed us to estimate VN depth at individual pixel level29,40 and to derive VN volume on a global scale with greater accuracy and efficiency. Our test on simulated landforms has achieved a relative accuracy of 96% and application to Ma'adim Vallis resulted in a volume value higher than previous estimates29.

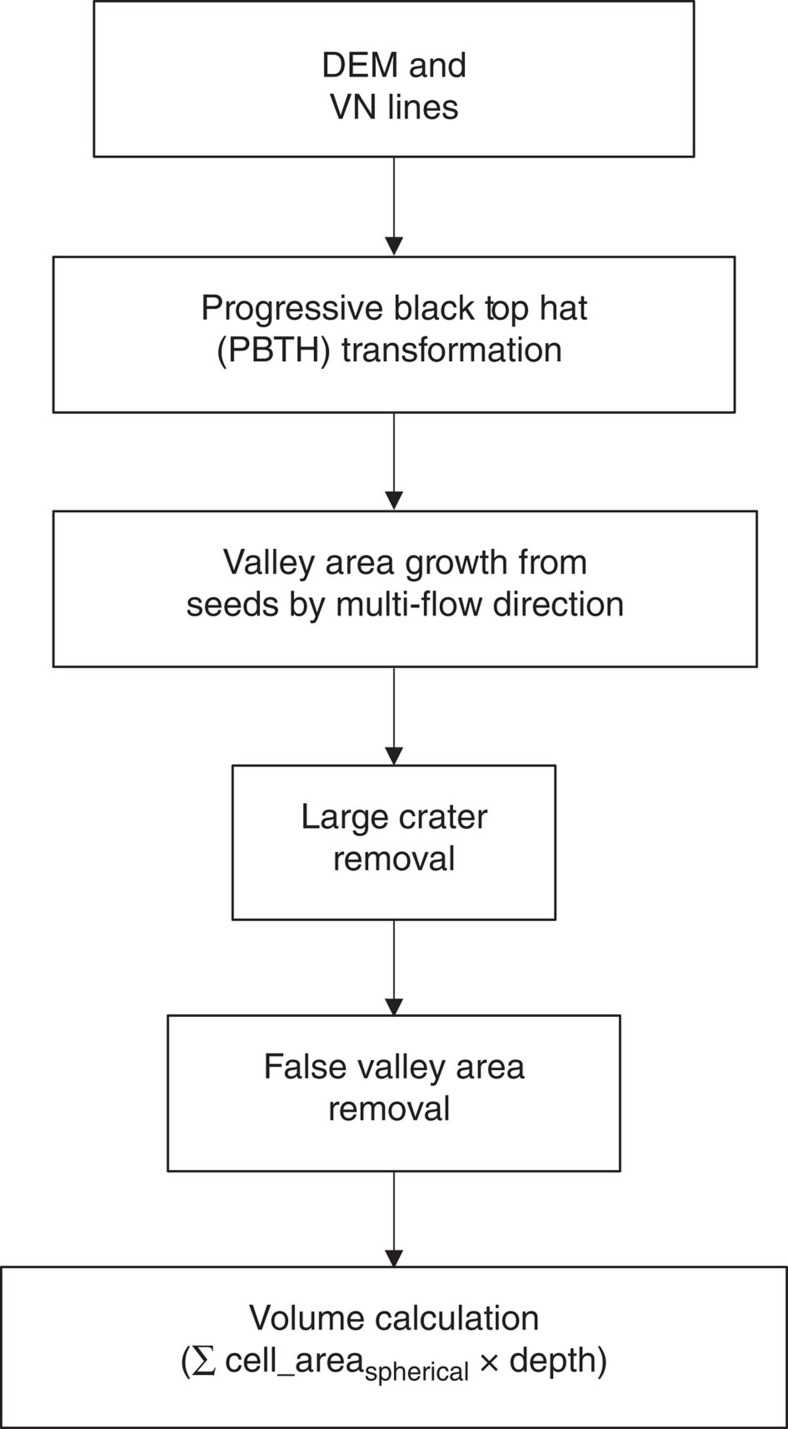
The application of the method to the whole of Mars required some special considerations and the process is outlined in the flow diagram in Fig. 1. To make the processing more tractable, we divided MOLA DEM into 20° × 20° tiles and processed one tile at a time. After all the tiles were processed, they were merged into one global dataset to estimate the global VN volume. To automate the process as much as possible, we took advantage of the previously extracted VN lines. Luo and Stepinksi16 extracted the global VNs using a morphology-based algorithm, which resulted in VNs that strictly follow topography but may be disconnected at places. Based primarily on images, Hynek et al.30 manually mapped another version of the global VNs, which are more connected but may not always follow topography. We derived two volume estimates: one based on the VN derived from topography and the other based on the combined VN from the two existing versions using a GIS conflation tool.

Figure 1. Overall flow diagram.

Figure 1

Open in a new tab

The process of applying the PBTH method to the whole of Mars. It is worth noting that the globe is divided into 20° × 20° tiles and is processed one tile at a time.

More details of PBTH method

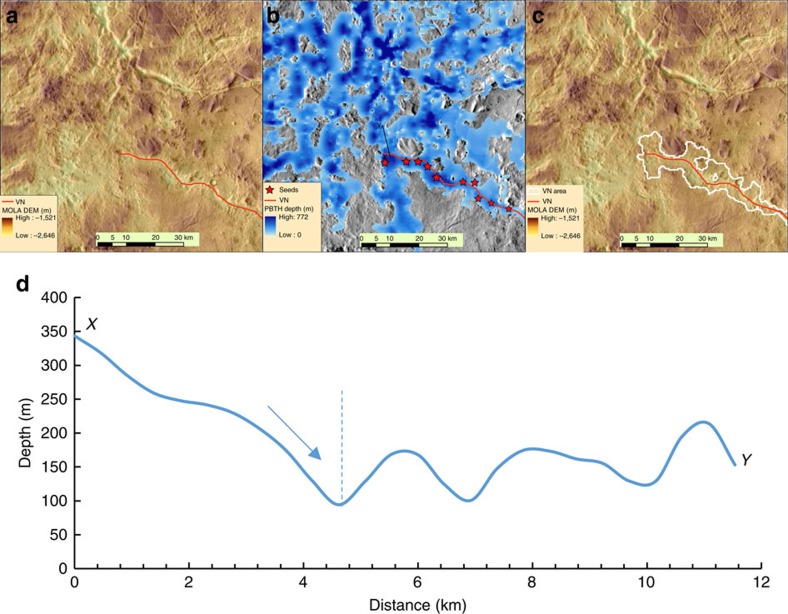
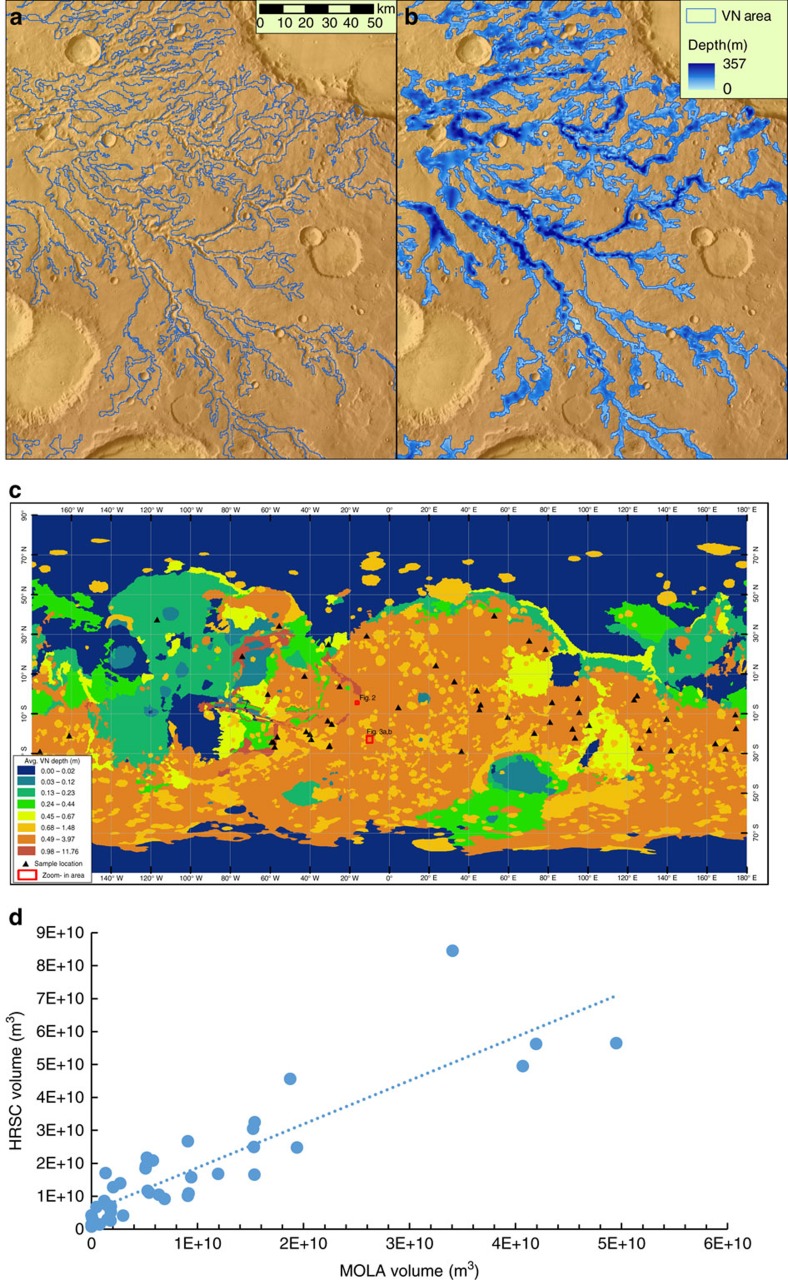
Black top hat (BTH) transformation is a mathematical morphology transformation used in image processing to extract dark features on an image with varied background40. It has been adapted to extract valley depth from DEM data40 (low elevations of the valleys are the dark features in image terms). Operationally, it involves finding focal maximum of the DEM within a moving circle (opening), then focal minimum of the opening result (closing) and subtracting the original DEM from the closing result40. The process essentially creates a pre-incision surface based on the present day topography under the assumption that the elevation of the valley shoulders did not change significantly, which is a reasonable assumption for Mars as the VNs carve into the highland surface29. To address the drawbacks of using a single window size in BTH, a series of windows with progressively bigger sizes (from 3 to 11 cells) were used to capture valleys of different sizes more effectively (hence, the name progressive BTH or PBTH)29. At the end of each BTH operation, the depth result was thresholded to remove noise. Following algorithms used in LiDAR data processing29, a slope factor (0.02) was introduced to scale the threshold value according to each progressive window size29. The VN depth grids were merged together, taking the maximum value if a cell location had multiple values from different window sizes. This final depth grid represents the depth of all the depressions (essentially an inverse of topography with deeper depression having higher depth value), most of which are indeed VNs, but may also include some non-VN depressions (Fig. 2a,b). To automatically generate the correct VN areas around the VN lines, we started at local maxima of the VN depth grid that are near the VN line (‘seeds') and followed a standard multiple flow direction algorithm to grow the area around the ‘seeds' to form the VN area polygon (Fig. 2c). Crater depressions that still remain after the multiple flow direction algorithm were removed using location and diameter information from an existing database of craters41. Some parts of shallow valleys do not meet the depth threshold, resulting in small gaps in the valley area polygon. These gaps were connected by buffering each pixel of under the VN line with a buffer size that is ten times the depth at that location (that is, assuming the width is about ten times the depth42, a conservative estimate). More details of the process is documented in the Python source code and is available as Supplemental Material. Finally, visual inspection and manual editing was conducted to remove any false positives not consistent with VN morphology based on Thermal Emission Imaging System images. An example of the final VN area and VN depth is shown in Fig. 3a,b and the zonal mean of VN depth by geologic unit43 is shown in Fig. 3c, illustrating its global spatial distribution.

Figure 2. Valley area growth from seeds by multi-flow direction.

Figure 2

Open in a new tab

(a) VN and shaded MOLA DEM (for location, see Fig. 3b). (b) VN, thresholded PBTH depth and local maxima ‘seeds' for generating VN area following multi-flow direction on depth grid. (c) VN, VN area polygon and shaded MOLA DEM. (d) Depth profile along XY in b. Dashed vertical line indicates where the flow would stop, which defines the boundary of VN area polygon as shown in c.

Figure 3. Example of PBTH-derived VN depth and spatial distribution.

Figure 3

Open in a new tab

(a) VN boundary overlain on MOLA DEM shaded relief (see c for location). (b) VN depth. (c) Global distribution of zonal mean VN depth by geologic unit43. (d) Regression relating volumes extracted from MOLA and HRSC data based on 50 random samples (location shown as triangles in c). The regression equation is: y=1.3215x+5 × 109, R2=0.79.

VN volume calculation

The volume of VNs was calculated by summing the volume of each pixel column (product of depth and area of each pixel) of the valley depth grid inside the VN area polygon. To avoid distortion associated with map projection for the global data, we used the spherical area of each pixel. The DEM data with global coverage is the MOLA DEM at ∼463 m per pixel resolution. The High/Super Resolution Stereo Colour Imager (HRSC) DEM data have higher resolution (∼75 m per pixel), but with limited coverage. We took 50 random sampled areas where both HRSC and MOLA data are available and extracted VN volumes from both resolutions. A regression line was established between the values at these two resolutions (Fig. 3d) and the final MOLA DEM-derived volume was scaled following the regression line as the estimate of volume under higher HRSC resolution.

Code availability

The Python scripts for performing the PBTH volume calculation in ArcGIS can be found in the Supplementary Software. These include readme.txt (Supplementary Software 1), main.py (Supplementary Software 2) and extract_vn_library.py (Supplementary Software 3).

Additional information

How to cite this article: Luo, W. et al. New Martian valley network volume estimate consistent with ancient ocean and warm and wet climate. Nat. Commun. 8, 15766 doi: 10.1038/ncomms15766 (2017).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Material

Supplementary Software 1

readme file

ncomms15766-s1.txt (1.7KB, txt)
Supplementary Software 2

Main Program

ncomms15766-s2.txt (1.5KB, txt)
Supplementary Software 3

Library

ncomms15766-s3.txt (9.2KB, txt)
Peer Review File
ncomms15766-s4.pdf (486KB, pdf)

Acknowledgments

This research was supported by NASA Mars Data Analysis Program Grant number NNX13AK65G. We thank V. Baker and two anonymous reviewers for their constructive reviews of manuscript, which greatly improved its quality. We thank B. Hynek and W. Nelson for calculating the volume of valleys in a simulated landscape for comparison.

Footnotes

The authors declare no competing financial interests.

Author contributions W.L. conceived this research study, devised the PBTH algorithm and wrote the paper. X.C. implemented the PBTH and multi-flow direction algorithms in Python, processed the data and contributed to the manuscript preparation. A.D.H. helped with the interpretation of the results and contributed to manuscript preparation.

References

  1. Craddock R. A. & Howard A. D. The case for rainfall on a warm, wet early Mars. J. Geophys. Res. 107, 21-1–21-36 (2002). [Google Scholar]
  2. Fassett C. I. & Head J. W. Valley network-fed, open-basin lakes on Mars: distribution and implications for Noachian surface and subsurface hydrology. Icarus 198, 37–56 (2008). [Google Scholar]
  3. Baker V. R. et al. Fluvial geomorphology on Earth-like planetary surfaces: a review. Geomorphology 245, 149–182 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Carr M. H. Mars: a water-rich planet? Icarus 68, 187–216 (1986). [Google Scholar]
  5. Fassett C. I. & Head J. W. Fluvial sedimentary deposits on Mars: ancient deltas in a crater lake in the Nili Fossae region. Geophys. Res. Lett. 32, (2005). [Google Scholar]
  6. Irwin R. P., Howard A. D., Craddock R. A. & Moore J. M. An intense terminal epoch of widespread fluvial activity on early Mars: 2. Increased runoff and paleolake development. J. Geophys. Res. Planets 110, (2005). [Google Scholar]
  7. Carr M. H. in Water on Mars 229 (Oxford Univ. Press, 1996).
  8. Clifford S. M. & Parker T. J. The evolution of the Martian hydrosphere: implications for the fate of a primordial ocean and the current state of the northern plains. Icarus 154, 40–79 (2001). [Google Scholar]
  9. Gulick V. C. Origin of the valley networks on Mars: a hydrological perspective. Geomorphology 37, 241–269 (2001). [Google Scholar]
  10. Carr M. H. & Head J. W. III Oceans on Mars: an assessment of the observational evidence and possible fate. J. Geophys. Res. 108, http://dx.doi.org/10.1029/2002JE001963 (2003). [Google Scholar]
  11. Villanueva G. L. et al. Strong water isotopic anomalies in the martian atmosphere: probing current and ancient reservoirs. Science 348, 218–221 (2015). [DOI] [PubMed] [Google Scholar]
  12. Parker T. J., Gorsline D. S., Saunders R. S., Pieri D. C. & Schneeberger D. M. Coastal geomorphology of the Martian Northern Plains. J. Geophys. Res. Planets 98, 11061–11078 (1993). [Google Scholar]
  13. Baker V. R. Ancient oceans, ice sheets and the hydrological cycle on Mars. Nature 352, 589–594 (1991). [Google Scholar]
  14. Di Achille G. & Hynek B. M. Ancient ocean on Mars supported by global distribution of deltas and valleys. Nat. Geosci. 3, 459–463 (2010). [Google Scholar]
  15. DiBiase R. A., Limaye A. B., Scheingross J. S., Fischer W. W. & Lamb M. P. Deltaic deposits at Aeolis Dorsa: sedimentary evidence for a standing body of water on the northern plains of Mars. J. Geophys. Res. Planets 118, 1285–1302 (2013). [Google Scholar]
  16. Luo W. & Stepinski T. F. Computer-generated global map of valley networks on Mars. J. Geophys. Res. Planets 114, (2009). [Google Scholar]
  17. Dohm J. M. et al. GRS evidence and the possibility of paleooceans on Mars. Planet. Space Sci. 57, 664–684 (2009). [Google Scholar]
  18. Malin M. C. & Edgett K. S. Oceans or seas in the Martian northern lowlands: High resolution imaging tests of proposed coastlines. Geophys. Res. Lett. 26, 3049–3052 (1999). [Google Scholar]
  19. Carr M. H. & Head J. W. Martian surface/near-surface water inventory: sources, sinks, and changes with time. Geophys. Res. Lett. 42, 726–732 (2015). [Google Scholar]
  20. McEwen A. S. et al. A closer look at water-related geologic activity on Mars. Science 317, 1706–1709 (2007). [DOI] [PubMed] [Google Scholar]
  21. Perron J. T., Mitrovica J. X., Manga M., Matsuyama I. & Richards M. A. Evidence for an ancient martian ocean in the topography of deformed shorelines. Nature 447, 840–843 (2007). [DOI] [PubMed] [Google Scholar]
  22. Rodriguez J. A. P. et al. Tsunami waves extensively resurfaced the shorelines of an early Martian ocean. Sci. Rep. 6, 25106 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Moscardelli L. Boulders of the Vastitas Borealis formation: potential origin and implications for an ancient martian ocean. GSA Today 24, 4–10 (2014). [Google Scholar]
  24. Rosenberg E. N. & Head J. W. III Late Noachian fluvial erosion on Mars: cumulative water volumes required to carve the valley networks and grain size of bed-sediment. Planet. Space Sci. 117, 429–435 (2015). [Google Scholar]
  25. Gulick V. & Baker V. R. Fluvial valleys and Martian palaeoclimates. Nature 341, 514–516 (1989). [Google Scholar]
  26. Goldspiel J. M. & Squyres S. W. Ancient aqueous sedimentation on Mars. Icarus 89, 392–410 (1991). [Google Scholar]
  27. Jaumann R., Nass A., Tirsch D., Reiss D. & Neukum G. The Western Libya Montes Valley System on Mars: evidence for episodic and multi-genetic erosion events during the Martian history. Earth Planet. Sci. Lett. 294, 272–290 (2010). [Google Scholar]
  28. Hoke M. R. T., Hynek B. M. & Tucker G. E. Formation timescales of large Martian valley networks. Earth Planet. Sci. Lett. 312, 1–12 (2011). [Google Scholar]
  29. Luo W., Pingel T., Heo J., Howard A. & Jung J. A progressive black top hat transformation algorithm for estimating valley volumes on Mars. Comput. Geosci. 75, 17–23 (2015). [Google Scholar]
  30. Hynek B. M., Beach M. & Hoke M. R. T. Updated global map of Martian valley networks and implications for climate and hydrologic processes. J. Geophys. Res. Planets 115, (2010). [Google Scholar]
  31. Abramov O. & McEwen A. Technical note: an evaluation of interpolation methods for Mars Orbiter Laser Altimeter (MOLA) data. Int. J. Remote Sens. 25, 669–676 (2004). [Google Scholar]
  32. Matsubara Y., Howard A. D. & Gochenour J. P. Hydrology of early Mars: valley network incision. J. Geophys. Res. Planets 118, 1365–1387 (2013). [Google Scholar]
  33. Sklar L. S. & Dietrich W. E. Sediment and rock strength controls on river incision into bedrock. Geology 29, 1087 (2001). [Google Scholar]
  34. Howard A. D., Breton S. & Moore J. M. Formation of gravel pavements during fluvial erosion as an explanation for persistence of ancient cratered terrain on Titan and Mars. Icarus 270, 100–113 (2016). [Google Scholar]
  35. Wordsworth R. et al. Global modelling of the early martian climate under a denser CO2 atmosphere: water cycle and ice evolution. Icarus 222, 1–19 (2013). [Google Scholar]
  36. Wordsworth R. D., Kerber L., Pierrehumbert R. T., Forget F. & Head J. W. Comparison of ‘warm and wet' and ‘cold and icy' scenarios for early Mars in a 3-D climate model. J. Geophys. Res. Planets 120, 1201–1219 (2015). [Google Scholar]
  37. Forget F. et al. 3D modelling of the early martian climate under a denser CO2 atmosphere: temperatures and CO2 ice clouds. Icarus 222, 81–99 (2013). [Google Scholar]
  38. Wordsworth R. D. The climate of early Mars. Annu. Rev. Earth Planet. Sci. 44, 381–408 (2016). [Google Scholar]
  39. Fastook J. L. & Head J. W. Glaciation in the Late Noachian Icy Highlands: ice accumulation, distribution, flow rates, basal melting, and top-down melting rates and patterns. Planet. Space Sci. 106, 82–98 (2015). [Google Scholar]
  40. Rodriguez F., Maire E., Courjault-Rade P. & Darrozes J. The Black Top Hat function applied to a DEM: a tool to estimate recent incision in a mountainous watershed (Estibere Watershed, Central Pyrenees). Geophys. Res. Lett. 29, 9-1–9-4 (2002). [Google Scholar]
  41. Robbins S. J. & Hynek B. M. A new global database of Mars impact craters ≥1 km: 1. Database creation, properties, and parameters. J. Geophys. Res. Planets 117, (2012). [Google Scholar]
  42. Williams R. M. E. & Phillips R. J. Morphometric measurements of Martian valley networks from Mars Orbiter Laser Altimeter (MOLA) data. J. Geophys. Res. 106, 23,737–23,752 (2001). [Google Scholar]
  43. Tanaka K. L. et al. Geologic Map of Mars: U.S. Geological Survey Scientific Investigations Map 3292, Scale 1:20,000,000 (2014).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Software 1

readme file

ncomms15766-s1.txt (1.7KB, txt)
Supplementary Software 2

Main Program

ncomms15766-s2.txt (1.5KB, txt)
Supplementary Software 3

Library

ncomms15766-s3.txt (9.2KB, txt)
Peer Review File
ncomms15766-s4.pdf (486KB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES